Workshop Facility Layout Optimization Based on Deep Reinforcement Learning
Abstract
:1. Introduction
- (1)
- The DRL is proposed to solve the facility layout optimization problem.
- (2)
- The engineering application requirements of virtual reality facility layout for a real-time solution of dual-objective workshop facility layout are realized.
- (3)
- A dual-objective mathematical model for facility layout optimization is constructed.
- (4)
- High-quality cases can provide a reference for the layout of other similar types of workshop facilities.
2. Mathematical Model
3. DRL Solves WFLOP
3.1. Decomposition Strategy
3.2. Parameter Transfer Strategy
3.3. DRL Solves WFLOP Subproblem
4. Case Application
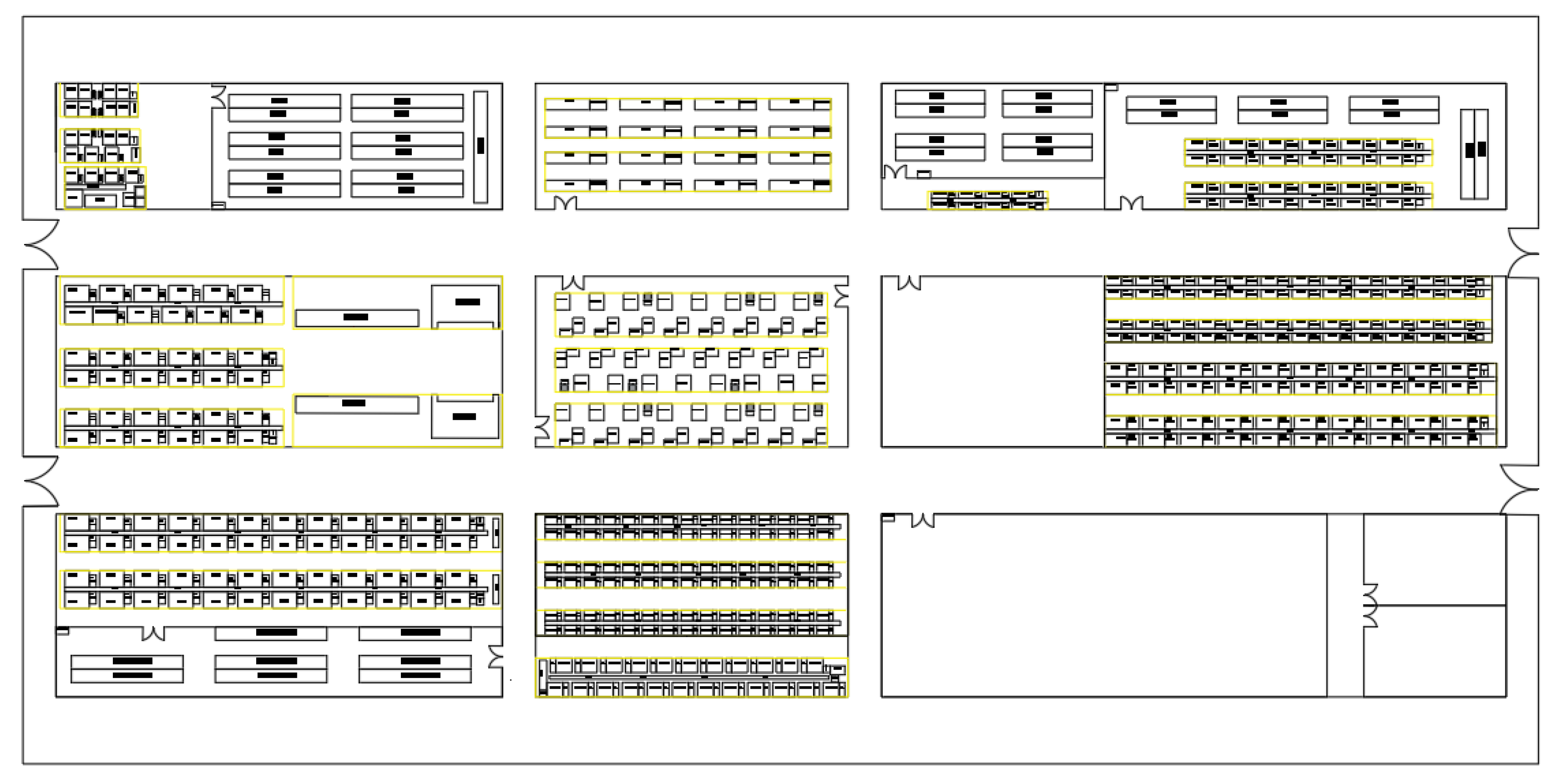
4.1. Chip Packaging Workshop Analysis
- (1)
- Chip packaging equipment
- (2)
- Packaging Process
- Dicing is the process of separating each chip with its own set of electrical characteristics. The dicing process is classified into two types: semi-automatic cutting and full-automatic cutting. The HJW CPW uses full-automatic cutting.
- Chip loading is the process of assembling the chip on the frame. Resin bonding, eutectic welding, and lead-tin alloy welding are all common chip loading processes employed by the HJW CPW.
- Bonding involves connecting the bonding wires between the electrodes in contact with the chip and the frame pins. This process places exceptionally high demands on the wires used for bonding, since the wires significantly impact the chip’s durability and stability.
- Plastic wrapping protects the item from environmental impacts and allows it to perform steadily and consistently for an extended time. Plastic packaging is classified into two types: air-tight packaging and non-airtight packaging. Because the air-tight packing effect is a better option, the HJW CPW uses air-tight packaging.
- The primary goal of electroplating is to cover the silicon wafer in the chip with a thick, homogeneous coating of gold free of holes, gaps, and other flaws to improve the chip’s conductivity and solderability.
- Printing entails performing laser engraving on the front or back of the chip, with the content of the engraving including product information, which is mostly utilized for chip identification and tracking. Ink printing and laser marking are two basic types of printing. The HJW CPW makes use of laser marking.
- Rib cutting consists mostly of two processes: rib cutting and bending. Rib cutting is a technology that divides a whole piece into multiple pieces. Bending is the removal of undesirable material from a work-in-process and pressing the work-in-process into certain predetermined forms.
- The test’s purpose is to complete the operation by collaborating between the sorting machine and the testing machine, checking the function and electrical characteristics of the finished chips, and the sorting machine marking, sorting, and receiving the chips.
- The packing procedure necessitates that the packed items be easily picked up.
- (3)
- Workshop Layout Analysis
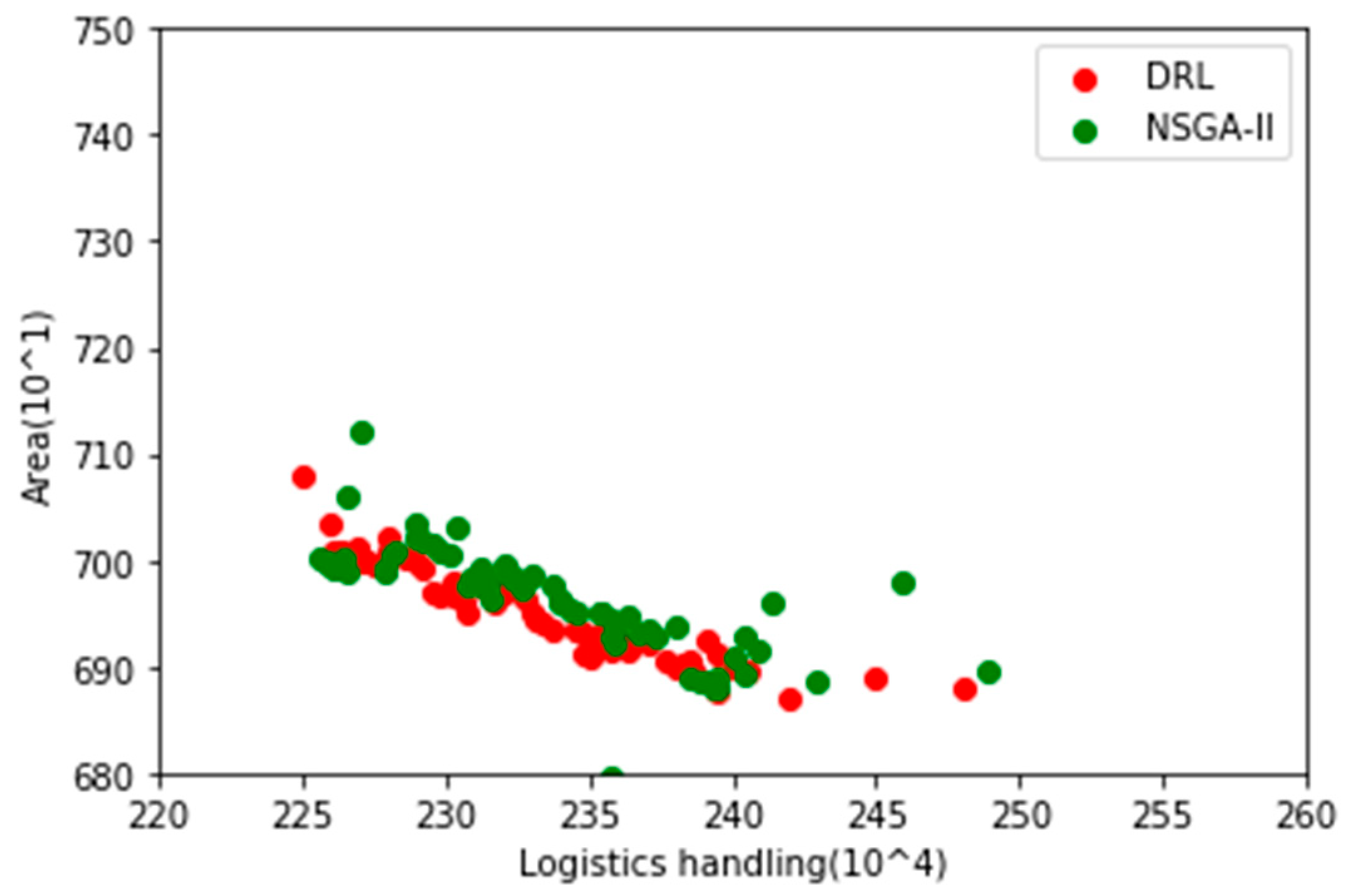
4.2. Solution Result Analysis
4.3. Optimization Algorithm Comparison
5. Discussion and Conclusions
- (1)
- This article only studies DRL (Deep Reinforcement Learning) to solve the dual-objective WFLOP (Workshop Facility Layout Optimization Problem). The DRL framework of the WFLOP for high-dimensional objectives needs further research.
- (2)
- The WFLOP platform for virtual reality technology has not yet been built. In the future, Unity 3D, Demo 3D, etc. will be used to build the WFLOP platform.
- (3)
- The generalization ability of DRL to solve the WFLOP needs further study to improve the compatibility of this method.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chao, G.; Zhang, Z.Q.; Liu, S.L. Multi-objective particle swarm optimization for multi-workshop facility layout problem. J. Manuf. Syst. 2019, 53, 32–48. [Google Scholar]
- Flavio, D.P.; Amy, R.C. An MINLP approach for safe process plant layout. Ind. Eng. Chem. Res. 1996, 35, 1354–1361. [Google Scholar]
- Zhao, Y.L. Manufacturing cell integrated layout method based on RNS-FOA algorithm in smart factory. Processes 2022, 10, 1759. [Google Scholar] [CrossRef]
- Guo, W.; Jiang, P.Y.; Yang, M.L. Unequal area facility layout problem-solving: A real case study on an air-conditioner production shop floor. Int. J. Prod. Res. 2022, 61, 1479–1496. [Google Scholar] [CrossRef]
- Andreas, K.; Vosniakos, G.C. An augmented reality approach to factory layout design embedding operation simulation. Int. J. Interact. Des. Manuf. 2019, 13, 1061–1071. [Google Scholar]
- Mona, S.; Emad, E.; Emad, E. Optimization of construction site layout using BIM generative design. Int. J. Constr. Manag. 2023, 24, 314–322. [Google Scholar]
- Seungnam, Y.; Jonghui, H. Virtual reality platform-based conceptual design and simulation of a hot cell facility. Int. J. Adv. Manuf. Technol. 2021, 116, 487–505. [Google Scholar]
- Chee, H.T.; Hwa, J.Y.; Siti, N.M. Augmented reality assisted facility layout digitization and planning. J. Mech. Sci. Technol. 2021, 35, 4115–4123. [Google Scholar]
- Mirco, P.; Giuseppe, F.; Fabio, S. V Digital Facility Layout Planning. Sustainability 2020, 12, 3349. [Google Scholar]
- Jiang, S.; Nee, A.Y.C. A novel facility layout planning and optimization methodology. CIRP Ann. Manuf. Technol. 2013, 32, 483–486. [Google Scholar] [CrossRef]
- Zhinan, Z.; Xin, W.; Xiaohan, W.; Fan, C.; Hui, C. A simulation-based approach for plant layout design and production planning. J. Ambient Intell. Humaniz. Comput. 2019, 10, 1217–1230. [Google Scholar]
- Goli, A.; Tirkolaee, E.B.; Aydın, N.S. Fuzzy integrated cell formation and production scheduling considering automated guided vehicles and human factors. IEEE Trans. Fuzzy Syst. 2021, 29, 3686–3695. [Google Scholar] [CrossRef]
- Kalyanmoy, D.; Proteek, C.R.; Rayan, H. Surrogate modeling approaches for multiobjective optimization: Methods, taxonomy, and results. Math. Comput. Appl. 2020, 26, 5. [Google Scholar]
- Julia, R.; Maria, A.Z.; Iva, K. Integrated multi-objective evolutionary optimization of production layout scenarios for parametric structural design of flexible industrial buildings. J. Build. Eng. 2022, 46, 103766. [Google Scholar]
- Oriol, V.; Meire, F.; Navdeep, J. Pointer networks. Adv. Neural Inf. Process. Syst. 2015, 475, 2692–2700. [Google Scholar]
- Kaiwen, L.; Tao, Z.; Rui, W. Deep reinforcement learning for multi-objective optimization. J. IEEE Transcations Cybern. 2020, 214, 2977661. [Google Scholar]
- Fei, F.; Guang, L.X. Spatiotemporal path tracking via deep reinforcement learning of robot for manufacturing internal logistics. J. Manuf. Syst. 2023, 69, 50–169. [Google Scholar]
- Yunmei, Y.; Hong, Y.L. Application of Deep Reinforcement Learning Algorithm in Uncertain Logistics Transportation Scheduling. Comput. Intell. Neurosci. 2021, 27, 5672227. [Google Scholar]
- Seamus, G.; Debin, D. China’s emerging role in the global semiconductor value chain. Telecommun. Policy 2022, 46, 101959. [Google Scholar]
- Jiancheng, G.; Nan, M. A bibliometric study of China’s semiconductor literature compared with other major asian countries. Scientometrics 2007, 70, 124–127. [Google Scholar]
- YouJin, P.; Sun, H. Improvement of productivity through the reduction of unexpected equipment faults in die attach equipment. Processes 2021, 8, 394. [Google Scholar]
- Pedro, E.C.; Radu, G.; Eduardo, M.G.R. A review of data mining applications in semiconductor manufacturing. Processes 2021, 9, 305. [Google Scholar]
- Madhav, D. Manufacturing processes for fabrication of flip-chip micro-bumps used in microelectronic packaging: An overview. J. Micromanuf. 2020, 3, 69–83. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]





| Number | Area Name | Length (m) | Width (m) |
|---|---|---|---|
| 1 | Dicing area | 7.64 | 9.78 |
| 2 | Raw material area | 26.00 | 11.30 |
| 3 | Loading area | 20.10 | 17.90 |
| 4 | Return cleaning area | 18.73 | 9.45 |
| 5 | Shelf area after loading | 40.00 | 6.27 |
| 6 | Gold wire bonding area | 28.00 | 6.90 |
| 7 | Aluminum wire bonding area | 28.00 | 3.49 |
| 8 | Plastic area | 28.00 | 15.30 |
| 9 | Plastic cold storage | 20.00 | 15.30 |
| 10 | Electroplating area | 28.00 | 11.30 |
| 11 | Printing area | 10.77 | 1.60 |
| 12 | Shelf area after printing | 20.00 | 8.50 |
| 13 | Rib cutting area | 36.00 | 11.30 |
| 14 | Testing area | 34.74 | 4.00 |
| 15 | Packaging area | 35.14 | 5.60 |
| 16 | Finished product Warehouse area | 39.94 | 16.40 |
| 17 | Bathroom | 12.77 | 16.40 |
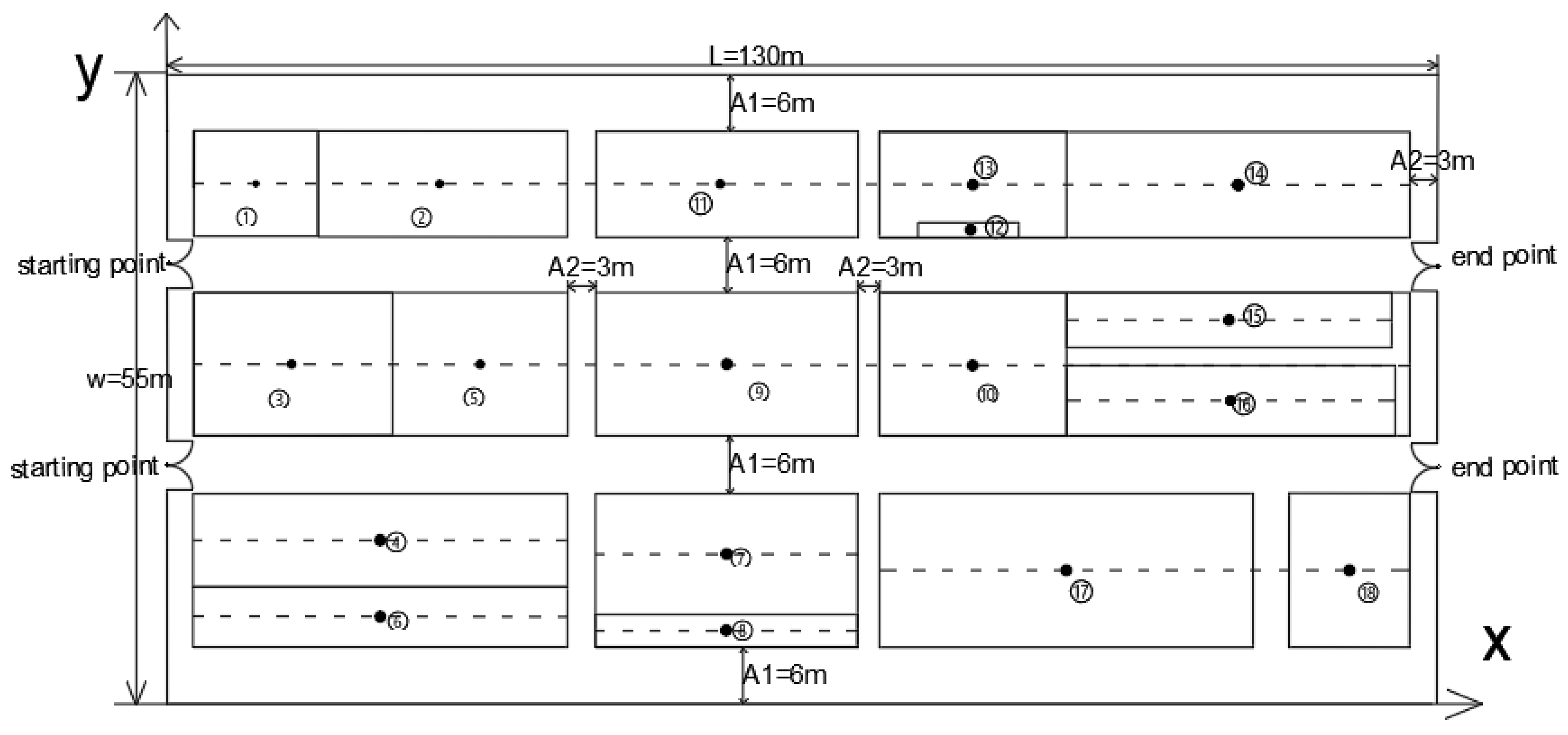
| Number | Coordinate Value | Number | Coordinate Value |
|---|---|---|---|
| 1 | [0, 20.65] or [0, 38.24] | 11 | [57.21, 45.48] |
| 2 | [9.07, 45.48] | 12 | [82.20, 41.45] |
| 3 | [27.86, 45.48] | 13 | [82.43, 45.48] |
| 4 | [21.78, 29.69] | 14 | [109.58, 45.48] |
| 5 | [21.78, 14.30] | 15 | [108.63, 33.56] |
| 6 | [32.01, 29.69] | 16 | [108.63, 26.52] |
| 7 | [57.21, 13.09] | 17 | [91.98, 11.68] |
| 8 | [57.21, 6.43] | 18 | [120.95, 11.68] [130, 20.65] or [130, 38.24] |
| 9 | [57.21, 29.69] | 19 | |
| 10 | [82.40, 29.69] |
| Number | O-D | Distance (m) | Output (pcs) | Logistics (m·pcs) |
|---|---|---|---|---|
| 1 | 0-2 | 28.79 | 4200 | 120,918 |
| 2 | 2-1 | 18.79 | 4200 | 78,918 |
| 3 | 1-3 | 16.21 | 2100 | 34,041 |
| 4 | 1-4 | 33.67 | 2100 | 70,707 |
| 5 | 3-5 | 19.29 | 3000 | 57,870 |
| 6 | 4-5 | 18.48 | 3000 | 55,440 |
| 7 | 5-6 | 24.33 | 3500 | 85,155 |
| 8 | 5-7 | 30.18 | 1500 | 45,270 |
| 9 | 5-8 | 34.29 | 1000 | 34,290 |
| 10 | 6-7 | 35.85 | 2000 | 71,700 |
| 11 | 6-8 | 35.45 | 1500 | 53,175 |
| 12 | 7-9 | 16.60 | 5000 | 83,000 |
| 13 | 8-9 | 23.26 | 4000 | 93,040 |
| 14 | 10-9 | 25.19 | 2000 | 50,380 |
| 15 | 9-11 | 15.79 | 11,000 | 173,690 |
| 16 | 11-12 | 25.31 | 12,500 | 316,375 |
| 17 | 12-13 | 4.04 | 10,000 | 40,400 |
| 18 | 12-14 | 27.67 | 2500 | 69,175 |
| 19 | 13-14 | 27.15 | 10,000 | 271,500 |
| 20 | 14-15 | 11.96 | 9000 | 107,640 |
| 21 | 15-16 | 7.04 | 9000 | 63,360 |
| 22 | 16-17 | 22.30 | 11,000 | 245,300 |
| 23 | 17-19 | 39.06 | 11,000 | 429,660 |
| total | 2,651,004 | |||
| Neural Network | Parameter |
|---|---|
| Actor network (Pointer network) | Encoder: 1D-Conv(Dinput, 128, kernel size = 1, stride = 1) |
| Decoder: GRU(hidden size = 128, number of layer = 1) | |
| Critic network | 1D-Conv(Dinput, 128, kernel size = 1, stride = 1) 1D-Conv(128, 20, kernel size = 1, stride = 1) 1D-Conv(20, 20, kernel size = 1, stride = 1) 1D-Conv(20, 1, kernel size = 1, stride = 1) |
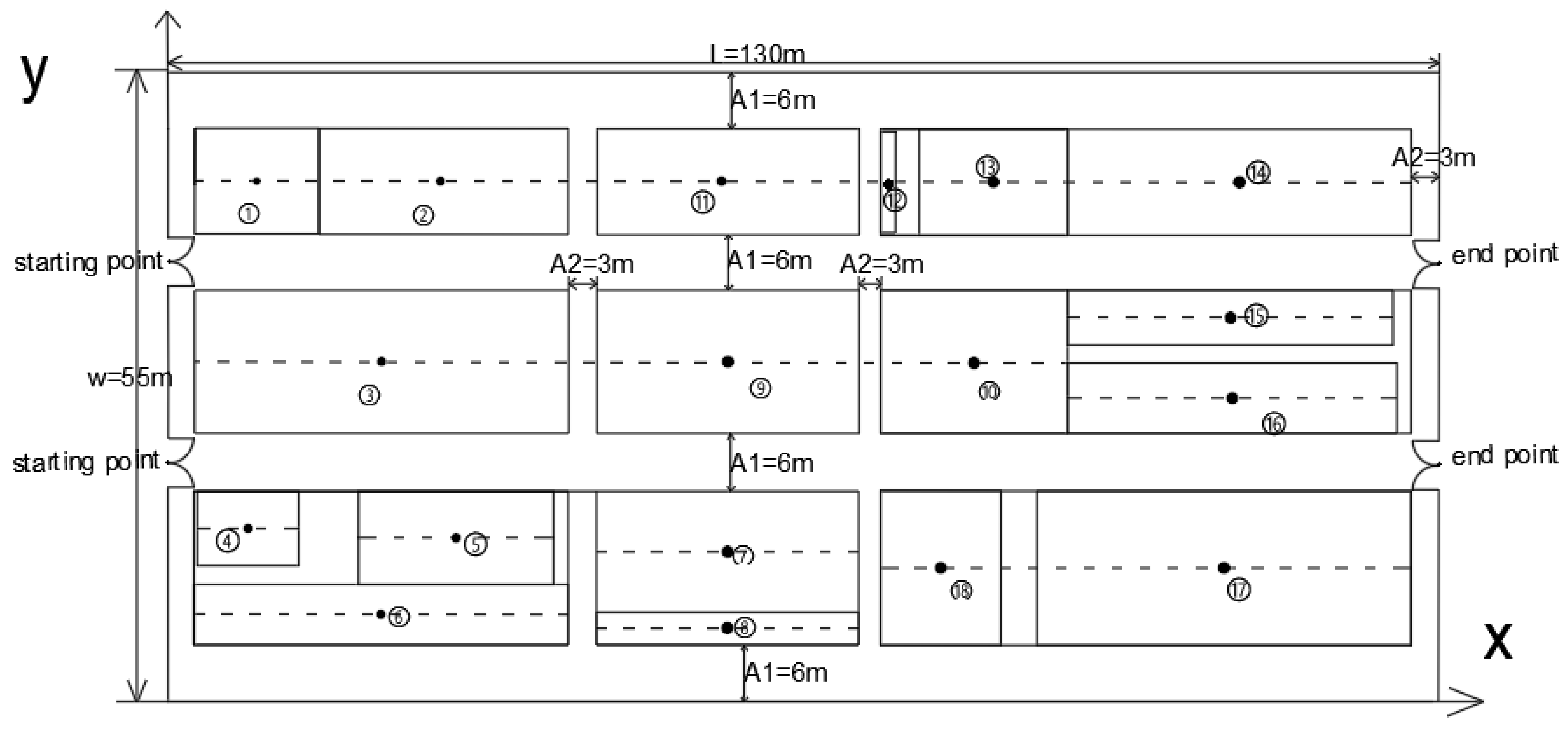
| Number | Coordinate Value | Number | Coordinate Value |
|---|---|---|---|
| 1 | [0, 20.65] or [0, 38.24] | 11 | [57.21, 42.48] |
| 2 | [9.07, 42.48] | 12 | [73.70, 42.48] |
| 3 | [27.86, 42.48] | 13 | [84.50, 42.48] |
| 4 | [21.84, 29.69] | 14 | [104.58, 42.48] |
| 5 | [8.15, 15.13] | 15 | [108.63, 33.56] |
| 6 | [29.44, 14.30] | 16 | [108.63, 26.52] |
| 7 | [57.21, 13.09] | 17 | [103.98, 11.68] |
| 8 | [57.21, 6.43] | 18 | [79.01, 11.68] [130, 20.65] or [130, 38.24] |
| 9 | [57.21, 29.69] | 19 | |
| 10 | [82.40, 29.69] |
| Number | O-D | Distance (m) | Output (pcs) | Logistics (m·pcs) |
|---|---|---|---|---|
| 1 | 0-2 | 28.79 | 4200 | 120,918 |
| 2 | 2-1 | 18.79 | 4200 | 78,918 |
| 3 | 1-3 | 20.31 | 3585 | 72,811.35 |
| 4 | 1-4 | 30.36 | 615 | 18,671.4 |
| 5 | 3-5 | 17.16 | 5121 | 87,876.36 |
| 6 | 4-5 | 21.31 | 879 | 18,731.49 |
| 7 | 5-6 | 10.16 | 3500 | 35,560 |
| 8 | 5-7 | 27.80 | 1500 | 41,700 |
| 9 | 5-8 | 28.86 | 1000 | 28,860 |
| 10 | 6-7 | 35.85 | 2000 | 71,700 |
| 11 | 6-8 | 35.45 | 1500 | 53,175 |
| 12 | 7-9 | 16.60 | 5000 | 83,000 |
| 13 | 8-9 | 23.26 | 4000 | 93,040 |
| 14 | 10-9 | 25.19 | 2000 | 50,380 |
| 15 | 9-11 | 15.79 | 11,000 | 173,690 |
| 16 | 11-12 | 16.49 | 12,500 | 206,125 |
| 17 | 12-13 | 10.80 | 10,000 | 108,000 |
| 18 | 12-14 | 35.88 | 2500 | 89,700 |
| 19 | 13-14 | 25.08 | 10,000 | 250,800 |
| 20 | 14-15 | 11.96 | 9000 | 107,640 |
| 21 | 15-16 | 7.04 | 9000 | 63,360 |
| 22 | 16-17 | 14.85 | 11,000 | 163,350 |
| 23 | 17-19 | 23.78 | 11,000 | 261,580 |
| total | 2,279,587 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Duan, D. Workshop Facility Layout Optimization Based on Deep Reinforcement Learning. Processes 2024, 12, 201. https://doi.org/10.3390/pr12010201
Zhao Y, Duan D. Workshop Facility Layout Optimization Based on Deep Reinforcement Learning. Processes. 2024; 12(1):201. https://doi.org/10.3390/pr12010201
Chicago/Turabian StyleZhao, Yanlin, and Danlu Duan. 2024. "Workshop Facility Layout Optimization Based on Deep Reinforcement Learning" Processes 12, no. 1: 201. https://doi.org/10.3390/pr12010201
APA StyleZhao, Y., & Duan, D. (2024). Workshop Facility Layout Optimization Based on Deep Reinforcement Learning. Processes, 12(1), 201. https://doi.org/10.3390/pr12010201






