A New Bottom-Hole Assembly Design Method to Maintain Verticality and Reduce Lateral Vibration
Abstract
:1. Introduction
2. Methods
2.1. BHA Modeling and Anti-Deviation Ability Evaluation
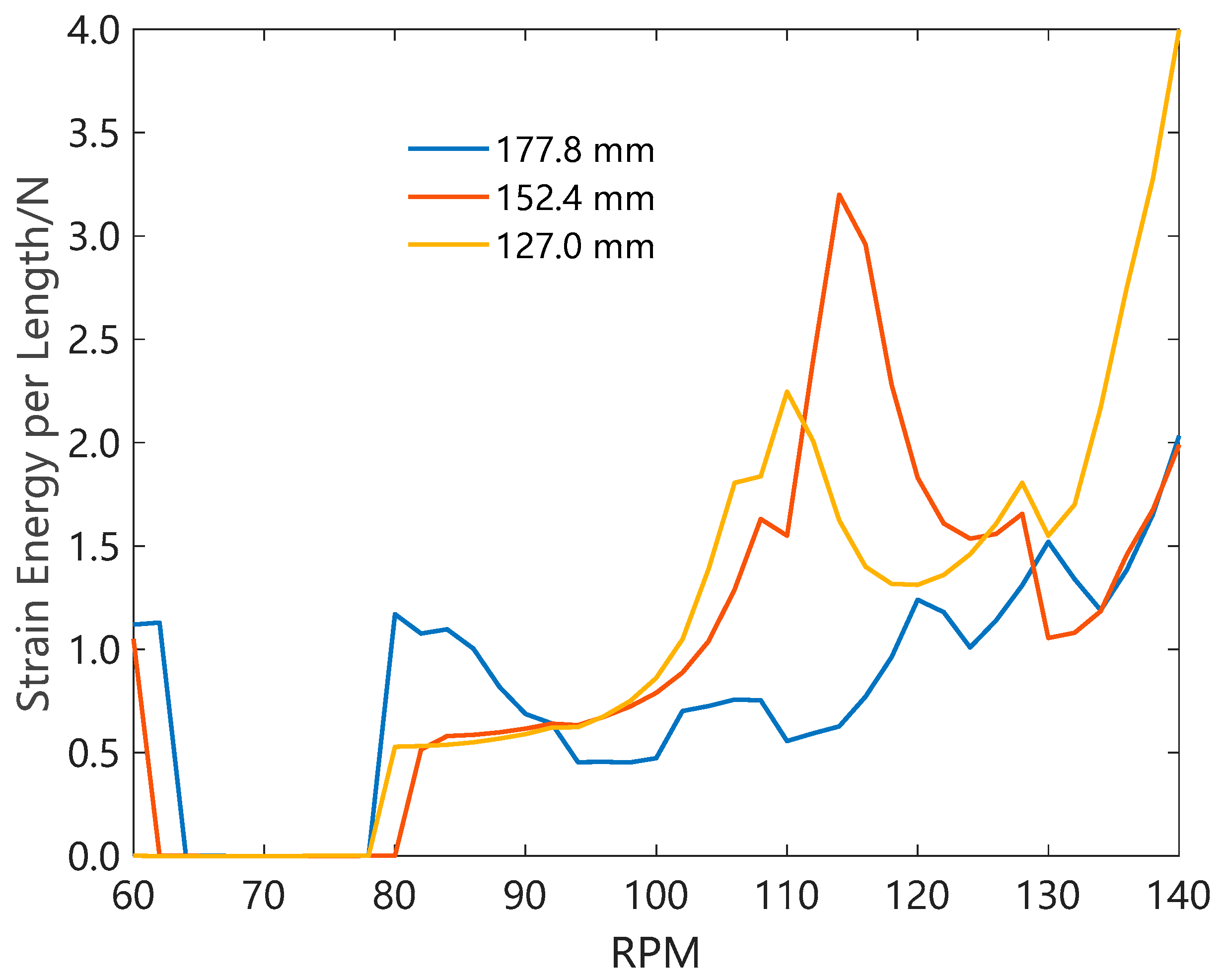
2.2. Forced Vibration Analysis Methods for Vertical Drilling BHAs
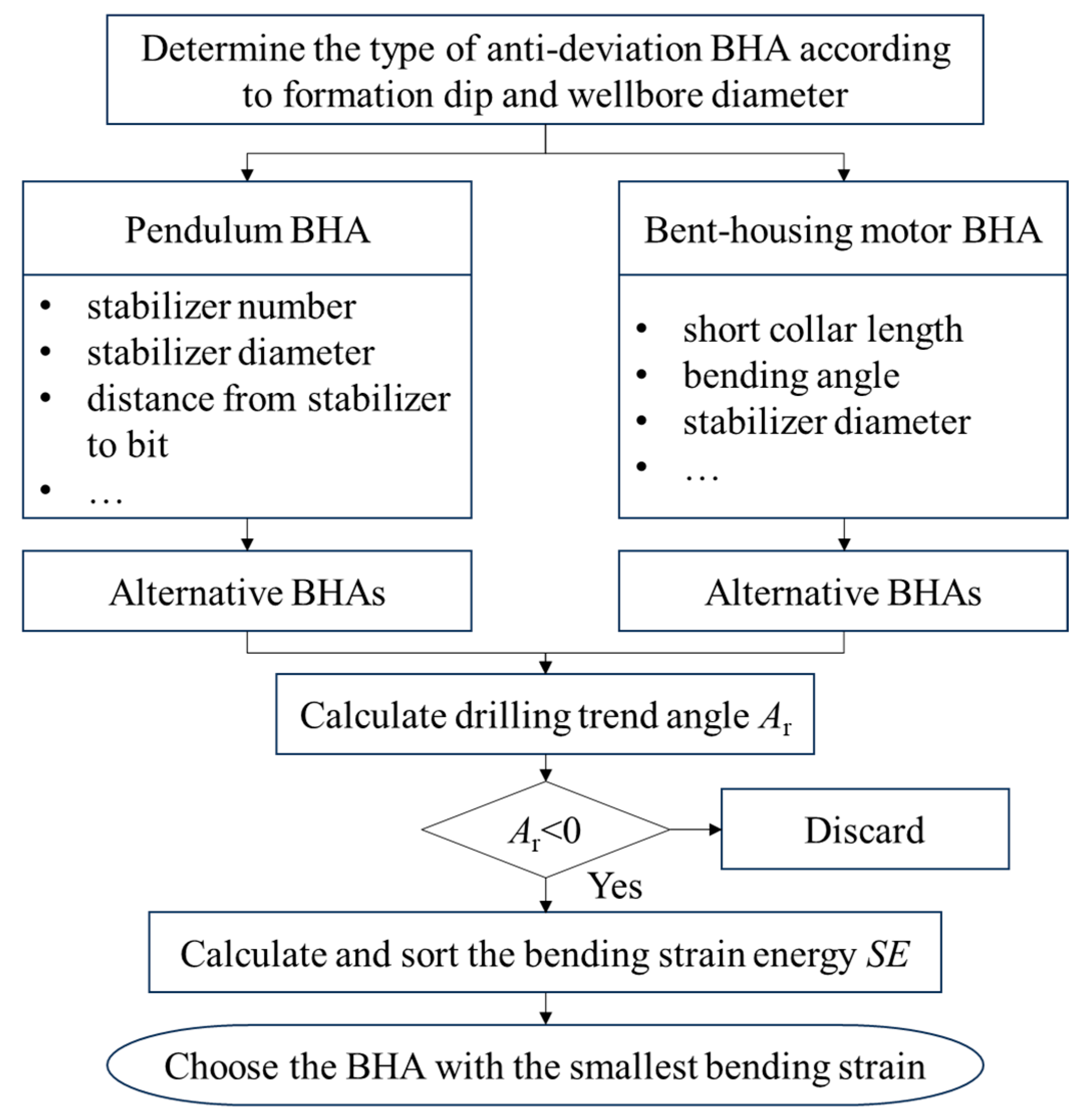
2.3. Integrated Anti-Deviation and Anti-Vibration BHA Design Method
3. Results and Discussions
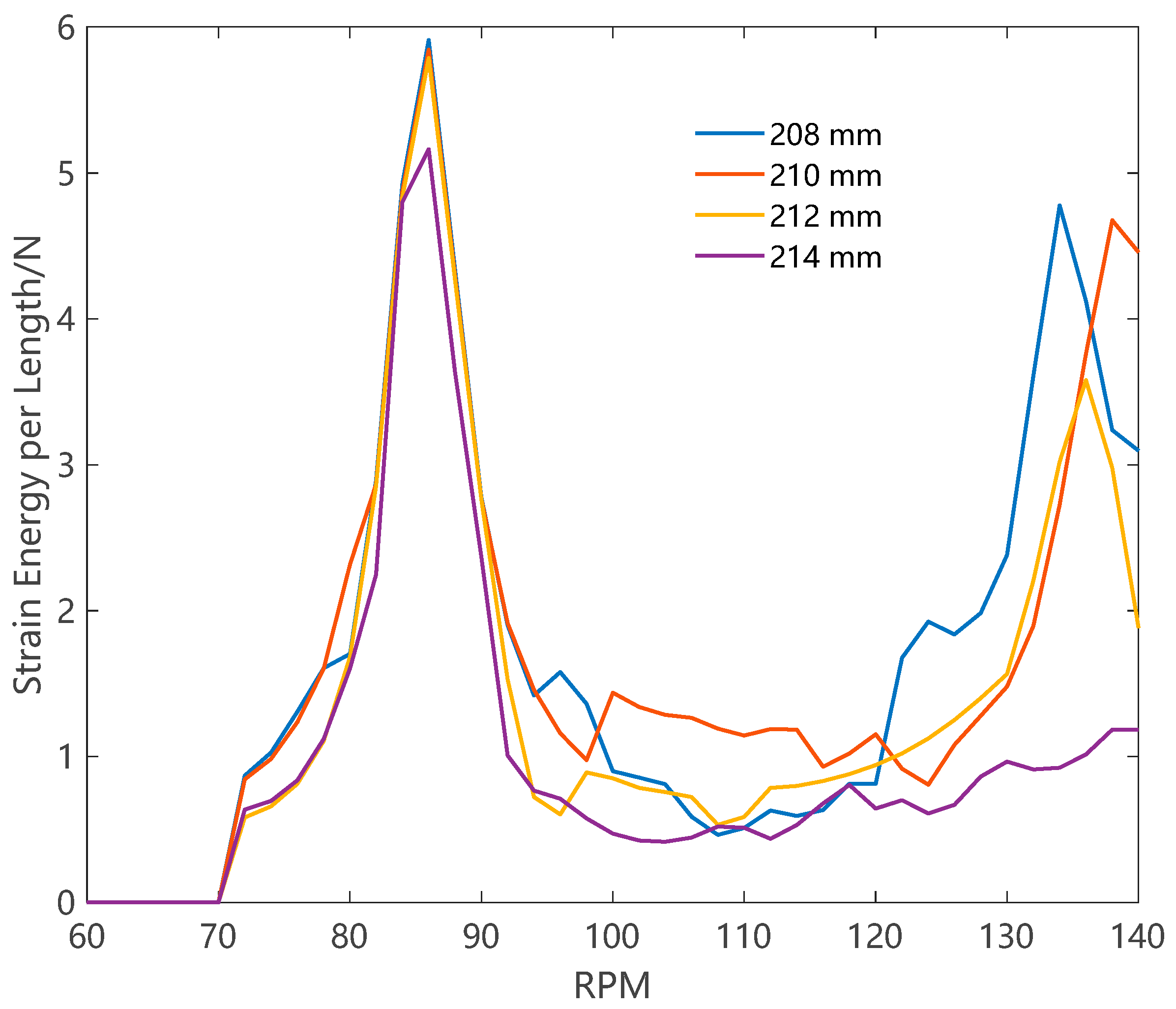
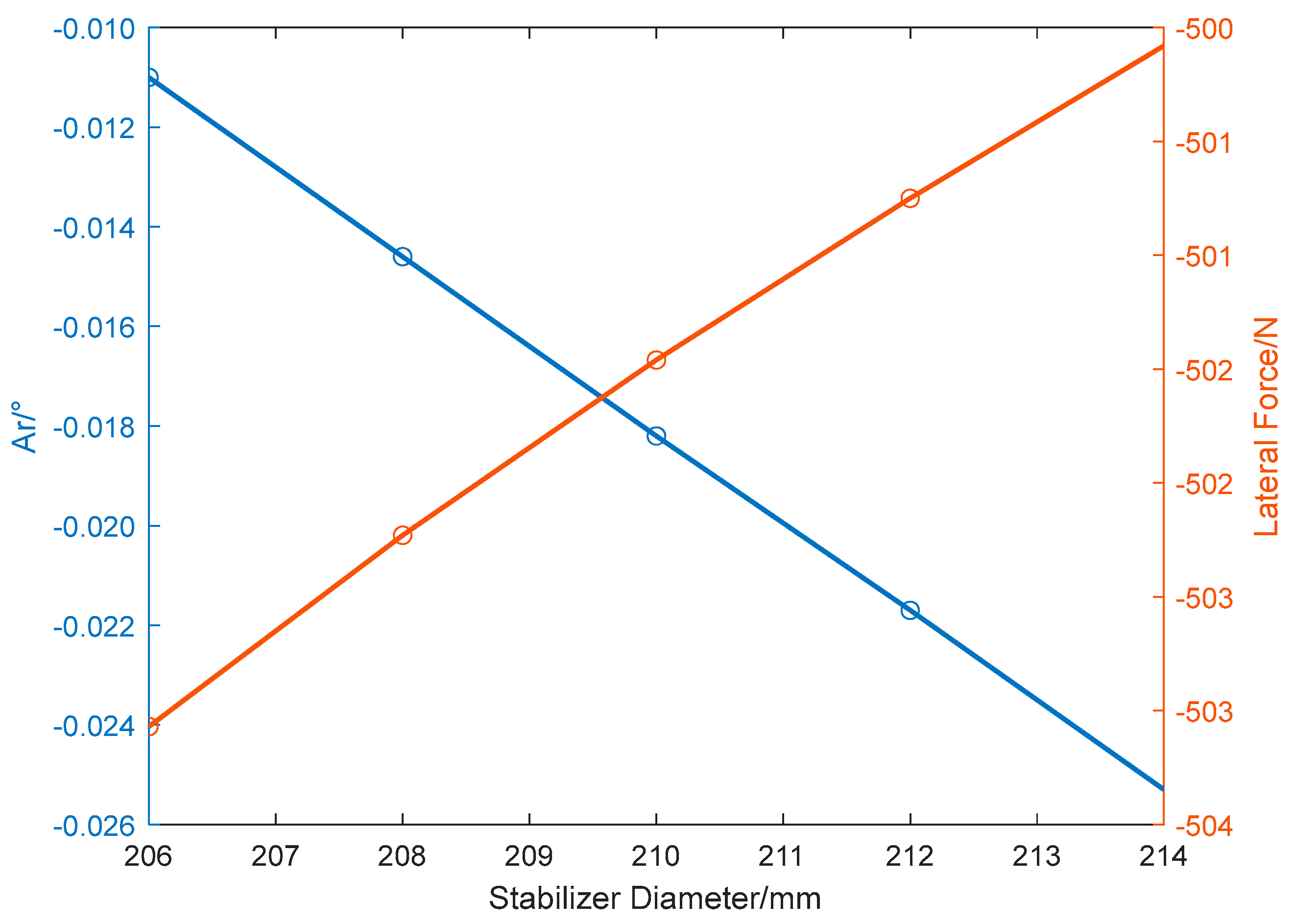
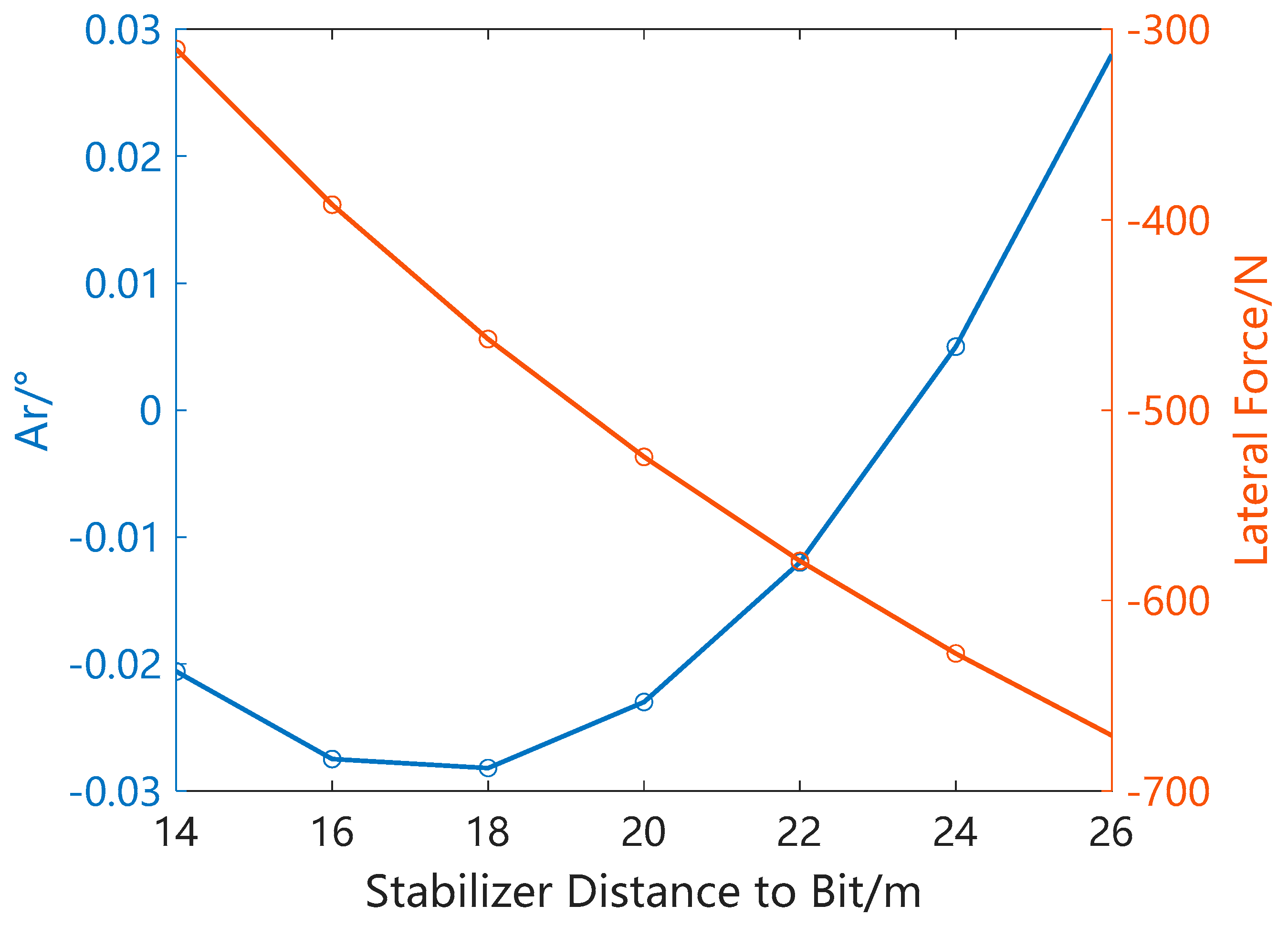
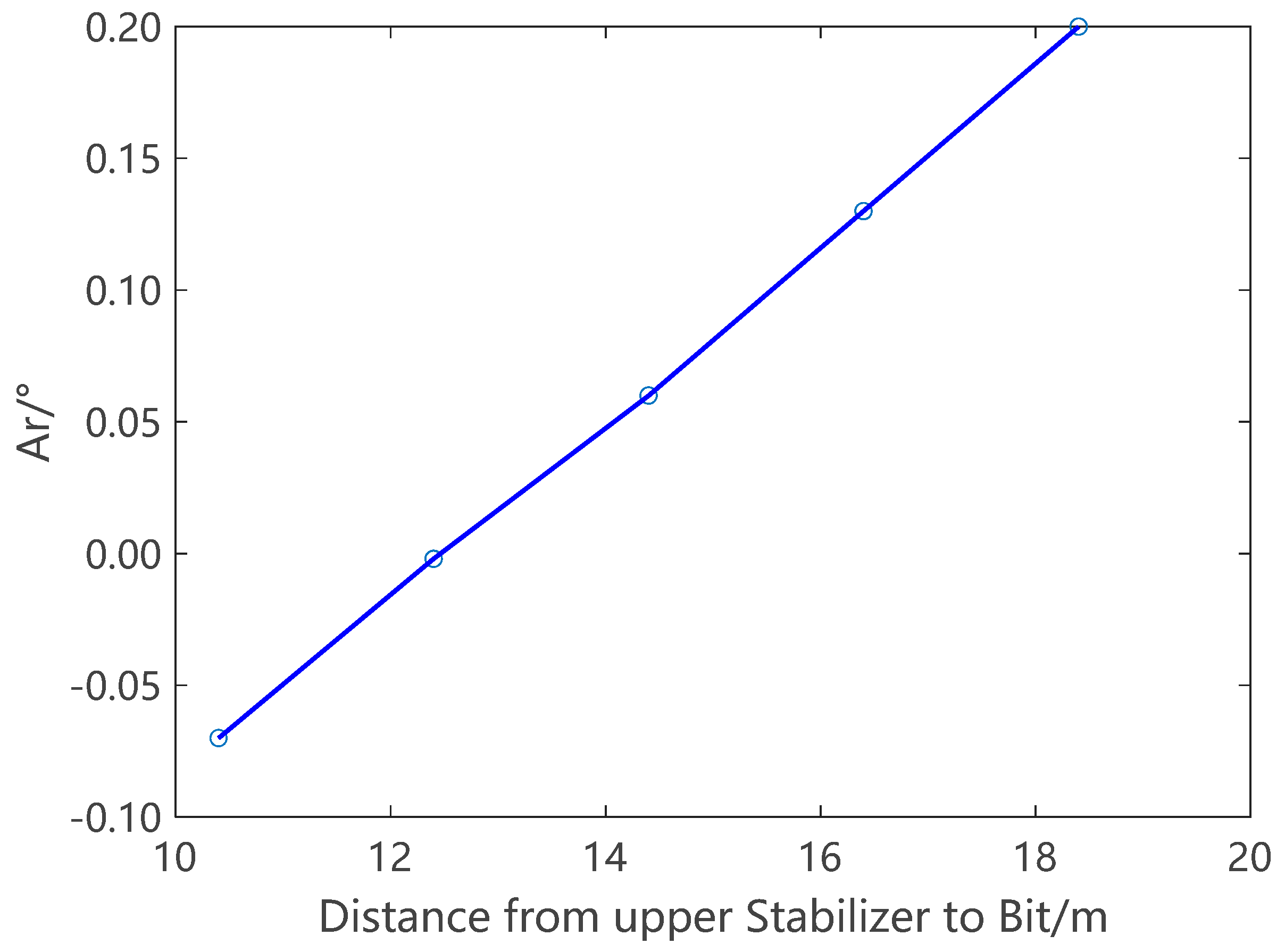
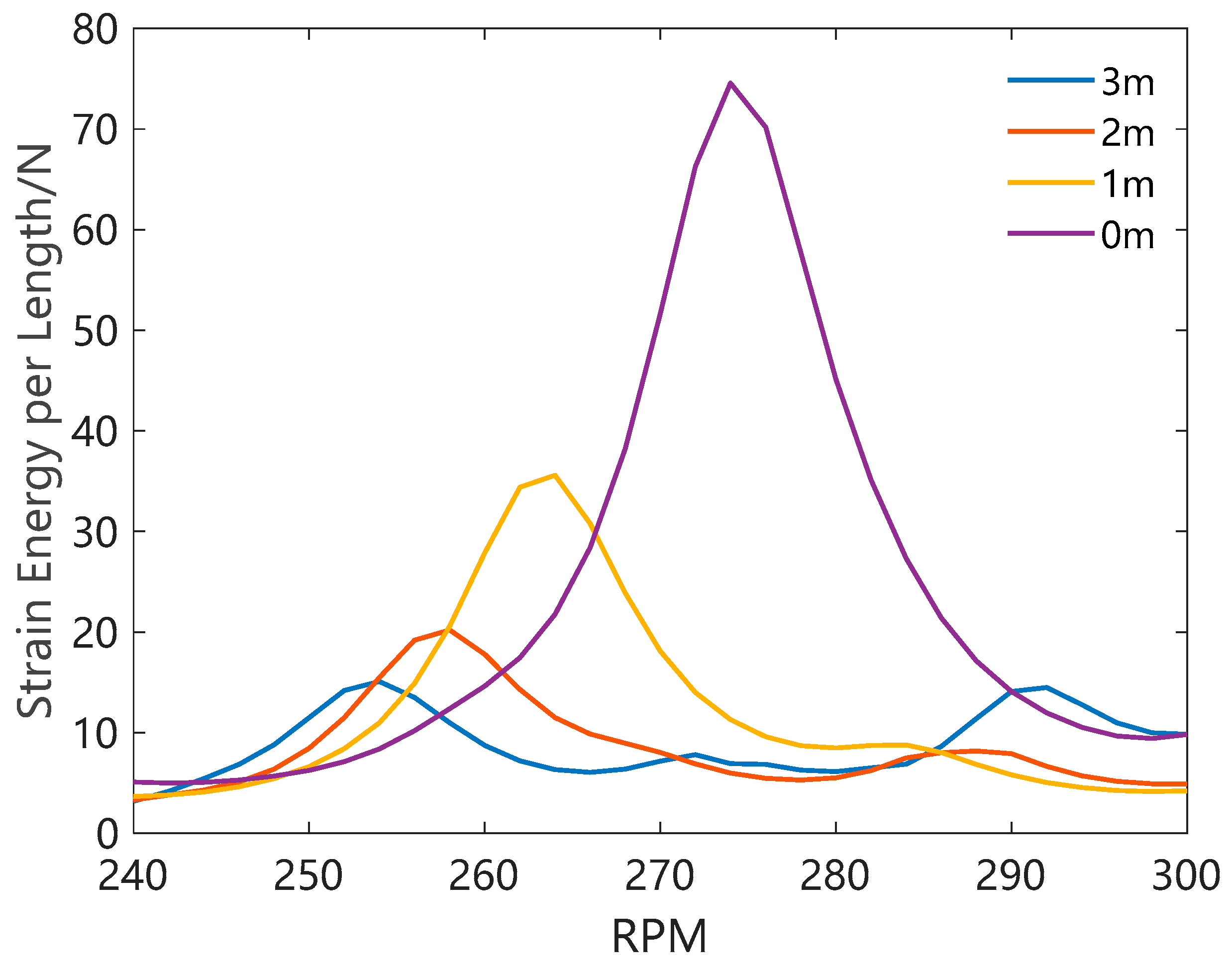
3.1. Important Design Factors of Pendulum BHA
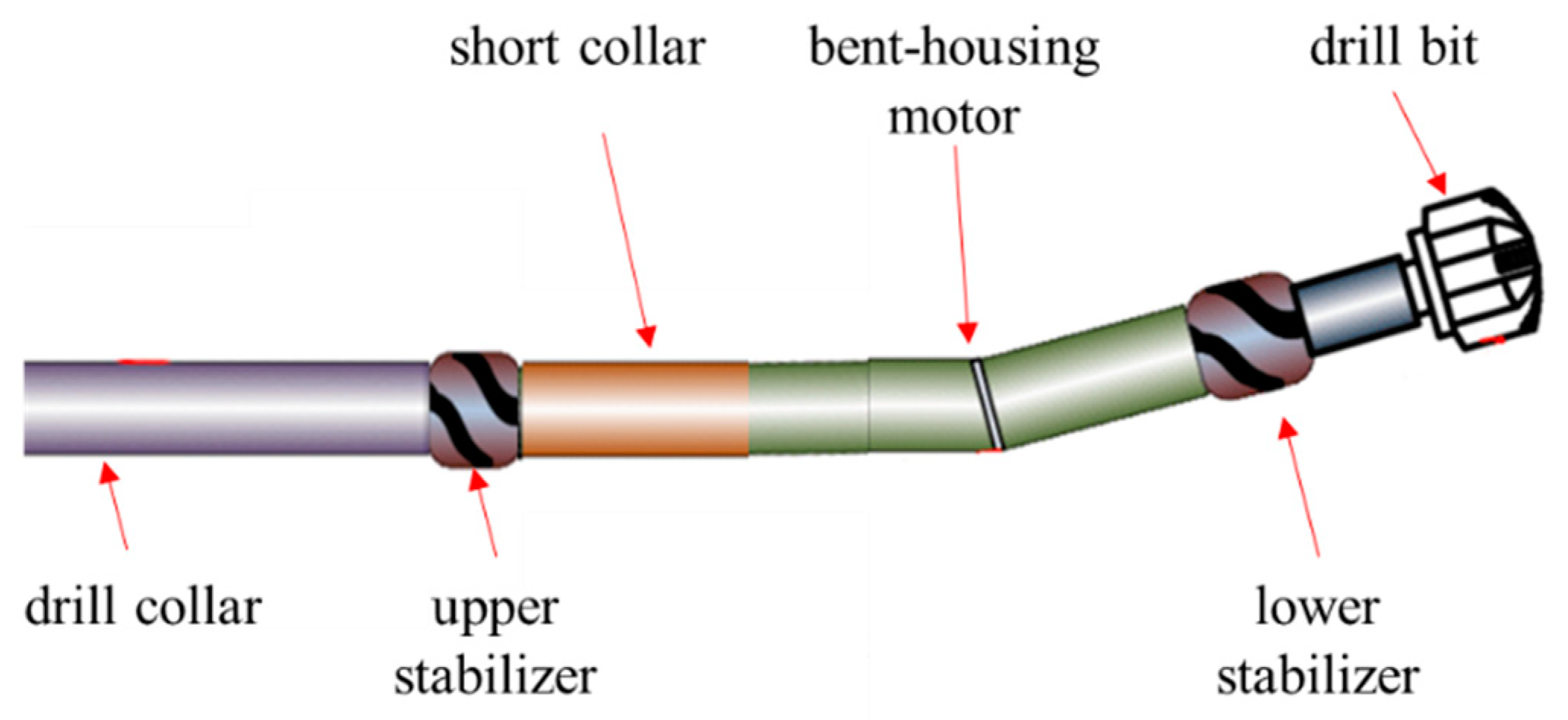
3.2. Important Design Factor of Bent Housing Mud Motor BHA
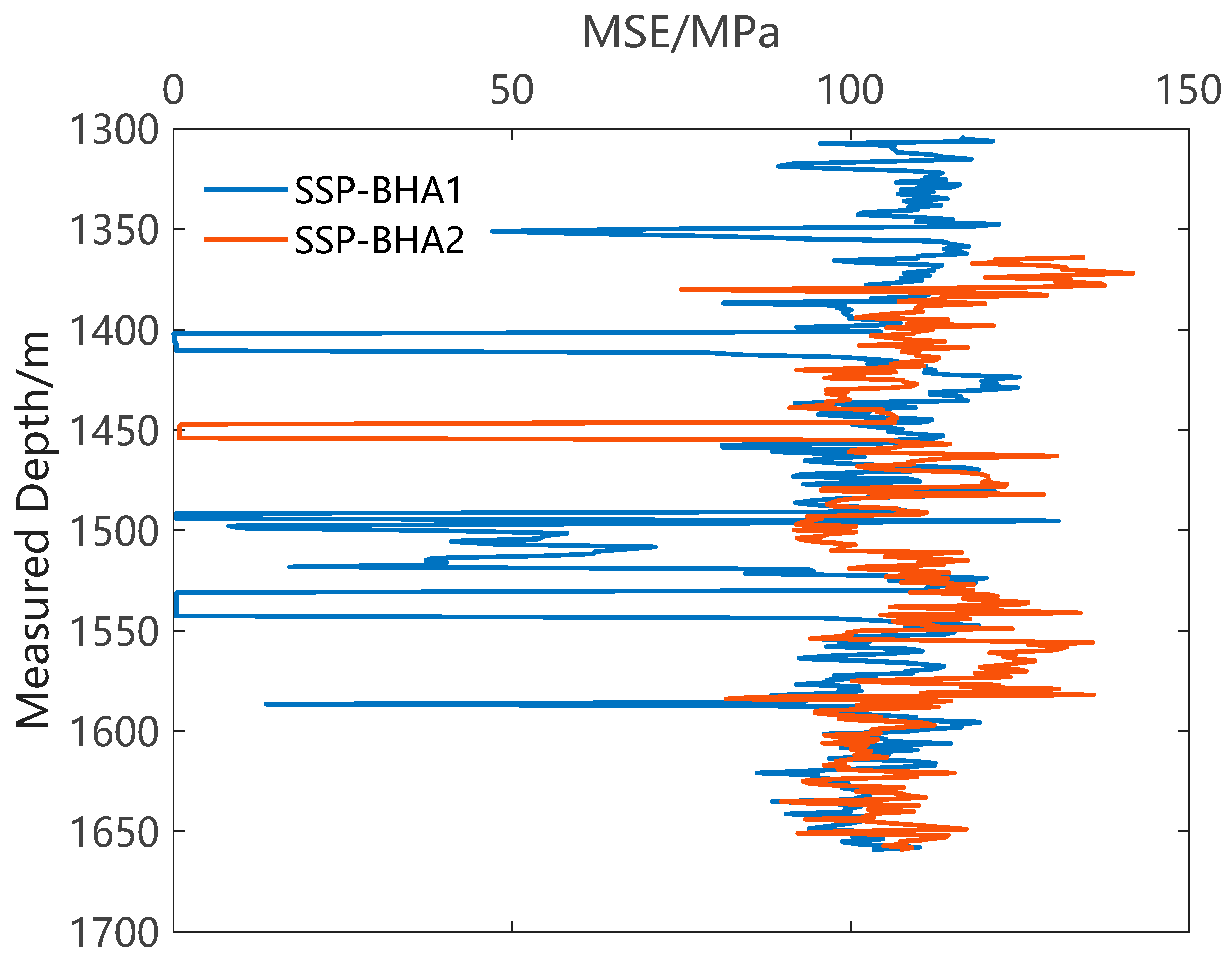
3.3. Field Tests of the Design Method
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BHA | bottom-hole assembly |
| BHMM | bent-housing mud motor |
| DSP | double-stabilizer pendulum |
| MSE | mechanical specific energy |
| RPM | revolutions per minute |
| SSP | single-stabilizer pendulum |
| WOB | weight on bit |
References
- Tan, B.; Xu, Q.; Fu, Q. Research and Application of Air Drilling Key Technologies in Bozi Block, Xinjiang. Drill. Prod. Technol. 2021, 44, 13–16. [Google Scholar]
- Jones, S.; Feddema, C.; Castro, J.; Sugiura, J. Fully Mechanical Vertical Drilling System Delivers RSS Performance in Vertical Drilling Applications While Providing an Economical Alternative to Conventional Rotary Steerable Systems Set-Up for Vertical Hold Mode. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, Fort Worth, TX, USA, 6–8 March 2016. [Google Scholar]
- Xi, C.; Zhang, W.; Zhang, N.; Chu, H. Study on factors affecting vertical drilling bottom hole assembly performance and a new bottom hole assembly design method considering formation uncertainties. Front. Energy Res. 2022, 10, 1073135. [Google Scholar] [CrossRef]
- Karlsson, H.; Brassfield, T.; Krueger, V. Performance Drilling Optimization. In Proceedings of the SPE/IADC Drilling Conference, New Orleans, LA, USA, 6–8 March 1985. [Google Scholar]
- Karlsson, H.; Cobbley, R.; Jaques, G.E. New Developments in Short-, Medium-, and Long-Radius Lateral Drilling. In Proceedings of the SPE/IADC Drilling Conference, New Orleans, LA, USA, 18–21 February 1989. [Google Scholar]
- Su, Y. Limiting curvature method and its application. Acta Pet. Sin. 1997, 18, 110–113. [Google Scholar]
- Ho, H.-S. Prediction of Drilling Trajectory in Directional Wells Via a New Rock-Bit Interaction Model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 27 September 1987. [Google Scholar]
- Shi, Y.; Guan, Z.; Zhao, H.; Huang, G. A new method for build-up rate prediction of bottom-hole assembly in well drilling. J. China Univ. Pet. 2017, 41, 85–89. [Google Scholar]
- Huang, W.; Wang, K.; Gao, D. A method for predicting the build-up rate of “push-the-bit” rotary steering tool. Nat. Gas Ind. 2021, 41, 101–106. [Google Scholar]
- Millheim, K.; Jordan, S.; Ritter, C.J. Bottom-Hole Assembly Analysis Using the Finite-Element Method. J. Pet. Technol. 1978, 30, 265–274. [Google Scholar] [CrossRef]
- Neubert, M.; Heisig, G.; Forstner, I.; Mounzer, F. Verification of an Advanced BHA Analysis Model with Downhole Bending Moment Measurements. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 5–7 April 2005. [Google Scholar]
- Wilson, J.K. Field Validation of a New BHA Model and Practical Case Studies in Unconventional Shale Plays, with a Framework for Automated Analysis for Operations Support. In Proceedings of the SPE/AAPG Eastern Regional Meeting, Pittsburgh, PA, USA, 7–11 October 2018. [Google Scholar]
- Greenwood, J.; Marck, J.; Nair, V.N.; Munguia, J. Drilling Performance Evaluation Using Advanced BHA Modeling and Field Validation. In Proceedings of the IADC/SPE International Drilling Conference and Exhibition, Galveston, TX, USA, 3–5 March 2020. [Google Scholar]
- Bai, J. Bottom Hole Assembly Problems Solved by Beam-Column Theory. In Proceedings of the International Petroleum Exhibition and Technical Symposium, Beijing, China, 16–24 March 1982. [Google Scholar]
- Bai, J.; Lin, X. Two-Dimensional Analysis of Bottom Hole Assembly by Beam-Column Theory. Acta Pet. Sin. 1985, 6, 75–84. [Google Scholar]
- Bai, J.; Huang, Z.; Liu, Y. Three-Dimensional Analysis of Bottom Hole Assembly by Beam-Column Theory. Acta Pet. Sin. 1989, 10, 60–66. [Google Scholar]
- Menand, S.; Sellami, H.; Tijani, M.; Stab, O.; Dupuis, D.; Simon, C. Advancements in 3D Drillstring Mechanics: From the Bit to the Topdrive. In Proceedings of the IADC/SPE Drilling Conference, Miami, FL, USA, 21–23 February 2006. [Google Scholar]
- Menand, S.; Mills, K.A.; Suarez, R. Micro Dogleg Detection with Continuous Inclination Measurements and Advanced BHA Modeling. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 7–10 November 2016. [Google Scholar]
- Goicoechea, H.; Buezas, F.S.; Rosales, M.B. A non-linear Cosserat rod model for drill-string dynamics in arbitrary borehole geometries with contact and friction. Int. J. Mech. Sci. 2019, 157, 98–110. [Google Scholar] [CrossRef]
- Yu, F.; Huang, G.; Li, W.; Ni, H.; Huang, B.; Li, J.; Duan, J. Modeling lateral vibration of bottom hole assembly using Cosserat theory and laboratory experiment verification. Geoenergy Sci. Eng. 2023, 222, 211359. [Google Scholar] [CrossRef]
- Bailey, J.R.; Biediger, E.A.O.; Gupta, V.; Ertas, D.; Elks, W.C.; Dupriest, F.E. Drilling Vibrations Modeling and Field Validation. In Proceedings of the IADC/SPE Drilling Conference, Orlando, FL, USA, 4–6 March 2008. [Google Scholar]
- Bailey, J.R.; Lathi, H.; Tenny, M.J.; Payette, G.S.; Wang, L. BHA Lateral Vibration Chatter Impedes Application of Weight to Bit. In Proceedings of the IADC/SPE International Drilling Conference and Exhibition, Galveston, TX, USA, 3–5 March 2020. [Google Scholar]
- Wilson, J.K.; Heisig, G.; Freyer, C. HFTO Solved: Proven Mitigation of High Frequency Torsional Oscillations in Motor-Assisted Rotary Steerable Applications. In Proceedings of the IADC/SPE International Drilling Conference and Exhibition, Galveston, TX, USA, 7 March 2022. [Google Scholar]
- Dushaishi, M.F.A.I.; Stutts, D.S. Vibration analysis of simultaneous drilling and reaming BHA. J. Pet. Explor. Prod. Technol. 2020, 10, 3409–3417. [Google Scholar] [CrossRef]
- Sugiura, J.; Jones, S. Simulation and Measurement of High-Frequency Torsional Oscillation HFTO/High-Frequency Axial Oscillation HFAO and Downhole HFTO Mitigation: Knowledge Gains Continue by Using Embedded High-Frequency Drilling Dynamics Sensors. In Proceedings of the IADC/SPE International Drilling Conference and Exhibition, Galveston, TX, USA, 3–5 March 2020. [Google Scholar]
- Chen, S.; Propes, C.; Lanning, C.; Dunbar, B. Mechanisms and Mitigation of 3D Coupled Vibrations in Drilling with PDC Bits. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 21–23 September 2021. [Google Scholar]
- Belkacem, L.; Abdelbaki, N.; Otegui, J.L.; Gaceb, M.; Bettayeb, M. Using a superficially treated 2024 aluminum alloy drill pipe to delay failure during dynamic loading. Eng. Fail. Anal. 2019, 104, 261–273. [Google Scholar] [CrossRef]
- Cheng, J.; Yu, Y.; Sun, Y. Numerical analysis of whirl for drill string with aluminum alloy drill pipes in deep vertical well. Geoenergy Sci. Eng. 2023, 231, 212314. [Google Scholar] [CrossRef]
- Vedernikov, A.; Gemi, L.; Madenci, E.; Özkılıç, Y.O.; Yazman, Ş.; Gusev, S.; Sulimov, A.; Bondareva, J.; Evlashin, S.; Konev, S.; et al. Effects of high pulling speeds on mechanical properties and morphology of pultruded GFRP composite flat laminates. Compos. Struct. 2022, 301, 116216. [Google Scholar] [CrossRef]
- Wilson, J.K. Nonlinear Drillstring Modeling with Applications to Induced Vibrations in Unconventional Horizontal Wells. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2017. [Google Scholar]
- Bailey, J.R.; Remmert, S.M. Managing Drilling Vibrations Through BHA Design Optimization. SPE Drill. Compl. 2010, 25, 458–471. [Google Scholar] [CrossRef]
- Burgess, T.M.; McDaniel, G.L.; Das, P.K. Improving BHA tool reliability with drillstring vibration models: Field experience and limitations. In Proceedings of the SPE/IADC Drilling Conference, New Orleans, LA, USA, 15–18 March 1987. [Google Scholar]
- Dykstra, M.W. Nonlinear Drill String Dynamics. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 1996. [Google Scholar]


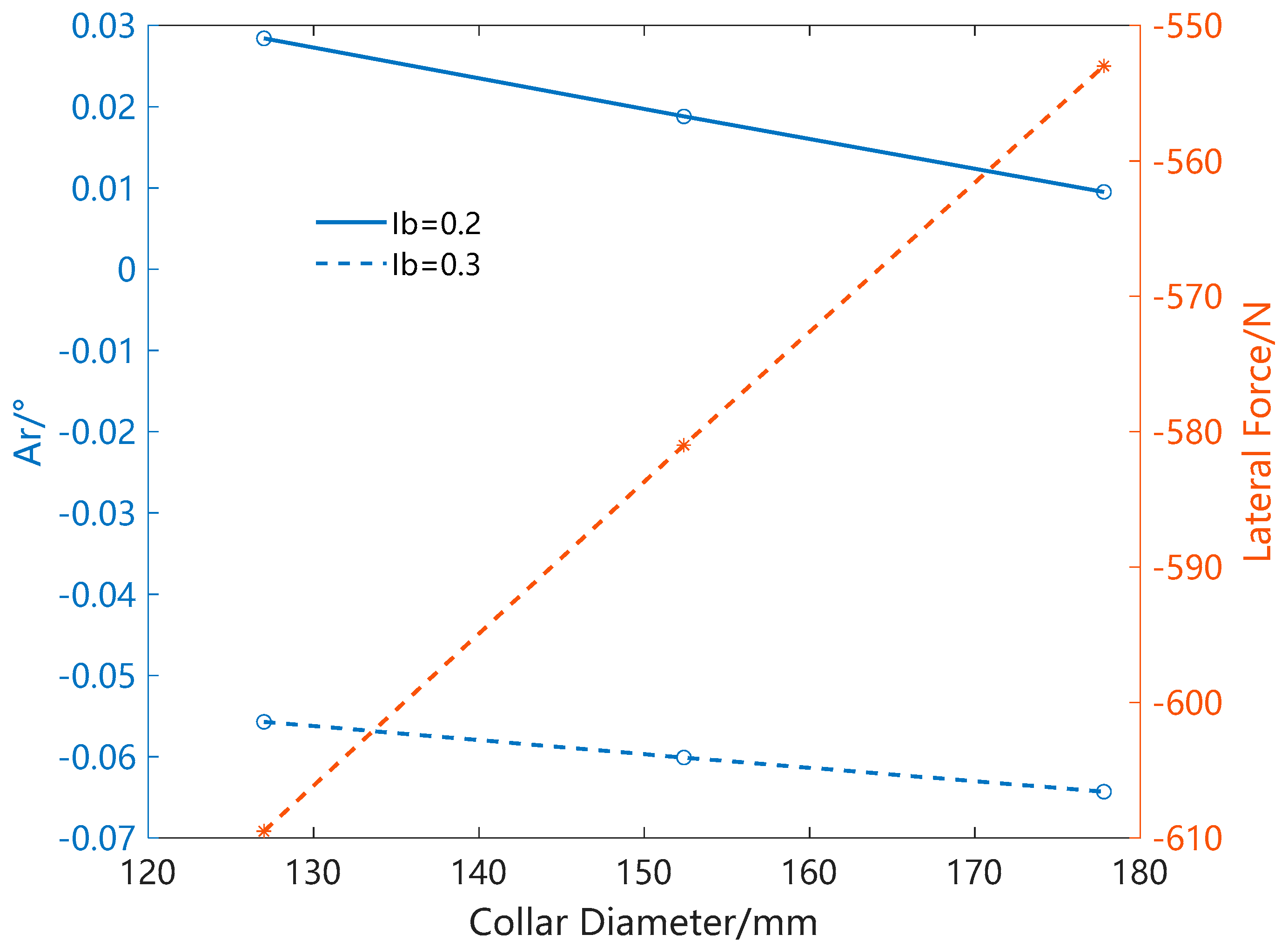

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Zhang, L.; Hao, Z.; Ding, X.; Liu, Z.; Li, T. A New Bottom-Hole Assembly Design Method to Maintain Verticality and Reduce Lateral Vibration. Processes 2024, 12, 95. https://doi.org/10.3390/pr12010095
Cheng Z, Zhang L, Hao Z, Ding X, Liu Z, Li T. A New Bottom-Hole Assembly Design Method to Maintain Verticality and Reduce Lateral Vibration. Processes. 2024; 12(1):95. https://doi.org/10.3390/pr12010095
Chicago/Turabian StyleCheng, Zhong, Liang Zhang, Zhouzheng Hao, Xiangxiang Ding, Zhikun Liu, and Tiantai Li. 2024. "A New Bottom-Hole Assembly Design Method to Maintain Verticality and Reduce Lateral Vibration" Processes 12, no. 1: 95. https://doi.org/10.3390/pr12010095
APA StyleCheng, Z., Zhang, L., Hao, Z., Ding, X., Liu, Z., & Li, T. (2024). A New Bottom-Hole Assembly Design Method to Maintain Verticality and Reduce Lateral Vibration. Processes, 12(1), 95. https://doi.org/10.3390/pr12010095






