Research on Dimension Reduction Method for Combustion Chamber Structure Parameters of Wankel Engine Based on Active Subspace
Abstract
:1. Introduction
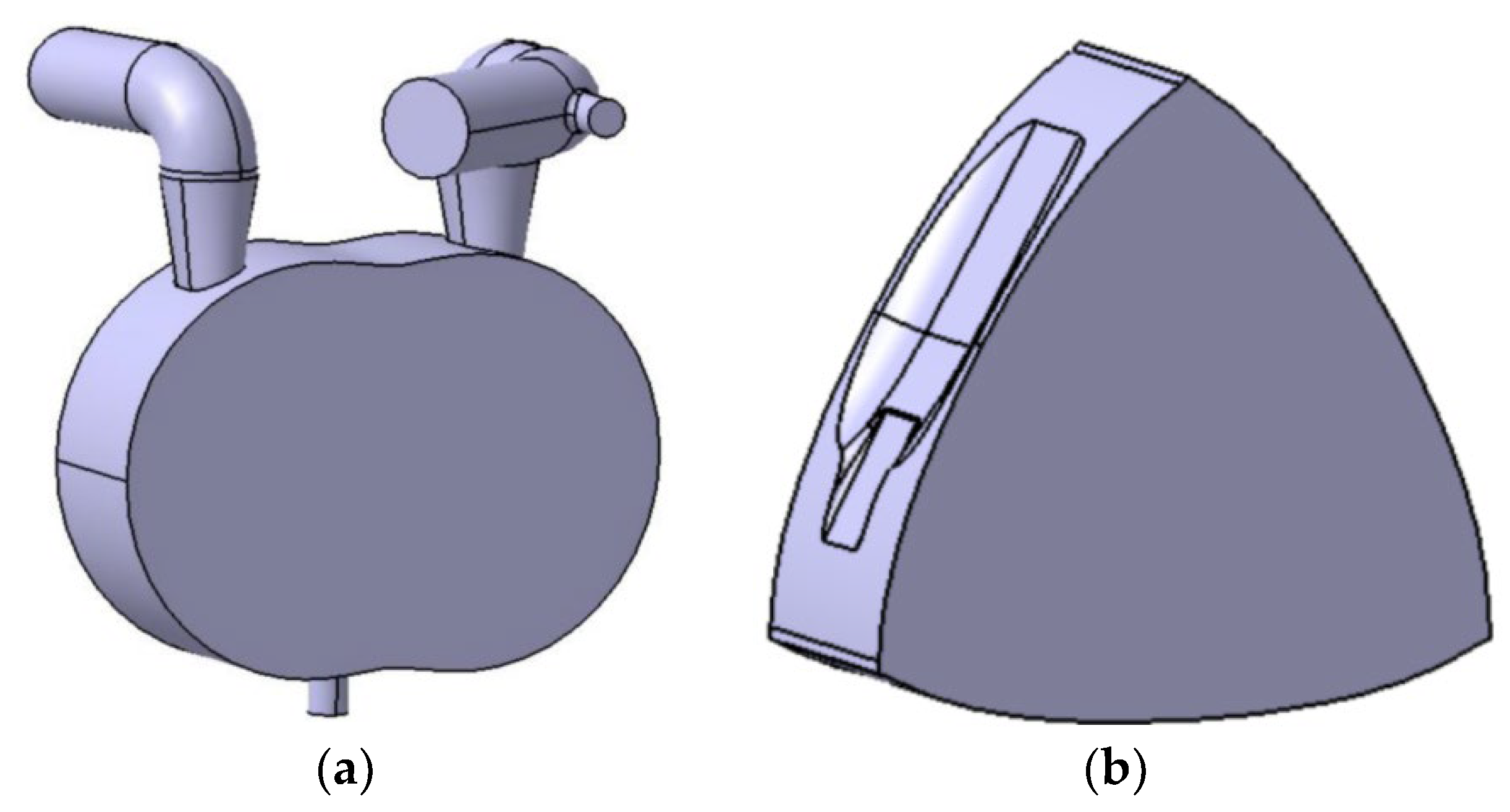
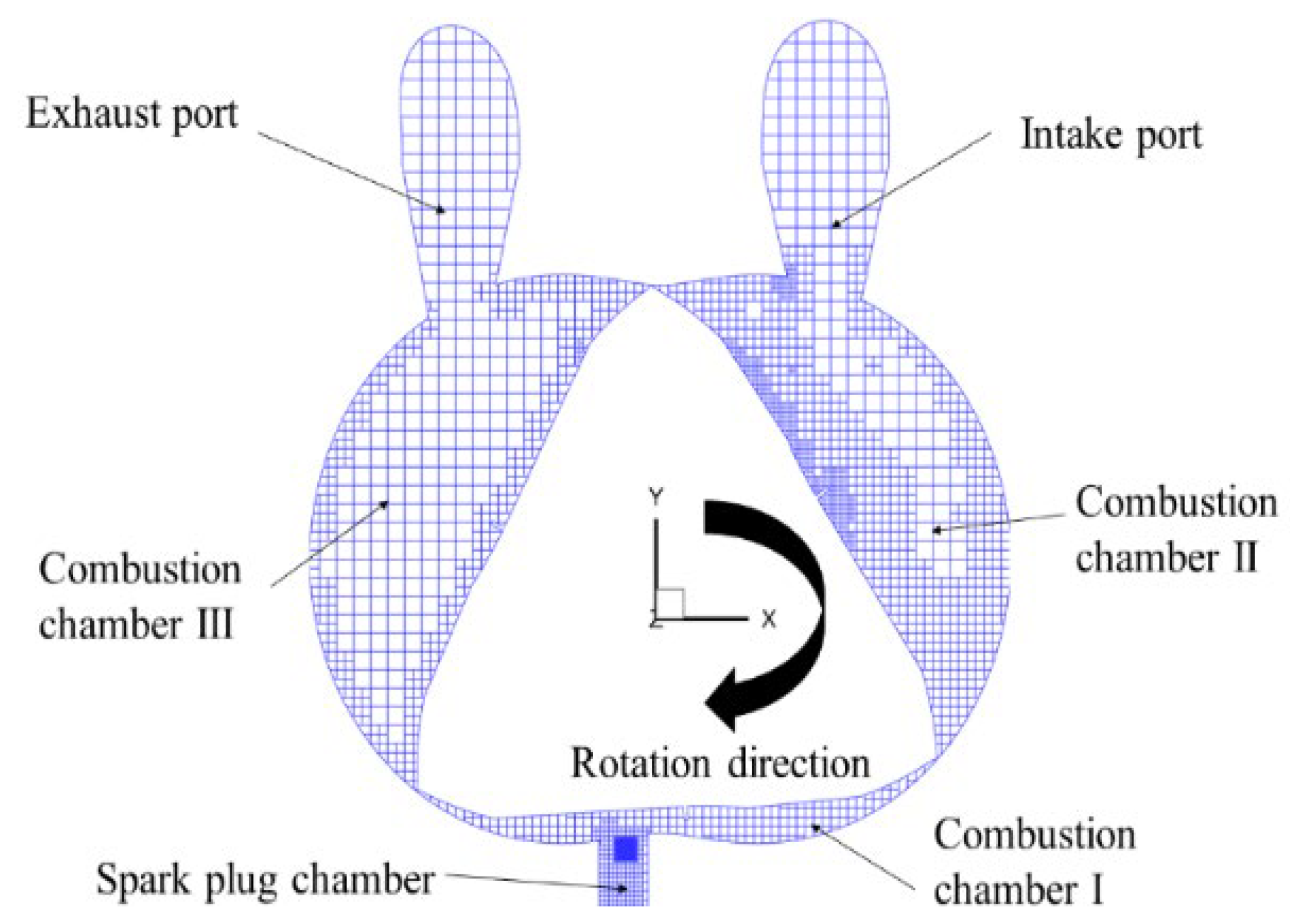
2. Uncertainty Analysis of Combustion Chamber Structure Parameters
- (1)
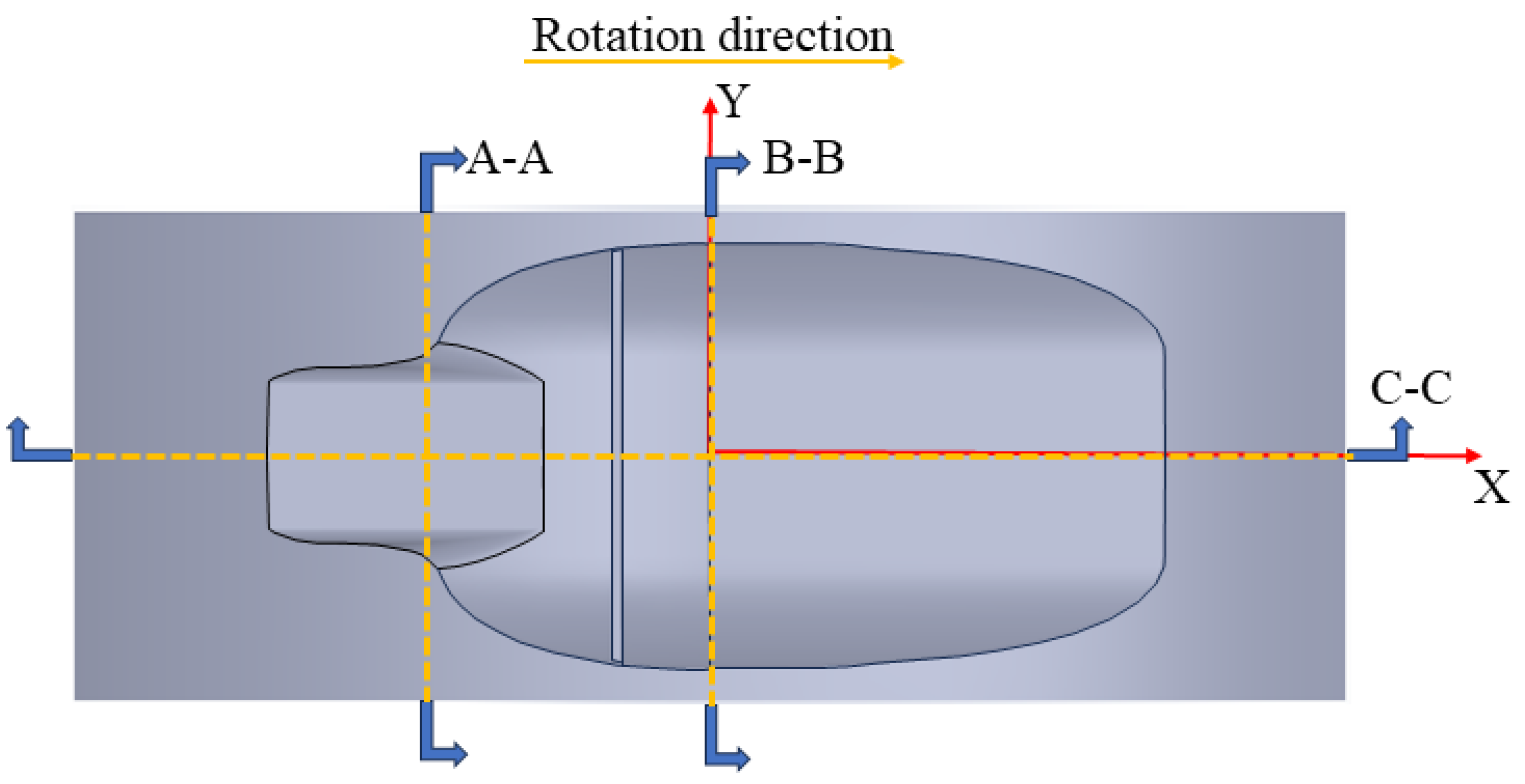
- The distance from the deepest part of the rotor combustion chamber to its center of gravity on the x-z plane must not exceed , considering structural strength, heat dissipation structure arrangement, and spindle assembly.
- (2)
- The maximum width of the chamber must not exceed , addressing seal arrangement and structural strength.
- (3)
- The distance between the chamber ends and the rotor tip on the y-z plane must not exceed , addressing radial seal arrangement and structural strength.
- (4)
- The width of the rotor spoiler plate must not exceed , ensuring spoiler plate strength.
- (5)
- (6)
- To simplify processing, the rotor spoiler should be positioned centrally or toward the rear of the combustion chamber, avoiding overlap between chamber sections.
- (7)
- The leading and middle parts of the combustion chamber must be connected, with a single recess on the rotor surface.
- (8)
- The arc radius of the transition section must not exceed .
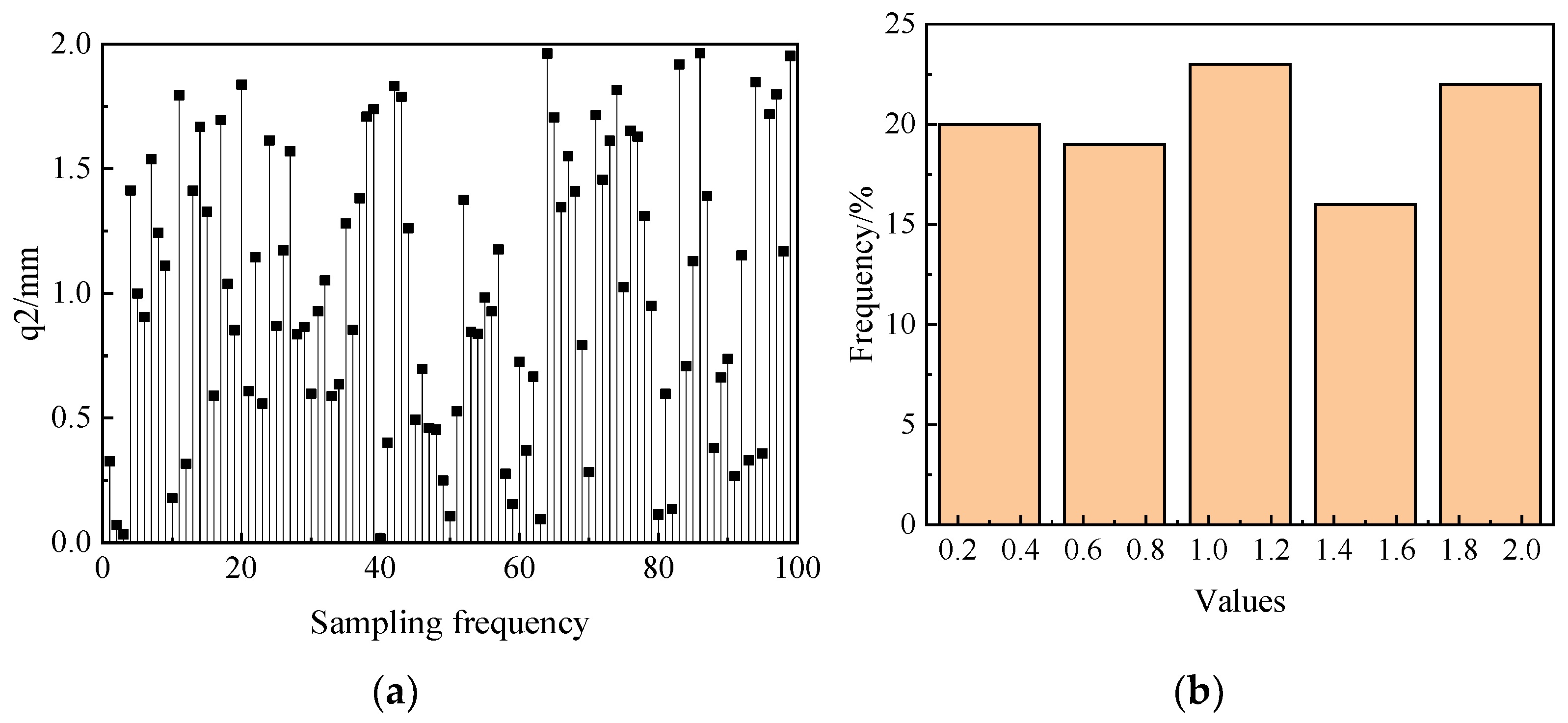
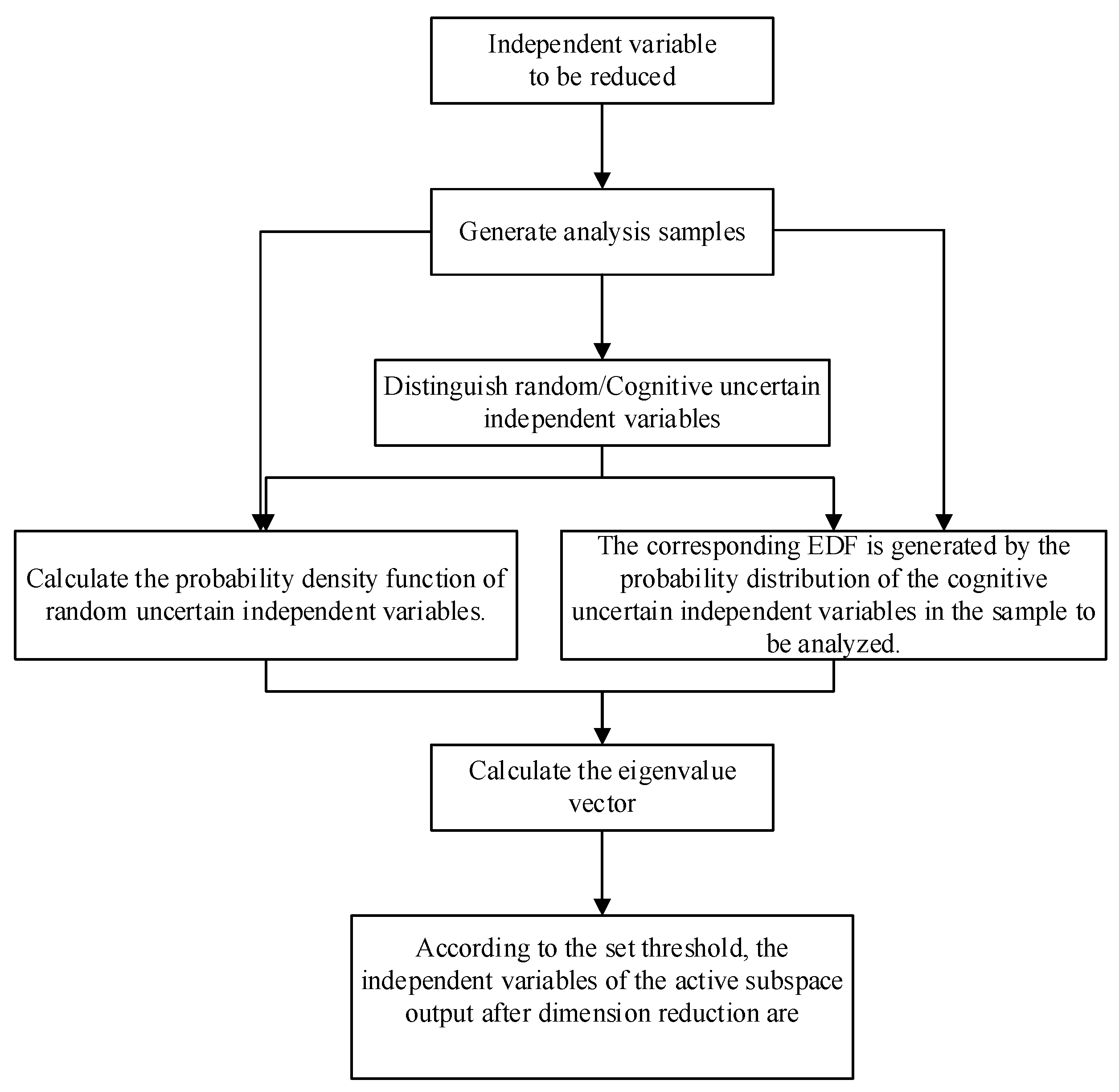
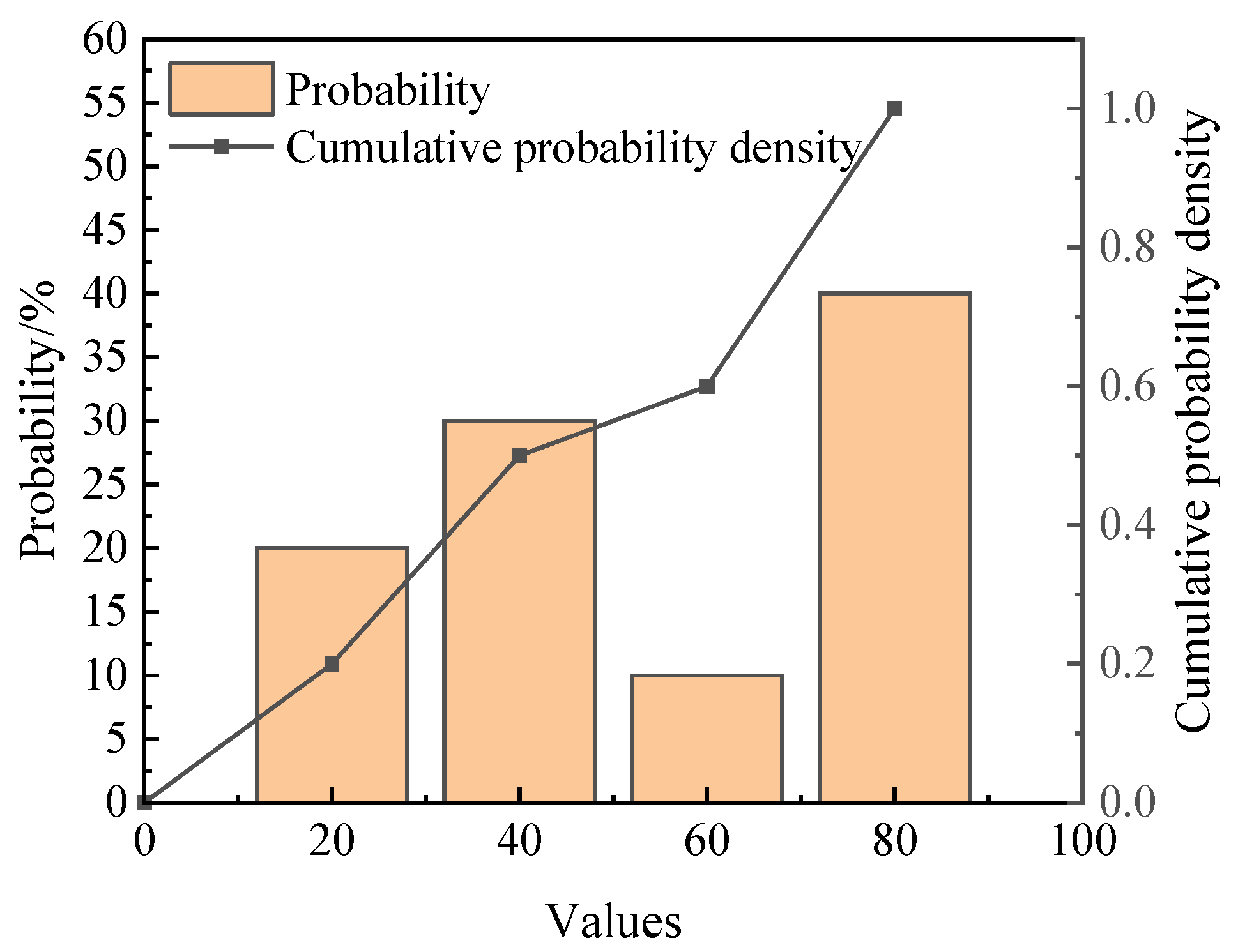
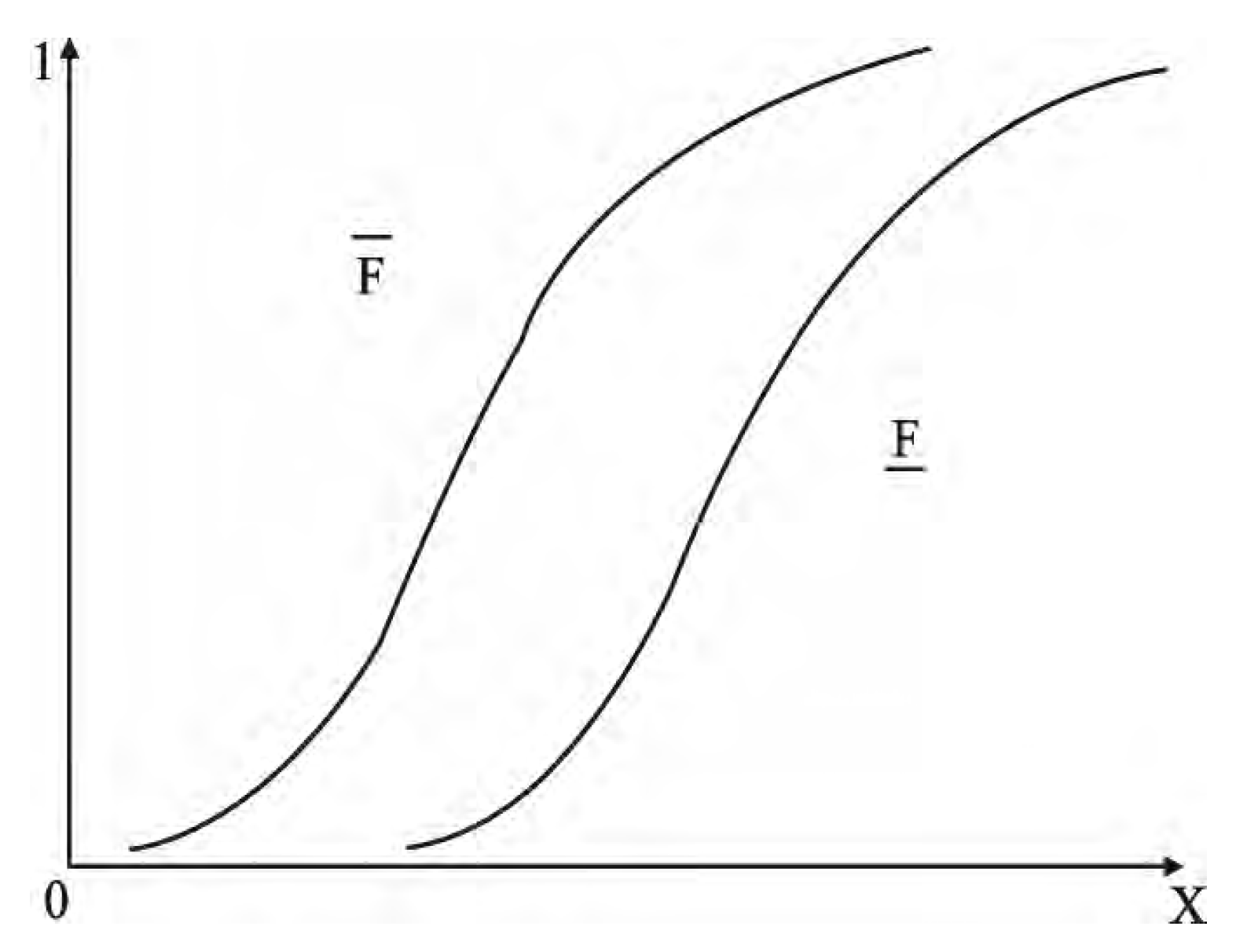
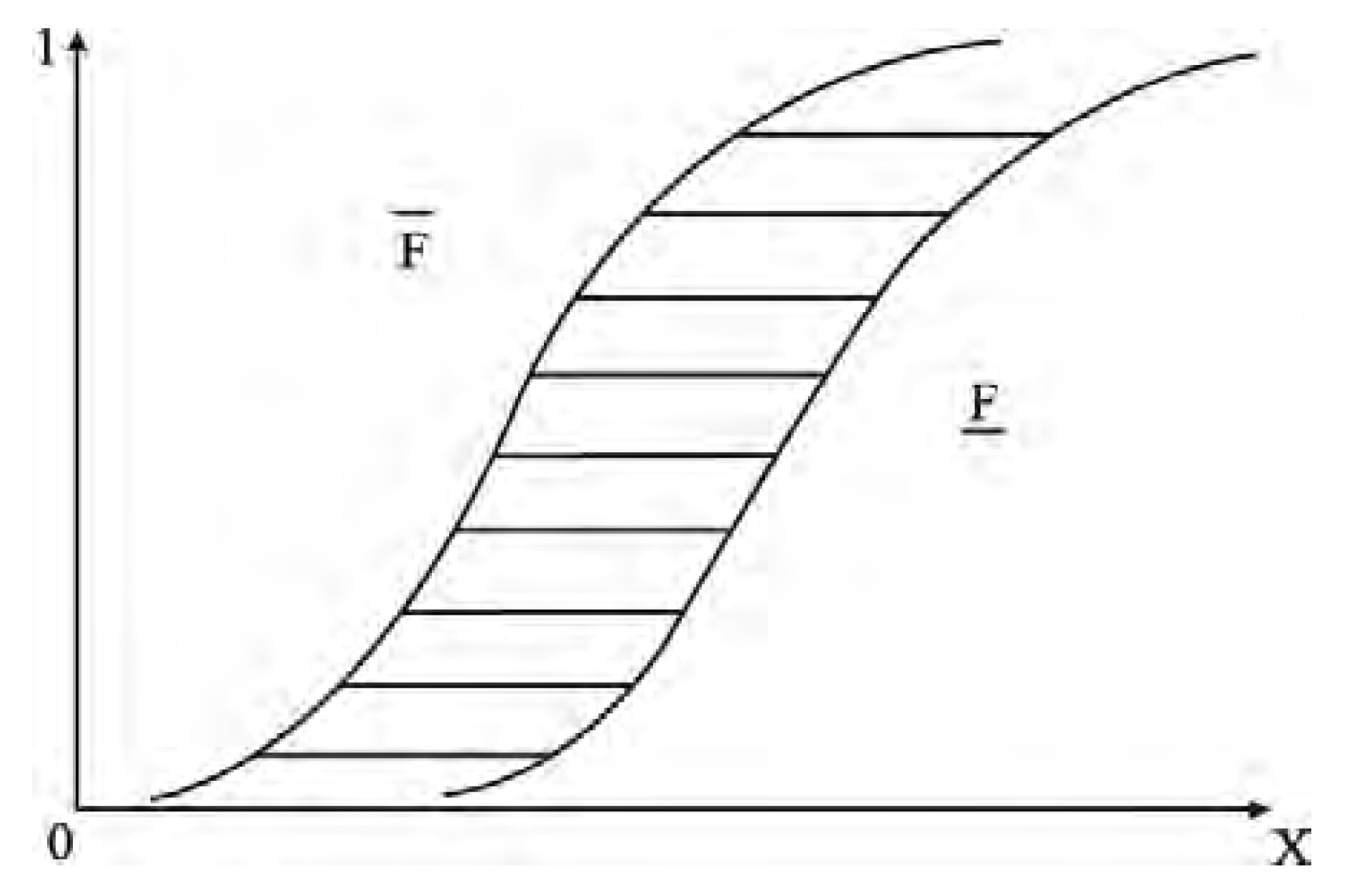
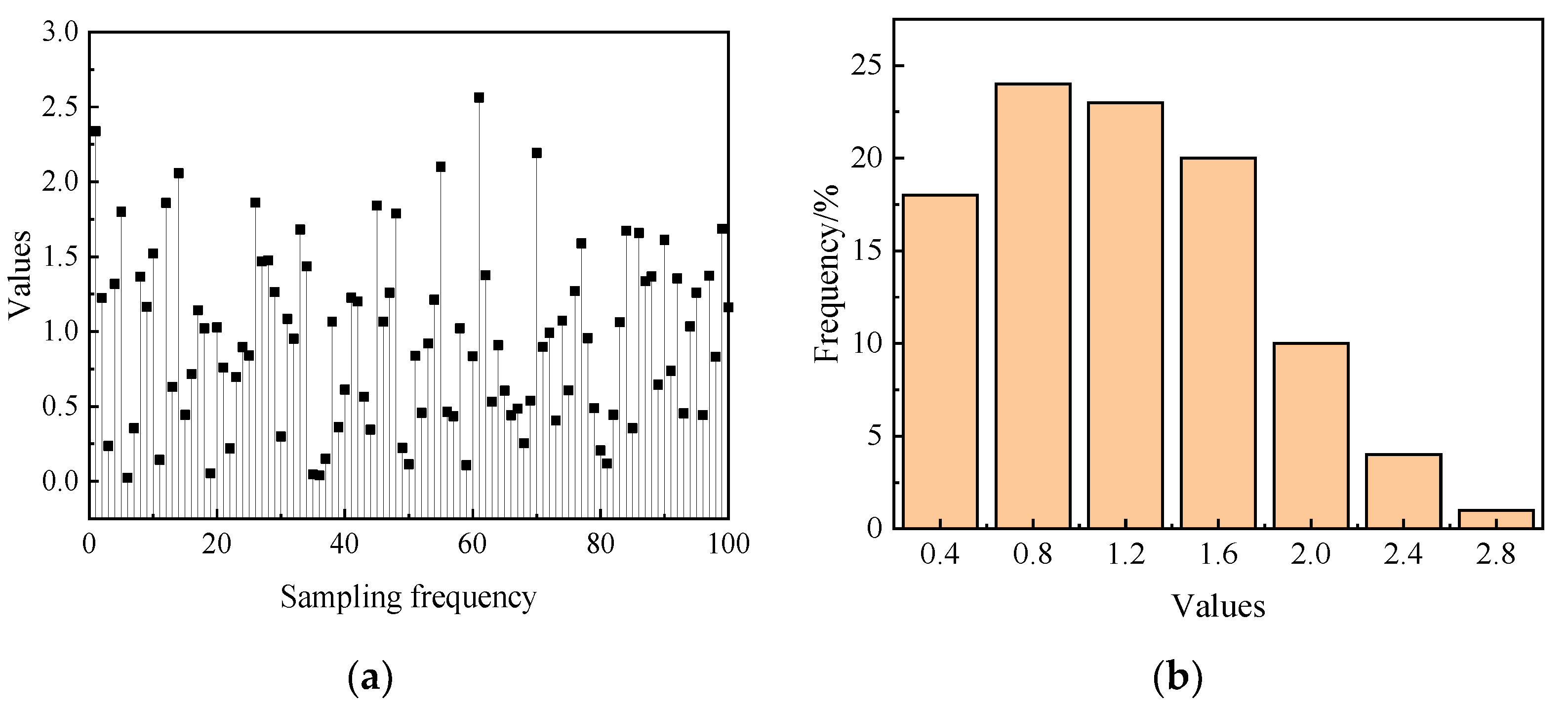
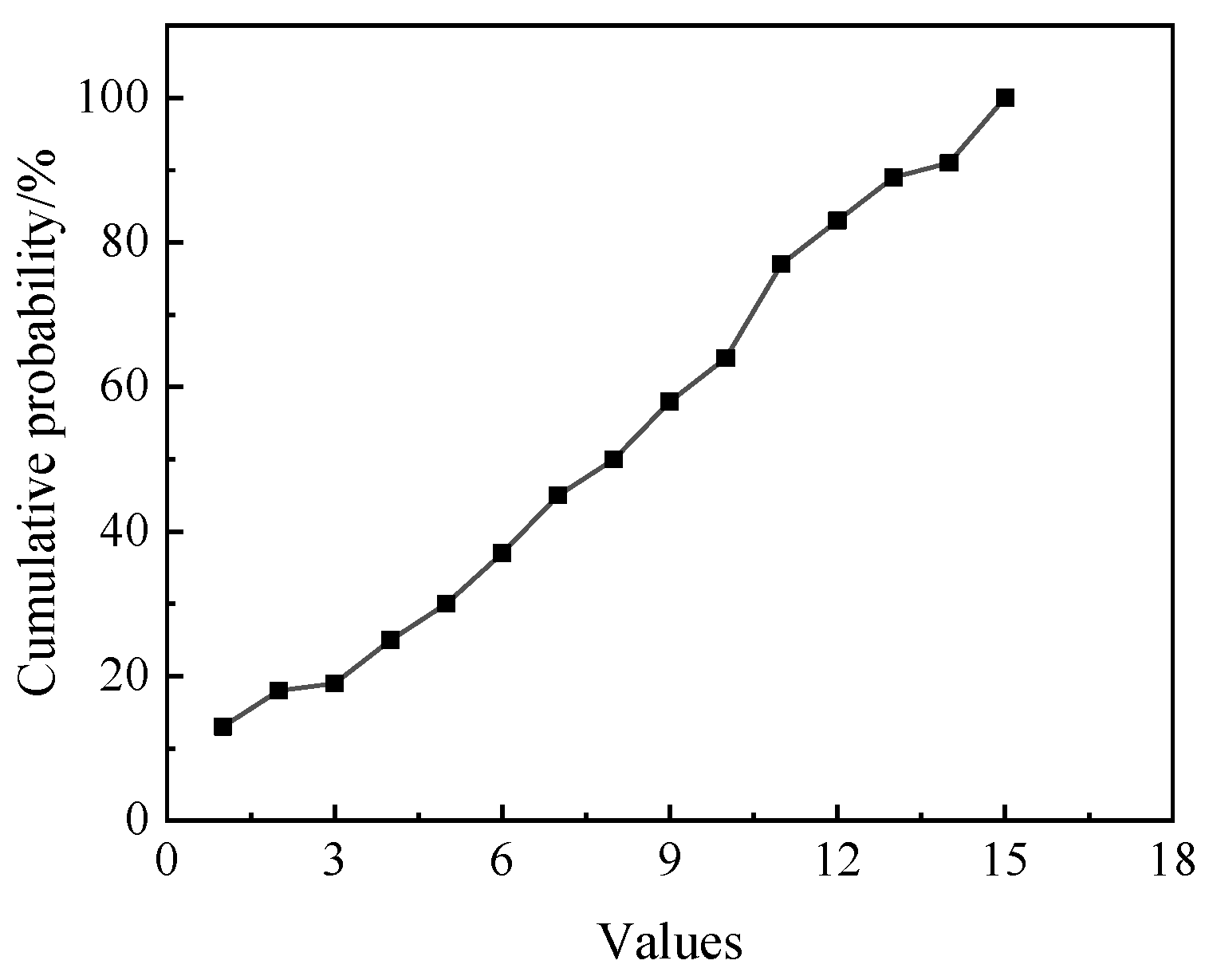
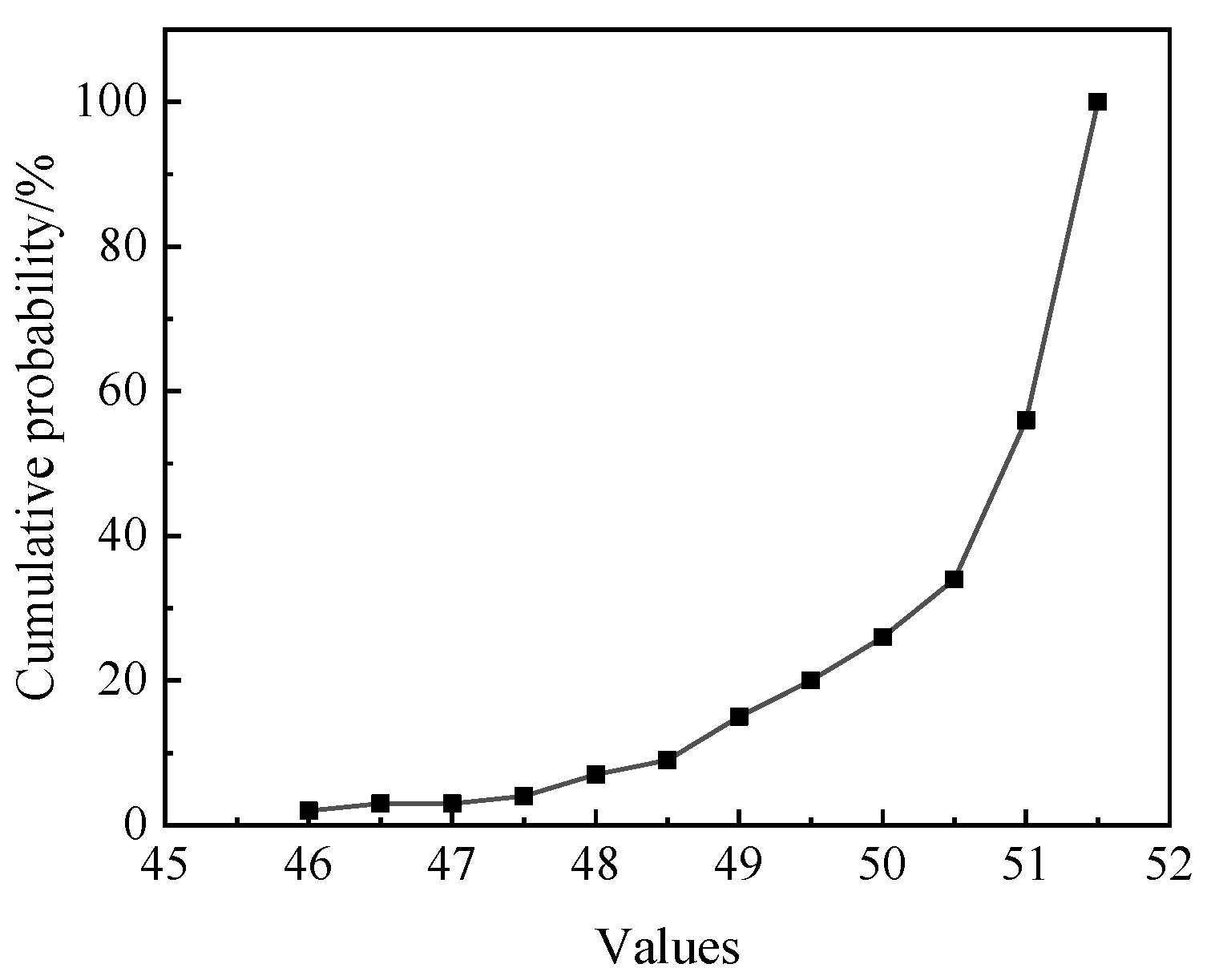
3. Estimation Method of Active Subspace Eigenvalues Based on Probability Box–EDF
- Step 1:
- Resample N samples into N groups, and divide each group into M segments from largest to smallest.
- Step 2:
- Use each segment’s maximum and minimum values as upper and lower bounds, respectively. If the distribution aligns with a certain distribution model, the upper and lower bounds of each group’s probability are obtained based on the distribution model; otherwise, the bounds are obtained based on the EDF probability distribution in Equation (28).
- Step 3:
- Average the maximum upper bounds and minimum lower bounds across N groups to obtain the fitted cumulative probability curve.
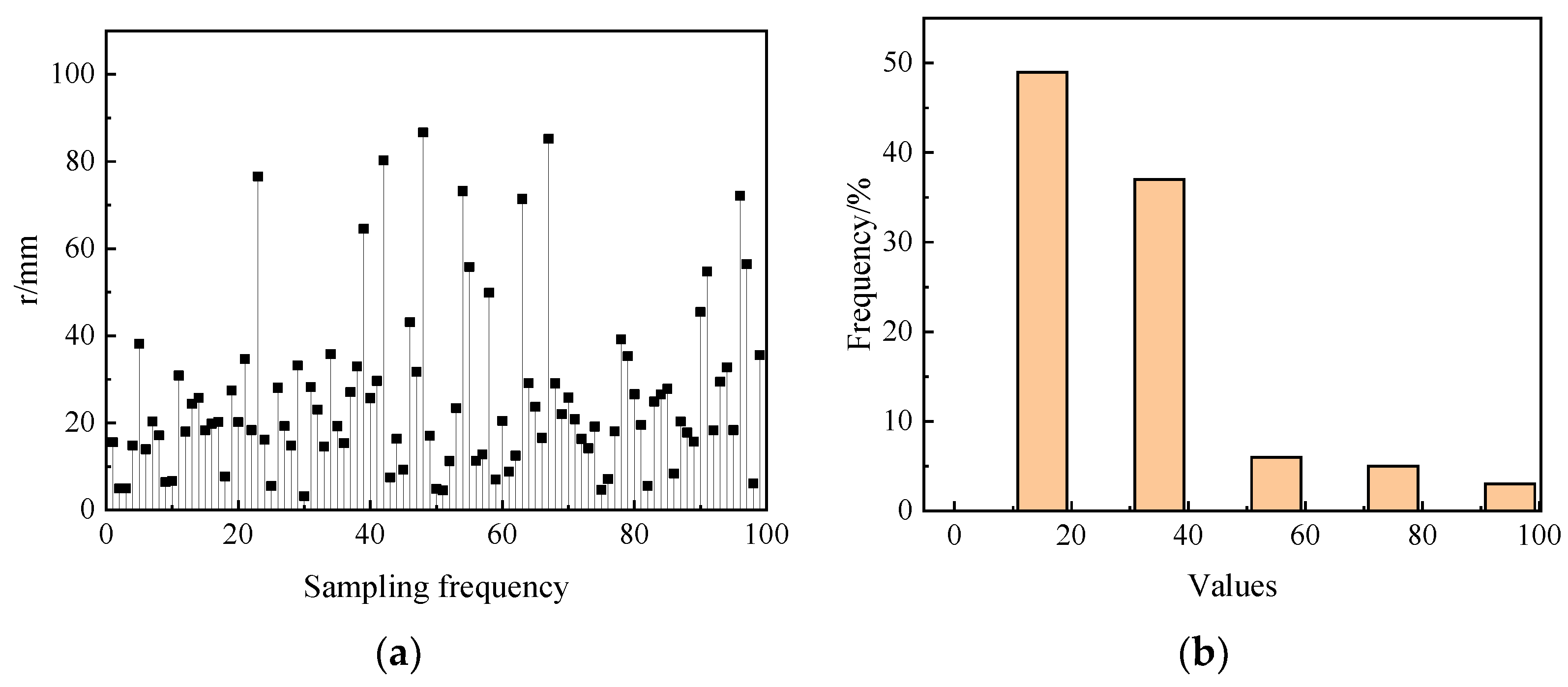
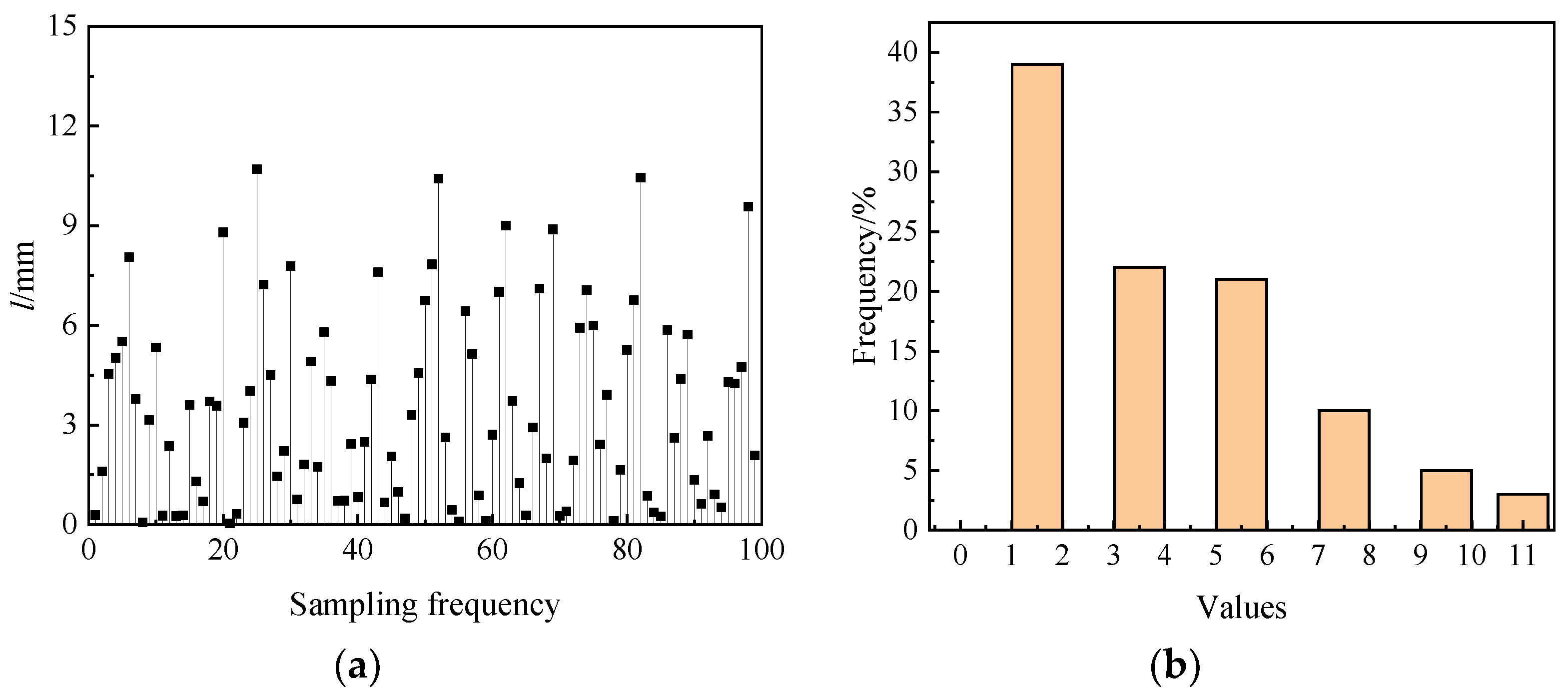
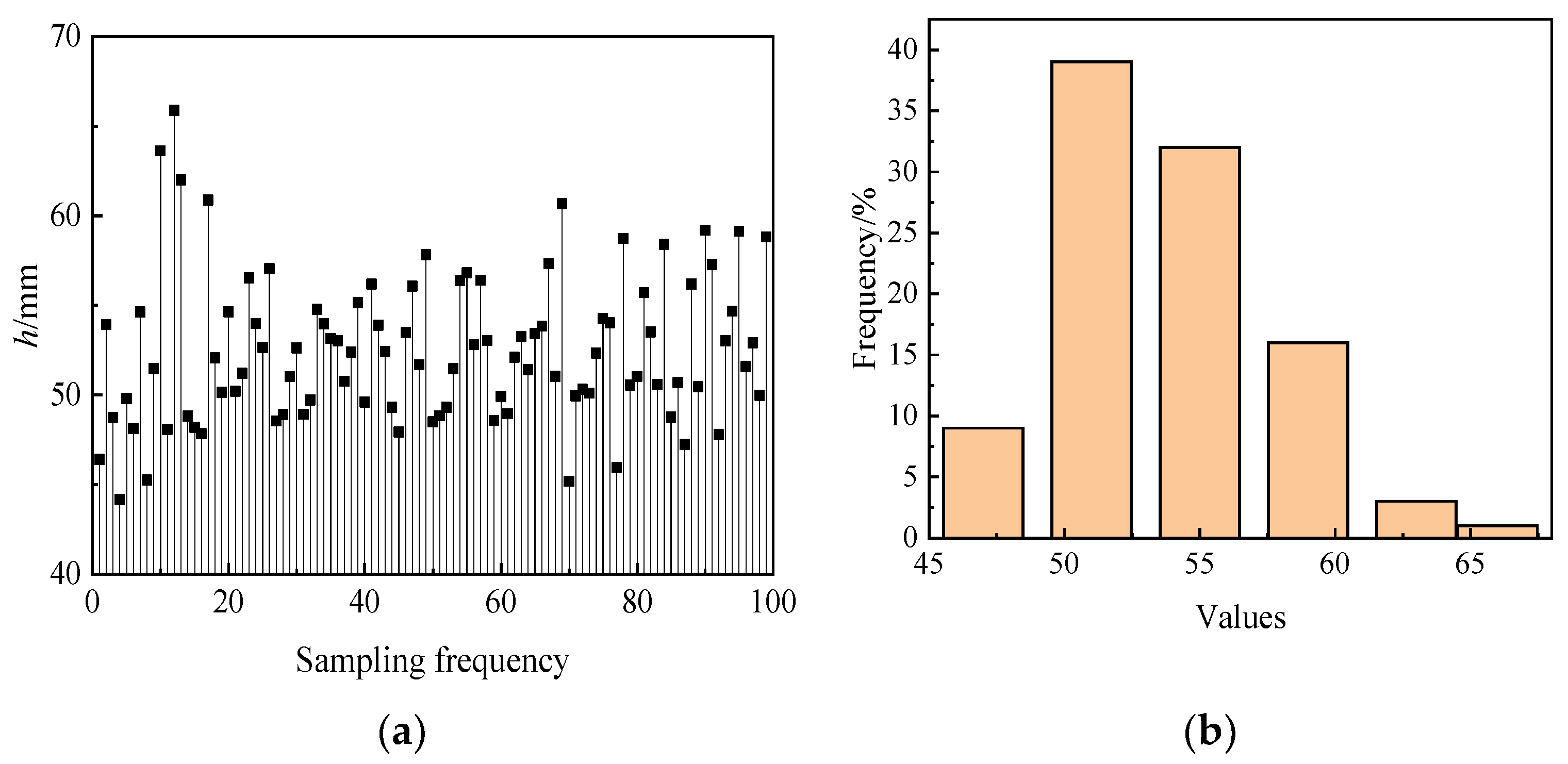
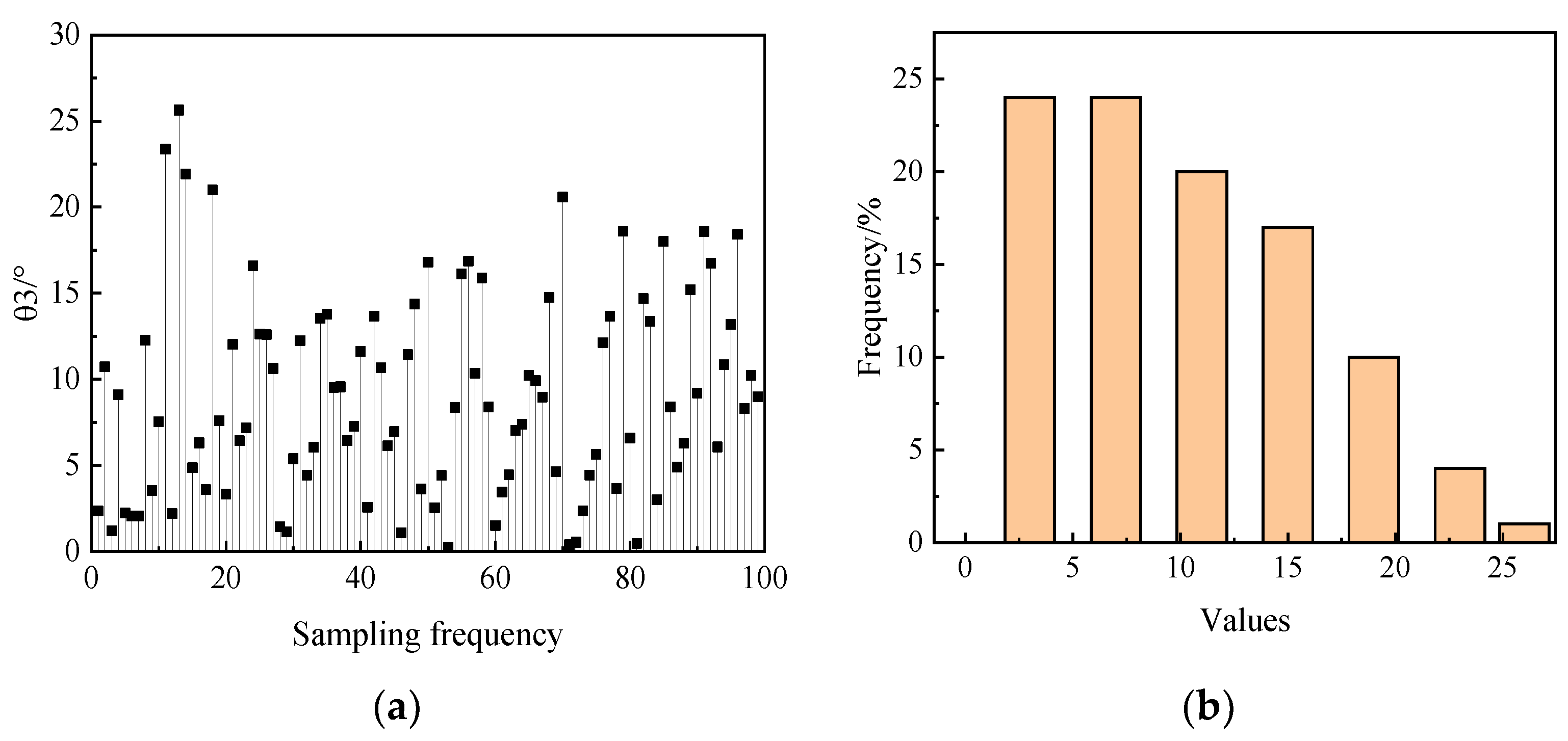
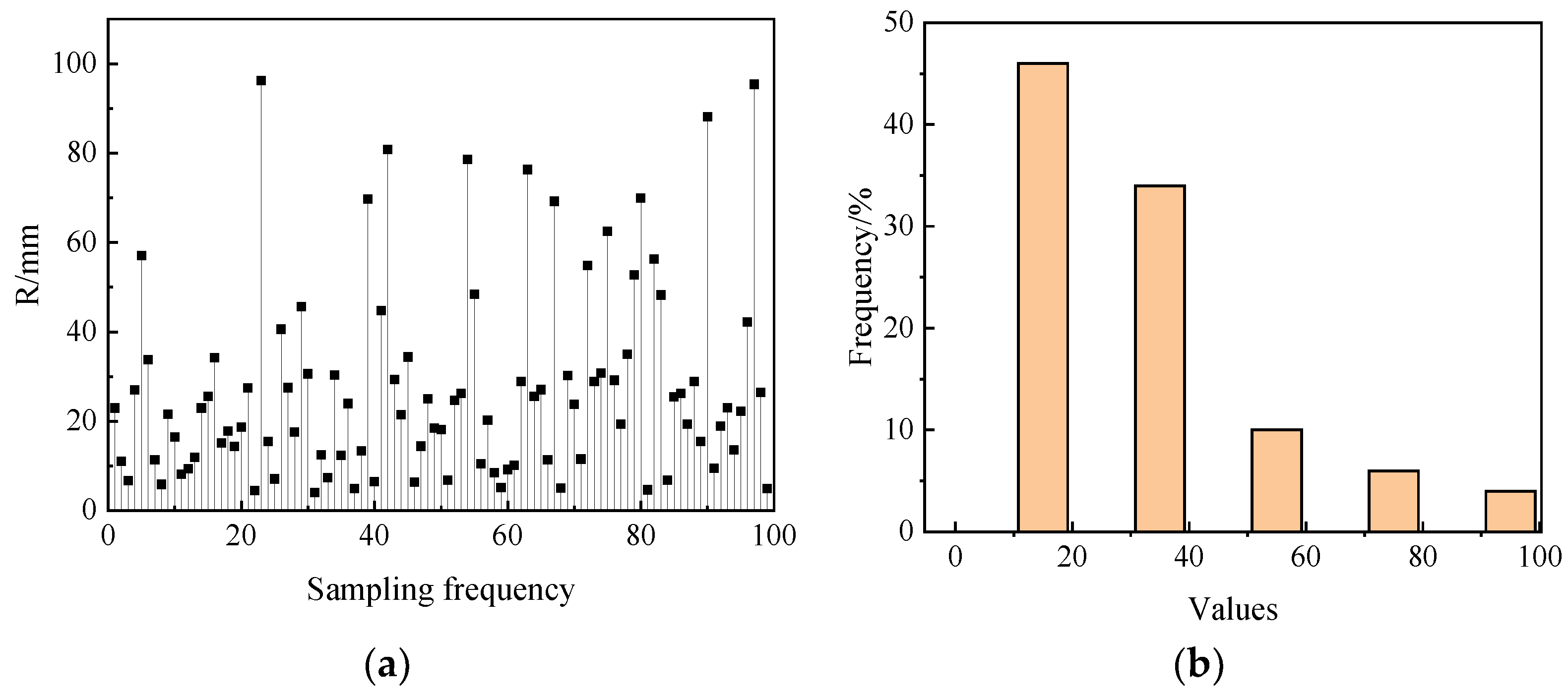
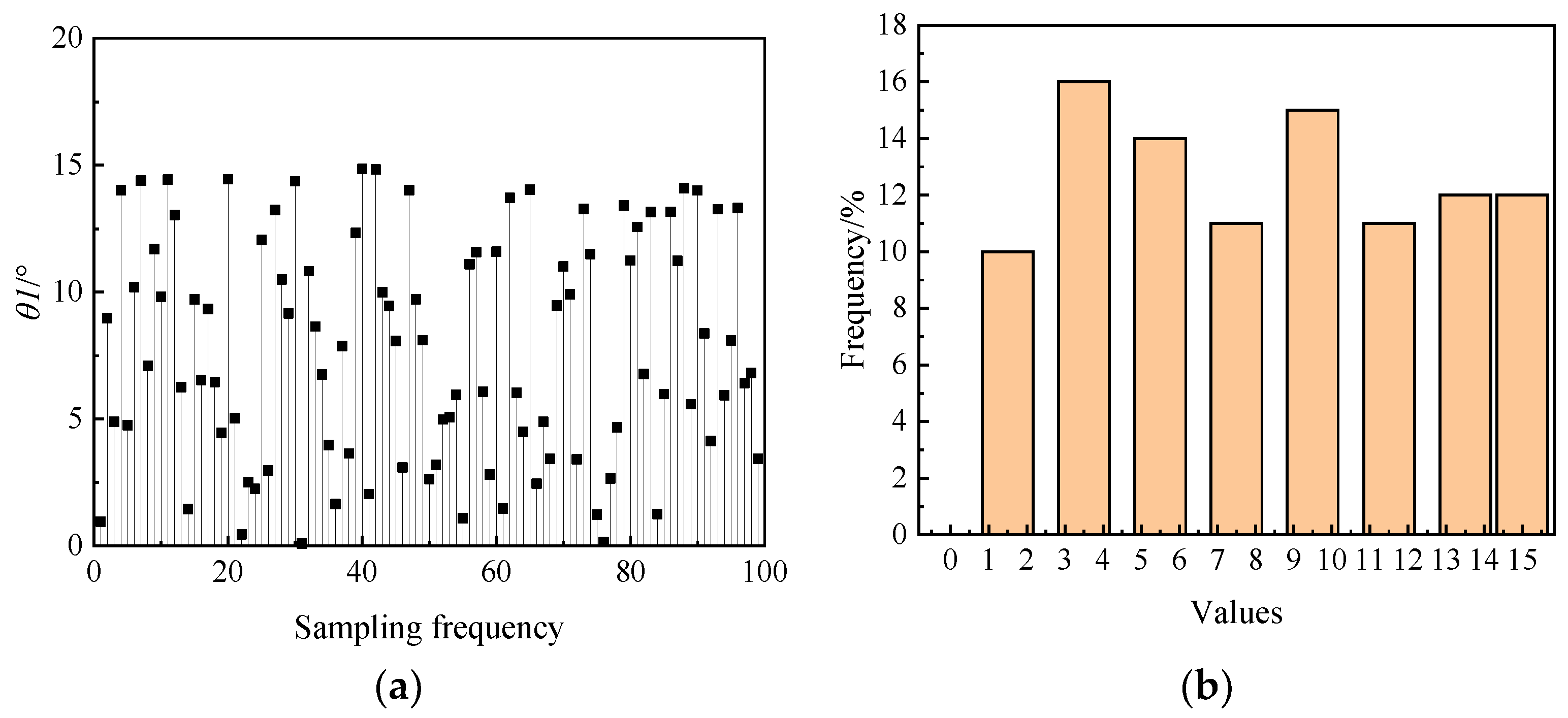
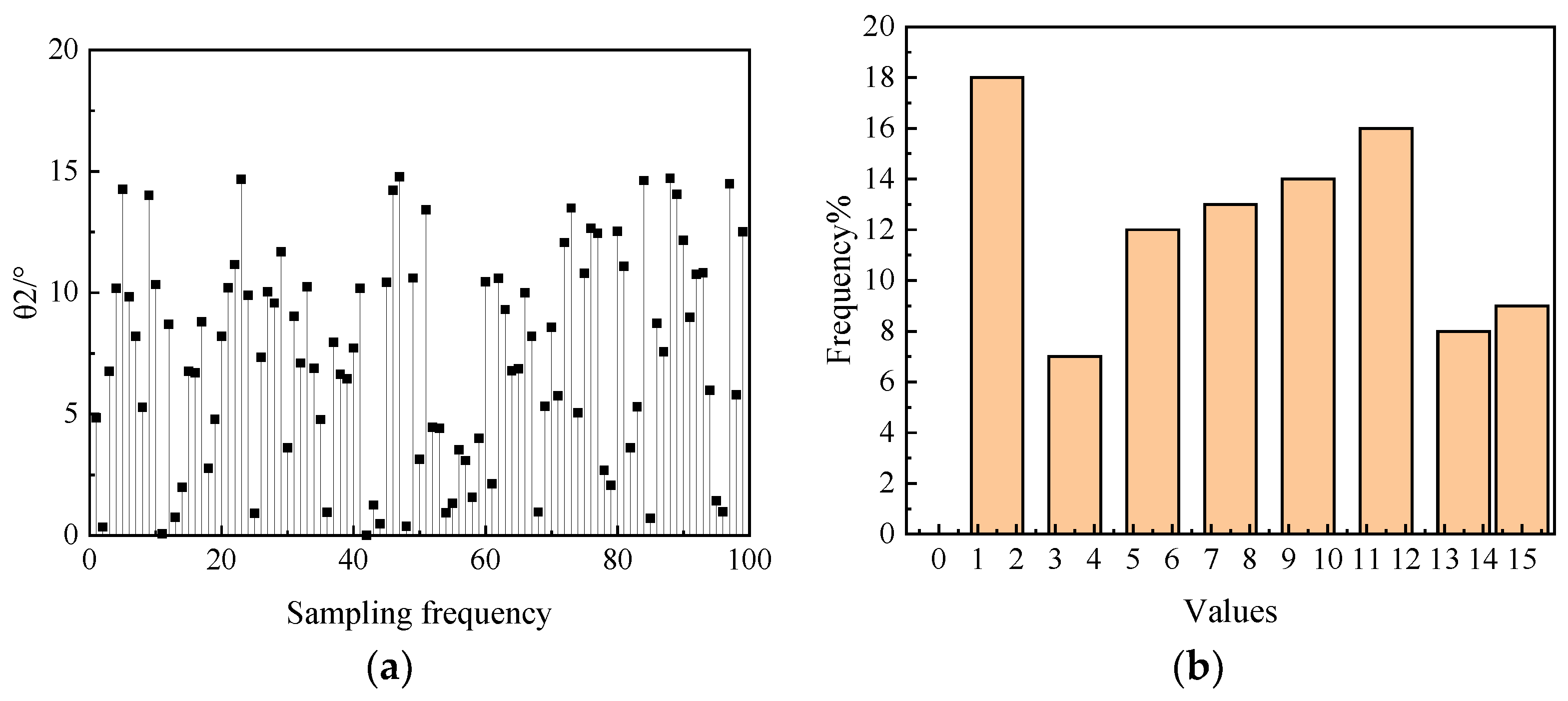
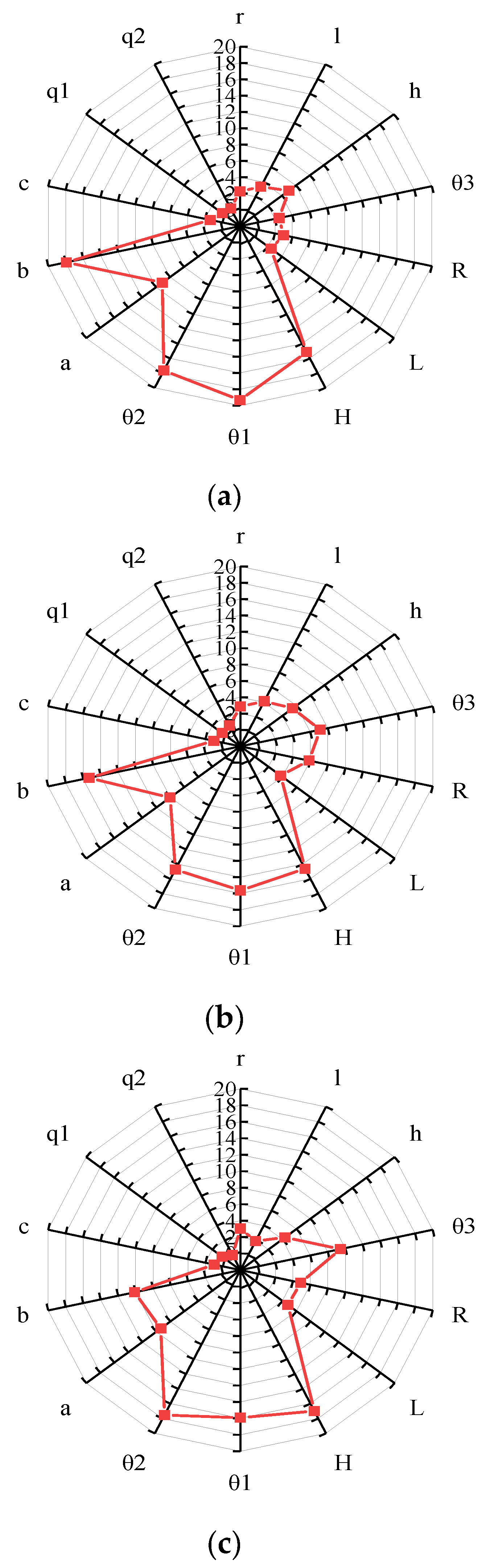
4. Dimensionality Reduction Analysis of Combustion Chamber Structure Parameters
5. Conclusions
- By analyzing the generation process of the active subspace and the composition of rotor structure parameters, based on active subspace, combined with the probability box and EDF, a dimension reduction method for rotary engine combustion chamber structure parameters is proposed, and the accuracy of the method is verified. The results show that the deviation between the calculated eigenvalues and the actual eigenvalues is only 1.2931%, and the estimation accuracy is high, which can be used for eigenvalue calculation and parameter dimension reduction of high-dimensional mixed uncertainty problems.
- Using the dimension reduction method proposed above, the dimension combination composed of 14 structural parameters is reduced to an important structural parameter composed of 8 structural parameters, including θ1, b, θ2, H, a, θ3, R, and h. The effects of the above eight structural parameters on the maximum cylinder pressure, the maximum cylinder temperature, and the indicated mean effective pressure are 89.5728%, 86.7924%, and 89.0677%, respectively.
- On this basis, three main structural parameters, with the influence of θ2 accounting for more than 45%, are obtained. And three adjustable structural parameters, including l, are obtained. The influence of the latter on the total proportion of each performance index is small, and the influence on the maximum cylinder pressure, the maximum cylinder temperature, and the indicated average effective pressure is 8.7753%, 13.7104%, and 11.5934%, respectively. Moreover, the change in parameters has a great influence on the compression ratio, process, and strength requirements. Therefore, the above three structural parameters can be used as adjustable structural parameters in the optimization of combustion chamber structure. When the main structural parameters are determined, the adjustable structural parameters are adjusted to make the combustion chamber meet many requirements, including compression ratio, process, and structure.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S. The Status of the Power Plants for UAVs in China. Aerosp. Power 2019, 2, 9–12. [Google Scholar]
- Dong, Y.; Huang, M.; Li, R. Overview of the Development of General Aviation Engines. J. Xi’an Aeronaut. Univ. 2017, 35, 8–13. [Google Scholar]
- Yin, Z.; Li, S.; Li, G. Current State and Development of the Unmanned Aerial Vehicle Power plant. Aeroengine 2007, 33, 10–15. [Google Scholar]
- Lu, D.; Zheng, J.; Hu, C.; Bian, S. Research on the development status of general aviation piston engine. Intern. Combust. Engine Parts 2019, 8, 64–66. [Google Scholar]
- Feng, G.; Zhou, M. Assessment of heavy fuel aircraft piston engine type. J. Tsinghua Univ. 2016, 56, 1114–1121. [Google Scholar]
- Jiao, H.; Liu, J.; Zou, R.; Wang, N. Combined influence of ignition chamber volume and spark plug channel diameter on the performance of small-scale natural gas Wankel rotary engine. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1775–1791. [Google Scholar] [CrossRef]
- Kong, X.; Liu, H. Research Progress of Key Technologies of Aviation Piston Engine for UAV. Small Intern. Combust. Engine Veh. Tech. 2021, 50, 79–87. [Google Scholar]
- Johar, T.; Hsieh, C.F. Design Challenges in Hydrogen-Fueled Rotary Engine-A Review. Energies 2023, 16, 607. [Google Scholar] [CrossRef]
- Wu, S. Research on Technical Characteristics and Application of Unmanned Aerial Vehicle Power Unit. Shanghai Energy Sav. 2022, 1536–1540. [Google Scholar]
- Wang, X.; Liu, J. GE Aerospace’s Roadmap for Next-Generation Aerospace Power Technology. Aerosp. Power 2023, 24–27. [Google Scholar]
- Li, H.; Sun, F. The Application Development and Key Technologies of Wankel engine. Small Intern. Combust. Engine Veh. 2023, 52, 68–74. [Google Scholar]
- Kotsiopoulos, P.; Yfantis, E.; Lois, E.; Hountalas, D. Diesel and JP-8 fuel performance on a Petter AVI diesel engine. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit (AIAA), Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef]
- Dutczak, J. Heavy fuel engines. Combust. Engines 2015, 163, 34–46. [Google Scholar] [CrossRef]
- Wu, H.; Wang, L.L.; Wu, Y.; Sun, B.; Zhao, Z.; Liu, F. Spray performance of air-assisted kerosene injection in a constant volume chamber under various in-cylinder GDI engine conditions. Appl. Therm. Eng. 2019, 150, 762–769. [Google Scholar] [CrossRef]
- Li, Z. Simulation Analys is on Cooperative Control of Ignition and Knock of Light-Weight, Spark Ignition, Heavy Oil Aeroengine. Master’s Thesis, Beijing Jiao Tong University, Beijing, China, 2016. [Google Scholar]
- Wang, Z. Experimental Study on Performance of 15kW Two-Stroke Ignited PFI Kerosene Piston Engine. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. [Google Scholar]
- Attard, W.P.; Blaxill, H.; Anderson, E.K.; Litke, P. Knock limit extension with a gasoline fueled pre -chamber jet igniter in a modern vehicle powertrain. SAE Int. J. Engines 2012, 5, 1201–1215. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhang, F.J.; Wang, E.H.; Yu, C.; Gao, H.; Liu, B.; Zhao, Z.; Zhao, C. Experimental study on knock suppression of spark -ignition engine fueled with kerosene via water injection. Appl. Energy 2019, 242, 248–259. [Google Scholar] [CrossRef]
- Chen, L.F.; Raza, M.; Xiao, J.H. Combustion analysis of an aviation compression ignition engine burning pentanol kerosene blends under different injection timings. Energy Fuel 2017, 31, 9429–9437. [Google Scholar] [CrossRef]
- Ning, L.; Duan, Q.M.; Wei, Y.H.; Zhang, X.; Yu, K.; Yang, B.; Zeng, K. Effects of injection timing and compression ratio on the combustion performance and emissions of a two -stroke DISI engine fuelled with aviation kerosene. Appl. Therm. Eng. 2019, 161, 114–124. [Google Scholar]
- Lu, Y.; Pan, J.F.; Fan, B.W.; Otchere, P.; Chen, W.; Cheng, B. Research on the application of aviation kerosene in a direct injection wankel engine -Part 1: Fundamental spray characteristics and optimized injection strategies. Energy Convers. Manag. 2019, 195, 519–532. [Google Scholar] [CrossRef]
- Yang, J.; Ji, C.; Wang, S.; Wang, D.; Ma, Z.; Zhang, B. Numerical investigation on the mixture formation and combustion processes of a gasoline wankel engine with direct injected hydrogen enrichment. Appl. Energy 2018, 224, 34–41. [Google Scholar] [CrossRef]
- Cao, B.W.; Liu, J.X. Design and optimization of orifice plates in the air-assisted kerosene injection system applied in the wankel rotary engine. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2023, 237, 2945–2953. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, X.; Feng, Z.; Zhu, R.; Su, X. Effects of Combustion Chamber Pit Shape on Combustion Process for Gasoline Wankel engine. Veh. Engine 2022, 40–46. [Google Scholar]
- Kuo, C.H.; Ma, H.L.; Chen, C.C. Chamber contour design and compression flow calculations of wankel engine. J. CCIT 2010, 39, 35–50. [Google Scholar]
- Tartakovsky, L.; Baibikov, V.; Gutman, M.; Veinblat, M.; Reif, J. Simulation of Wankel engine performance using commercial software for piston engines. In Proceedings of the 2012 Small Engine Technology Conference & Exhibition, Madison, WI, USA, 16–18 October 2012. SAE Technical Paper 2012–32-0098. [Google Scholar]
- Jeng, D.Z.; Hsieh, M.J.; Lee, C.C.; Han, Y. The numerical investigation on the performance of wankel engine with leakage, different fuels and recess sizes. In Proceedings of the JSAE/SAE 2013 Small Engine Technology Conference, Taipei, Taiwan, 8–10 October 2013. SAE Technical Paper 2013–32-9160. [Google Scholar]
- Wei, F.B.; Feng, P.J.; Xian, L.Y.; Rui, C.; Di, W.U. Effect of pocket location on combustion process in natural gas-fueled wankel engine. Appl. Mech. Mater. 2013, 316–317, 73–79. [Google Scholar] [CrossRef]
- Fan, B.W.; Pan, J.F.; Pan, Z.H.; Tang, A.K.; Zhu, Y.J.; Xue, H. Effects of pocket shape and ignition slot locations on the combustion processes of a wankel engine fueled with natural gas. Appl. Therm. Eng. 2015, 89, 11–27. [Google Scholar] [CrossRef]
- Ji, C.W.; Su, T.; Zhang, S.F.; Yu, M.; Cong, X. Effect of hydrogen addition on combustion and emissions performance of a gasoline wankel engine at part load and stoichiometric conditions. Energy Convers. Manag. 2016, 121, 272–280. [Google Scholar] [CrossRef]
- Amrouche, F.; Varnhagen, S.; Erickson, P.A.; Park, J. An experimental study of a hydrogen-enriched ethanol fueled Wankel wankel engine at ultra lean and full load conditions. Energy Convers. Manag. 2016, 123, 174–184. [Google Scholar] [CrossRef]
- Su, T.; Ji, C.; Wang, S.; Shi, L.; Cong, X. Effect of ignition timing on performance if a hydrogen-enriched n-butanol wankel engine at lean condition. Energy Convers. Manag. 2018, 161, 27–34. [Google Scholar] [CrossRef]
- Chen, W.; Pan, J.; Fan, B.; Liu, Y.; Peter, O. Effect of injection strategy on fuel-air mixing and combustion process in a direct injection diesel wankel engine (DI-DRE). Energy Convers. Manag. 2017, 154, 68–80. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, P.; Ji, C. Understanding the role of turbulence-induced blade configuration in improving combustion process for hydrogen-enriched wankel engine. Fuel 2022, 319, 123807. [Google Scholar] [CrossRef]
- Bienner, A.; Gloerfelt, X.; Cinnella, P. Leading-Edge Effects on Freestream Turbulence Induced Transition of an Organic Vapor. Flow Turbul. Combust. 2024, 224, 345–373. [Google Scholar] [CrossRef]
- Li, M.; Hamel, J.; Azarm, S. Optimal uncertainty reduction for multi-disciplinary multi-output systems using sensitivity analysis. Struct. Multidiscip. Optim. 2010, 40, 77–96. [Google Scholar] [CrossRef]
- Davey, K.; Sadeghi, H.; Darvizeh, R. The theory of scaling. Contin. Mech. Thermodyn. 2023, 35, 471–496. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis; Wiley Online Library: Hoboken, NJ, USA, 2002. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wang, J. Geometric Structure of High-Dimensional Data and Dimensionality Reduction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Donoho, D.L.; Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proc. Natl. Acad. Sci. USA 2003, 100, 5591–5596. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Constantine, P.G. Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies; SIAM: Philadelphia, PA, USA, 2015. [Google Scholar]
- Scott, D.W. The Curse of Dimensionality and Dimension Reduction. In Multivariate Density Estimation; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wang, B.X.; Huang, X.Z.; Chang, M.X. Regional reliability sensitivity analysis based on dimension reduction technique. Probabilistic Eng. Mech. 2023, 74, 1394–1419. [Google Scholar] [CrossRef]
- Russi, T.M. Uncertainty Quantification with Experimental Data and Complex System Models. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2010. [Google Scholar]
- Stewart, G.W. Error and perturbation bounds for subspaces associated with certain eigenvalue problems. SIAM Rev. 1973, 15, 727–764. [Google Scholar] [CrossRef]
- Davey, K.; Abd Malek, M.I.; Ali, Z.; Sadeghi, H.; Darvizeh, R. The theory of scaled electromechanics. Int. J. Eng. Sci. 2024, 203, 1041–1068. [Google Scholar] [CrossRef]
- Fujimori, K.; Goto, Y.; Liu, Y.; Taniguchi, M. Sparse principal component analysis for high-dimensional stationary time series. Scand. J. Stat. 2023, 50, 1953–1983. [Google Scholar] [CrossRef]
- Wang, M.; Lu, Y.; Pan, W. An improved pattern-based prediction model for a class of industrial processes. Trans. Inst. Meas. Control. 2022, 44, 1410–1423. [Google Scholar] [CrossRef]
- Chib, S.; Greenberg, E. Understanding the metropolis-hastings algorithm. Am. Stat. 1995, 49, 327–335. [Google Scholar] [CrossRef]
- Ray, T. Golinski’s speed reducer problem revisited. AIAA J. 2003, 41, 556–558. [Google Scholar] [CrossRef]
- Allen, M.; Maute, K. Reliability-based design optimization of aeroelastic structures. Struct. And. Multidiscip. Optim. 2004, 27, 228–242. [Google Scholar] [CrossRef]
- Lillacci, G.; Khammash, M. A distribution-matching method for parameter estimation and model selection in computational biology. Int. J. Robust Nonlinear Control 2012, 22, 1065–1081. [Google Scholar] [CrossRef]
- Seshadri, P.; Constantine, P.; Iaccarino, G.; Parks, G. Aggressive design: A density-matching approach for optimization under uncertainty. arXiv 2014, arXiv:1409.7089. [Google Scholar]
- Ferson, S.; Kreinovich, V.; Ginzburg, L.; Myers, D.S.; Sentz, K. Constructing Probability Boxes and Dempster-Shafer Structures; SAND2003-4015; Sandia National Laboratories: Albuquerque, NM, USA, 2003. [Google Scholar]
- Yang, X. Research on Highly Efficient and Precise Methods for Reliability Analysis with Epistemic Uncertainties. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2016. [Google Scholar]
- Huang, X.; Wang, Q.; Ding, J. Faculty of Information Engineering and Automation: Index Uncertainty Modeling in Grid Planning Based on Probability Box Theory. Inf. Control 2016, 45, 272–277. [Google Scholar]
- Ferson, S.; Tucker, W.T. Sensitivity in Risk Analyses with Uncertain Numbers; Sandia National Laboratories: Albuquerque, NM, USA, 2006; pp. 156–159. [Google Scholar]
- Crespo, L.G.; Kenny, S.P.; Giesy, D.P. Reliability analysis of polynomial systems subject to p-box uncertainties. Mech. Syst. Signal Process. 2013, 37, 121–136. [Google Scholar] [CrossRef]
- Beer, M.; Ferson, S.; Kreinovich, V. Imprecise probabilities in engineering analyses. Mech. Syst. Signal Process. 2013, 37, 4–29. [Google Scholar] [CrossRef]
- Jiao, H.; Ye, X.; Zou, R.; Wang, N.; Liu, J. Comparative study on ignition and combustion between conventional spark-ignition method and near-wall surface ignition method for small-scale Wankel rotary engine. Energy 2022, 255, 1049–1072. [Google Scholar] [CrossRef]
- Zou, R.; Liu, J.; Jiao, H.; Zhao, J.; Wang, N. Combined effect of intake angle and chamber structure on flow field and combustion process in a small-scaled rotary engine. Appl. Therm. Eng. 2022, 203, 1497–1521. [Google Scholar] [CrossRef]
- Hege, J. The Wankel Wankel Engine: A History; McFarland and Company Inc.: Jefferson, NC, USA, 2006. [Google Scholar]
- Wladyslaw, M. Modelling and Simulation of Working Processes in Wankel Engine with Direct Hydrogen Injection System. Combust. Engines 2015, 161, 42–52. [Google Scholar]
- Peden, M. Study of Direct Injection Limitations on a Wankel Engine. Master’s Thesis, University of Bath, Bath, UK, 2017. [Google Scholar]
- Wendeker, M.; Grabowski, L.; Pietrykowski, K.; Margryta, P. Phenomenological Model of a Wankel Engine; Lublin University of Technology: Lublin, Poland, 2012. [Google Scholar]
- Tomlinson, A. Modelling of Wankel Engine Performance in Commercial Piston Engine Software. Master’s Thesis, University of Bath, Bath, UK, 2016. [Google Scholar]
- Georgios, Z. Mathematical and Numerical Modelling of Flow and Combustion Processes in a Spark Ignition Engine. Master’s Thesis, Department of Applied Mathematics, University of Wisconsin, Madison, WI, USA, 2005. [Google Scholar]










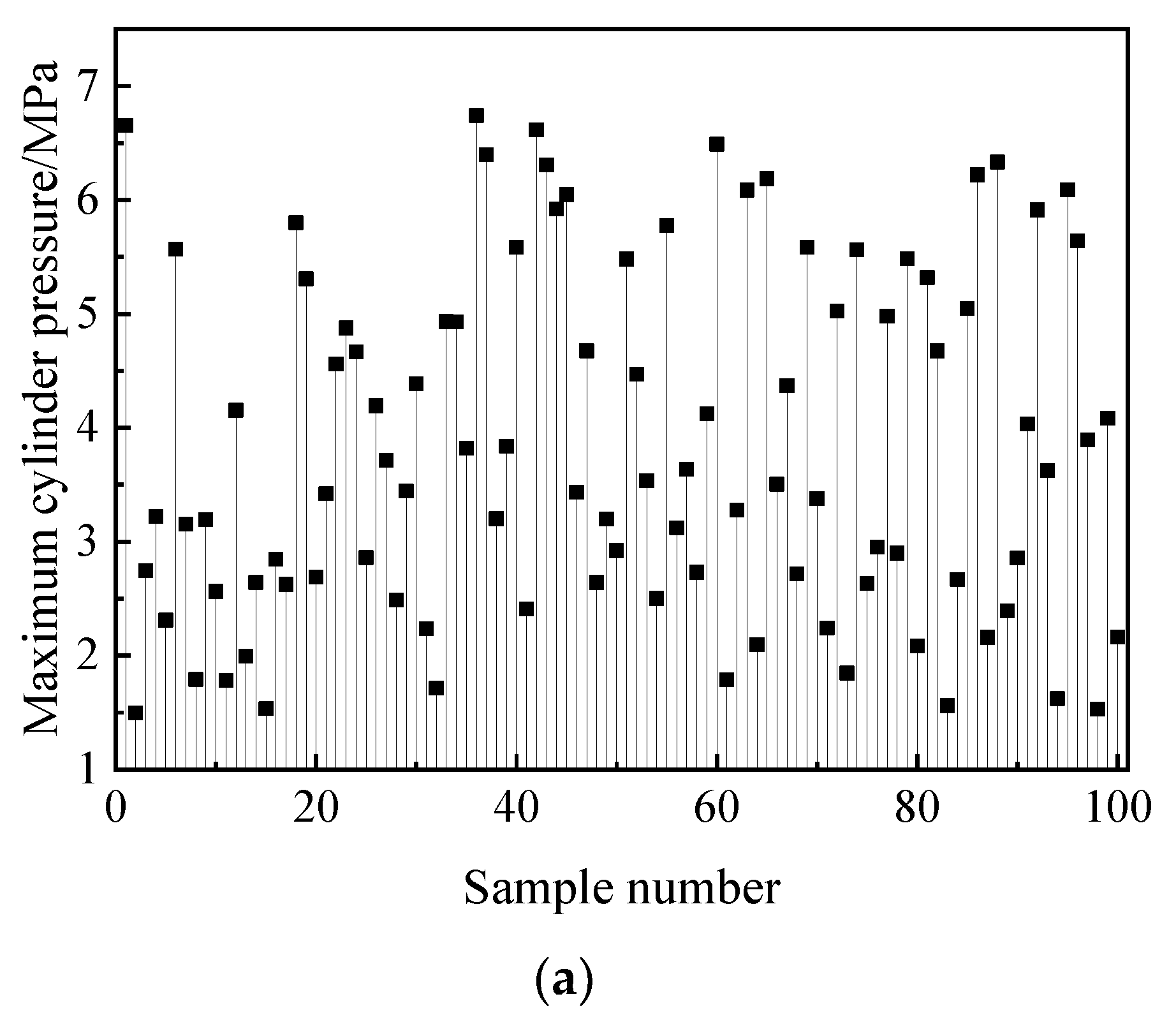
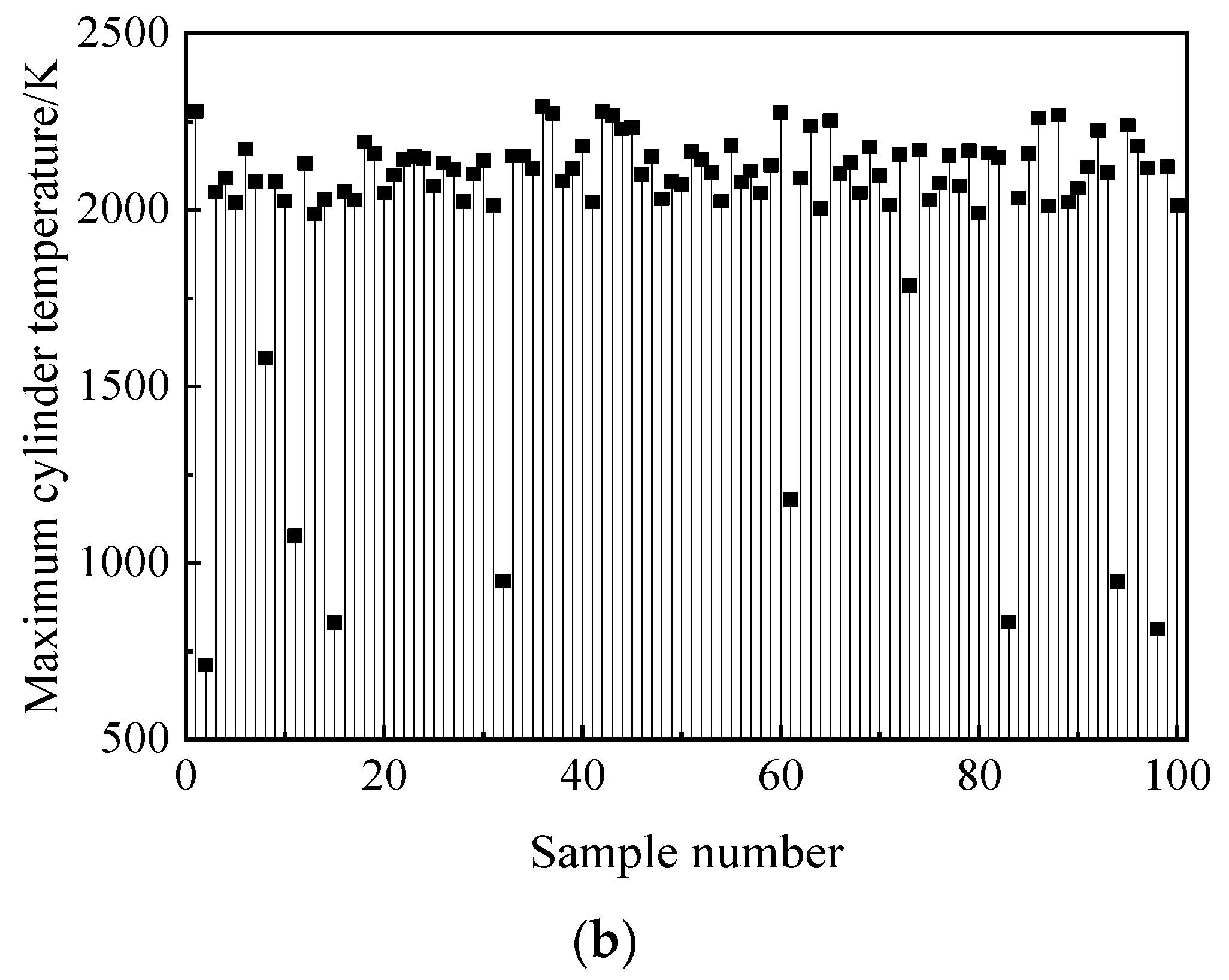
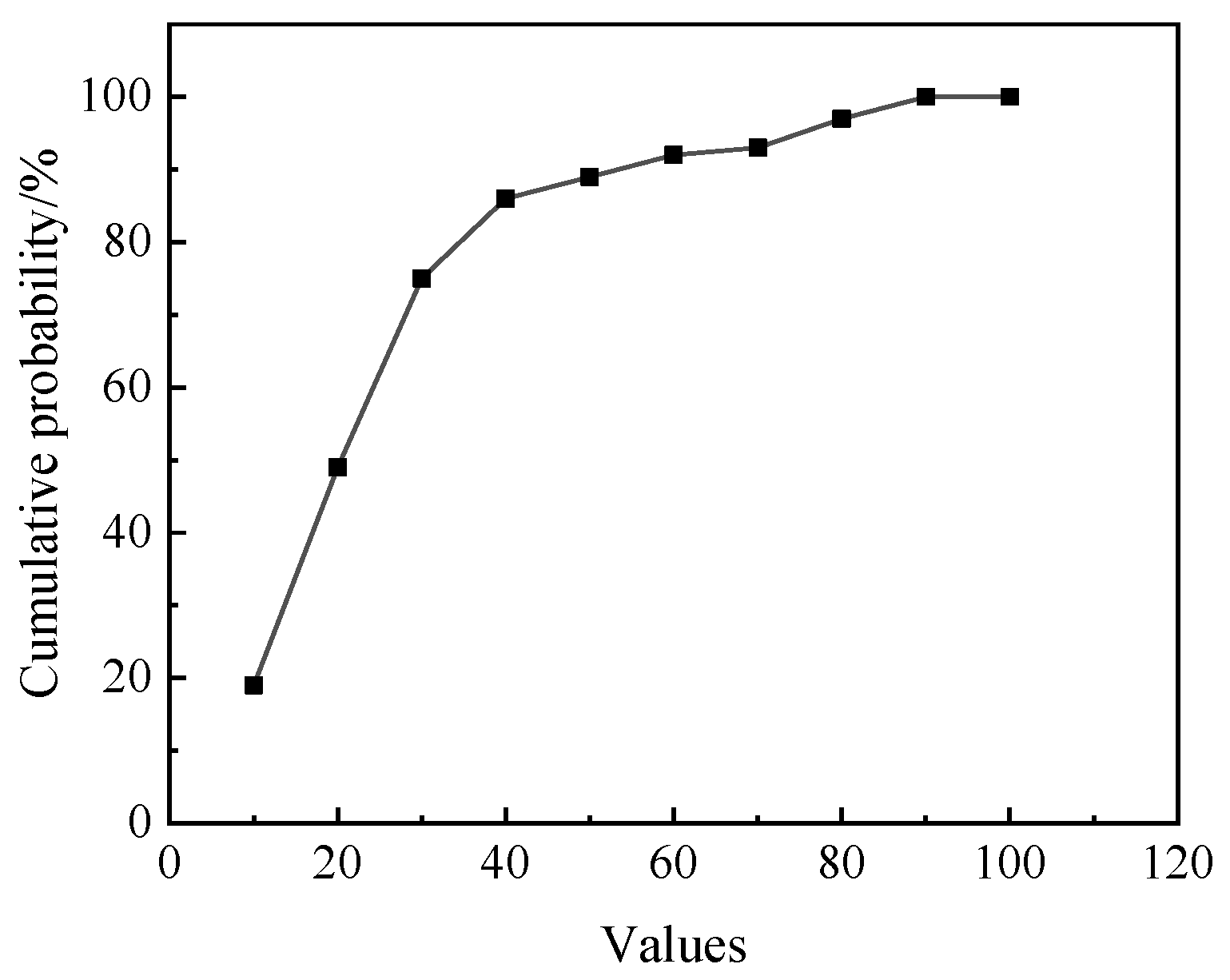
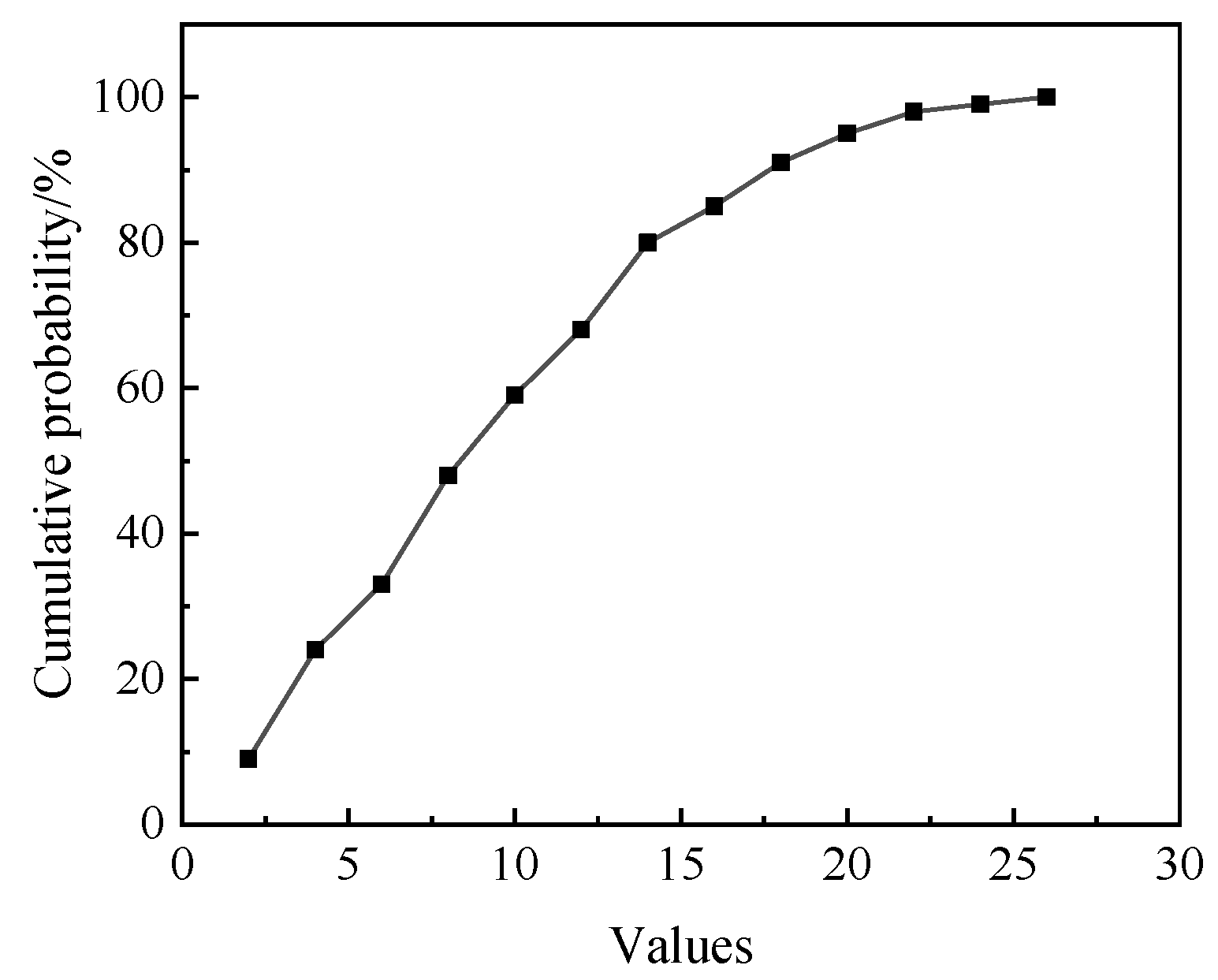

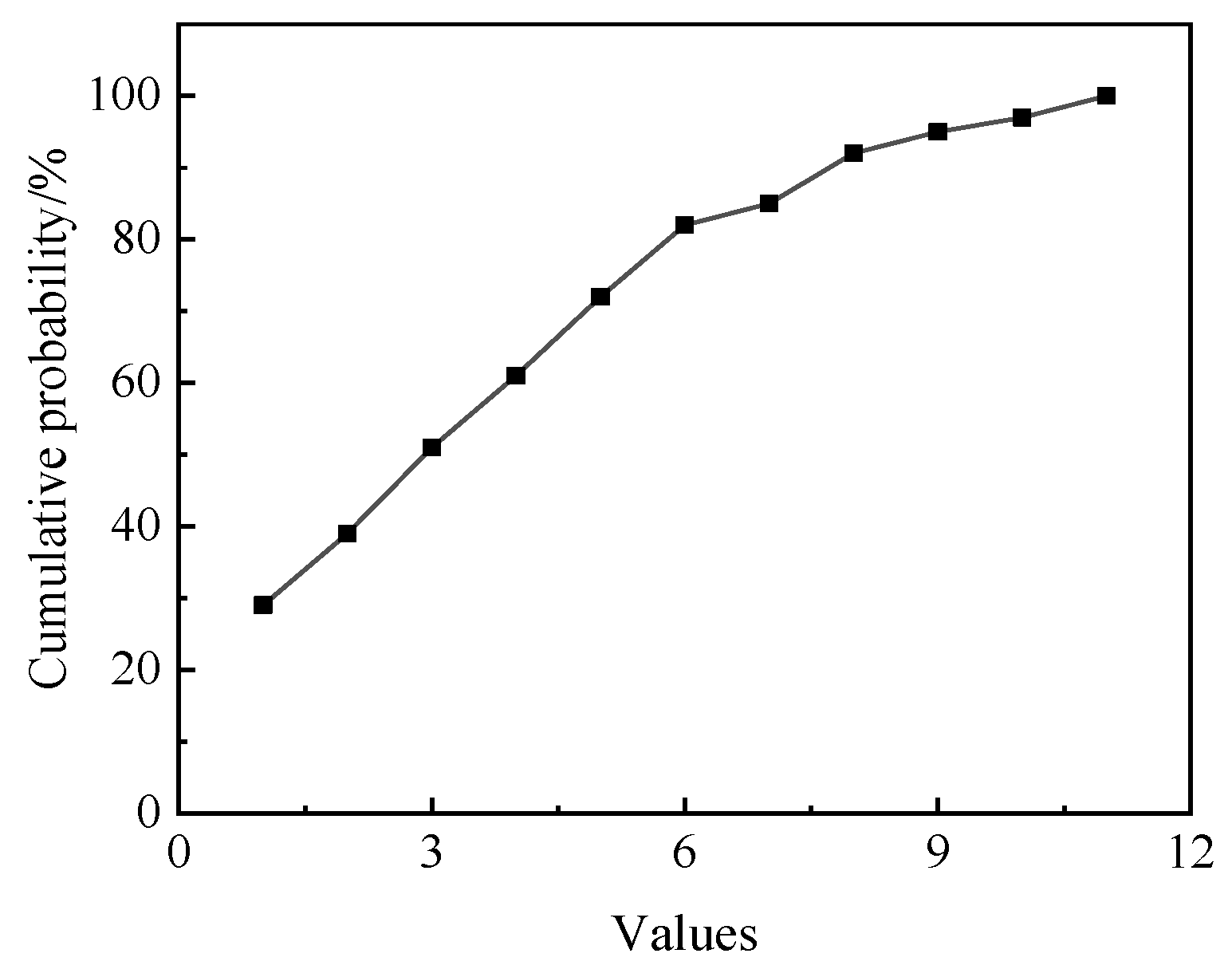

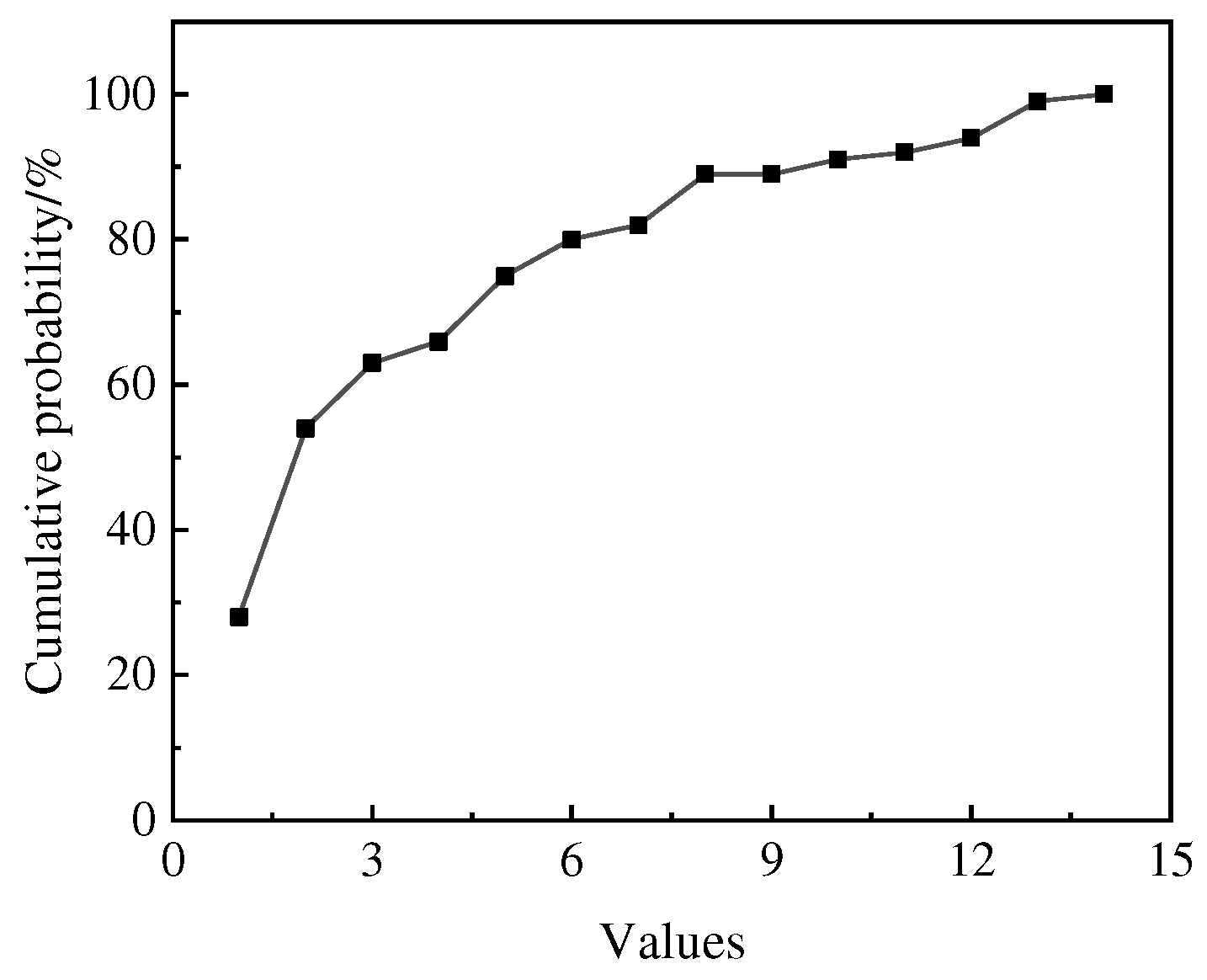
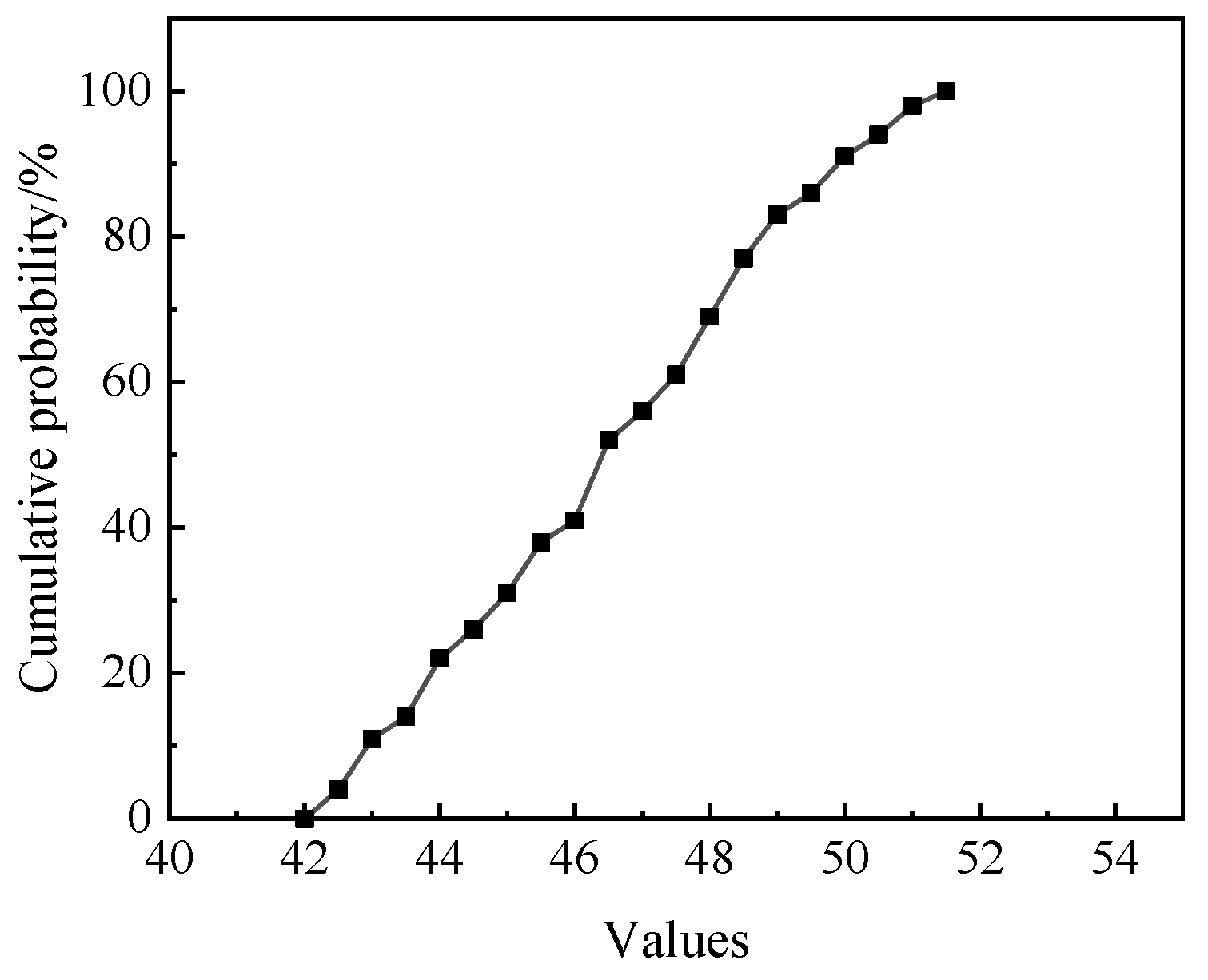
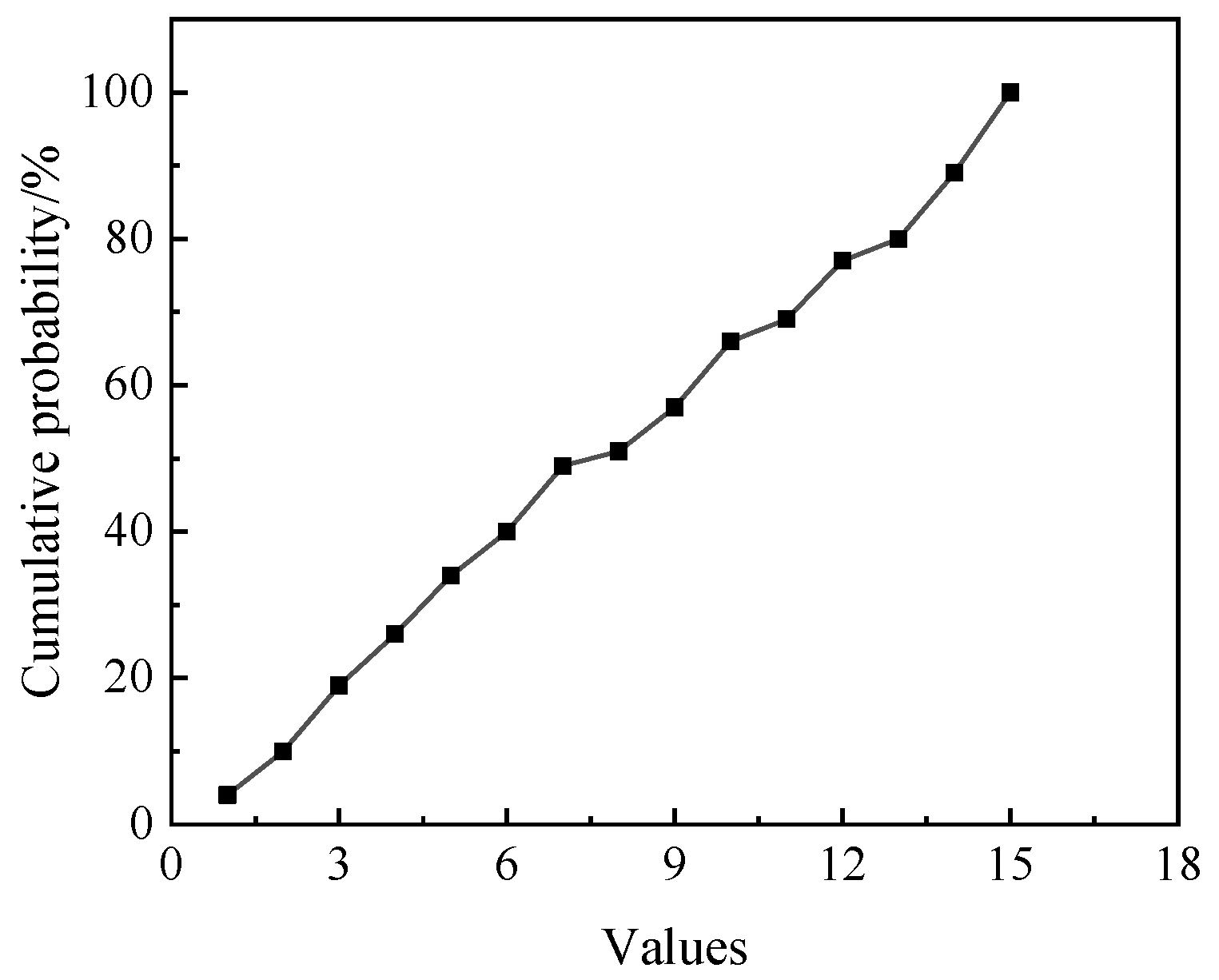
| Parameter | Value |
|---|---|
| Creation radius (mm) | 60 |
| Eccentricity (mm) | 10 |
| Rotor width (mm) | 42 |
| Translational distance (mm) | 1.45 |
| Speed (r/min) | 8000 |
| Single cylinder volume (cc) | 133 |
| Compression ratio | 10 |
| Ignition advance angle | 30° BTDC |
| Ignition source | Single spark plug |
| Fuel type | Gasoline |
| Jet strategy | Pre-mixed intake duct |
| Air–fuel ratio | 1 |
| Ignition diameter (mm) | 8 |
| Ignition energy (J) | 0.08 |
| Engine power (kw) | 12.3 |
| Torque (N.m) | 15.66 |
| Oil consumption (g/kw·h) | 402.3 |
| Variable | Structure Name |
|---|---|
| r | Combustion chamber leading arc radius |
| l | Length of the leading bottom edge of the combustion chamber |
| h | The distance from the bottom of the combustion chamber’s leading section to the rotor’s center of gravity at the x-z plane |
| θ3 | The angle between the combustion chamber’s leading bottom edge and the y-z plane |
| R | Trailing arc radius in the combustion chamber |
| L | Trailing bottom edge length of the combustion chamber |
| H | The distance from the bottom of the trailing section of the combustion chamber to the rotor’s center of gravity at the x-z plane |
| θ1 | The angle between the middle bottom edge of the combustion chamber and the y-z plane |
| θ2 | The angle between the trailing bottom edge of the combustion chamber and the y-z plane |
| a | The vertical distance between the spoiler plate and the rotor x-z section |
| b | The distance from the spoiler’s top center to the combustion chamber’s bottom edge |
| c | The spoiler plate’s width |
| q1 | The excessive arc radius from the leading part to the middle of the combustion chamber |
| q2 | The excessive arc radius from the middle to the trailing part of the combustion chamber |
| Constraint Name | Variable Name | Value |
|---|---|---|
| The minimum distance from the bottom of the combustion chamber to the center of gravity of the rotor | 42 mm | |
| Maximum width of the combustion chamber | 40 mm | |
| The projection distance between the two ends of the rotor combustion chamber and the rotor tip on the y-z section | 10 mm | |
| Maximum width of the spoiler plate | 3 mm | |
| The maximum radius of the excessive arc | 2 mm |
| Eigenvalue Calculation Method | Proportion | |||
|---|---|---|---|---|
| Formula calculation | 12.3058 | 62.1078% | 7.5078 | 37.8922% |
| Probability box–EDF estimation | 12.8423 | 60.8148% | 8.2748 | 39.1852% |
| Boundary | Type | Temperature (K) | Pressure (MPa) |
|---|---|---|---|
| Inlet | Inflow | 300 | 0.101325 |
| Intake port | Fixed wall | 300 | / |
| Outlet | Outflow | 570 | 0.101325 |
| Exhaust port | Fixed wall | 550 | / |
| Rotor | Moving wall | 400 | / |
| Rotor flank 1 | Fixed wall | 624 | 0.117210 |
| Rotor flank 2 | Fixed wall | 600 | / |
| Structural Parameter | Performance Index | ||
|---|---|---|---|
| Maximum Cylinder Pressure | Maximum Cylinder Temperature | Indicated Average Effective Pressure | |
| r | 2.1339 | 3.3178 | 2.5761 |
| l | 3.1528 | 4.7906 | 1.6218 |
| h | 4.6812 | 6.3345 | 3.7114 |
| θ3 | 2.3218 | 8.2688 | 8.0427 |
| R | 2.8055 | 6.7792 | 4.1701 |
| L | 2.2952 | 4.3389 | 4.0759 |
| H | 14.2391 | 16.9644 | 14.4644 |
| θ1 | 18.1673 | 18.1360 | 13.5508 |
| θ2 | 16.6057 | 17.0970 | 14.9315 |
| a | 8.5642 | 9.3406 | 7.9712 |
| b | 16.8614 | 17.7883 | 8.6039 |
| c | 1.3363 | 1.2064 | 0.8551 |
| q1 | 0.5012 | 0.7131 | 0.5182 |
| q2 | 0.3877 | 0.9580 | 0.0224 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Shi, Y.; Tian, Y.; Liu, W.; Zou, R. Research on Dimension Reduction Method for Combustion Chamber Structure Parameters of Wankel Engine Based on Active Subspace. Processes 2024, 12, 2238. https://doi.org/10.3390/pr12102238
Li L, Shi Y, Tian Y, Liu W, Zou R. Research on Dimension Reduction Method for Combustion Chamber Structure Parameters of Wankel Engine Based on Active Subspace. Processes. 2024; 12(10):2238. https://doi.org/10.3390/pr12102238
Chicago/Turabian StyleLi, Liangyu, Yaoyao Shi, Ye Tian, Wenyan Liu, and Run Zou. 2024. "Research on Dimension Reduction Method for Combustion Chamber Structure Parameters of Wankel Engine Based on Active Subspace" Processes 12, no. 10: 2238. https://doi.org/10.3390/pr12102238
APA StyleLi, L., Shi, Y., Tian, Y., Liu, W., & Zou, R. (2024). Research on Dimension Reduction Method for Combustion Chamber Structure Parameters of Wankel Engine Based on Active Subspace. Processes, 12(10), 2238. https://doi.org/10.3390/pr12102238







