Simulation of PSDF (Photovoltaic, Storage, Direct Current and Flexibility) Energy System for Rural Buildings
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Work
2. Methodology
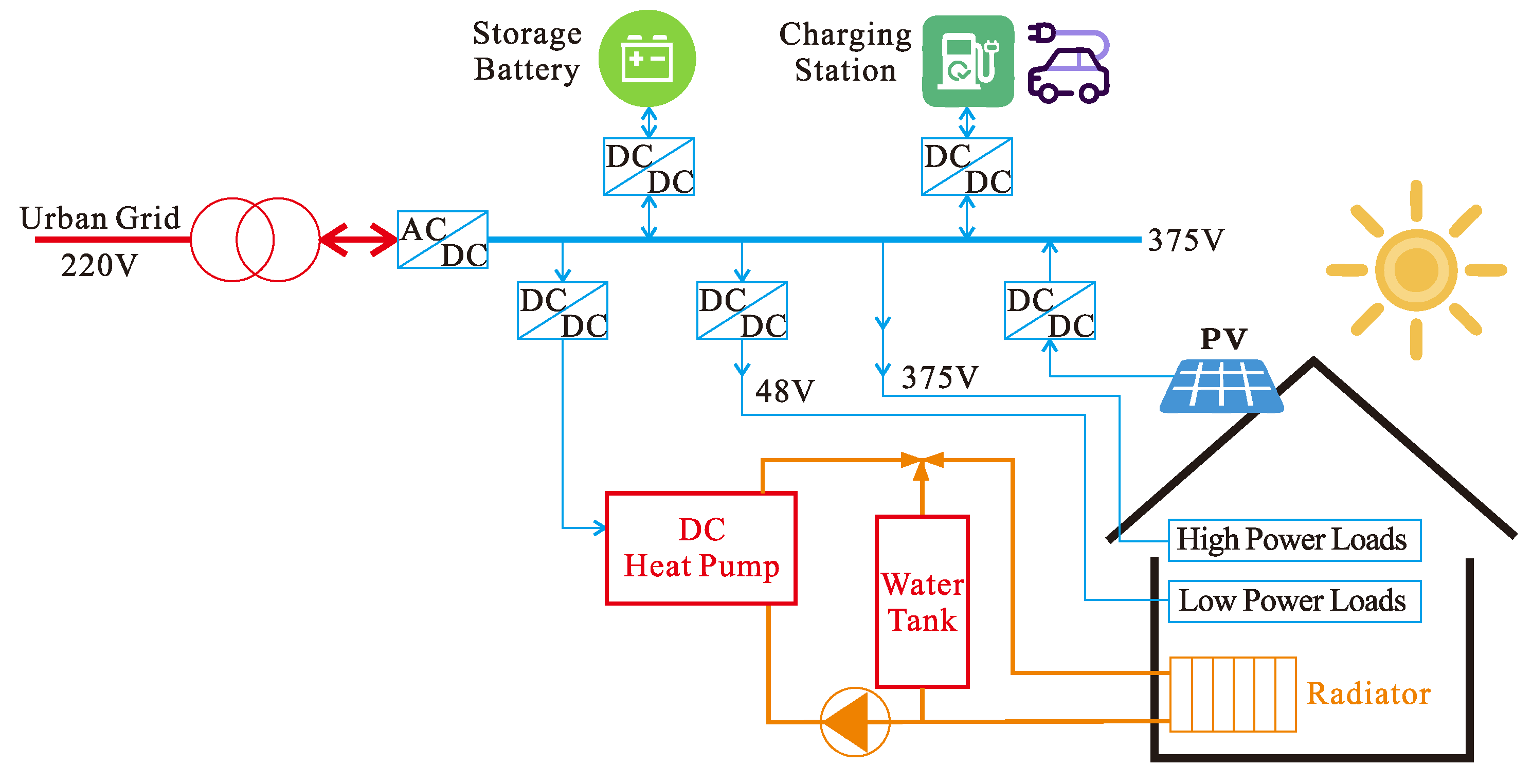
2.1. System Topological Structure
2.2. System Model
2.2.1. Architectural Overview
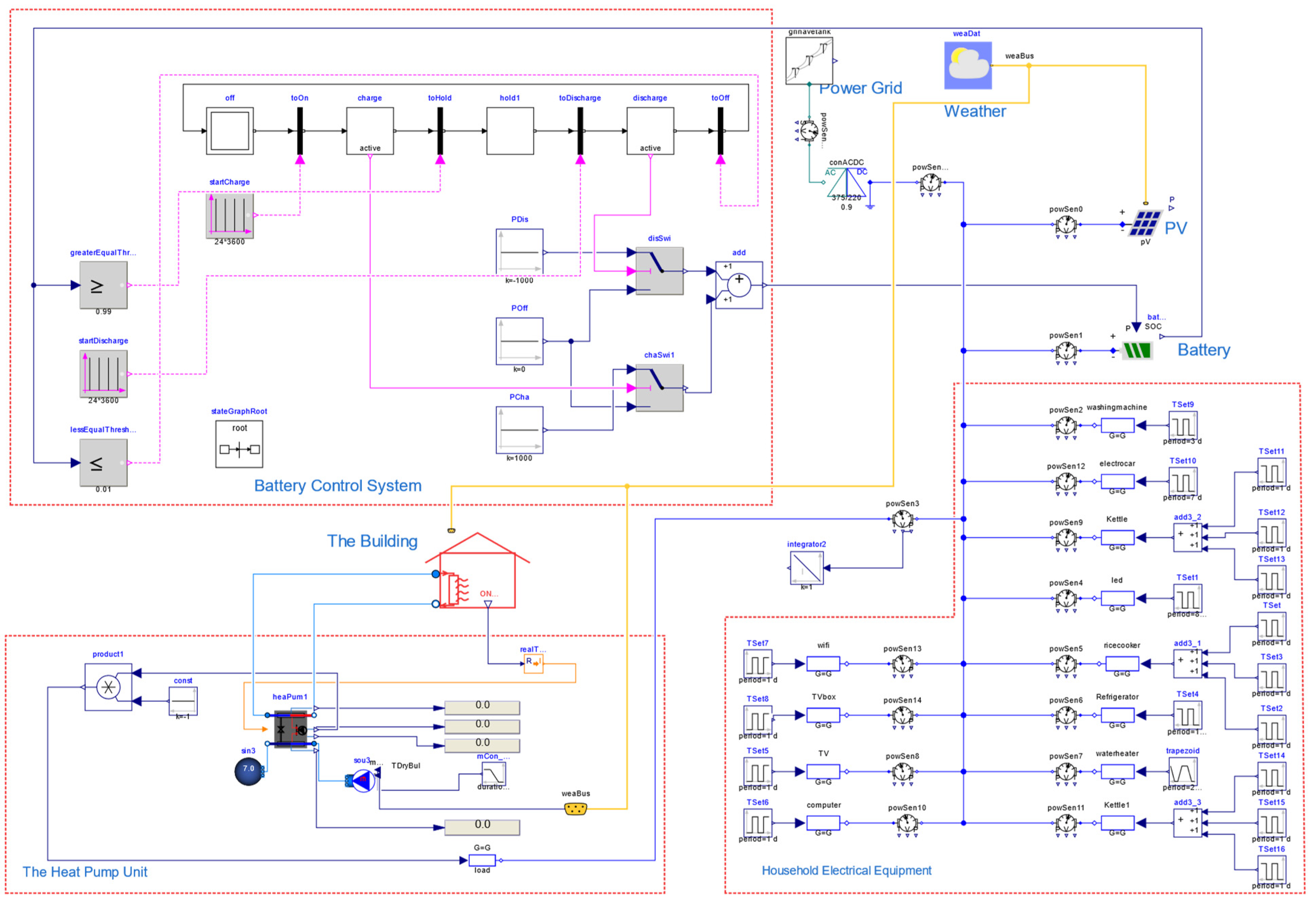
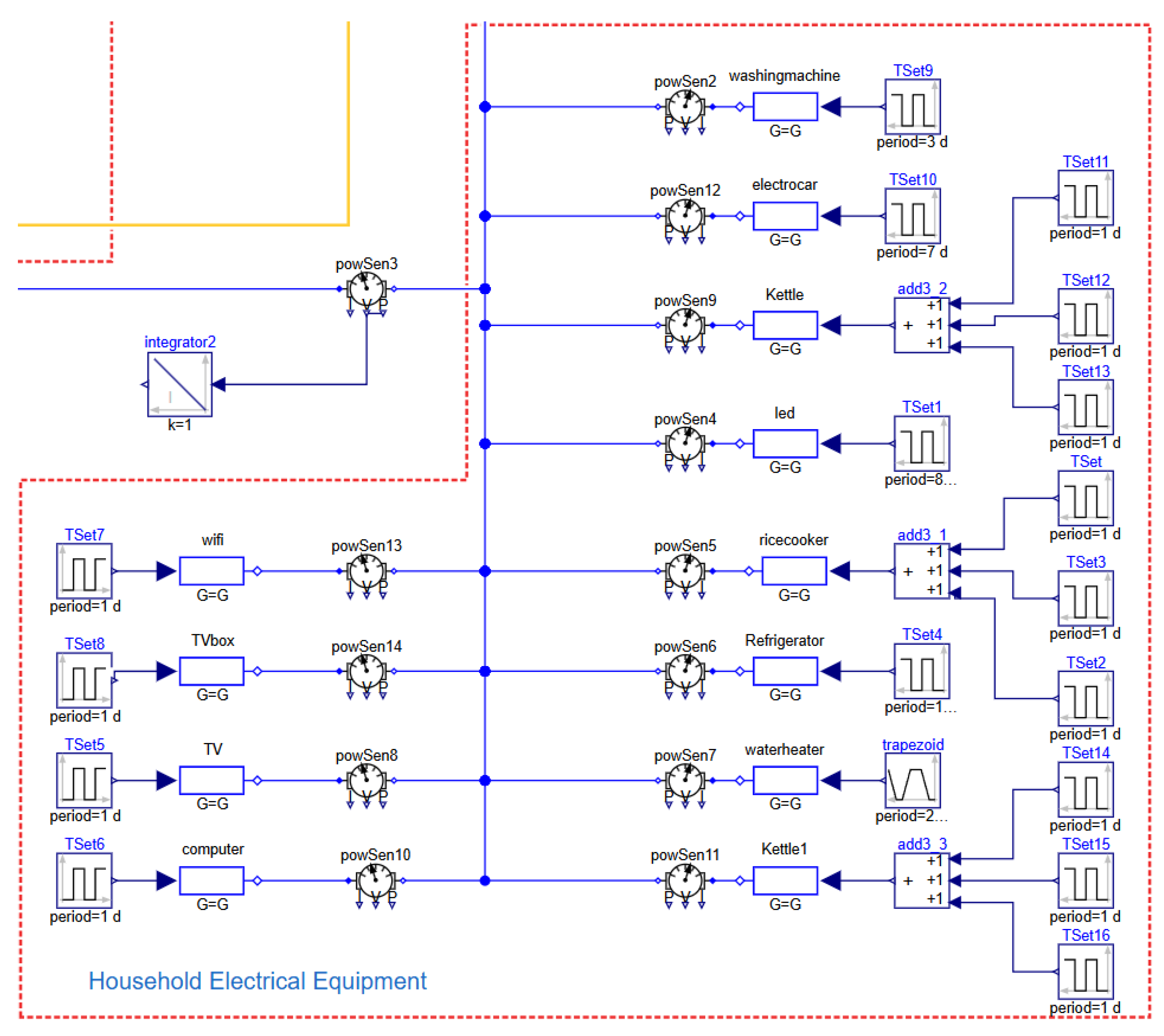
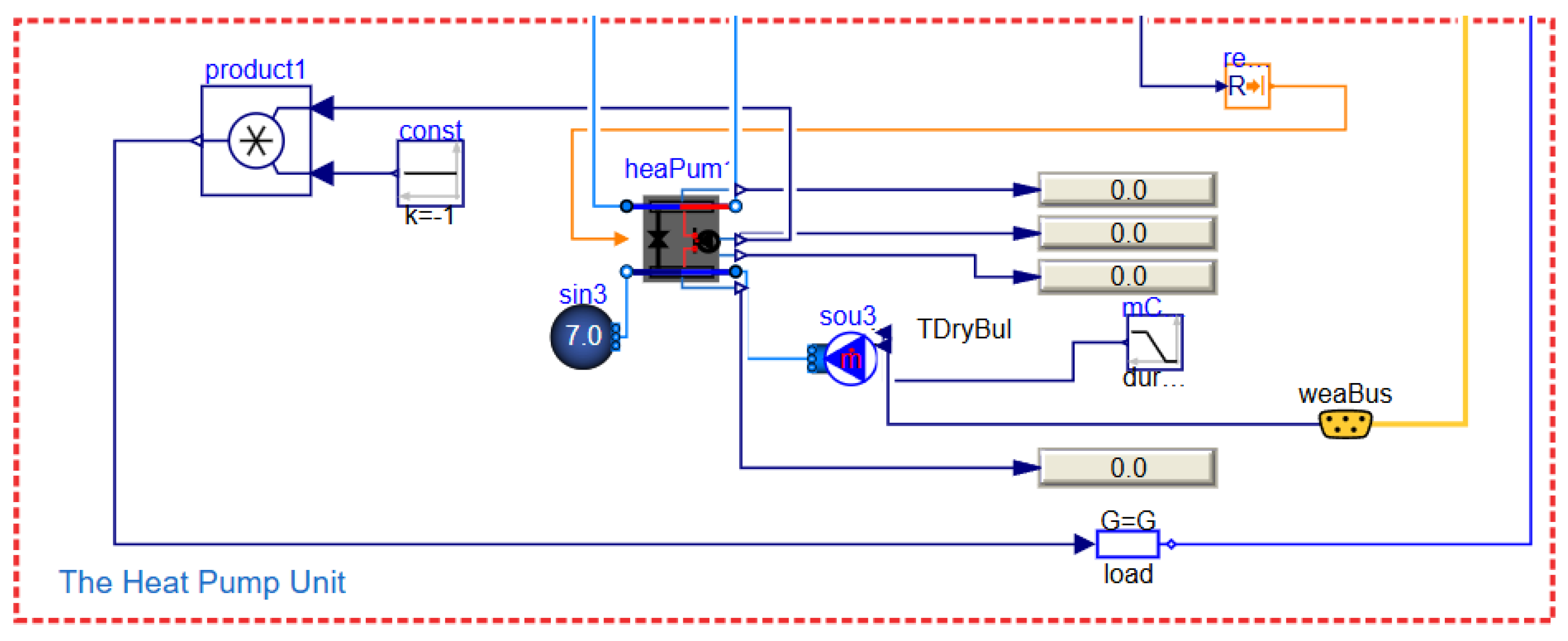
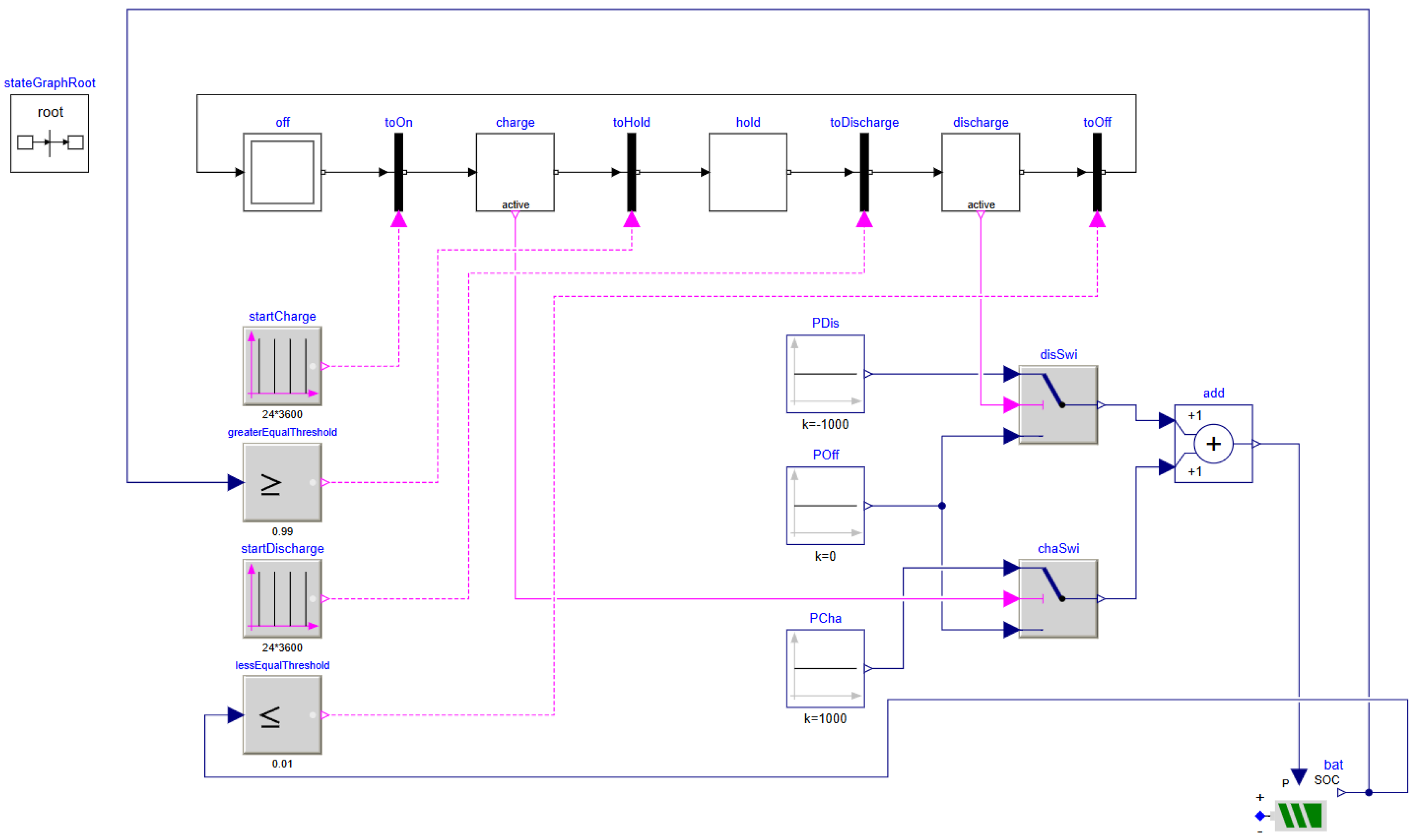
2.2.2. Simulation Model
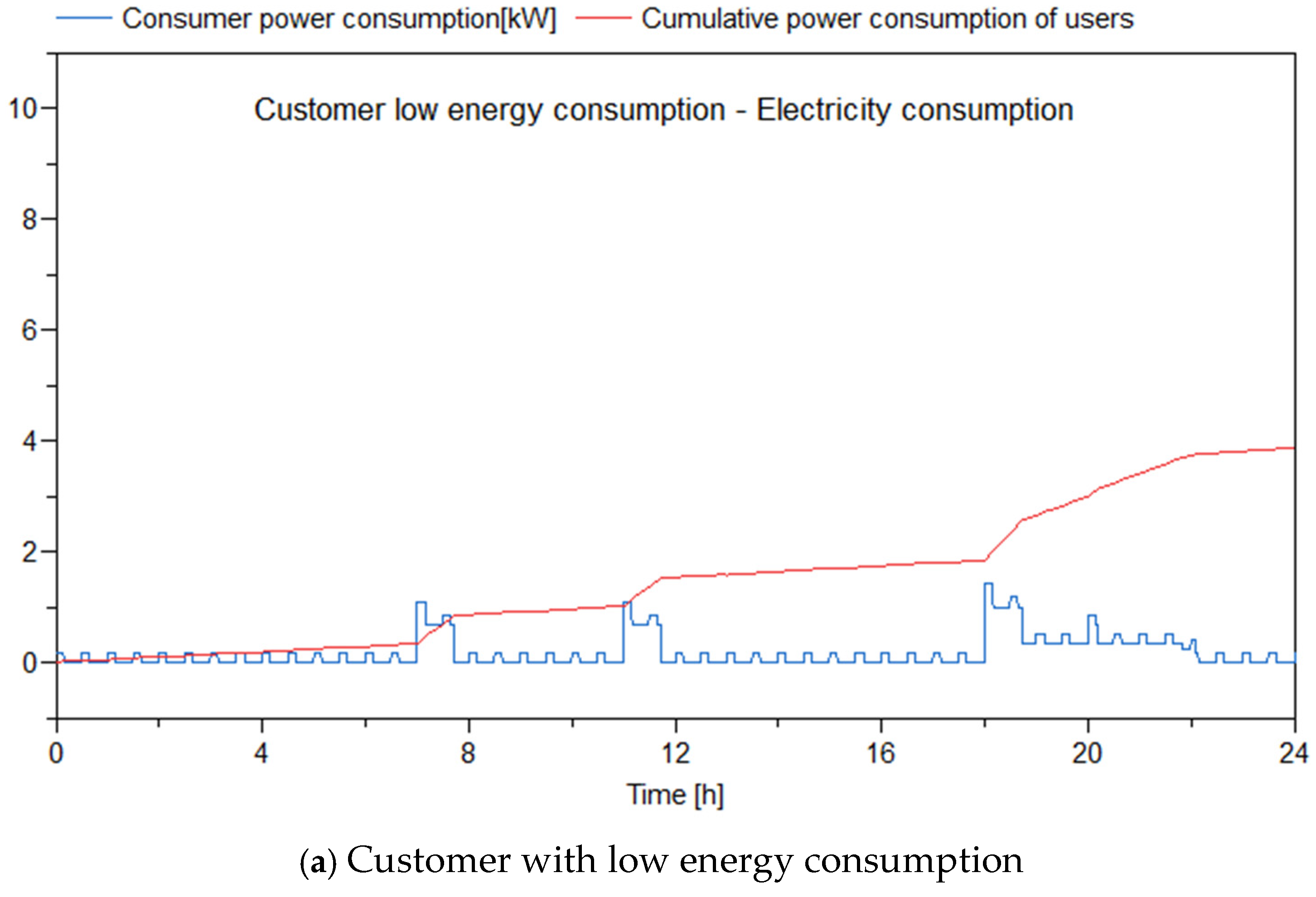
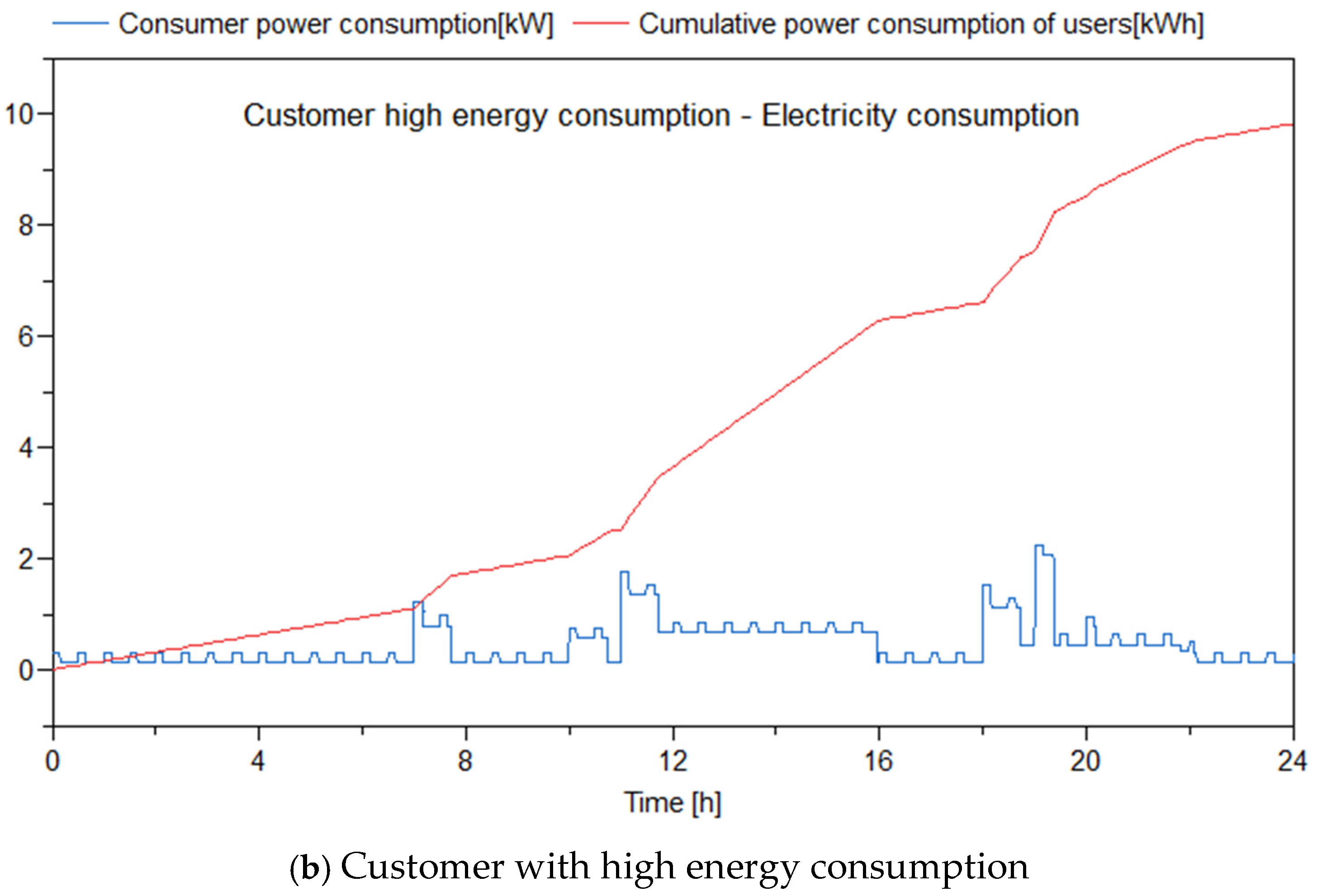
3. Results
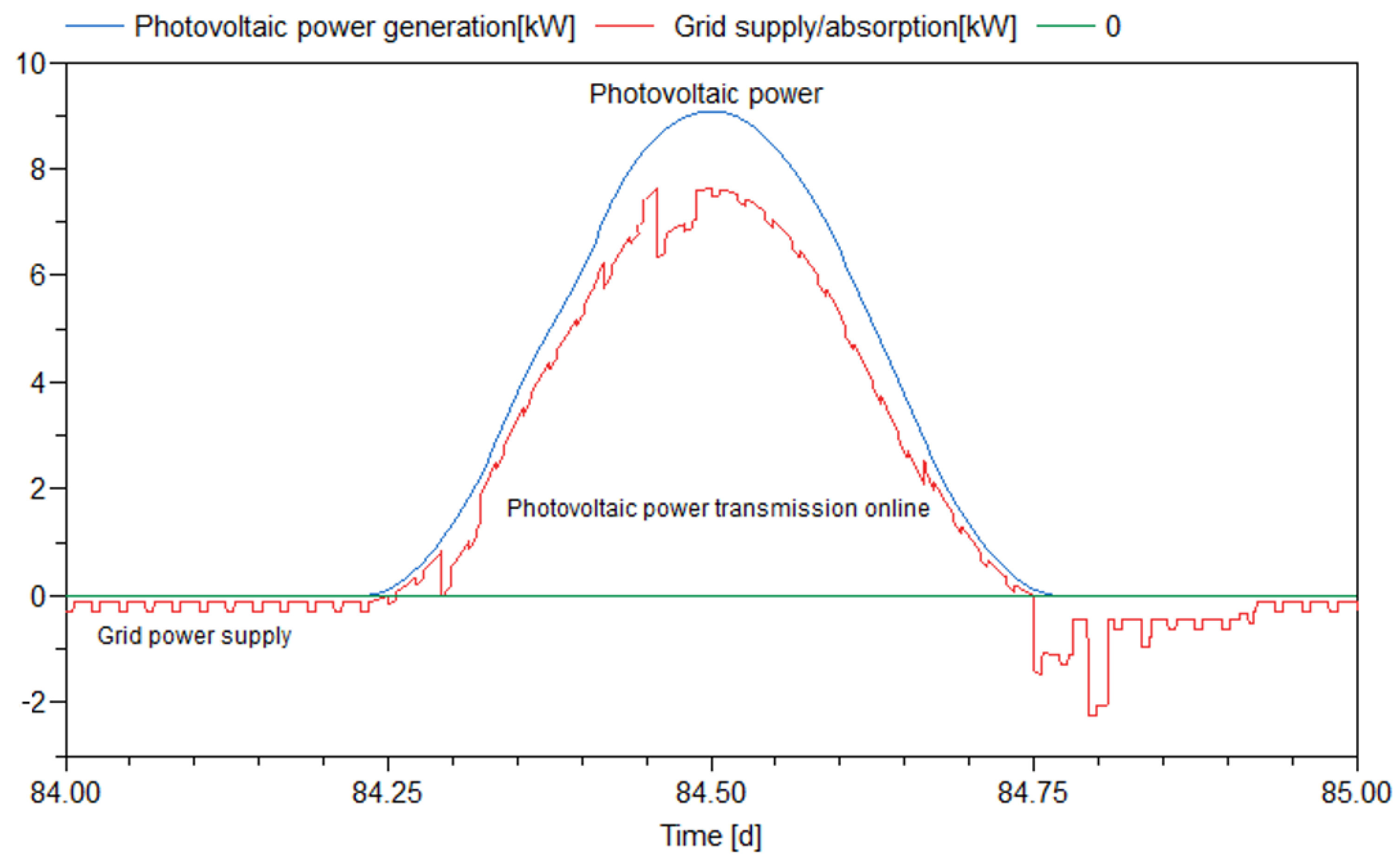
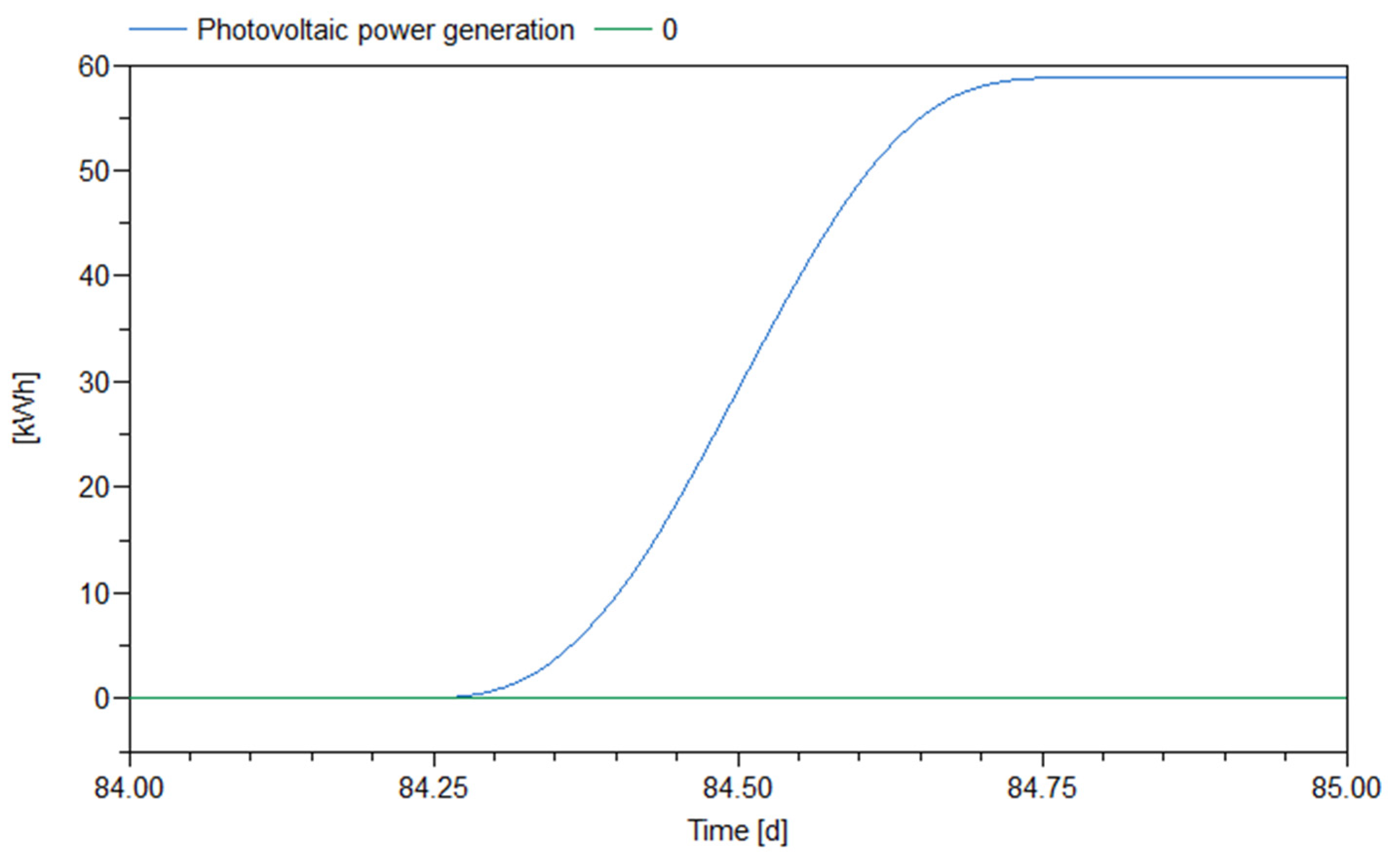
3.1. Power Production of the PSDF System
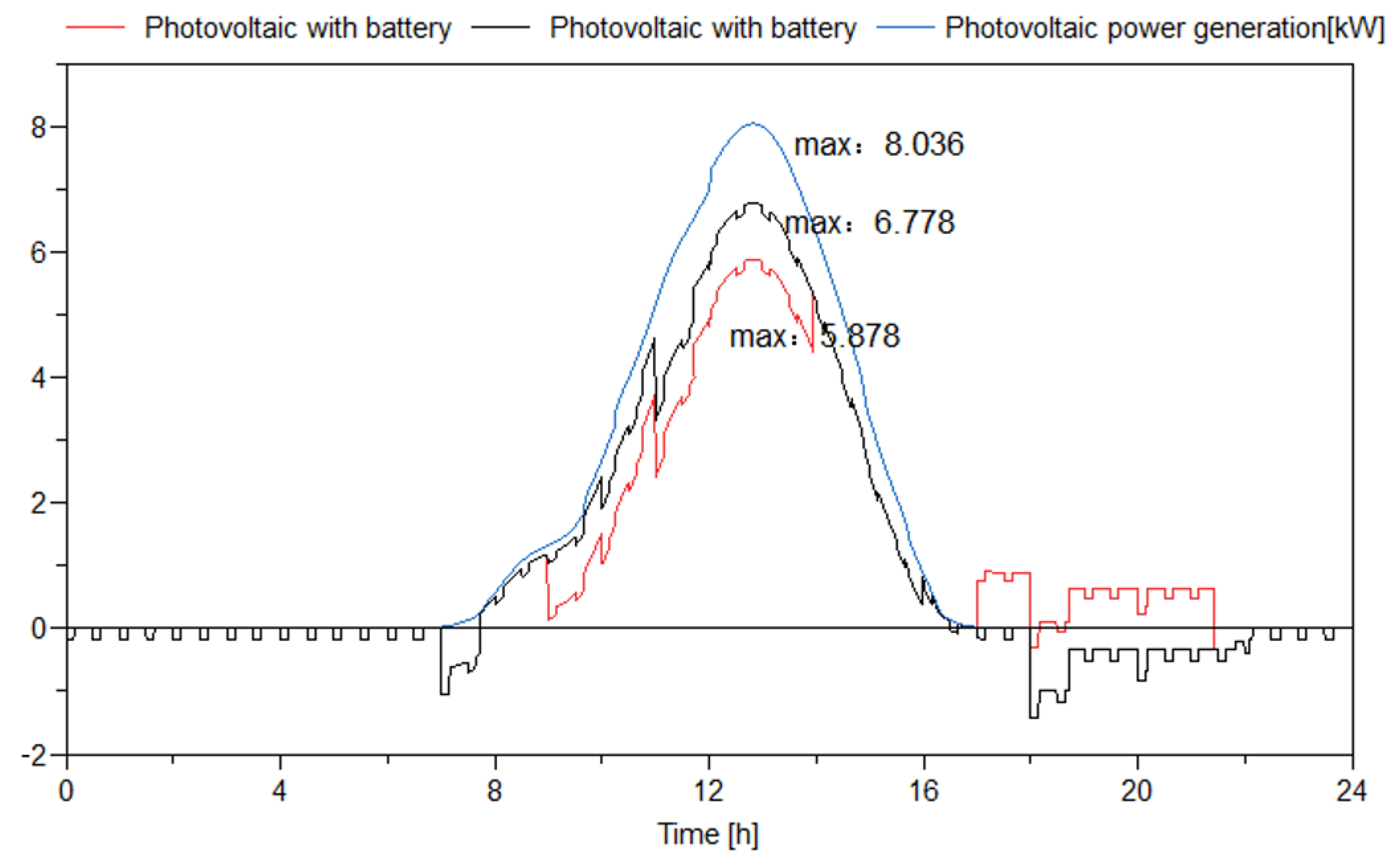
3.2. Impacts of the Battery on PSDF System
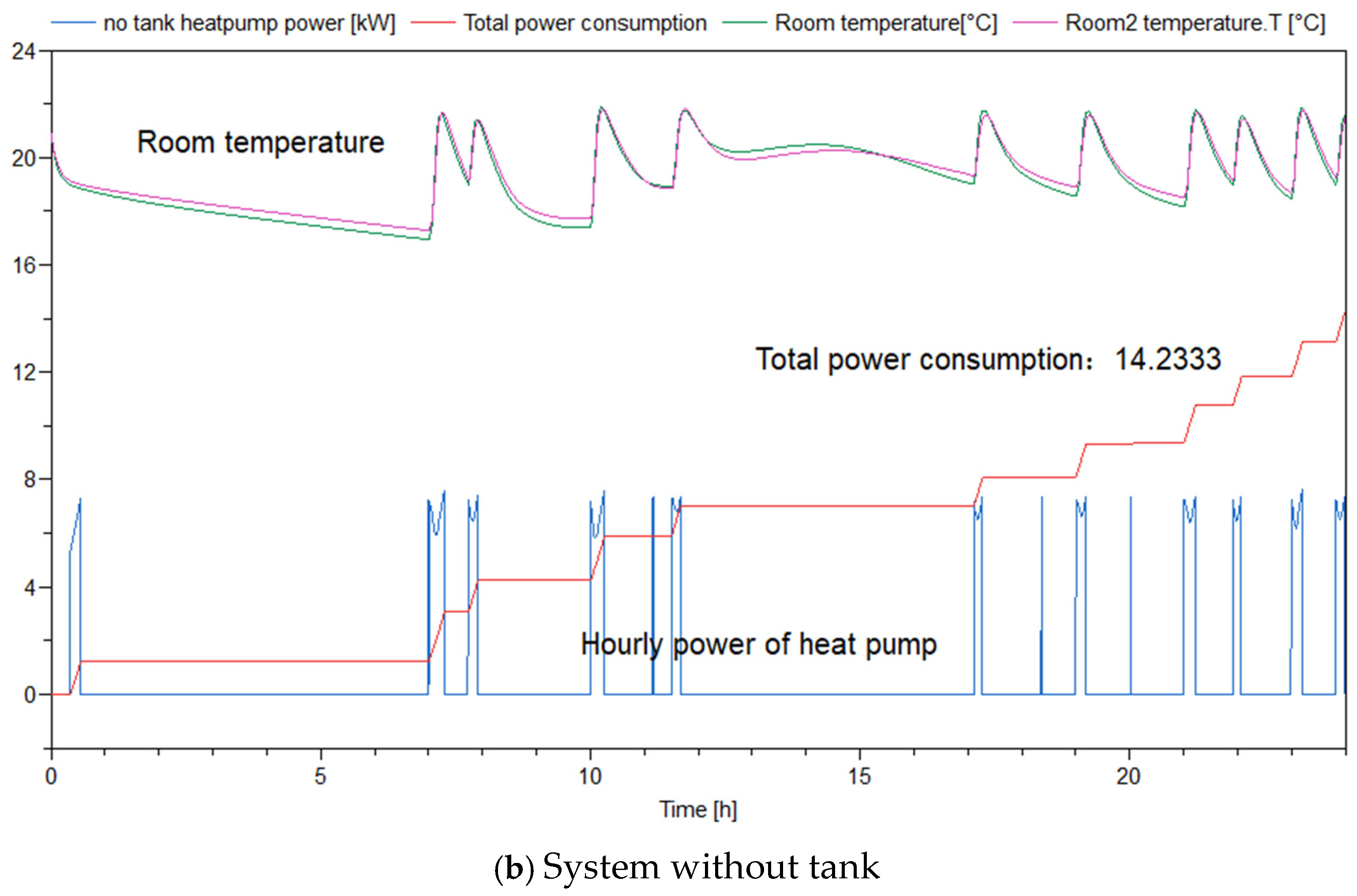
3.3. Impacts of the Thermal Inertia on PSDF System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H. Innovation “carbon” road booster industry development. China Construction News, 23 May 2023. (In Chinese) [Google Scholar]
- Su, W.; Han, Y.; Liu, Z.; Jin, X.; Liu, Z.; Yang, D.; Zhang, X. Absorption heat pumps for low-grade heat utilization: A comprehensive review on working pairs, classification, system advances and applications. Energy Convers. Manag. 2024, 315, 118760. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, J.; Gao, Y.; Xiong, F. Application of Renewable Energy in Passive Ultra Low-energy Consumption Building. Build. Sci. 2016, 32, 25–29. (In Chinese) [Google Scholar] [CrossRef]
- Zou, F.; Zhu, X.; Yin, J. Analysis of development trend of building energy system under the goal of carbon peak and parbon neutrality. Integr. Smart Energy 2023, 1–5. [Google Scholar]
- Oliver, M.; Jackson, T. Energy and economic evaluation of building-integrated photovoltaics. Energy 2001, 26, 431–439. [Google Scholar] [CrossRef]
- Yi, J. PSDF (Photovoltaic, Storage, DC, Flexible) a new type of building power distribution system for zero carbon powers system. HVAC 2019, 51, 1–12. (In Chinese) [Google Scholar]
- Wu, X.; Sun, K.; Lou, J.; Liu, Y.; Zhang, S.; Sun, Y.; Li, K. Research on topology selection of low carbon “photovoltaics, energy storage, direct current and flexibility” system. Power Supply 2022, 33, 21–29. (In Chinese) [Google Scholar]
- Hao, B. Building “light storage straight and soft” and zero-carbon electricity go hand in hand. Architecture 2021, 23, 27–29. (In Chinese) [Google Scholar]
- Su, W.; Li, J.; Lu, Z.; Jin, X.; Zhang, J.; Liu, Z.; Zhang, X. Performance analysis and optimization of a solar assisted heat pump-driven vacuum membrane distillation system for liquid desiccant regeneration. Energy Convers. Manag. 2024, 301, 118047. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, T.; Liu, X.; Jiang, Y. Development Statuses and research Prospect of PEDF(photovoltaics, energy storage, direct current and flexibility) building energy systems. HVAC 2022, 52, 1–9, 82. (In Chinese) [Google Scholar]
- Jiang, Y.; Hu, S. Research on the development strategy of production and consumption integrated roof-top PV system in rural China. Clim. Change Res. 2022, 18, 272–282. (In Chinese) [Google Scholar]
- Wang, C.; Xiao, T.; Li, S.; Zhang, J. Performance investigation of PEDF system applied in rural areas. Electr. Power 2024, 57, 160–169. (In Chinese) [Google Scholar]
- Chen, W.; Hao, B. Analysis of rural PEDF system toward carbon neutral-case study of Dongyao Village, Ruicheng County, Shanxi Province. Constr. Sci. Technol. 2021, 427, 86–89. (In Chinese) [Google Scholar]
- Dou, X.; Yuan, J.; Wu, Z.; Ni, Y.; Fan, C.; Xiao, Y. Improved configuration optimization of PV-wind-storage capacities for grid-connected microgrid. Electr. Power Autom. Equip. 2016, 36, 26–32. (In Chinese) [Google Scholar]
- Zhang, L.; Xiao, W.; Jiang, C.; Liu, Y.; Li, S.; Zhang, J. Research on Capacity Allocation Method of Key Equipment in PV System Applied in Office Buildings. Electr. Power 2024, 57, 152–159, 169. (In Chinese) [Google Scholar]
- Jiang, J.; Ni, Z.; Chen, C.; Cai, X.; Qian, H.; Hu, L.; Yu, C.; Shi, G.; Cao, H.; Lu, W.; et al. Capacity configuration and economic calculation of household PV+storage energy system. Sol. Energy 2020, 319, 44–48. (In Chinese) [Google Scholar]
- Zhao, A.; Wang, P.; Jing, J.; Gao, Z.; Li, W. Optimal Configuration Method of New Energy Capacity for Rural Households Considering Impact of Electric Vehicles. Electr. Power 2022, 55, 31–39, 50. (In Chinese) [Google Scholar]
- Cervantes, J.; Choobineh, F. Optimal Sizing of a Nonutility-Scale Solar Power System and Its Battery Storage. Appl. Energy 2018, 216, 105–115. [Google Scholar] [CrossRef]
- Javeed, I.; Khezri, R.; Mahmoudi, A.; Yazdani, A.; Shafiullah, G.M. Optimal Sizing of Rooftop PV and Battery Storage for Grid-Connected Houses Considering Flat and Time-of-Use Electricity Rates. Energies 2021, 14, 3520. [Google Scholar] [CrossRef]
- Khezri, R.; Mahmoudi, A.; Haque, M.H. Optimal Capacity of Solar PV and Battery Storage for Australian Grid-Connected Households. IEEE Trans. Ind. Appl. 2020, 56, 5319–5329. [Google Scholar] [CrossRef]
- Pan, X.; Khezri, R.; Mahmoudi, A.; Muyeen, S.M. Optimal Planning of Solar PV and Battery Storage with Energy Management Systems for Time-of-Use and Flat Electricity Tariffs. IET Renew. Power Gener. 2022, 16, 1206–1219. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Doorman, G.; Fischer, D.; Korpås, M.; Ånestad, A.; Sartori, I. Methodology for optimal energy system design of Zero Energy Buildings using mixed-integer linear programming. Energy Build. 2016, 127, 194–205. [Google Scholar] [CrossRef]
- Huang, B.; Li, Q.; Gao, F.; Huang, Z.; Wang, J. Cost analysis of distributed photovoltaic integration with high penetration rate in rural network. CSU-EPSA 2017, 29, 102–106. (In Chinese) [Google Scholar]
- Hofer, J.; Svetozarevic, B.; Schlueter, A. Hybrid AC/DC building microgrid for solar PV and battery storage integration. In Proceedings of the 2017 IEEE Second International Conference on DC Microgrids (ICDCM), Nuremburg, Germany, 27–29 June 2017. [Google Scholar] [CrossRef]
- Miglani, S.; Orehounig, K.; Carmeliet, J. Integrating a thermal model of ground source heat pumps and solar regeneration within building energy system optimization. Appl. Energy 2018, 218, 78–94. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, X.; Liu, X. Exploration of vehicle-building-grid(VBG) collaboration interaction under dual carbon target. HVAC 2023, 53, 1–11. (In Chinese) [Google Scholar]
- Rong, X.; Zhang, H.; Zhu, L.; Li, X.; Wang, J.; Ma, J. Research on ‘Photovoltaic, Storage and DC Flexibility’ Based Constant Power Operation in Commercial Buildings under Targets of ‘Carbon Peak’ and ‘Carbon Neutral’. Mach. Build. Autom. 2022, 51, 223–227. (In Chinese) [Google Scholar]
- Wang, B. Research on Building Power Distribution System and Scheduling Strategy Based on PEDF (Photovoltaic, Energy storge, DC, Flexible). Master’s Thesis, Beijing University of Civil Engineering and Architecture, Beijing, China, 2023. (In Chinese). [Google Scholar]
- Luo, Z.; Peng, J.; Cao, J.; Yin, R.; Zou, B.; Tan, Y.; Yan, J. Demand Flexibility of Residential Buildings: Definitions, Flexible Loads, and Quantification Methods. Engineering 2022, 18, 123–140. [Google Scholar] [CrossRef]
- Liang, W.; Li, H.; Zhan, S.; Chong, A.; Hong, T. Energy flexibility quantification of a tropical net-zero office building using physically consistent neural network-based model predictive control. Adv. Appl. Energy 2024, 14, 100167. [Google Scholar] [CrossRef]
- Peng, J.; Luo, Z.; Tan, Y.; Jiang, H.; Yin, R.; Yan, J. Balancing stakeholder benefits: A many-objective optimal dispatch framework for home energy systems inspired by Maslow’s Hierarchy of needs. Adv. Appl. Energy 2024, 13, 100160. [Google Scholar] [CrossRef]
- Shi, L. Virtual Inertia and Auxiliary Frequency Modulation Control Strategy of Optical Storage Direct Flexible System. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2022. (In Chinese). [Google Scholar]
- Dymola Dassault Systèmes®WWW Document, n.d. Available online: https://www.3ds.com/products/catia/dymola (accessed on 10 August 2024).
- Wetter, M.; Zuo, W.; Nouidui, T.S.; Pang, X. Modelica buildings library. J. Build. Perform. Simul. 2014, 7, 253–270. [Google Scholar] [CrossRef]
- Tang, C. Equation Fit Based Models of Water Source Heat Pumps. Master’s Thesis, Oklahoma State University, Oklahoma, OK, USA, 2005. [Google Scholar]






| Month | Air Temperature (°C) | Sunshine Duration (hour) |
|---|---|---|
| January | 5.1 | 135 |
| February | 7.1 | 117 |
| March | 11.7 | 140 |
| April | 17.4 | 153 |
| May | 22.2 | 174 |
| June | 25.4 | 162 |
| July | 29.9 | 232 |
| August | 29.0 | 243 |
| September | 24.8 | 161 |
| October | 19.5 | 162 |
| November | 13.5 | 149 |
| December | 7.4 | 150 |
| Wall U Value | Door U Value | Window U Value | Floor U Value | Roof U Value |
|---|---|---|---|---|
| W/m2·K | W/m2·K | W/m2·K | W/m2·K | W/m2·K |
| 0.384 | 1.7 | 1.27 | 0.431 | 0.411 |
| Season | The Total Photovoltaic Power Generation (kWh) |
|---|---|
| Spring | 5265.85 |
| Summer | 5244.03 |
| Autumn | 4785.2 |
| Winter | 3125.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Miao, W.; Xu, C.; Li, Y.; Liu, Z.; Sha, S. Simulation of PSDF (Photovoltaic, Storage, Direct Current and Flexibility) Energy System for Rural Buildings. Processes 2024, 12, 2380. https://doi.org/10.3390/pr12112380
Li X, Miao W, Xu C, Li Y, Liu Z, Sha S. Simulation of PSDF (Photovoltaic, Storage, Direct Current and Flexibility) Energy System for Rural Buildings. Processes. 2024; 12(11):2380. https://doi.org/10.3390/pr12112380
Chicago/Turabian StyleLi, Xianfeng, Wenjie Miao, Chuanzi Xu, Yubao Li, Zhongyan Liu, and Shuai Sha. 2024. "Simulation of PSDF (Photovoltaic, Storage, Direct Current and Flexibility) Energy System for Rural Buildings" Processes 12, no. 11: 2380. https://doi.org/10.3390/pr12112380
APA StyleLi, X., Miao, W., Xu, C., Li, Y., Liu, Z., & Sha, S. (2024). Simulation of PSDF (Photovoltaic, Storage, Direct Current and Flexibility) Energy System for Rural Buildings. Processes, 12(11), 2380. https://doi.org/10.3390/pr12112380





