A Modified Control Strategy for Three-Phase Four-Switch Active Power Filters Based on Fundamental Positive Sequence Extraction
Abstract
:1. Introduction
2. Topology of Three-Phase Four-Switch APFs
3. Control Strategy for Three-Phase Four-Switch APFs
3.1. Fundamental Positive Sequence Extraction Method
3.2. Coordinate Transformation Method Without PLLs
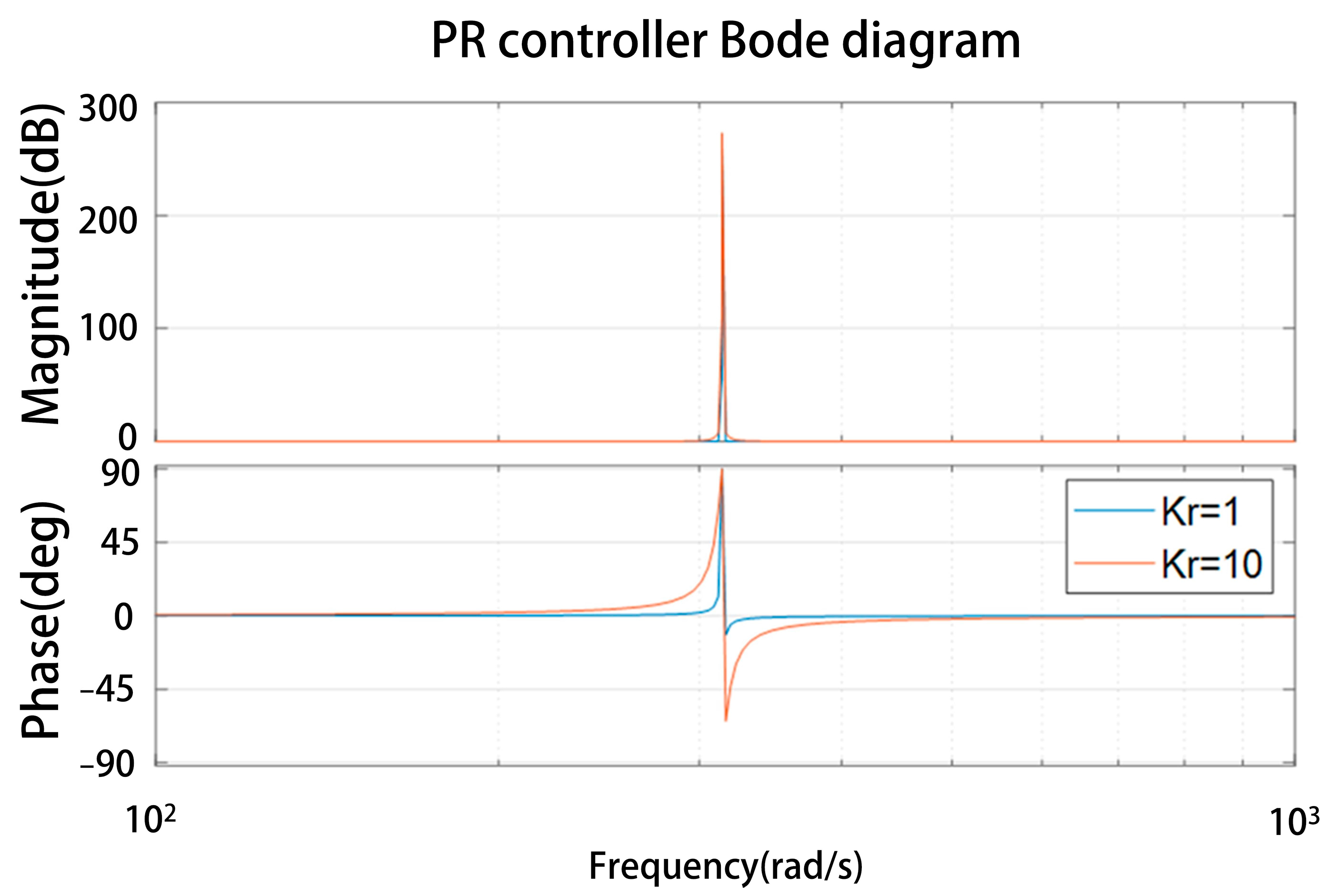
3.3. Quasi-PR Control Strategy
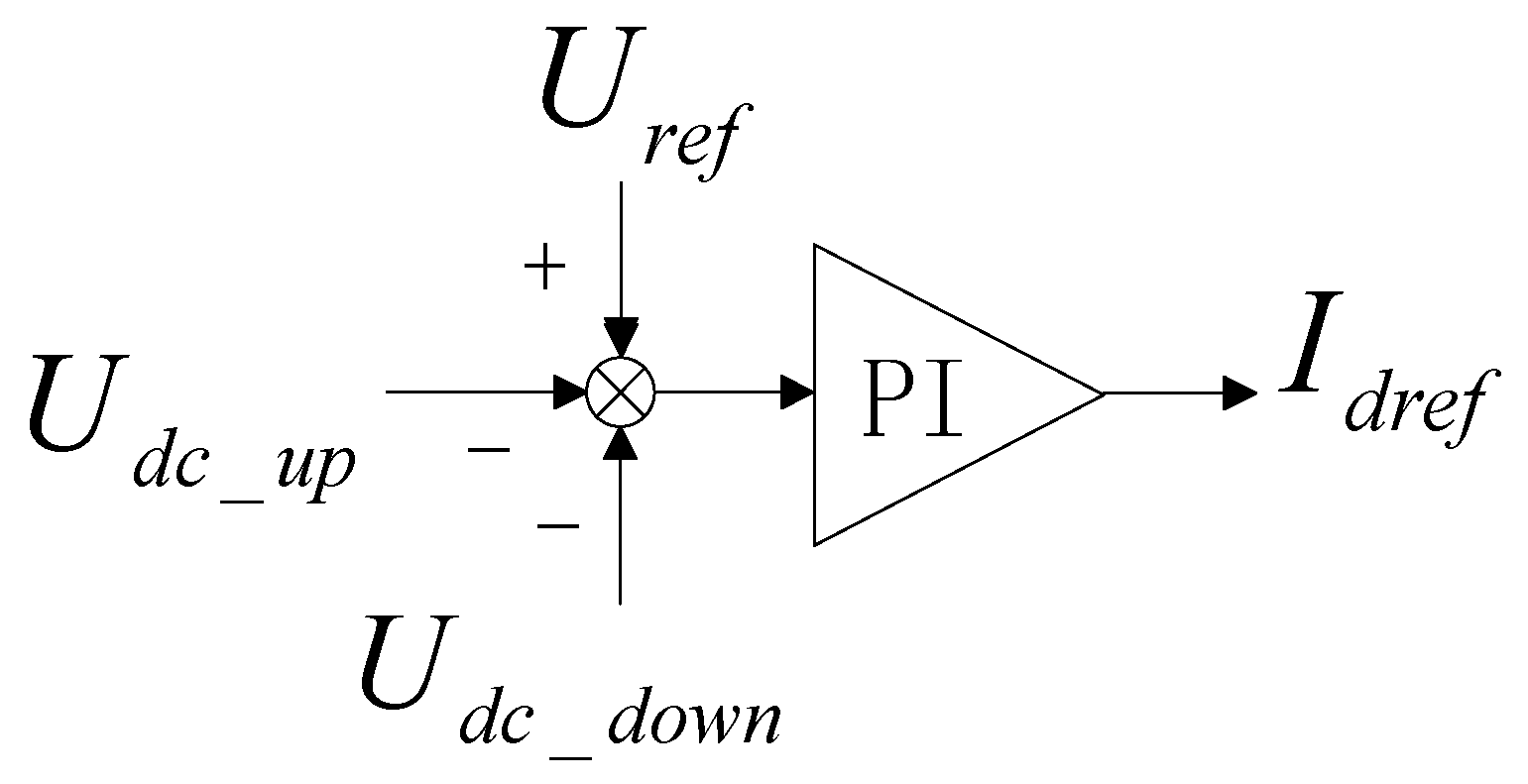
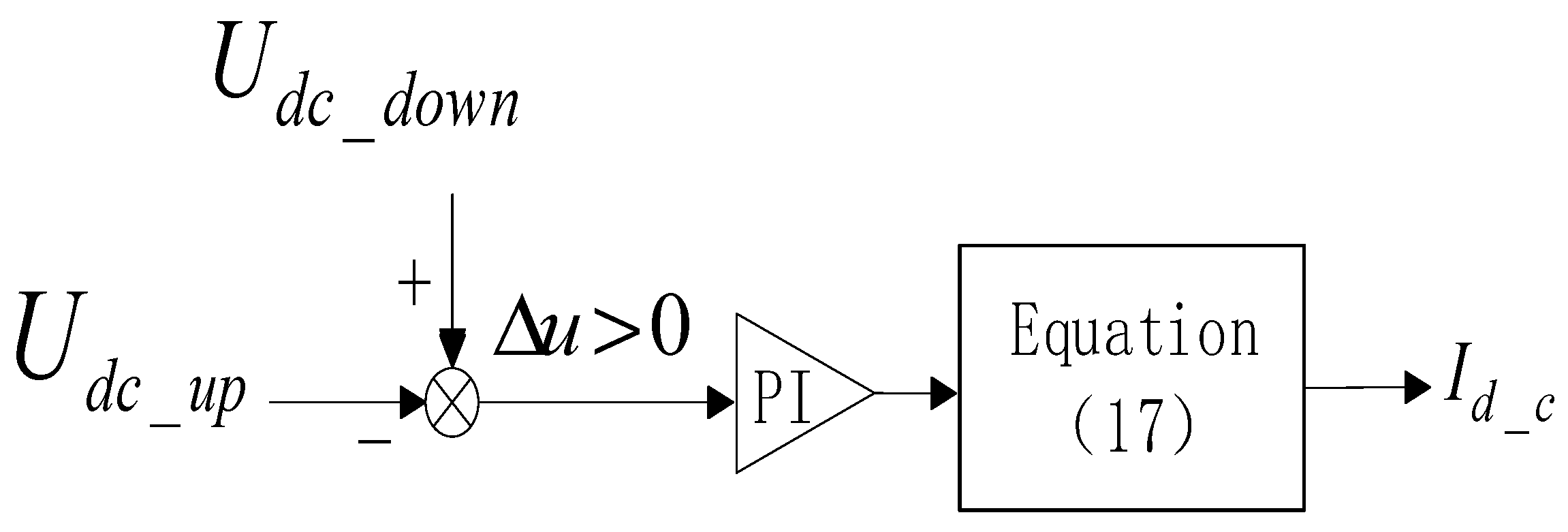
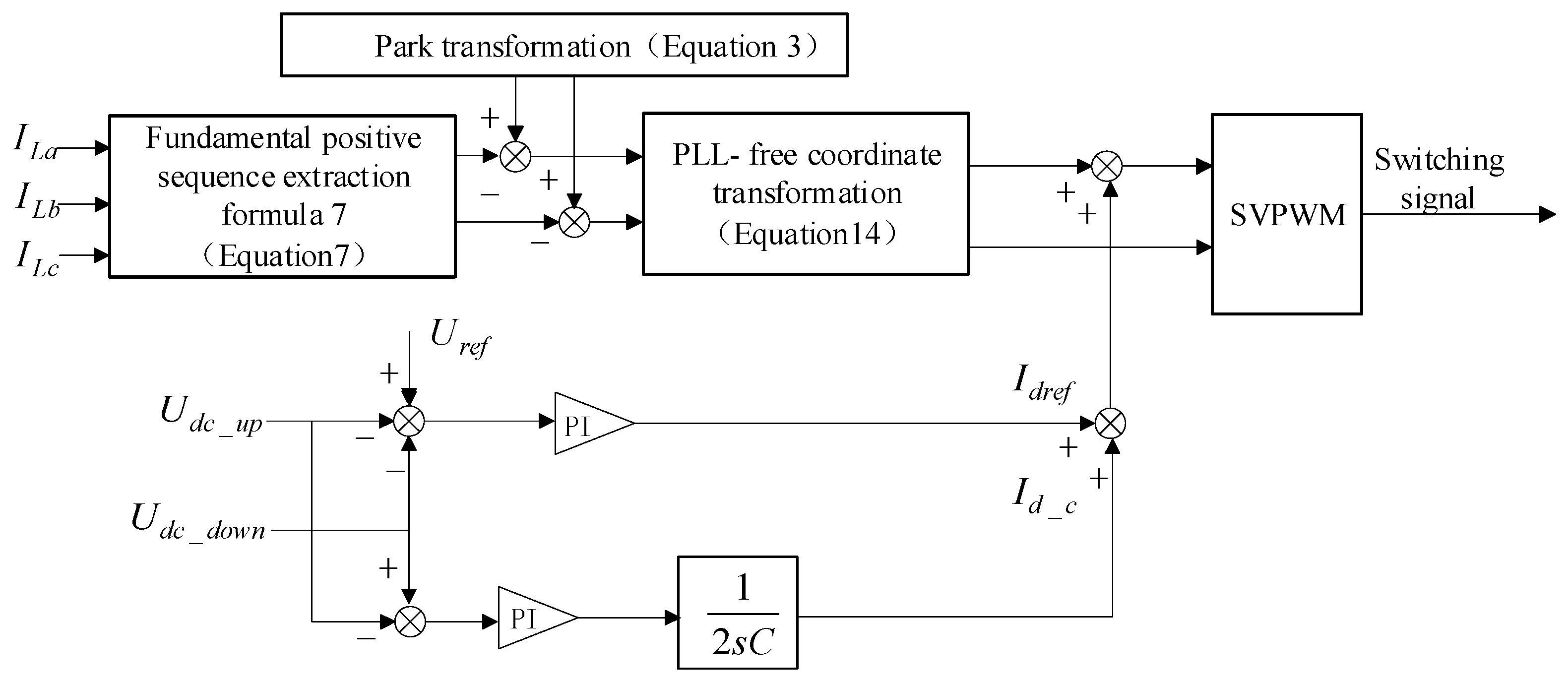
3.4. DC Voltage Control Strategy
4. SVPWM Method for the Three-Phase Four-Switch Topology
5. Simulation Analysis
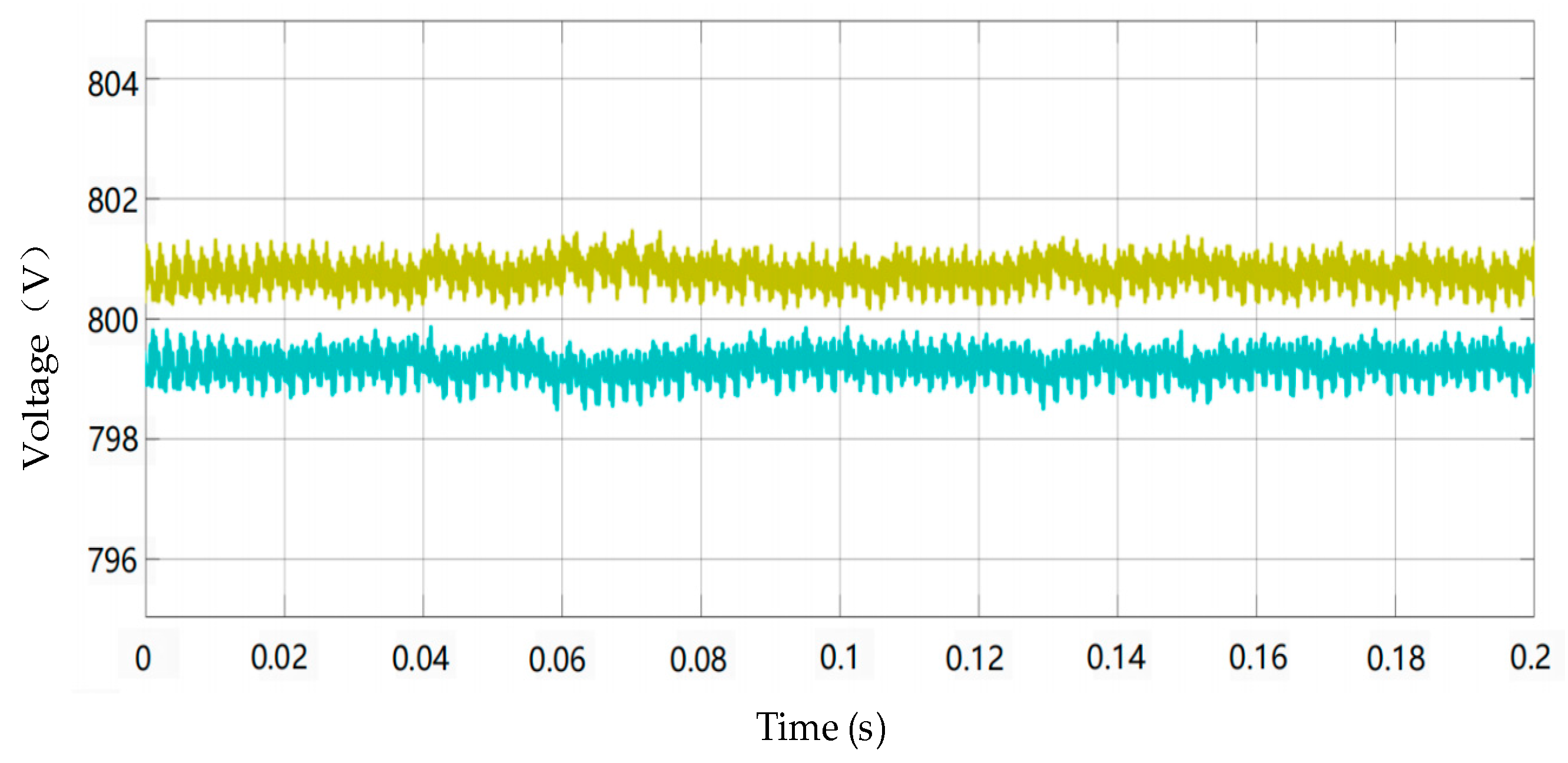
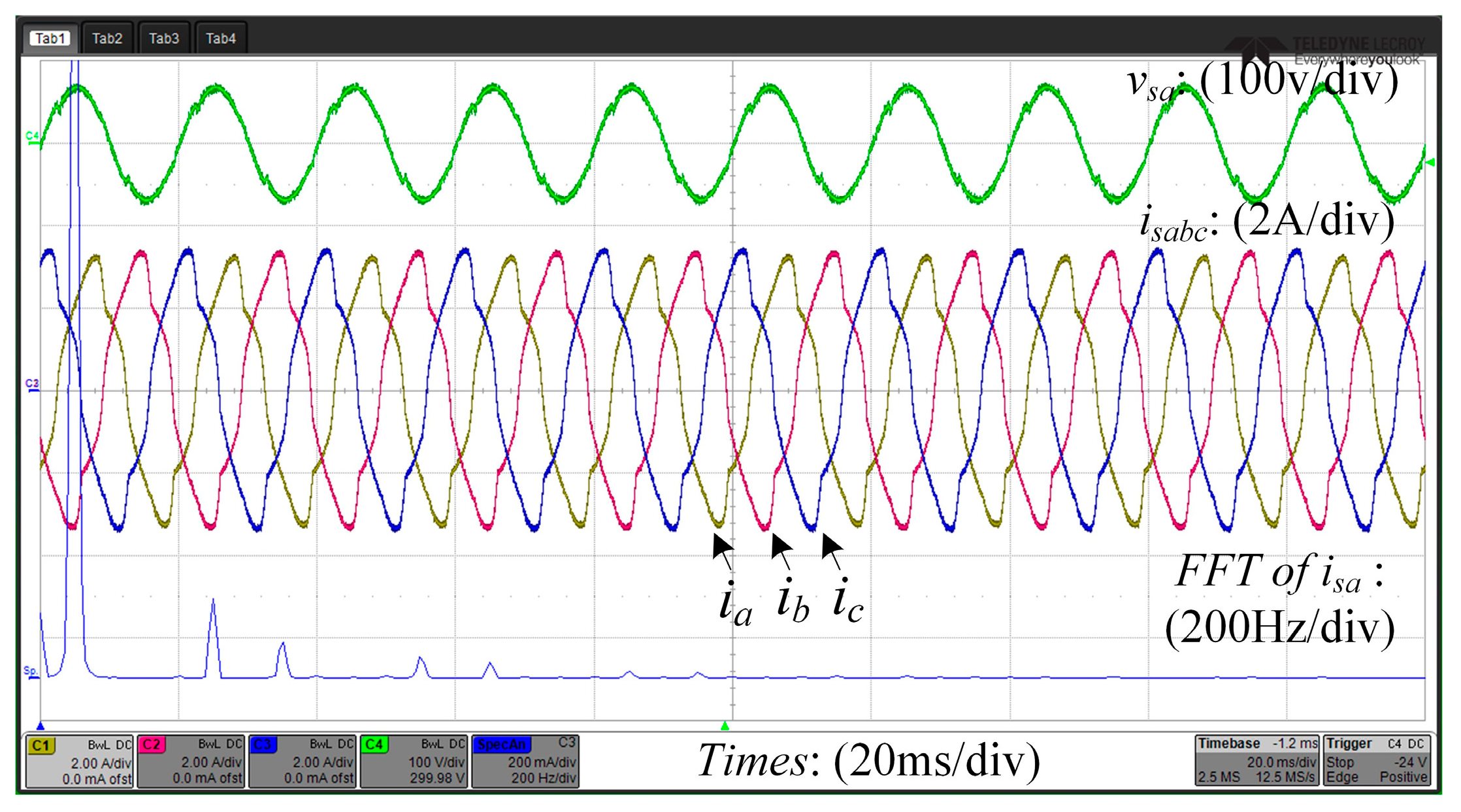
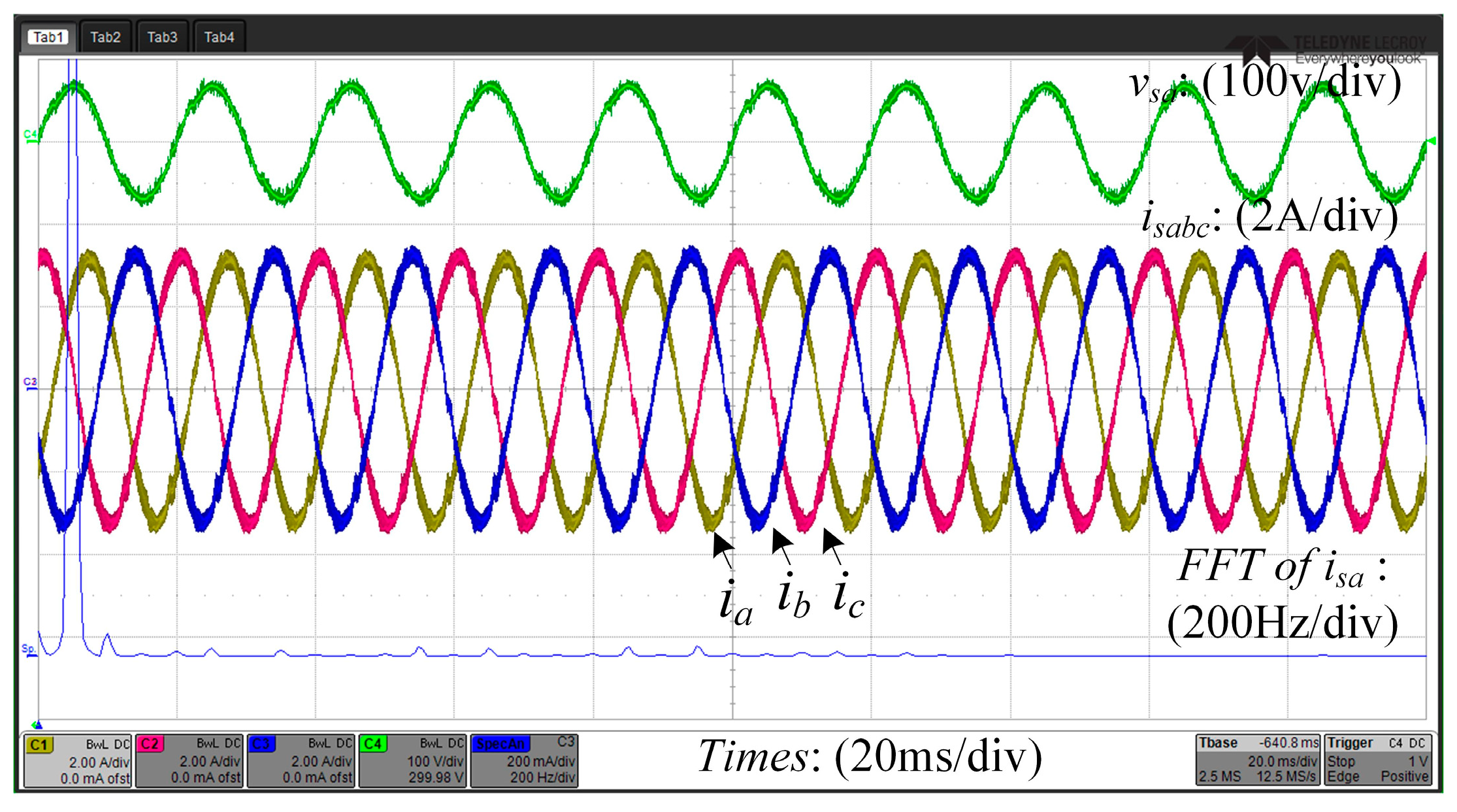
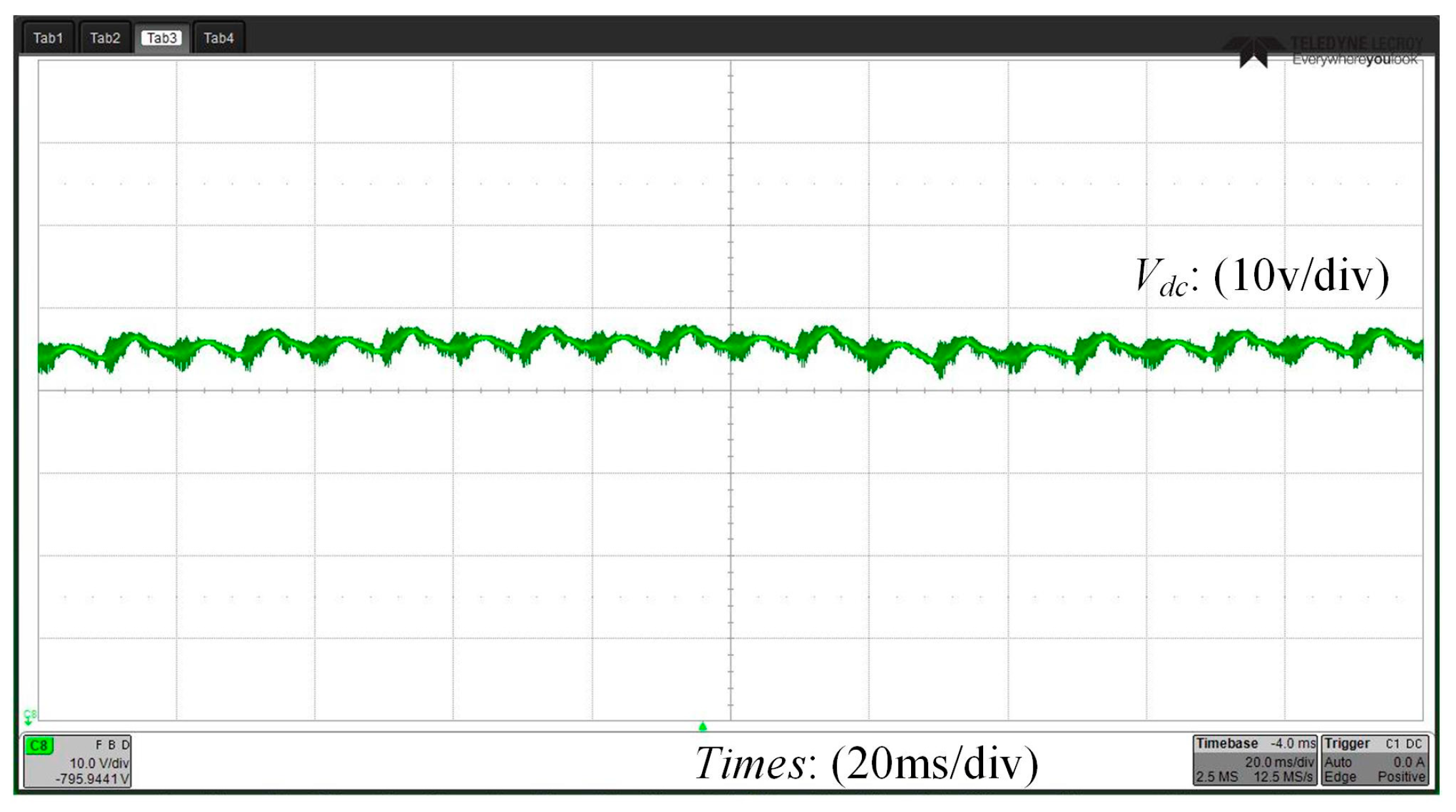
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liang, X. Emerging Power Quality Challenges Due to Integration of Renewable Energy Sources. IEEE Trans. Ind. Appl. 2017, 53, 855–866. [Google Scholar] [CrossRef]
- Anzalchi, A.; Sundararajan, A.; Moghadasi, A.; Sarwat, A. High penetration grid-tied photovoltaics: Analysis of power quality and feeder voltage profile. IEEE Ind. Appl. Mag. 2019, 25, 83–94. [Google Scholar] [CrossRef]
- Honrubia-Escribano, A.; García-Sánchez, T.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, A. Power Quality Surveys of Photovoltaic Power Plants: Characterisation and Analysis of Grid-Code Requirements. IET Renew. Power Gener. 2015, 9, 466–473. [Google Scholar] [CrossRef]
- Abdel-Aziz, A.; Elgenedy, M.A.; Williams, B.W. Two-Leg Neutral-Point Diode-Clamped Active Front-End Rectifier. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 405–419. [Google Scholar] [CrossRef]
- Bollen, M.H.; Das, R.; Djokic, S.; Ciufo, P.; Meyer, J.; Rönnberg, S.K.; Zavodam, F. Power Quality Concerns in Implementing Smart Distribution-Grid Applications. IEEE Trans. Smart Grid 2017, 8, 391–399. [Google Scholar] [CrossRef]
- Peng, F.Z.; Lai, J.S. Reactive Power and Harmonic Compensation Based on the Generalized Instantaneous Reactive Power Theory for Three-phase Power Systems. In Proceedings of the 7th International Conference on Harmonics and Quality of Power, Las Vegas, NV, USA, 16 October 1996; pp. 83–89. [Google Scholar]
- Hirofumi, A.; Yoshihira, K.; Akira, N. Instantaneous Reactive Power Compensators Comprising Switching Devices without Energy Storage Components. IEEE Trans. Ind. Appl. 1984, IA-20, 625–630. [Google Scholar]
- Gong, C.; Cheng, Z.; Sou, W.K.; Lam, C.S.; Chow, M.Y. Collaborative Distributed Optimal Control of Pure and Hybrid Active Power Filters in Active Distribution Network. IEEE Trans. Power Deliv. 2023, 38, 2326–2337. [Google Scholar] [CrossRef]
- Fan, Y.; Zhou, Q.; Wang, J.; Mu, S.; Wang, L. Application of Superconducting-Magnetic-Energy-Storage-Based Current-Source Active Power Filter in Photovoltaics for Harmonic Mitigation. IEEE Trans. Appl. Supercond. 2021, 31, 1–4. [Google Scholar] [CrossRef]
- Li, D.; Wang, T.; Pan, W.; Ding, X.; Gong, J. A Comprehensive Review of Improving Power Quality Using Active Power Filters. Electr. Power Syst. Res. 2021, 199, 107389. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Ahmadi, A.; Sharaf, A.M.; Siano, P.; Pou, J.; Hredzak, B.; Agelidis, V.G. Review of FACTS Technologies and Applications for Power Quality in Smart Grids with Renewable Energy Systems. Renew. Sustain. Energy Rev. 2018, 82, 502–514. [Google Scholar] [CrossRef]
- Rachit, A.; Sood, V.K. Development of EMTP-based active filter model for distribution system studies. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering, Waterloo, ON, Canada, 25–28 May 1998; Volume 1, pp. 77–80. [Google Scholar]
- Kesler, M.; Ozdemir, E. Synchronous-Reference-Frame-Based Control Method for UPQC Under Unbalanced and Distorted Load Conditions. IEEE Trans. Ind. Electron. 2011, 58, 3967–3975. [Google Scholar] [CrossRef]
- Serra, F.M.; Montoya, O.D.; De Angelo, C.H.; Forchetti, D.G. On The Use of The P-Q Theory for Harmonic Current Cancellation with Shunt Active Filters. Adv. Electr. Electron. Eng. 2019, 17, 262–269. [Google Scholar] [CrossRef]
- Masiha, A.; Ikhlaq, H.; Shameem, A.L.; Mukul, C. GRLF-LAD Control Based Active Power Filter Operation With QSG-SOGI Algorithm for Grid Voltage Harmonics Disturbance Rejection. IEEE Access 2023, 11, 135753–135763. [Google Scholar]
- Asiminoaei, L.; Blaabjerg, F.; Hansen, S. Detection Is Key—Harmonic Detection Methods for Active Power Filter Applications. IEEE Ind. Appl. Mag. 2007, 13, 22–33. [Google Scholar] [CrossRef]
- Rai, K.B.; Kumar, N.; Singh, A. Three-Phase Grid Connected Shunt Active Power Filter Based on Adaptive Q-LMF Control Technique. IEEE Trans. Power Electron. 2024, 39, 10216–10225. [Google Scholar] [CrossRef]
- Karbasforooshan, M.S.; Monfared, M. Adaptive Self-Tuned Current Controller Design for an LCL-Filtered LC-Tuned Single-Phase Shunt Hybrid Active Power Filter. IEEE Trans. Power Deliv. 2022, 37, 2747–2756. [Google Scholar] [CrossRef]
- Mykhailo, A.; Vasyl, C.; Serhii, P.; Valerii, M.; Ivan, S. Integral Power Theory and Active Filtering Using the α-β Reference Frame. IEEE Access 2024, 12, 60004–60014. [Google Scholar]
- Ferreira, S.C.; Gonzatti, R.B.; Pereira, R.R.; da Silva, C.H.; da Silva, L.E.B.; Lambert-Torres, G. Finite Control Set Model Predictive Control for Dynamic Reactive Power Compensation with Hybrid Active Power Filters. IEEE Trans. Ind. Electron. 2018, 65, 2608–2617. [Google Scholar] [CrossRef]
- Komurcugil, H.; Bayhan, S.; Guler, N.; Blaabjerg, F. An Effective Model Predictive Control Method with Self-Balanced Capacitor Voltages for Single-Phase Three-Level Shunt Active Filters. IEEE Access 2021, 9, 103811–103821. [Google Scholar] [CrossRef]
- Iqbal, M.; Jawad, M.; Jaffery, M.H.; Akhtar, S.; Rafiq, M.N.; Qureshi, M.B.; Ansari, A.R.; Nawaz, R. Neural Networks Based Shunt Hybrid Active Power Filter for Harmonic Elimination. IEEE Access 2021, 9, 69913–69925. [Google Scholar] [CrossRef]
- Kumar, R.; Bansal, H.O.; Gautam, A.R.; Mahela, O.P.; Khan, B. Experimental Investigations on Particle Swarm Optimization Based Control Algorithm for Shunt Active Power Filter to Enhance Electric Power Quality. IEEE Access 2022, 10, 54878–54890. [Google Scholar] [CrossRef]
- Behnam, A.; Hasan, R.; Mohammad, P. A New Fractional-Order Proportional-Resonant Control of Shunt Active Power Filter Based on Genetic Algorithm Optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 4612–4622. [Google Scholar]
- Basha, S.G.; Mani, V.; Mopidevi, S. Single-phase Thirteen-level Dual-boost Inverter Based Shunt Active Power Filter Control Using Resonant and Fuzzy Logic Controllers. CSEE J. Power Energy Syst. 2022, 8, 849–863. [Google Scholar]
- Çelik, D.; Ahmed, H.; Meral, M.E. Kalman Filter-Based Super-Twisting Sliding Mode Control of Shunt Active Power Filter for Electric Vehicle Charging Station Applications. IEEE Trans. Power Deliv. 2023, 38, 1097–1107. [Google Scholar] [CrossRef]
- Fei, J.; Yang, J. Chebyshev Fuzzy Neural Network Super-Twisting Terminal Sliding-Mode Control for Active Power Filter. IEEE Internet Things J. 2023, 10, 13587–13600. [Google Scholar] [CrossRef]
- Serra, F.M.; De Angelo, C.H. Direct Power Control of a Shunt Active Power Filter Using a Modified IDA–PBC Approach with Integral Action. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 1991–1995. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G.; Mahela, O.P.; Padmanaban, S.; Holm-Nielsen, J.B. Comprehensive review of distributed FACTS control algorithms for power quality enhancement in utility grid with renewable energy penetration. IEEE Access 2020, 8, 107614–107634. [Google Scholar] [CrossRef]
- Khodabakhsh, J.; Moschopoulos, G. A Four-Switch Three-Phase AC– DC Converter with Galvanic Isolation. IEEE Trans. Power Electron. 2020, 35, 1699–1710. [Google Scholar] [CrossRef]
- Shanmugam, S.K.; Ramachandran, S.; Arumugam, S.; Pandiyan, S.; Nayyar, A.; Hossain, E. Design and Implementation of Improved Three Port Converter and B4-Inverter Fed Brushless Direct Current Motor Drive System for Industrial Applications. IEEE Access 2020, 8, 149093–149112. [Google Scholar] [CrossRef]
- Tareen, W.U.K.; Mekhielf, S. Three-Phase Transformerless Shunt Active Power Filter with Reduced Switch Count for Harmonic Compensation in Grid-Connected Applications. IEEE Trans. Power Electron. 2018, 33, 4868–4881. [Google Scholar] [CrossRef]
- Aboutaleb, A.M.; Azazi, H.Z.; Osheba, D.S.M.; El-Abbe, A.E. Active Power Filter with Reduced Number of Semiconductor Switches Based on Synchronous Reference Frame. In Proceedings of the 2019 IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019; pp. 151–155. [Google Scholar]
- Trinh, Q.N.; Lee, H.H. An Advanced Current Control Strategy for Three-Phase Shunt Active Power Filters. IEEE Trans. Ind. Electron. 2013, 60, 5400–5410. [Google Scholar] [CrossRef]
- Joos, G.; Chen, S.; Haddad, K. Four Switch Three Phase Active Filter with Reduced Current Sensors. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference. Conference Proceedings, Galway, Ireland, 23 June 2000; pp. 1318–1323. [Google Scholar]
- Abdel-Aziz, A.Z.; Elgenedy, M.A.; Williams, B.W. Model Predictive Current Control for Low-Cost Shunt Active Power Filter. CSEE J. Power Energy Syst. 2024, 10, 1589–1598. [Google Scholar]
- Bala, S.; Patel, N.; Femandes, B.G. Reduced-Switch Three-Phase Active Power Filter with One Cycle Control. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 2333–2339. [Google Scholar]
- Komurcugil, H.; Kukrer, O. A Double-Band Hysteresis Control Approach for Three-Phase Four-Switch Active Filters with Switching Frequency Mitigation. In Proceedings of the IECON 2014–40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 1021–1027. [Google Scholar]
- Biricik, S.; Komurcugil, H. Three-Level Hysteresis Current Control Strategy for Three-Phase Four-Switch Shunt Active Filters. IET Power Electron. 2016, 9, 1732–1740. [Google Scholar] [CrossRef]
- Hoseinpour, A.; Ghazi, R. Using of A Three-Phase Four-Switch Inverter Equipped with A Variable Index PWM to Improve The Power Quality of A Wind Power Plant. Int. J. Ind. Electron. Control Optim. 2020, 3, 213–222. [Google Scholar]




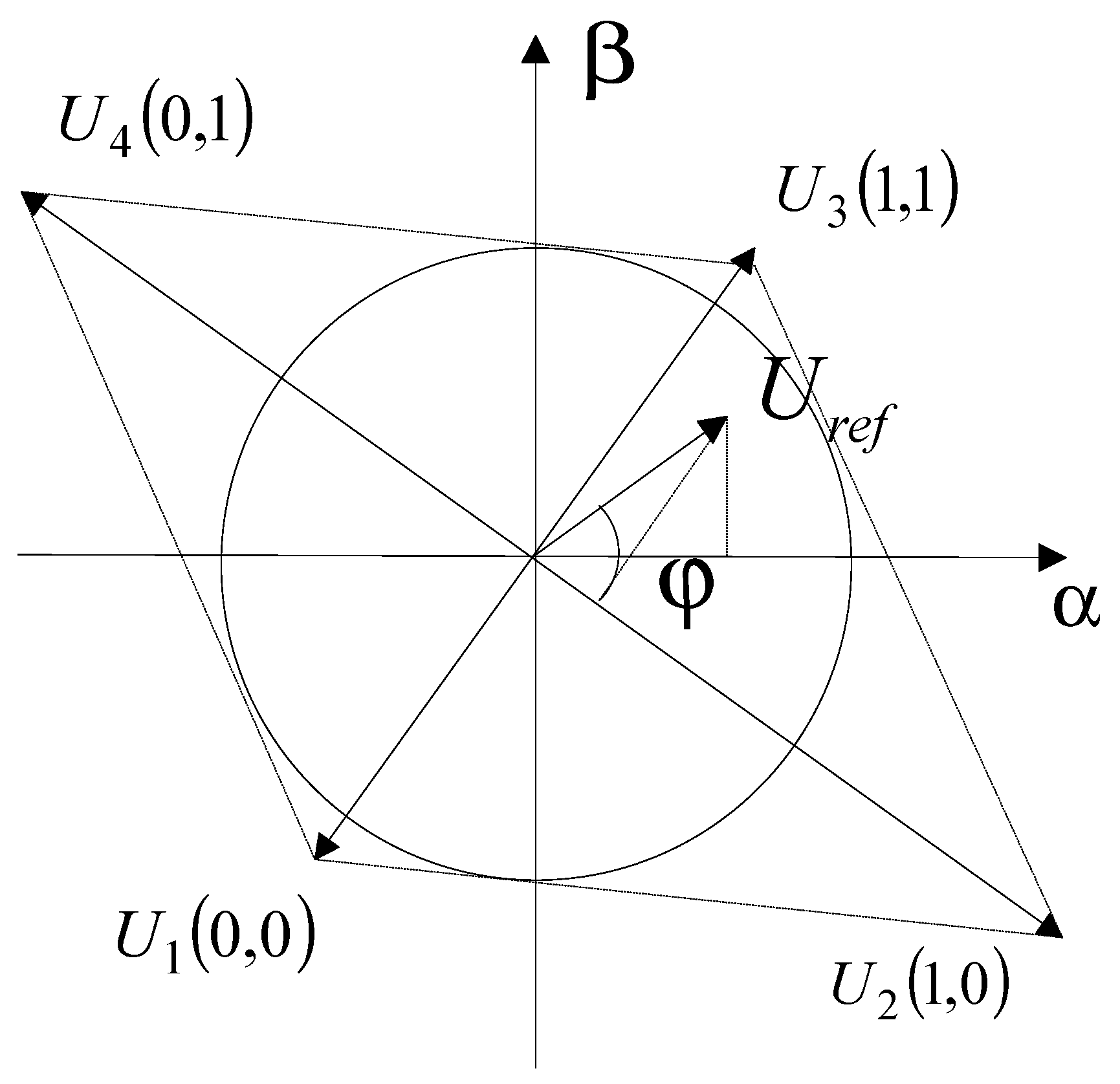

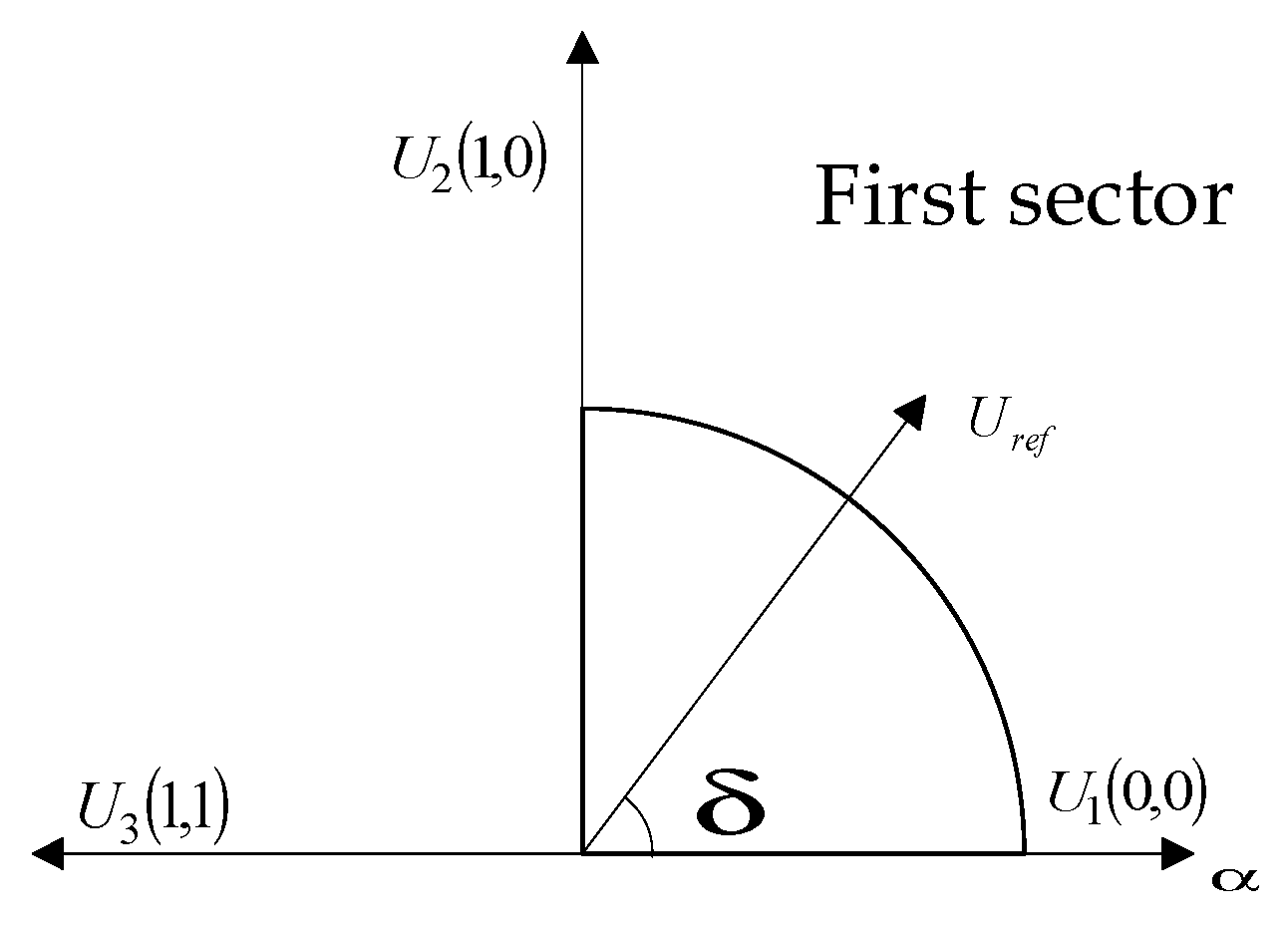
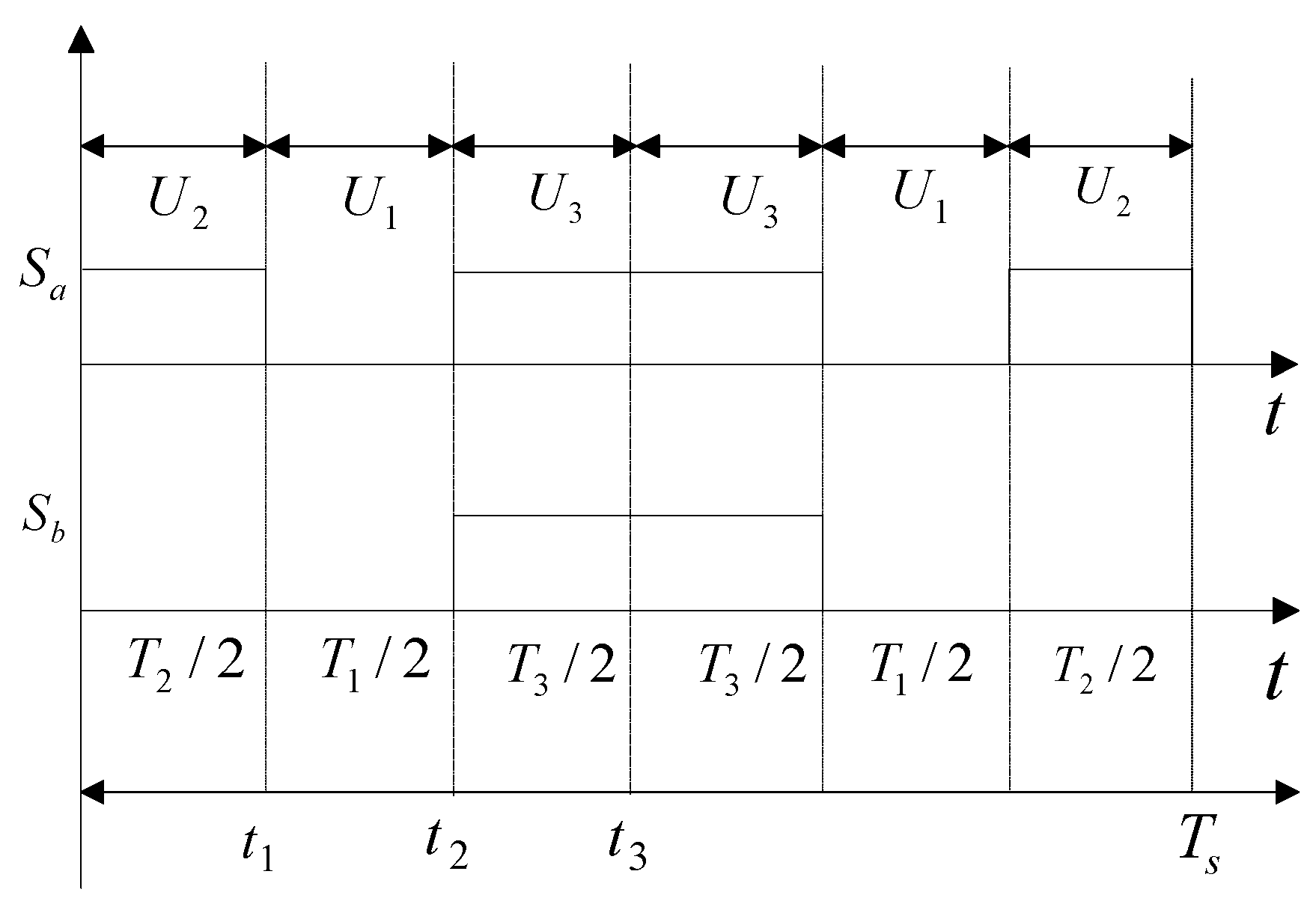






| Voltage Vector | |||
|---|---|---|---|
| 0 | 0 | ||
| 1 | 0 | ||
| 1 | 1 | ||
| 0 | 1 |
| N | Disk Sector (Computing) |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| Sector | Order | Time |
|---|---|---|
| First sector | U2, U1, U3, U1, U2 | T2/2, T1/2, T3, T1/2, T2/2 |
| Second sector | U2, U3, U1, U3, U2 | T2/2, T3/2, T1, T3/2, T2/2 |
| Third sector | U4, U3, U1, U3, U4 | T4/2, T3/2, T1, T3/2, T4/2 |
| Fourth sector | U4, U1, U3, U1, U4 | T4/2, T1/2, T3, T1/2, T4/2 |
| Sector | First Sector | Second Sector | Third Sector | Fourth Sector |
|---|---|---|---|---|
| , | , | |||
| , | , |
| Parameter | Value |
|---|---|
| Grid voltage and frequency | 380 V, 50 Hz |
| Nonlinear load | 5 Ω, 2 mH |
| Filter inductors | 2 mH |
| DC voltage | 1600 V |
| Capacitance on DC side | 5000 µF |
| Parameter | Value |
|---|---|
| Grid voltage and frequency | 50 V,50 Hz |
| Nonlinear load | 5 Ω, 2 mH |
| Filter inductors | 3 mH |
| DC voltage | 800 V |
| Capacitance on DC side | 5000 µF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Ren, Y.; Cao, Q.; Wang, L.; Yin, J. A Modified Control Strategy for Three-Phase Four-Switch Active Power Filters Based on Fundamental Positive Sequence Extraction. Processes 2024, 12, 2586. https://doi.org/10.3390/pr12112586
Xiao C, Ren Y, Cao Q, Wang L, Yin J. A Modified Control Strategy for Three-Phase Four-Switch Active Power Filters Based on Fundamental Positive Sequence Extraction. Processes. 2024; 12(11):2586. https://doi.org/10.3390/pr12112586
Chicago/Turabian StyleXiao, Chun, Yulu Ren, Qiong Cao, Lei Wang, and Jingyu Yin. 2024. "A Modified Control Strategy for Three-Phase Four-Switch Active Power Filters Based on Fundamental Positive Sequence Extraction" Processes 12, no. 11: 2586. https://doi.org/10.3390/pr12112586
APA StyleXiao, C., Ren, Y., Cao, Q., Wang, L., & Yin, J. (2024). A Modified Control Strategy for Three-Phase Four-Switch Active Power Filters Based on Fundamental Positive Sequence Extraction. Processes, 12(11), 2586. https://doi.org/10.3390/pr12112586






