Next Article in Journal
Comparative Evaluation of Wound Healing Efficacy of Bombyx mori L. Body Extracts, Gland Extracts, and Cocoon for the Treatment of Second-Degree Burns: A Pilot Study
Previous Article in Journal
The Influence of Mg, Na, and Li Oxides on the CO2 Sorption Properties of Natural Zeolite
Previous Article in Special Issue
Hydrogen in Burners: Economic and Environmental Implications
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 12
Issue 11
10.3390/pr12112593
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Growth Optimizer Algorithm for Economic Load Dispatch Problem: Analysis and Evaluation

by
Ahmed Ewis Shaban
1,
Alaa A. K. Ismaeel
2,
Ahmed Farhan
1,
Mokhtar Said
1,* and
Ali M. El-Rifaie
3,*
1
Electrical Engineering Department, Faculty of Engineering, Fayoum University, Fayoum 43518, Egypt
2
Faculty of Computer Studies (FCS), Arab Open University (AOU), Muscat 130, Oman
3
College of Engineering and Technology, American University of the Middle East, Egaila 54200, Kuwait
*
Authors to whom correspondence should be addressed.
Processes 2024, 12(11), 2593; https://doi.org/10.3390/pr12112593
Submission received: 28 October 2024 / Revised: 12 November 2024 / Accepted: 15 November 2024 / Published: 18 November 2024
(This article belongs to the Special Issue Advances in Renewable Energy Systems (2nd Edition))
Browse Figures
Versions Notes

Abstract

:
The Growth Optimizer algorithm (GO) is a novel metaheuristic that draws inspiration from people’s learning and introspection processes as they progress through society. Economic Load Dispatch (ELD), one of the primary problems in the power system, is resolved by the GO. To assess GO’s dependability, its performance is contrasted with a number of methods. These techniques include the Rime-ice algorithm (RIME), Grey Wolf Optimizer (GWO), Elephant Herding Optimization (EHO), and Tunicate Swarm Algorithm (TSA). Also, the GO algorithm has the competition of other literature techniques such as Monarch butterfly optimization (MBO), the Sine Cosine algorithm (SCA), the chimp optimization algorithm (ChOA), the moth search algorithm (MSA), and the snow ablation algorithm (SAO). Six units for the ELD problem at a 1000 MW load, ten units for the ELD problem at a 2000 MW load, and twenty units for the ELD problem at a 3000 MW load are the cases employed in this work. The standard deviation, minimum fitness function, and maximum mean values are measured for 30 different runs in order to evaluate all methods. Using the GO approach, the ideal power mismatch values of 3.82627263206814 × 10−12, 0.0000622209480241054, and 5.5893360695336 × 10−7 were found for six, ten, and twenty generator units, respectively. The GO’s dominance over all other algorithms is demonstrated by the results produced for the ELD scenarios.

1. Introduction

The growing complexity of societal and technological challenges, such as the parameter extraction problem in photovoltaic (PV) [1,2], fuel cell [3,4], charging station [5], unit commitment [6], and economic load dispatch (ELD) [7], has engineers of the twenty-first century intrigued. The aim of the economic load dispatch (ELD) is allocating power generation to satisfy load requirements at the lowest generation cost while also adhering to the practical constraints [8]. These constraints include the power balance, power generation, valve point loading effect, restricted operating zones, power transmission capability, and ramp rate limitation [9,10]. Due to these constraints, the ELD problem became a non-linear, non-smooth, non-convex, and non-differentiable optimization problem [11,12,13]. In recent years, researchers have proposed many different algorithms for tackling the difficult complex optimization ELD problem [14,15]. The output of each generating unit can be optimized such that the best output from each generating unit is achieved, resulting in reducing the fuel expenditures [16].
The term “Global optimization” refers to algorithms and strategies created for identifying the global optimum solution for an optimization problem, which means finding the optimal solution over the whole space of feasible solutions considering every potential solution [17].
Conventional calculus-based methods such as linear programming [18], LaGrange relaxation [19], dynamic programming [20], quadratic programming [21], and the interior point technique [22] are utilized for solving the ELD problem. However, these methods require a long running time and suffer from computational complexity, which makes them unsuitable for handling the large-scale optimization problems of power systems [23]. Also, conventional methods can be trapped in local optima and the global optimum solution may not be achieved when handling the ELD problem [24,25].
Recently, meta-heuristic algorithms (MH) have been utilized for tackling the complex ELD problem [26]. Unlike mathematical approaches, the MH techniques randomly solve problems in spite of the problem complexity and the constraints; also, they have the potential of controlling their exploration and exploitation aspects. Due to this advantage, MH approaches are being used more frequently to address actual optimization problems with wide search spaces [27]. Some of the most recently used MH algorithms in solving ELD problems are the enhanced social network search (ESNS) algorithm [16], golden jackal optimization (GJO) algorithm [28], hybrid moth-flame and mayfly optimization algorithm (MFMFOA) [29], Gorilla Troop Optimization (GTO) [30], Walrus Optimizer (WO) [12], Improved Yellow Saddle Goat Fish Algorithm (IYSGA) [31], Enhanced Cheetah Optimization Algorithm (ECOA) [32], Updated Differential Evolution (UDE) algorithm [33], Snow Ablation Optimizer (SAO) [16], Enhanced Beluga Whale Optimizer (EBWO) [34], Osprey Optimization Algorithm (OOA) [35], Eagle strategy supply–demand optimizer with chaotic (ESCSDO) [11], Dingo coot optimization [36], Modified weighted water cycle algorithm [37], hybrid algorithm of the exchange market algorithm (EMA) and grasshopper optimization algorithm (GOA) [27], hybrid Harris Hawks Optimizer (HHO) with the adaptive-hill-climbing optimizer [38], hybrid capuchin search algorithm with the gradient search algorithm [10], Modified Particle Swarm Optimization (MPSO) [8], adaptive backtracking algorithm with a dual learning strategy (DABSA) [26], improved manta ray foraging optimizer (IMRFO) [9], multi-objective Salp Swarm Algorithm (MSSA) [39], constrained cooperative adaptive multi-population differential evolutionary (CCAM-PDE) algorithm [24], Search and Rescue (SAR) algorithm (SAR) [40], hybrid Multi-verse Optimizer (MVO) with sequential quadratic programming (SQP) termed as Hybrid MVO (MVO-SQP) [41], Hybrid Genetic–Artificial Fish Swarm Algorithm (HGAFSA) [42], gradient-based optimizer (GBO) [7], multi-gradient particle swarm optimization (MG-PSO) algorithm [43], Chameleon Swarm Algorithm (CSA) [44], Turbulent Flow of Water Optimization (TFWO) algorithm [45], Quasi Oppositional Population-Based Global Particle Swarm Optimizer With Inertial Weights (QPGPSO-W) [46], hybrid Multi-objective Spotted Hyena Optimizer (MOSHO) and Emperor Penguin Optimizer (EPO) (MOSHEPO) [46], clustering cuckoo search optimization (CCSO) [47], Improved Bird Swarm Algorithm (IBSA) [48], artificial cooperative search (ACS) optimization algorithm [49], phasor particle swarm optimization (PPSO) [50], and Grey Wolf Optimization (GWO) algorithm [51].
As the literature demonstrates, numerous meta-heuristic optimization algorithms exist. Consequently, the no free lunch theory [52] is worth being mentioned here. This theory logically demonstrated that no single meta-heuristic algorithm is ideal for resolving every optimization issue. That is to say, a certain meta-heuristic might demonstrate extremely promising results for one set of problems but fail for other kind of problems. This reality fuels the dynamic nature of meta-heuristic research, leading to the continual development of new algorithms and improvements to existing ones. A brief summary of the literature review is presented in Table 1.
The following serves as an illustration of the primary contributions and goals of this paper:
  • The Growth Optimizer (GO), a novel metaheuristic method, is utilized to address the ELD problem.
  • Talk about ELD for the 6-, 10-, and 20-unit systems network studies.
  • The Rime-ice algorithm (RIME), Tunicate Swarm Algorithm (TSA), Grey Wolf Optimizer (GWO), and Elephant Herding Optimization (EHO) are compared with the proposed GO approach for the identical case study.
  • Also, the GO algorithm is compared with various approaches in the literature such as Monarch butterfly optimization (MBO), the Sine Cosine algorithm (SCA), the chimp optimization algorithm (ChOA), the moth search algorithm (MSA), and the snow ablation algorithm (SAO).
  • For the statistical data of all used methods, the mean, standard deviation, maximum, and minimum fitness function values over 30 runs are utilized.
  • The power imbalance between the unit’s generated power and the load demand is used to evaluate GO and all other approaches.
  • Every method is tested over thirty runs based on the robustness and convergence statistics.
  • The effectiveness of GO and all other approaches is determined by the power differential between the unit’s generated power and the load demand.
The paper is structured as follows: Section 2 discusses the ELD concerns. Section 3 discusses the GO technique. Section 4 analyzes the outcomes. Section 5 provides illustrations for the conclusion and future work.

2. Economic Load Dispatch Problem

One of the problems with the way power systems function is ELD. The primary barrier to resolving the ELD issue and optimizing the financial advantage for power plants is lowering fuel consumption expenses. The resource distribution vector in the ELD issue that maximizes power production per unit is defined by the primary variable. The ELD mathematical equations with losses can be categorized using the following names. The following formula will be used to calculate the cost of fuel used to operate generators [12]:
M i n F = F 1 P 1 + ⋯ F n P n
where F stands for the net fuel cost, F n stands for the nth generator fuel cost, and F 1 stands for the first generator fuel cost. The following techniques will be used to derive the gasoline cost function in quadratic form:
M i n F = ∑ k = 1 n F i P i = ∑ k = 1 n a k P k 2 + b k P k + c k
where c, b, and a stand for the fuel cost’s weight parameters.
∑ k = 1 n P k − P D − P L = 0
where P D indicates the total network demand and P L   is the transmission losses, which can be obtained as follows:
P L = ∑ i = 1 n ∑ j = 1 n P i B i j P j
In this case, P i stands for the generated power at the ith generator, P j stands for the generated power at the jth generator, and B i j stands for the loss factor.
P k m i n ≤ P k ≤ P k m a x

3. Growth Optimizer

The mathematical foundation of the Growth Optimizer (GO) [54], its structure and flow, and its distinctions from other humanoid metaheuristic technologies are all covered in this section. Interestingly, this section’s algorithm only addresses the minimization problem [54].

3.1. The GO Process

There are two steps to the process. The ‘learning phase’ makes up the first section, while the ‘reflection phase’ makes up the second. The ‘learning phase’ is when the person fills in the gaps left by other unique people, and the ‘reflection phase’ is when the person employs various techniques to identify and correct their own inadequacies.

3.1.1. The Learning Phase

An individual’s progress can be substantially aided by confronting and analyzing the gaps that exist between them as well as by investigating and learning from these gaps. Four frequent gaps are mathematically modelled in the GO learning phase: G a p → 1 between the leader and the elite, G a p → 2 between the leader and the bottom, G a p → 3 between the elite and the bottom, and G a p → 4 between two random people. Equation (6) describes the mathematical model for each set of gaps.
G a p → 1 = x → best − x → better G a p → 2 = x → best − x → worse G a p → 3 = x → better − x → worse G a p → 4 = x → L 1 − x → L 2  
where the society’s leader is represented by x → best and one of the next P1-1 best people referred to as an elite is represented by x → better . The elites and the leader combined comprise the upper class in GO. At the bottom of the social ladder, x → worse is among the P_1 lowest-ranking people in the population. Random people distinct from the ith individual are x → L 1 and x → L 2 . The distance between two people is expressed as G a p → k (k = 1.2.3.and 4). G a p → k enables students to properly comprehend and reap the benefits of the distinctions between two people. It is important to note that in order to make the update and the selection of these people easier, GR should be arranged in ascending order within the current iteration (It) of the GO algorithm.
For every one of the four disparity measurements, a learning factor (LF) is added to account for this fluctuation, LFk, which is modelled as shown in Equation (7), and will affect the ith individual’s learning effect on the kth group gap.
L F k = G a → p k ∑ k = 1 4   G a → p k , k = 1,2 , 3,4
When G a → p k   , the kth group gap’s Euclidean distance is represented by the normalized ratio L F k   , which has a range of [0,1]. The ith individual will gain more knowledge from the kth gap when the kth group’s gap is greater, and L F k will also be greater.
People view themselves differently depending on where they are in the growing process. The i t h person determines for himself the extent of acceptable knowledge by using S F i   . A higher SFi indicates that in order to better himself, individual i has to learn more. Equation (8) models S F i .
S F i = G R i G R m a x
where G R m a x   is the greatest growth resistance of all and G R i   is the growth resistance of the ith person. Generally speaking, a smaller G R i   indicates that an individual will extract and assimilate knowledge more to the extent that his level is higher. As a result, the person ought to receive a reduced S F i   , which is skewed towards engaging in local exploitation practises. If G R i   is greater, it indicates that the ith individual is insufficient and that the individual needs to close the knowledge gaps. As a result, the individual is biased towards executing global search patterns and ought to receive a higher S F i .
Knowledge transformation and learning are lossy processes. The person I learns something from the k t h group of gaps G a p → k   , and this information is the kth group of knowledge acquisition K A → k   . Equation (9) describes the method by which L F k and S F i operate on the kth group gap to obtain K A → k for the i t h individual.
K A → k = S F i · L F k · G a p → k , k = 1,2 , 3,4
where the knowledge that the ith person from the kth group of the gap has learned is denoted by K A → k , L F k evaluates the external environment, and S F i evaluates its internal circumstance. The ith person completes the learning process by determining his own needed knowledge ( K A → k from G a p → k ) as a result of both assessments’ influence.
The ith individual completes a rich knowledge accumulation process by absorbing the knowledge gaps between distinct individuals; the ith individual’s specialized learning process is provided by Equation (10).
x → i I t + 1 = x → i I t + K A → 1 + K A → 2 + K A → 3 + K A → 4
where It is the number of current iterations, and x → i is the ith individual who absorbs the knowledge acquired during the learning phase to grow.
Following the modification of the learning phase, each individual’s candidate solution quality may advance or regress. Therefore, it is imperative to confirm whether it has actually advanced. The ith individual’s GRi will drop and its rank will rise if progress is accomplished. The ith individual has a high chance of losing part of the knowledge they have learned if they regress, but because learning takes time and effort, there is a slim chance that they will retain the knowledge they have learned. In this case, P2 is in charge of regulating this retention probability. Equation (11) describes this procedure.
x i → I t + 1 = → I t + 1           i f   f x i → i t + 1 < f x i → i t → I t + 1           i f   r 1 < P 2 → I t          
where P 2 decides whether the newly learned information is kept when the ith person fails to update, r 1 is a uniformly distributed random number in the range [0,1], and ind (i) is the ranking of the ith individual in accordance with the GR ascending order. P 2 in this case is 0.001. The full conditional judgement statement for holding onto the newly learned information (in the event that the individual update fails) is provided here because of space constraints in Equation (11): r 1 < P 2 && i n d ⁡ ( i ) ∼ = i n d ⁡ ( 1 ) . This guarantees that the existing global optimal solution cannot be replaced, which might prevent the algorithm from converging. It also indicates that when an individual update fails, the individual has a 0.001 probability of joining the population of the following generation.
Using five vectors to provide four bits of information about the convergence direction, the learning operator is a cooperative search approach. The likelihood of the algorithm slipping into a local optimum trap is significantly decreased by balancing this four-directional information through the fitness value and distance between the vectors.

3.1.2. The Reflection Phase

Reflection and learning go hand in hand. As a result, a person ought to acquire both learning and reflecting skills. This suggests that a person should retain his competence and review and make up for any areas where he may have failed. They should learn from great people about their undesirable traits while retaining their positive traits. Resuming systematic learning is the best course of action when prior information is discarded and a particular feature of the lesson cannot be corrected. Equations (12) and (13) provide a mathematical model of the reflecting process of GO.
x i . j I t + 1 = l b + r 4 × u b − l b           i f   r 3 < A F x i . j I t + r 5 × R j − x i . j I t             i f   r 2 < P 3 x i . j I t
F = 0.01 + 0.99 × 1 − F E s M a x F E s
where r 2 , r 3 , r 4 ,   a n d   r 5   are uniformly distributed random values in the interval [0,1], and ub and lb are the upper and lower bounds of the search domain. The probability of reflection is determined by P 3 , which is typically set to 0.3. The current number of evaluations (FEs) and the maximum number of evaluations (MaxFEs) combine to form the attenuation factor (AF). The value of AF will progressively converge to 0.01 as the algorithm iterates, preventing wasting needless time from frequent initialization as a person advances. During the reflection phase, an upper-level individual R → . R → will provide guidance to the i t h individual’s j t h aspect. This indicates a high-level individual and acts as a guide for introspective learning for the present individual I. The knowledge of the j t h aspect of R ‗ is denoted by R j   . If the jth aspect of the i t h individual really needs to learn from others, there will be an upper-level individual as R → to guide it. This is because the range of R → is specified as the top P 1 + 1 individuals (the leader or the elite) in the population.
The same is true for the learning stage: after finishing his reflection, the individual should assess whether he has improved. Equation (11) is still used for the entire verification procedure as well as the ensuing actions.

3.2. The GO Pseudocode

The comprehensive implementation of GO is given in this subsection. Algorithm 1 provides the GO pseudocode.
Algorithm 1: This is the GO algorithm pseudocode.
Input: N, M a x F E s , D, u b , l b , P 3 = 0.3, P 2 = 0.001, P 1 = 0.3
Result: worldwide ideal outcome g b e s t x →
Use x → = lb + (ub − lb) − rand(N, D) to initialize the population and then evaluate (i = 1, ……, N)
while FEs <= MaxFEs
X b e s t = X(ind(1).:)
for i = 1 : N
Calculate Gapk using Equation (6).
Calculate L F k using Equation (7).
Calculate S F i using Equation (8).
Calculate K A → k using Equation (9).
As Equation (10), finish the learning process for the ith individual once.
Finalize the ith individual’s update in accordance with Equation (11) Real-time update g b e s t x →
end
for i = 1: N
Follow Equations (12) and (13) to finish the reflection process for the ith individual once.
Finalize the ith individual’s update in accordance with Equation (11) Real-time update g b e s t x →
End
End
Export g b e s t x →
The core operator in the GO learning phase is designed with inspiration from the effect of several persons. This means that the operator itself avoids the strong influence of a few individuals and may reduce the likelihood of errors in the algorithm’s search direction. In order to enhance the algorithm’s capacity for local exploitation, the reflection phase of GO depends on an exceptional individual to provide guidance or facilitate relearning with a low likelihood, all while retaining the majority of its benefits.

4. ELD Results

The GO performance is donated to the ELD. The proposed GO approach was evaluated using the Rime-ice algorithm (RIME) [55], Tunicate Swarm Algorithm (TSA) [56], Grey Wolf Optimizer (GWO) [51], and Elephant Herding Optimization (EHO) [57]. The following case studies took advantage of the ELD issue:
  • Six generators operating at a load of 1000 MW comprise the first case study.
  • There are 10 generators in the second case study operating at a 2000 MW load.
  • The third case study has 20 generators operating at a 3000 MW load.

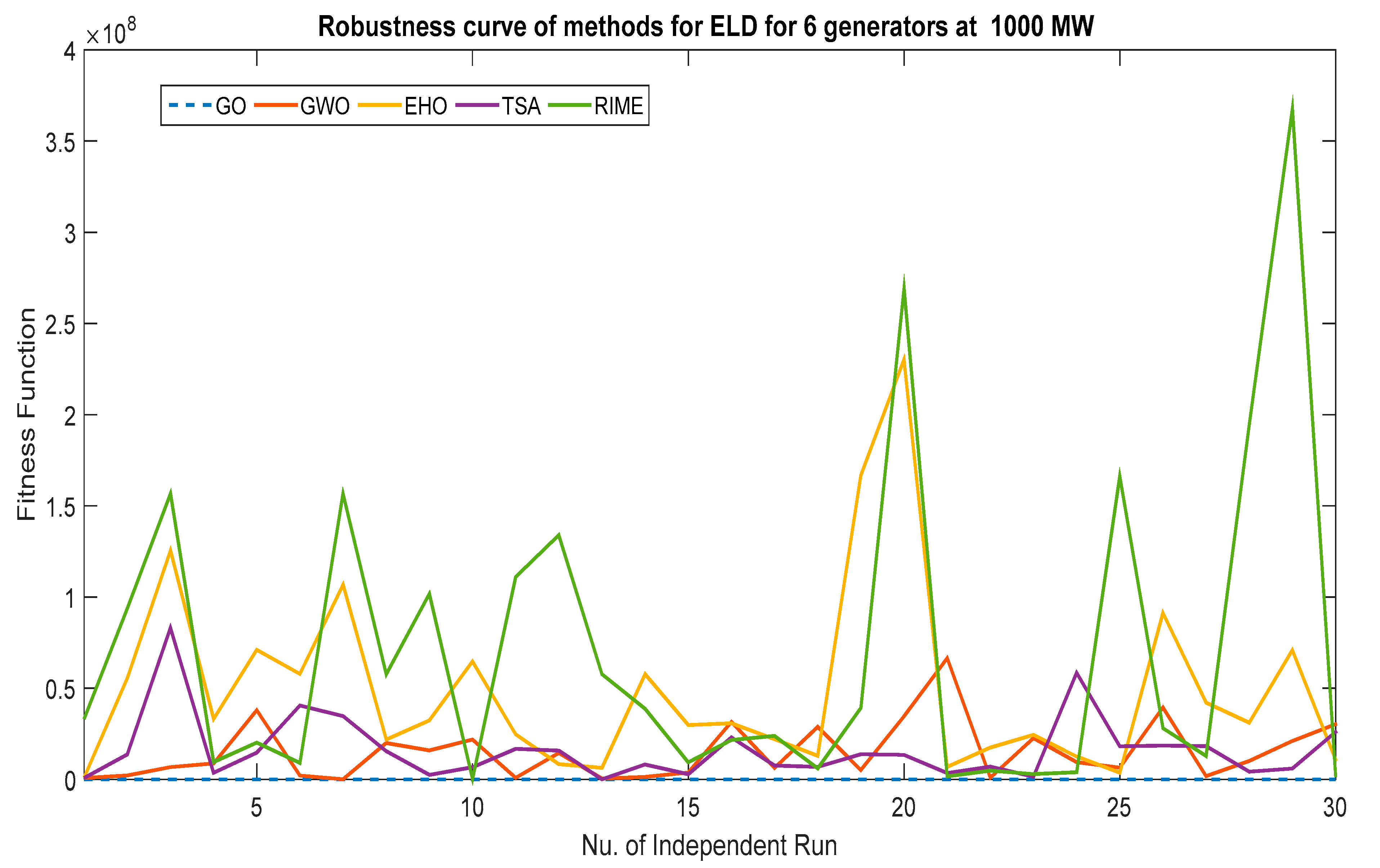
4.1. Analysis Results of Six Generators

A case study with six generators running at a 1000 MW load is donated in order to examine the ELD issue. Numerous methods were employed, such as the GWO, TSA, RIME, EHO, and GO algorithms. The effectiveness of each competing method was evaluated over thirty runs. Using these runs, the mean, maximum, minimum, and standard deviation values were recorded as statistical data for every load, as indicated in Table 2. The GO calculates the ideal goal function and standard deviation using these data. Thus, the most accurate and dependable algorithm for ELD is the GO algorithm. Table 3 shows the optimal gasoline price. The ideal power supplied by each unit to recover the 1000 MW load need is displayed in Table 4, which was produced using the best objective function across all strategies. Based on the outcomes of every technique recorded over the course of the 30 runs, the robustness curve calculates the fitness function value for each run. Figure 1 displays the robustness curve attribute for the six-unit system. Based on the GO approach, Table 5 provides an explanation of the anticipated sharing power from each unit across the thirty runs for six units.

4.2. Analysis Results of Ten Generators

A case study with ten generators running at a 2000 MW load is donated in order to examine the ELD issue. Numerous methods were employed, such as the GWO, TSA, RIME, EHO, and GO algorithms. The effectiveness of each competing method was evaluated over thirty runs. Using these runs, the mean, maximum, minimum, and standard deviation values were recorded as statistical data for every load, as indicated in Table 6. The GO calculates the ideal goal function and standard deviation using these data. Thus, the most accurate and dependable algorithm for ELD is the GO algorithm. Table 7 shows the optimal gasoline price. The ideal power supplied by each unit to recover the 2000 MW load need is displayed in Table 8, which was produced using the best objective function across all strategies. Based on the outcomes of every technique recorded over the course of the 30 runs, the robustness curve calculates the fitness function value for each run. Figure 2 displays the robustness curve attribute for the ten-unit system. Based on the GO approach, Table 9 provides an explanation of the anticipated sharing power from each unit across the thirty runs for ten units.

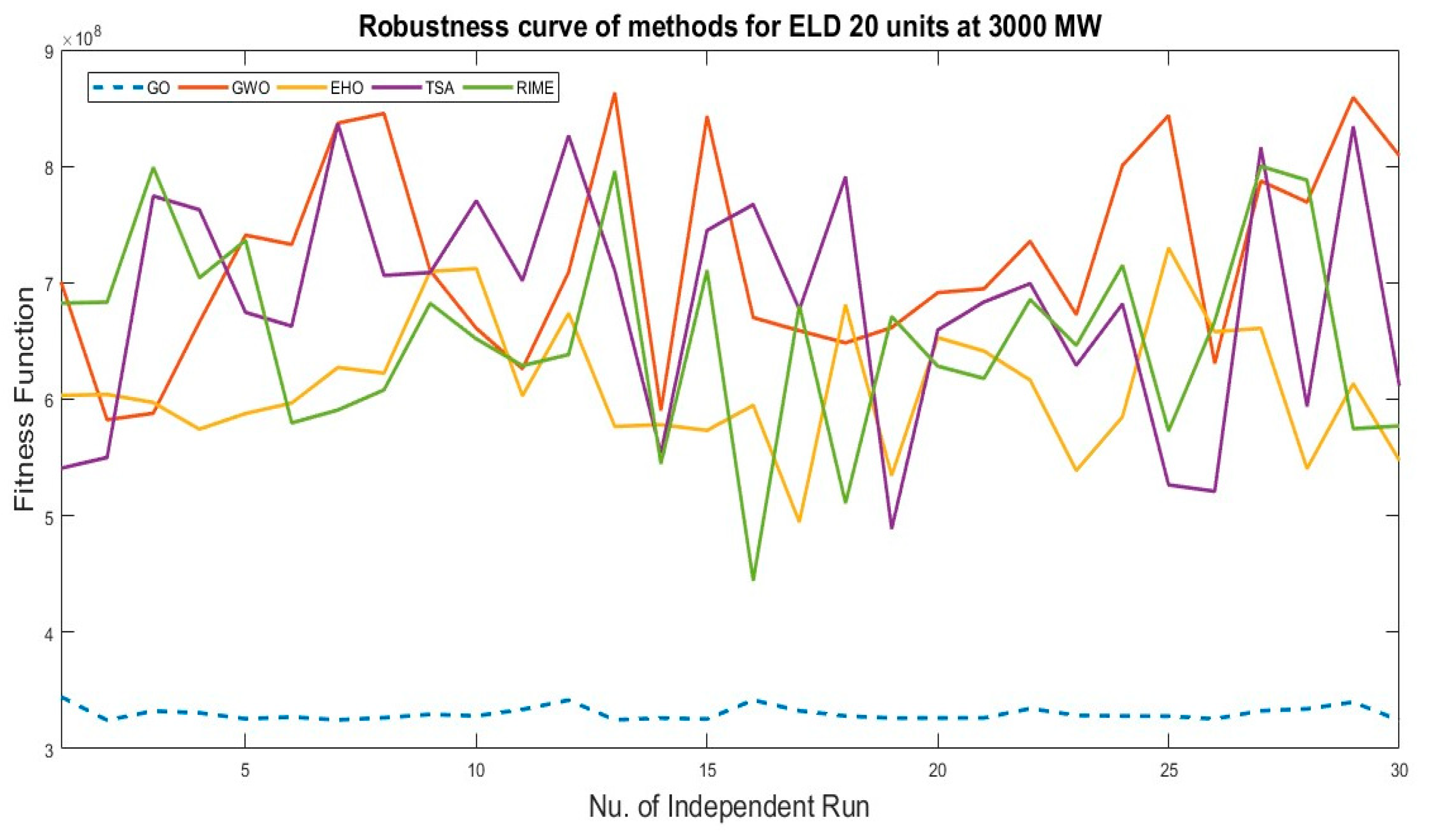
4.3. Analysis Results of Twenty Generators

A case study with twenty generators running at a 3000 MW load is donated in order to examine the ELD issue. Numerous methods were employed, such as the GWO, TSA, RIME, EHO, and GO algorithms. The effectiveness of each competing method was evaluated over thirty runs. Using these runs, the mean, maximum, minimum, and standard deviation values were recorded as statistical data for every load, as indicated in Table 10. The GO calculates the ideal goal function and standard deviation using these data. Thus, the most accurate and dependable algorithm for ELD is the GO algorithm. Table 11 shows the optimal gasoline price. The ideal power supplied by each unit to recover the 3000 MW load need is displayed in Table 12, which was produced using the best objective function across all strategies. Based on the outcomes of every technique recorded over the course of the 30 runs, the robustness curve calculates the fitness function value for each run. Figure 3 displays the robustness curve attribute for the ten-unit system. Based on the GO approach, Table 13 provides an explanation of the anticipated sharing power from each unit across the thirty runs for ten units.

4.4. Discussion

The power mismatch value is the primary cause of ELD issues, the exact discrepancy between the total demand plus transmission losses and the power units generated. Since the power mismatch value is almost zero, high-performance techniques are used to obtain it. The significance of this element for ELD is explained in Table 14. Along with the five techniques employed in the run, the suggested GO algorithm is compared to other techniques from the literature, including the snow ablation algorithm (SAO), chimp optimization algorithm (ChOA), moth search algorithm (MSA), Monarch butterfly optimization (MBO), and Sine Cosine algorithm (SCA) [12].

5. Conclusions

Growth Optimizer (GO) is a novel metaheuristic algorithm that mimics and takes inspiration from people’s learning and self-reflection throughout society. Furthermore, GO’s efficacy is compared to that of twelve different algorithms. In this study, GO is used to solve a critical problem: Economic Load Dispatch (ELD). In particular, ELD reduces fuel consumption expenditures. The primary concern in optimizing the ELD problem is fuel consumption, and GO aims to minimize this expense while maximizing the power system’s economic value. The unit-specific allocation vector that establishes the optimal output for every system unit is reflected in the major variable of the ELD problem. A number of techniques, such the Grey Wolf Optimizer (GWO), Tunicate Swarm Algorithm (TSA), Rime-ice algorithm (RIME), and Elephant Herding Optimization (EHO), are used to compare the performance of GO. When compared to the alternatives, the results ultimately confirmed that GO was beneficial in reducing the cost of fuel for ELD. For six generating units operating at a demand load of 1000 MW, the GO method yields the optimal fuel cost value of 12,119.2864397972. For ten generator units with a demand load of 2000 MW, the GO technique yields the optimal fuel cost value of 402,837,175.865899. For 20 generating units with a demand load of 3000 MW, the GO technique yields the optimal fuel cost value of 324,256,382.003049. The optimal power mismatch values for six, ten, and twenty generator units were determined using the GO technique to be 3.82627263206814 × 10−12, 0.0000622209480241054, and 5.5893360695336 × 10−7, respectively. The GO approach will be used in the future to solve other large-scale, real-world optimization problems pertaining to photovoltaic energy and power systems.

Author Contributions

Conceptualization, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; methodology, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; software, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; validation, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; formal analysis, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; investigation, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; resources; data curation, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; writing—original draft preparation, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; writing—review and editing, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; visualization, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; supervision, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; project administration, A.E.S., A.A.K.I., M.S., A.F. and A.M.E.-R.; funding acquisition, A.M.E.-R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Said, M.; Shaheen, A.M.; Ginidi, A.R.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Estimating Parameters of Photovoltaic Models Using Accurate Turbulent Flow of Water Optimizer. Processes 2021, 9, 627. [Google Scholar] [CrossRef]
  2. Ben Aribia, H.; El-Rifaie, A.M.; Tolba, M.A.; Shaheen, A.; Moustafa, G.; Elsayed, F.; Elshahed, M. Growth Optimizer for Parameter Identification of Solar Photovoltaic Cells and Modules. Sustainability 2023, 15, 7896. [Google Scholar] [CrossRef]
  3. Houssein, E.H.; Samee, N.A.; Alabdulhafith, M.; Said, M. Extraction of PEM Fuel Cell Parameters using Walrus Optimizer. AIMS Math. 2024, 9, 12726–12750. [Google Scholar] [CrossRef]
  4. Ismaeel, A.A.; Houssein, E.H.; Khafaga, D.S.; Aldakheel, E.A.; Said, M. Performance of rime-ice algorithm for estimating the PEM fuel cell parameters. Energy Rep. 2024, 11, 3641–3652. [Google Scholar] [CrossRef]
  5. Said, M.; Houssein, E.H.; Deb, S.; Alhussan, A.A.; Ghoniem, R.M. A Novel Gradient Based Optimizer for Solving Unit Commitment Problem. IEEE Access 2022, 10, 18081–18092. [Google Scholar] [CrossRef]
  6. Houssein, E.H.; Deb, S.; Oliva, D.; Rezk, H.; Alhumade, H.; Said, M. Performance of Gradient-Based Optimizer on Charging Station Placement Problem. Mathematics 2021, 9, 2821. [Google Scholar] [CrossRef]
  7. Deb, S.; Abdelminaam, D.S.; Said, M.; Houssein, E.H. Recent methodology-based gradient-based optimizer for economic load dispatch problem. IEEE Access 2021, 9, 44322–44338. [Google Scholar] [CrossRef]
  8. Singh, N.; Chakrabarti, T.; Chakrabarti, P.; Margala, M.; Gupta, A.; Praveen, S.P.; Krishnan, S.B.; Unhelkar, B. Novel heuristic optimization technique to solve economic load dispatch and economic emission load dispatch problems. Electronics 2023, 12, 2921. [Google Scholar] [CrossRef]
  9. Chen, C.; Qu, L.; Tseng, M.L.; Li, L.; Chen, C.C.; Lim, M.K. Reducing fuel cost and enhancing the resource utilization rate in energy economic load dispatch problem. J. Clean. Prod. 2022, 364, 132709. [Google Scholar] [CrossRef]
  10. Braik, M.; Awadallah, M.A.; Al-Betar, M.A.; Hammouri, A.I. A hybrid capuchin search algorithm with gradient search algorithm for economic dispatch problem. Soft Comput. 2023, 27, 16809–16841. [Google Scholar] [CrossRef]
  11. Hassan, M.H.; Kamel, S.; Eid, A.; Nasrat, L.; Jurado, F.; Elnaggar, M.F. A developed eagle-strategy supply-demand optimizer for solving economic load dispatch problems. Ain Shams Eng. J. 2023, 14, 102083. [Google Scholar] [CrossRef]
  12. Said, M.; Houssein, E.H.; Aldakheel, E.A.; Khafaga, D.S.; Ismaeel, A.A.K. Performance of the Walrus Optimizer for solving an economic load dispatch problem. AIMS Math. 2024, 9, 10095–10120. [Google Scholar] [CrossRef]
  13. Mohammadi, F.; Abdi, H. A modified crow search algorithm (MCSA) for solving economic load dispatch problem. Appl. Soft Comput. 2018, 71, 51–65. [Google Scholar] [CrossRef]
  14. He, X.; Rao, Y.; Huang, J. A novel algorithm for economic load dispatch of power systems. Neurocomputing 2016, 171, 1454–1461. [Google Scholar] [CrossRef]
  15. Ali, M.H.; El-Rifaie, A.M.; Youssef, A.A.F.; Tulsky, V.N.; Tolba, M.A. Techno-Economic Strategy for the Load Dispatch and Power Flow in Power Grids Using Peafowl Optimization Algorithm. Energies 2023, 16, 846. [Google Scholar] [CrossRef]
  16. Ismaeel, A.A.K.; Houssein, E.H.; Khafaga, D.S.; Aldakheel, E.A.; AbdElrazek, A.S.; Said, M. Performance of Snow Ablation Optimization for Solving Optimum Allocation of Generator Units. IEEE Access 2024, 12, 17690–17707. [Google Scholar] [CrossRef]
  17. Hassan, M.H.; Kamel, S.; Jurado, F.; Desideri, U. Global optimization of economic load dispatch in large scale power systems using an enhanced social network search algorithm. Int. J. Electr. Power Energy Syst. 2024, 156, 109719. [Google Scholar] [CrossRef]
  18. Jabr, R.; Coonick, A.; Cory, B. A homogeneous linear programming algorithm for the security constrained economic dispatch problem. IEEE Trans. Power Syst. 2000, 15, 930–936. [Google Scholar] [CrossRef]
  19. Raj, V.M.; Chanana, S. Analysis of unit commitment problem through Lagrange relaxation and priority listing method. In Proceedings of the 2014 6th IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014. [Google Scholar]
  20. Xu, Y.; Zhang, W.; Liu, W. Distributed Dynamic Programming-Based Approach for Economic Dispatch in Smart Grids. IEEE Trans. Ind. Inform. 2015, 11, 166–175. [Google Scholar] [CrossRef]
  21. Papageorgiou, L.G.; Fraga, E.S. A mixed integer quadratic programming formulation for the economic dispatch of generators with prohibited operating zones. Electr. Power Syst. Res. 2007, 77, 1292–1296. [Google Scholar] [CrossRef]
  22. Lin, W.-M.; Chen, S.-J. Bid-based dynamic economic dispatch with an efficient interior point algorithm. Int. J. Electr. Power Energy Syst. 2002, 24, 51–57. [Google Scholar] [CrossRef]
  23. Mishra, S.; Shaik, A.G. Solving bi-objective economic-emission load dispatch of diesel-wind-solar microgrid using African vulture optimization algorithm. Heliyon 2024, 10, e24993. [Google Scholar] [CrossRef] [PubMed]
  24. Fu, L.; Ouyang, H.; Zhang, C.; Li, S.; Mohamed, A.W. A constrained cooperative adaptive multi-population differential evolutionary algorithm for economic load dispatch problems. Appl. Soft Comput. 2022, 121, 108719. [Google Scholar] [CrossRef]
  25. Sharifzadeh, H. Two efficient logarithmic formulations to solve nonconvex economic dispatch. Electr. Power Syst. Res. 2024, 229, 110123. [Google Scholar] [CrossRef]
  26. Hu, Z.; Dai, C.; Su, Q. Adaptive backtracking search optimization algorithm with a dual-learning strategy for dynamic economic dispatch with valve-point effects. Energy 2022, 248, 123558. [Google Scholar] [CrossRef]
  27. Sharifian, Y.; Abdi, H. Solving multi-area economic dispatch problem using hybrid exchange market algorithm with grasshopper optimization algorithm. Energy 2023, 267, 126550. [Google Scholar] [CrossRef]
  28. Ragunathan, R.; Ramadoss, B. Golden jackal optimization for economic load dispatch problems with complex constraints. Bull. Electr. Eng. Inform. 2024, 13, 781–793. [Google Scholar] [CrossRef]
  29. Jain, A.K.; Gidwani, L. Dynamic economic load dispatch in microgrid using hybrid moth-flame optimization algorithm. Electr. Eng. 2024, 106, 3721–3741. [Google Scholar] [CrossRef]
  30. Wadood, A.; Ghani, A. An application of Gorilla troops optimizer in solving the problem of economic load dispatch considering valve point loading effect. Eng. Res. Express 2024, 6, 015310. [Google Scholar] [CrossRef]
  31. Brar, M.S.; Brar, G.S. Economic Load Dispatch using IYSGA. Eur. J. Theor. Appl. Sci. 2024, 2, 595–606. [Google Scholar] [CrossRef]
  32. Nagarajan, K.; Rajagopalan, A.; Bajaj, M.; Sitharthan, R.; Mohammadi, S.A.D.; Blazek, V. Optimizing dynamic economic dispatch through an enhanced Cheetah-inspired algorithm for integrated renewable energy and demand-side management. Sci. Rep. 2024, 14, 3091. [Google Scholar] [CrossRef] [PubMed]
  33. Tiwari, P.; Mishra, V.N.; Parouha, R.P. Optimization of economic dispatch using updated differential evolution algorithm. Int. J. Inf. Technol. 2024, 16, 2315–2329. [Google Scholar] [CrossRef]
  34. Hassan, M.H.; Kamel, S.; Jurado, F.; Ebeed, M.; Elnaggar, M.F. Economic load dispatch solution of large-scale power systems using an enhanced beluga whale optimizer. Alex. Eng. J. 2023, 72, 573–591. [Google Scholar] [CrossRef]
  35. Ismaeel, A.A.K.; Houssein, E.H.; Khafaga, D.S.; Aldakheel, E.A.; AbdElrazek, A.S.; Said, M. Performance of osprey optimization algorithm for solving economic load dispatch problem. Mathematics 2023, 11, 4107. [Google Scholar] [CrossRef]
  36. Singh, P.; Singh, S.; Paprzycki, M. DICO: Dingo coot optimization-based ZF net for pansharpening. Int. J. Knowl.-Based Intell. Eng. Syst. 2022, 26, 271–288. [Google Scholar] [CrossRef]
  37. Bisoi, R.; Parhi, P.; Dash, P. Hybrid modified weighted water cycle algorithm and Deep Analytic Network for forecasting and trend detection of forex market indices. Int. J. Knowl.-Based Intell. Eng. Syst. 2022, 26, 249–269. [Google Scholar] [CrossRef]
  38. Al-Betar, M.A.; Awadallah, M.A.; Makhadmeh, S.N.; Abu Doush, I.; Abu Zitar, R.; Alshathri, S.; Elaziz, M.A. A hybrid Harris Hawks optimizer for economic load dispatch problems. Alex. Eng. J. 2023, 64, 365–389. [Google Scholar] [CrossRef]
  39. Hassan, M.H.; Kamel, S.; Domínguez-García, J.L.; El-Naggar, M.F. MSSA-DEED: A multi-objective salp swarm algorithm for solving dynamic economic emission dispatch problems. Sustainability 2022, 14, 9785. [Google Scholar] [CrossRef]
  40. Said, M.; Houssein, E.H.; Deb, S.; Ghoniem, R.M.; Elsayed, A.G. Economic load dispatch problem based on search and rescue optimization algorithm. IEEE Access 2022, 10, 47109–47123. [Google Scholar] [CrossRef]
  41. Iqbal, M.N.; Bhatti, A.R.; Butt, A.D.; Sheikh, Y.A.; Paracha, K.N.; Ashique, R.H. Solution of economic dispatch problem using hybrid multi-verse optimizer. Electr. Power Syst. Res. 2022, 208, 107912. [Google Scholar] [CrossRef]
  42. Kabir, A.M.; Kamal, M.; Ahmad, F.; Ullah, Z.; Albogamy, F.R.; Hafeez, G.; Mehmood, F. Optimized economic load dispatch with multiple fuels and valve-point effects using hybrid genetic–artificial fish swarm algorithm. Sustainability 2021, 13, 10609. [Google Scholar] [CrossRef]
  43. Al-Bahrani, L.; Seyedmahmoudian, M.; Horan, B.; Stojcevski, A. Solving the real power limitations in the dynamic economic dispatch of large-scale thermal power units under the effects of valve-point loading and ramp-rate limitations. Sustainability 2021, 13, 1274. [Google Scholar] [CrossRef]
  44. Said, M.; El-Rifaie, A.M.; Tolba, M.A.; Houssein, E.H.; Deb, S. An efficient chameleon swarm algorithm for economic load dispatch problem. Mathematics 2021, 9, 2770. [Google Scholar] [CrossRef]
  45. Deb, S.; Houssein, E.H.; Said, M.; Abdelminaam, D.S. Performance of Turbulent Flow of Water Optimization on Economic Load Dispatch Problem. IEEE Access 2021, 9, 77882–77893. [Google Scholar] [CrossRef]
  46. Salaria, U.A.; Menhas, M.I.; Manzoor, S. Quasi Oppositional Population Based Global Particle Swarm Optimizer With Inertial Weights (QPGPSO-W) for Solving Economic Load Dispatch Problem. IEEE Access 2021, 9, 134081–134095. [Google Scholar] [CrossRef]
  47. Yu, J.; Kim, C.-H.; Rhee, S.-B. Clustering cuckoo search optimization for economic load dispatch problem. Neural Comput. Appl. 2020, 32, 16951–16969. [Google Scholar] [CrossRef]
  48. Fu, C.; Zhang, S.; Chao, K.-H. Energy management of a power system for economic load dispatch using the artificial intelligent algorithm. Electronics 2020, 9, 108. [Google Scholar] [CrossRef]
  49. Kaboli, S.H.A.; Alqallaf, A.K. Solving non-convex economic load dispatch problem via artificial cooperative search algorithm. Expert Syst. Appl. 2019, 128, 14–27. [Google Scholar] [CrossRef]
  50. Gholamghasemi, M.; Akbari, E.; Asadpoor, M.B.; Ghasemi, M. A new solution to the non-convex economic load dispatch problems using phasor particle swarm optimization. Appl. Soft Comput. 2019, 79, 111–124. [Google Scholar] [CrossRef]
  51. Xu, J.; Yan, F.; Yun, K.; Su, L.; Li, F.; Guan, J. Noninferior Solution Grey Wolf Optimizer with an Independent Local Search Mechanism for Solving Economic Load Dispatch Problems. Energies 2019, 12, 2274. [Google Scholar] [CrossRef]
  52. Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
  53. Dhiman, G. MOSHEPO: A hybrid multi-objective approach to solve economic load dispatch and micro grid problems. Appl. Intell. 2020, 50, 119–137. [Google Scholar] [CrossRef]
  54. Zhang, Q.; Gao, H.; Zhan, Z.-H.; Li, J.; Zhang, H. Growth Optimizer: A powerful metaheuristic algorithm for solving continuous and discrete global optimization problems. Knowl.-Based Syst. 2022, 261, 110206. [Google Scholar] [CrossRef]
  55. Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
  56. Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
  57. Wang, G.G.; Deb, S.; Coelho, L.D.S. Elephant herding optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI), Bali, Indonesia, 7–9 December 2015; pp. 1–5. [Google Scholar]
Processes 12 02593 g001
Figure 1. Robustness curves for six generators under a 1000 MW load.
Figure 1. Robustness curves for six generators under a 1000 MW load.
Processes 12 02593 g001
Processes 12 02593 g002
Figure 2. Robustness curves for ten generators under a 2000 MW load.
Figure 2. Robustness curves for ten generators under a 2000 MW load.
Processes 12 02593 g002
Processes 12 02593 g003
Figure 3. Robustness curves for twenty generators under a 3000 MW load.
Figure 3. Robustness curves for twenty generators under a 3000 MW load.
Processes 12 02593 g003
Table 1. Brief summary of the literature review.
Table 1. Brief summary of the literature review.
YearRef.Brief Summary
2024[17]The Enhanced Social Network Search (ESNS) optimizer is used for solving the ELD problem. The algorithm is applied on four test cases containing 11, 15, 40, and 110 generating units. The outcomes of the ESNS are compared with the results of well-known algorithms. The ESNS demonstrated better performance in terms of the speed of convergence and solution quality.
2024[28]The golden jackal optimization (GJO) is used for solving the ELD problem considering the two constraints restricted operating zones and valve point loading effect (VPL). To assess the effectiveness of the suggested GJO method, six distinct test systems, each comprising 6, 10, 13, 40, or 140 units with several constraints, are employed. The results of the GTO algorithm showed minimum fuel costs and good convergence compared with the results of other used algorithms for comparison.
2024[29]The paper proposed the hybrid moth-flame and mayfly optimization algorithm (MFMFOA) to solve the complex problem of ELD and emission dispatch. When the results of MFMFOA are in comparison with the results of other approaches presented in the literature for different case studies, it demonstrated minimum operational costs, better convergence, and a closer optimum point.
2024[30]Gorilla Troop Optimization (GTO) is applied for addressing the ELD problem with and without the VPL. The performance of the GTO is assessed using four distinct IEEE unit systems, with 3, 6, 10, and 40-units.GTO consistently outperforms other algorithms in minimizing total fuel costs, accelerating convergence, and reducing the computation time to reach the global optima across all case studies.
2024[12]Walrus Optimizer (WO) is used for addressing the ELD problem. In order to test its reliability, the performance of the WO is in comparison with the performance of other MH algorithms in the same case study with different scenarios including 6, 10, 20, and 30 generators at different load demands. The WO algorithm demonstrated superior performance compared to all other algorithms, as confirmed by the comparative analysis
2024[31]An Improved Yellow Saddle Goat Fish Algorithm (IYSGA) is proposed for resolving ELD issues. The objective of the proposed algorithm is to minimize the difference between the generated load and the required demand along with the unit cost. The performance of IYSGA showed an enhanced solution quality, convergence rate, and exploring ability over the other tested algorithm.
2024[32]Enhanced Cheetah Optimization Algorithm (ECOA) is utilized for solving the dynamic ELD problem. The study also includes renewable energy resources along with conventional resources. The Efficacy of the algorithm is evaluated using two test cases using 10 units and 20 units and the comparative analysis of the results is conducted with COA and GWA. The comparison revealed that ECOA has better reliability and adaptability.
2024[33]The updated differential evolution (UDE) algorithm is used for resolving the ELD issue. The UDE is investigated using a collection of bench-mark suites of IEEE CEC2006. The simulation outputs revealed that UDE surpasses other modern approaches used in the comparison.
2024[16]The snow ablation optimizer (SAO) is used for tackling the ELD issue. The SAO’s reliability is evaluated by comparing its performance to that of other techniques using the same six case studies. The results obtained for the test cases indicate that the SAO significantly outperforms the other algorithms, thus proving its excellence.
2023[34]The enhanced beluga whale optimizer (EBWO) is utilized for tackling the complex ELD problem on a large scale. To validate EBWO, seven benchmark functions are used in the simulation; then, it is applied on systems with 11, 40, and 110 generating units, and a comparative analysis of performance is conducted against literature algorithms. From the comparison results, it is clear that EBWO is very competitive in obtaining a low fuel cost.
2023[35]The osprey optimizer algorithm (OOA) is utilized for solving both the ELD problem and emission dispatch problem. The algorithm is validated by carrying out simulations on six case studies for ELD and six case studies for emission dispatch, and the algorithm showed superiority over the other algorithms for the same case studies.
2023[11]The eagle strategy supply–demand optimizer with chaotic (ESCSDO) is utilized for tackling the ELD issue. The algorithm’s ability to produce accurate results for ELD issues with generator constraints, power loss, VPL, and restricted operating zones is proven using four test studies including 6, 13, 15, and 40 generators.
2023[27]The ELD problem is solved using a hybrid exchange market and grasshopper algorithm. The research also considered the constrains of VPL, the restricted operating zones, the limits of the ramp rate, and the power loss. The robustness and solution quality are proven by the comparison of the results with those of other well-known algorithms.
2023[38]A hybrid algorithm of the Harris hawks optimizer and adaptive hill-climbing optimizer is provided for resolving the ELD problem. To evaluate its efficiency, six different case studies are utilized, and the results are compared against the results of the optimizers presented in published research for the same case study.
2023[10]A hybrid algorithm of the capuchin search algorithm and gradient search algorithm is applied for the ELD issue; the algorithm is assessed by applying it to six different case studies with 3, 13, 40, 80, and 140 units. The algorithm proved its superiority over the other test algorithms for large-scale systems (80 and 140 units).
2023[8]Modified particle swarm optimization (MPSO) is used for solving both ELD and economic emission load dispatch (EELD) considering the power loss and generator limit constraints. The algorithm was applied to three different cases with 6, 13, and 15 units. From the comparative results from other algorithms, this algorithm demonstrated superior performance.
2022[26]An adaptive backtracking algorithm with a dual learning strategy (DABSA) is utilized for solving the ELD problem with a valve point effect. The algorithm is tested for four different cases with 5, 10, and 30 units. The results showed a low cost with high robustness compared to other algorithms.
2022[9]An improved manta ray foraging optimization (IMRFO) algorithm is utilized for assessing the ELD issue. Three test cases are utilized to test the efficiency of the IMRFO algorithm. The outputs revealed that the IMRFO algorithm produced the best strategy for scheduling the unit compared with the other techniques.
2022[39]The salp swarm algorithm (SSA) is utilized for tackling the dynamic economic emission dispatch (DEED), taking into account realistic considerations such as the VPL, power loss, and ramp rate limitations. Three cases are studied to prove the efficiency of the algorithm; these cases are the IEEE 30-bus six-unit, New England power system consisting of a 39-bus 10-unit, and the IEEE 118-bus 14-unit system. The proposed algorithm’s robustness and efficacy were demonstrated by the results.
2022[24]The CCAM-PDE algorithm is used for solving the ELD problem. Eight ELD problems are solved using the algorithm, and the outcomes are contrasted by those of other popular algorithms to validate the algorithm. The outcomes comparison showed that the suggested algorithm has a better global searching capability, higher accuracy, and faster convergence speed.
2022[40]The Search and Rescue (SAR) algorithm is proposed for resolving the Combined Emission and Economic load Dispatch problem (CEED). The algorithm is verified by applying it to seven different cases with three and six generating units. The results approved the efficiency of the SAR optimizer in identifying the minimum fuel cost over the other used algorithms.
2022[41]The hybrid algorithm (MVO-SQP) is utilized for solving the ELD problem. This algorithm is validated on standard typical test systems containing 6, 13, 15, and 40 units, and the simulation results are compared with those of the literature techniques, showing higher savings in fuel costs.
2021[42]The hybrid algorithm (HGAFSA) is provided for solving the ELD problem, taking into account the valve point loading and multi-fuels. The validity of HGAFSA is verified using five test case studies with 13, 40, 110, 140, and 160 units. The results demonstrated higher cost savings than the approaches used in the literature.
2021[7]The GBO algorithm is provided for resolving the Combined Emission and Economic load Dispatch problem (CEED) and ELD, taking into account the VPL and transmission line losses. The experimental results indicated that GBO outperformed eight other metaheuristic algorithms.
2021[43]The MG-PSO algorithm is used for solving the ELD problem considering the VPL and ramp rate limitations. The algorithm’s authentication was demonstrated on five power systems, ranging from a medium to very large scale. Four case studies incorporating five generators are utilized for demonstrating the efficacy of the algorithm.
2021[44]The CSA algorithm is utilized for resolving ELD and CEED. The effectiveness of the CSA was in comparison with that of some advanced approaches in resolving the CEED and ELD problems, and it provided the minimum power mismatch. Three test cases are provided for both ELD and CEED.
2021[45]The TFWO algorithm is applied for addressing both the ELD and CEED problems, incorporating VPL and power losses. In comparison with seven meta-heuristic algorithms, TFWO provides the minimum cost and a robust solution for all test cases. The ELD and CEED are tested three times under different loading conditions.
2021[46]The QPGPSO-w algorithm is used to solve the ELD problem. The validation of the algorithm is carried out on IEEE standards with 3, 6, 13, 15, 40, and 140 generating units on the Korean grid. The simulation results showed an excellent cost reduction compared to other recent algorithms.
2020[53]The (MOSHEPO) algorithm is suggested for solving ELD problems, taking into account practical constraints such as VPL, transmission losses, and restricted operating zones. To assess MOSHEPO’s effectiveness, it was tested on various benchmarks, and its performance was compared to that of other well-known approaches. The comparison shows that MOSHEPO outperforms other algorithms in solving economic and microgrid power dispatch problems while requiring less computational effort.
2020[47]A clustering cuckoo search optimizer (CCSO) is used for tackling the ELD issue. CCSO’s effectiveness was verified on six benchmark functions along with ELD problems with 6, 10, 13, 15, and 40 generators. A comparative analysis of CCSO and CSO is conducted, focusing on the rate of convergence, the value of the objective function, and the robustness. CCSO is much better than CSO for the same test conditions
2020[48]An Improved Bird Swarm Algorithm (IBSA) is proposed for resolving the ELD problem. IBSA’s performance was verified on two systems with 6 and 15 units, considering generator limits, prohibited operating zones, and the ramp rate. The simulation results demonstrate IBSA’s excellent performance and robustness, making it a reliable solution for ELD.
2019[49]The artificial cooperative search (ACS) algorithm is utilized for tackling the ELD problem, considering practical constraints such as the VPL, generation limits, and demand constraint. The ACS is applied on medium- to relatively large-scale power systems and demonstrated its efficiency and robustness in tackling ELD problems compared to other methods in the literature.
2019[50]The (PPSO) algorithm is applied for solving the ELD problem in multiple benchmark power systems comprising 10, 15, 80, and 140 generating units, taking into account the restricted operating zones, VPL, and power losses. Based on the comparative results, PPSO is a reliable algorithm for resolving the ELD problem with higher quality.
2019[51]The novel grey wolf optimizer (NGWO) is used for solving the ELD problem. The suggested NGWO technique was tested on five different case studies and compared to other techniques in terms of the solution quality, robustness, and rate of convergence. The results indicate that NGWO efficiently solves ELD problems with superior solutions
Table 2. Statistical result of all algorithms in ($/h) for six generators.
Table 2. Statistical result of all algorithms in ($/h) for six generators.
Demand (MW)AlgorithmMinimumSDMeanMaximum
1000GO12,119.335511.62313712,140.1989112,165.96105
GWO84,448.7983815,832,763.4915,078,181.5166,411,534.85
EHO1,088,084.87951,872,22149,024,054.01230,237,965
TSA19,012.9547118,026,304.7116,185,322.4483,109,107.03
RIME318,009.046789,701,754.0171,123,668.37367,689,162.8
Table 3. The optimal cost of fuel usage ($/h) for six generators.
Table 3. The optimal cost of fuel usage ($/h) for six generators.
Algorithm1000 MW
GO12,119.28644
GWO12,176.17786
EHO13,765.64252
TSA12,473.50544
RIME12,628.2995
Table 4. The optimal power (MW) distribution among six generators for a 1000 MW load.
Table 4. The optimal power (MW) distribution among six generators for a 1000 MW load.
GOGWOEHOTSARIME
397.1006415348.726273181.83572392500175.5031567
122.4463005120.754963897.55273028192.3015638160.2451283
225.3470349230.7033553123.045057180300
100.957066291.71239042138.577895759.71743169143.7008257
118.2791771182.6622628237.646817670.03386672166.9615517
59.4782105250.75167398346.213691112082.05115898
Table 5. Based on the GO technique at 1000 MW, the anticipated sharing power from all units during the thirty runs is for six units.
Table 5. Based on the GO technique at 1000 MW, the anticipated sharing power from all units during the thirty runs is for six units.
Unit 1Unit 2Unit 3Unit 4Unit 5Unit 6
430.8358487129.2546847213.610266975.3842310796.5953102977.12548932
410.6400887118.3408164187.8061594129.570654119.944102557.05322438
400.9699598142.2327289185.593255991.78501966136.257600866.67548157
414.2817848155.3612806213.244777864.9857365124.819201950.46736454
413.0616712160.3041676202.131753355.03198666141.742174351.08214766
390.0561863110.8082995232.4863322129.1651389104.123287457.1184943
394.0318994153.5156338176.4458905111.9300222119.396984468.06671545
393.1467777122.261174244.056059575.27733429136.087154653.18367501
415.8312482164.762351191.098451382.1618717494.665888374.25947916
384.0366828140.2183982217.1301621100.1398789112.964927569.15215532
407.453584197.99122461248.4397975119.1577658100.559136250.01059831
442.3959205143.7183225200.68230676.52947254104.931862254.21100516
408.7413629146.2226372228.831803568.5276114198.5808181372.26552271
412.301574392.87959688197.9060904117.1533216137.057136766.50433164
429.9549046148.4895731180.485951792.30747803107.481876763.93795414
388.9500522112.8676999232.734466788.53688165131.075660969.89694002
365.2263045132.1840528242.976884191.20497302118.870586773.78324518
390.6331267100.7957729217.3316904120.5736453126.729036267.97175834
409.2320312125.320755221.663087592.4025191195.374122379.21863624
387.8497325132.3743384218.1615536106.916623113.848823564.47739293
418.1116178162.1247676195.376479672.06570765123.406420251.89322157
397.1006415122.4463005225.3470349100.9570662118.279177159.47821052
376.1792134137.4335834226.562441986.01676132105.212344992.4929281
389.5617582165.4196117181.6106999101.6665181125.693728859.48528249
383.9548808106.3390585224.638701498.33858186135.733107575.2387894
398.4834552120.2498329210.358418393.06238595110.287111591.1668325
410.3303361113.7569697231.058432655.22596366137.824716175.68047151
449.0598655143.6256636209.526970966.7760342691.3572528261.96214444
377.5594302141.0882913194.4608049139.514183698.7385364272.27467699
428.145696110.7854683229.4498195101.2197572101.436057251.96212016
Table 6. Statistical result of all algorithms in ($/h) for ten generators.
Table 6. Statistical result of all algorithms in ($/h) for ten generators.
Demand (MW)AlgorithmMinimumSDMeanMaximum
2000GO403,459,385.316,662,253.57433,268,828.7462,151,691.8
GWO527,874,749.635,406,315.44600,680,060.3661,612,752.3
EHO1,404,633,41049,679,972,83657,284,262,8951.77439 E+11
TSA525,137,956.442,260,639.63618,326,865.6744,209,124
RIME496,656,222.783,146,797.78618,351,049.1811,012,244.4
Table 7. The optimal cost of fuel usage ($/h) for ten generators.
Table 7. The optimal cost of fuel usage ($/h) for ten generators.
Algorithm2000 MW
GO402,837,175.9
GWO520,113,057.2
EHO361,676,723.3
TSA491,249,989.9
RIME496,561,378.6
Table 8. The optimal power (MW) distribution among ten generators for a 2000 MW load.
Table 8. The optimal power (MW) distribution among ten generators for a 2000 MW load.
GOGWOEHOTSARIME
376.2896401437.830971622.42124296470470
267.1462651379.598951536.24554906312.3805006309.239895
337.6176172318.249748771.82349206292.4108881330.4433964
292.881171249.8132669104.3039646300291.7305541
241.3085143243119.3405633243227.8630641
157.4291746159.831227240.9191078160160
125.6344364129.9919094297.876191466.4529746637.09020184
118.933414956.69647937323.9950929120120
78.6488376920.23780916408.908153963.6851228139.26091535
43.0175853452.78954207418.908465514.4671497155
Table 9. Based on the GO technique at 2000 MW, the anticipated sharing power from all units during the thirty runs is for ten units.
Table 9. Based on the GO technique at 2000 MW, the anticipated sharing power from all units during the thirty runs is for ten units.
Unit 1Unit 2Unit 3Unit 4Unit 5
380.2494914331.8006265301.6774621297.8671518229.0491311
449.6441249263.0092621331.6238948270.6563075234.1253704
364.453935309.3232555336.1288937297.1636285225.0922042
419.6653232285.3448651339.7774821261.4387284224.8880913
416.5108903253.6906765335.9493243273.6601303238.6826124
449.4454276288.4422758288.8694957297.2300037223.5472982
425.5633808273.2725331334.210842297.4948363242.6106644
410.9640604304.9725913330.755091277.5056006232.8629403
388.4499093288.6528381335.1453611298.8031111239.6495138
399.9018278327.2431035314.8593363256.7404665206.8329373
379.6820635334.3543131339.8859414284.449539219.6040339
373.3812304299.0848993336.5529262290.1078815220.1613079
391.0516328280.1120505321.0139149277.2181002239.0124535
312.7340947356.2391644321.2342631298.7572993240.2354473
401.9600621357.8271587268.0777811274.0577876231.8798377
376.6919422319.4697901303.8616384288.7822861242.8600135
396.5516752291.5967522334.357437288.3458404236.0239482
399.0583109290.1611223304.816709297.4329539236.7615549
449.0294732272.4804372285.4993883292.9300515222.6425763
427.2825971281.4435153325.3946603281.3832356220.3409501
421.8321927301.9801493333.4973204276.4360542239.0311975
384.0303609335.4695756318.899372292.8099183234.5810609
410.577226248.4549836321.311956294.8992057240.6532707
423.0858666314.1088467337.4104893286.9632695233.2014233
401.826815270.379897311.6007366292.9928131242.949654
376.2896401267.1462651337.6176172292.881171241.3085143
457.8899305299.0812389254.628556298.4213924236.9314229
402.2268267266.3001613322.7044322291.949112236.9276004
383.2168299277.3121047339.962803299.1078492239.991673
407.0242638274.1393198314.7458724270.9477607241.0491811
Unit 6Unit 7Unit 8Unit 9Unit 10
159.4569064129.853415108.24239250.9376985453.32468654
157.411427126.64102114.68480436.9402268754.6785473
150.5674262125.0177997117.159023878.4993175436.63504968
159.3766901127.2063103109.361404265.071861647.87149283
158.7791947124.1957045104.529922578.4321006254.99231309
139.4129798127.150023119.531980174.964804932.62447842
154.140504128.787169893.097478542.4328135149.0936045
142.1677855112.4177676112.39083677.5897060538.68361299
128.18861129.9045099119.845497859.91520150.64081774
159.8197165128.9324752119.959500476.7530477650.18568946
158.3919978129.220725770.5508166673.4001072753.99476675
158.5515875129.5822262110.729493268.9235152752.96221859
156.8307277127.329371117.288362378.6120506251.25367877
143.6750386129.2642016115.746783474.292470950.55050269
133.2087174127.8495872119.058910379.1563152851.0839217
157.5928295109.4706138119.631786868.1021649654.757631
154.5997747120.9885881105.185979278.8286553133.96049925
147.4869951125.3670511116.556332475.7876769546.95688553
156.6833142115.7275079118.149879773.2168299754.40650337
135.5568776126.7370231109.969774579.8544918951.85508029
149.9174467126.4986958100.758438561.6899596429.7267201
159.2504086115.07876891.8309628755.9430995554.99096611
153.6581912127.6778879107.57068979.8098447954.71422371
134.8109135126.992091553.1383766779.9934630454.27427682
160129.3163684108.524787269.5954059853.05668684
157.4291746125.6344364118.933414978.6488376943.01758534
159.5863288128.986476594.0434953270.0892769445.11184526
156.3784049124.9686671112.854144671.2722679153.82234183
158.4730228128.7299932108.8135775.3323448228.95000466
155.0357049129.5728585119.883705274.4684174652.82509064
Table 10. Statistical results of all algorithms in ($/h) for twenty generators.
Table 10. Statistical results of all algorithms in ($/h) for twenty generators.
Demand (MW)AlgorithmMinimumSDMeanMaximum
3000GO324,261,971.35,647,315.714330,118,085.8344,637,144.1
GWO582,356,264.786,555,080.36720,998,567.9863,176,003.3
EHO494,550,252.656,173,293.3610,979,905.4729,867,203.6
TSA488,707,354.5100,431,720.7683,484,980.6836,449,616.9
RIME444,191,182.285,324,517.25653,856,793.2800,012,129.5
Table 11. The optimal cost of fuel usage ($/h) for twenty generators.
Table 11. The optimal cost of fuel usage ($/h) for twenty generators.
Algorithm2000 MW
GO324,256,382
GWO572,724,405.9
EHO372,737,291.7
TSA423,002,638.7
RIME433,885,024.3
Table 12. The optimal power (MW) distribution among twenty generators for a 3000 MW load.
Table 12. The optimal power (MW) distribution among twenty generators for a 3000 MW load.
GOGWOEHOTSARIME
150.1347081303.654094938.11359116239.213034204.46305
137.8538918144.384690648.36819253195.0223431147.4943195
214.5679581122.487182950.08283235142.8655093315.8349621
219.985949697.829448265.22808351297.1640127109.3843499
229.4665139150.003012465.5076667193.69698485148.0017622
159.9864227119.4008876.3925957160111.0190778
127.973151913088.8522563116.6391609105.6950967
118.415268568.4436180199.8410962612098.34335255
79.7072544826.79155925116.216289249.5570318555.10157814
54.99480419.52133913118.238075234.1886925748.52283803
150.3492831303.548469146.8093287293.4601473292.3427023
143.1246464388.2926001159.1722972201.1054248180.9273613
171.2109225340165.4529989184.8154601340
262.8101639223.672651178.6073159222.1119065279.7630038
242.7260986158.9818987191.6397931221.9981631135.2156712
156.884144585.68947992205.403052108.9005199125.8035734
129.9911335130264.7240765107.2258899108.9980269
117.004517670.6942127271.4257399104.2166573112.8727886
79.8431630267.24758355319.88076248027.1361492
52.9700044149.35824278330.03588727.8256324353.07930548
Table 13. Based on the GO technique at 3000 MW, the anticipated sharing power from all units during the thirty runs is for twenty units.
Table 13. Based on the GO technique at 3000 MW, the anticipated sharing power from all units during the thirty runs is for twenty units.
Unit 1Unit 2Unit 3Unit 4Unit 5
179.5807021143.6533007202.4957511285.4635644242.6052033
150.0217934135.1487191186.0876065250.5781886236.7853441
152.6374569137.0632346218.7851029239.137835228.8101049
150.2353164135.3110578219.2274789190.1959436239.5341889
151.9276018135.0039869218.3096582219.4628714242.1344252
150.3004969138.608888189.3471362250.6519157174.8402066
151.0400241137.2149477199.0675424292.7432751239.0177953
151.8651819135.0000574188.4943644257.299267240.2900648
157.6300365141.2615827169.2282857232.9094678230.5825914
150.0089723135.0219135180.1450282277.5909378241.2463306
152.20423135.0003903214.8993561276.337515242.9985665
179.8652364157.6705445246.5103097259.7617037242.9986903
152.2588436135.0243436180.6444875279.2688473232.0368129
150.0366853135.400814232.0835246270.0495706201.2728638
174.3436904135.9967003215.8148177217.7171134242.9910283
150.0476747135.0012754200.0366356299.98183212.7870825
150.01002135.0248993246.1622037255.4358481201.6441658
155.5138367139.4908169189.0083715285.0175362238.9551059
150.0987074135.0030777175.0958843267.2164568229.222801
150.1457417135.101566216.346181281.8146651242.5765715
152.6853664135.1452853187.4796828232.4793472202.3543068
150.1117258135.1422721181.1973826201.1472388231.6877228
150.0141091136.1428412205.8272704263.0081496216.157885
150.6815783139.0834407184.2996395263.3111516233.5688791
163.8852015135.1540293197.3977402283.3810965202.4146275
151.4486276135.0104964217.4682192262.0665143241.7933881
152.7862739135.1410224216.4417993265.2573983214.0861293
151.2837259135.2773683179.0233647279.578706230.3200586
150.1462752135.2255805244.6975715291.1316338242.8308342
150.1347081137.8538918214.5679581219.9859496229.4665139
Unit 6Unit 7Unit 8Unit 9Unit 10
159.6071133128.2248201119.412454860.9191471322.25343163
156.2458253129.998044109.620017179.8780424654.99962846
153.1173496129.532493571.1809021479.9405618154.91304993
147.1801462129.981923119.989184179.9997586454.91059276
141.014391129.979635119.958634879.9147743446.7459475
152.3942434129.8322517119.943045279.9946551653.42403429
158.7472358127.9300113119.499726876.0900400852.94271817
143.4551017128.5212054119.982499574.8654932154.99356614
144.294757117.3979839119.812372878.6460419854.90345637
159.9967153120.733818192.9905024579.8209383254.70211983
158.6077299129.9998999119.993096379.8535893916.48794946
119.3645573128.1154723119.903361979.9797077554.86715214
157.8686626129.6454432119.999405879.9985546954.23922039
155.2511123129.2655473104.594398579.9485524154.99269654
142.3902517129.991262107.589466479.9927862654.52099243
152.9434074129.85067118.772540622.675681854.30300161
159.9622766126.8940207119.980948479.9595383454.82704351
159.9298982129.9860725104.784970958.0540825754.25152691
145.0748375129.4372678119.168466379.9906011640.98013232
122.6832857129.989344119.426574179.4859194746.56445201
153.9102491126.2093543107.902156679.9460700950.68969523
131.8863195108.4068981111.037509575.3100656154.85476363
159.8272413127.2417015119.289508579.9935172348.51668141
159.97221129.984346116.224169579.9986587534.68278715
158.076051129.945586114.104831177.8084003253.6657387
159.9790266129.0847428119.908321777.0382327853.99889027
156.4948638129.7824241119.832597337.5282592954.88312116
159.9322747129.4839435119.109750822.889020654.99791032
158.3260423129.892538752.7745865379.9773549144.7843366
159.9864227127.9731519118.415268579.7072544854.994804
Unit 11Unit 12Unit 13Unit 14Unit 15
163.9714219135.2857218226.8835763253.8607253218.3425489
150.1073911135.0069405239.4990776241.83748211.3983519
165.4211208135.1763477209.2265595299.8641235192.9770205
151.6567153151.092975195.6860209278.9956422242.9998245
164.4830205135.1304851177.8301433257.55773242.8966889
167.9131672137.2493631230.4827677251.9429259236.3931901
155.9612027135.0422724180.4341837203.2142802226.5626607
150.0010082136.0622371191.13657293.0957233216.2115426
152.5359708135.1487893251.107523261.0659056233.1404916
150.0003557144.5522934195.5011934283.8063539195.1444996
161.3714465138.6959055201.7071607250.2727825210.6681699
163.3672551135.1865186167.2094506265.2657888234.571584
150.4006307135.0491182194.9220775248.2108678223.723122
150.0674432135.0031397209.9860468252.26862220.8399793
151.0287309135.0615175183.1769845246.3623588238.051573
153.1286326135.0015821207.5830441299.7925328242.936154
150.036499135.5345527183.8706041299.3815277242.9788396
153.3524219135.1443598180.8035128245.3192621227.4360925
150.9989258135.0008874182.4898976286.0980579239.4184178
150.0025446135.0017993200.9379405222.9370261228.8781296
150.1806045135.0207224226.3587728282.4387782242.6676528
185.5805862135.7915104240.862454285.1801767242.9896496
150.0003818136.459248219.0233956245.8566655242.9367538
152.3737494135.6004609198.2873227250.6099577242.7592839
150.1935987135.0315858206.3861712236.8870903233.108755
150.0691408135.1762192206.1210885257.9775751160.3210936
164.3192048136.0036645205.9741368236.5811709242.9894127
150.0913954135.0232752221.4542619258.6821827241.644435
169.0346926135.2602349189.4649965254.692806242.9804725
150.3492831143.1246464171.2109225262.8101639242.7260986
Unit 16Unit 17Unit 18Unit 19Unit 20
75.10666095129.9699161119.997674879.3428691153.02341349
157.897968129.9564725110.088796679.8500785954.99423415
159.3319587129.8315905110.755658977.3111219254.98640407
153.5321558129.9935616119.420331179.92600430.13117879
157.7831465129.9688278117.547352877.4467368954.90394198
159.936876129.9966044113.979742279.8762525652.89223678
159.8412134129.8432973119.876258379.973116654.9581964
153.5296836111.70183119.966370878.5382294254.99000339
159.9914986123.0710183102.45398879.9236123454.89462543
155.6313734128.1253351119.993474479.9913098354.99653496
159.3828433129.999112886.5349083479.9965044354.98884311
107.3895089127.242150476.170251879.627558454.93321042
159.9993451128.9258557119.978211179.9907326237.8154179
137.0933932129.9175857117.591079379.4482288154.88871871
159.9938017129.9844538119.997457179.9954044354.99960931
159.947747696.5268622793.7947753279.9541332154.93473633
109.9394483118.362048102.960157872.5345448554.50081514
159.9927371129.3049782119.939524178.9188092754.79608051
156.2077493129.5070589119.97530774.2542609154.76120082
159.6995205128.224356115.191317279.9934804354.999584
159.9803278129.0824742112.959657177.8318364754.67766056
158.3190154129.9870703112.108685573.9930491154.40590394
159.672906100.7382081111.246685979.9546717448.09217884
159.9875307129.9984778119.995492179.9995667338.58129767
159.2488955129.1460247119.953188959.8611591954.35022834
159.7734066129.8243007119.358751179.9624449753.61951966
159.9103087126.6175612118.756073478.1420608448.47252174
159.9987868116.250261119.999592179.9701224354.98956435
117.437771108.7568617117.633320379.9897662154.9623243
156.8841445129.9911335117.004517679.8431630252.97000441
Table 14. The power mismatch for all unit generators based on all methods.
Table 14. The power mismatch for all unit generators based on all methods.
CaseAlgorithm1000 MW
6-Generators unitGO3.82627 × 10−12
GWO7.22726 × 10−6
EHO11.52188186
TSA6.53945 × 10−7
RIME3.05381 × 10−5
MSA [5]12.80174784
ChOA [5]0.000232386
SAO [5]4.85414 × 10−10
MBO [5]10.11850299
SCA [5]0.000182
CaseAlgorithm2000 MW
10-Generators unitGO6.22209 × 10−5
GWO0.000776169
EHO14.83826809
TSA0.003388797
RIME9.48441 × 10−6
MSA [5]
ChOA [5]
SAO [5]
CaseAlgorithm3000 MW
20-Generators unitGO5.58934 × 10−7
GWO0.000963186
EHO0.008069445
TSA0.006570472
RIME0.001030616
MSA [5]4.47608 × 10−6
ChOA [5]0.00868658
SAO [5]0.000356058
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Shaban, A.E.; Ismaeel, A.A.K.; Farhan, A.; Said, M.; El-Rifaie, A.M. Growth Optimizer Algorithm for Economic Load Dispatch Problem: Analysis and Evaluation. Processes 2024, 12, 2593. https://doi.org/10.3390/pr12112593

AMA Style

Shaban AE, Ismaeel AAK, Farhan A, Said M, El-Rifaie AM. Growth Optimizer Algorithm for Economic Load Dispatch Problem: Analysis and Evaluation. Processes. 2024; 12(11):2593. https://doi.org/10.3390/pr12112593

Chicago/Turabian Style

Shaban, Ahmed Ewis, Alaa A. K. Ismaeel, Ahmed Farhan, Mokhtar Said, and Ali M. El-Rifaie. 2024. "Growth Optimizer Algorithm for Economic Load Dispatch Problem: Analysis and Evaluation" Processes 12, no. 11: 2593. https://doi.org/10.3390/pr12112593

APA Style

Shaban, A. E., Ismaeel, A. A. K., Farhan, A., Said, M., & El-Rifaie, A. M. (2024). Growth Optimizer Algorithm for Economic Load Dispatch Problem: Analysis and Evaluation. Processes, 12(11), 2593. https://doi.org/10.3390/pr12112593

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop