Establishment of a Temperature–Pressure Coupling Model for a Tubular String in a Carbon Dioxide Injection Well
Abstract
:1. Introduction
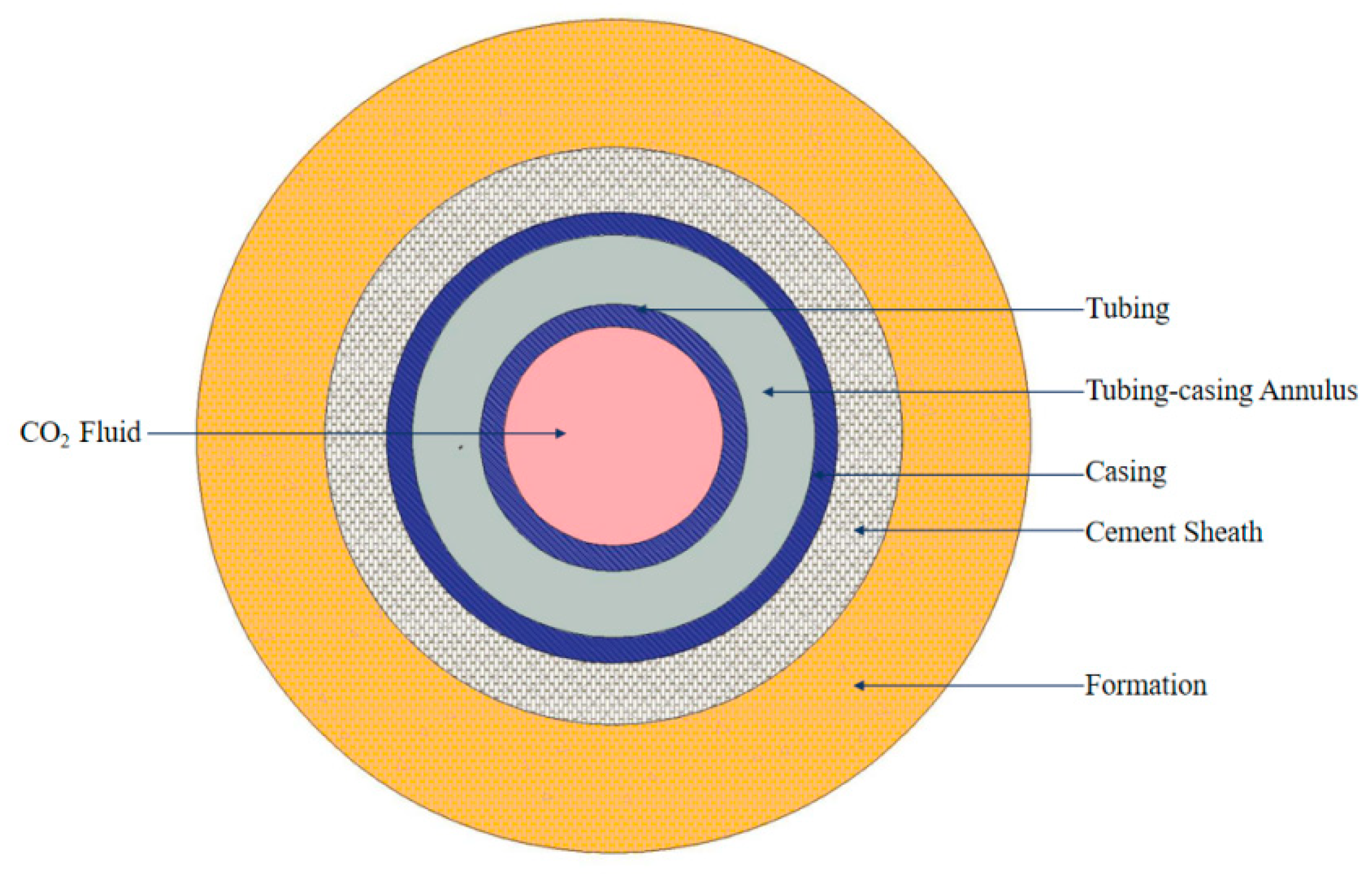
2. Establishing and Solving the Temperature–Pressure Prediction Model
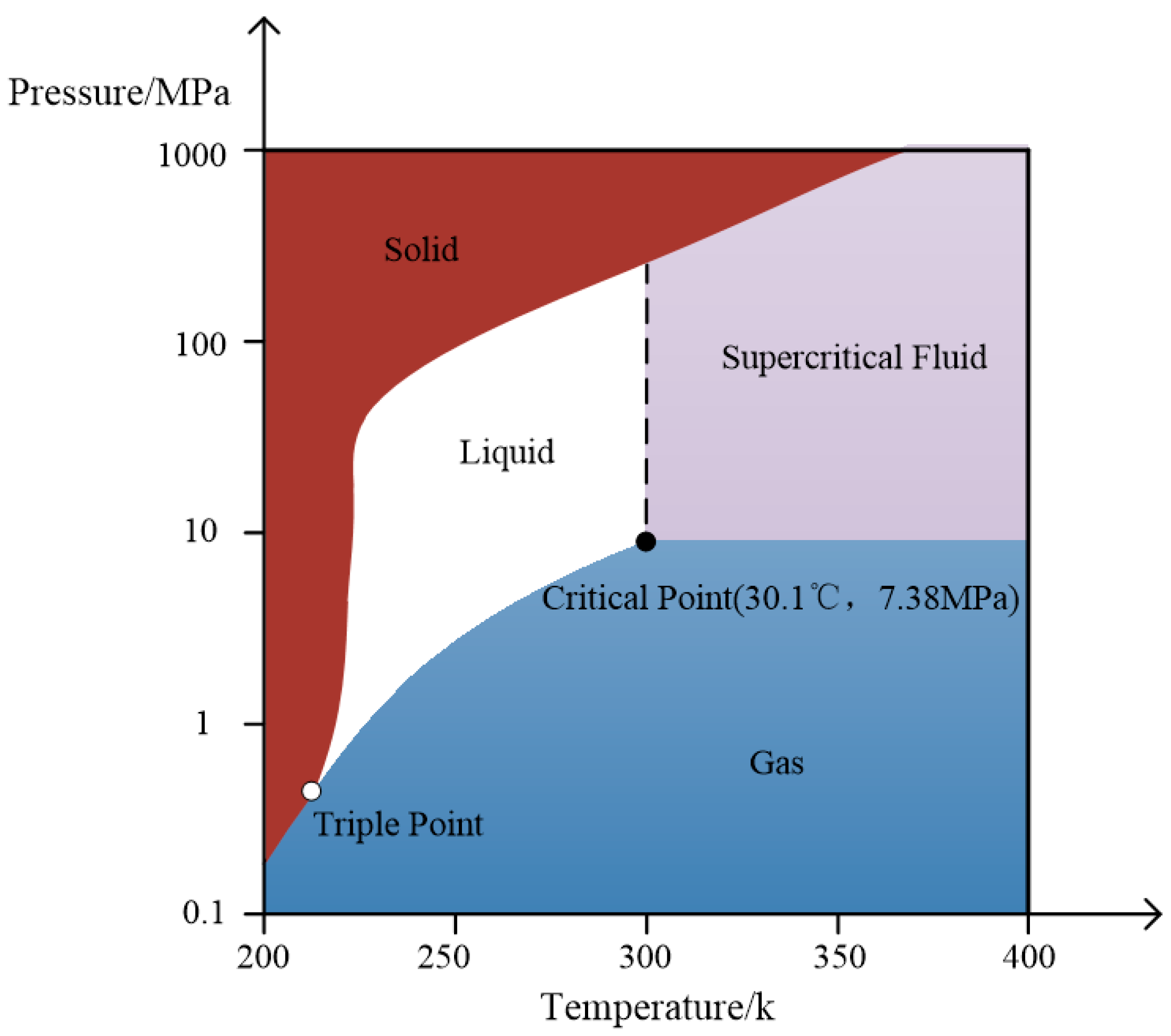
2.1. Physical Property Parameters Analysis of CO2
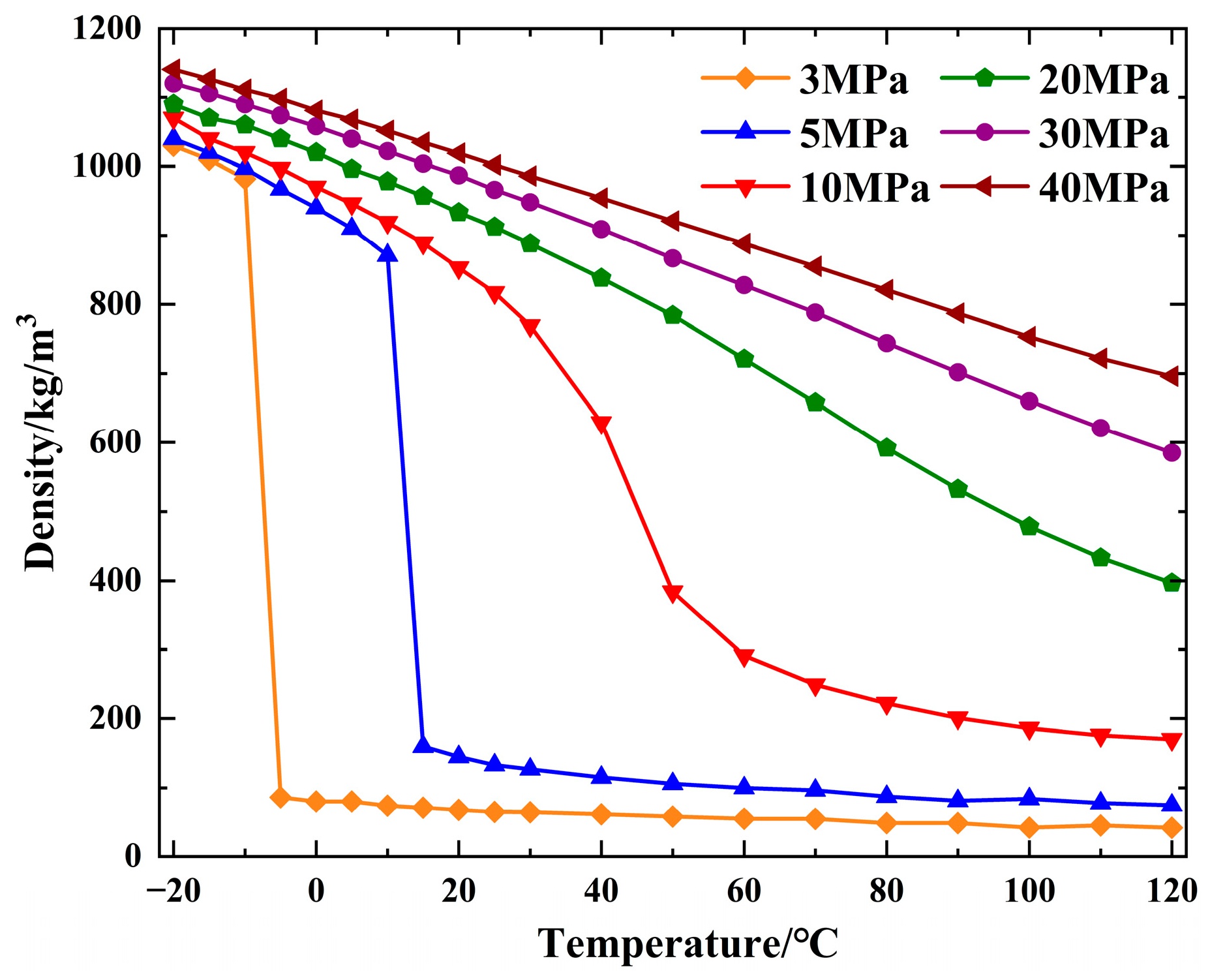
2.1.1. Density Analysis of CO2
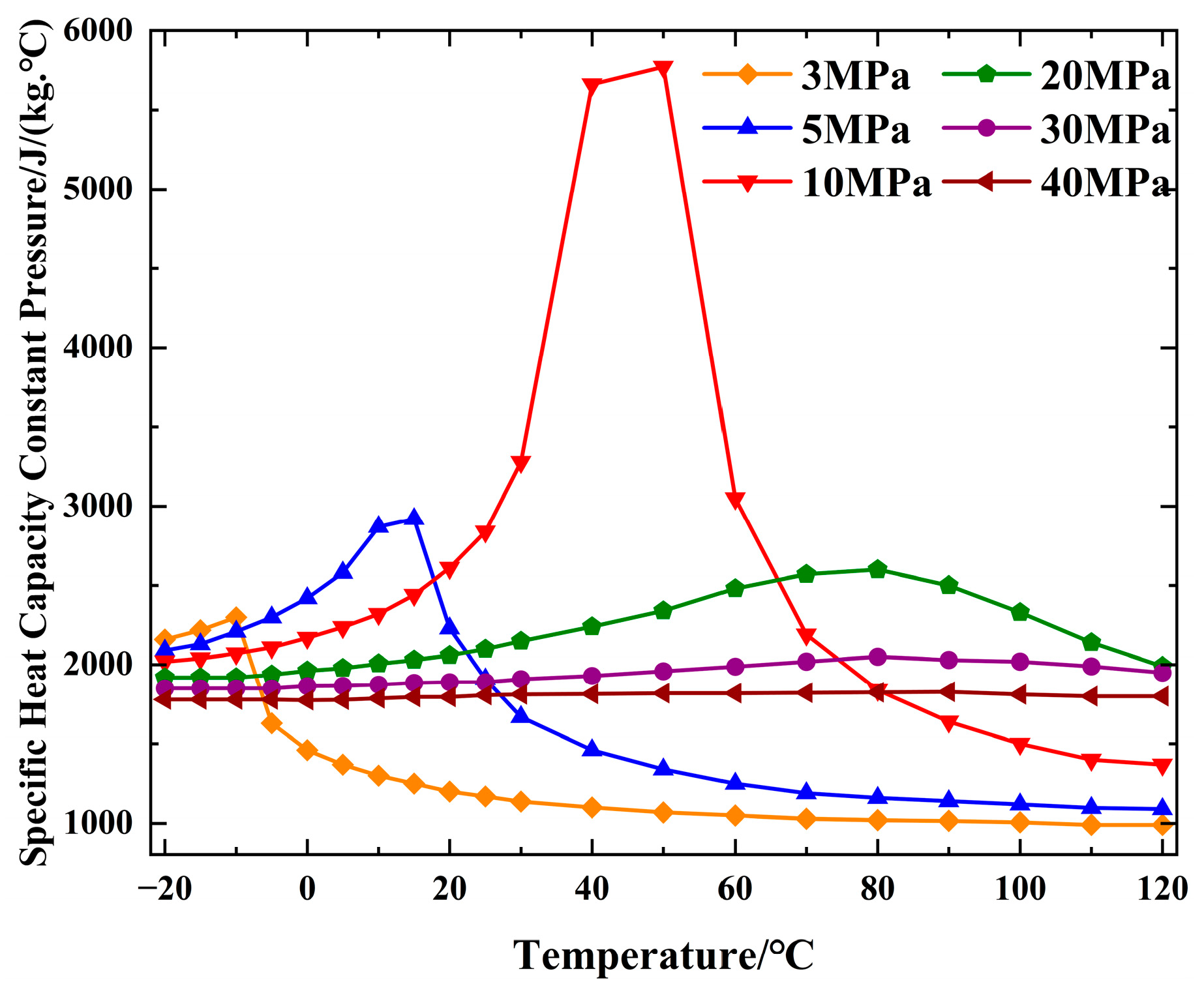
2.1.2. Specific Heat Capacity Analysis of CO2
2.1.3. Joule–Thomson Coefficient Analysis of CO2
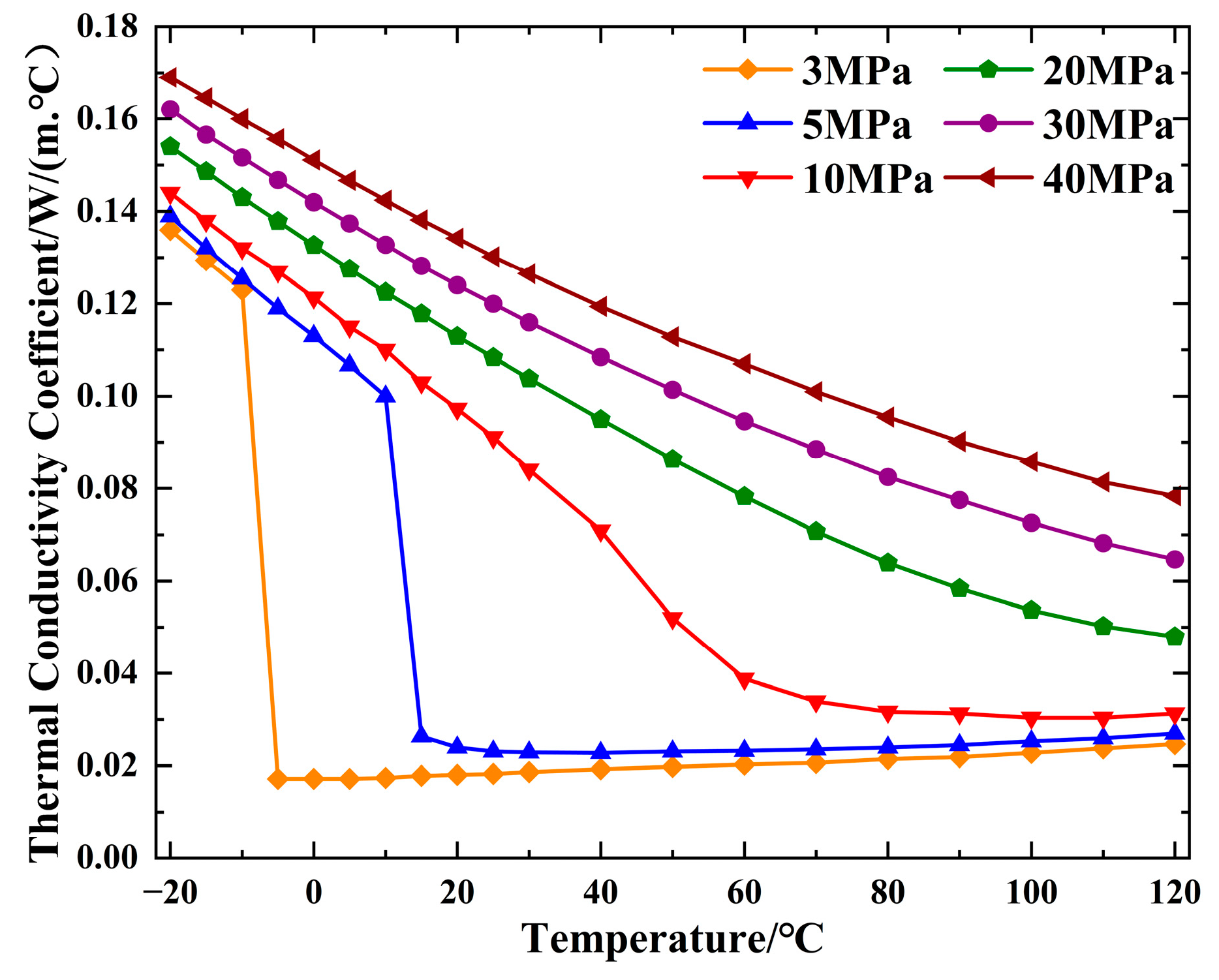
2.1.4. Thermal Conductivity Analysis of CO2
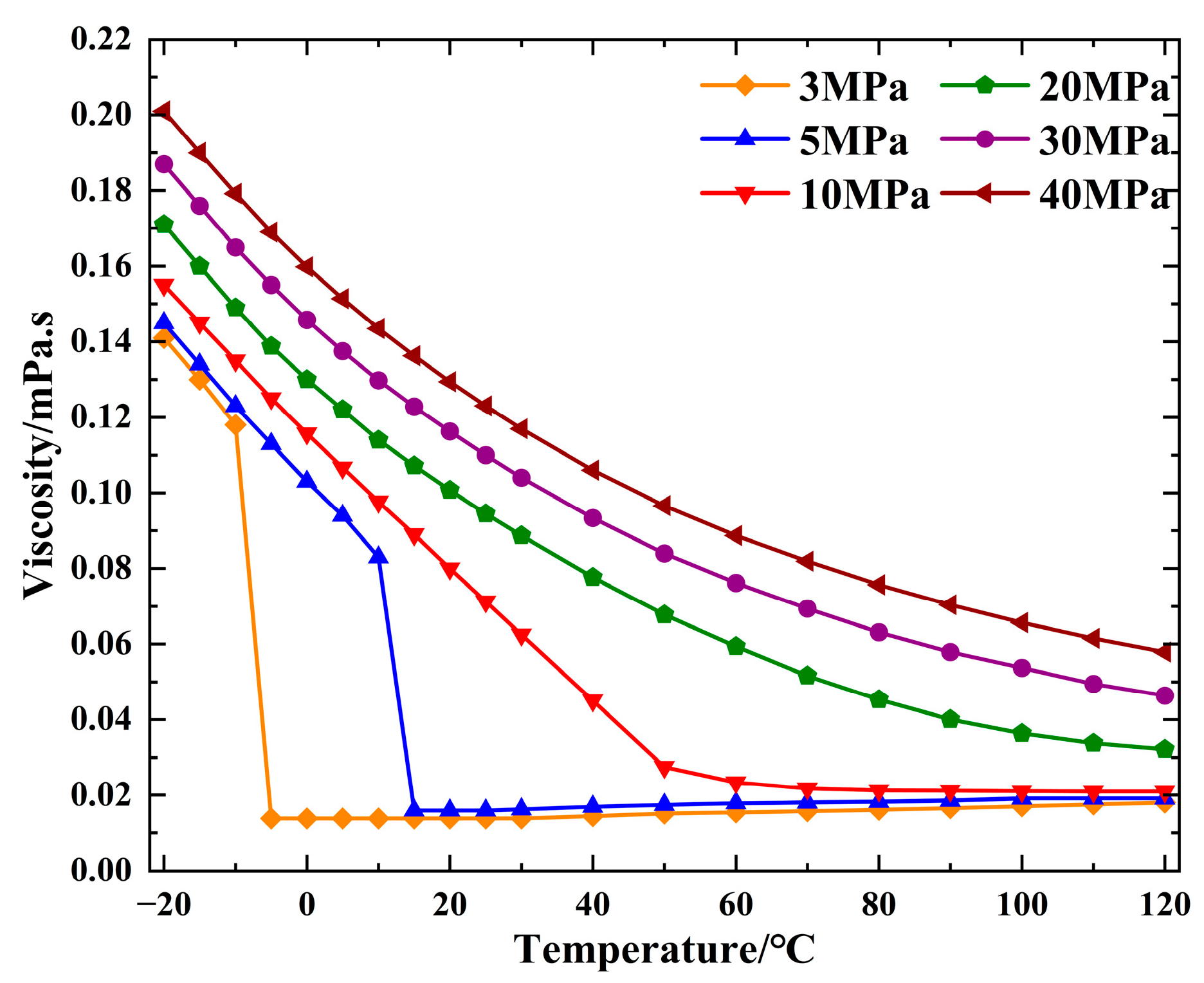
2.1.5. Viscosity Analysis of CO2
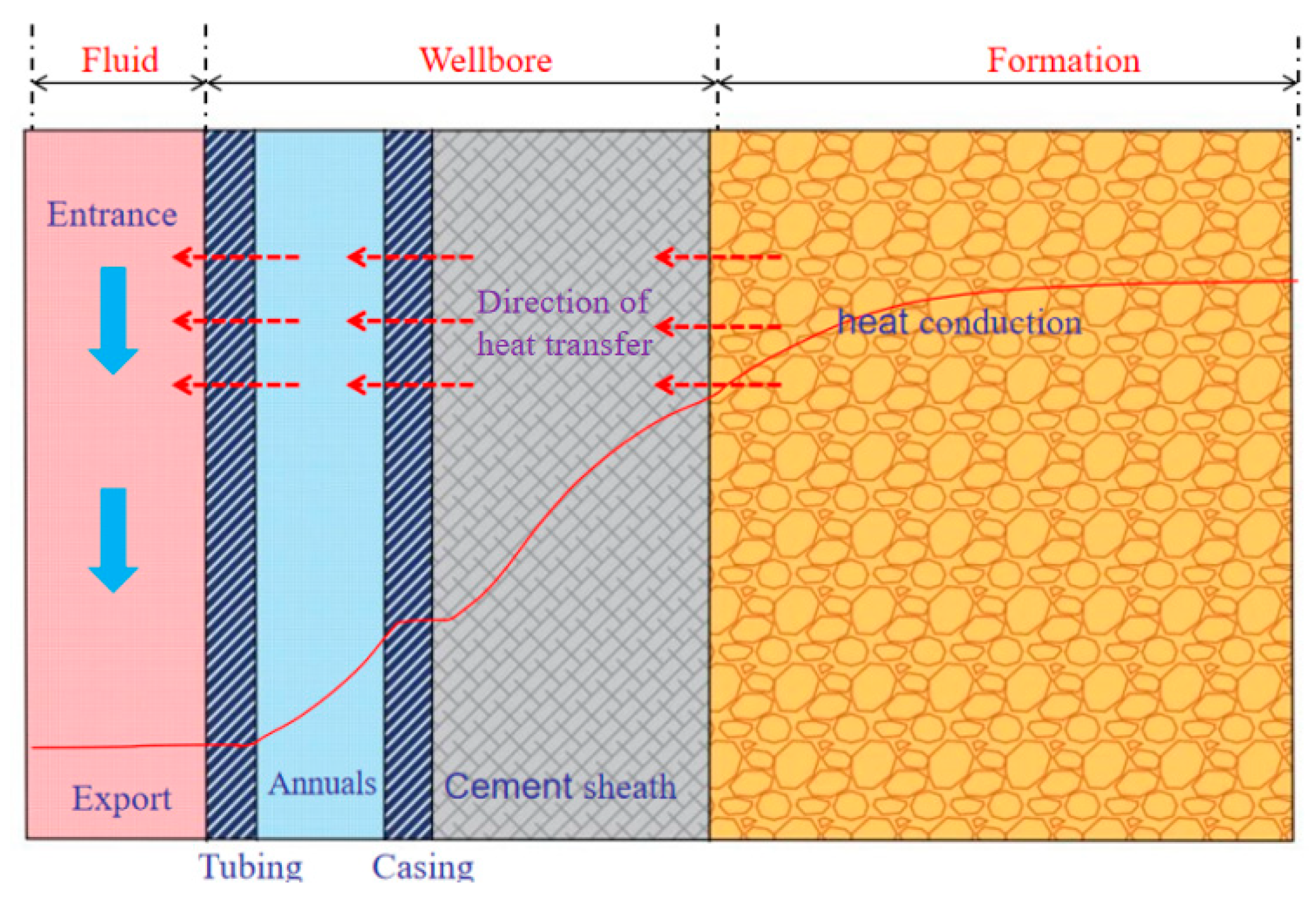
2.2. Temperature Distribution Model
2.3. Pressure Drop Model
2.4. Model Solution
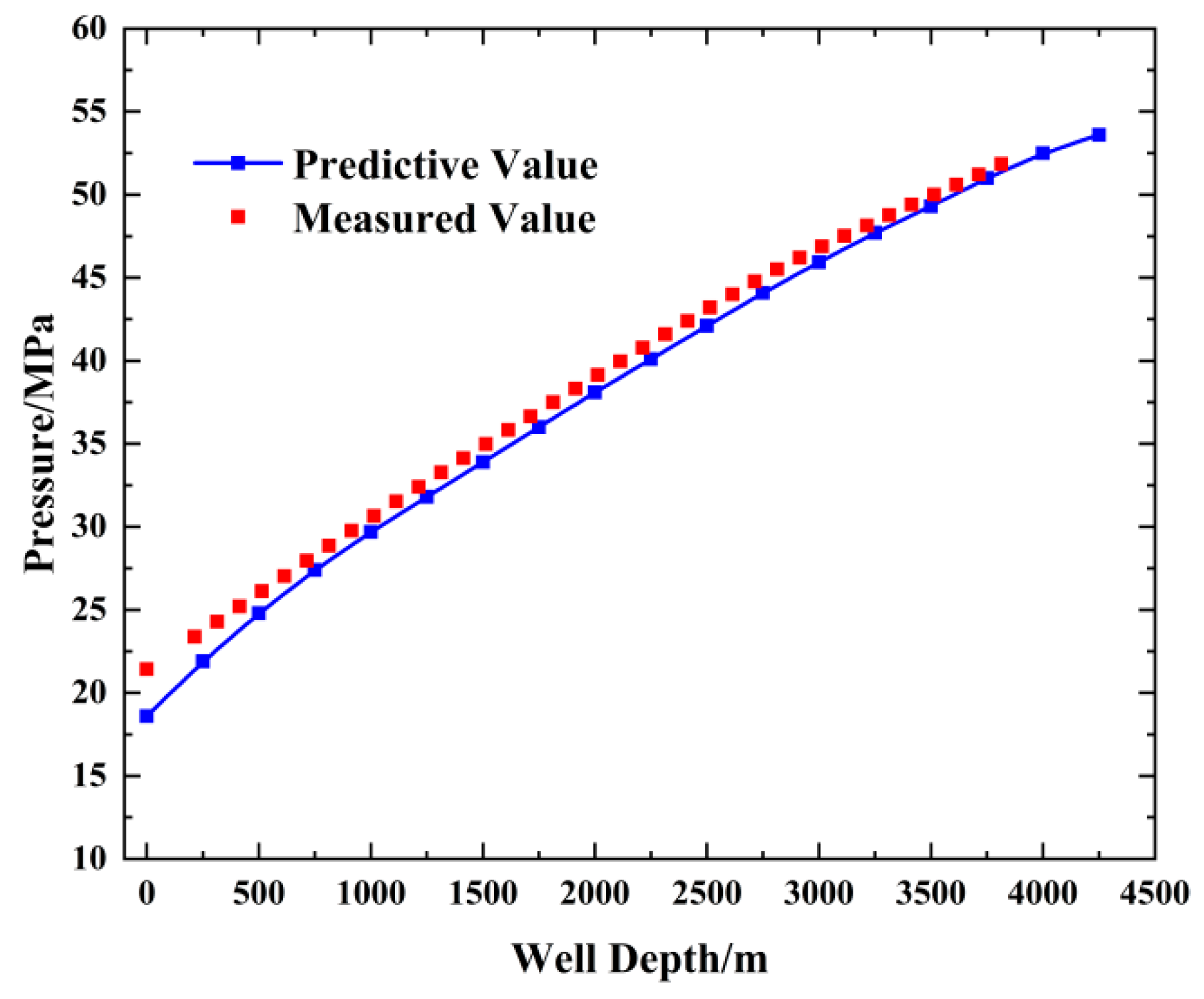
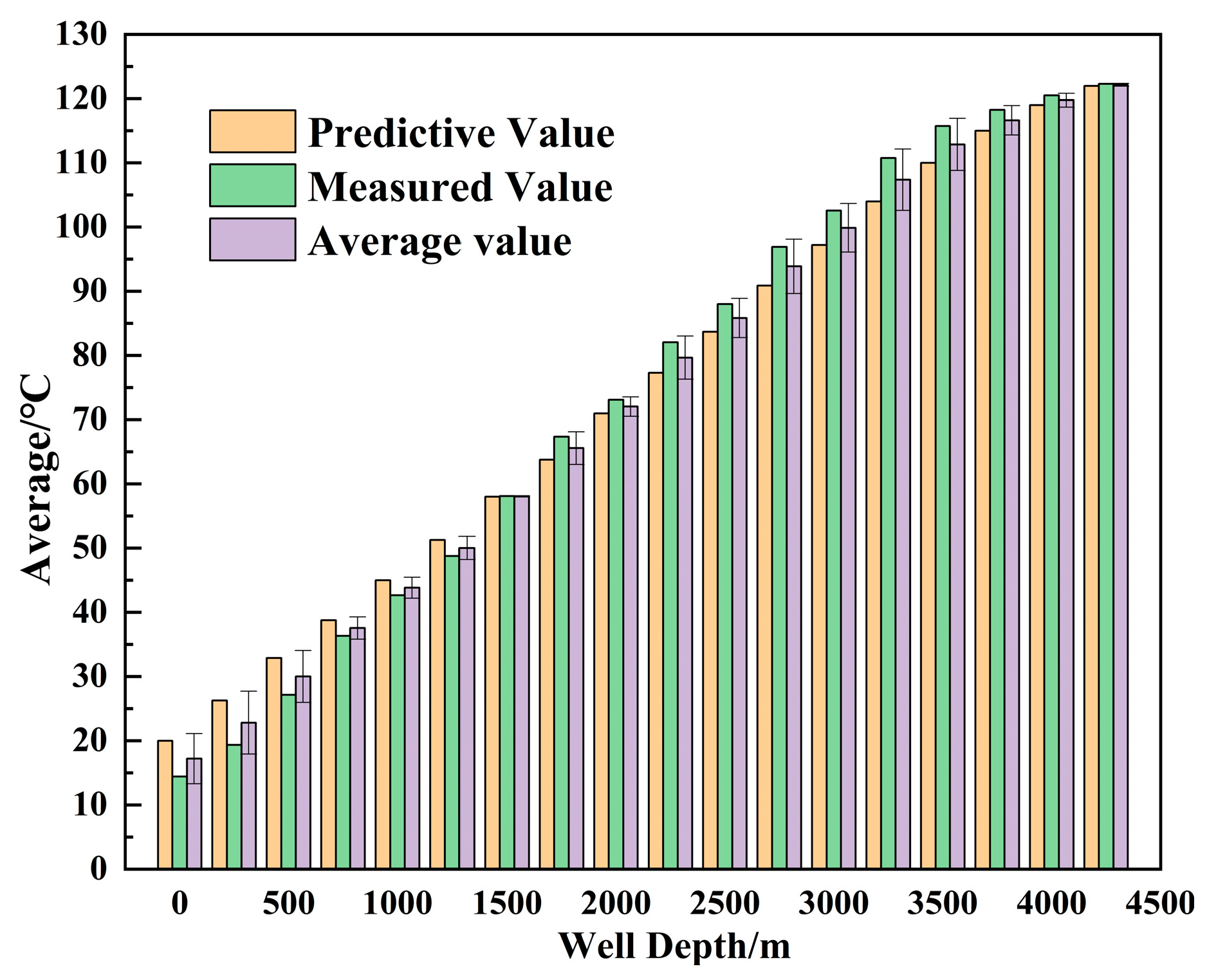
3. Model Validation
4. Discussion
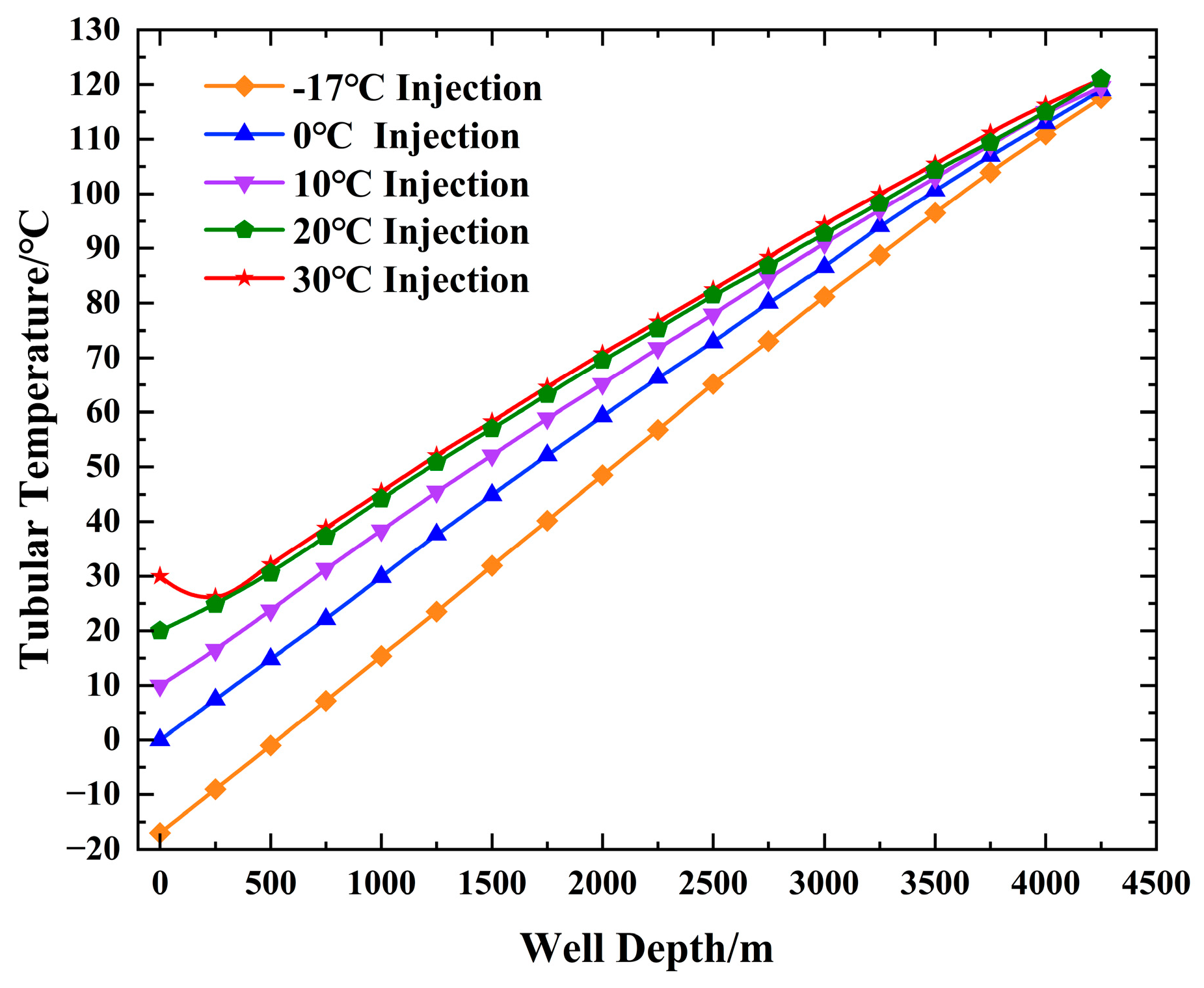
4.1. Change in the Tubular String Temperature and Pressure with the Injection Temperature
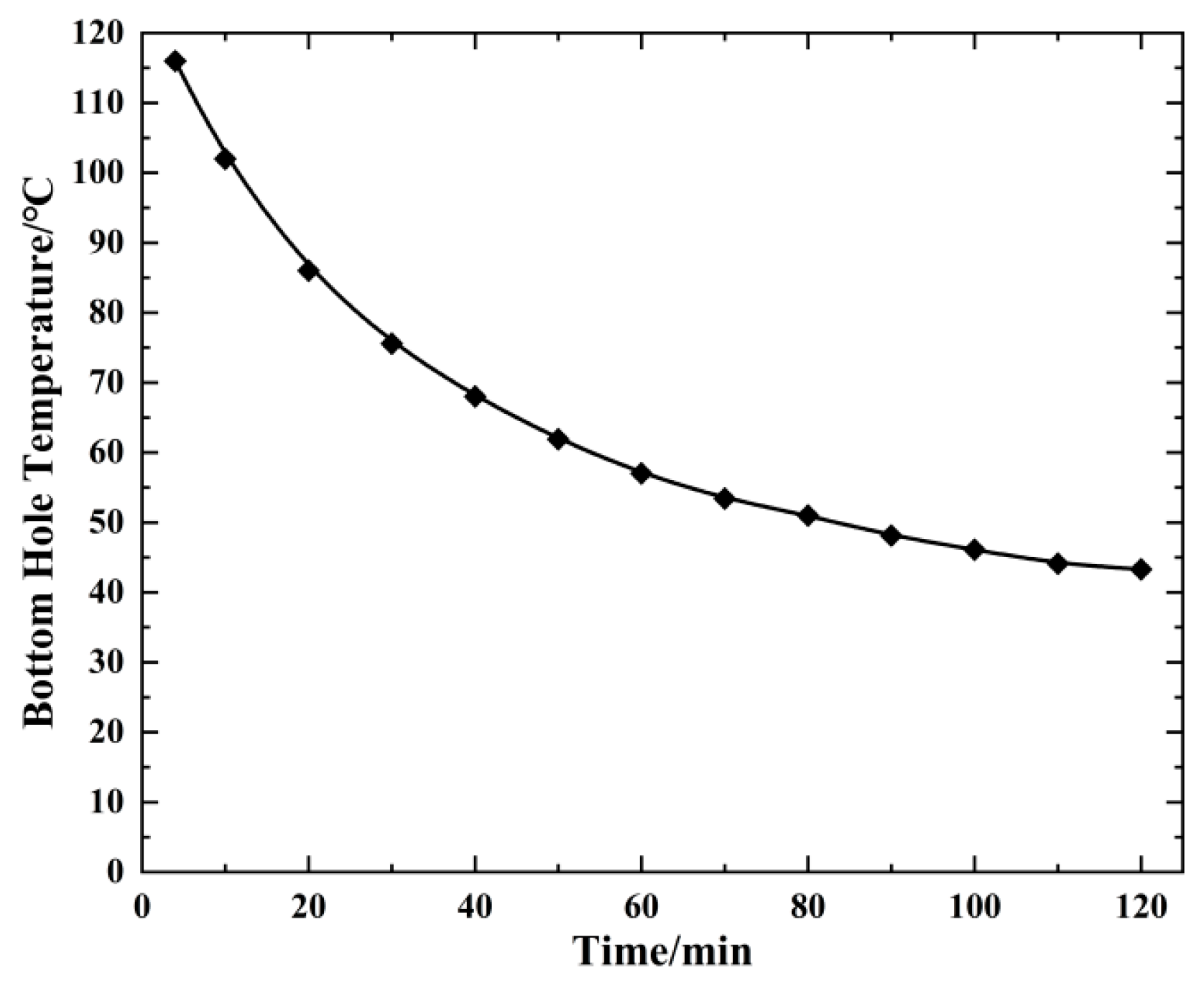
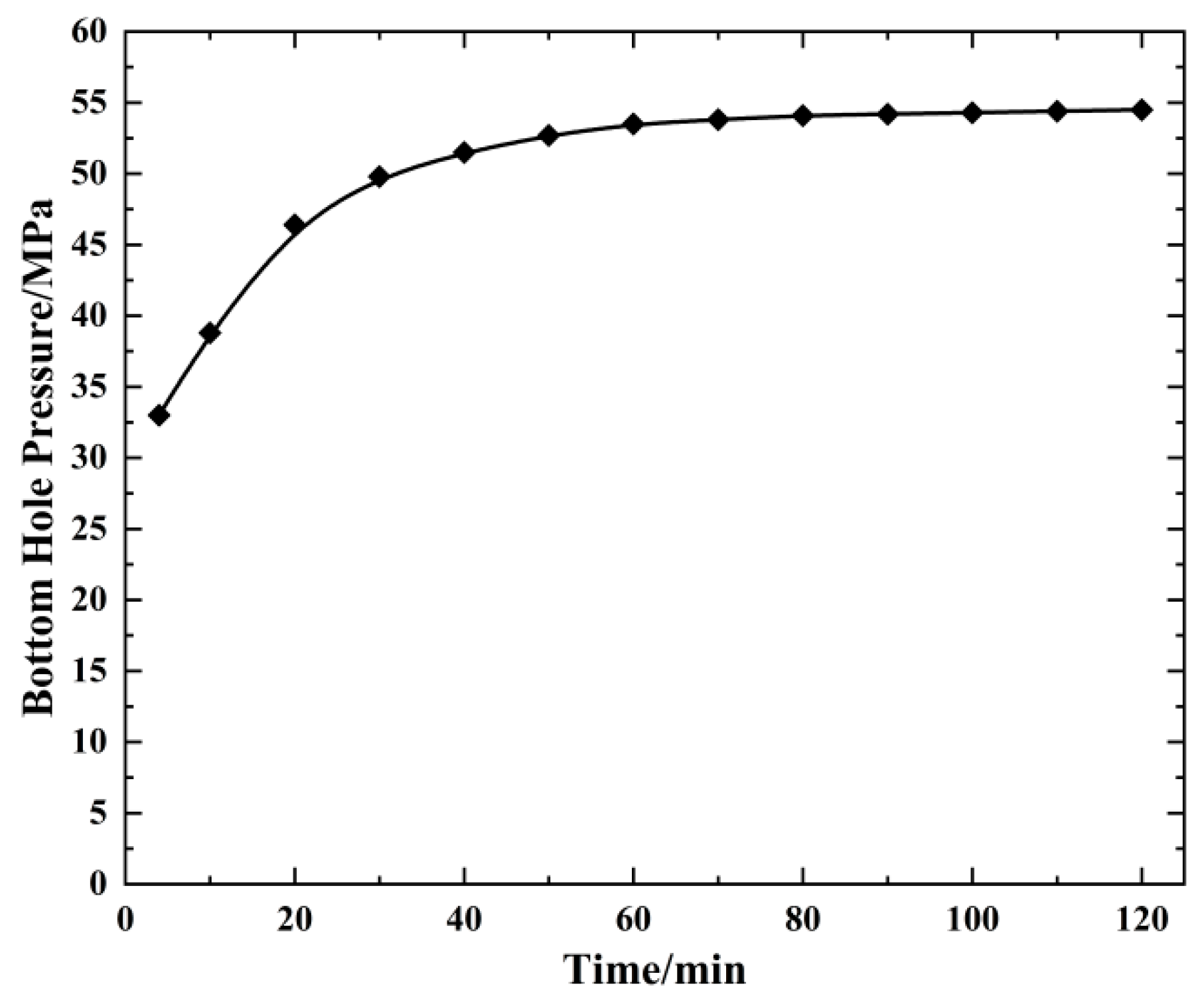
4.2. Change in Bottom Hole Temperature Pressure with Injection Time (20 °C)
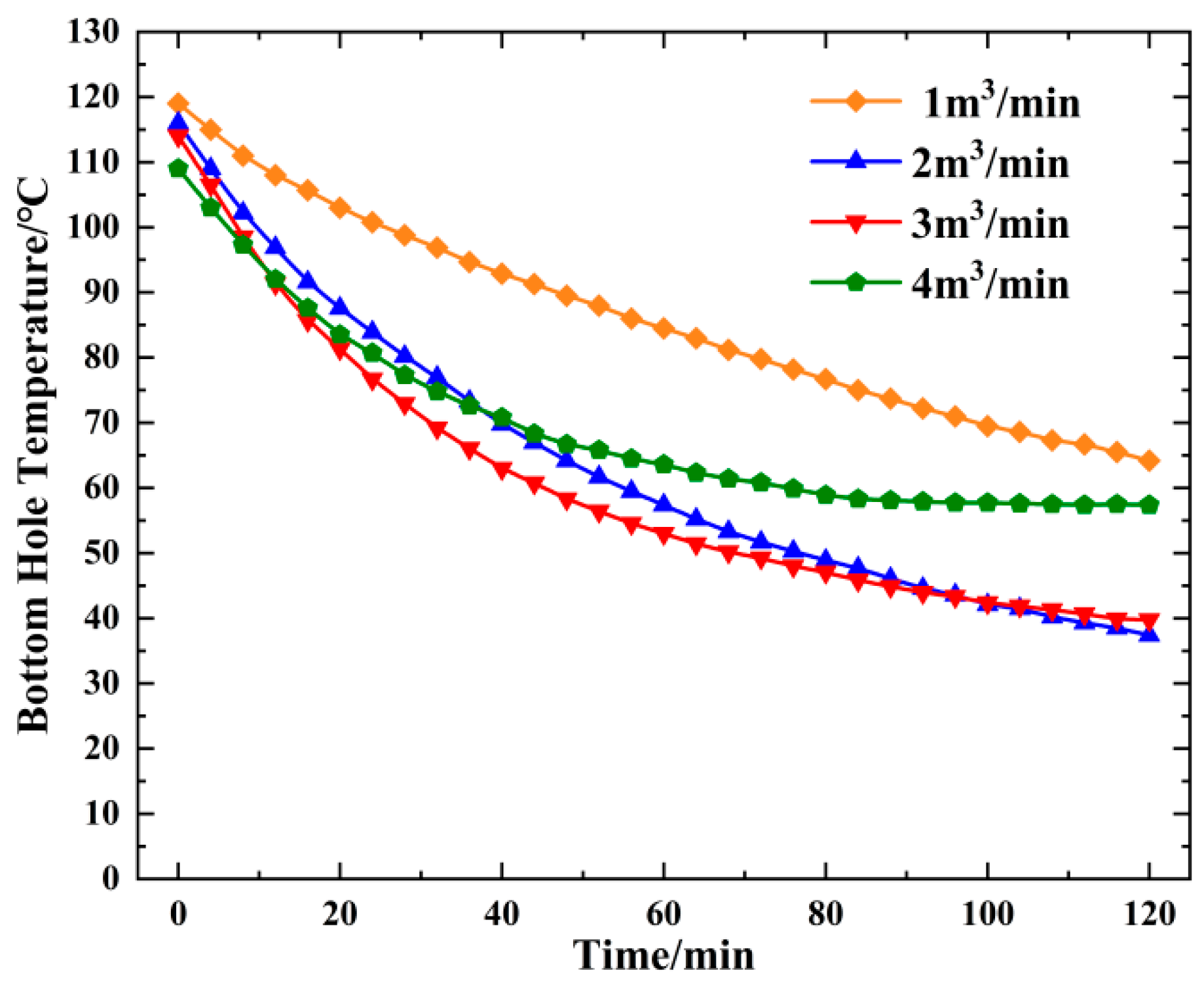
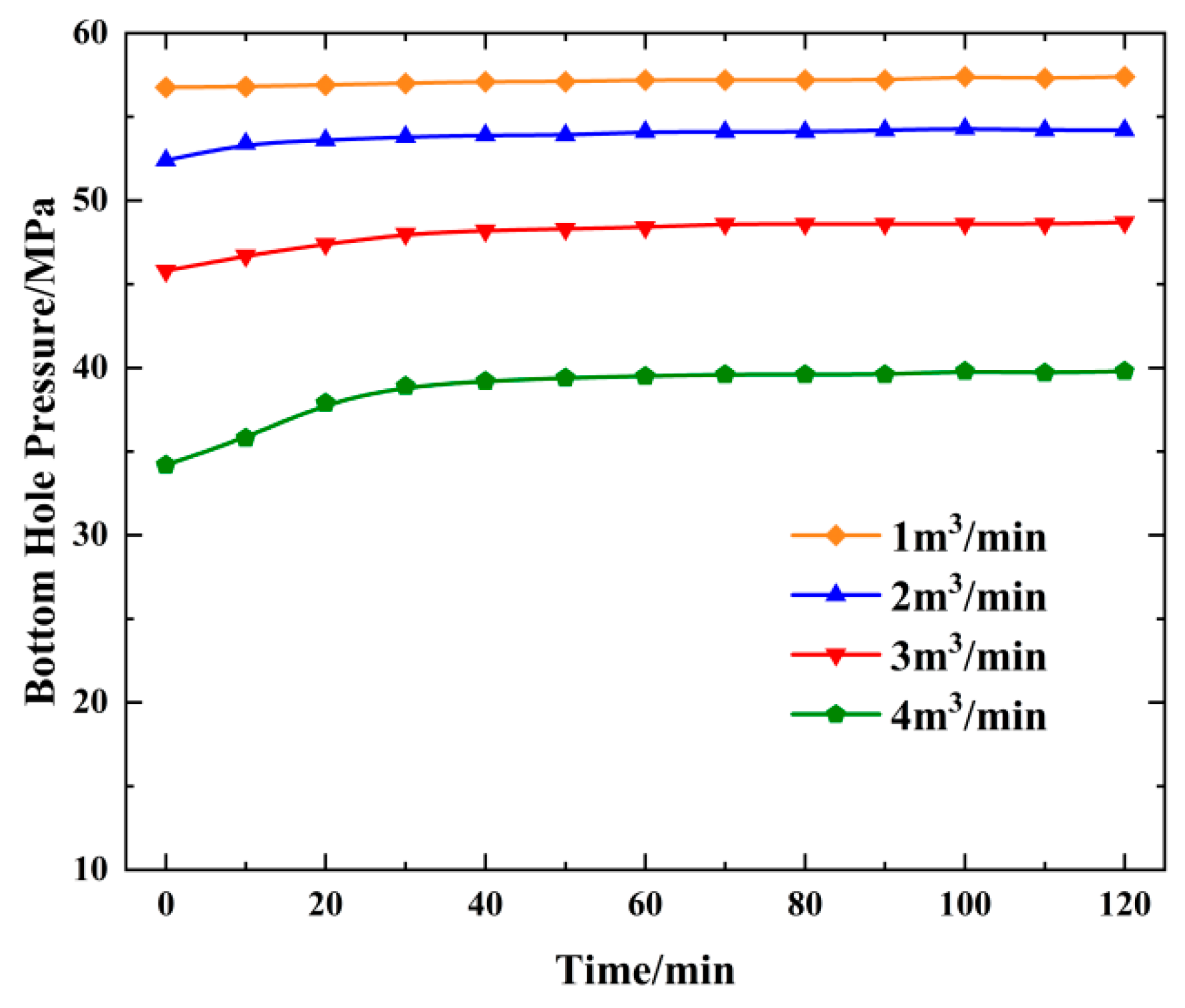
4.3. Change in Bottom Hole Temperature and Pressure with Displacement
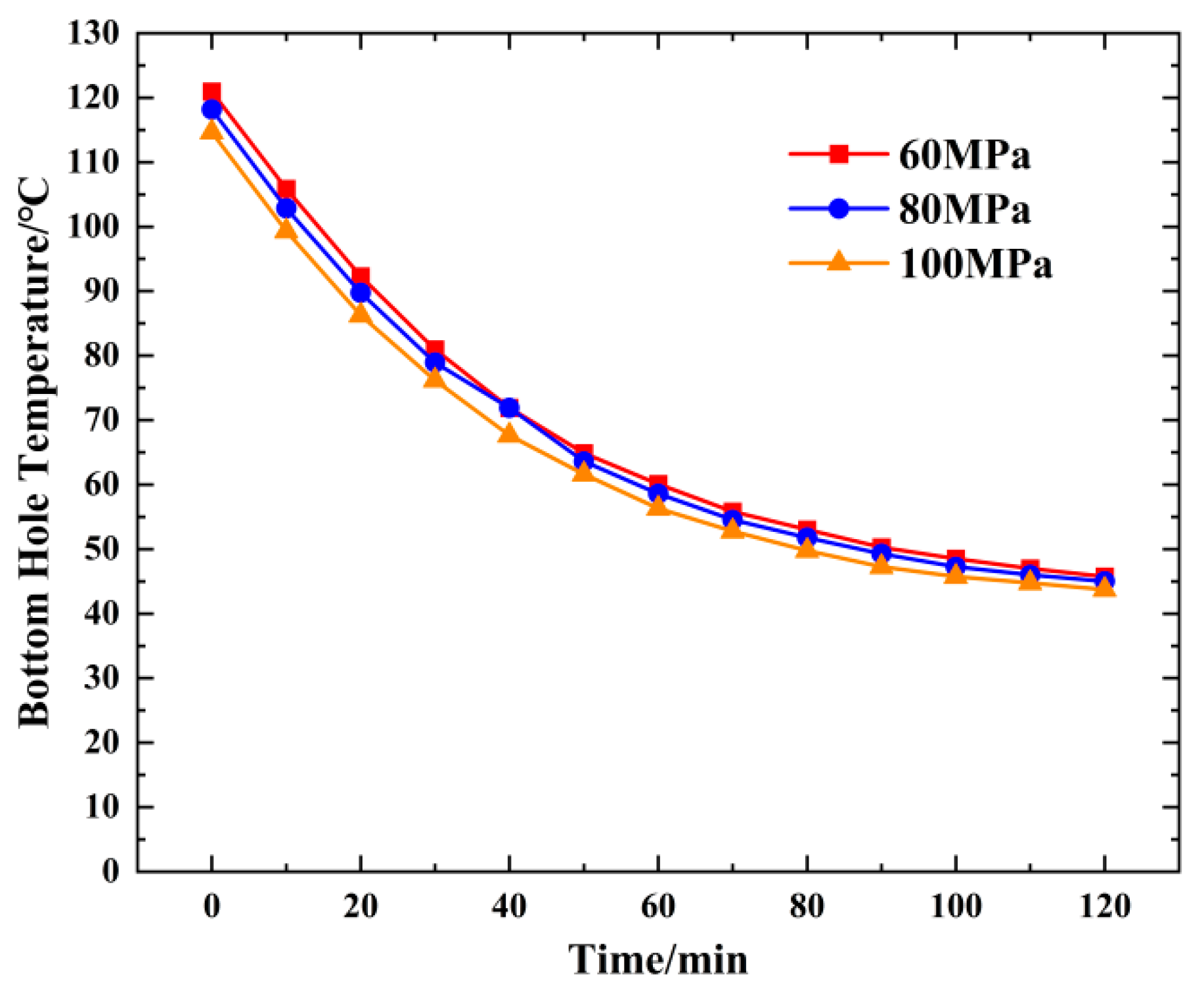
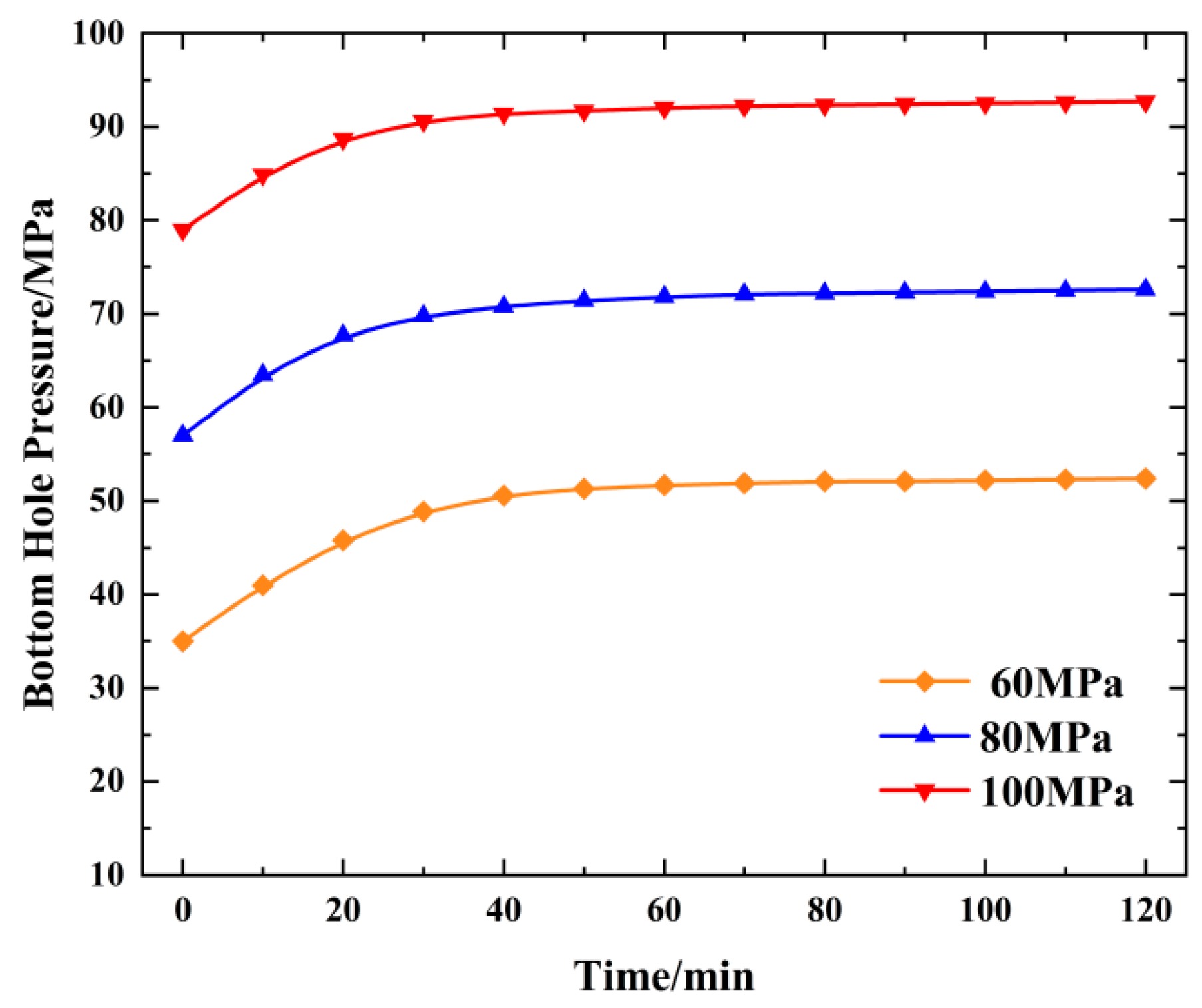
4.4. Change in the Bottom Hole Temperature Pressure with the Injection Pressure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pires da Mata Costa, L.; Micheline Vaz de Miranda, D.; Couto de Oliveira, A.; Falcon, L.; Stella Silva Pimenta, M.; Guilherme Bessa, I.; Juarez Wouters, S.; Andrade, M.; Pinto, J. Capture and Reuse of Carbon Dioxide (CO2) for a Plastics Circular Economy: A Review. Processes 2021, 9, 759. [Google Scholar] [CrossRef]
- He, Y.; Gao, H.; Zhou, X. Study on method for improving displacement effect of CO2 drive in extra-low permeability reservoir. Fault-Block Oil Gas Field 2011, 18, 512–515. [Google Scholar]
- Yang, Y. Research and application of CO2 flooding technology in extra-low permeability reservoirs of Shengli Oilfield. Oil Gas Geol. Oil Recovery Ratio 2020, 27, 11–19. [Google Scholar] [CrossRef]
- Brown, D. A hot dry rock geothermal energy concept utilizing supercritical CO2 instead of water. In Proceedings of the Twenty-Fifth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 24–26 January 2000; pp. 233–238. Available online: https://api.semanticscholar.org/CorpusID:2049110 (accessed on 1 January 2000).
- Sodeifian, G.; Usefi, M.M.B. Solubility, extraction, and nanoparticles production in supercritical carbon dioxide: A mini-review. ChemBioEng Rev. 2023, 10, 133–166. [Google Scholar] [CrossRef]
- Jiang, P.; Zhang, L.; Xu, R. Experimental study of convective heat transfer of carbon dioxide at supercritical pressures in a horizontal rock fracture and its application to enhanced geothermal systems. Appl. Therm. Eng. 2017, 117, 39–49. [Google Scholar] [CrossRef]
- Zhang, S.; Fu, J.; Peng, C.; Su, Y.; Zhang, H.; Yang, M. The Analysis of Transient Temperature in the Wellbore of a Deep Shale Gas Horizontal Well. Processes 2024, 12, 1402. [Google Scholar] [CrossRef]
- Shi, Y.; Weng, D.; Cai, B.; Zhang, Y.; Zhang, Y.; Wang, B.; Wang, H. Flow and Heat Transfer of Shale Oil Reservoir during CO2 Enhanced Pyrolysis: A Pore-Scale Modeling. Processes 2024, 12, 1694. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, F.; Zhang, B.; Liu, T.; Hong, Y. The Three-Dimensional Heterogeneous Simulation Study of CO2 Flooding in Low-Permeability Reservoirs. Processes 2024, 12, 1843. [Google Scholar] [CrossRef]
- Ramey, H.J. Wellbore heat transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Abdelhafiz, M.; Hegele, J.; Oppelt, J. Temperature modeling for wellbore circulation and shut-in with application in vertical geothermal wells. J. Pet. Sci. Eng. 2021, 204, 108660. [Google Scholar] [CrossRef]
- Klinkby, L.; Nielsen, C.; Krogh, E. Sim-ulating rapidly fluctuating CO2 flow into the Vedsted CO2 pipeline, injection well and reservoir. Energy Procedia 2011, 4, 4291–4298. [Google Scholar] [CrossRef]
- Li, X.; Li, G.; Wang, H. A wellbore flow model and coupling solution for supercritical CO2 fracturing. Pet. Drill. Technol. 2018, 42, 87–94. [Google Scholar] [CrossRef]
- Qiu, Z.; Xie, B.; Wang, Z. Research on the key technology of supercritical carbon dioxide drilling fluid. Pet. Drill. Technol. 2012, 40, 1–7. [Google Scholar] [CrossRef]
- Lesem, L.; Greytok, F.; Marotta, F. A Method of Calculating the Distribution of Temperature in Flowing Gas Wells. Soc. Pet. Eng. 1957, 210, 1–8. [Google Scholar] [CrossRef]
- Sproull, R. The conduction of heat in solids. Sci. Am. 1962, 207, 92–107. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, Y.; Li, Y. Mechanistic model for predicting bore pressure and temperature distribution. J. Xi’an Inst. Pet. Technol. 2003, 18, 40–44. [Google Scholar]
- Gu, H.; Cheng, L.; Huang, S. Thermophysical properties estimation and performance analysis of superheated-steam injection in horizontal wells considering phase change. Energy Convers. Manag. 2015, 99, 119–131. [Google Scholar] [CrossRef]
- Dong, W.; Shen, R.; Liang, Q. Model Calculations and Factors Affecting Wellbore Temperatures During SRV Fracturing. Arab. J. Sci. Eng. 2018, 43, 6475–6480. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Q.; He, Y. Temperature-pressure field coupling calculation model considering phase behavior change in CO2 injection wellbore hole. J. China Univ. Pet. Nat. Sci. Ed. 2009, 33, 73–77. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, X. Study on Temperature and Pressure Profiles and Its Influencing Factors in CO2 Injection Wellbore. Sci. Technol. Eng. 2009, 9, 5330–5334. [Google Scholar]
- Paterson, L.; Lu, M.; Connell, L. Numerical modeling of pressure and temperature profiles including phase transitions in carbon dioxide wells. SPE 2008, 115946. [Google Scholar] [CrossRef]
- Yasunami, T.; Sasaki, K.; Sugai, Y. CO2 temperature prediction in injection tubing considering supercritical condition at Yubari ECBM pilot-test. J. Can. Pet. Technol. 2010, 49, 44–50. [Google Scholar] [CrossRef]
- Cheng, L.; Xu, J.; Wang, Q. The influence of tube diameter parameters on the flow resistance and heat transfer characteristics of supercritical CO2 in horizontal tubes. Appl. Therm. Eng. 2024, 241, 122361. [Google Scholar] [CrossRef]
- Hou, J.; Zhou, Y.; Yuan, Y. Numerical study on flow structure and heat transfer of supercritical CO2 in tubes with different inclination angles. Prog. Nucl. Energy 2024, 168, 105028. [Google Scholar] [CrossRef]
- Sun, F.; Xie, G.; Song, J.; Li, S. Thermal characteristics of in-tube upward supercritical CO2 flows and a new heat transfer prediction model based on artificial neural networks (ANN). Appl. Therm. Eng. 2021, 194, 117067. [Google Scholar] [CrossRef]
- Chen, X.; He, M.; Xu, M. Fully transient coupled prediction model of wellbore temperature and pressure for multi-phase flow during underbalanced drilling. Geoenergy Sci. Eng. 2023, 223, 211540. [Google Scholar] [CrossRef]
- Jing, J.; Shan, H.; Zhu, X.; Huangpu, Y. Wellbore temperature and pressure calculation of offshore gas well based on gas–liquid separated flow model. Processes 2022, 10, 2043. [Google Scholar] [CrossRef]
- Liu, X.; Liu, L.; Yu, Z.; Zhang, L. Study on the coupling model of wellbore temperature and pressure during the production of high temperature and high pressure gas well. Energy Rep. 2022, 8, 1249–1257. [Google Scholar] [CrossRef]
- Pang, Z.; Wang, L. A model to calculate heat loss of flowing superheated steam in pipe or wellbore. Comput. Comput. Therm. Sci. 2016, 8, 249–263. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, X.; Zheng, X. Numerical investigation on heat transfer of the supercritical fluid upward in vertical tube with constant wall temperature. Int. J. Heat Mass Transf. 2019, 128, 875–884. [Google Scholar] [CrossRef]
- Tang, Y.; Hu, S.; Wang, Y. Phase behaviors of CO2 in the whole process of injection–fracturing–flowback: A case study of Well SH52 in a tight sandstone gas reservoir of the Shenmu Gas Field. Ordos Basin Nat. Gas Ind. 2019, 39, 58–64. [Google Scholar] [CrossRef]
- Khan, N.U.; May, R. A generalized mathematical model to predict transient bottomhole temperature during drilling operation. J. Pet. Sci. Eng. 2016, 147, 435–450. [Google Scholar] [CrossRef]
- Dang, Z.; Chen, X.; Yao, X.; Xu, Z.; Zhou, M.; Yang, W.; Song, X. Wellbore Temperature Prediction Model and Influence Law of Ultra-Deep Wells in Shunbei Field, China. Processes 2024, 12, 1715. [Google Scholar] [CrossRef]
- Cao, J.; Ma, G.; Zhao, G.; Yang, S.; Han, L.; Wang, J.; Mou, Y.; Cai, M. Research on Wellbore Integrity Evaluation Model of CO2 Enhanced Composite Fracturing. Processes 2024, 12, 2338. [Google Scholar] [CrossRef]
- Zhang, H. Study on Heat Transfer Characteristics in Wellbore during Cryogenic Fracturing. Ph.D. Dissertation, Oil and Gas Well Engineering, China University of Petroleum, Beijing, China, 2020. Available online: https://link.cnki.net/doi/10.27643/d.cnki.gsybu.2020.000002 (accessed on 11 March 2022).
- Span, R. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Vesovic, V.; Wakeham, W.; Olchowy, G.; Sengers, J. The transport properties of carbon dioxide. J. Phys. Chem. Ref. Data 1990, 19, 763–808. [Google Scholar] [CrossRef]
- Fenghour, A.; Wakeham, W. The viscosity of carbon dioxide. J. Phys. Chem. Ref. Data 1998, 27, 31–44. [Google Scholar] [CrossRef]
- Bo, X. Coupling solving method of temperature and pressure fieldduring supereritical carbon dioxide dry fracturing. China Sci. 2020, 15, 119–124. [Google Scholar] [CrossRef]
- Guo, C.Q.; Li, Y.C. Comprehensive numerical simulation of pressure and temperature prediction in gas well. Acta Pet. Sin. 2001, 22, 100. [Google Scholar] [CrossRef]
- Lan, J.P.; Gong, Q.; Xu, Z.G. Effect of CO2 fracturing parameters on well temperature and pressure. China Pet. Mach. 2018, 46, 101–107. [Google Scholar] [CrossRef]



| Property | Parameter | Property | Parameter |
|---|---|---|---|
| Boiling Point/°C | −78.5 | Density/kg/m3 | 468 |
| Volume/cm3/mol | 93.9 | Viscosity/mPas | 0.404 |
| Gas Density/kg/m3 | 7.74 | Compressibility Factor | 0.315 |
| Liquid Density/kg/m3 | 1178 | Deviation Factor | 0.274 |
| Critical Point | 31.1 °C, 7.38 MPa | Triple Point | −56.67 °C, 0.527 MPa |
| Basic Data | Parameter | Basic Data | Parameter |
|---|---|---|---|
| Drilling Depth (m) | 4399 | Artificial Bottom (m) | 4326.28 |
| Casing Outer Diameter (mm) | 139.7 | Casing Inner Diameter (mm) | 121.36 |
| Tubing Outer Diameter (mm) | 73.02 | Tubing Wall Thickness (mm) | 5.51 |
| Injection Temperature (°C) Density/kg/m3 | −17 | Surface Temperature (°C) | 26 |
| Geothermal Gradient (°C/100 m) | 2.8 | Injection Pressure (MPa) | 39 |
| Injection Rate (m3/min) | 2.0 | Formation Thermal Conductivity W/(m°C) | 2.0 |
| Tubing Thermal Conductivity W/(m°C) | 44.66 | Casing Thermal Conductivity W/(m°C) | 44.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Chen, X.; Lin, W.; Du, H.; Hu, Y. Establishment of a Temperature–Pressure Coupling Model for a Tubular String in a Carbon Dioxide Injection Well. Processes 2024, 12, 2848. https://doi.org/10.3390/pr12122848
Cao Y, Chen X, Lin W, Du H, Hu Y. Establishment of a Temperature–Pressure Coupling Model for a Tubular String in a Carbon Dioxide Injection Well. Processes. 2024; 12(12):2848. https://doi.org/10.3390/pr12122848
Chicago/Turabian StyleCao, Yinping, Xinwei Chen, Wenwen Lin, Heng Du, and Yijie Hu. 2024. "Establishment of a Temperature–Pressure Coupling Model for a Tubular String in a Carbon Dioxide Injection Well" Processes 12, no. 12: 2848. https://doi.org/10.3390/pr12122848
APA StyleCao, Y., Chen, X., Lin, W., Du, H., & Hu, Y. (2024). Establishment of a Temperature–Pressure Coupling Model for a Tubular String in a Carbon Dioxide Injection Well. Processes, 12(12), 2848. https://doi.org/10.3390/pr12122848






