Feature Extraction and Diagnosis of Periodic Transient Impact Faults Based on a Fast Average Kurtogram–GhostNet Method
Abstract
:1. Introduction
2. Optimized Algorithm Based on the Fast Kurtogram
2.1. Spectral Kurtosis Definition
2.2. Fast Kurtogram Algorithm Definition
- As shown in Equations (4) and (5), two quasi-analytic filters are constructed, namely, a low-pass filter and high-pass filter , where is a low-pass filter with a cutoff frequency ; is a quasi-analytic low-pass filter with a bandwidth of and the frequency shift of is 0.125; is a quasi-analytic high-pass filter with a bandwidth of obtained via a frequency shift of 0.375 from .
- As shown in Figure 1a, the filters and are used to filter the signal, and the twofold downsampling method is adopted for iteration to keep the total amount of data unchanged. In Figure 1a, is the coefficient sequence of the th filter at the th level , where is the number of decomposition levels of the filter, and two new sequences and are generated in layer after filtering. It is worth noting that multiplying the filter by is to convert the high-pass sequence to the low-pass sequence, thus complying with the frequency ordering. This process iterates from layer and continues to , resulting in a tree-like filter bank at each layer with sub-bands, as shown in Figure 1b. Therefore, the coefficient can be interpreted as a complex envelope of the signal located at the central frequency , and is the bandwidth.
- The spectral kurtosis value of each frequency band is calculated. From Formula (3), the spectral kurtosis of the complex envelope ci can be calculated at the center frequency with bandwidth . Therefore, Formula (3) can be rewritten as
2.3. Fast Averaging Kurtogram Algorithm Definition
- Original signal segmentation by dividing the vibration signal x(t) into M equal-length sub-signals {x_m (t)|m = 1,2, …, M}.
- Sub-signal spectral kurtosis value calculation of the kurtosis values of each sub-signal after the dual-tree complex wavelet packet transform (DTCWPT):
- Average the kurtosis values of each sub-band and sum the corresponding positions of the M group spectral kurtosis arrays obtained in the previous step to find the average:
- Select the optimal demodulation band to determine the best frequency band based on the center frequency and bandwidth at the point of maximum kurtosis () value.
- Perform an envelope analysis on the optimal frequency band to extract the fault characteristic frequencies.
3. Bearing Fault Diagnosis Method Based on the FAK
- Ball pass frequency, outer race:
- Ball pass frequency, inner race:
- Fundamental train frequency, also known as the cage speed:
- Ball (roller) spin frequency:
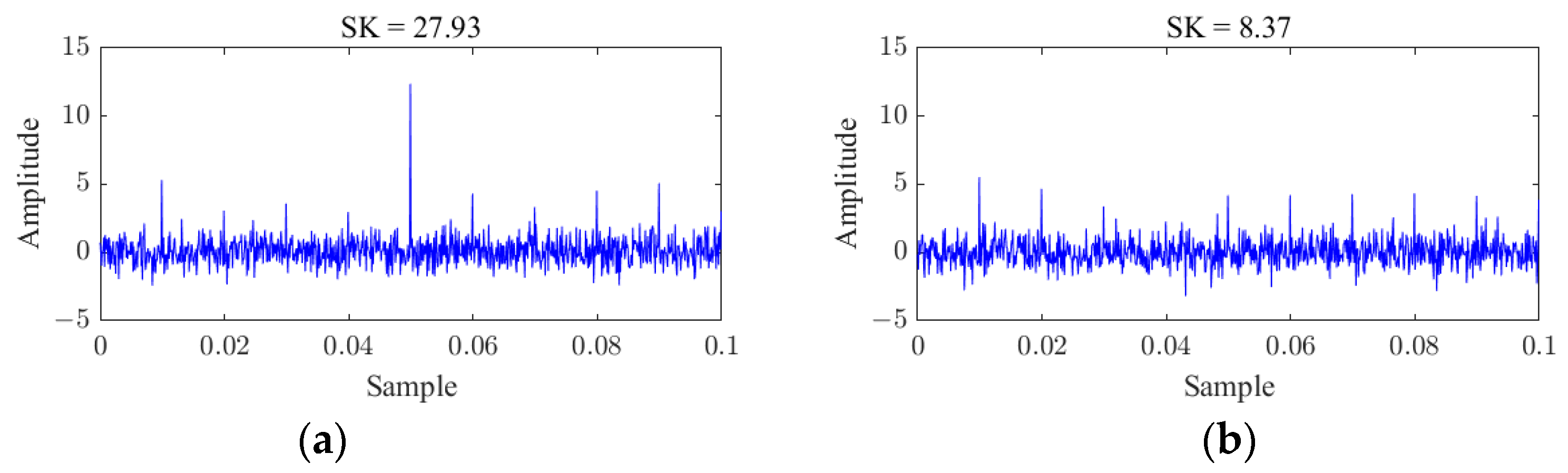
3.1. Simulation Verification
- The signal represents a simulated bearing fault signal, which is constructed by superimposing a series of decaying transient sinusoidal waves to model periodic transient impacts caused by faults during the bearing’s operation:
- represents an interference signal composed of two low-frequency sinusoidal harmonics:
- represents two oscillatory decaying pulse interferences:
- represents Gaussian white noise:
3.2. Open Dataset Test Analysis
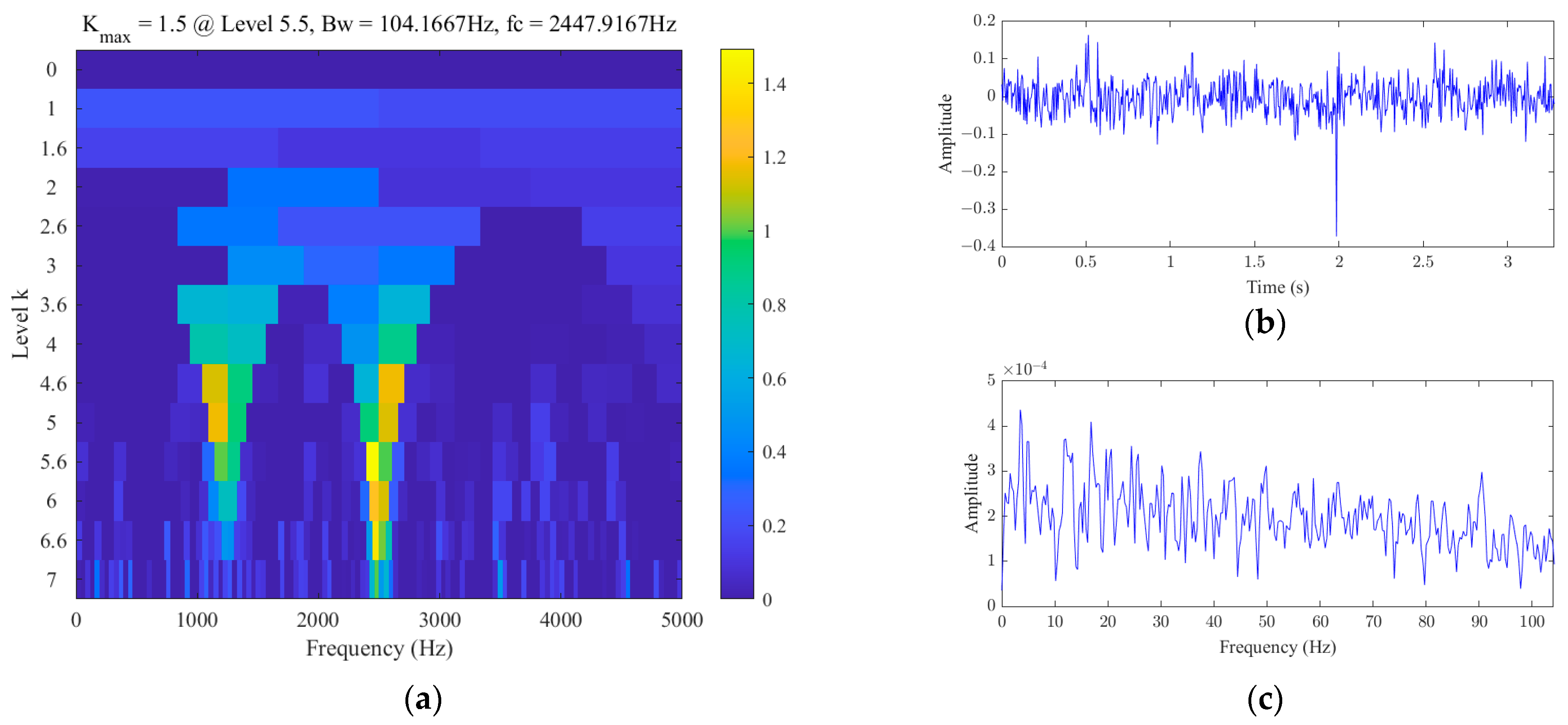
3.2.1. Data Source
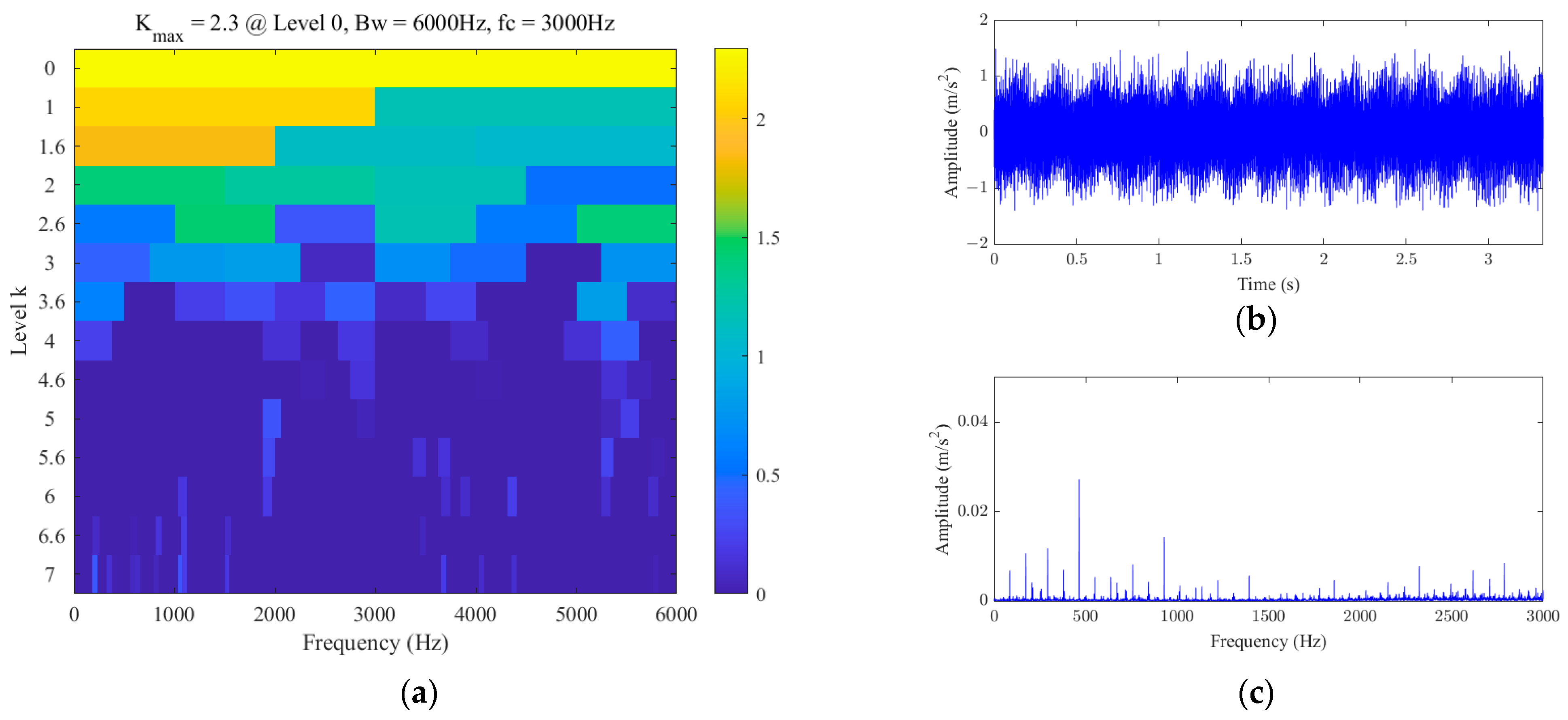
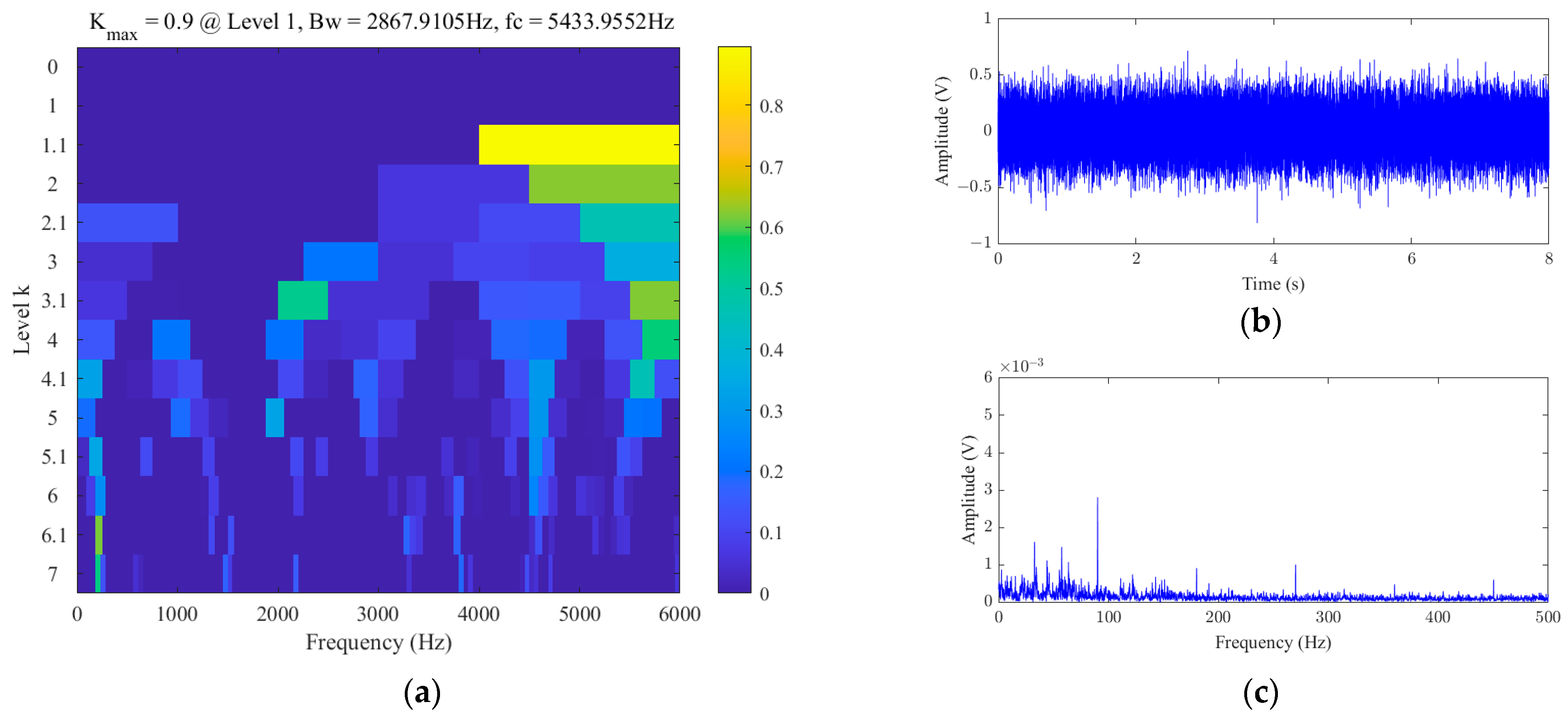
3.2.2. Results Analysis
3.3. Laboratory Data Testing Analysis
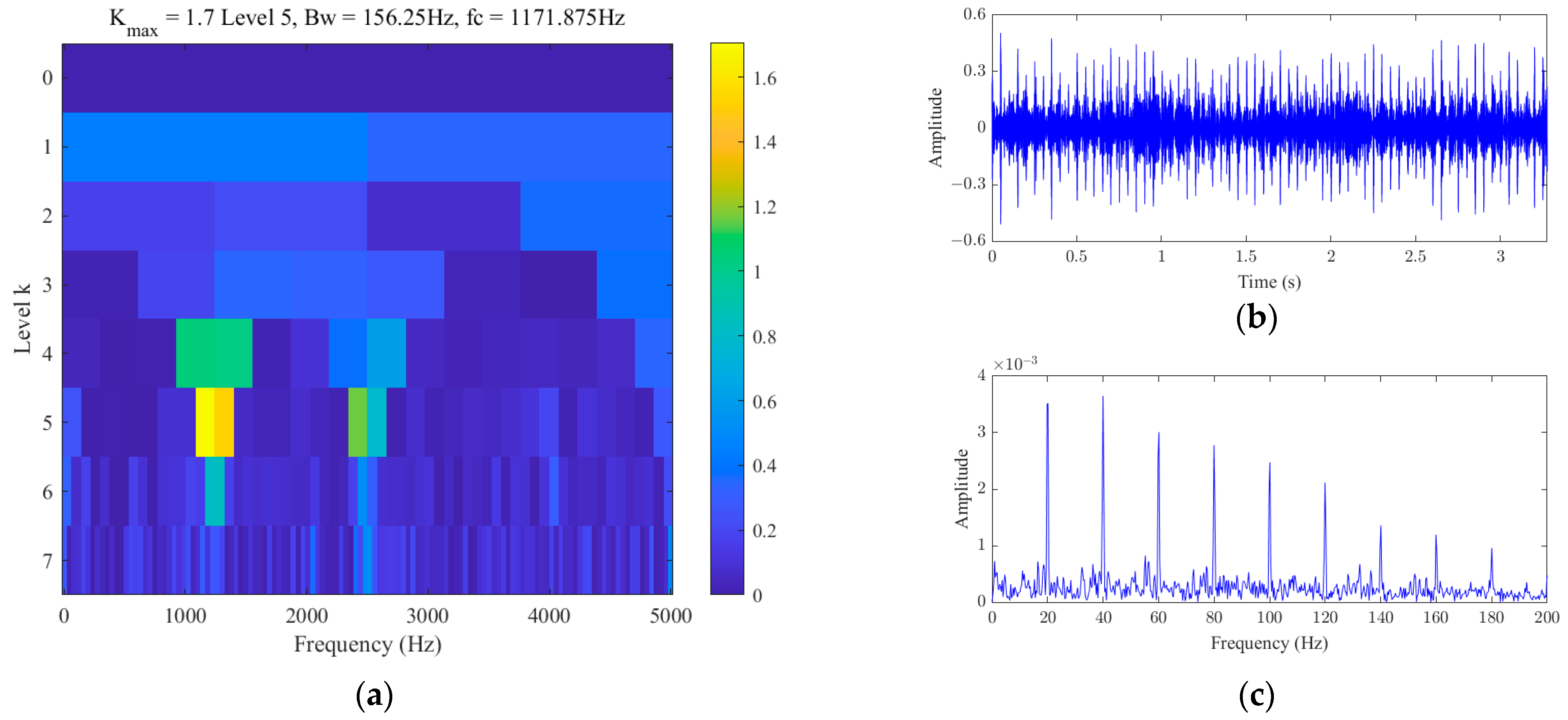
3.3.1. Experimental Setup
3.3.2. Results Analysis
4. Application of Deep Learning in Fault Diagnosis
4.1. Introduction to Convolutional Neural Networks
4.2. GhostNet Model
- Model compression: As the Ghost Module performs real convolution operations on only a subset of channels, it requires significantly fewer parameters than traditional convolutions. This design strategy reduces the model’s storage requirements and makes it more suitable for resource-limited environments.
- Design flexibility: the Ghost Module introduces a new hyperparameter, namely, the ratio of output channels that undergo actual convolution, offering researchers the possibility to adjust the balance between computation and performance, facilitating optimization according to actual application needs.
- High integrability: the Ghost Module is highly adaptable and can be used as a plug-and-play module to upgrade existing convolutional neural networks for various image classification tasks.
- For a typical convolutional layer, as shown in Figure 16a, its computational process can be represented as
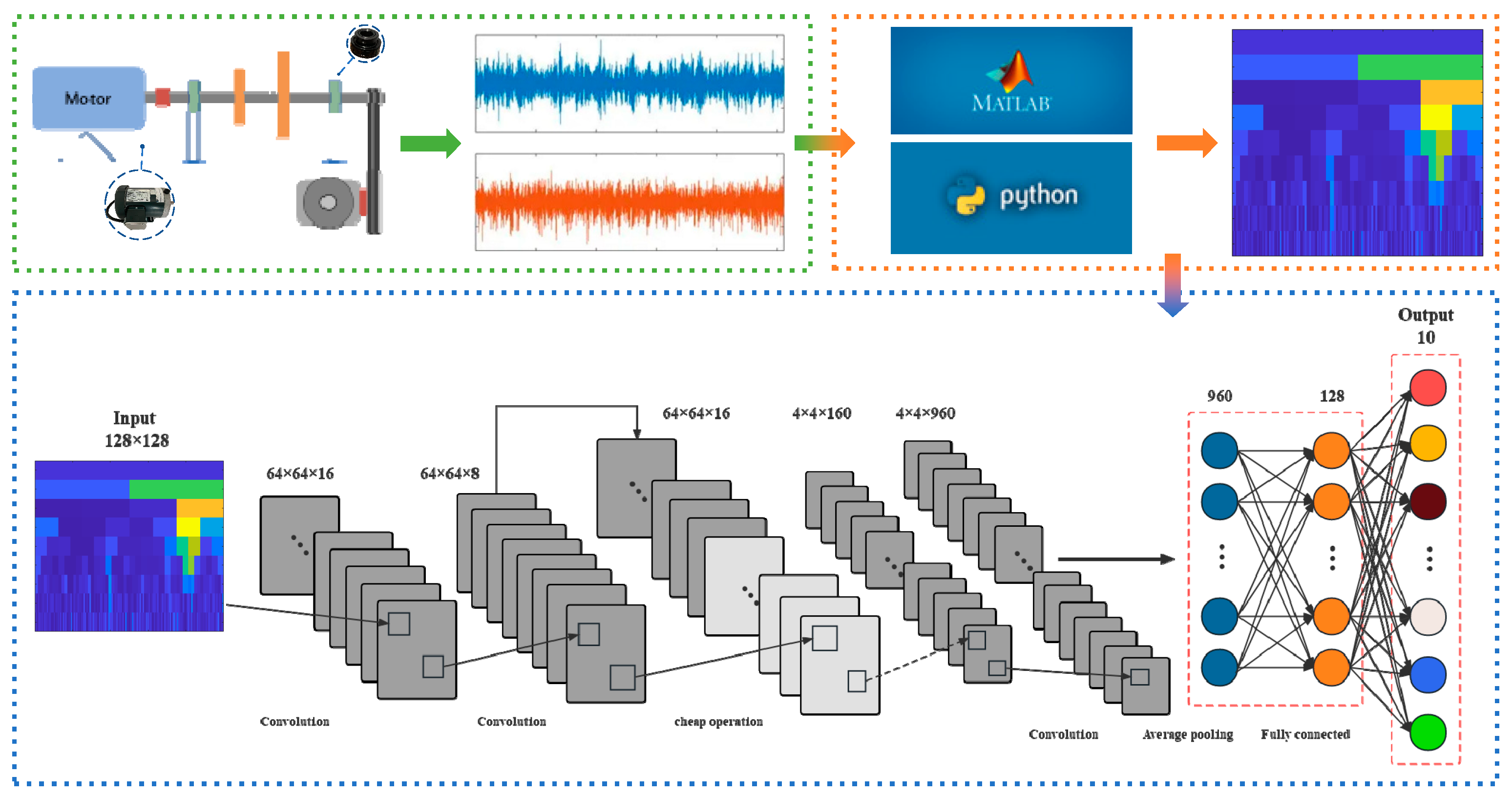
5. Intelligent Fault Diagnosis Method Based on FAK-GhostNet
5.1. Method Overview
5.2. Rolling Bearing Fault Diagnosis Experiment
5.2.1. Experimental Setup
5.2.2. Results Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.Y.; Jiang, W.L.; Yue, Y.; Zhang, S.Q. Research on Prediction Method of Gear Pump Remaining Useful Life Based on DCAE and Bi-LSTM. Symmetry 2022, 14, 1111. [Google Scholar] [CrossRef]
- Dwyer, R. Use of the Kurtosis Statistic in the Frequency Domain as an Aid in Detecting Random Signals. IEEE J. Ocean. Eng. 1984, 9, 85–92. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zi, Y. Application of an Improved Kurtogram Method for Fault Diagnosis of Rolling Element Bearings. Mech. Syst. Signal Process. 2011, 25, 1738–1749. [Google Scholar] [CrossRef]
- Zhang, Y.; Randall, R.B. Rolling Element Bearing Fault Diagnosis Based on the Combination of Genetic Algorithms and Fast Kurtogram. Mech. Syst. Signal Process. 2009, 23, 1509–1517. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Z.; Zi, Y.; He, Z.; Sun, C. Detecting of Transient Vibration Signatures Using an Improved Fast Spatial–Spectral Ensemble Kurtosis Kurtogram and Its Applications to Mechanical Signature Analysis of Short Duration Data from Rotating Machinery. Mech. Syst. Signal Process. 2013, 40, 1–37. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Tan, H.; Shi, P.; Qiao, Z. Cyclogram: An Effective Method for Selecting Frequency Bands for Fault Diagnosis of Rolling Element Bearings. Meas. Sci. Technol. 2023, 34, 094003. [Google Scholar] [CrossRef]
- Dai, S.-C.; Guo, Y.; Wu, X.; Na, J. Improvement of fast spectral kurtograph algorithm based on subband spectral kurtosis average. Vib. Shock 2015, 34, 98–102. [Google Scholar]
- Wang, L.; Liu, Z.; Cao, H.; Zhang, X. Subband Averaging Kurtogram with Dual-Tree Complex Wavelet Packet Transform for Rotating Machinery Fault Diagnosis. Mech. Syst. Signal Process. 2020, 142, 106755. [Google Scholar] [CrossRef]
- Tian, Z.; Wong, L.; Safaei, N. A Neural Network Approach for Remaining Useful Life Prediction Utilizing Both Failure and Suspension Histories. Mech. Syst. Signal Process. 2010, 24, 1542–1555. [Google Scholar] [CrossRef]
- Wang, J.; Yu, L.-C.; Lai, K.R.; Zhang, X. Dimensional Sentiment Analysis Using a Regional CNN-LSTM Model. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers), Berlin, Germany, 7–12 August 2016; Erk, K., Smith, N.A., Eds.; Association for Computational Linguistics: Berlin, Germany, 2016; pp. 225–230. [Google Scholar]
- Huang, C.; Kong, C.; Lucey, S. CNNs Are Globally Optimal Given Multi-Layer Support. arXiv 2017, arXiv:1712.02501. [Google Scholar]
- Chu, D.C.; Humphrey, M. Mobile OGSI.NET: Grid Computing on Mobile Devices. In Proceedings of the Fifth IEEE/ACM International Workshop on Grid Computing, Pittsburgh, PA, USA, 8 November 2004; pp. 182–191. [Google Scholar]
- Paul, R.R.; Valgenti, V.C.; Kim, M.S. Real-Time Netshuffle: Graph Distortion for on-Line Anonymization. In Proceedings of the 2011 19th IEEE International Conference on Network Protocols, Vancouver, BC, Canada, 17–20 October 2011; pp. 133–134. [Google Scholar]
- Gholami, A.; Kwon, K.; Wu, B.; Tai, Z.; Yue, X.; Jin, P.; Zhao, S.; Keutzer, K. SqueezeNext: Hardware-Aware Neural Network Design. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1719–171909. [Google Scholar]
- Cao, M.; Fu, H.; Zhu, J.; Cai, C. Lightweight Tea Bud Recognition Network Integrating GhostNet and YOLOv5. Math. Biosci. Eng. 2022, 19, 12897–12914. [Google Scholar] [CrossRef]
- Antoni, J. The Spectral Kurtosis: A Useful Tool for Characterising Non-Stationary Signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J. Fast Computation of the Kurtogram for the Detection of Transient Faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Borghesani, P.; Ricci, R.; Chatterton, S.; Pennacchi, P. A New Procedure for Using Envelope Analysis for Rolling Element Bearing Diagnostics in Variable Operating Conditions. Mech. Syst. Signal Process. 2013, 38, 23–35. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J.; Chobsaard, S. The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals. Mech. Syst. Signal Process. 2001, 15, 945–962. [Google Scholar] [CrossRef]
- Yu, L.; Hai, L. Fault diagnosis method of rolling bearings with different specifications based on federated model migration. Vib. Shock 2023, 42, 184–192. [Google Scholar]
- Zhi, C.; Xu, C. Application of deep learning in equipment failure prediction and health management. Chin. J. Sci. Instrum. 2020, 40, 206–226. [Google Scholar]
- Randall, R.B. Rolling Element Bearing Diagnostics—A Tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: A Benchmark Study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Liu, H.; Ma, R.; Li, D.; Yan, L.; Ma, Z. Machinery Fault Diagnosis Based on Deep Learning for Time Series Analysis and Knowledge Graphs. J. Signal Process. Syst. 2021, 93, 1433–1455. [Google Scholar] [CrossRef]
- Shao, S.; Zhang, S.; Jiang, W.; Li, Z. Study on the Health Condition Monitoring Method of Hydraulic Pump Based on Convolutional Neural Network. In Proceedings of the 2020 12th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Phuket, Thailand, 28–29 February 2020; pp. 149–153. [Google Scholar]
- Ming, D.; Bao, W. Fault diagnosis of hydraulic pump based on empirical wavelet decomposition and convolutional neural network. Chin. Hydraul. Pneum. 2020, 1, 163–170. [Google Scholar]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A Survey of the Recent Architectures of Deep Convolutional Neural Networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, S.; Wang, Y.; Huan, W. Review of Research on Lightweight Convolutional Neural Networks. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 1713–1720. [Google Scholar]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. GhostNet: More Features from Cheap Operations. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1577–1586. [Google Scholar]
- Lang, X.; Han, F. MFL Image Recognition Method of Pipeline Corrosion Defects Based on Multilayer Feature Fusion Multiscale GhostNet. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- Li, S.; Sultonov, F.; Tursunboev, J.; Park, J.-H.; Yun, S.; Kang, J.-M. Ghostformer: A GhostNet-Based Two-Stage Transformer for Small Object Detection. Sensors 2022, 22, 6939. [Google Scholar] [CrossRef] [PubMed]
- Chi, J.; Guo, S.; Zhang, H.; Shan, Y. L-GhostNet: Extract Better Quality Features. IEEE Access 2023, 11, 2361–2374. [Google Scholar] [CrossRef]
- Udmale, S.S.; Patil, S.S.; Phalle, V.M.; Singh, S.K. A Bearing Vibration Data Analysis Based on Spectral Kurtosis and ConvNet. Soft Comput. 2019, 23, 9341–9359. [Google Scholar] [CrossRef]
- Huang, B.; Liu, J.; Zhang, Q.; Liu, K.; Li, K.; Liao, X. Identification and Classification of Aluminum Scrap Grades Based on the Resnet18 Model. Appl. Sci. 2022, 12, 11133. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]

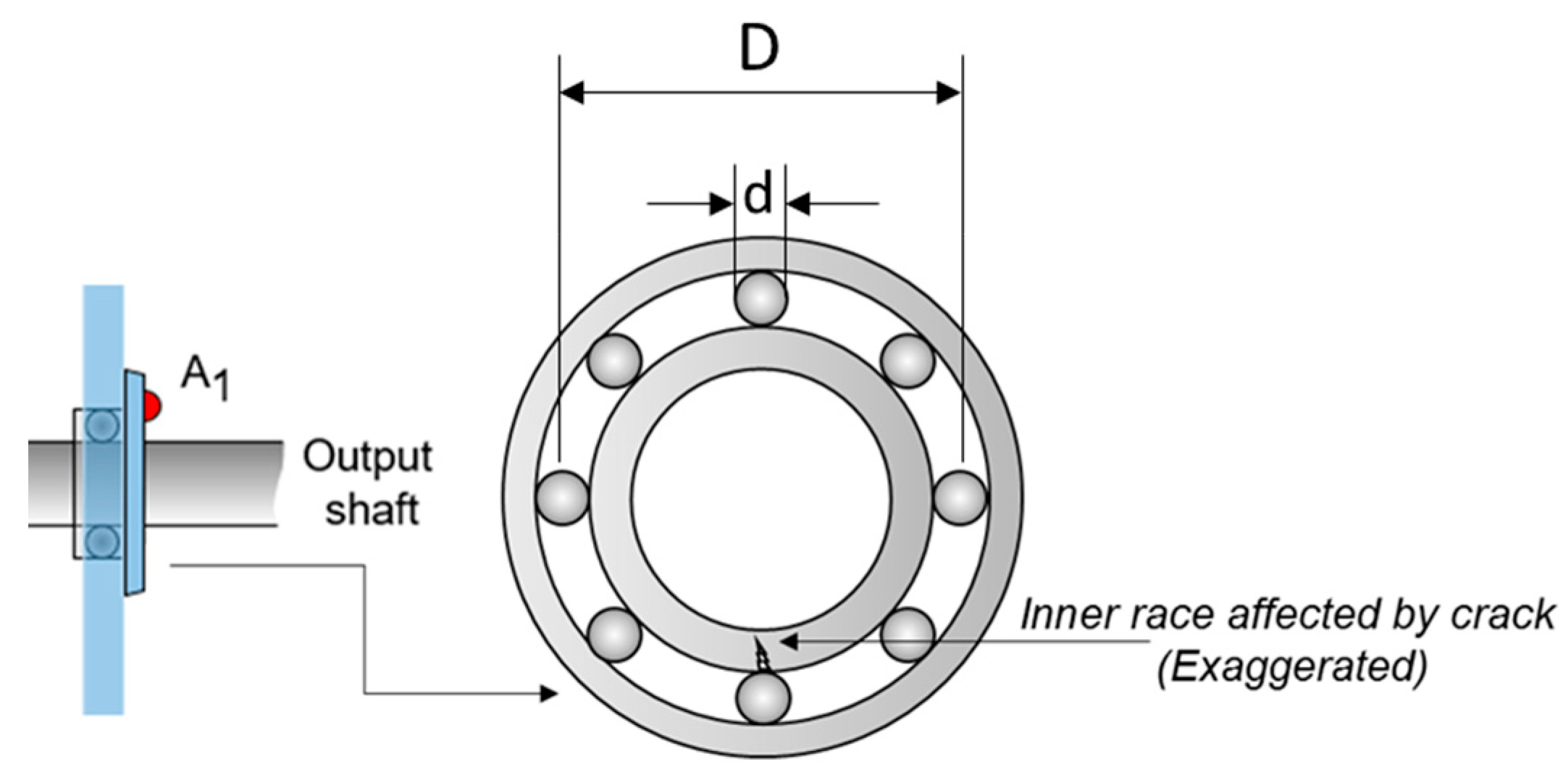












| Number of Rolling Elements (z) | Rolling Element Size (d/mm) | Pitch Diameter (D/mm) | Contact Angle () |
|---|---|---|---|
| 9 | 7.94 | 39.04 | 0 |
| Number of Rolling Elements (z) | Rolling Element Size (d/in) | Pitch Diameter (D/in) | Contact Angle () |
|---|---|---|---|
| 8 | 0.3125 | 1.319 | 0 |
| Number of Rolling Elements (z) | Rolling Element Size (d/in) | Pitch Diameter (D/in) | Contact Angle () |
|---|---|---|---|
| 8 | 0.3125 | 1.318 | 0 |
| Input | Output | Operator | #exp | SE | Stride |
|---|---|---|---|---|---|
| 128 × 128 × 3 | 64 × 64 × 16 | Conv2d 3 × 3 | - | - | 2 |
| 64 × 64 × 16 | 64 × 64 × 16 | G-bneck | 16 | - | 1 |
| 64 × 64 × 16 | 32 × 32 × 24 | G-bneck | 48 | - | 2 |
| 32 × 32 ×24 | 32 × 32 × 24 | G-bneck | 72 | - | 1 |
| 32 × 32 × 24 | 16 × 16 × 40 | G-bneck | 72 | 1 | 2 |
| 16 × 16 × 40 | 16 × 16 × 40 | G-bneck | 120 | 1 | 1 |
| 16 × 16 × 40 | 8 × 8 × 80 | G-bneck | 240 | - | 2 |
| 8 × 8 × 80 | 8 × 8 × 80 | G-bneck | 200 | - | 1 |
| 8 × 8 × 80 | 8 × 8 × 80 | G-bneck | 184 | - | 1 |
| 8 × 8 × 80 | 8 × 8 × 80 | G-bneck | 184 | - | 1 |
| 8 × 8 × 80 | 8 × 8 × 112 | G-bneck | 480 | 1 | 1 |
| 8 × 8 × 112 | 8 × 8 × 112 | G-bneck | 672 | 1 | 1 |
| 8 × 8 × 112 | 4 × 4 × 160 | G-bneck | 672 | 1 | 2 |
| 4 × 4 × 160 | 4 × 4 × 160 | G-bneck | 960 | - | 1 |
| 4 × 4 × 160 | 4 × 4 × 160 | G-bneck | 960 | 1 | 1 |
| 4 × 4 × 160 | 4 × 4 × 160 | G-bneck | 960 | - | 1 |
| 4 × 4 × 160 | 4 × 4 × 160 | G-bneck | 960 | 1 | 1 |
| 4 × 4 × 160 | 4 × 4 × 960 | Conv2d 1 × 1 | - | - | 1 |
| 4 × 4 × 960 | 1 × 1 × 960 | AvgPool4 × 4 | - | - | - |
| 1 × 1 × 960 | 1 × 1 × 128 | FC | - | - | - |
| 1 × 1 × 128 | 1 × 1 × 5 | FC | - | - | - |
| Model | Acc. (%) | MFLOPs | Params/106 | MemR + W(MB) | Images/s |
|---|---|---|---|---|---|
| FK–GhostNet | 0.9848 | 49.51 | 2.79 | 36.5 | 82 |
| FAK–GhostNet | 0.9902 | 49.51 | 2.79 | 36.5 | 85 |
| FAK–ResNet18 | 0.9930 | 594.58 | 11.18 | 59.77 | 59 |
| FAK-MobileNetV2 | 0.9820 | 104.16 | 2.23 | 57.11 | 57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.-L.; Zhao, Y.-H.; Zang, Y.; Qi, Z.-Q.; Zhang, S.-Q. Feature Extraction and Diagnosis of Periodic Transient Impact Faults Based on a Fast Average Kurtogram–GhostNet Method. Processes 2024, 12, 287. https://doi.org/10.3390/pr12020287
Jiang W-L, Zhao Y-H, Zang Y, Qi Z-Q, Zhang S-Q. Feature Extraction and Diagnosis of Periodic Transient Impact Faults Based on a Fast Average Kurtogram–GhostNet Method. Processes. 2024; 12(2):287. https://doi.org/10.3390/pr12020287
Chicago/Turabian StyleJiang, Wan-Lu, Yong-Hui Zhao, Yan Zang, Zhi-Qian Qi, and Shu-Qing Zhang. 2024. "Feature Extraction and Diagnosis of Periodic Transient Impact Faults Based on a Fast Average Kurtogram–GhostNet Method" Processes 12, no. 2: 287. https://doi.org/10.3390/pr12020287
APA StyleJiang, W.-L., Zhao, Y.-H., Zang, Y., Qi, Z.-Q., & Zhang, S.-Q. (2024). Feature Extraction and Diagnosis of Periodic Transient Impact Faults Based on a Fast Average Kurtogram–GhostNet Method. Processes, 12(2), 287. https://doi.org/10.3390/pr12020287






