Exploration of Temperature Inversion in Intermediate Joints of 10 kV Three-Core Cable
Abstract
:1. Introduction
2. Numerical Computation of Temperature Distribution in a Three-Core Cable Joint
2.1. Establishment of Simulation Model
2.2. Temperature Field Control Equation
2.3. Loading Conditions
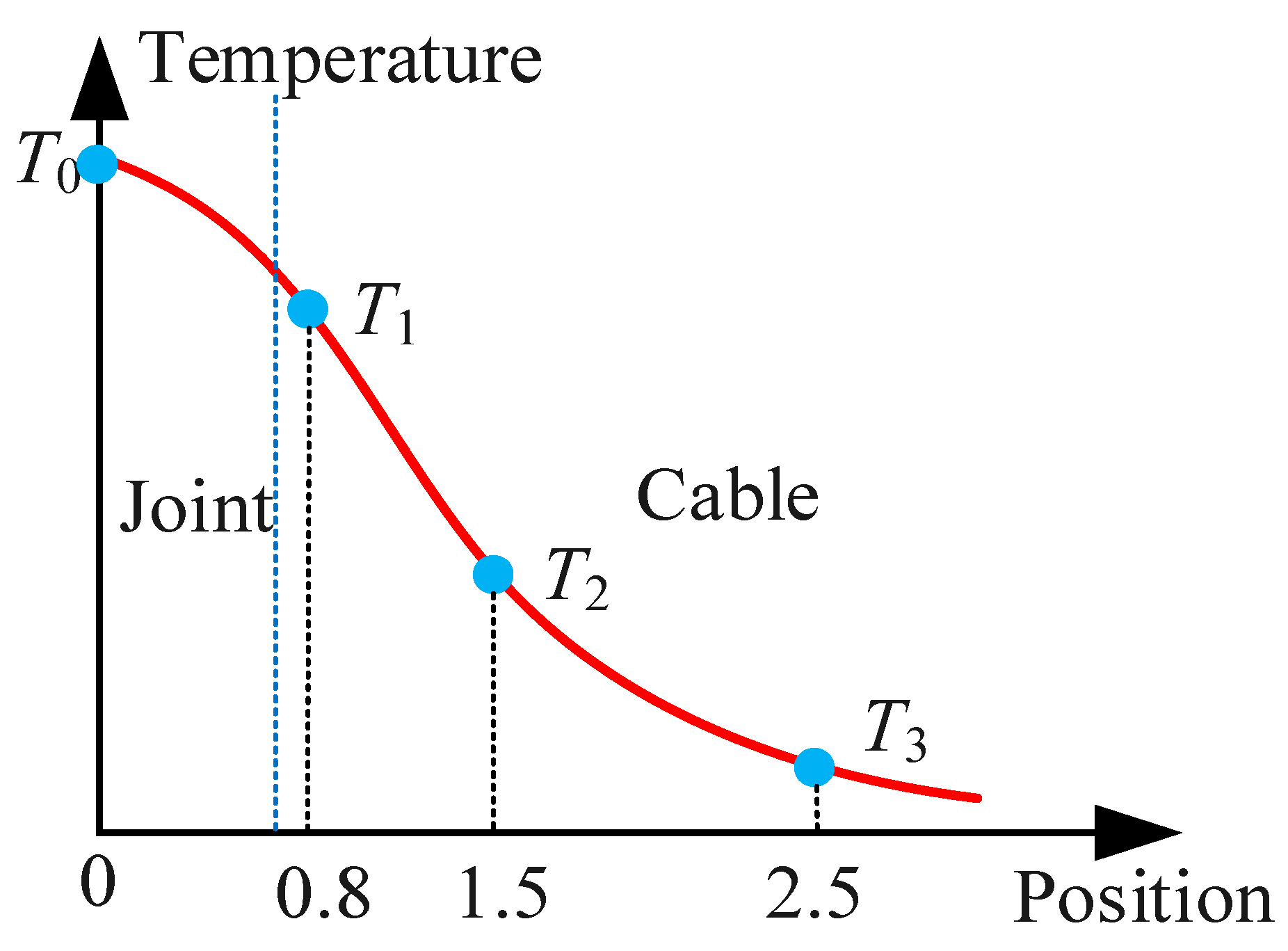
2.4. Analysis of the Temperature Distribution in Cable Joints
3. Temperature Inversion Method for Three-Core Cable Joints
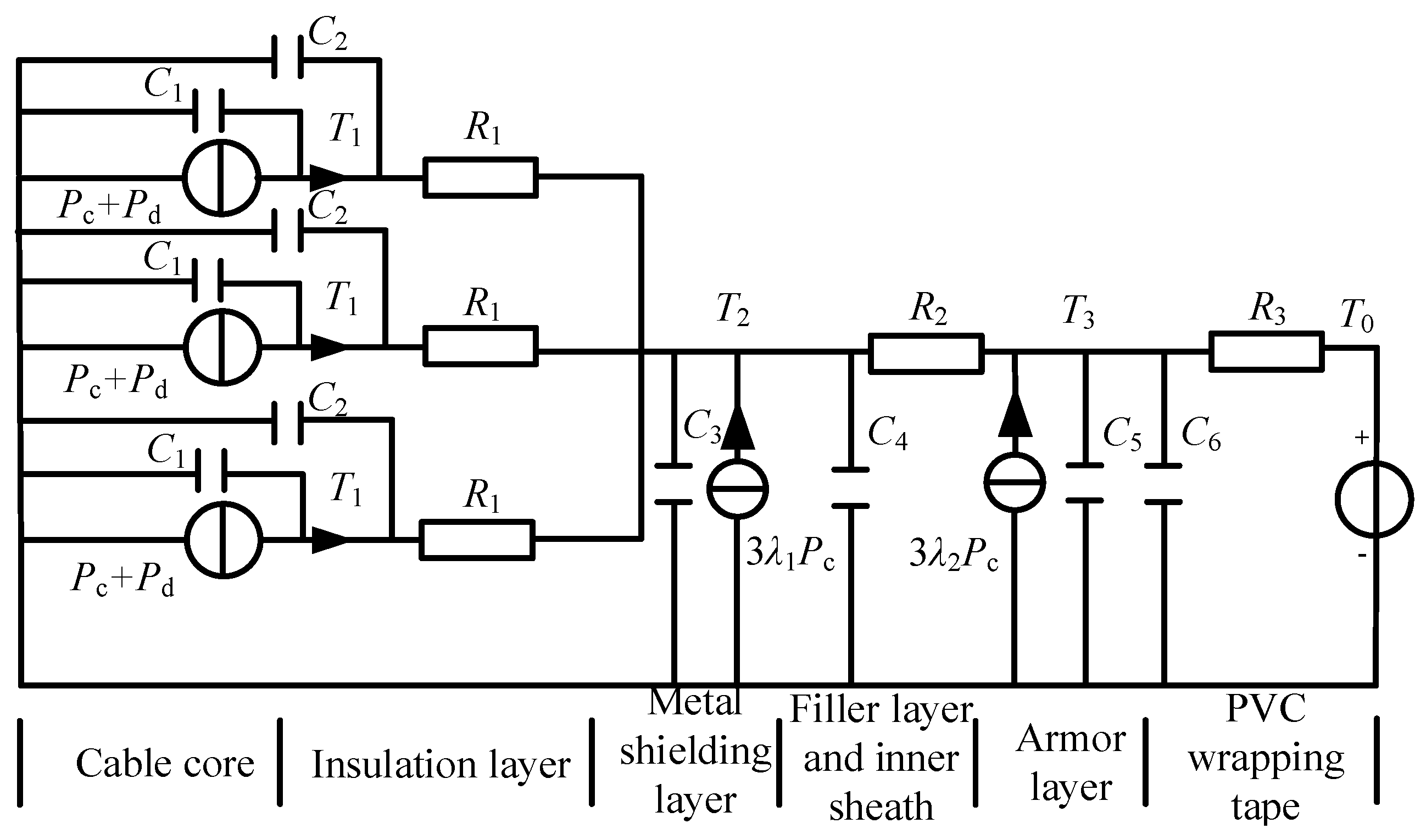
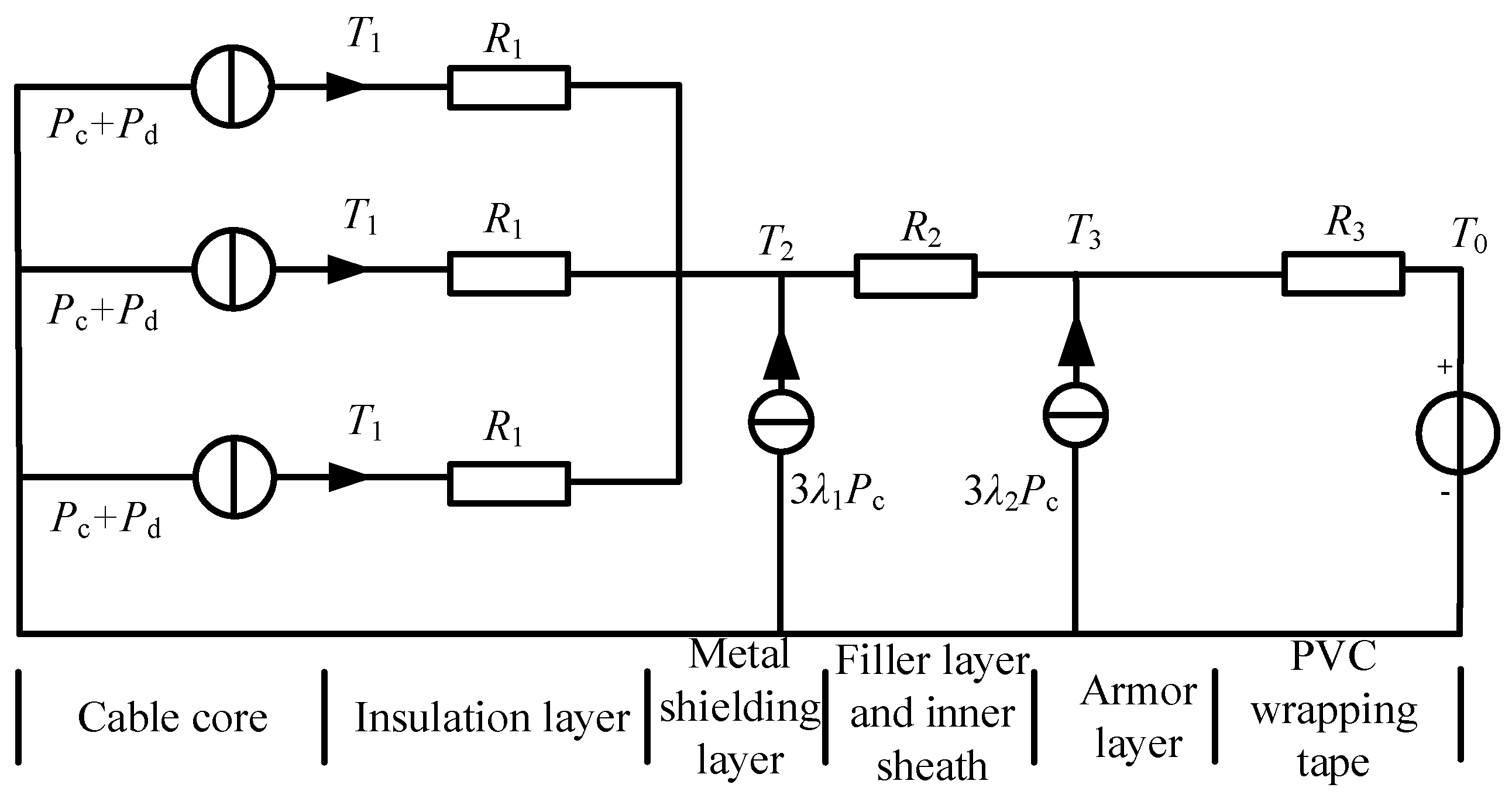
3.1. Establishment of Radial Thermal Path Model
- (1)
- Thermal resistance calculation
- (2)
- Heat capacity calculation
3.2. Calculation Method for Axial Fitting
4. Verification of Joint Temperature Inversion Model
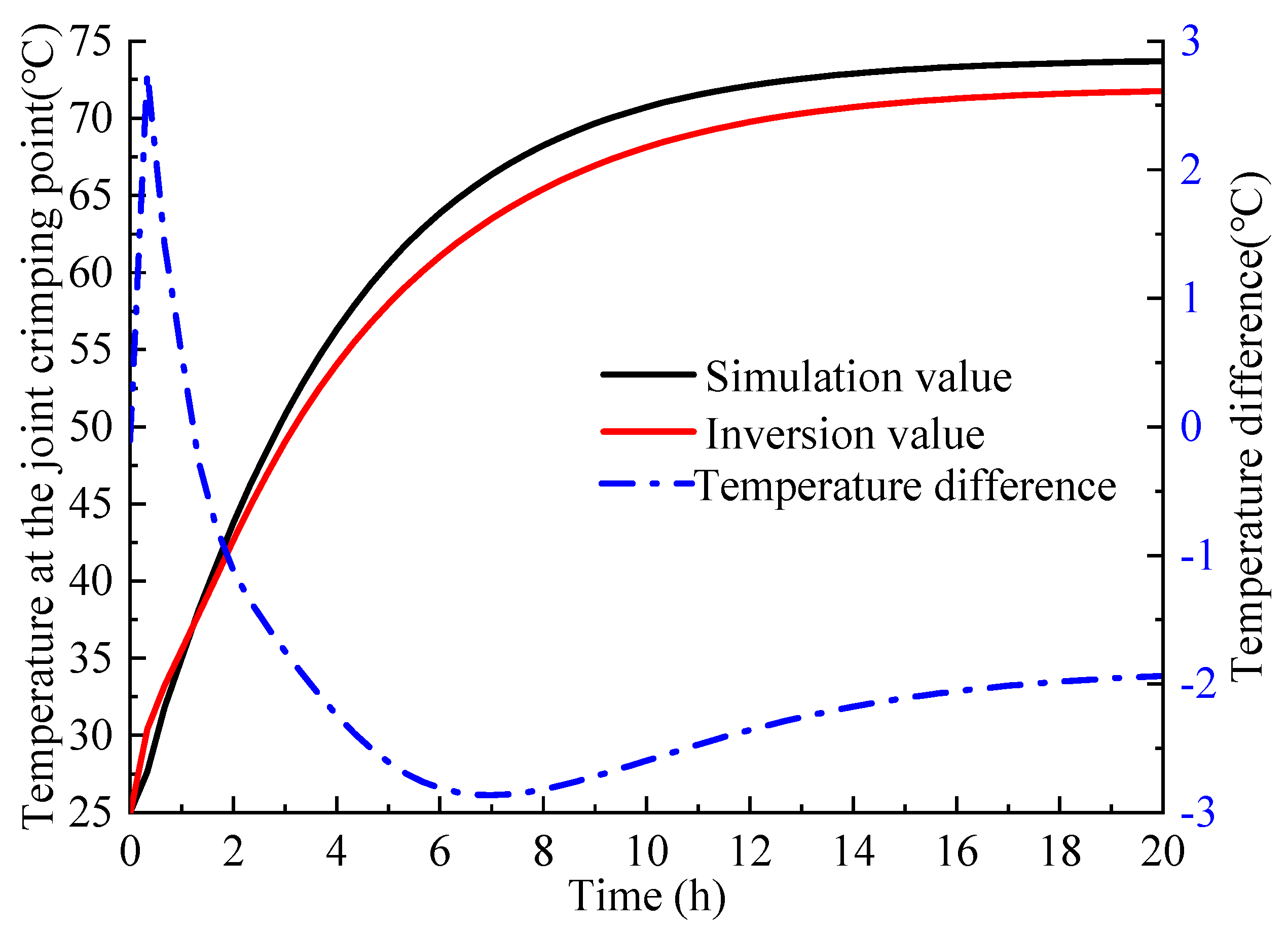
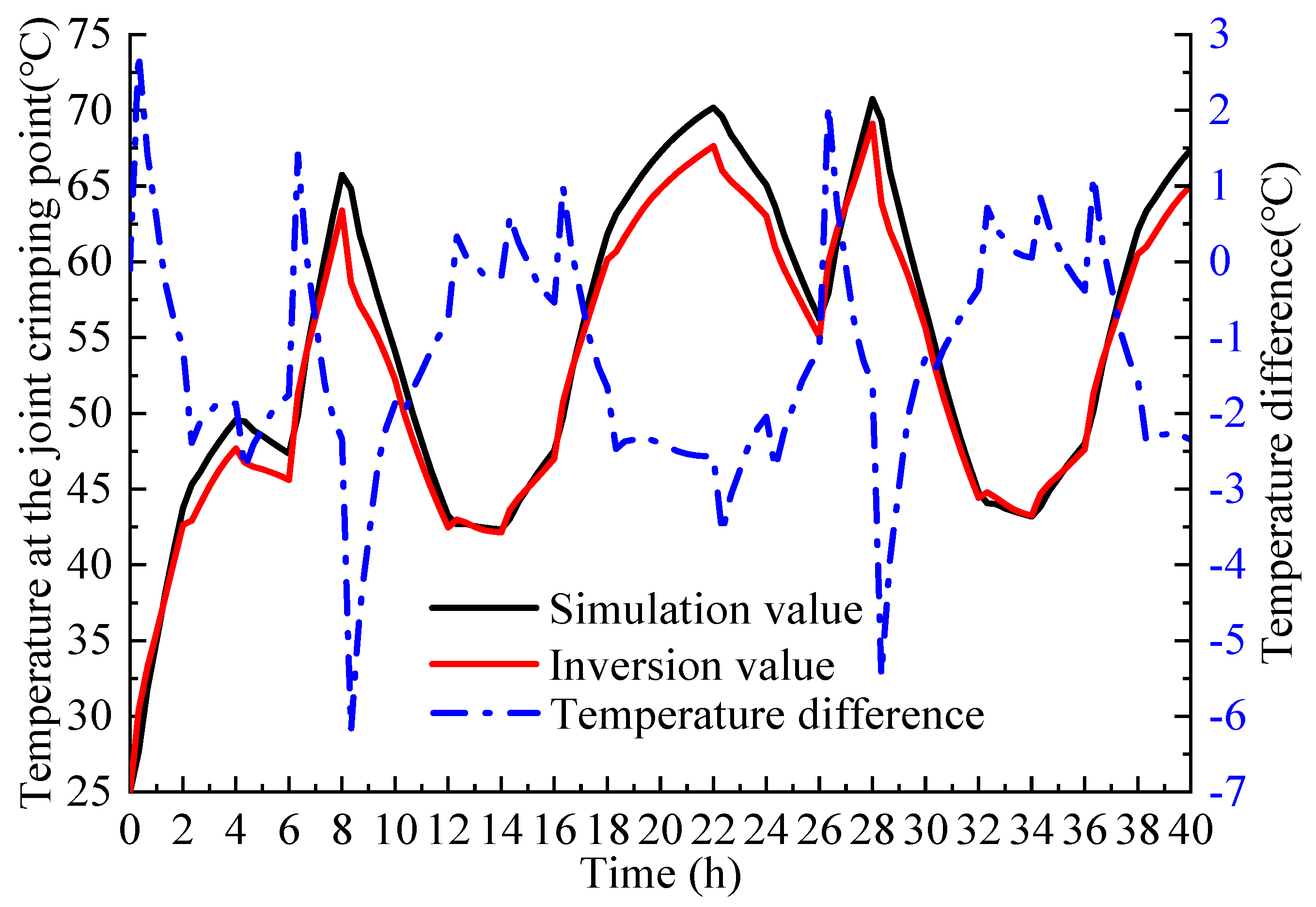
4.1. Continuous Load
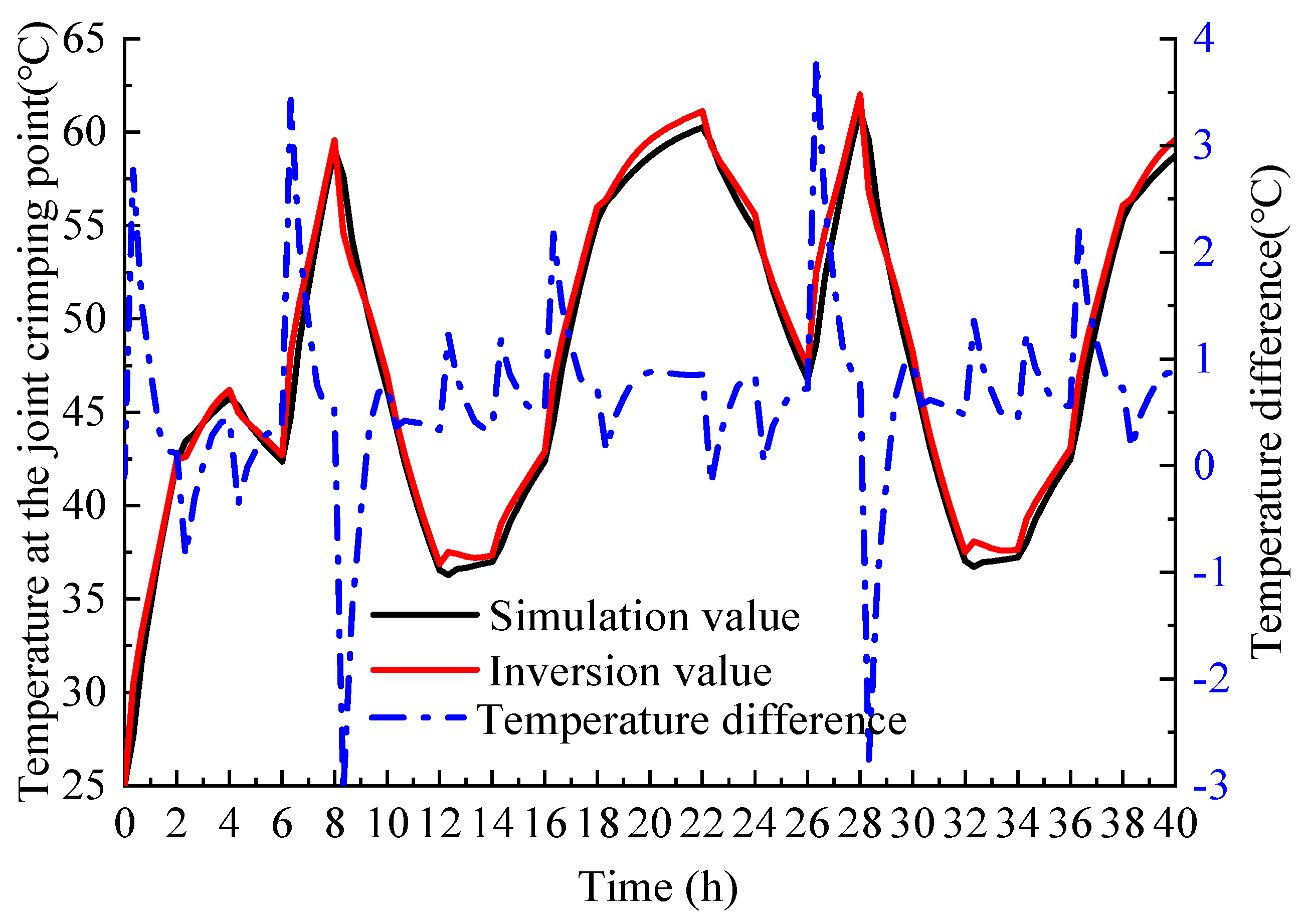
4.2. Periodic Load
4.3. Taking into Account the Influence of Material Parameter Dispersion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- The National Development and Reform Commission. Guiding Opinions on Accelerating the Construction and Renovation of Distribution Networks; The National Development and Reform Commission: Beijing, China, 2015. [Google Scholar]
- Liu, G.; Lei, C.; Liu, Y. Analysis on transient error of simplified thermal circuit model for calculating conductor temperature by cable surface temperature. Power Syst. Technol. 2011, 35, 212–217. [Google Scholar]
- Guo, W.; Zhou, S.L.; Wang, L.; Pei, H.; Zhang, C.; Li, H.C. Design and application of online monitoring system for electrical cable states. High Volt. Eng. 2019, 45, 3459–3466. [Google Scholar]
- Xia, C.; Liu, H.; Wu, G.; Xia, Z. Research on the Heat Dissipation Performance and Current Carrying Capacity of the Intermediate Joint of Three Core Cables with Explosion Proof Boxes. Electr. Meas. Instrum. 2022, 59, 47–52. [Google Scholar]
- Yuan, Y.; Gao, L.; Zhu, C.; Dong, J.; Ye, Z.; Zou, H. Method for calculating the temperature of high-voltage three-core cable joints based on support vector regression. Power Supply Consum. 2023, 40, 85–91. [Google Scholar]
- Bucolo, M.; Buscarino, A.; Carlo, F.; Fortuna, L. Chaos Addresses Energy in Networks of Electrical Oscillators. IEEE Access 2021, 9, 153258–153265. [Google Scholar] [CrossRef]
- Guo, X.; Wang, Q.; He, X.; Wang, Z. Temperature Trend Simulation and System Design of Cable Conductors in Distribution Networks. Power Supply Consum. 2020, 37, 83–88. [Google Scholar]
- Lv, G.; Zhang, D.; Fu, C.; Yang, L.; Zhou, C.; Wu, X.; Liu, B. Split Conductor in Preset Temperature Fiber XLPE Cables and Accessories of the Development and Test. Electr. Wire Cable 2013, 5, 8–11. [Google Scholar]
- Lis, J.; Thelwell, M.J. Analogue investigation of water cooling of e.h.v cables. Proc. IEEE 1965, 112, 335–341. [Google Scholar] [CrossRef]
- Weedy, B.M.; Thelwell, M.J. Transient thermal performance of ehv-cable joints. Proc. IEEE 1972, 119, 472–478. [Google Scholar]
- Xu, Y.; Wang, L.; Gao, H.; Xie, X. Theoretical study on temperature field distribution of power cable joints. Power Syst. Prot. Control 2008, 36, 4–7. [Google Scholar]
- Hu, W.; Hu, Q.; Lin, X.; Lin, S. Research on Cable Joint Temperature Monitoring System Based on Temperature Field. Ind. Min. Autom. 2013, 39, 90–93. [Google Scholar]
- Lin, S.; Hu, W. Theoretical research on temperature field of power cable joint with FEM. In Proceedings of the International Conference on System Science and Engineering, Dalian, China, 30 June–2 July 2012. [Google Scholar]
- Chang, W.; Han, X.; Li, C.; Ge, Z. Experimental Study on Table Joint Temperature Measurement Technology under Step Current. High Volt. Eng. 2013, 39, 1156–1162. [Google Scholar]
- Han, X. Research on Online Monitoring System for Temperature of Intermediate Joints in Power Cables; North China Electric Power University: Beijing, China, 2012. [Google Scholar]
- Xiao, W.; Han, Q.; Zhu, W.; Zhan, Q.; Yi, S. Temperature prediction of cable joints based on generalized regression neural network. Electr. Power 2013, 32, 34–37. [Google Scholar]
- Gao, Y.; Tan, T.; Liu, K.; Ruan, J. Research on Temperature Retrieval and Fault Diagnosis of Cable Joint. High Volt. Eng. 2016, 42, 535–542. [Google Scholar]
- Chen, M. Simulation Study on Temperature Field of 10 kV Three Core Cable Joint; Xi’an University of Science and Technology: Xi’an, China, 2019. [Google Scholar]
- Yu, J. Temperature and Electric Field Simulation Analysis of 35 kV Three Core XLPE Cable Changing to Three Pole DC Operation. Electrotech. J. 2017, 8, 6–7, 49. [Google Scholar]
- Li, J.; Liu, G.; Li, L. Optimization study of thermal evaluation model for cable laying in pipeline clusters. Guangdong Electric Power. 2023, 36, 115–125. [Google Scholar]
- Li, X.; Chen, Y.; Liu, J.; Wang, X. Analysis of steady-state thermal path model for intermediate joints of 10 kV three core cables considering axial heat dissipation. Power Grid Clean Energy 2023, 39, 56–62, 69. [Google Scholar]
- Tao, W. Heat Transfer; Version 5; Higher Education Press: Beijing, China, 2019. [Google Scholar]
- Cengel, Y. Heat Transfer—A Practical Approach; Mc-Graw Hill: New York, NY, USA, 2003. [Google Scholar]
- Ruan, J.; Deng, Y.; Huang, D.; Duan, C.; Gong, R.; Quan, Y.; Hu, Y.; Rong, Q. HST Calculation of a 10 kV Oil-immersed Transformer With 3D Coupled-field Method. IET Electr. Power Appl. 2020, 14, 921–928. [Google Scholar] [CrossRef]
- IEC 60287-1-1: 2023; Electric Cables-Calculation of the Current Rating-Part 1-1: Current Rating Equations (100% Load Factor) and Calculation of Losses-General. IEC: Geneva, Switzerland, 2023.
- IEC 60287-2-1: 2023; Electric Cables-Calculation of the Current Rating-Part 2-1: Thermal Resistance-Calculation of Thermal Resistance. IEC: Geneva, Switzerland, 2023.
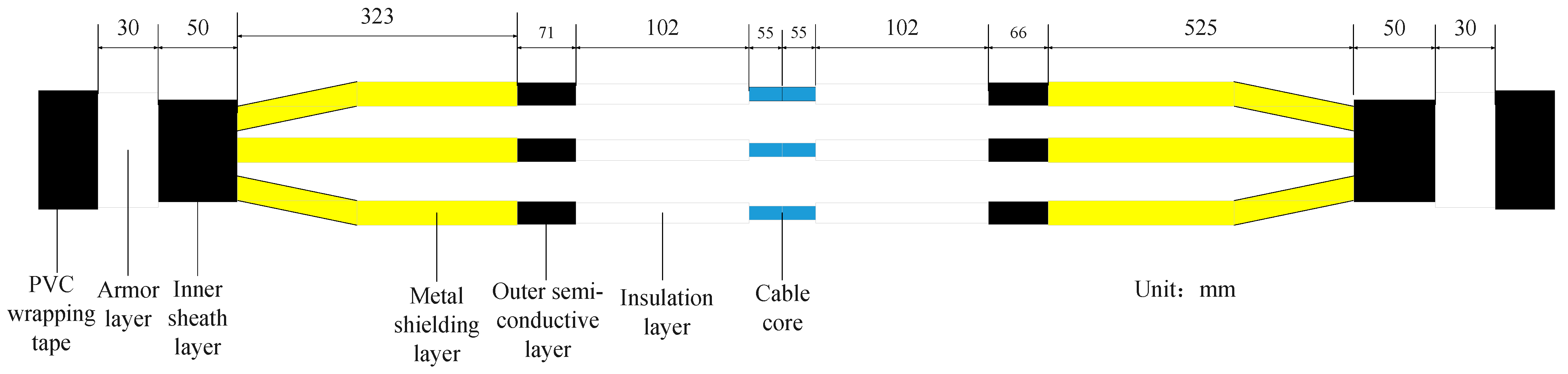
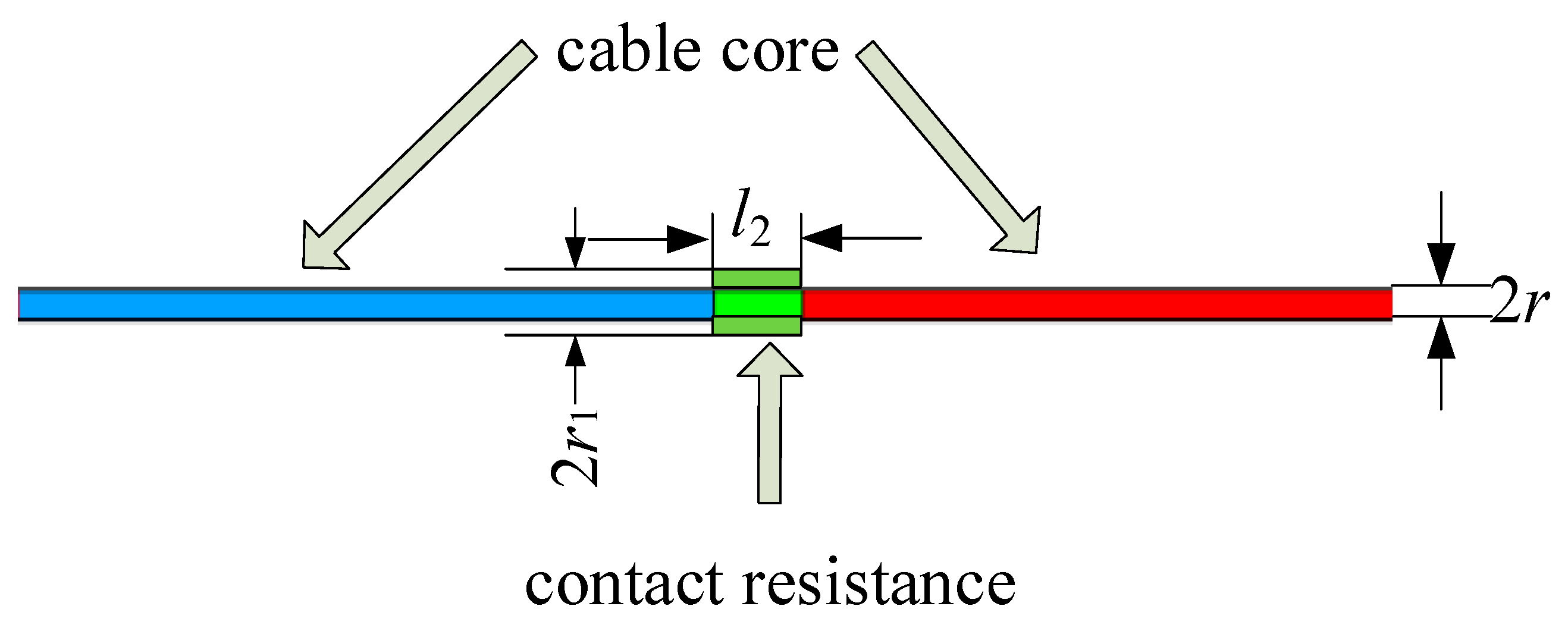

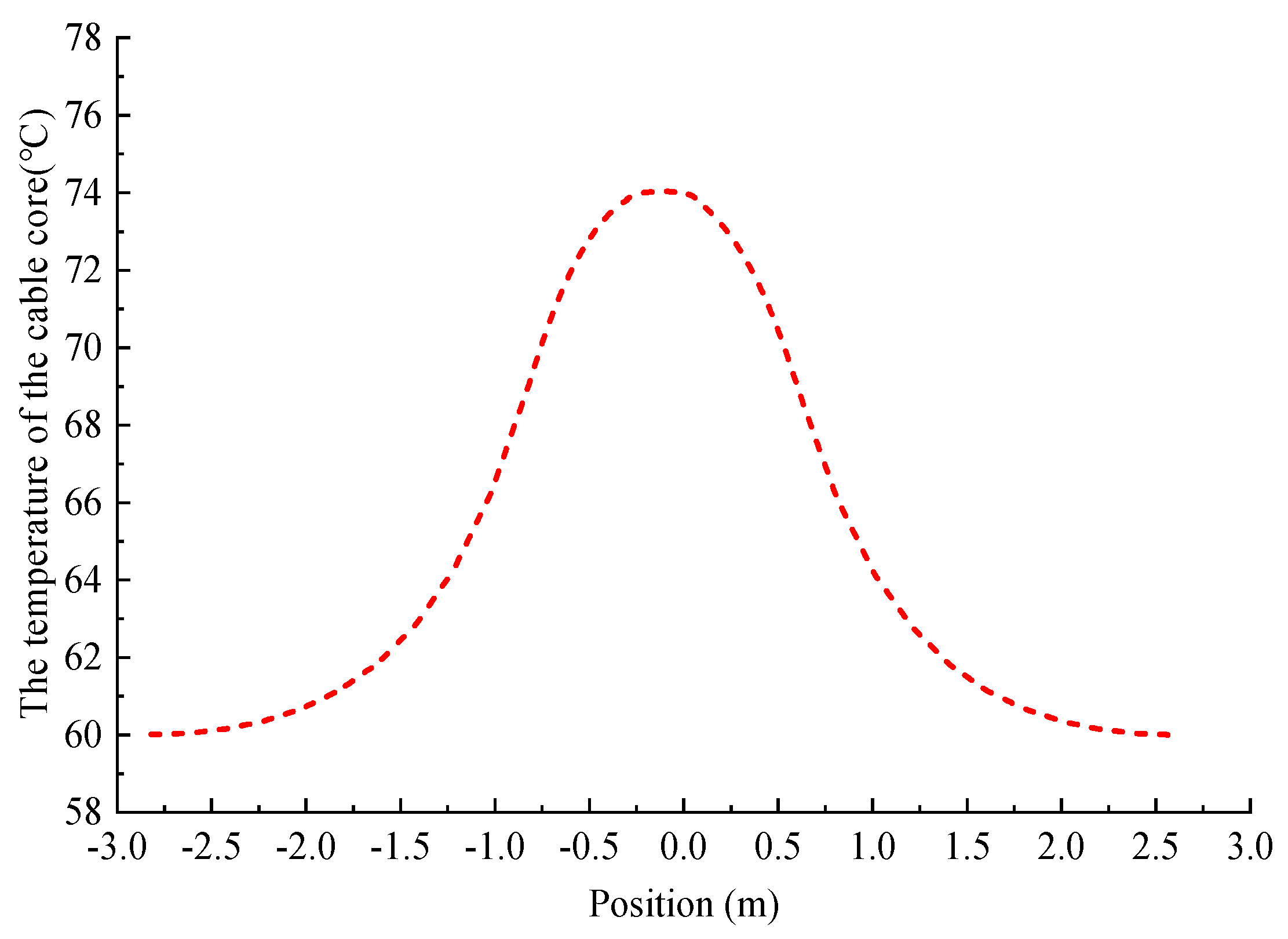
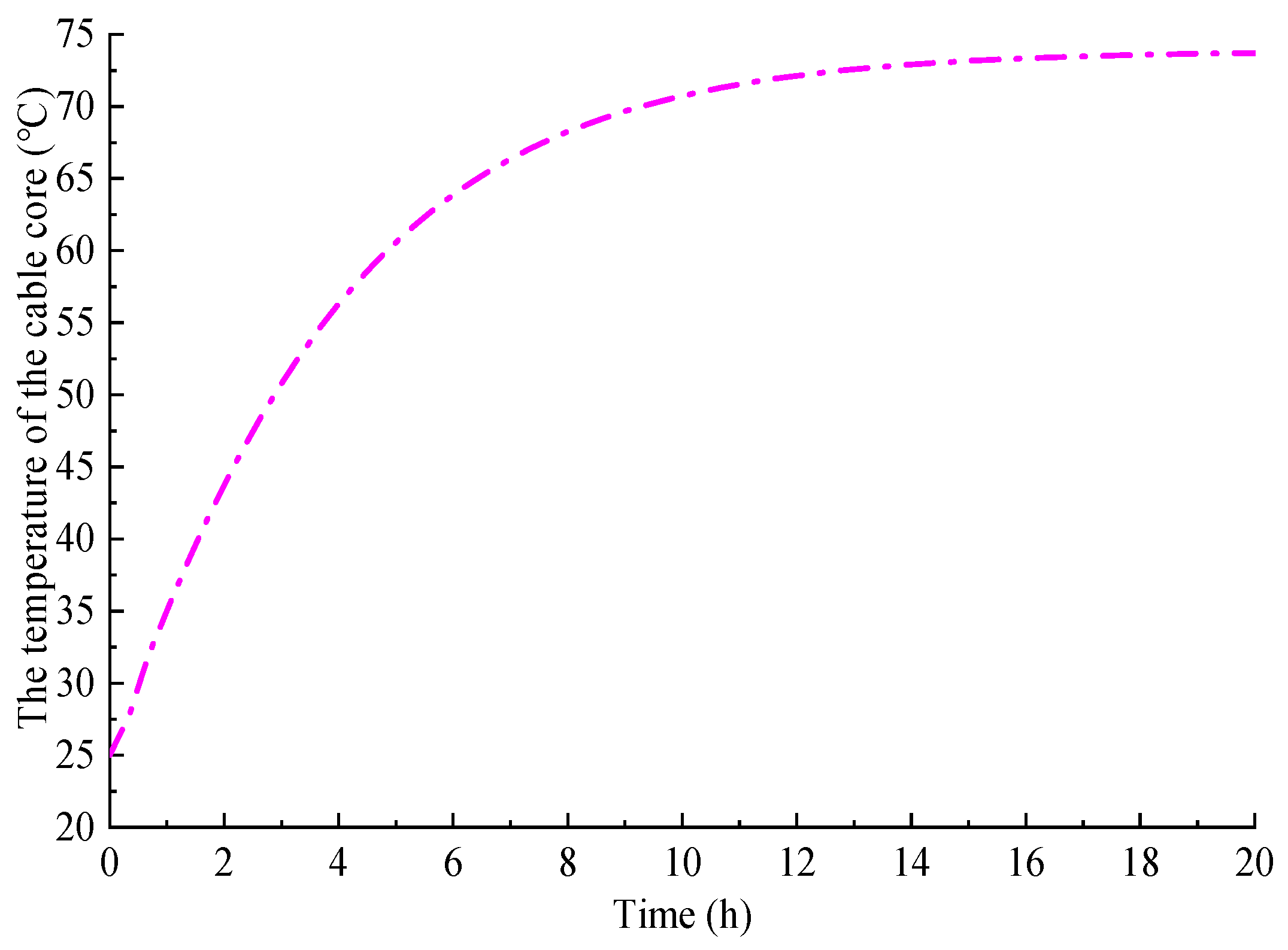
| Parameter | Material | Thermal Conductivity (W/(m·K)) | Density (kg/m3) | Specific Heat Capacity (J/(kg·K)) | |
|---|---|---|---|---|---|
| Component | |||||
| Cable core | Copper | 383 | 8889 | 390 | |
| Crimping sleeve | Copper | 401 | 7830 | 390 | |
| Prefabricated insulation component | Rubber | 0.45 | 1100 | 2219 | |
| Insulation layer | XLPE | 0.286 | 920 | 2500 | |
| Air | Air | 0.023 | 1.293 | 1004 | |
| PVC wrapping tape | Polyvinyl chloride | 0.167 | 1450 | 1005 | |
| Armoring tape | Fiberglass tape | 0.036 | 2500 | 794.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chan, Q.; Ma, Y.; Ruan, J.; Hou, A. Exploration of Temperature Inversion in Intermediate Joints of 10 kV Three-Core Cable. Processes 2024, 12, 460. https://doi.org/10.3390/pr12030460
Li X, Chan Q, Ma Y, Ruan J, Hou A. Exploration of Temperature Inversion in Intermediate Joints of 10 kV Three-Core Cable. Processes. 2024; 12(3):460. https://doi.org/10.3390/pr12030460
Chicago/Turabian StyleLi, Xinhai, Qizhong Chan, Yue Ma, Jiangjun Ruan, and Aogang Hou. 2024. "Exploration of Temperature Inversion in Intermediate Joints of 10 kV Three-Core Cable" Processes 12, no. 3: 460. https://doi.org/10.3390/pr12030460
APA StyleLi, X., Chan, Q., Ma, Y., Ruan, J., & Hou, A. (2024). Exploration of Temperature Inversion in Intermediate Joints of 10 kV Three-Core Cable. Processes, 12(3), 460. https://doi.org/10.3390/pr12030460






