A Fault-Tolerant Soft Sensor Algorithm Based on Long Short-Term Memory Network for Uneven Batch Process
Abstract
:1. Introduction
- An algorithm based on a two-layer LSTM model is proposed to develop a fault-tolerant soft sensor for modeling long-time nonlinear dependent batch processes. Historical batch data quality measurements are applied to the soft sensor to enhance the robustness of the model in case of sensor failure;
- The problem of estimating the quality variable of uneven batch processes is transformed into rate estimation within a fixed window, which addresses the issue of uneven batch data. The model’s reliability is verified on normal data and datasets with various failures in simulated penicillin production;
- An algorithm for endpoint detection is proposed to estimate the quality variable using the soft sensor model, which can accurately determine when to terminate production once the expected yield is reached.
2. Related Work
2.1. Sensor Fault-Tolerant
2.2. Uneven Batches
2.3. LSTM-Based Soft Sensor
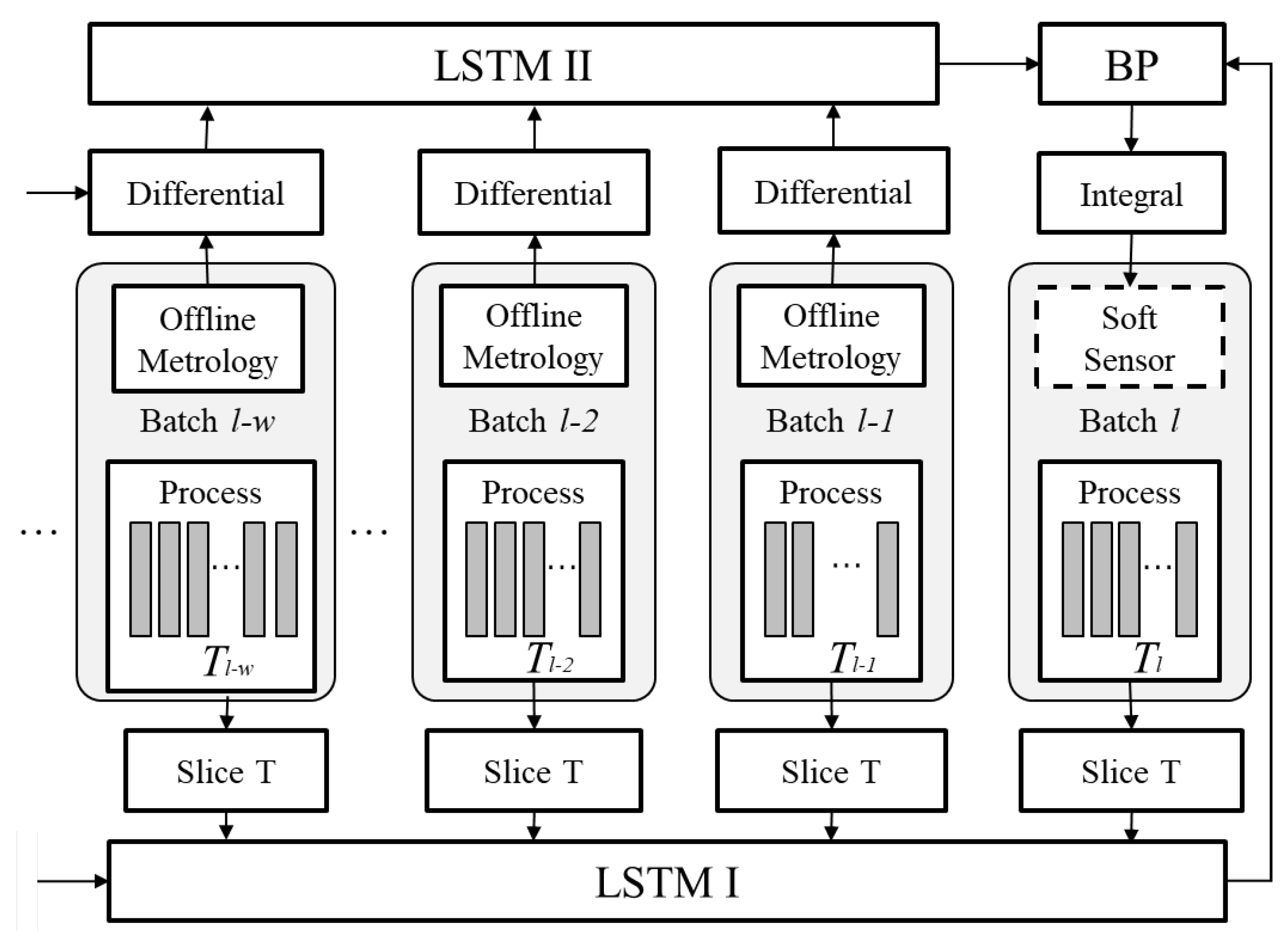
3. Methodology
3.1. Estimation by LSTM I
3.2. Compensation by LSTM II
3.3. Endpoint Detection
4. Case Study
4.1. Simulation
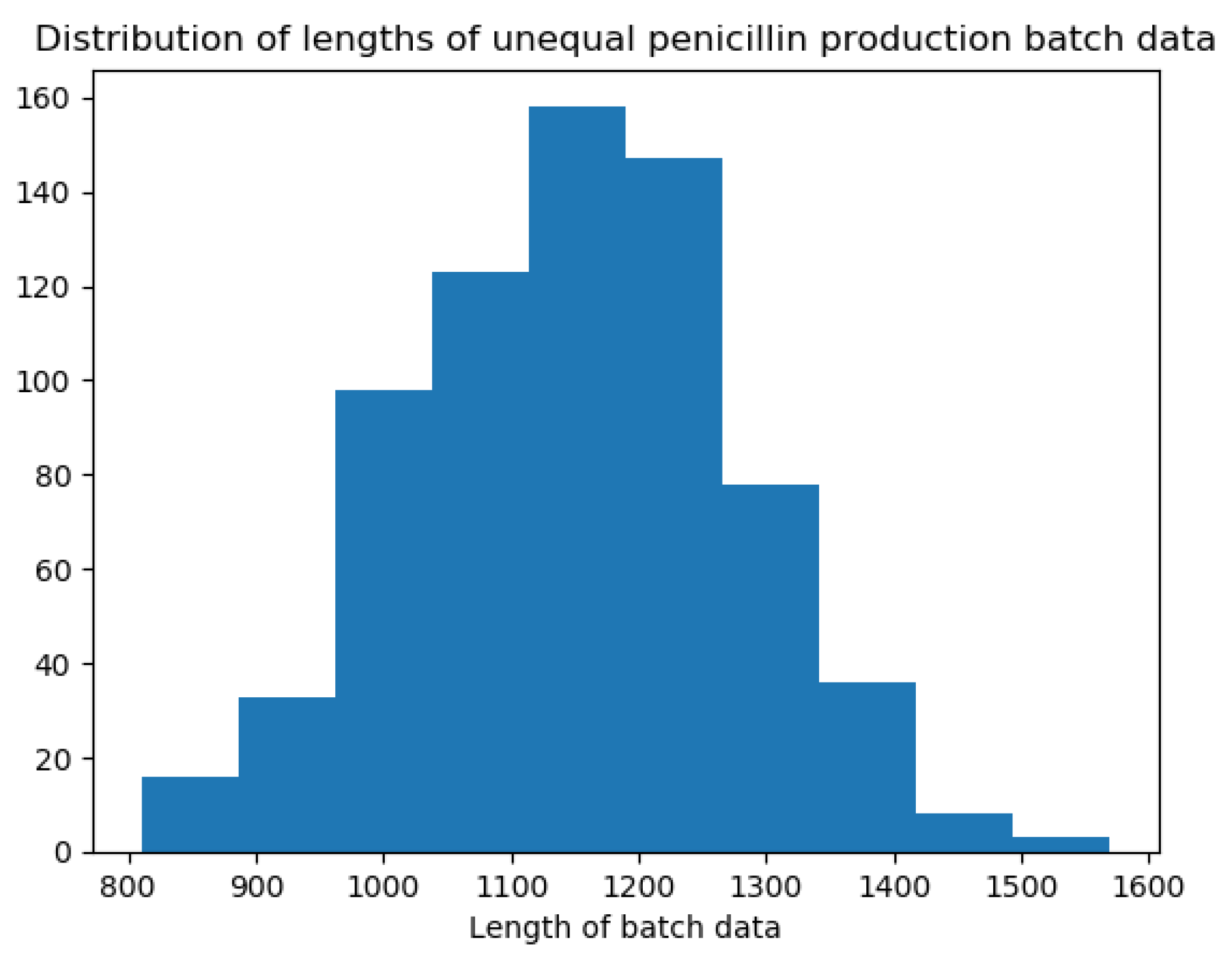
4.2. Data Description
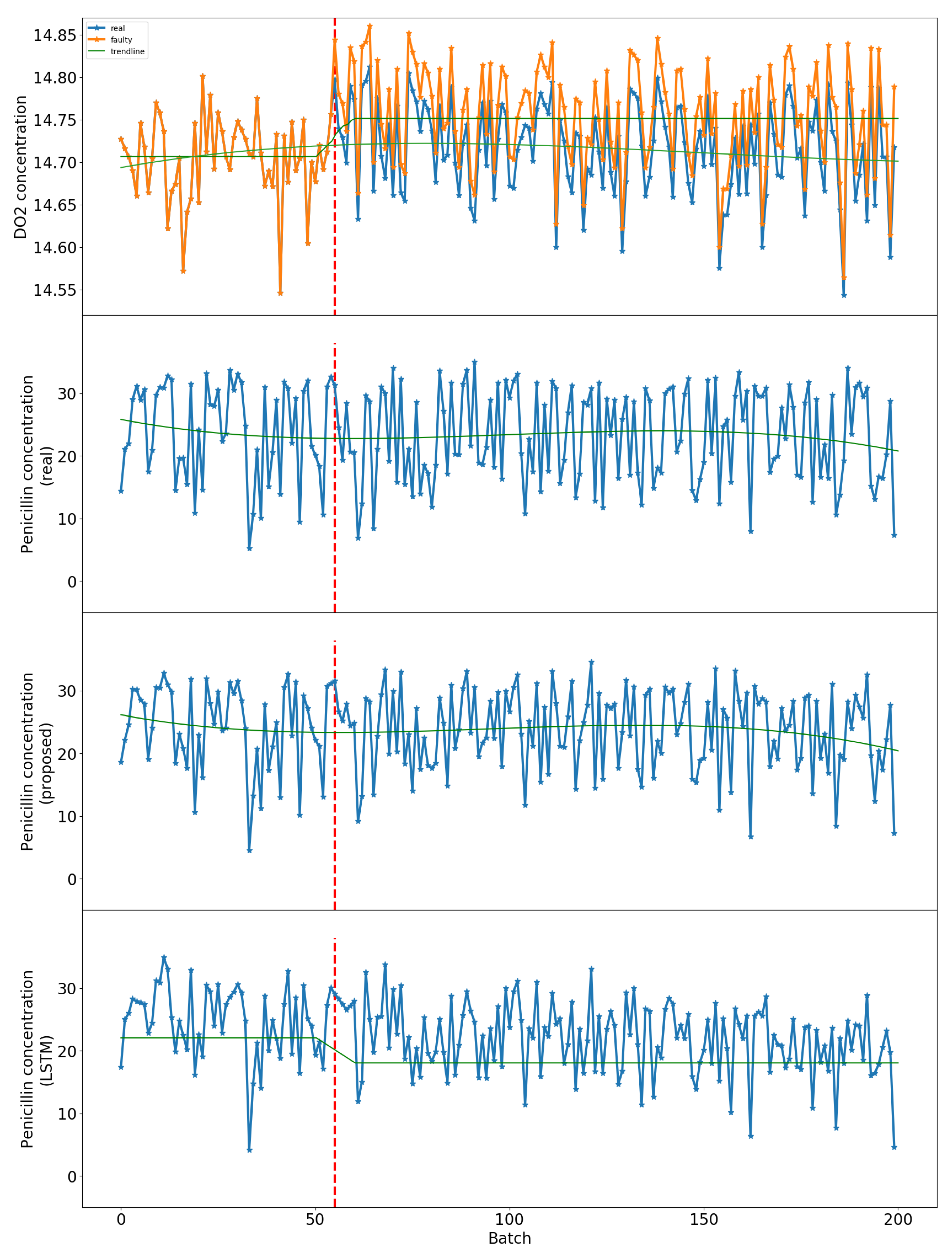
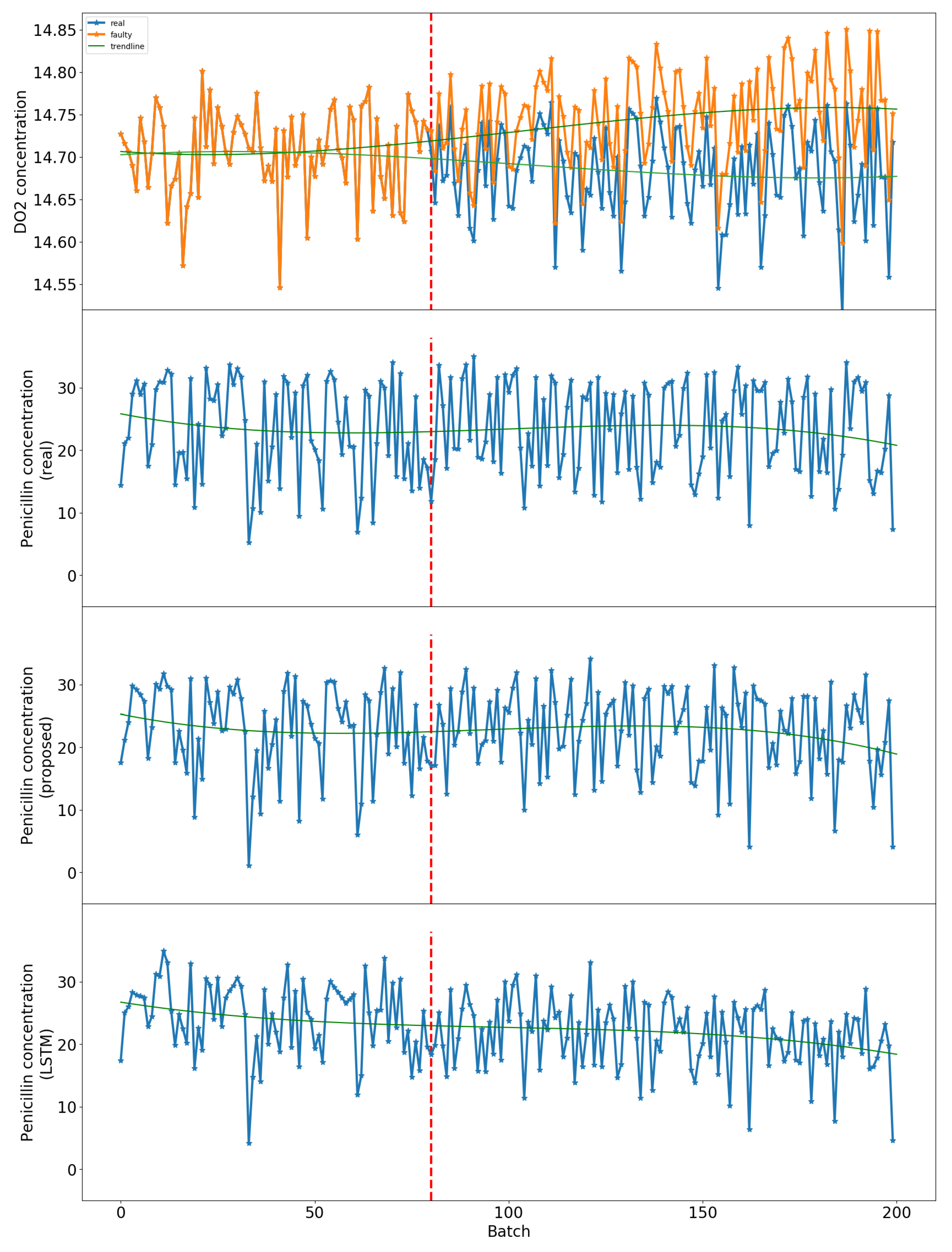
4.3. Sensor Faults
5. Discussion
5.1. Model Structure and Parameters
5.2. Model Comparisons
5.3. Performance Measures
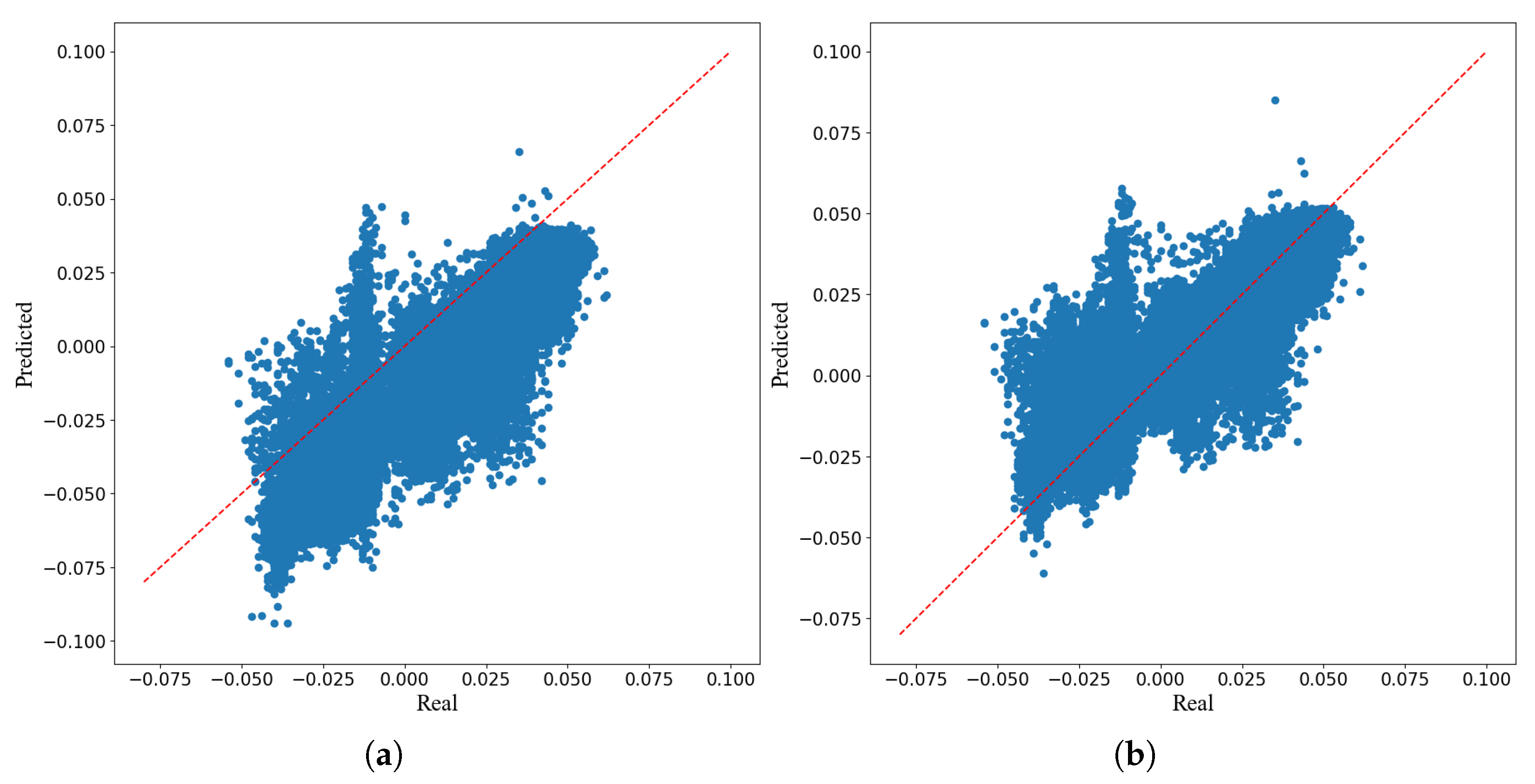
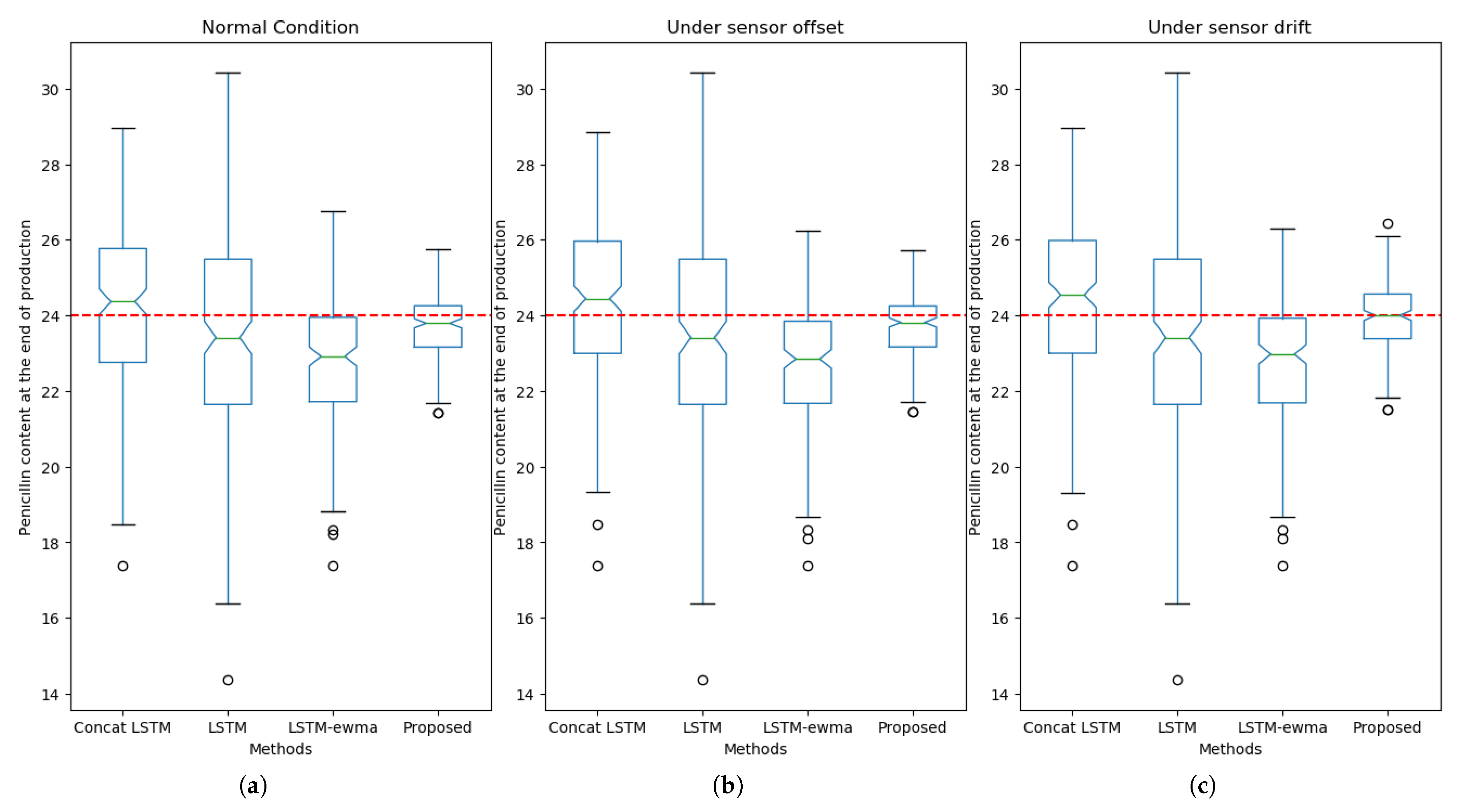
5.4. Comparison Results on Normal Condition
5.5. Comparison Results on Fault Condition
5.6. Methods for Aligning Uneven Batches
5.7. Endpoint Detection Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LSTM | Long short-term memory |
| PLS | Partial least square |
| SAEs | Stacked self-encoders |
| MLR | Multiple linear regression |
| SVR | Support vector regression |
| ANN | Artificial neural network |
| RNN | Recurrent neural network |
| DNN | Deep neural network |
| CNN | Convolutional neural network |
| EWMA | Exponential weighted moving average |
| RMSE | Root mean squared error |
| MAE | Mean absolute error |
| R-square score |
References
- Hsiao, Y.D.; Kang, J.L.; Wong, D.S.H. Development of Robust and Physically Interpretable Soft Sensor for Industrial Distillation Column Using Transfer Learning with Small Datasets. Processes 2021, 9, 667. [Google Scholar] [CrossRef]
- Souza, F.A.; Araújo, R.; Mendes, J. Review of soft sensor methods for regression applications. Chemom. Intell. Lab. Syst. 2016, 152, 69–79. [Google Scholar] [CrossRef]
- Wang, D.; Liu, J.; Srinivasan, R. Data-Driven Soft Sensor Approach for Quality Prediction in a Refining Process. IEEE Trans. Ind. Inform. 2010, 6, 11–17. [Google Scholar] [CrossRef]
- Hargrove, M.; Wen, S.; Yim, D.; Ruegger, K.E.; Nanja, P.; Sarkar, S.; Lowe, B.; Vincent, B.; Ervin, J.; Fried, D. Review of virtual wafer process modeling and metrology for advanced technology development. J. Micro/Nanopatterning Mater. Metrol. 2023, 22, 031209. [Google Scholar] [CrossRef]
- Kang, P.; Lee, H.j.; Cho, S.; Kim, D.; Park, J.; Park, C.K.; Doh, S. A virtual metrology system for semiconductor manufacturing. Expert Syst. Appl. 2009, 36, 12554–12561. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S.; Dong, J.; Kaynak, O. A review on soft sensors for monitoring, control, and optimization of industrial processes. IEEE Sens. J. 2020, 21, 12868–12881. [Google Scholar] [CrossRef]
- Gonzaga, J.; Meleiro, L.A.C.; Kiang, C.; Maciel Filho, R. ANN-based soft-sensor for real-time process monitoring and control of an industrial polymerization process. Comput. Chem. Eng. 2009, 33, 43–49. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Xibilia, M.G. Soft sensors for product quality monitoring in debutanizer distillation columns. Control. Eng. Pract. 2005, 13, 499–508. [Google Scholar] [CrossRef]
- Hirai, T.; Kano, M. Adaptive virtual metrology design for semiconductor dry etching process through locally weighted partial least squares. IEEE Trans. Semicond. Manuf. 2015, 28, 137–144. [Google Scholar] [CrossRef]
- Kang, S.; Kim, D.; Cho, S. Efficient Feature Selection-Based on Random Forward Search for Virtual Metrology modelling. IEEE Trans. Semicond. Manuf. 2016, 29, 391–398. [Google Scholar] [CrossRef]
- Dilmi, S. Calcium Soft Sensor Based on the Combination of Support Vector Regression and 1-D Digital Filter for Water Quality Monitoring. Arab. J. Sci. Eng. 2022, 48, 6111–6136. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, X.; Zhao, J.; Pan, C.; Sun, K. Development of a Robust Data-Driven Soft Sensor for Multivariate Industrial Processes with Non-Gaussian Noise and Outliers. Mathematics 2022, 10, 3837. [Google Scholar] [CrossRef]
- Zhang, F.; Li, N.; Li, L.; Wang, S.; Du, C. A local semi-supervised ensemble learning strategy for the data-driven soft sensor of the power prediction in wind power generation. Fuel 2022, 333, 126435. [Google Scholar] [CrossRef]
- Medl, M.; Rajamanickam, V.; Striedner, G.; Newton, J. Development and Validation of an Artificial Neural-Network-Based Optical Density Soft Sensor for a High-Throughput Fermentation System. Processes 2023, 11, 297. [Google Scholar] [CrossRef]
- Zhang, D.; Duan, L.; Xu, Y.; Gao, H.; Liu, N. An ANN-based soft-sensor to estimate the sand content of drilling fluid. In Proceedings of the 2022 IEEE 6th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Beijing China, 3–5 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1598–1602. [Google Scholar]
- Shen, F.; Zheng, J.; Ye, L.; Ma, X. LSTM Soft Sensor Development of Batch Processes with Multivariate Trajectory Based Ensemble Just-in-time Learning. IEEE Access 2020, 8, 73855–73864. [Google Scholar] [CrossRef]
- Ke, W.; Huang, D.; Yang, F.; Jiang, Y. Soft sensor development and applications based on LSTM in deep neural networks. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Yuan, X.; Li, L.; Shardt, Y.; Wang, Y.; Yang, C. Deep learning with spatiotemporal attention-based LSTM for industrial soft sensor model development. IEEE Trans. Ind. Electron. 2020, 68, 4404–4414. [Google Scholar] [CrossRef]
- Pisa, I.; Santín, I.; Vicario, J.; Morell, A.; Vilanova, R. ANN-Based Soft Sensor to Predict Effluent Violations in Wastewater Treatment Plants. Sensors 2019, 19, 1280. [Google Scholar] [CrossRef]
- Lee, K.B.; Kim, C.O. Recurrent feature-incorporated convolutional neural network for virtual metrology of the chemical mechanical planarization process. J. Intell. Manuf. 2018, 31, 73–86. [Google Scholar] [CrossRef]
- Yuan, X.; Huang, B.; Wang, Y.; Yang, C.; Gui, W. Deep learning-based feature representation and its application for soft sensor modeling with variable-wise weighted SAE. IEEE Trans. Ind. Inform. 2018, 14, 3235–3243. [Google Scholar] [CrossRef]
- Yuan, X.; Ou, C.; Wang, Y.; Yang, C.; Gui, W. Deep quality-related feature extraction for soft sensing modeling: A deep learning approach with hybrid VW-SAE. Neurocomputing 2020, 396, 375–382. [Google Scholar] [CrossRef]
- Ahmad, I.; Ayub, A.; Kano, M.; Cheema, I.I. Gray-box Soft Sensors in Process Industry: Current Practice, and Future Prospects in Era of Big Data. Processes 2020, 8, 243. [Google Scholar] [CrossRef]
- Zhang, X.; Song, C.; Zhao, J.; Xu, Z.; Deng, X. Deep subdomain learning adaptation network: A sensor fault-tolerant soft sensor for industrial processes. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.J.; Ni, D.; Shao, X.; Gong, D.L.; Li, J.J. A hierarchical model-based method for wafer level virtual metrology under process information deficiency. Qual. Eng. 2023, 1–14. [Google Scholar] [CrossRef]
- Du, P.; Zhong, W.; Peng, X.; Li, L.; Li, Z. Data-Driven Fault Compensation Tracking Control for Coupled Wastewater Treatment Process. IEEE/CAA J. Autom. Sin. 2023, 10, 294–297. [Google Scholar] [CrossRef]
- Yang, X.B.; Jin, X.Q.; Du, Z.M.; Fan, B.; Zhu, Y.H. Optimum operating performance based online fault-tolerant control strategy for sensor faults in air conditioning systems. Autom. Constr. 2014, 37, 145–154. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Y.; Gou, B. Current sensor fault diagnosis and fault-tolerant control for single-phase PWM rectifier based on a hybrid model-based and data-driven method. IET Power Electron. 2020, 13, 4150–4157. [Google Scholar] [CrossRef]
- Belchior, C.A.C.; Araújo, R.A.M.; Souza, F.A.A.; Landeck, J.A.C. Sensor-fault tolerance in a wastewater treatment plant by means of ANFIS-based soft sensor and control reconfiguration. Neural Comput. Appl. 2018, 30, 3265–3276. [Google Scholar] [CrossRef]
- Chen, H.; Huang, B. Fault-Tolerant Soft Sensors for Dynamic Systems. IEEE Trans. Control. Syst. Technol. 2023, 31, 2805–2818. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, C. Stationarity test and Bayesian monitoring strategy for fault detection in nonlinear multimode processes. Chemom. Intell. Lab. Syst. 2017, 168, 45–61. [Google Scholar] [CrossRef]
- Kourti, T. Multivariate dynamic data modeling for analysis and statistical process control of batch processes, start-ups and grade transitions. J. Chemom. 2003, 17, 93–109. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Wang, D. Wavelet functional principal component analysis for batch process monitoring. Chemom. Intell. Lab. Syst. 2020, 196, 103897. [Google Scholar] [CrossRef]
- Kassidas, A.; MacGregor, J.F.; Taylor, P.A. Synchronization of batch trajectories using dynamic time warping. AIChE J. 1998, 44, 864–875. [Google Scholar] [CrossRef]
- Qiu, K.; Wang, J.; Wang, R.; Guo, Y.; Zhao, L. Soft sensor development based on kernel dynamic time warping and a relevant vector machine for unequal-length batch processes. Expert Syst. Appl. 2021, 182, 115223. [Google Scholar] [CrossRef]
- CUI, L.; ZHANG, Q.; SHI, Y.; YANG, L.; WANG, Y.; WANG, J.; BAI, C. A method for satellite time series anomaly detection based on fast-DTW and improved-KNN. Chin. J. Aeronaut. 2023, 36, 149–159. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, X.; Hui, Y.; Liu, K. Online monitoring and fault diagnosis for uneven length batch process based on multi-way orthogonal enhanced neighborhood preserving embedding. Asia-Pac. J. Chem. Eng. 2022, 17, e2763. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, P.; Liu, C.; Xu, Y.; Zhang, H. A sequential resampling approach for imbalanced batch process fault detection in semiconductor manufacturing. J. Intell. Manuf. 2022, 33, 1057–1072. [Google Scholar] [CrossRef]
- Wang, K.; Rippon, L.; Chen, J.; Song, Z.; Gopaluni, R.B. Data-driven dynamic modeling and online monitoring for multiphase and multimode batch processes with uneven batch durations. Ind. Eng. Chem. Res. 2019, 58, 13628–13641. [Google Scholar] [CrossRef]
- Yuan, X.; Li, L.; Wang, K.; Wang, Y. Sampling-Interval-Aware LSTM for Industrial Process Soft Sensing of Dynamic Time Sequences With Irregular Sampling Measurements. IEEE Sens. J. 2021, 21, 10787–10795. [Google Scholar] [CrossRef]
- Xie, W.; Wang, J.; Xing, C.; Guo, S.; Guo, M.; Zhu, L. Variational autoencoder bidirectional long and short-term memory neural network soft-sensor model based on batch training strategy. IEEE Trans. Ind. Inform. 2020, 17, 5325–5334. [Google Scholar] [CrossRef]
- Yuan, X.; Li, L.; Wang, Y. Nonlinear dynamic soft sensor modeling with supervised long short-term memory network. IEEE Trans. Ind. Inform. 2019, 16, 3168–3176. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, Y.; Wang, B.; Shen, F. A Multi-Step Sequence-to-Sequence Model with Attention LSTM Neural Networks for Industrial Soft Sensor Application. IEEE Sens. J. 2023, 23, 10801–10813. [Google Scholar] [CrossRef]
- Bono, F.; Radicioni, L.; Cinquemani, S. A novel approach for quality control of automated production lines working under highly inconsistent conditions. Eng. Appl. Artif. Intell. 2023, 122, 106149. [Google Scholar] [CrossRef]
- Ji, C.; Ma, F.; Wang, J.; Sun, W. Profitability related industrial-scale batch processes monitoring via deep learning based soft sensor development. Comput. Chem. Eng. 2023, 170, 108125. [Google Scholar] [CrossRef]
- Bajpai, R.; Reuss, M. A mechanistic model for penicillin production. J. Chem. Technol. Biotechnol. 1980, 30, 332–344. [Google Scholar] [CrossRef]
- Birol, G.; Ündey, C.; Cinar, A. A modular simulation package for fed-batch fermentation: Penicillin production. Comput. Chem. Eng. 2002, 26, 1553–1565. [Google Scholar] [CrossRef]
- Goldrick, S.; Duran-Villalobos, C.A.; Jankauskas, K.; Lovett, D.; Farid, S.S.; Lennox, B. Modern day monitoring and control challenges outlined on an industrial-scale benchmark fermentation process. Comput. Chem. Eng. 2019, 130, 106471. [Google Scholar] [CrossRef]
- Gins, G.; Van Impe, J.F.; Reis, M.S. Finding the optimal time resolution for batch-end quality prediction: MRQP—A framework for multi-resolution quality prediction. Chemom. Intell. Lab. Syst. 2018, 172, 150–158. [Google Scholar] [CrossRef]
- Jan, S.U.; Lee, Y.D.; Shin, J.; Koo, I. Sensor fault classification based on support vector machine and statistical time-domain features. IEEE Access 2017, 5, 8682–8690. [Google Scholar] [CrossRef]
- Tobias, P.A.; Trindade, D. Applied Reliability; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Suhir, E. Static fatigue lifetime of optical fibers assessed using Boltzmann–Arrhenius–Zhurkov (BAZ) model. J. Mater. Sci. Mater. Electron. 2017, 28, 11689–11694. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Offermans, T.; Wijker, T.H.; Folcarelli, R.; Heemskerk, R.; Lamers, P.P.; Proenca, M.; Tran, T.N.; Buydens, L.M.C.; Jansen, J.J. ENDBOSS: Industrial endpoint detection using batch-specific control spaces of spectroscopic data. Chemom. Intell. Lab. Syst. 2021, 209, 209. [Google Scholar] [CrossRef]



| Variable | ||
|---|---|---|
| Time (h) | Base flow rate (L/h) | Vessel weight (Kg) |
| Aeration rate (L/h) | Cooling water flow rate (L/h) | PH |
| Agitator RPM (RPM) | Heating water flow rate (L/h) | Temperature (K) |
| Sugar feed rate (L/h) | Dissolved oxygen concentration (mg/L) | Vessel Volume (L) |
| Acid flow rate (L/h) | Carbon dioxide in off-gas (%) | Oxygen in off-gas (%) |
| Train | Test | |||
|---|---|---|---|---|
| Normal | Normal | Offset | Drift | |
| RMSE | 0.00580 | 0.00579 | 0.00623 | 0.00602 |
| 0.93367 | 0.93355 | 0.92292 | 0.92813 | |
| MAE | 0.00378 | 0.00379 | 0.00491 | 0.00397 |
| Methods | RMSE | MAE | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Normal | Offset | Drift | Normal | Offset | Drift | Normal | Offset | Drift | |
| Proposed | 0.00579 | 0.00623 | 0.00602 | 0.93355 | 0.92292 | 0.92813 | 0.00379 | 0.00491 | 0.00397 |
| LSTM-ewma | 0.00721 | 0.00747 | 0.00780 | 0.89680 | 0.88927 | 0.87943 | 0.00518 | 0.00532 | 0.00563 |
| Concat LSTM | 0.00809 | 0.01030 | 0.00977 | 0.87020 | 0.78952 | 0.81066 | 0.00541 | 0.00725 | 0.00684 |
| LSTM | 0.01033 | 0.01138 | 0.01214 | 0.76372 | 0.70767 | 0.68392 | 0.00892 | 0.01024 | 0.01114 |
| Methods | RMSE | MAE | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Normal | Offset | Drift | Normal | Offset | Drift | Normal | Offset | Drift | |
| Proposed | 0.00579 | 0.00623 | 0.00602 | 0.93355 | 0.92292 | 0.92813 | 0.00379 | 0.00491 | 0.00397 |
| Padding | 0.00700 | 0.00839 | 0.00683 | 0.90427 | 0.86237 | 0.88750 | 0.00542 | 0.00591 | 0.00562 |
| Resample | 0.00679 | 0.00793 | 0.00736 | 0.91006 | 0.87706 | 0.89425 | 0.00521 | 0.00592 | 0.00502 |
| Normal | Offset | Drift | |
|---|---|---|---|
| Proposed | 0.64123 | 0.65597 | 0.70415 |
| LSTM-EWMA | 1.66602 | 1.68973 | 1.68063 |
| Concat LSTM | 1.79287 | 1.80891 | 1.83912 |
| LSTM | 2.03024 | 2.14383 | 2.16533 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ni, D.; Wang, Z. A Fault-Tolerant Soft Sensor Algorithm Based on Long Short-Term Memory Network for Uneven Batch Process. Processes 2024, 12, 495. https://doi.org/10.3390/pr12030495
Liu Y, Ni D, Wang Z. A Fault-Tolerant Soft Sensor Algorithm Based on Long Short-Term Memory Network for Uneven Batch Process. Processes. 2024; 12(3):495. https://doi.org/10.3390/pr12030495
Chicago/Turabian StyleLiu, Yujun, Dong Ni, and Zongyi Wang. 2024. "A Fault-Tolerant Soft Sensor Algorithm Based on Long Short-Term Memory Network for Uneven Batch Process" Processes 12, no. 3: 495. https://doi.org/10.3390/pr12030495
APA StyleLiu, Y., Ni, D., & Wang, Z. (2024). A Fault-Tolerant Soft Sensor Algorithm Based on Long Short-Term Memory Network for Uneven Batch Process. Processes, 12(3), 495. https://doi.org/10.3390/pr12030495







