Study on Heat Transfer Synergy and Optimization of Capsule-Type Plate Heat Exchangers
Abstract
:1. Introduction
2. Structure Parameters
3. Simulating Calculation
3.1. Physical Condition Setting
3.2. Parameter Setting
3.3. Comparison with the Experiment
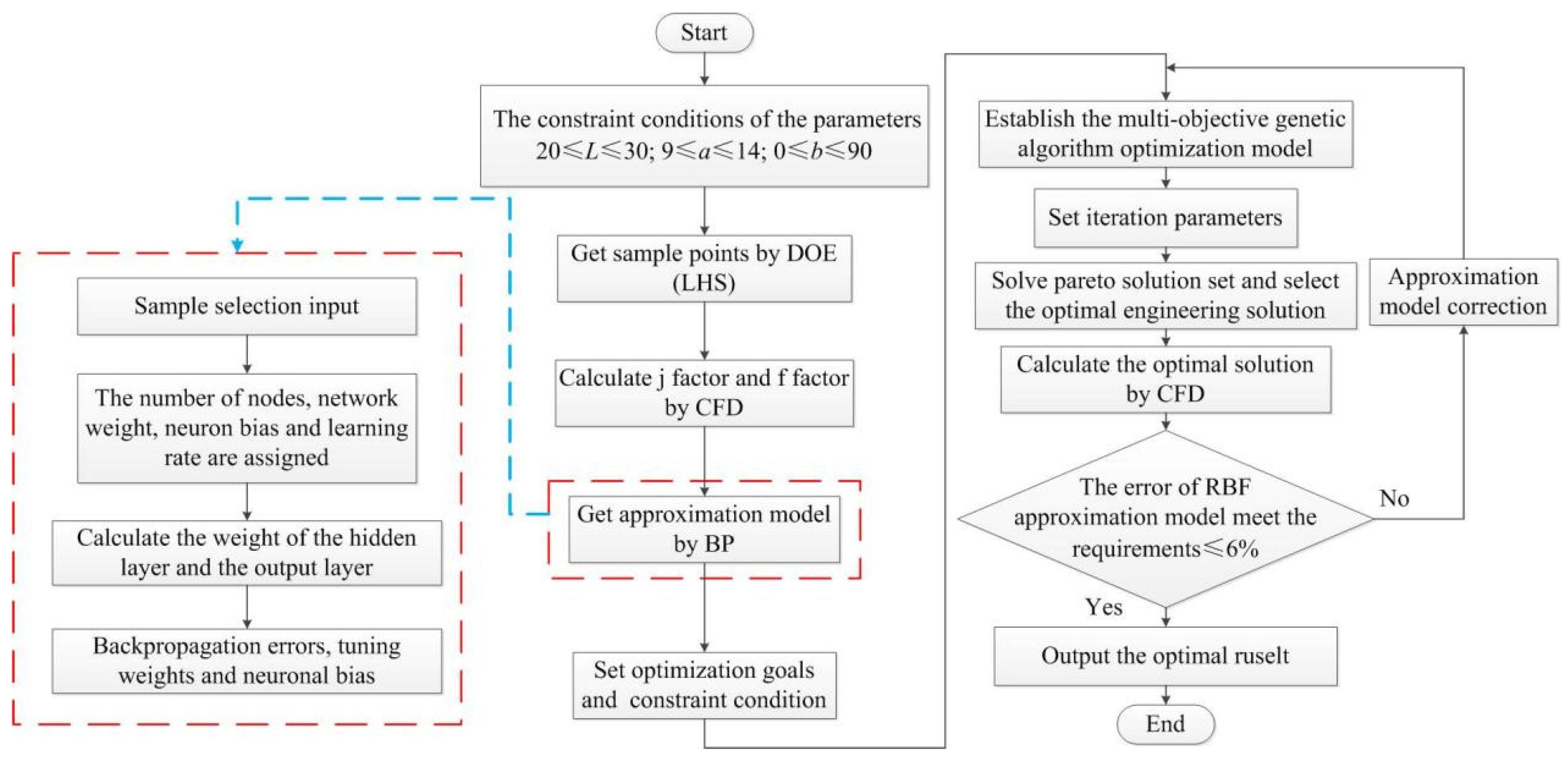
4. Optimal Structure of Capsule-Type Plate
5. Optimal Result Analysis
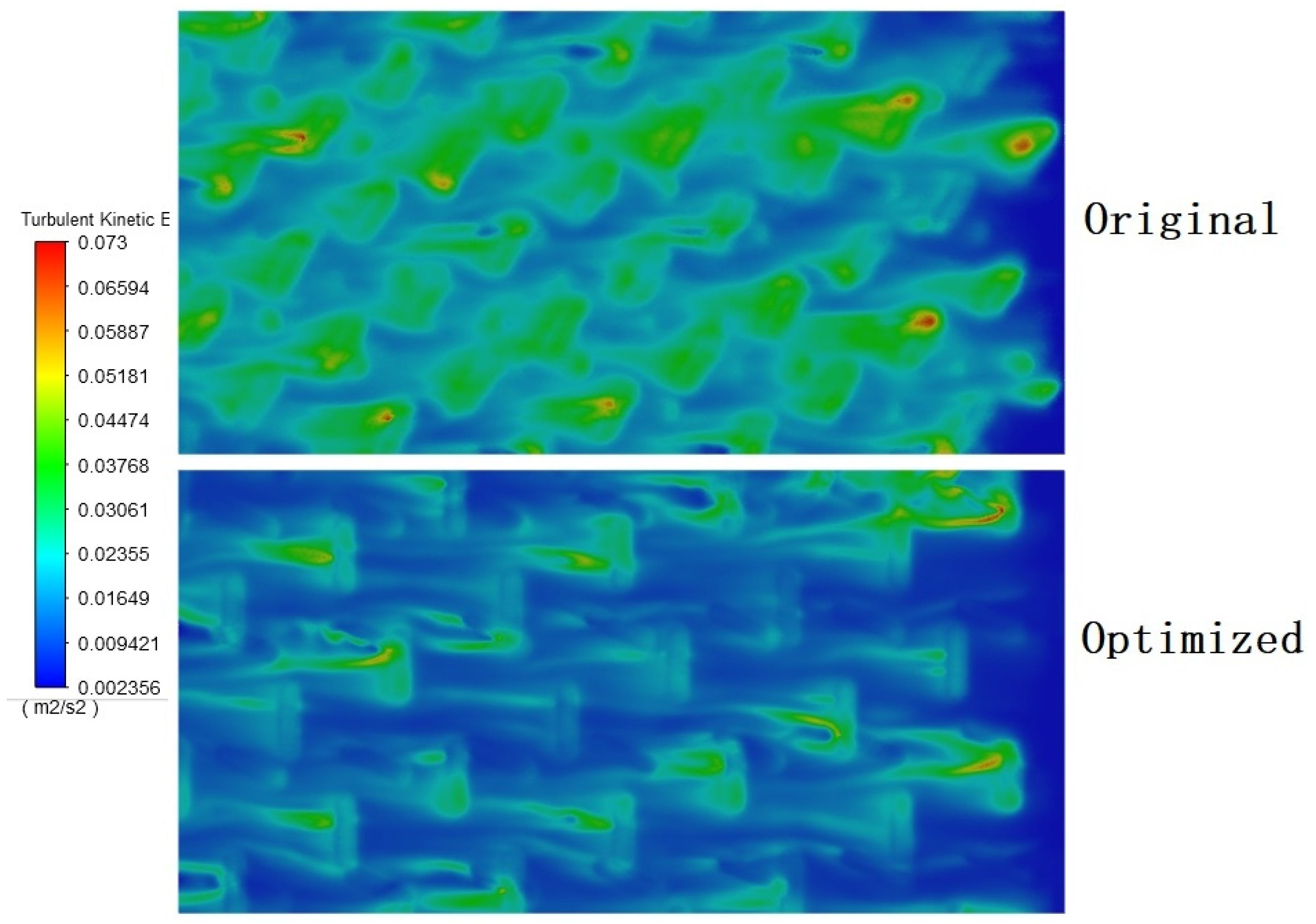
5.1. Physical Field Analysis
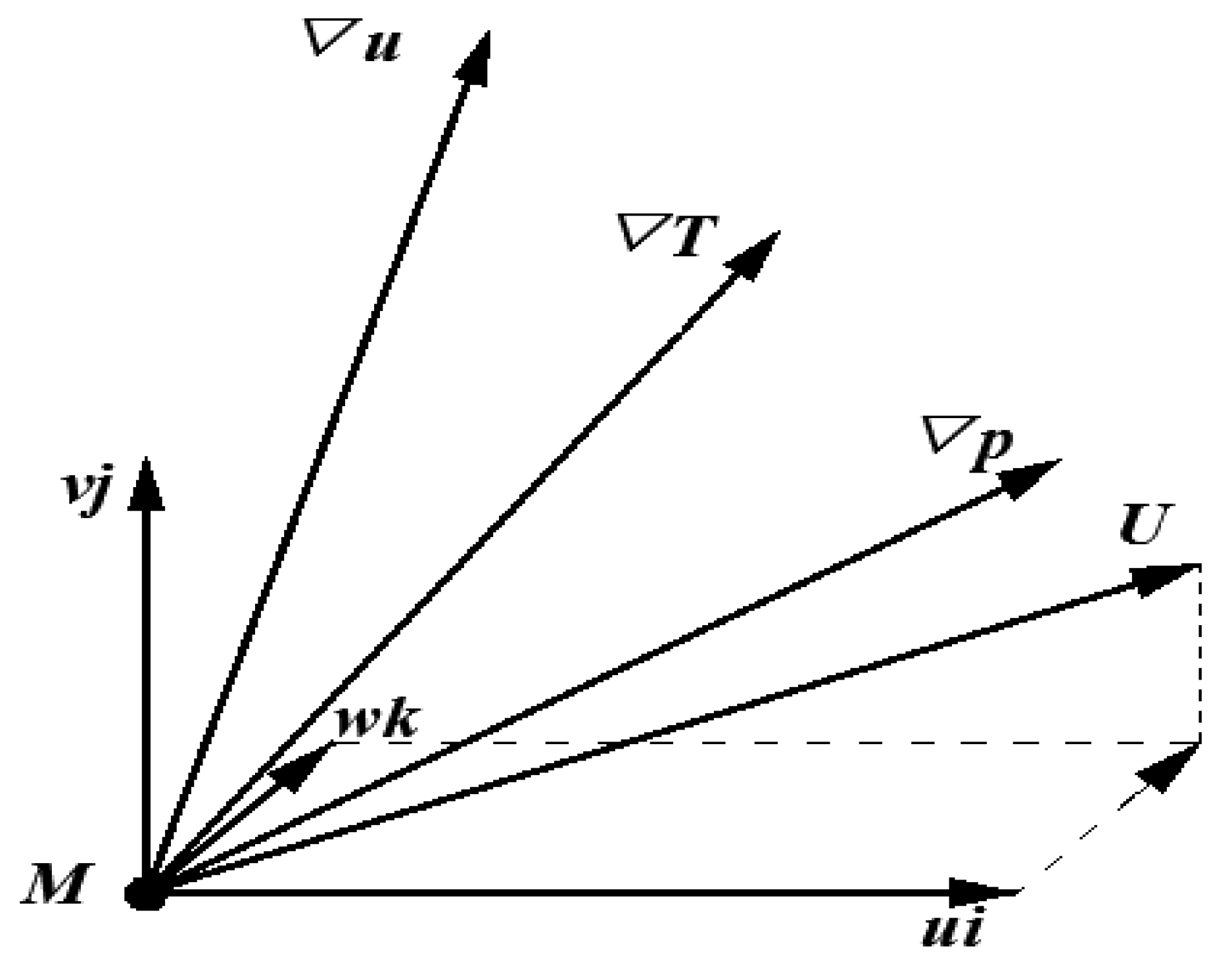
5.2. The Field Synergy Analysis
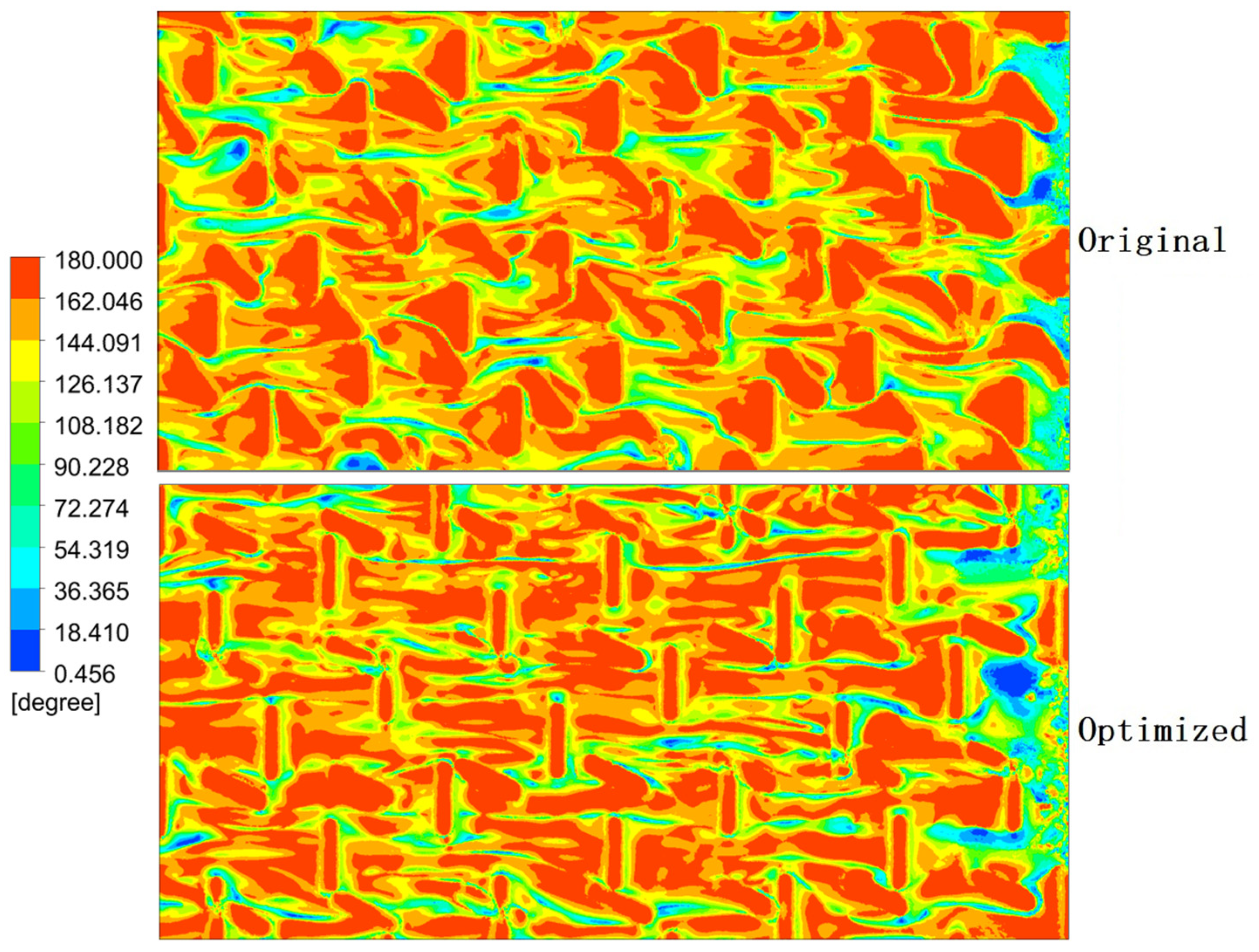
5.2.1. Synergy Angle β
5.2.2. Synergy Angle θ
5.2.3. Synergy Angle γ
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| l | capsule length (mm) | ci | center of clustering |
| a | capsule angle ) | ∇T | temperature gradient (K/m) |
| b | capsule width (mm) | ∇p | pressure gradient (Pa/m) |
| t | capsule plate thickness (mm) | ∇u | velocity gradient (1/s) |
| j | Heat transfer factor | ||
| f | friction factor | Re | Reynolds number |
| T | temperature (K) | Pr | Prandtl number |
| D | hydraulic diameter (m) | Nu | Nusselt number |
| ΔP | pressure difference (Pa) | ||
| m | mass flow (kg/s) | ρ | density (kg/m3) |
| cp | constant-pressure specific heat (J/(kg °C)) | μ | dynamic viscosity (N s/m2) |
| w | weight | λt | thermal conductivity (W/(m °C)) |
| n | number of samples | σ | variance of basis function |
| ui, vj, wk | velocity component in co-ordinate system (m/s) | ||
Appendix A
| 50 sets of Structural Parameter Sample Points | |||||||
| Num | l (mm) | a (°) | b (mm) | Num | l (mm) | a (°) | b (mm) |
| 1 | 26 | 5 | 12.2 | 26 | 25 | 43 | 13 |
| 2 | 21 | 12 | 9.8 | 27 | 24 | 74 | 13.7 |
| 3 | 30 | 49 | 13.7 | 28 | 27 | 61 | 10.5 |
| 4 | 29 | 72 | 11.5 | 29 | 29 | 51 | 12.9 |
| 5 | 26 | 47 | 13.9 | 30 | 23 | 26 | 9.6 |
| 6 | 22 | 41 | 11.3 | 31 | 25 | 65 | 12.7 |
| 7 | 22 | 68 | 9.8 | 32 | 24 | 22 | 12.1 |
| 8 | 20 | 38 | 10.7 | 33 | 21 | 4 | 9.1 |
| 9 | 30 | 84 | 11.5 | 34 | 26 | 15 | 11.4 |
| 10 | 29 | 30 | 10.1 | 35 | 28 | 17 | 9.5 |
| 11 | 20 | 57 | 11 | 36 | 21 | 33 | 11.9 |
| 12 | 20 | 38 | 9.3 | 37 | 23 | 9 | 11.7 |
| 13 | 26 | 44 | 13.3 | 38 | 28 | 52 | 10.1 |
| 14 | 23 | 61 | 13.1 | 39 | 25 | 1 | 10.5 |
| 15 | 24 | 19 | 10.8 | 40 | 28 | 77 | 12.5 |
| 16 | 26 | 28 | 13.1 | 41 | 22 | 31 | 12.3 |
| 17 | 24 | 21 | 11.8 | 42 | 28 | 7 | 14 |
| 18 | 23 | 55 | 9.1 | 43 | 27 | 82 | 13.4 |
| 19 | 25 | 59 | 10.2 | 44 | 29 | 46 | 12.6 |
| 20 | 22 | 13 | 11.2 | 45 | 23 | 63 | 10.3 |
| 21 | 20 | 85 | 12.7 | 46 | 22 | 90 | 12.2 |
| 22 | 21 | 69 | 11.8 | 47 | 27 | 7 | 10.9 |
| 23 | 21 | 75 | 9.7 | 48 | 27 | 87 | 10.7 |
| 24 | 24 | 24 | 10 | 49 | 21 | 35 | 13.5 |
| 25 | 25 | 80 | 13.2 | 50 | 20 | 77 | 9.3 |
Appendix B. Nonlinear Relationship between Parameters and Performances
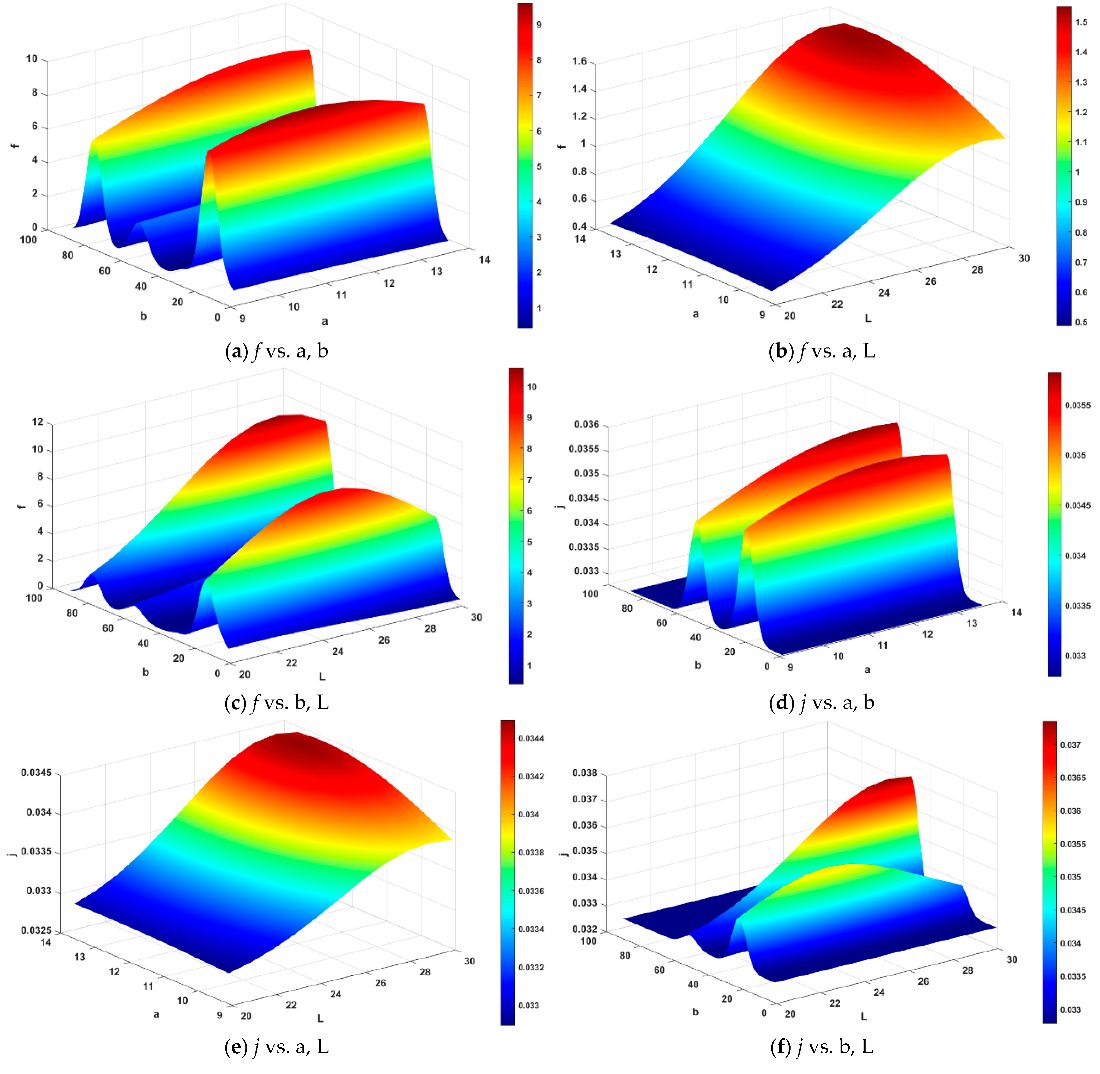
References
- Arsenyeva, O.; Tran, J.; Piper, M.; Kenig, E. An approach for pillow plate heat exchangers design for single-phase applications. Appl. Therm. Eng. 2019, 147, 579–591. [Google Scholar] [CrossRef]
- Arsenyeva, O.; Piper, M.; Zibart, A.; Olenberg, A.; Kenig, E.Y. Investigation of heat transfer and hydraulic resistance in small-scale pillow-plate heat exchangers. Energy 2019, 181, 1213–1224. [Google Scholar] [CrossRef]
- Piper, M.; Olenberg, A.; Tran, J.M.; Kenig, E.Y. Determination of the geometric design parameters of pillow-plate heat exchangers. Appl. Therm. Eng. 2015, 91, 1168–1175. [Google Scholar] [CrossRef]
- Piper, M.; Zibart, A.; Djakow, E.; Springer, R.; Homberg, W.; Kenig, E.Y. Heat transfer enhancement in pillow-plate heat exchangers with dimpled surfaces: A numerical study. Appl. Therm. Eng. 2019, 153, 142–146. [Google Scholar] [CrossRef]
- Piper, M.; Zibart, A.; Kenig, E.Y. New design equations for turbulent forced convection heat transfer and pressure loss in pillow-plate channels. Int. J. Therm. Sci. 2017, 120, 459–468. [Google Scholar] [CrossRef]
- Piper, M.; Zibart, A.; Tran, J.M.; Kenig, E.Y. Numerical investigation of turbulent forced convection heat transfer in pillow plates. Int. J. Heat Mass Transf. 2016, 94, 516–527. [Google Scholar] [CrossRef]
- Tran, J.M.; Piper, M.; Kenig, E.Y. Experimental Investigation of Convective Heat Transfer and Pressure Drop in Pillow Plates under Single-Phase Through-Flow Conditions. Chem. Ing. Tech. 2015, 87, 226–234. [Google Scholar] [CrossRef]
- Tran, J.M.; Sommerfeld, S.; Piper, M.; Kenig, E.Y. Investigation of pillow-plate condensers for the application in distillation columns. Chem. Eng. Res. Des. 2015, 99, 67–74. [Google Scholar] [CrossRef]
- Shirzad, M.; Ajarostaghi, S.S.M.; Delavar, M.A.; Sedighi, K. Improve the thermal performance of the pillow plate heat exchanger by using nanofluid: Numerical simulation. Adv. Powder Technol. 2019, 30, 1356–1365. [Google Scholar] [CrossRef]
- Song, J.; Wang, F.; Cheng, L. Experimental study and analysis of a novel multi-media plate heat exchanger. Sci. China-Technol. Sci. 2012, 55, 2157–2162. [Google Scholar] [CrossRef]
- Pei, B.; Chen, Z.; Li, F.; Bai, B. Flow and heat transfer of supercritical CO2 in the honeycomb ultra-compact plate heat exchanger. J. Supercrit. Fluids 2019, 148, 1–8. [Google Scholar] [CrossRef]
- Wenjing, D.U.; Wang, F.; Zhang, S.H.; Gao, X.D.; Cheng, L. Thermodynamic Analysis on The Regular Hexagonal Plate Heat Exchanger. J. Eng. Thermophys. 2010, 31, 1763–1766. [Google Scholar]
- Jamzad, P.; Kenna, J.; Bahrami, M. Development of novel plate heat exchanger using natural graphite sheet. Int. J. Heat Mass Transf. 2019, 131, 1205–1210. [Google Scholar] [CrossRef]
- Durmus, A.; Benli, H.; Kurtbas, I.; Gul, H. Investigation of heat transfer and pressure drop in plate heat exchangers having different surface profiles. Int. J. Heat Mass Transf. 2009, 52, 1451–1457. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, D.; Han, Y.; Zhu, Y.; Peng, X. Experimental and numerical investigation on the exergy and entransy performance of a novel plate heat exchanger. Exp. Heat Transf. 2017, 30, 162–177. [Google Scholar] [CrossRef]
- Jeong, J.Y.; Hong Hk Kim, S.K.; Kang, Y.T. Impact of plate design on the performance of welded type plate heat exchangers for sorption cycles. Int. J. Refrig. 2009, 32, 705–711. [Google Scholar] [CrossRef]
- Jiang, C.; Bai, B.F. Flow patterns and pressure drop of downward two-phase flow in a capsule-type plate heat exchanger. Exp. Therm. Fluid Sci. 2019, 103, 347–354. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, C.; Yang, Z.; Zhang, Y.; Bai, B. Numerical study on heat transfer enhancement in capsule-type plate heat exchangers. Appl. Therm. Eng. 2016, 108, 1237–1242. [Google Scholar] [CrossRef]
- Alqutub, A.M.; Linjawi, M.T.; Alrawi, I.M. Performance Study of a Dimpled-Protruded Air-to-Air Plate Heat Exchanger. In Proceedings of the International Conference on ASME Power Conference Collocated with the ASME International Conference on Energy Sustainability, San Diego, CA, USA, 28 June–2 July 2015. [Google Scholar]
- Kim, M.; Baik, Y.-J.; Park, S.-R.; Ra, H.-S.; Lim, H. Experimental study on corrugated cross-flow air-cooled plate heat exchangers. Exp. Therm. Fluid Sci. 2010, 34, 1265–1272. [Google Scholar] [CrossRef]
- Doo, J.H.; Ha, M.Y.; Min, J.K.; Stieger, R.; Rolt, A.; Son, C. An investigation of cross-corrugated heat exchanger primary surfaces for advanced intercooled-cycle aero engines (Part-I: Novel geometry of primary surface). Int. J. Heat Mass Transf. 2012, 55, 5256–5267. [Google Scholar] [CrossRef]
- Lee, J.M.; Kwan, P.W.; Son, C.M.; Ha, M.Y. Characterizations of aerothermal performance of novel cross-corrugated plate heat exchangers for advanced cycle aero-engines. Int. J. Heat Mass Transf. 2015, 85, 166–180. [Google Scholar] [CrossRef]
- Kanaris, A.G.; Mouza, A.A.; Paras, S.V. Optimal design of a plate heat exchanger with undulated surfaces. Int. J. Therm. Sci. 2009, 48, 1184–1195. [Google Scholar] [CrossRef]
- Imran, M.; Pambudi, N.A.; Farooq, M. Thermal and hydraulic optimization of plate heat exchanger using multi objective genetic algorithm. Case Stud. Therm. Eng. 2017, 10, 570–578. [Google Scholar] [CrossRef]
- Giurgiu, O.; Pleşa, A.; Socaciu, L. Plate Heat Exchangers—Flow Analysis through Mini Channels. Energy Procedia 2016, 85, 244–251. [Google Scholar] [CrossRef]
- Jin, S.; Hrnjak, P. Effect of end plates on heat transfer of plate heat exchanger. Int. J. Heat Mass Transf. 2017, 108, 740–748. [Google Scholar] [CrossRef]
- Longo, G.A.; Gasparella, A.; Sartori, R. Experimental heat transfer coefficients during refrigerant vaporisation and condensation inside herringbone-type plate heat exchangers with enhanced surfaces. Int. J. Heat Mass Transf. 2004, 47, 4125–4136. [Google Scholar] [CrossRef]
- Hu, S.; Ma, X.; Zhou, W. Condensation heat transfer of ethanol-water vapor in a plate heat exchanger. Appl. Therm. Eng. 2017, 113, 1047–1055. [Google Scholar] [CrossRef]
- Yu, C.; Xue, X.; Shi, K.; Shao, M. A Three-Dimensional Numerical and Multi-Objective Optimal Design of Wavy Plate-Fins Heat Exchangers. Processes 2021, 9, 9. [Google Scholar] [CrossRef]
- Khodabandeh, E.; Toghraie, D.; Chamkha, A.; Mashayekhi, R.; Akbari, O.; Rozati, S.A. Energy saving with using of elliptic pillows in turbulent flow of two-phase water-silver nanofluid in a spiral heat exchanger. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 2025–2049. [Google Scholar] [CrossRef]
- Hwang, S.D.; Kwon, H.G.; Cho, H.H. Local Heat Transfer and Thermal Performance on Periodically Dimple-protrusion Patterned Walls for Compact Heat Exchangers. Energy 2010, 35, 5357–5364. [Google Scholar] [CrossRef]
- Yu, C.; Xue, X.; Shi, K.; Wang, R.; Zhang, L. Optimization of wavy fin-and-elliptical tube heat exchanger using CFD, multi-objective genetic algorithm and radical basis function. Energy Sci. Eng. 2021, 9, 1359–1372. [Google Scholar] [CrossRef]
- Li, P.P. Research on Performance of the Plate Oil Radiator for Construction Vehicle. Doctoral Dissertation, Jilin University, Changchun, Jilin, 2016. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1fabe1d7768e0820f565bb672e9b17d5&site=xueshu_se (accessed on 1 January 2024).









| Capsule Dimensions | Values | Core Dimensions | Values |
|---|---|---|---|
| Capsule length (mm) | l | Plate length (mm) | 200 |
| Capsule angle (°) | a | Plate width (mm) | 100 |
| Capsule width (mm) | b | Plate thickness (mm) | 0.5 |
| Coolant Liquid | Aluminum | |
|---|---|---|
| Density (kg/m3) | 1009.86 | 2719 |
| Specific heat (J/(kg·K)) | 3679.4 | 871 |
| Thermal conductivity (W/(m·K)) | 0.643 | 237 |
| Viscosity (Pa·s) | 7.13 × 10−4 | —— |
| l (mm) | a (°) | b (mm) | Heat Transfer Factor j | Friction Factor f | |
|---|---|---|---|---|---|
| Before optimization | 22 | 41 | 11.3 | 1.869 | 0.042 |
| After optimization | 25 | 65 | 12.7 | 2.025 | 0.036 |
| Variable quantity | 13.6% | 58.5% | 12.3% | 8.3% | 14.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Shao, M.; Zhang, W.; Wang, G.; Huang, M. Study on Heat Transfer Synergy and Optimization of Capsule-Type Plate Heat Exchangers. Processes 2024, 12, 604. https://doi.org/10.3390/pr12030604
Yu C, Shao M, Zhang W, Wang G, Huang M. Study on Heat Transfer Synergy and Optimization of Capsule-Type Plate Heat Exchangers. Processes. 2024; 12(3):604. https://doi.org/10.3390/pr12030604
Chicago/Turabian StyleYu, Chao, Mingzhen Shao, Wenbao Zhang, Guangyi Wang, and Mian Huang. 2024. "Study on Heat Transfer Synergy and Optimization of Capsule-Type Plate Heat Exchangers" Processes 12, no. 3: 604. https://doi.org/10.3390/pr12030604
APA StyleYu, C., Shao, M., Zhang, W., Wang, G., & Huang, M. (2024). Study on Heat Transfer Synergy and Optimization of Capsule-Type Plate Heat Exchangers. Processes, 12(3), 604. https://doi.org/10.3390/pr12030604






