Research on a Sensorless ADRC Vector Control Method for a Permanent Magnet Synchronous Motor Based on the Luenberger Observer
Abstract
1. Introduction
2. Mathematical Model of PMSM
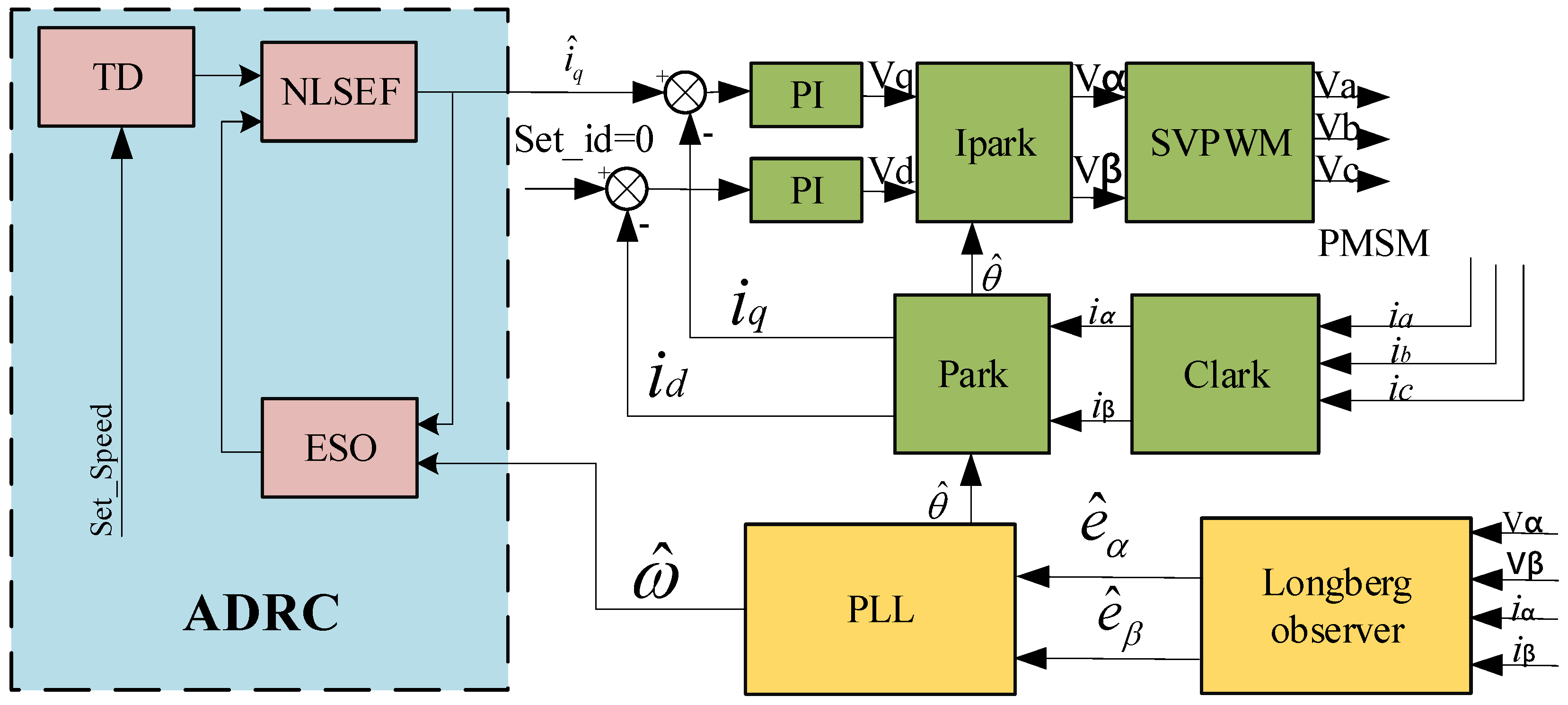
3. Construction of the Luenberger Observer and Estimation of the Rotor Position
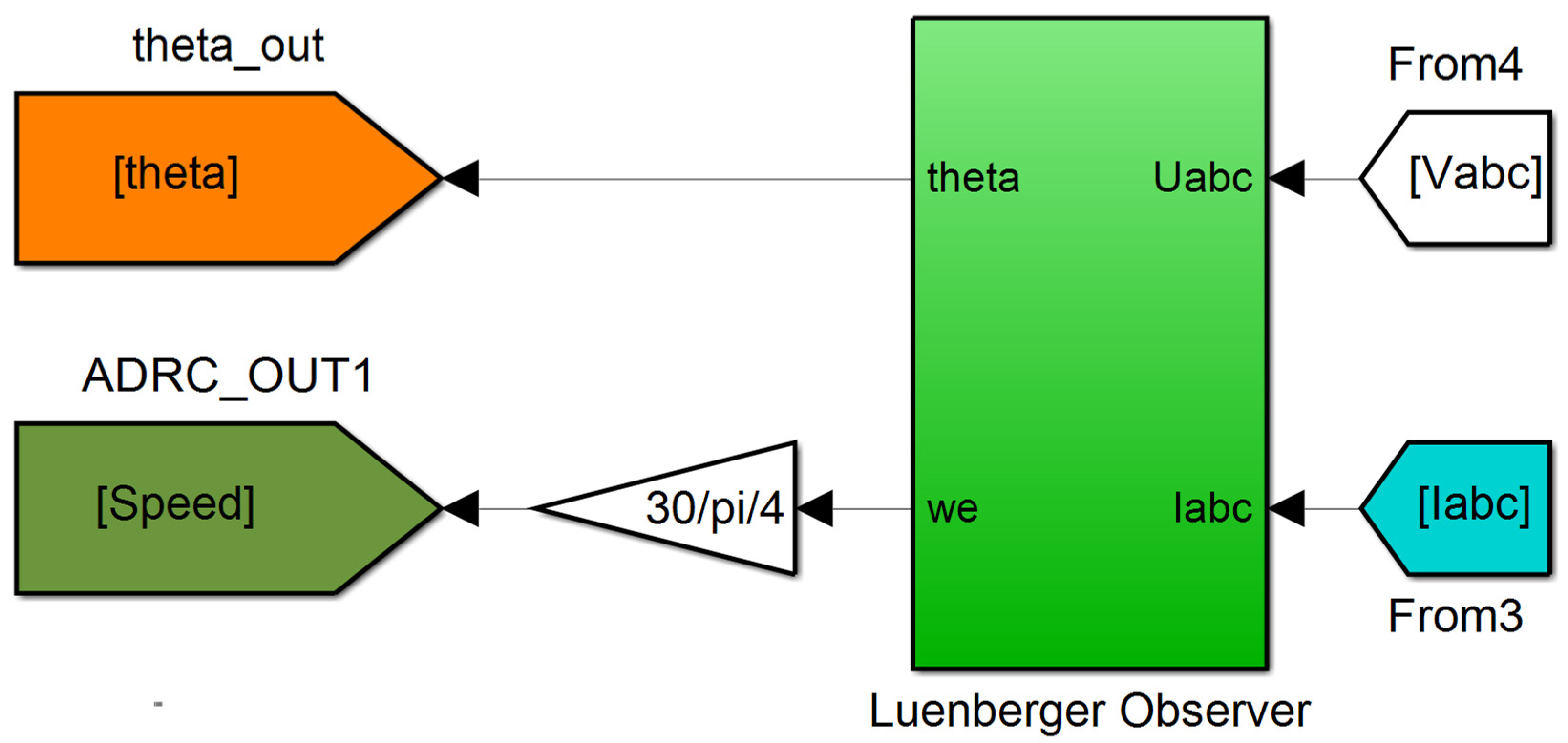
3.1. Construction of the Luenberger Observer
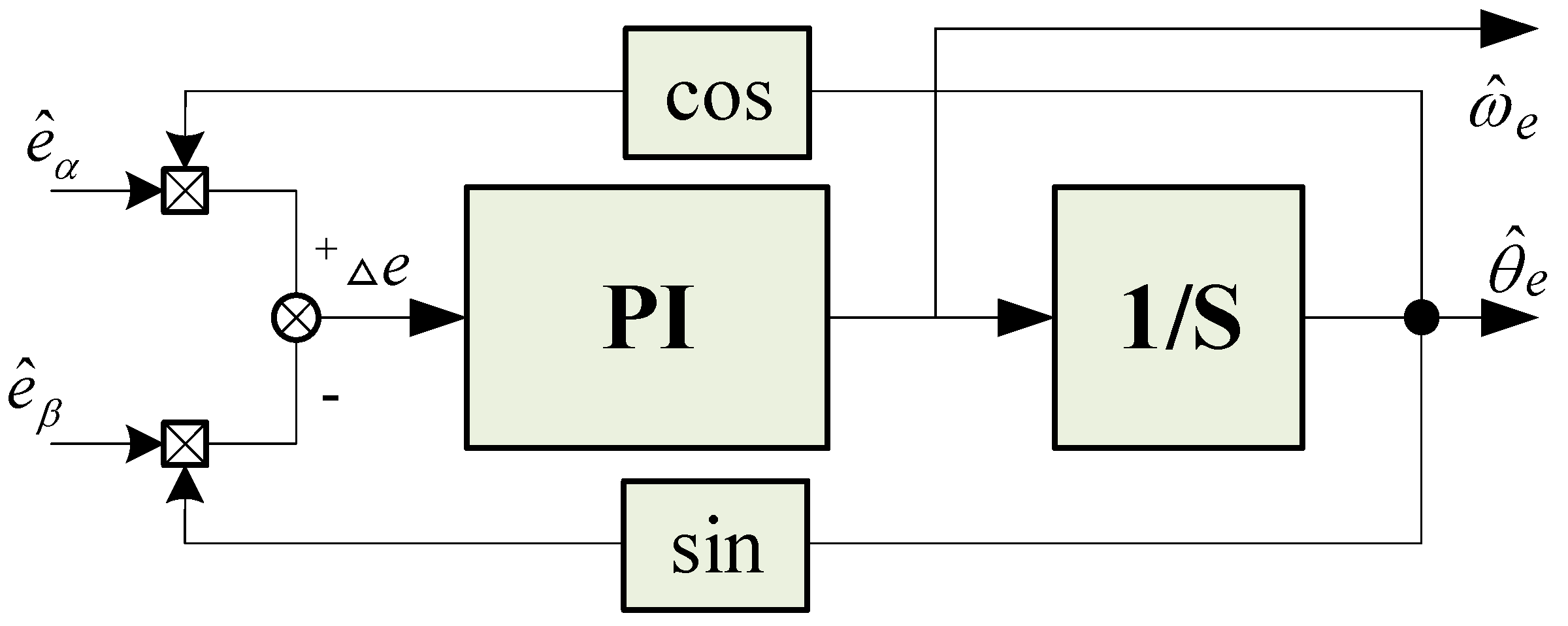
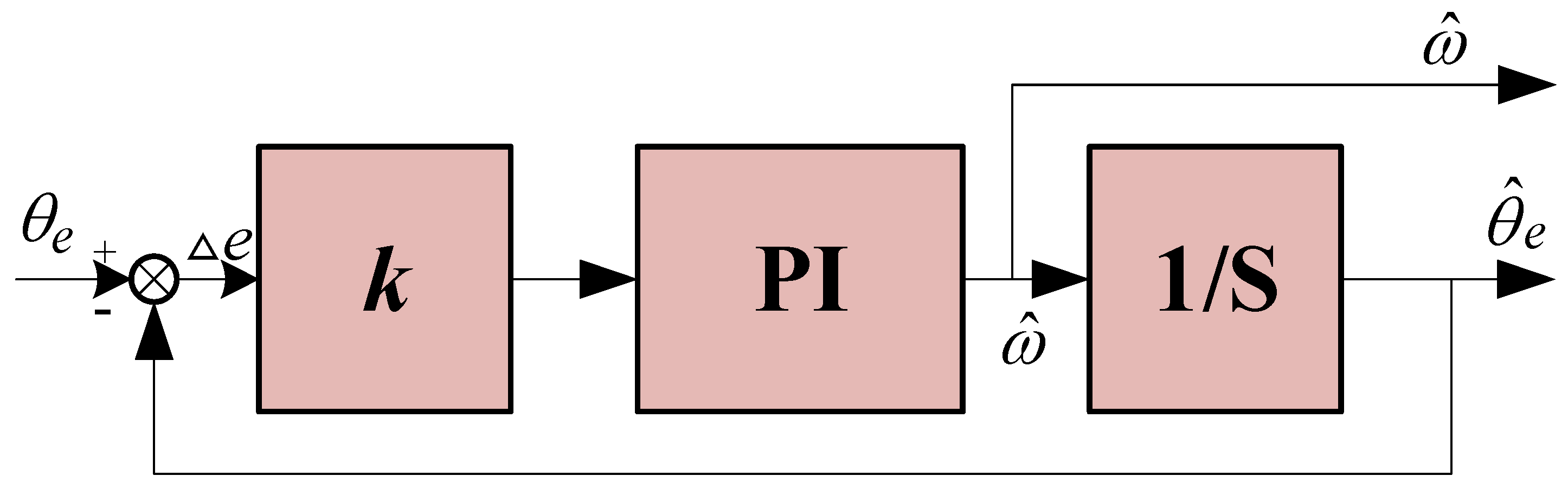
3.2. Estimation of Rotor Position and Speed
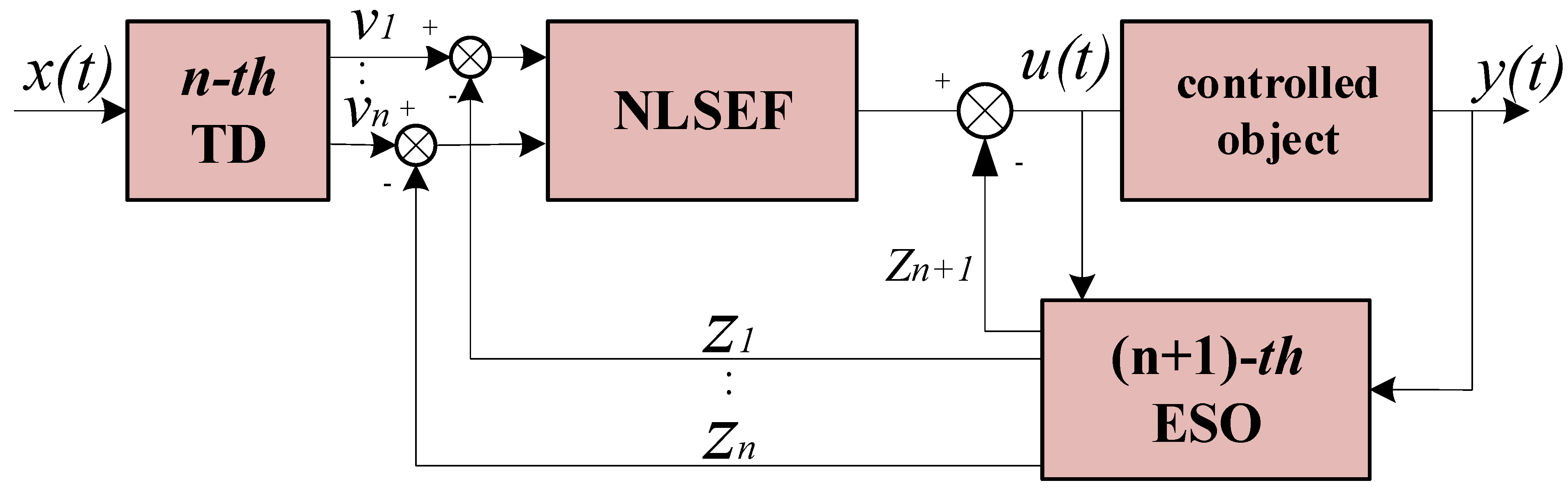
4. Construction of the PMSM Second-Order ADRC
5. Analysis of the Experimental Results
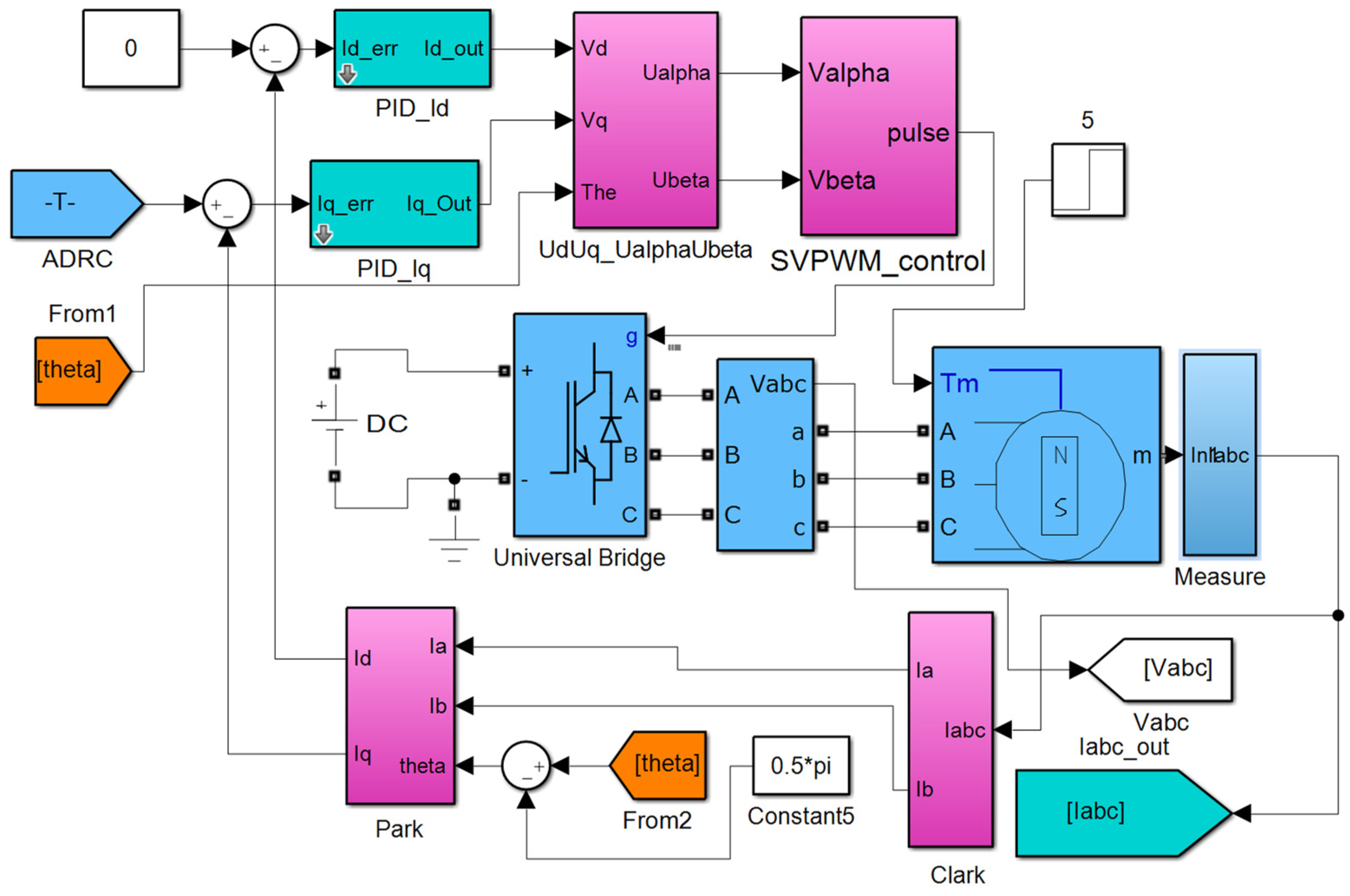
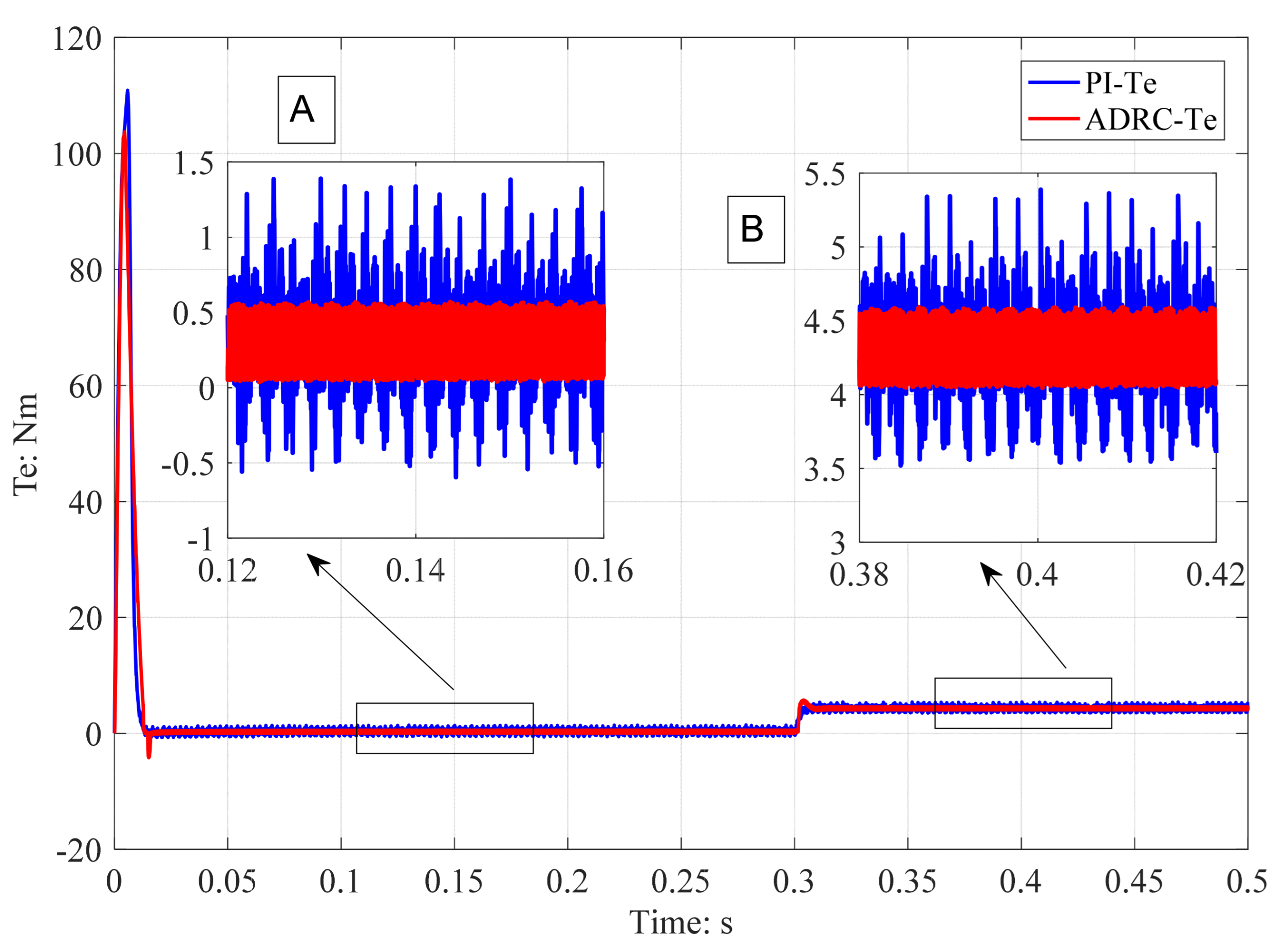
5.1. Model Simulation and Results Analysis
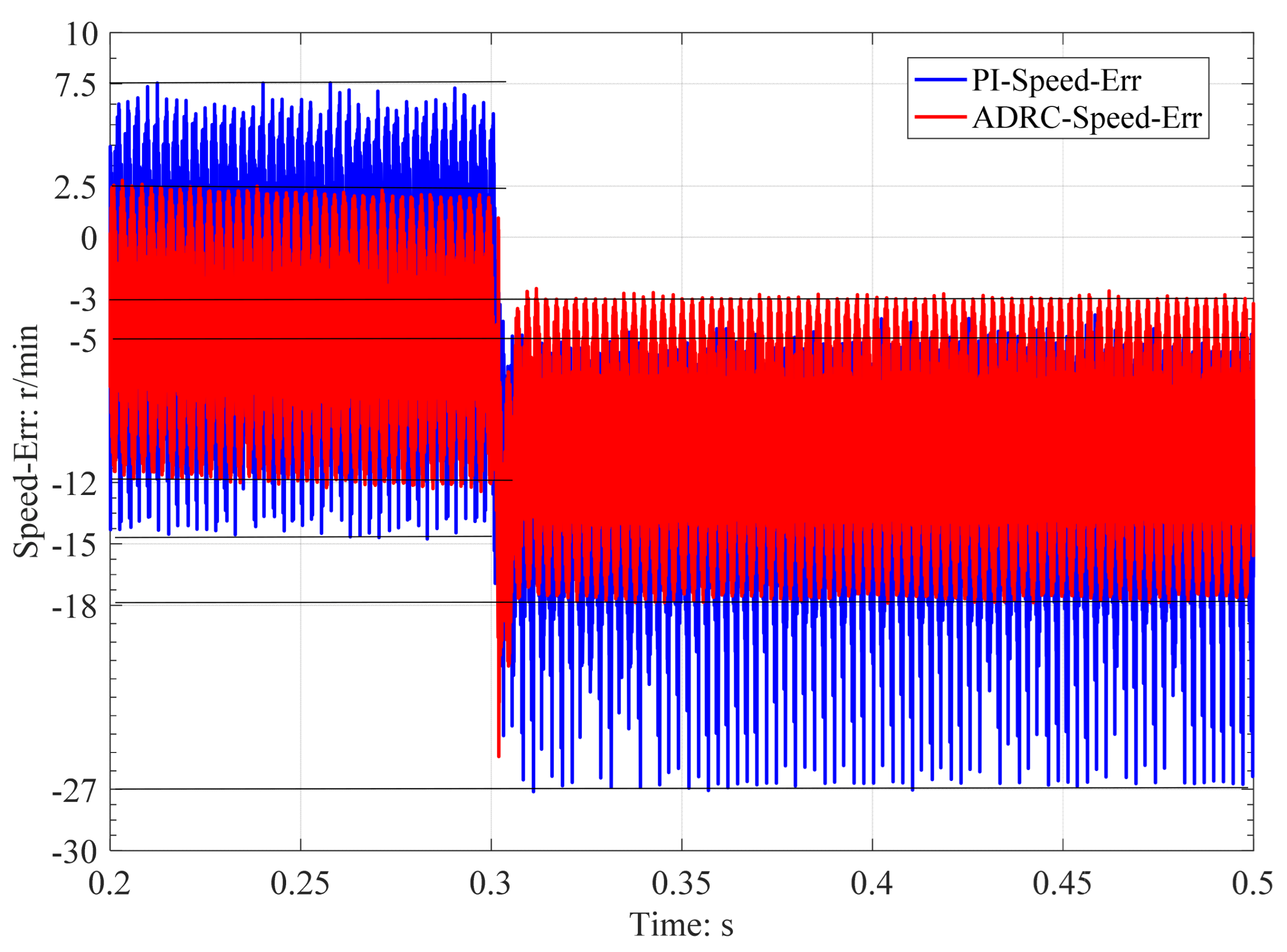
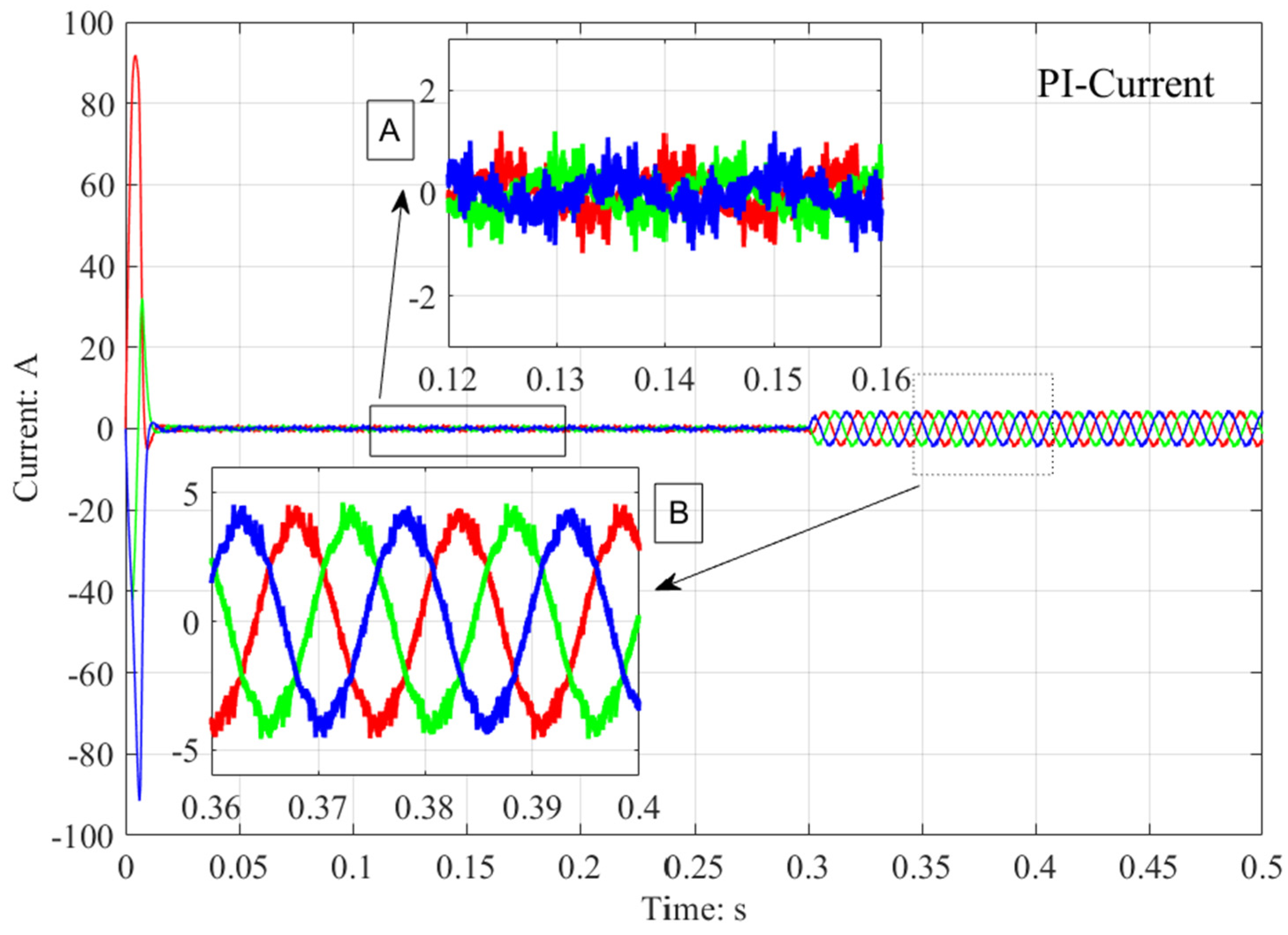
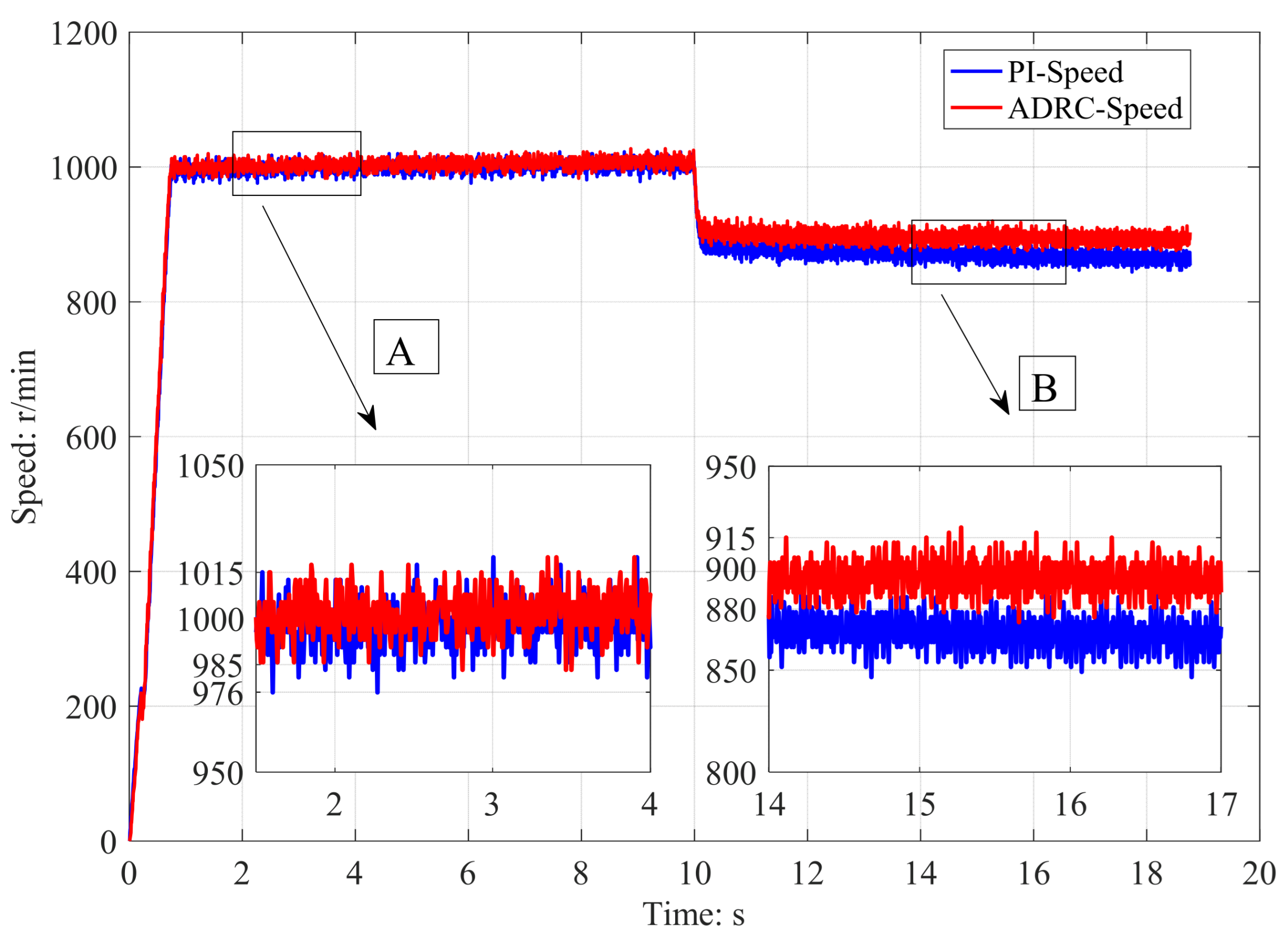
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, H.; Li, S. Speed control for PMSM servo system using predictive functional control and extended state observer. IEEE Trans. Ind. Electron. 2011, 59, 1171–1183. [Google Scholar] [CrossRef]
- Ahn, H.; Park, H.; Kim, C.; Lee, H. A Review of State-of-the-art Techniques for PMSM Parameter Identification. J. Electr. Eng. Technol. 2020, 15, 1177–1187. [Google Scholar] [CrossRef]
- Ullah, K.; Guzinski, J.; Mirza, A.F. Critical review on robust speed control techniques for permanent magnet synchronous motor (PMSM) speed regulation. Energies 2022, 15, 1235. [Google Scholar] [CrossRef]
- Niu, S.; Luo, Y.; Fu, W.; Zhang, X. Robust model predictive control for a three-phase PMSM motor with improved control precision. IEEE Trans. Ind. Electron. 2020, 68, 838–849. [Google Scholar] [CrossRef]
- Hong, D.-K.; Hwang, W.; Lee, J.-Y.; Woo, B.-C. Design, analysis, and experimental validation of a permanent magnet synchronous motor for articulated robot applications. IEEE Trans. Magn. 2017, 54, 1–4. [Google Scholar] [CrossRef]
- Vafaie, M.H.; Dehkordi, B.M.; Moallem, P.; Kiyoumarsi, A. A new predictive direct torque control method for improving both steady-state and transient-state operations of the PMSM. IEEE Trans. Power Electron. 2015, 31, 3738–3753. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Chen, C. Review of sensorless control techniques for PMSM drives. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 1543–1552. [Google Scholar] [CrossRef]
- Kim, H.; Son, J.; Lee, J. A High-Speed Sliding-Mode Observer for the Sensorless Speed Control of a PMSM. IEEE Trans. Onindustrial Electron. 2011, 58, 4069. [Google Scholar]
- Abdelrahem, M.; Hackl, C.M.; Kennel, R. Finite Position Set-Phase Locked Loop for Sensorless Control of Direct-Driven Permanent-Magnet Synchronous Generators. IEEE Trans. Power Electron. 2018, 33, 3097. [Google Scholar] [CrossRef]
- Yang, H.; Xu, A.; Zhang, Y.; Chai, X. Error Analysis and Design of Sliding Mode Observer-based Sensorless PMSM Drives under Low Sampling Ratio. IEEE Trans. Power Electron. 2024. [Google Scholar] [CrossRef]
- Li, Y.; Hu, H.; Shi, P. A Review of Position Sensorless Compound Control for PMSM Drives. World Electr. Veh. J. 2023, 14, 34. [Google Scholar] [CrossRef]
- Benchabane, F.; Titaouine, A.; Bennis, O.; Yahia, K.; Taibi, D. Sensorless fuzzy sliding mode control for permanent magnet synchronous motor fed by AC/DC/AC converter. Int. J. Syst. Assur. Eng. Manag. 2012, 3, 221–229. [Google Scholar] [CrossRef]
- Teymoori, V.; Kamper, M.; Wang, R.-J.; Kennel, R. Sensorless control of dual three-phase permanent magnet synchronous machines—A review. Energies 2023, 16, 1326. [Google Scholar] [CrossRef]
- Quang, N.K.; Hieu, N.T.; Ha, Q.P. FPGA-based sensorless PMSM speed control using reduced-order extended Kalman filters. IEEE Trans. Ind. Electron. 2014, 61, 6574–6582. [Google Scholar] [CrossRef]
- Liang, D.; Li, J.; Qu, R. Sensorless control of permanent magnet synchronous machine based on second-order sliding-mode observer with online resistance estimation. IEEE Trans. Ind. Appl. 2017, 53, 3672–3682. [Google Scholar] [CrossRef]
- Qiao, Z.; Shi, T.; Wang, Y.; Yan, Y.; Xia, C.; He, X. New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor. IEEE Trans. Ind. Electron. 2012, 60, 710–719. [Google Scholar] [CrossRef]
- Antti, P.; Marko, H. Adaptation of motor parameters in sensorless PMSM drives. IEEE Trans. Ind. Appl. 2009, 45, 203–212. [Google Scholar]
- Antti, P.; Jorma, L. Adaptive observer combined with HF signal injection for sensorless control of PMSM drives. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 674–681. [Google Scholar]
- Faten, G.; Lassaâd, S. Speed sensorless IFOC of PMSM based on adaptive Luenberger observer. Int. J. Electr. Electron. Eng. 2009, 2, 7–13. [Google Scholar]
- Huang, X.; Guan, P.; Pan, H.; Liu, S.; Du, G.; Huang, X.; Wang, X. Research on grey predictive control of PMSM based on reduced-order luenberger observer. J. Electr. Eng. Technol. 2021, 16, 2635–2646. [Google Scholar] [CrossRef]
- Wang, B.; Tian, M.; Yu, Y.; Dong, Q.; Xu, D. Enhanced ADRC with quasi-resonant control for PMSM speed regulation considering aperiodic and periodic disturbances. IEEE Trans. Transp. Electrif. 2021, 8, 3568–3577. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, L. Robust current and speed control of a permanent magnet synchronous motor using SMC and ADRC. Control Theory Technol. 2019, 17, 190–199. [Google Scholar] [CrossRef]
- Lu, W.; Li, Q.; Lu, K.; Lu, Y.; Guo, L.; Yan, W.; Xu, F. Load adaptive PMSM drive system based on an improved ADRC for manipulator joint. IEEE Access 2021, 9, 33369–33384. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Discrete-time repetitive control-based ADRC for current loop disturbances suppression of PMSM drives. IEEE Trans. Ind. Inform. 2021, 18, 3138–3149. [Google Scholar] [CrossRef]
- Ahcene, F.; Bentarzi, H. Synthesis of ADRC and its Application to an Electrical Power System. Alger. J. Signals Syst. 2022, 7, 122–134. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, G.; Liu, Y.; Yang, Z.; Zhu, H. Research of a six-pole active magnetic bearing system based on a fuzzy active controller. Electronics 2022, 11, 1723. [Google Scholar] [CrossRef]
- Tao, L.; Chen, Q.; Nan, Y.; Dong, F.; Jin, Y. Speed tracking and synchronization of a multimotor system based on fuzzy ADRC and enhanced adjacent coupling scheme. Complexity 2018, 2018, 5632939. [Google Scholar] [CrossRef]
- Su, G. Fuzzy ADRC controller design for PMSM speed regulation system. Adv. Mater. Res. 2011, 201, 2405–2408. [Google Scholar] [CrossRef]
- Li, J.; Ren, H.; Zhong, Y. Robust speed control of induction motor drives using first-order autodisturbance rejection controllers. IEEE. Trans. Ind. Appl. 2015, 51, 712–720. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Luenberger−K1 | 155,000 | ADRC−β1 | 250 |
| Luenberger−K2 | 140,000 | ADRC−β2 | 1.2 |
| ADRC−r | 0.1 | ADRC−β01 | 2000 |
| ADRC−h | 0.25 | ADRC−β02 | 2100 |
| ADRC−α1 | 0.5 | ADRC−β03 | 2400 |
| ADRC−α2 | 0.75 | PI−kp/ki | 0.4/0.02 |
| Name | Value | Unit |
|---|---|---|
| Maximum speed | 5000 | r/min |
| Rated voltage | 24 | V |
| Rated torque | 0.318 | Nm |
| Rated current | 4.6 | A |
| Moment of inertia | 0.0588 | kg·m2 10−4 |
| Line resistance | 0.75 | Ω |
| Weight | 0.8 | kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Shi, Z.; Yu, B.; Qi, H. Research on a Sensorless ADRC Vector Control Method for a Permanent Magnet Synchronous Motor Based on the Luenberger Observer. Processes 2024, 12, 906. https://doi.org/10.3390/pr12050906
Zhang P, Shi Z, Yu B, Qi H. Research on a Sensorless ADRC Vector Control Method for a Permanent Magnet Synchronous Motor Based on the Luenberger Observer. Processes. 2024; 12(5):906. https://doi.org/10.3390/pr12050906
Chicago/Turabian StyleZhang, Pan, Zhaoyao Shi, Bo Yu, and Haijiang Qi. 2024. "Research on a Sensorless ADRC Vector Control Method for a Permanent Magnet Synchronous Motor Based on the Luenberger Observer" Processes 12, no. 5: 906. https://doi.org/10.3390/pr12050906
APA StyleZhang, P., Shi, Z., Yu, B., & Qi, H. (2024). Research on a Sensorless ADRC Vector Control Method for a Permanent Magnet Synchronous Motor Based on the Luenberger Observer. Processes, 12(5), 906. https://doi.org/10.3390/pr12050906






