Fault Diagnosis of Wind Turbine Gearbox Using Vibration Scatter Plot and Visual Geometric Group Network
Abstract
1. Introduction
2. Research System Architecture and Fault Design
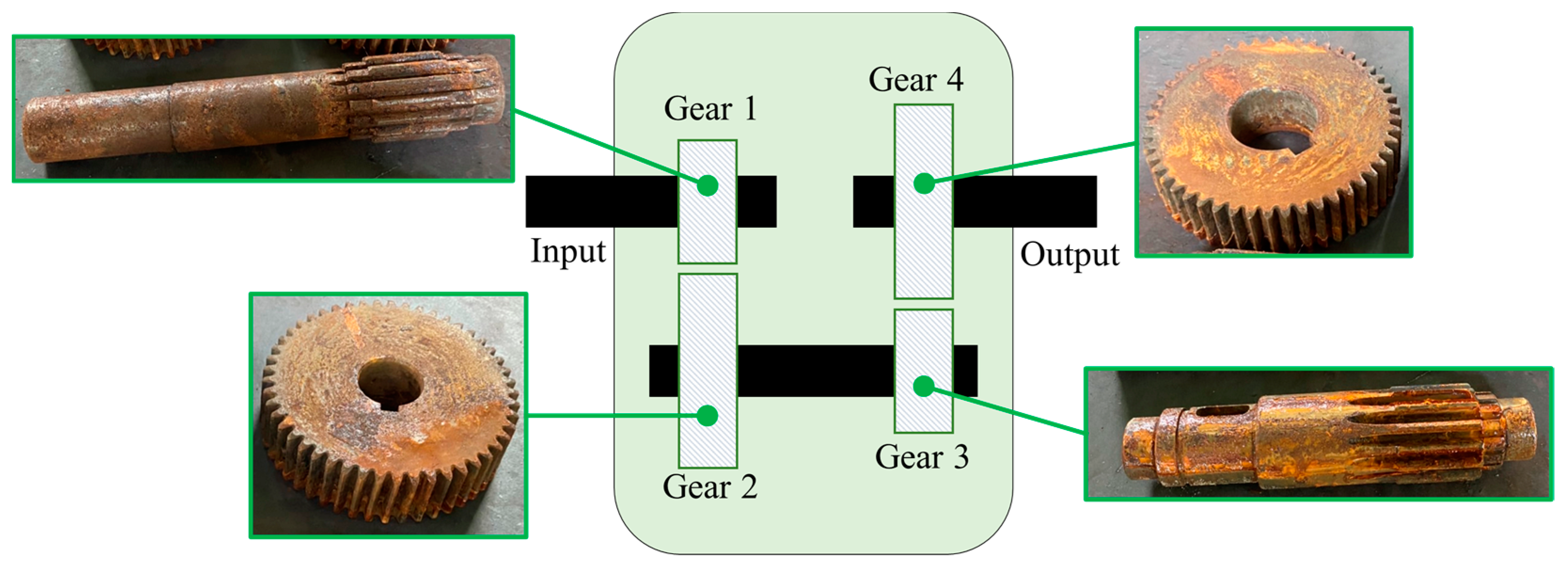
2.1. Fault Testing Platform and Gearbox Fault Design
2.1.1. No-Fault (Type A)
2.1.2. Rusty (Type B)
2.1.3. Chipped (Type C)
2.1.4. Gear Worn (Type D)
2.1.5. Gear Aged (Type E)
3. Methodology
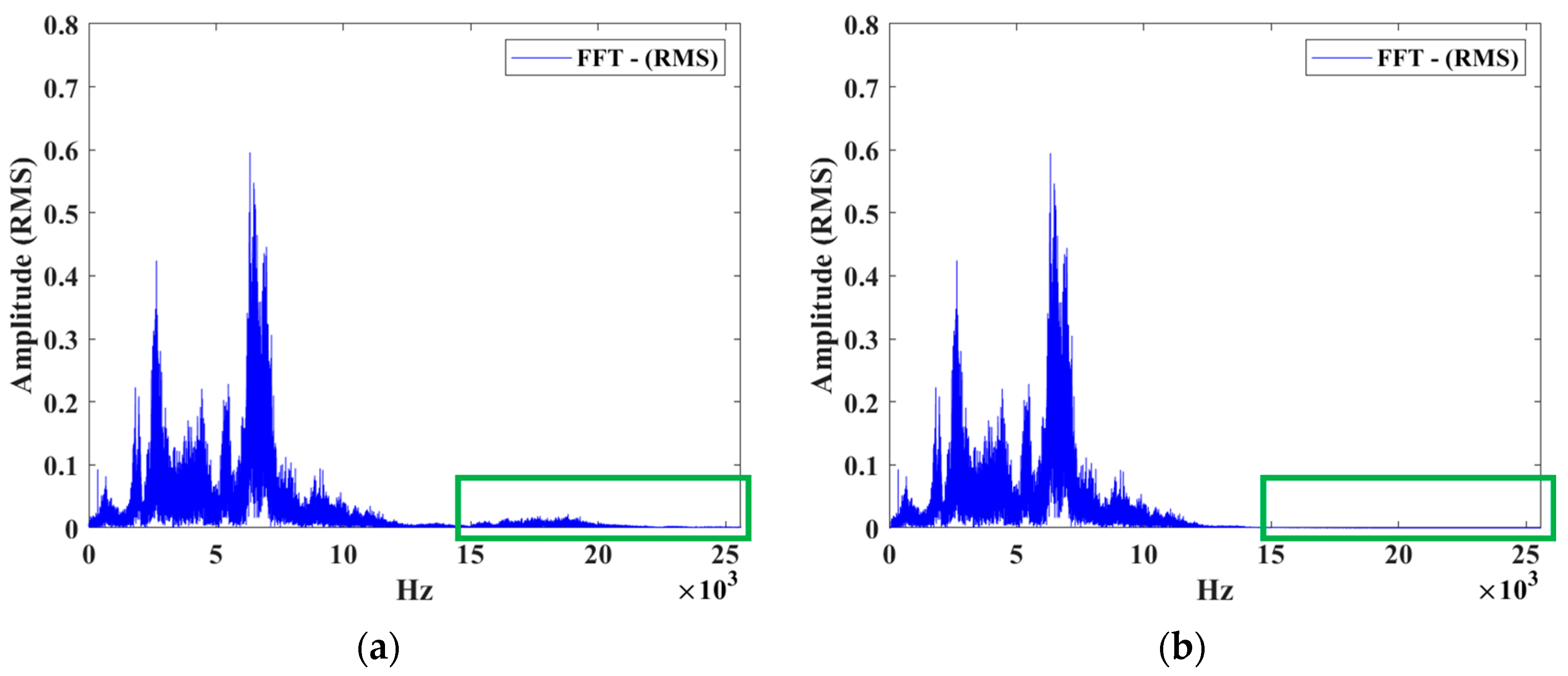
3.1. Signal Processing
3.2. Gaussian White Noise
3.3. Scatter Plot
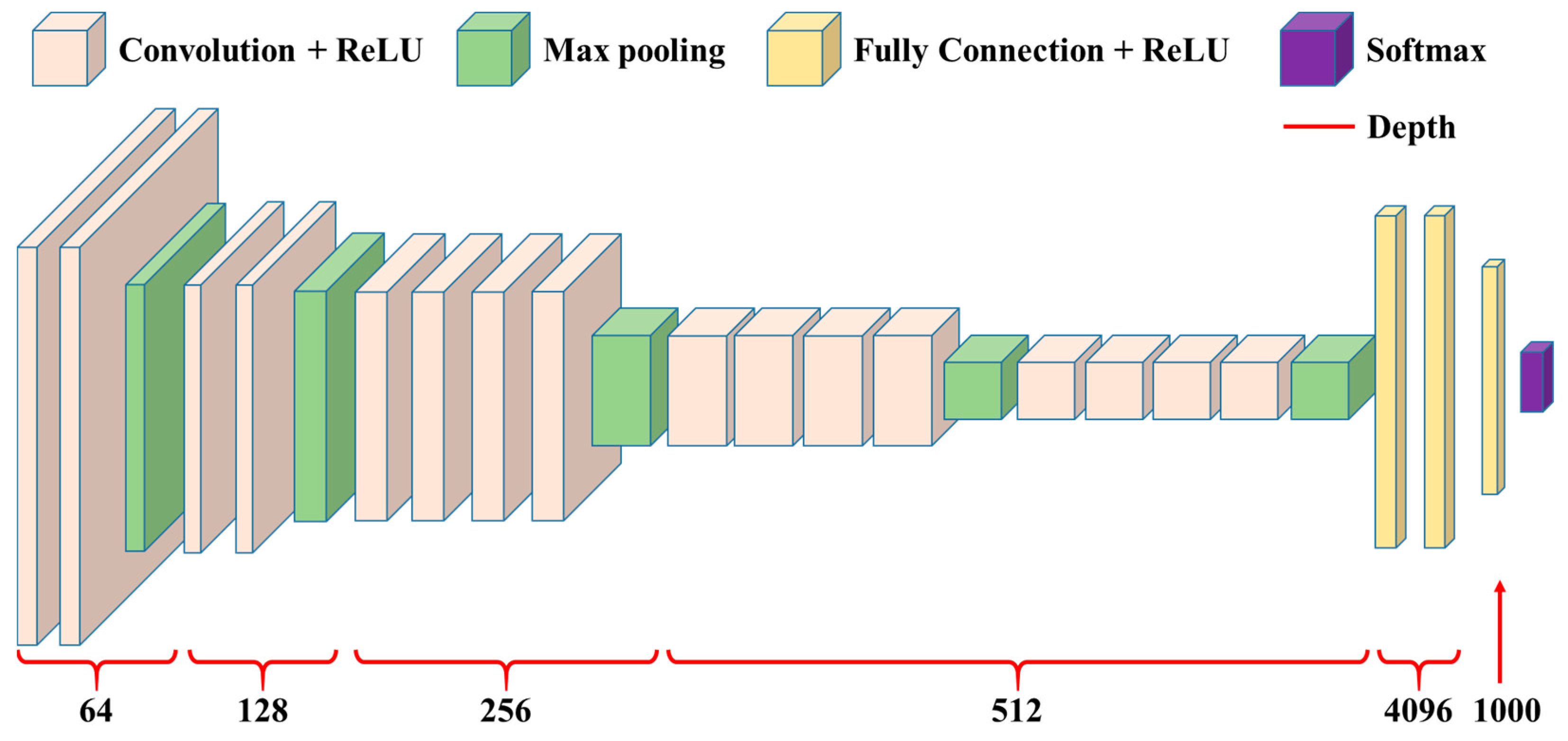
3.4. Visual Geometric Group
3.4.1. VGG 19
3.4.2. Convolutional Kernel and Convolution Layer
3.4.3. Pooling Layer
3.4.4. Fully Connected Layer
4. Experimental Results
4.1. Scatter Plot
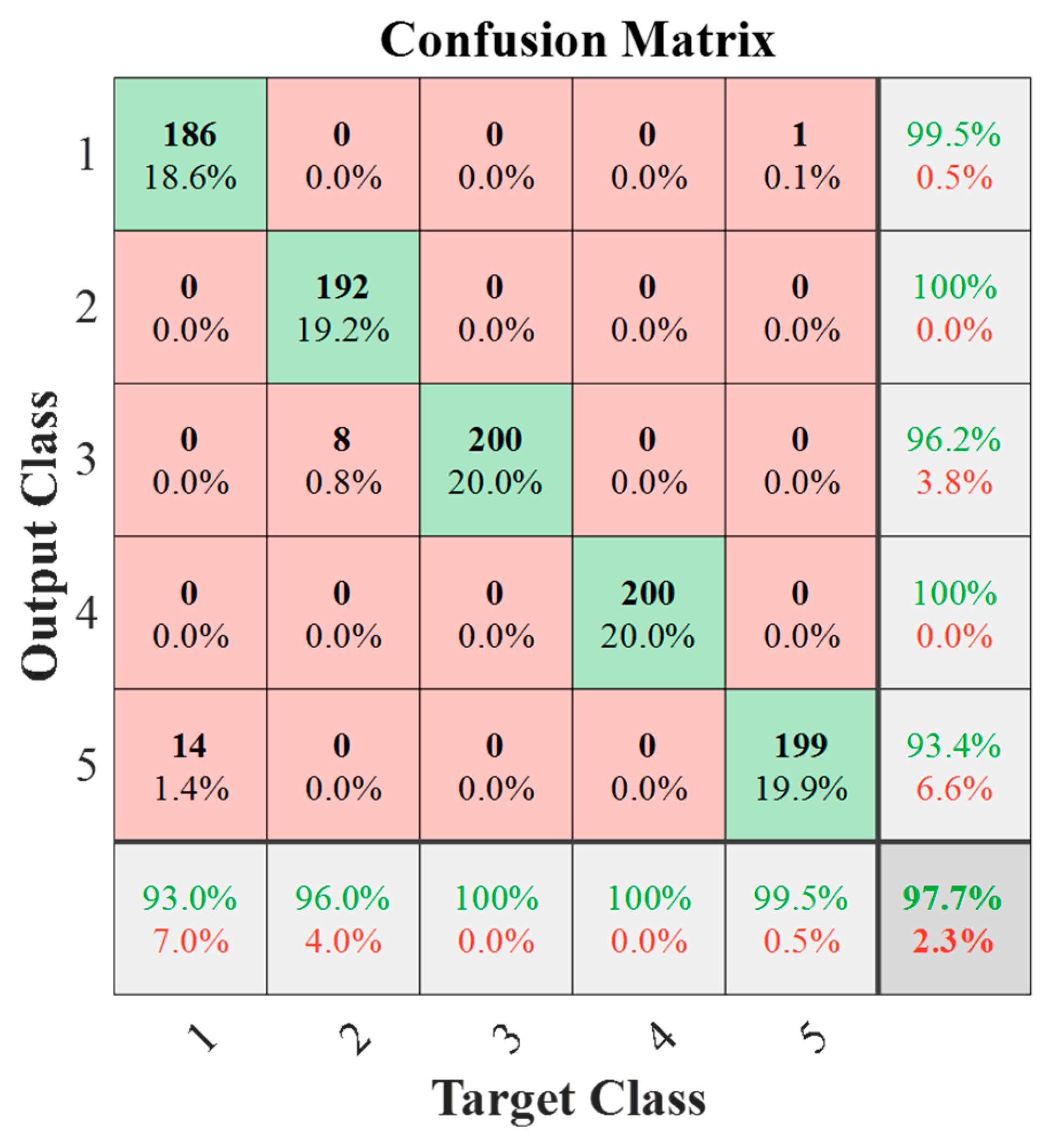
4.2. VGG 19
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Wang, X.; Zhang, L. Fault Diagnosis of Industrial Wind Turbine Blade Bearing Using Acoustic Emission Analysis. IEEE Trans. Instrum. Meas. 2020, 69, 6630–6639. [Google Scholar] [CrossRef]
- He, Q.; Zhao, J.; Jiang, G.; Xie, P. An Unsupervised Multiview Sparse Filtering Approach for Current-Based Wind Turbine Gearbox Fault Diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 5569–5578. [Google Scholar] [CrossRef]
- Assoumane, A.; Ravier, P.; Capdessus, C.; Sekko, E. H∞ estimator for gearbox diagnosis in variable speed conditions. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017. [Google Scholar]
- Huang, N.; Chen, Q.; Cai, G.; Xu, D.; Zhang, L.; Zhao, W. Fault Diagnosis of Bearing in Wind Turbine Gearbox Under Actual Operating Conditions Driven by Limited Data with Noise Labels. IEEE Trans. Instrum. Meas. 2021, 70, 3502510. [Google Scholar] [CrossRef]
- Artigao, E.; Honrubia-Escribano, A.; Gómez-Lázaro, E. In-Service Wind Turbine DFIG Diagnosis Using Current Signature Analysis. IEEE Trans. Ind. Electron. 2020, 67, 2262–2271. [Google Scholar] [CrossRef]
- Dao, C.; Kazemtabrizi, B.; Crabtree, C. Wind turbine reliability data review and impacts on levelised cost of energy. Wind Energy 2019, 22, 1848–1871. [Google Scholar] [CrossRef]
- Xiong, Z.; Qiu, Y.; Feng, Y.; Chen, L. Fatigue Damage of Wind Turbine Gearbox Under Extreme Wind Conditions. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018. [Google Scholar]
- Bechhoefer, E.; Wadham-Gagnon, M.; Boucher, B. Initial Condition Monitoring Experience on a Wind Turbine. Annu. Conf. PHM Soc. 2012, 4, 63–70. [Google Scholar] [CrossRef]
- Qu, Y.; He, D.; Yoon, J.; Van Hecke, B.; Bechhoefer, E.; Zhu, J. Gearbox Tooth Cut Fault Diagnostics Using Acoustic Emission and Vibration Sensors—A Comparative Study. Sensors 2014, 14, 1372–1393. [Google Scholar] [CrossRef]
- He, M.; He, D.; Bechhoefer, E. Using Deep Learning Based Approaches for Bearing Fault Diagnosis with AE Sensors. Annu. Conf. PHM Soc. 2016, 8, 282–291. [Google Scholar] [CrossRef]
- Bechhoefer, E.; Butterworth, B. A Comprehensive Analysis of the Performance of Gear Fault Detection Algorithms. Annu. Conf. PHM Soc. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Peng, Y.; Cheng, F.; Qiao, W.; Qu, L. Fault prognosis of drivetrain gearbox based on a recurrent neural network. In Proceedings of the 2017 IEEE International Conference on Electro Information Technology (EIT), Lincoln, NE, USA, 14–17 May 2017. [Google Scholar]
- Huang, C.; Li, Y.; Zhang, T.; Hou, G.; Zhang, J. Fault diagnosis of wind turbine gearbox by diminishing step fruit fly algorithm optimized SVM. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017. [Google Scholar]
- Liu, Q.; Yang, J. Fault Diagnosis of Wind Turbine Gearbox Based on Dual-tree Complex Wavelet and Information Entropy. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018. [Google Scholar]
- Zhong, J.H.; Zhang, J.; Liang, J.; Wang, H. Multi-Fault Rapid Diagnosis for Wind Turbine Gearbox Using Sparse Bayesian Extreme Learning Machine. IEEE Access 2019, 7, 773–781. [Google Scholar] [CrossRef]
- Amin, A.; Bibo, A.; Panyam, M.; Tallapragada, P. Vibration-based Condition Monitoring in Wind Turbine Gearbox Using Convolutional Neural Network. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022. [Google Scholar]
- Yu, X.; Tang, B.; Zhang, K. Fault Diagnosis of Wind Turbine Gearbox Using a Novel Method of Fast Deep Graph Convolutional Networks. IEEE Trans. Instrum. Meas. 2021, 70, 6502714. [Google Scholar] [CrossRef]
- Pu, Z.; Li, C.; Zhang, S.; Bai, Y. Fault Diagnosis for Wind Turbine Gearboxes by Using Deep Enhanced Fusion Network. IEEE Trans. Instrum. Meas. 2021, 70, 2501811. [Google Scholar] [CrossRef]
- Qiu, G.; Gu, Y.; Cai, Q. A deep convolutional neural networks model for intelligent fault diagnosis of a gearbox under different operational conditions. Measurement 2019, 145, 94–107. [Google Scholar] [CrossRef]
- Rapp, T.; Peters, C.; Dachsbacher, C. Visual Analysis of Large Multivariate Scattered Data using Clustering and Probabilistic Summaries. IEEE Trans. Visual Comput. Graphics. 2021, 27, 1580–1590. [Google Scholar] [CrossRef] [PubMed]
- Pangilinan, J.R.; Legaspi, J.; Linsangan, N. InceptionV3, ResNet50, and VGG19 Performance Comparison on Tomato Ripeness Classification. In Proceedings of the 2022 5th International Seminar on Research of Information Technology and Intelligent Systems (ISRITI), Yogyakarta, Indonesia, 8–9 December 2022. [Google Scholar]
- Singh, D.K.; Kurien, J.; Villayamore, A. Study and analysis of wind turbine gearbox lubrication failure and its mitigation process. Mater. Proc. 2021, 44, 3976–3983. [Google Scholar] [CrossRef]
- CNS15176-1: Wind Turbines—Part 1: Design Requirements. Available online: https://www.cnsonline.com.tw/?node=detail&generalno=15176-1&locale=en_US (accessed on 11 May 2024).
- Wang, X.; Yang, C.; Zhang, Z.; Du, Y. DCT-Based Deep Learning of Polarimetric Scattering from a Dielectric Cylinder. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4021905. [Google Scholar] [CrossRef]
- Pang, X.Y.; Tong, Y.; Zhang, B.W.; Wei, J.G. NSP-CNN Rolling Bearing Fault Diagnosis Method. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021. [Google Scholar]
- Zhu, X.; Zhao, J.; Hou, D.; Han, Z. An SDP characteristic information fusion-based CNN vibration fault diagnosis method. Shock Vib. 2019, 2019, 3926963. [Google Scholar] [CrossRef]
- Ahmad, S.; Choudhury, P.K. On the Performance of Deep Transfer Learning Networks for Brain Tumor Detection Using MR Images. IEEE Access 2022, 10, 59099–59114. [Google Scholar] [CrossRef]









| Wind Turbine Measurement Platform Specifications | |
|---|---|
| Induction motor | 1.5 hp |
| Gearbox | 1:12.25 gear ratio |
| Three-axis accelerometer (voltage sensitivity) | 100 ± 5% (mV/g) sensitivity |
| NI-9234 DAQ (Manufactured by National Instruments in the U. S.) | 51.2 kHz, 32-bit resolution, four synchronous channels |
| Gearbox Fault Testing Specifications | |
|---|---|
| Gearbox | Gear ratio 1:12.25 |
| Gearbox fault types in wind turbines | |
| Type A | No-fault |
| Type B | Rust |
| Type C | Chipped |
| Type D | Gear worn |
| Type E | Gear aged |
| Fault Types | Training Pattern | Testing Pattern | Accuracy (%) |
|---|---|---|---|
| Type A | 200 | 186 | 97.7 |
| Type B | 200 | 192 | |
| Type C | 200 | 200 | |
| Type D | 200 | 200 | |
| Type E | 200 | 199 |
| Algorithm | Training Time (s) | Testing Time (s) | Epoch | Accuracy (%) | |
|---|---|---|---|---|---|
| Non-Noise | 5 dB | ||||
| Scatter plot + VGG 19 | 95.2 | 0.0049 | 50 | 99.6 | 97.7 |
| Scatter plot + VGG 19 | 228.4 | 0.0050 | 100 | 97.7 | 96.6 |
| Scatter plot + VGG 19 | 344.0 | 0.0050 | 150 | 97.1 | 95.4 |
| Scatter plot + VGG 16 | 93.2 | 0.0053 | 50 | 98.2 | 96.8 |
| Scatter plot + VGG 16 | 156.5 | 0.0048 | 100 | 97.1 | 95.8 |
| Scatter plot + VGG 16 | 223.5 | 0.0051 | 150 | 97.0 | 93.9 |
| SDP + VGG 16 | 81.3 | 0.0049 | 50 | 92.1 | 85.5 |
| SDP + VGG 19 | 100.1 | 0.0132 | 50 | 91.0 | 84.6 |
| Scatter plot + CNN | 85.1 | 0.0008 | 50 | 93.3 | 88.4 |
| Scatter plot + HOG + SVM | 4.2 | 0.19 | 87.3 | 79.2 | |
| Algorithm | Accuracy (%) | Precision | Recall | F1-Score | Kappa |
|---|---|---|---|---|---|
| Scatter plot + VGG 19 | 97.7 | 0.9947 | 0.930 | 0.9612 | 0.971 |
| Scatter plot + VGG 19 | 96.6 | 0.9946 | 0.920 | 0.9558 | 0.958 |
| Scatter plot + VGG 19 | 95.4 | 0.9891 | 0.910 | 0.9479 | 0.943 |
| Scatter plot + VGG 16 | 96.8 | 0.9946 | 0.915 | 0.9531 | 0.960 |
| Scatter plot + VGG 16 | 95.8 | 0.9943 | 0.870 | 0.9280 | 0.948 |
| Scatter plot + VGG 16 | 93.9 | 0.9836 | 0.900 | 0.9399 | 0.924 |
| SDP + VGG 16 | 85.5 | 0.8458 | 0.850 | 0.8479 | 0.819 |
| SDP + VGG 19 | 84.6 | 0.8458 | 0.850 | 0.8479 | 0.808 |
| Scatter plot + CNN | 88.4 | 0.6491 | 0.925 | 0.7629 | 0.855 |
| Scatter plot + HOG + SVM | 79.2 | 0.5217 | 0.900 | 0.6606 | 0.740 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.-H.; Hung, C.-C.; Lu, S.-D.; Chen, F.-H.; Su, Y.-X.; Kuo, C.-C. Fault Diagnosis of Wind Turbine Gearbox Using Vibration Scatter Plot and Visual Geometric Group Network. Processes 2024, 12, 985. https://doi.org/10.3390/pr12050985
Wang M-H, Hung C-C, Lu S-D, Chen F-H, Su Y-X, Kuo C-C. Fault Diagnosis of Wind Turbine Gearbox Using Vibration Scatter Plot and Visual Geometric Group Network. Processes. 2024; 12(5):985. https://doi.org/10.3390/pr12050985
Chicago/Turabian StyleWang, Meng-Hui, Chun-Chun Hung, Shiue-Der Lu, Fu-Hao Chen, Yu-Xian Su, and Cheng-Chien Kuo. 2024. "Fault Diagnosis of Wind Turbine Gearbox Using Vibration Scatter Plot and Visual Geometric Group Network" Processes 12, no. 5: 985. https://doi.org/10.3390/pr12050985
APA StyleWang, M.-H., Hung, C.-C., Lu, S.-D., Chen, F.-H., Su, Y.-X., & Kuo, C.-C. (2024). Fault Diagnosis of Wind Turbine Gearbox Using Vibration Scatter Plot and Visual Geometric Group Network. Processes, 12(5), 985. https://doi.org/10.3390/pr12050985








