Advancing Decarbonization Efforts in the Glass Manufacturing Industry through Mathematical Optimization and Management Accounting

Abstract

This study explores the integration of activity-based costing (ABC) and the theory of constraints (TOC) with carbon tax policies to drive decarbonization in the Taiwanese glass industry. Employing a mathematical programming approach, four distinct models are developed to assess the impact of different carbon tax structures, carbon trading mechanisms, and recycled material utilization on corporate profitability and carbon emissions. The findings reveal that strategically applying ABC and the TOC with well-designed carbon tax policies can effectively incentivize emission reduction while maintaining industrial competitiveness. The models incorporating carbon trading and tax allowances demonstrate the potential for creating win–win situations, where companies can increase profitability by investing in cleaner technologies and processes. This study contributes to the literature on sustainable manufacturing and provides actionable insights for policymakers and industry leaders seeking to implement effective carbon pricing mechanisms that drive economic growth and environmental sustainability in tandem.

1. Introduction

Research Background

Glass is an incredibly versatile and ubiquitous material in our modern society, despite often being taken for granted [1]. Its unique combination of properties—fragile yet transparent, impermeable, non-toxic, inert, and non-crystalline—make it suitable for a wide range of applications [2]. From smartphone screens and car windows to drinking glasses and even more specialized uses like fiber optic cables, biomedical implants, lasers, and optics, glass is all around us [3,4].

Recently, glass has also emerged as a key enabler of low-carbon technologies like high-capacity batteries, data storage, 3D printing [5], energy-efficient buildings [6], solar panels [7], and wind turbines [8]. This has propelled global glass production to nearly 130 million tons in 2020 [1].

The history of glass spans thousands of years, with the oldest artifacts dating back to 3500 BC [9]. Originating in Egypt, glass production later developed independently in China, Greece, and Northern Tyrol [10]. Major milestones include the invention of the glass blowing pipe in 1st century AD Syria, a return to plant ash-based recipes in the Levant in the 8th–9th century [9,11], large mirrors in 17th-century France [12], the rise of Murano, Swarovski, and Waterford as glass art centers, the regenerative furnace enabling mass production in the 19th century [13], automatic bottle manufacturing in the 1920s [12], and the revolutionary float glass process invented by Pilkington in 1952 [14]. Modern float glass lines can produce up to 1000 ton per day [12].

The advantages provided by glass are overshadowed by its environmental impacts, as increasing carbon emissions contribute to global climate change and the greenhouse effect. This urgency is underscored by disasters like European floods and Spanish wildfires, prompting nations to aim for “net zero by 2050” goals. Aligning with these objectives, Taiwan saw 27 companies, including notable ones like Sinosteel and Chunghwa Telecom, form the “Taiwan Net Zero Action Alliance” in 2021 with the ambition of achieving zero emissions at office locations by 2030 and at production sites by 2050. Following suit, the Taiwanese government introduced “Taiwan’s 2050 Net Zero Emissions Pathway and Strategy” in 2022, detailing necessary shifts across energy, industry, lifestyle, and societal domains to meet this target.

To facilitate reaching these net zero ambitions, mechanisms such as carbon fees, taxes, trading, and carbon footprinting are being implemented. Notably, in early 2023, Taiwan’s Legislative Yuan enacted the “Climate Change Response Act”, making the 2050 net zero target a legal obligation and establishing a carbon fee from 2024 on entities emitting more than 25,000 tons of carbon annually, along with setting up a carbon trading system.

This research delves into the glass industry’s adaptation to a green economy, exploring the integration of carbon taxation, trading, recycling, and the comprehensive accounting of emissions and operational costs. The objective is to develop carbon tax formulas and trading frameworks tailored for the glass manufacturing process, incorporating the recycling of raw materials. Through simulation, this study aims to identify production strategies that optimize profit across various product lines, cost structures, and output levels. It also assesses the effects of different carbon policy implementations and recycling initiatives on emission reduction and financial performance, employing activity-based costing for precise cost estimation and the theory of constraints for bottleneck management.

The findings are expected to guide companies in understanding the financial implications of impending carbon taxes and trading systems, thus informing both corporate strategies and governmental policies towards the “net zero by 2050” goal. Emphasizing recycling and other circular economy practices not only aids firms and consumers but also contributes to long-term environmental sustainability. Achieving net zero is a collective global endeavor requiring coordinated efforts from individuals, governments, and industries to regulate and oversee supply and production chains.

The rest of the paper is structured as follows: Section 2 reviews glass industry emissions, circular economy development, carbon tax and trading systems, and applications of green ABC and the TOC. Section 3 describes the production process and planning models for eight carbon emission functions under single- and multi-phase scenarios. Section 4 presents enterprise sample data (model parameters from Section 3), compares simple models, and analyzes the integrated results. Section 5 provides a brief discussion and conclusion.

2. Background and Literature

2.1. Background

To meet the ambitious targets of the Paris Climate Convention (2015), which aims to limit the global average temperature rise to below 1.5 °C above pre-industrial levels, comprehensive decarbonization efforts need to extend beyond the energy sector, encompassing transportation, residential, and industrial sectors [15,16,17]. Among these, energy-intensive industries (EIIs) represent a significant challenge due to their capital-intensive nature, high cost-competitiveness, and sensitivity to product quality, which are compounded by their substantial energy consumption per unit of output [18,19,20]. Specific industries such as aluminum [21,22], steel [23], cement [21,22], and glass [24,25] are highlighted for their energy intensiveness.

The glass industry, in particular, requires significant energy primarily for the high-temperature melting of raw materials, presenting a microcosm of the broader challenges faced by EIIs [26]. The industry’s diversity, with sub-sectors such as container glass, flat glass, special glass, and glass fibers, each with different energy needs and quality standards, underscores the complexity of implementing effective decarbonization strategies. This sector’s substantial CO₂ emissions, with container and flat glass production accounting for a significant share of global output and emissions [27,28,29], highlight the urgent need for targeted mitigation strategies.

Research efforts aimed at both quantifying and mitigating the glass industry’s carbon footprint have led to insightful findings. Schmitz et al. [30] analyzed energy consumption and CO₂ emissions across the EU ETS countries, identifying container and flat glass as major emitters, with natural gas as the predominant fuel source. In contrast, Hu et al. [31] examined the CO₂ emissions from China’s container glass industry, noting significant differences in emission intensity due to variations in fuel mix and recycling rates compared to Europe. Additionally, efforts to forecast and reduce energy demand through energy efficiency measures (EEMs) have been documented, with Frassine et al. [32] predicting a decrease in energy demand for European glass furnaces by 2030, despite an increase in glass demand.

The comprehensive discussion on emissions and EEMs within the glass industry, including the evaluation of technical options and the Best Available Techniques (BATs) for emission reduction, is provided by Delgado Sancho et al. [25]. Further assessments by Springer and Hasanbeigi [27] and Worrell et al. [33] on technologies for improving energy efficiency in glass production estimate potential savings and highlight the multifaceted approach required for effective decarbonization. Finally, Papadogeorgos and Schure [34] outline various decarbonization options for the Dutch glass industry, emphasizing strategies like fuel and feedstock substitution and carbon capture, storage, and utilization (CCS/CCU).

2.2. Activity-Based Costing and Theory of Constraints

Cooper and Kaplan [35] introduced activity-based costing (ABC), a method that allocates costs to objects in two stages, widely applied in industries like aviation and manufacturing, as shown by research [36,37,38]. ABC’s applications extend to environmental management and project management, highlighting its utility in providing detailed cost information for environmental initiatives [39,40]. The United Nations Division for Sustainable Development views environmental costs as those related to protecting the environment, including efforts to manage carbon emissions [41]. ABC helps managers make sustainable decisions by offering accurate environmental cost data, aiding in pricing and outsourcing decisions [42].

Goldratt and Cox’s [43] theory of constraints (TOC), introduced in 1984 [44], emphasizes managing limited resources through a five-step model aimed at improving system throughput. This methodology is especially relevant in manufacturing, where it addresses production bottlenecks to enhance output [45]. Carbon emissions, categorized into direct, indirect, and those from broader production activities, are considered significant constraints in production systems.

ABC, primarily a long-term analysis tool, assumes variable costs for most production resources, not directly addressing system constraints like the TOC, which is more short-term-oriented [46]. The Green Activity-Based Management approach merges ABC, the TOC, and the Critical Path Method (CPM) to measure and report carbon emissions effectively, illustrating the impact of exceeding emission limits or extending working hours on costs [46].

Integrating ABC and the TOC with environmental considerations, this paper proposes a mathematical programming model for green product portfolio decision-making, incorporating carbon emission costs. This integration allows for optimizing product mixes and maximizing profitability by leveraging limited resources and accurate cost data from ABC [47].

This research seeks to fill the literature gap on the use of advanced costing methods, like ABC and the TOC, combined with carbon reduction strategies in the glass industry. It aims to enhance cost allocation precision and optimize production for environmental sustainability, offering insights into aligning industry practices with the global decarbonization agenda [48,49,50,51,52,53,54,55]. This approach underscores the potential synergies between ABC, the TOC, and carbon reduction practices, marking a significant advancement in sustainable industrial practices within the glass sector.

2.3. Emission Reduction-Contributing Industries

In the steel manufacturing industry, a framework for carbon reduction targeting energy-intensive industries has been proposed. By integrating digitalization and high-efficiency energy-saving equipment, carbon emissions in steel manufacturing can be significantly reduced. Although the initial costs are high, combining digital tools and energy-saving equipment is effective in the long term [56]. Secondly, in the power sector, a study in Fangshan District, Beijing, proposed a low-carbon demand response mechanism using dynamic carbon accounting technology and electricity planning data. This mechanism, which sends carbon reduction signals from the user side, helps the power sector realize its carbon reduction potential. The study showed that a low-carbon demand response can effectively reduce corporate carbon emissions, with enterprise capacity and industry attributes significantly impacting the reduction effect [57]. Additionally, in the field of enhanced oil recovery, carbon capture, utilization, and storage (CCUS) technology is considered an important means of reducing CO₂ emissions. A study on large-scale CO₂ enhanced oil recovery projects globally indicated that these projects have potential in reducing carbon emissions, though the lack of standardized methodologies makes estimating their lifecycle emissions challenging [58]. In Asia, an analysis of carbon emissions data from 38 countries between 1991 and 2018 identified policies and carbon trading systems as factors influencing the cost of carbon reduction. The results showed that optimizing the energy structure and implementing policies significantly impacted carbon emission reductions [56]. Research explored the impact of policy support and corporate behavior on carbon reduction for Chinese listed companies, indicating that these factors are crucial for effectively alleviating environmental pressure [57]. The study found that in 2050, Brazilian steel production is expected to emit 64 million tons of carbon dioxide (MtCO₂). If steel recycling reaches 36% of total production, carbon emissions can be reduced by 20%. Converting 86% of the remaining blast furnace production to charcoal could achieve a total emission reduction of 65%. Although the abatement cost of charcoal is higher and the uncertainty of recycling is greater, the abatement potential of charcoal production is relatively stable. The study also highlights that economic policies and regulations need to be strengthened to cope with the additional cost of charcoal, ensure sustainable charcoal production, and improve logistics and scrap market differentiation [59]. Additionally, the study found that changes in carbon emissions in Portugal between 1960 and 2016 were mainly influenced by fossil fuel dependence and the efficiency and structure of the energy system. Electrification promotes decarbonization if terminal electrification, renewable resources, and natural gas each account for more than one-third of the energy mix [60]. In summary, various industries have made significant contributions to carbon reduction. However, the glass industry has not been explored in depth. This study will focus on the glass industry in Taiwan, elaborating on the model construction process in the next section.

3. Materials and Methods

This study used LINGO 18, a powerful software tool for solving both linear and nonlinear optimization problems. The methodology applied in our analysis involves calculating profitability by subtracting the total operational and production costs from generated revenues and then accounting for carbon tax implications as a final adjustment. This approach allows us to assess the net profit under different regulatory and market conditions.

By employing LINGO 18, we defined our objective function explicitly to maximize profit, factoring in these costs and revenues. For reproducibility, researchers should set up their LINGO model to calculate the revenue from the sale of glass products, subtract the associated costs of materials, labor, and operations, and finally include the carbon tax costs as specified by the scenarios tested in our study.

Firstly, we identify the glass furnace, a critical process, as the ‘bottleneck resource’ limiting production capacity and focus our analysis around it, reflecting the basic TOC concept of focusing on constraints. Secondly, only variable costs are considered in the objective function, treating fixed costs as ‘sunk costs’, which aligns with the TOC’s ‘throughput accounting’ philosophy. Moreover, in setting resource constraints, we follow the TOC logic of ‘time compression’, optimizing production batches and minimizing work-in-progress to maximize the efficiency of bottleneck resource utilization. Although the model does not directly reflect the complete steps of the ‘Five Focusing Steps’, the underlying constraint theory significantly influences problem formulation and solution.

3.1. Glass Industry Production Process

Glassware has a storied past, with its earliest use by humans traced back to around 2000 BC. As civilizations evolved, so did the techniques for crafting glass, leading to the sophisticated manufacturing processes we see today. Illustrated in Figure 1, the production of modern glass involves five key stages: batching, melting, forming, annealing, and finishing. Initially, the composition of raw materials is determined based on the specific glass items to be produced. These materials are then thoroughly mixed in a batch mixer. Following this, the blend is transferred to a melting furnace where it is liquefied. After melting, the molten glass is moved to an annealing furnace where it is slowly cooled to relieve internal stresses. The final stage involves various treatments such as cleaning and polishing to achieve the desired shape and quality of the glass product.

3.2. Research Hypothesis

This study’s primary considerations for selecting three time periods are as follows: First, given the production characteristics and equipment renewal cycles of the glass industry, three years (2019–2021) is typically a suitable timescale for medium- to long-term planning; second, considering the phased implementation of carbon tax policies and the gradual increase in carbon prices, three years also represents a typical policy adjustment period; third, in terms of data availability, a three-year span makes it easier to collect relevant information on production, sales volume, prices, and costs. Of course, our model is not limited to three periods and can be adjusted flexibly according to actual needs. Additionally, we will clarify the positioning of the first period in the model as a baseline scenario and reference point for the multi-period model to help understand the impacts and changes across different periods. We believe that these additions will enable readers to clearly understand our considerations in the selection of time periods. Companies aim to achieve the highest possible profits. Spanning from t = 1 to t = 3, this denotes a model that covers three time periods. There are four categories of products indexed as i = 1 to i = 4, where flat glass is designated as product 1 (i = 1), reflective glass as product 2 (i = 2), lacquered glass as product 3 (i = 3), and tempered glass as product 4 (i = 4). Each product, numbered from 1 to 4, has its own selling price per unit. The quantity produced for each product is also numbered from 1 to 4. Seven different materials are used as inputs, labeled j = 1 to j = 7, where silicon dioxide is j = 1, sodium carbonate is j = 2, lime is j = 3, petroleum coke is j = 4, metal film is j = 5, paint is j = 6, and recycled waste glass is j = 7. The proportion of recycled waste glass in the total raw material mix is also considered. The cost per unit for each type of material is also labeled (j = 1 to j = 7). Glass manufacturing involves batching, where raw materials (silica sand, soda ash, limestone, additives) are mixed in precise proportions. The batch is then fed into a furnace at high temperatures (up to 1700 °C/3090 °F) for melting, creating a homogeneous liquid. Next, the molten glass is formed into the desired shape using techniques like blowing, pressing, drawing, or rolling. After forming, the glass undergoes annealing, where it is slowly cooled to relieve internal stresses and prevent cracking. Finally, the glass is inspected for imperfections and finished according to specifications, which may include cutting, polishing, and further shaping.

The amount of each material type j needed to manufacture one unit of product i is considered, for i ranging from 1 to 4 and j from 1 to 7. For labor costs, there are standard hours (HR1), the cost for the first level of overtime (HR2), and the cost for the second level of overtime (HR3), with the constraint that only up to two of these costs can be non-zero.

The cost associated with performing a single unit of job type o (o = 5 or 6).

The amount of product needed for material handling jobs (o = 5).

The total volume processed in a single batch for material handling jobs (o = 5).

The required quantity of product type i for setup jobs (o = 6).

The batch size for product type i in setup jobs (o = 6).

Includes all other costs that are constant.

The ratio of recycled waste glass from the last production cycle to the total mass of all products produced in the preceding period.

3.3. Basic Production Model

3.3.1. General Formula of Objective Function

This part of the paper outlines the goal function and the constraints used in the production process: The firm aims to maximize its profit (π), which is calculated as the revenue from sales of glass products minus the expenses incurred, including the cost of raw materials, wages for direct labor, expenses for handling operations, costs associated with setting up, charges related to carbon emissions, and any other fixed expenses. The single-period model is used to quickly assess the impact of policy changes, while the multi-period model is suitable for long-term strategic analysis to evaluate the impact of decisions over a large time span. The single-period model, also known as the static model or the current-period model, is mainly used to portray the optimal decision-making of glass enterprises within a single production cycle. In this model, we consider the main economic parameters, such as the sales revenue, raw material cost, labor cost, equipment depreciation, and energy consumption of glass products, and introduce environmental parameters such as the carbon emission coefficient and carbon tax rate to establish a linear programming model with the goal of maximizing profit. By solving the model, we can determine the optimal product mix for glass enterprises under given production conditions and carbon tax levels. The advantage of this model is that it can meticulously depict the input–output relationship of glass production and incorporate the impact of carbon tax, thereby providing a quantitative basis for the company’s current production decisions. However, this model also has certain limitations; that is, it fails to reflect the dynamic adjustment process of production decisions and does not consider the cross-period constraints of enterprises in terms of production capacity and capital budget.

To make up for the deficiencies of static analysis, we further developed a multi-period model, also known as a dynamic model. Compared with the single-period model, the time span of the multi-period model is longer, usually covering 3–5 production cycles. In this model, we not only consider the production and operation decisions of each period but also portray the association and constraints between different decision-making periods in terms of capacity planning and capital budgeting. At the same time, we also introduce dynamic factors such as technological updates and learning effects to reflect the gradual improvement in corporate production efficiency. Moreover, in the objective function, we replace the maximization of current-period profit with the maximization of the cumulative value of cross-period profit, so as to reflect the behavioral orientation of enterprises pursuing long-term benefits. Through multi-period optimization, we can obtain a dynamic optimal decision-making path, that is, in different periods, what product mix, production scale, and technology level the enterprise should choose in order to obtain the maximum long-term revenue while meeting the carbon tax constraints. The advantage of this model is that it can capture the dynamic change characteristics of corporate production and operation and provide forward-looking decision-making solutions. However, this model also has higher requirements for data and needs to make reasonable predictions on the changing trends of product demand, price, cost, and other parameters.

The single-period model is used to quickly assess the impact of policy changes, while the multi-period model is suitable for long-term strategic analysis to evaluate the impact of decisions over a large time span.

Single period general formula:

$$\pi ={\displaystyle \sum }_{i=1}^4{S}_i{P}_i-Re{\displaystyle \sum }_{i=1}^4\{[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_i\}$$

$$\left(1-Re\right){\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_i-\left[H{R}_1+{\epsilon }_1\left(H{R}_2-H{R}_1\right)+{\epsilon }_2\left(H{R}_3-H{R}_1\right)\right]$$

$$-C_o{Q}_o{B}_o-{\displaystyle \sum }_{i=1}^4{C}_o{d}_{io}{B}_{io}-Carbon tax-$$

Multiple periods general formula

$$\pi ={\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4{S}_i{P}_{it}-{\displaystyle \sum }_{t=1}^3\left(R{e}_t\left\{{\displaystyle \sum }_{i=1}^4[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_{it}\right\}\right)$$

$$-{\displaystyle \sum }_{t=1}^3[\left(1-R{e}_t\right){\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_{it}]+MRe{\displaystyle \sum }_{t=2}^3{\displaystyle \sum }_{i=1}^4{P}_{it}M{C}_7-{\displaystyle \sum }_{t=1}^3$$

$$\left[H{R}_1+{\epsilon }_{1t}\left(H{R}_2-H{R}_1\right)+{\epsilon }_{2t}\left(H{R}_3-H{R}_1\right)\right]-{\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4(C_o{d}_{io}{B}_{iot}+C_o{Q}_o{B}_{ot})-{\displaystyle \sum }_{t=1}^3\left(Carbon tax\right)$$

$$-{\displaystyle \sum }_{t=1}^3+F$$

Symbol Description:

π	Profit Maximization by Companies: Businesses aim to achieve the highest possible profits.
t	The Definition of the Timeframe in the Model: The multi-period model is identified with labels t = 1 to 3, indicating a span of three time periods.
i	The Classification of Products: Within the product categories numbered 1 through 4, we have the following: for category 1 (i = 1), the product is flat glass; for category 2 (i = 2), the product is reflective glass; for category 3 (i = 3), the product is lacquered glass; and for category 4 (i = 4), the product is tempered glass.
Si	The Sale Price per Unit for Each Product: For products numbered 1 through 4, we have a distinct selling price per unit.
Pi	The Volume of Production for Each Product: The amount of each product (numbered 1 to 4) that is produced.
j	Types of Raw Materials Used: We categorize raw materials into seven types, labeled 1 through 7, with each type representing a different material such as silicon dioxide, sodium carbonate, lime, petroleum coke, metal film, paint, and waste glass.
Re	Waste Glass Usage Ratio: The fraction of waste glass in comparison to the total raw materials used.
MCj	The Cost per Unit of Raw Materials: For each of the seven types of raw materials (numbered 1 to 7), there is a specific cost associated.
qij	Raw Material Consumption per Product Unit: This details how much of each raw material (1 through 7) is required to produce one unit of each product (1 through 4).
HR1, HR2, HR3	Direct and Overtime Labor Costs: There are three categories of labor costs: regular hours (HR1), first level of overtime (HR2), and second level of overtime (HR3), with a constraint that at most two of these can be non-zero for any given situation.
ε0, ε1, ε2	Non-negative Variable Constraints: All variables in the set should be greater than or equal to zero, with the stipulation that no more than two of these variables can have values above zero at any given time.
Co	Cost for Each Job Operation: The expense incurred for executing one unit of a specific operation, designated as operations 5 and 6.
Qo	Required Quantity for Material Handling: This refers to the amount needed for operation 5, which deals with handling materials.
Bo	Material Handling Batch Size: The number of units processed in a single batch for material handling operation 5.
dio	Product Demand for Setup Operations: The quantity of each product (i) needed for the setup operation labeled as number 6.
Bio	Setup Operation Batch Size: The total number of units of product i that are prepared in one batch for setup operation 6.
F	Fixed Overhead Costs: Expenses that remain constant regardless of the volume of production.
MRe	The Ratio of Recycled Waste Glass: This describes the share of waste glass from the last production cycle relative to the total mass of products produced in the same period.
UMQj	The upper limit of the available quantity of raw material j.
uio	Labor Hours per Product Unit: The amount of labor time required to manufacture one unit of product i during operation o.
CHR1, CHR2, CHR3	The Allocation of Labor Hours: Typically, there are caps on labor hours categorized as the maximum regular labor hours (CHR1), hours for the first overtime phase (CHR2), and hours for the second overtime phase (CHR3).
${\alpha }_1$, ${\alpha }_2$	Binary Variable Constraints: For a set of binary variables (0 or 1), if one variable is assigned the value 1, the remaining must be set to 0 to ensure exclusivity.
${\eta }_o$	The quantity for each batch size in terms of tons during material handling operations is set at 5.
$P{C}_o$	The maximum energy allocation for these material handling operations is also established at 5.
mhio	The machine hours required to produce a unit of product i under o operation.
LMPo	The maximum capacity of machines under job o (o = 1,2,3,4).
UNTQ1, UNTQ2	The maximum carbon emissions for the first (CTFQ1) and second (CTFQ2) scenarios.
$m_1$, $m_2$, $m_3$	Dummy variable (0,1); only one of the three can be 1.
$k{r}_1$,$k{r}_2$,$k{r}_3$	The first carbon tax rate ($kr$1), the second carbon tax rate ($kr$2), and the third carbon tax rate ($kr$3).
${\lambda }_0,{\lambda }_1,{\lambda }_2,{\lambda }_3$	Dummy variable (0,1); only one of the four can be 1.
$F{Q}_0$	Tax-free carbon emissions.
$FNT{Q}_1$,$FNT{Q}_2$,$FNT{Q}_3$	The amount of carbon emissions falling in the first segment ($FNT{Q}_1$), the amount of carbon emissions falling in the second segment ($FNT{Q}_2$), and the amount of carbon emissions falling in the third segment ($FNT{Q}_3$).
$F{Q}_0$, $F{Q}_1$, $F{Q}_2$	Tax-free carbon emissions ($F{Q}_0$) and the maximum carbon emissions in the first stage ($F{Q}_1$) and the second stage ($F{Q}_2$). Exempt carbon emissions ($F{Q}_0$) and the upper limit of carbon emissions for the initial stage ($F{Q}_1$) and for the subsequent stage ($F{Q}_2$).

3.3.2. Direct Material Cost Function

This study posits that the manufacturing of glass predominantly relies on seven key materials. The foundational components include silicon dioxide (identified as j = 1), sodium carbonate (j = 2), and lime (j = 3). For fuel, petroleum coke (j = 4) is utilized, with its quantity varying based on the specific product requirements. Materials such as a metal film (j = 5) and paint (j = 6) are essential for the production of reflective glass (i = 2) and painted glass (i = 3), respectively. Additionally, waste glass (j = 7) serves as a recyclable material that can substitute a portion of the primary raw materials.

One-period direct material cost function:

$$Re{\displaystyle \sum }_{i=1}^4\{[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_i\}+$$

$$\left(1-Re\right){{\displaystyle \sum }}_{i=1}^4\left({{\displaystyle \sum }}_{j=1}^{6}M{C}_j{q}_{ij}\right)P_i$$

Related constraints:

$${\displaystyle \sum }_{i=1}^4{P}_i{q}_{ij} \leqq UM{Q}_j \left(j=1,2,\dots ,6\right)$$

(1)

Multi-period direct material cost function:

$$\begin{gathered} {\displaystyle \sum }_{t=1}^3(R{e}_t\left\{{\displaystyle \sum }_{i=1}^4[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_{it}\right\})+{\displaystyle \sum }_{t=1}^3[\left(1-R{e}_t\right){\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_{it}] \\ -MRe{\displaystyle \sum }_{t=2}^3{\displaystyle \sum }_{i=1}^4{P}_{it}M{C}_7 \end{gathered}$$

Related constraints:

$${\displaystyle \sum }_{i=1}^4{P}_{it}{q}_{ij}\leqq UM{Q}_j \left(j=1\dots 6,t=1,2,3\right)$$

(2)

Symbol Description:

UMQj	The upper limit of the available quantity of raw material j.
$(q_{i4}-0.06$)	The 0.06 adjustment effectively represents the losses or inefficiencies in the use of this material during the production process.

3.3.3. Direct Labor Cost Function

In the process of producing glass, wages for direct labor encompass both regular hours and overtime, divided into two tiers. The workforce is primarily engaged in monitoring the production flow and managing the machinery. Typically, labor expenses are constant, as salaries are owed to workers irrespective of the production needs. Overtime is incurred for expedited orders or when the existing workforce is insufficient to manage a surge in orders within a brief timeframe. During such instances, the escalation in work hours sequentially triggers the costs associated with the first and then the second tier of overtime. Illustrated in Figure 2, the function representing labor costs is a piecewise continuous function, activating different overtime pay rates in a stepwise manner as work hours extend beyond the standard schedule.

Single-period direct labor cost function:

$$H{R}_1+{\epsilon }_1\left(H{R}_2-H{R}_1\right)+{\epsilon }_2\left(H{R}_3-H{R}_1\right)$$

Related constraints:

$${\displaystyle \sum }_{i=1}^4{\displaystyle \sum }_{o=1}^6{u}_{io}{P}_i\le CH{R}_1+{\epsilon }_1\left(CH{R}_2-CH{R}_1\right)+{\epsilon }_2\left(CH{R}_3-CH{R}_1\right)$$

(3)

$${\epsilon }_0-{\alpha }_1\le 0$$

(4)

$${\epsilon }_1-{\alpha }_1-{\alpha }_2\le 0$$

(5)

$${\epsilon }_2-{\alpha }_2\le 0$$

(6)

$${\epsilon }_0+{\epsilon }_1+{\epsilon }_2=1$$

(7)

$${\alpha }_1+{\alpha }_2=1$$

(8)

$${\displaystyle \sum }_{t=1}^3\left[H{R}_1+{\epsilon }_{1t}\left(H{R}_2-H{R}_1\right)+{\epsilon }_{2t}\left(H{R}_3-H{R}_1\right)\right]$$

Related constraints:

$${\displaystyle \sum }_{i=1}^4{\displaystyle \sum }_{o=1}^6{u}_{io}{P}_{it}\le CH{R}_1+{\epsilon }_{1t}\left(CH{R}_2-CH{R}_1\right)+{\epsilon }_{2t}\left(CH{R}_3-CH{R}_1\right) \mathrm{t} =1,2,3$$

(9)

$${\epsilon }_{0t}-{\alpha }_{1t}\le 0 \mathrm{t} =1,2,3$$

(10)

$${\epsilon }_{1t}-{\alpha }_{1t}-{\alpha }_{2t}\le 0 \mathrm{t} =1,2,3$$

(11)

$${\epsilon }_{2t}-{\alpha }_{2t}\le 0 \mathrm{t} =1,2,3$$

(12)

$${\epsilon }_{0t}+{\epsilon }_{1t}+{\epsilon }_{2t}=1 \mathrm{t} =1,2,3$$

(13)

$${\alpha }_{1t}+{\alpha }_{2t}=1 \mathrm{t} =1,2,3$$

(14)

Symbol Description:

uio	Labor Hours per Product Unit: The amount of labor time required to manufacture one unit of product i during operation o.
CHR1, CHR2, CHR3	The Allocation of Labor Hours: Typically, there are caps on labor hours categorized as the maximum regular labor hours (CHR1), hours for the first overtime phase (CHR2), and hours for the second overtime phase (CHR3).
${\alpha }_1$, ${\alpha }_2$	Binary Variable Constraints: For a set of binary variables (0 or 1), if one variable is assigned the value 1, the remaining must be set to 0 to ensure exclusivity.

The number of hours worked by employees and the corresponding expenses are determined by a set of indicator variables ${\alpha }_1$ and ${\alpha }_2$; for example, if ${\alpha }_1$ is 1, then ${\alpha }_2$ = 0 must Given the conditions outlined in Constraints (3) to (8), it is established that ${\epsilon }_0$ and ${\epsilon }_1$ both lie within the range (0, 1), and their combined total equals 1. Under these circumstances, the total labor hours allocated by the company are $CH{R}_1+{\epsilon }_1\left(CH{R}_2-CH{R}_1\right)$, which will fall in the second paragraph in Figure 2 (paragraph The total labor cost is $H{R}_1+{\epsilon }_1\left(H{R}_2-H{R}_1\right)$).

3.3.4. Material Handling Costs

This research posits that operations for handling materials take place exclusively during the transition from storage to the production area, ensuring that all raw materials for glass are moved to the machinery area for manufacturing activities.

One-period material handling cost function:

$$C_o{Q}_o{B}_o$$

Related constraints:

$${\displaystyle \sum }_{j=1}^6{q}_{ij}{P}_i\le {\eta }_o{B}_o \left(i=1\dots 4,o=5\right)$$

(15)

$$Q_o{B}_o\le P{C}_o \left(o=5\right)$$

(16)

Multi-period material handling cost function:

$${\displaystyle \sum }_{t=1}^3{C}_o{Q}_o{B}_{ot}$$

Related constraints:

$${\displaystyle \sum }_{j=1}^6{q}_{ij}{P}_{it}\le {\eta }_o{B}_{ot} \left(i=1\dots 4,o=5\right) \mathrm{t} =1,2,3$$

(17)

$$Q_o{B}_{ot}\le P{C}_o \left(o=5\right) \mathrm{t} =1,2,3$$

(18)

Symbol Description:

${\eta }_o$	The quantity for each batch size in terms of tons during material handling operations is set at 5.
$P{C}_o$	The maximum energy allocation for these material handling operations is also established at 5.

3.3.5. Batch Level Job—Set Job Cost Function

This research presumes that the adjustment activities will be carried out in processes numbered o = 1 to 4. For instance, during the batching process, the machine’s parameters are adjusted to set the mixture ratio, thereby controlling the quality of the glass. Similarly, in the process designated as o = 3, which involves the treatment of lacquered glass, the color of the lacquer is controlled through specific adjustments to the machinery settings.

Single-period setting activity cost function:

$${\displaystyle \sum }_{i=1}^4{C}_o{d}_{io}{B}_{io}$$

Related constraints:

$$P_i\le {\Gamma }_{io}{B}_{io} \left(i=1\dots 4, o=6\right)$$

(19)

$${\displaystyle \sum }_{i=1}^4{d}_{io}{B}_{io}\le P{C}_o\left(o=6\right)$$

(20)

Multi-period setting activity cost function:

$${\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4{C}_o{d}_{io}{B}_{iot}$$

Related constraints:

$$P_{it}\le {\Gamma }_{io}{B}_{iot} \left(i=1\dots 4, o=6\right) \mathrm{t} =1,2,3$$

(21)

$${\displaystyle \sum }_{i=1}^4{d}_{io}{B}_{iot}\le P{C}_o\left(o=6\right) \mathrm{t} =1,2,3$$

(22)

Symbol Description:

$P{C}_o$	Capacity for batch design operations (o = 6).
${\Gamma }_{io}$	The batch-level workload of each batch of product i produced under the setting operation, that is, the number of glass products to be applied in one setting (o = 6).

3.3.6. Machine Hour Limit

In the manufacturing process of glass, a significant portion of the requirements are fulfilled by machinery and equipment. Throughout the stages of mixing ingredients, melting, shaping, further processing, and finally during the coating and printing of specialized products, the use of machinery and equipment is essential. There exists a maximum output capacity for these machines, meaning there is a cap on how much can be produced, which in turn can indirectly influence profits. Here is the formula related to the limitations on machine hours for a single period:

$${\displaystyle \sum }_{i=1}^{4}m{h}_{io}{P}_i\le LM{P}_o \left(o=1,2,3,4\right)$$

(23)

Multi-period:

$${\displaystyle \sum }_{i=1}^{4}m{h}_{io}{P}_{it}\le LM{P}_o \left(o=1,2,3,4\right) \mathrm{t} =1,2,3$$

(24)

Symbol Description:

mhio	The machine hours required to produce a unit of product i under o operation.
LMPo	The maximum capacity of machines under job o (o = 1,2,3,4).

3.4. Carbon Tax Cost Function

This paper develops four distinct models considering the variables of being continuous or discontinuous, incorporating or excluding tax benefits, and including or excluding carbon trading options. Additionally, it differentiates between single-period and multi-period models, designating three periods for the latter. In this research, the single-period model specifies that waste glass (j = 7) constitutes 30% of all raw materials used. In the multi-period scenario, the proportion of waste glass utilized increases progressively over time: starting at 30% in the first period, then escalating to 50% in the second, and reaching 70% in the final period. This incremental approach aims to enhance the recycling of waste glass as a substitute for raw materials, thereby contributing to carbon reduction objectives. Such a strategy is anticipated to lower costs and boost profits. Regarding carbon credits, this study applies a simple linear model for carbon pricing, indicating a uniform rate for either purchasing or selling carbon credits.

3.4.1. Discontinuous Carbon Tax Cost Function

Single-period objective function:

$$\pi ={\displaystyle \sum }_{i=1}^4{S}_i{P}_i-Re{\displaystyle \sum }_{i=1}^4\{[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_i\}-\left(1-Re\right)$$

$${\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_i-\left[H{R}_1+{\epsilon }_1\left(H{R}_2-H{R}_1\right)+{\epsilon }_2\left(H{R}_3-H{R}_1\right)\right]-C_o{Q}_o{B}_o-$$

$${\displaystyle \sum }_{i=1}^4{C}_o{d}_{io}{B}_{io}-(k_{1}NT{Q}_1+k_{2}NT{Q}_2+k_{3}NT{Q}_3)-F$$

Multi-period objective function:

$$\pi ={\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4{S}_i{P}_{it}-{\displaystyle \sum }_{t=1}^3(R{e}_t\left\{{\displaystyle \sum }_{i=1}^4[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_{it}\right\})-{\displaystyle \sum }_{t=1}^3[\left(1-R{e}_t\right)$$

$${\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_{it}]+MRe{\displaystyle \sum }_{t=2}^3{\displaystyle \sum }_{i=1}^4{P}_{it}M{C}_7-{\displaystyle \sum }_{t=1}^3\left[H{R}_1+{\epsilon }_{1t}\left(H{R}_2-H{R}_1\right)+{\epsilon }_{2t}\left(H{R}_3-H{R}_1\right)\right]$$

$$-{\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4(C_o{d}_{io}{B}_{iot}+C_o{Q}_o{B}_{ot})-{\displaystyle \sum }_{t=1}^3(k_{1}NT{Q}_{1t}+k_{2}NT{Q}_{2t}+k_{3}NT{Q}_{3t})-{\displaystyle \sum }_{t=1}^3+F$$

Symbol Description:

$k_1$,$k_2$,$k_3$	The first carbon tax rate (($k$1), the second carbon tax rate ($k$2), and the third carbon tax rate ($k$3).
$NT{Q}_1$,$NT{Q}_2$,$NT{Q}_3$	The amount of carbon emissions falling in the first segment ($NT{Q}_1$), the amount of carbon emissions falling in the second segment ($NT{Q}_2$), and the amount of carbon emissions falling in the third segment ($NT{Q}_3$).

The discontinuous (full progressive tax rate) carbon tax cost function, as shown in Figure 3 and Functions (25) and (26), uses three discontinuous tax rates, which means that when the upper limit of each segment is exceeded, all carbon emissions will be taxed at the new rate. In Figure 3, the segments are clearly delineated, demonstrating the points at which the tax rates change., UNTQ₁ the initial tax rate, represented by k_1, applies when the total carbon emissions fall within the range of 0 to UNTQ1. This range defines the first stage of taxation. The second stage introduces a higher tax rate and takes effect when emissions exceed UNTQ1 but do not surpass UNTQ2, with UNTQ2 marking the upper boundary of this stage, then $k_1$ is used as the tax rate. $k_2$ is used as the tax rate; when the total carbon emission is greater than UNTQ₂, $k_3$ is used as the tax rate. The following are all constraints related to the cost of these carbon single-period functions:

$$f_3\left(TCTQ\right)=\{k_{1}TCTQ, 0\le TCTQ\le UNT{Q}_1 k_{2}TCTQ, UNT{Q}_1<TCTQ\le UNT{Q}_2 k_{3}TCTQ, TCTQ>UNT{Q}_2$$

(25)

Multi-period functions:

$$f_3\left(TCT{Q}_t\right)=\{k_{1}TCT{Q}_t, 0\le TCT{Q}_t\le UNT{Q}_1 k_{2}TCT{Q}_t, UNT{Q}_1<TCT{Q}_t\le UNT{Q}_2 k_{3}TCT{Q}_t, TCT{Q}_t>UNT{Q}_2$$

(26)

Single-period

$${\displaystyle \sum }_{i=1}^{n}CT{e}_i{P}_i=NT{Q}_1+NT{Q}_2+NT{Q}_3$$

(27)

$$0\le NT{Q}_1\le m_{1}UNT{Q}_1$$

(28)

$$m_{2}UNT{Q}_1<NT{Q}_2 \le m_{2}UNT{Q}_2$$

(29)

$$m_{3}UNT{Q}_2<NT{Q}_3$$

(30)

$$m_1+m_2+m_3=1$$

(31)

Multi-period

$${\displaystyle \sum }_{i=1}^{n}CT{e}_i{P}_i=NT{Q}_1+NT{Q}_2+NT{Q}_3, \mathrm{t} =1,2,3$$

(32)

$$0\le NT{Q}_{1t}\le m_{1t}UNT{Q}_1, \mathrm{t} =1,2,3$$

(33)

$$m_{2t}UNT{Q}_1<NT{Q}_{2t} \le m_{2t}UNT{Q}_2, \mathrm{t} =1,2,3$$

(34)

$$m_{3t}UNT{Q}_2<NT{Q}_{3t}, \mathrm{t} =1,2,3$$

(35)

$$m_{1t}+m_{2t}+m_{3t}=1, \mathrm{t} =1,2,3$$

(36)

Symbol Description:

UNTQ1, UNTQ2	The maximum carbon emissions for the first (CTFQ1) and second (CTFQ2) scenarios.
$m_1$, $m_2$, $m_3$	Dummy variable (0,1); only one of the three can be 1.

The carbon tax cost will be influenced by the specific mix of dummy variables. For $m_1$, $m_2$, $m_3$, for example, if $m_1$ is 1, then $m_2$ and $m_3$ must be 0, and from restriction Formulas (28)–(31), at this time, the company’s total carbon emission is $NT{Q}_1$, which will fall in the first range (0, $UNT{Q}_1$), and the total carbon tax cost is $k_{1}NT{Q}_1$.

3.4.2. Discontinuous Carbon Tax Cost Function of Carbon-Containing Rights

Single-period objective function:

$$\pi ={\displaystyle \sum }_{i=1}^4{S}_i{P}_i-Re{\displaystyle \sum }_{i=1}^4\{[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_i\}-\left(1-Re\right)$$

$$\begin{gathered} {\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_i-\left[H{R}_1+{\epsilon }_1\left(H{R}_2-H{R}_1\right)+{\epsilon }_2\left(H{R}_3-H{R}_1\right)\right]-C_o{Q}_o{B}_o-{\displaystyle \sum }_{i=1}^4{C}_o{d}_{io}{B}_{io} \\ -\{\left[(k_{1}NT{Q}_1+k_{2}NT{Q}_2+k_{3}NT{Q}_3)-\theta \left(GCQ-TCTQ\right)\right]{\sigma }_1+\left[(k_{1}NT{Q}_1+k_{2}NT{Q}_2+k_{3}NT{Q}_3)+\theta \left(TCTQ-GCQ\right)\right]{\sigma }_2\}-F \end{gathered}$$

Multi-period objective function:

$$\pi ={\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4{S}_i{P}_{it}-{\displaystyle \sum }_{t=1}^3\left(R{e}_t\left\{{\displaystyle \sum }_{i=1}^4[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_{it}\right\}\right)$$

$$-{\displaystyle \sum }_{t=1}^3\left[\left(1-R{e}_t\right){\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_{it}\right]+MRe{\displaystyle \sum }_{t=2}^3{\displaystyle \sum }_{i=1}^4{P}_{it}M{C}_7-{\displaystyle \sum }_{t=1}^3$$

$$\left[H{R}_1+{\epsilon }_{1t}\left(H{R}_2-H{R}_1\right)+{\epsilon }_{2t}\left(H{R}_3-H{R}_1\right)\right]-{\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4(C_o{d}_{io}{B}_{iot}+C_o{Q}_o{B}_{ot})$$

$$-\left\{\left[{\displaystyle \sum }_{t=1}^3(k_{1}NT{Q}_{1t}+k_{2}NT{Q}_{2t}+k_{3}NT{Q}_{3t})-\theta ({\displaystyle \sum }_{i=1}^{3}GC{Q}_t-{\displaystyle \sum }_{t=1}^{3}TCT{Q}_t)\right]{\sigma }_1 \right\}$$

$$\left\{+\left[{\displaystyle \sum }_{t=1}^3(k_{1}NT{Q}_{1t}+k_{2}NT{Q}_{2t}+k_{3}NT{Q}_{3t})+\theta ({\displaystyle \sum }_{i=1}^{3}TCT{Q}_t-{\displaystyle \sum }_{t=1}^{3}GC{Q}_t)\right]{\sigma }_2 \right\}-{\displaystyle \sum }_{t=1}^{3}F$$

The following are the relevant restrictions:

Single-period:

$${\displaystyle \sum }_{i=1}^{n}CT{e}_i{P}_i={\Omega }_1+{\Omega }_2=TCTQ$$

(37)

$$0\le {\Omega }_1\le GCQ{\sigma }_1$$

(38)

$$GCQ{\sigma }_2<{\Omega }_2\le \left(GCQ+UCQ\right){\sigma }_2$$

(39)

$${\sigma }_1+{\sigma }_2=1$$

(40)

Multi-period:

$${\displaystyle \sum }_{i=1}^{n}CT{e}_i{P}_{it}={\Omega }_{1t}+{\Omega }_{2t}=TCT{Q}_t, \mathrm{t} =1,2,3$$

(41)

$$0\le {\Omega }_{1t}\le GCQ{\sigma }_{1t}, \mathrm{t} =1,2,3$$

(42)

$$GCQ{\sigma }_{2t}<{\Omega }_{2t}\le \left(GCQ+UCQ\right){\sigma }_{2t}, \mathrm{t} =1,2,3$$

(43)

$${\sigma }_{1t}+{\sigma }_{2t}=1, \mathrm{t} =1,2,3$$

(44)

For example, when ${\sigma }_1$ is 1, ${\sigma }_2$ = 0, the company’s carbon emissions will be between 0 and GCQ, eliminating the need to buy carbon credits and allowing for the sale of surplus allowances, resulting in zero carbon emission costs. $\left[(k_{1}NT{Q}_1+k_{2}NT{Q}_2+k_{3}NT{Q}_3)-\theta \left(GCQ-TCTQ\right)\right]{\sigma }_1$.

3.4.3. Discontinuous Carbon Tax Cost Function with Allowance

Single-period objective function:

$$\pi ={\displaystyle \sum }_{i=1}^4{S}_i{P}_i-Re{\displaystyle \sum }_{i=1}^4\{[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_i\}$$

$$-\left(1-Re\right){\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_i-\left[H{R}_1+{\epsilon }_1\left(H{R}_2-H{R}_1\right)+{\epsilon }_2\left(H{R}_3-H{R}_1\right)\right]$$

$$-C_o{Q}_o{B}_o-{{\displaystyle \sum }}_{i=1}^4{C}_o{d}_{io}{B}_{io}-\left[{\lambda }_{1}k{r}_1(FNT{Q}_1-F{Q}_0\right)+{\lambda }_{2}k{r}_2(FNT{Q}_2-F{Q}_0) +{\lambda }_{3}k{r}_3\left(FNT{Q}_3-F{Q}_0\right)]-\mathrm{F}$$

Multi-period objective function:

$$\begin{gathered} \pi ={\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4{S}_i{P}_{it}-{\displaystyle \sum }_{t=1}^3\left(R{e}_t\left\{{\displaystyle \sum }_{i=1}^4[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_{it}\right\}\right) \\ -{\displaystyle \sum }_{t=1}^3\left[\left(1-R{e}_t\right){\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_{it}\right]+MRe{\displaystyle \sum }_{t=2}^3{\displaystyle \sum }_{i=1}^4{P}_{it}M{C}_7-{\displaystyle \sum }_{t=1}^3 \\ \left[H{R}_1+{\epsilon }_{1t}\left(H{R}_2-H{R}_1\right)+{\epsilon }_{2t}\left(H{R}_3-H{R}_1\right)\right]-{\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4(C_o{d}_{io}{B}_{iot}+C_o{Q}_o{B}_{ot})-{\displaystyle \sum }_{t=1}^3 \\ \left[{\lambda }_{1t}k{r}_1(FNT{Q}_{1t}-F{Q}_0\right)+{\lambda }_{2t}k{r}_2(FNT{Q}_{2t}-F{Q}_0)+{\lambda }_{3t}k{r}_3\left(FNT{Q}_{3t}-F{Q}_0\right)]-{\displaystyle \sum }_{t=1}^{3}F \end{gathered}$$

Symbol Description:

$k{r}_1$,$k{r}_2$,$k{r}_3$	The first carbon tax rate ($kr$1), the second carbon tax rate ($kr$2), and the third carbon tax rate ($kr$3).
${\lambda }_0,{\lambda }_1,{\lambda }_2,{\lambda }_3$	Dummy variable (0,1); only one of the four can be 1.
$F{Q}_0$	Tax-free carbon emissions.
$FNT{Q}_1$,$FNT{Q}_2$,$FNT{Q}_3$	The amount of carbon emissions falling in the first segment ($FNT{Q}_1$), the amount of carbon emissions falling in the second segment ($FNT{Q}_2$), and the amount of carbon emissions falling in the third segment ($FNT{Q}_3$).

Figure 4 and Formula (45) illustrate a non-continuous (incrementally increasing tax rate) carbon tax cost function that incorporates tax exemptions. This setup presumes that the government provides businesses with a specific quota of tax credits. Companies will not be taxed as long as their emissions stay within this allocated limit. However, if their emissions exceed this threshold, a tiered tax rate system comes into effect, applying progressively higher rates in three distinct segments. This means any emissions surpassing the cap of a given tier will be taxed at the higher rate applicable to the next tier.

The tax rate applies as follows: $k{r}_1$ between FQ₀ and FQ₁, $k{r}_2$ between FQ₁ and FQ₂, and $k{r}_3$ for emissions over FQ₂.

Single-period functions:

The following are all constraints related to the cost of this carbon tax:

$$\begin{gathered} f_4\left(TCTQ\right)=\{ 0, 0\le TCTQ\le F{Q}_0 k{r}_1\left(TCTQ-F{Q}_0\right), \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}F{Q}_0\le TCTQ\le F{Q}_1 k{r}_2\left(TCTQ-F{Q}_0\right), \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} F{Q}_1<TCTQ\le F{Q}_2 k{r}_3\left(TCTQ-F{Q}_0\right), TCTQ>F{Q}_2 \end{gathered}$$

(45)

Multi-period functions:

Single-period:

$${\displaystyle \sum }_{i=1}^{n}CT{e}_i{P}_i=FNT{Q}_0+FNT{Q}_1+FNT{Q}_2+FNT{Q}_3$$

(46)

$$0\le FNT{Q}_0\le {\lambda }_{0}F{Q}_0$$

(47)

$${\lambda }_{1}F{Q}_0<FNT{Q}_1 \le {\lambda }_{1}F{Q}_1$$

(48)

$${\lambda }_{2}F{Q}_1<FNT{Q}_2\le {\lambda }_{2}F{Q}_2$$

(49)

$${\lambda }_{3}F{Q}_2<FNT{Q}_3$$

(50)

$${\lambda }_0+{\lambda }_1+{\lambda }_2+{\lambda }_3=1$$

(51)

Multi-period:

$${\displaystyle \sum }_{i=1}^{n}CT{e}_i{P}_{it}=FNT{Q}_{0t}+FNT{Q}_{1t}+FNT{Q}_{2t}+FNT{Q}_{3t}, \mathrm{t} =1,2,3$$

(52)

$$0\le FNT{Q}_{0t}\le {\lambda }_{0t}F{Q}_0, \mathrm{t} =1,2,3$$

(53)

$${\lambda }_{1t}F{Q}_0<FNT{Q}_{1t} \le {\lambda }_{1t}F{Q}_1 \mathrm{t} =1,2,3$$

(54)

$${\lambda }_{2t}F{Q}_1<FNT{Q}_{2t}\le {\lambda }_{2t}F{Q}_2, \mathrm{t} =1,2,3$$

(55)

$${\lambda }_{3t}F{Q}_2<FNT{Q}_{3t}, \mathrm{t} =1,2,3$$

(56)

$${\lambda }_{0t}+{\lambda }_{1t}+{\lambda }_{2t}+{\lambda }_{3t}=1, \mathrm{t} =1,2,3$$

(57)

Symbol Description:

$F{Q}_0$, $F{Q}_1$, $F{Q}_2$

Tax-free carbon emissions ($F{Q}_0$), the maximum carbon emissions in the first stage ($F{Q}_1$) and the second stage ($F{Q}_2$). Exempt carbon emissions ($F{Q}_0$) and the upper limit of carbon emissions for the initial stage ($F{Q}_1$) and for the subsequent stage ($F{Q}_2$).

The carbon tax cost will depend on the combination of dummy variables ${\lambda }_0, {\lambda }_1, {\lambda }_2, {\lambda }_3$; for example, if ${\lambda }_1$ is 1, then ${\lambda }_0, {\lambda }_2$, and ${\lambda }_3$ must be 0 and can be determined by Constraints (47)–(51). It is known that the total carbon emission of the company at this time is $FNT{Q}_1$, which will fall in the first range in Figure 4 ($F{Q}_0$, $F{Q}_1$), and the total carbon tax cost is ${\lambda }_{1}k{r}_1(FNT{Q}_1-F{Q}_0)$.

3.4.4. Discontinuous Carbon Tax Cost Function of Carbon Rights and Tax Allowances

Single-period objective function:

$$\begin{gathered} \pi ={\displaystyle \sum }_{i=1}^4{S}_i{P}_i-Re{\displaystyle \sum }_{i=1}^4\{[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_i\}-\left(1-Re\right){\displaystyle \sum }_{i=1}^4 \\ \left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_i-\left[H{R}_1+{\epsilon }_1\left(H{R}_2-H{R}_1\right)+{\epsilon }_2\left(H{R}_3-H{R}_1\right)\right]-C_o{Q}_o{B}_o-{\displaystyle \sum }_{i=1}^4{C}_o{d}_{io}{B}_{io} \\ \left\{\{\left[{\lambda }_{1}k{r}_1(FNT{Q}_1-F{Q}_0\right)+{\lambda }_{2}k{r}_2(FNT{Q}_2-F{Q}_0)+{\lambda }_{3}k{r}_3\left(FNT{Q}_3-F{Q}_0\right)]-\theta \left(GCQ-TCTQ\right)\}{\sigma }_1 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\{{\lambda }_{1}k{r}_1(FNT{Q}_1-F{Q}_0)+{\lambda }_{2}k{r}_2(FNT{Q}_2-F{Q}_0)+{\lambda }_{3}k{r}_3\left(FNT{Q}_3-F{Q}_0\right)]+\theta \left(GCQ-TCTQ\right)\}{\sigma }_2 \right\}-F \end{gathered}$$

Multi-period objective function:

$$\begin{gathered} \pi ={\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4{S}_i{P}_{it}-{\displaystyle \sum }_{t=1}^3\left(R{e}_t\left\{{\displaystyle \sum }_{i=1}^4[M{C}_7{q}_{i7}+M{C}_4(q_{i4}-0.06)+({\displaystyle \sum }_{j=5}^{6}M{C}_j{q}_{ij})]P_{it}\right\}\right) \\ -{\displaystyle \sum }_{t=1}^3\left[\left(1-R{e}_t\right){\displaystyle \sum }_{i=1}^4\left({\displaystyle \sum }_{j=1}^{6}M{C}_j{q}_{ij}\right)P_{it}\right]+MRe{\displaystyle \sum }_{t=2}^3{\displaystyle \sum }_{i=1}^4{P}_{it}M{C}_7 \\ -{\displaystyle \sum }_{t=1}^3\left[H{R}_1+{\epsilon }_{1t}\left(H{R}_2-H{R}_1\right)+{\epsilon }_{2t}\left(H{R}_3-H{R}_1\right)\right]-{\displaystyle \sum }_{t=1}^3{\displaystyle \sum }_{i=1}^4(C_o{d}_{io}{B}_{iot}+C_o{Q}_o{B}_{ot}) \\ -[{\displaystyle \sum }_{t=1}^3[{\lambda }_{1t}k{r}_1(FNT{Q}_{1t}-F{Q}_0)+{\lambda }_{2t}k{r}_2(FNT{Q}_{2t}-F{Q}_0)+{\lambda }_{3t}k{r}_3\left(FNT{Q}_{3t}-F{Q}_0\right)]-\theta ({\displaystyle \sum }_{i=1}^{3}GC{Q}_t-{\displaystyle \sum }_{t=1}^{3}TCT{Q}_t) {\sigma }_1 \\ +[{\displaystyle \sum }_{t=1}^3[{\lambda }_{1t}k{r}_1(FNT{Q}_{1t}-F{Q}_0)+{\lambda }_{2t}k{r}_2(FNT{Q}_{2t}-F{Q}_0)+{\lambda }_{3t}k{r}_3\left(FNT{Q}_{3t}-F{Q}_0\right)]+\theta ({\displaystyle \sum }_{i=1}^{3}TCT{Q}_t-{\displaystyle \sum }_{t=1}^{3}GC{Q}_t) {\sigma }_{2)} \\ -{\displaystyle \sum }_{t=1}^3+F \end{gathered}$$

The following are the relevant restrictions:

Single-period:

$${\displaystyle \sum }_{i=1}^{n}CT{e}_i{P}_i={\Omega }_1+{\Omega }_2=TCTQ$$

(58)

$$0\le {\Omega }_1\le GCQ{\sigma }_1$$

(59)

$$GCQ{\sigma }_2<{\Omega }_2\le \left(GCQ+UCQ\right){\sigma }_2$$

(60)

$${\sigma }_1+{\sigma }_2=1$$

(61)

Multi-period:

$${\displaystyle \sum }_{i=1}^{n}CT{e}_i{P}_{it}={\Omega }_{1t}+{\Omega }_{2t}=TCT{Q}_t \mathrm{t} =1,2,3$$

(62)

$$0\le {\Omega }_{1t}\le GCQ{\sigma }_{1t} \mathrm{t} =1,2,3$$

(63)

$$GCQ{\sigma }_{2t}<{\Omega }_{2t}\le \left(GCQ+UCQ\right){\sigma }_{2t}, \mathrm{t} =1,2,3$$

(64)

$${\sigma }_{1t}+{\sigma }_{2t}=1, \mathrm{t} =1,2,3$$

(65)

For example, when ${\sigma }_1$ is 1, ${\sigma }_2$ will be nonexistent. Under these circumstances, the company’s total carbon emissions will be between 0 and GCQ, indicating that there is no necessity for the company to buy additional carbon credits. Instead, it has the option to sell any surplus credits to other companies. At this point, the cost associated with carbon emissions is $\{\left[{\lambda }_{1}k{r}_1(FNT{Q}_1-F{Q}_0\right)+{\lambda }_{2}k{r}_2(FNT{Q}_2-F{Q}_0)+{\lambda }_{3}k{r}_3\left(FNT{Q}_3-F{Q}_0\right)]-\theta \left(GCQ-TCTQ\right)\}{\sigma }_1$.

4. Model Research Results and Analysis

4.1. Model Data Assumptions

Building on the mathematical model established previously, this section explores the emission reduction potential and optimal decarbonization pathways for the glass industry in Taiwan under various carbon pricing scenarios through a case study. We selected a representative glass company as our research subject, inputting relevant parameters such as production, cost, and emissions, and used Lingo 18.0 software to solve the optimization model. By setting different carbon pricing levels and constraints, we constructed a series of scenarios to assess the impact of carbon pricing policies on the emission reduction behaviors and operational performance of glass enterprises.

Table 1. Model data.

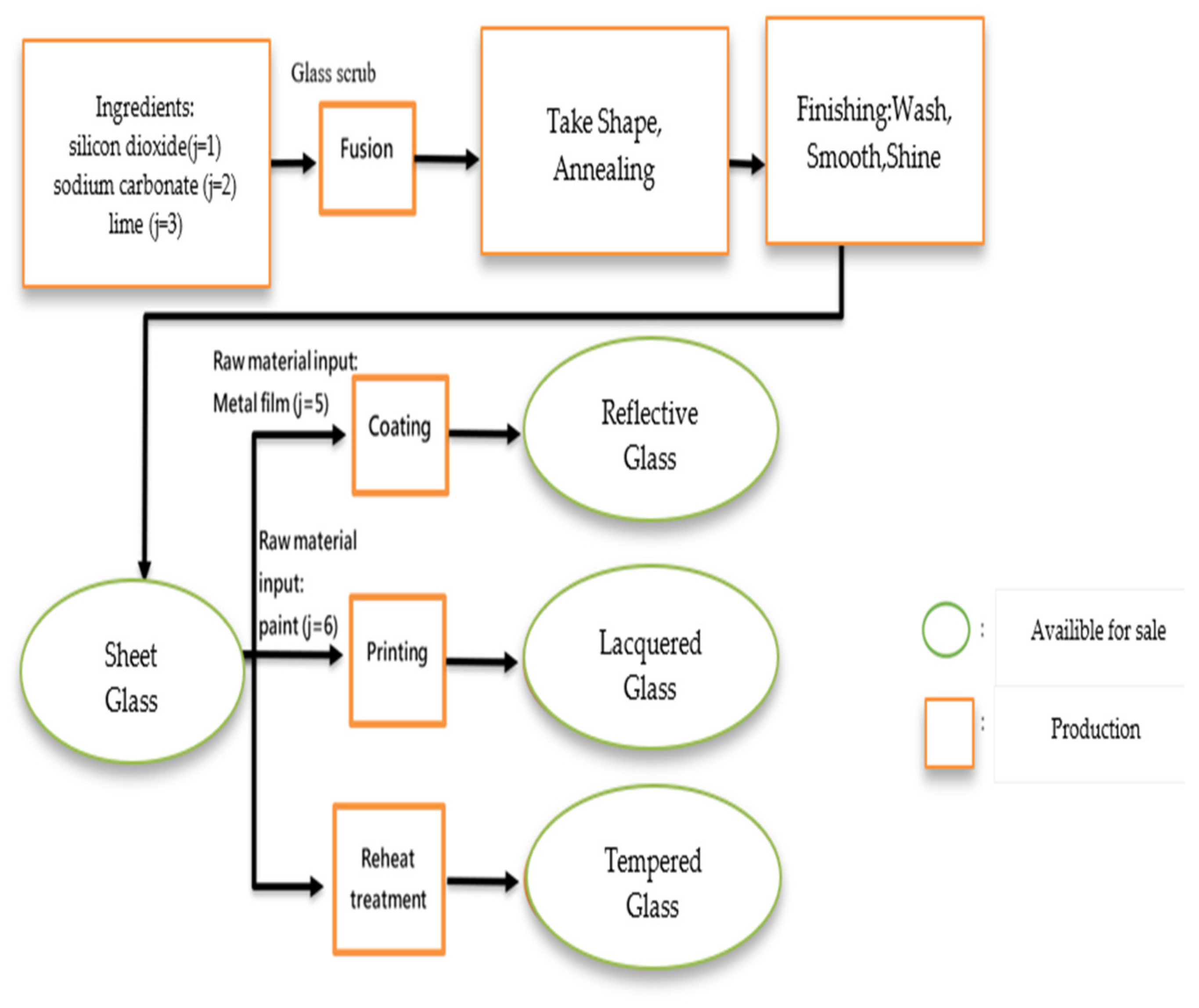
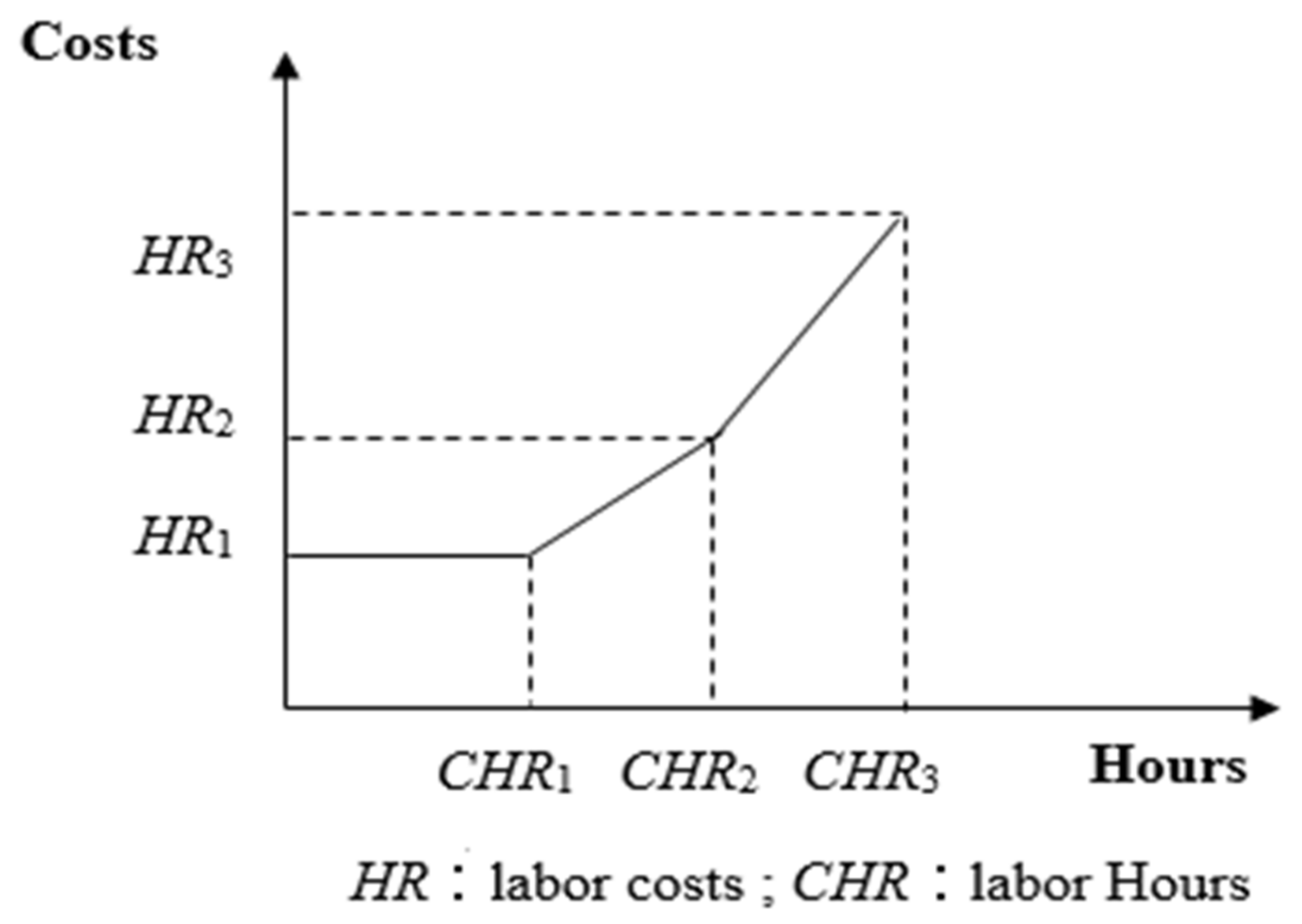
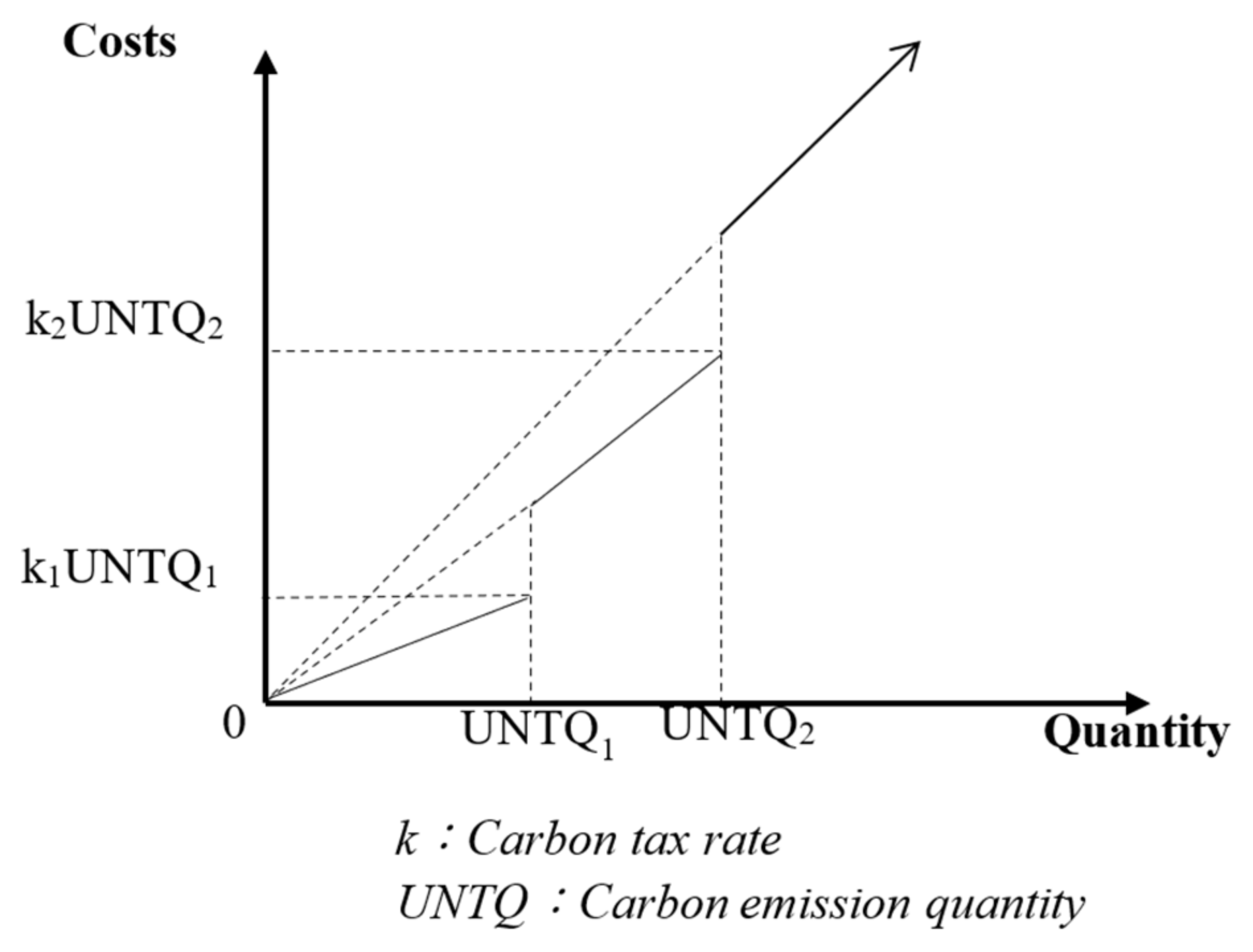
					Products
			Symbol		Sheet Glass	Reflective Glass	Lacquered Glass	Tempered Glass	Capacity Cap
Minimum demand (production volume)/ton			Pi		>280,000	>28,333	>30,000	>52,500
Sales price/ton			Si		USD 243	USD 384	USD 486	USD 332
Unit-level material price
silicon dioxide (j = 1)	MC1 = USD 52/ton		qi1		0.7	0.7	0.7	0.7
sodium carbonate (j = 2)	MC2 = USD 439/ton		qi2		0.2	0.2	0.2	0.2
lime (j = 3)	MC3 = USD 56/ton		qi3		0.1	0.1	0.1	0.1
fuel: Petroleum Coke (j = 4)	MC4 = USD 420/ton		qi4		0.2	0.25	0.25	0.3
metallic film raw material (j = 5)	MC5 = USD 600/ton		qi5		0	0.1	0	0
paint (j = 6)	MC6 = USD 660/ton		qi6		0	0	0.2	0
glass (j = 7)	MC7 = USD 100/ton		qi7		1	1	1	1
Unit-level Activity		o
labor hours	Ingredients for Processing	1	ui1		2	2	2	2
	coating	2	ui2		0	2	0	0
	print	3	ui3		0	0	2	0
	reheat	4	ui4		0	0	0	1.5
machine hours	Ingredients for Processing	1	mhi1		5	5	5	5	LMP1 = 2,394,594
	coating	2	mhi2		0	3	0	0	LMP2 = 163,680
	print	3	mhi3		0	0	3	0	LMP3 = 169,912
	reheat	4	mhi4		0	0	0	2	LMP4 = 135,589
					Products
			o	Symbol	Sheet Glass	Reflective Glass	Lacquered Glass	Tempered Glass	Capacity Cap
Batch-Level Activity
Material handling	C5 = USD 10,000/batch	5	Q5	1					PC5 = 20,000
			η5	10,000
Set	C6 = USD 27,000/batch	6	di6	2	3	4	3		PC6 = 500,000
			Γi6	100	50	50	70
Direct labor cost
Cost	HR1 = USD 4,988,641	HR2 = USD 9,243,464	HR3 = USD 15,762,636
Labor hour	CHR1 = 28,345	CHR2 = 39,334	CHR3 = 53,433
Wage rate	USD 176/h	USD 235/h	USD 295/h
Carbon tax			CTei	0.5	0.8	0.8	0.7
Cost of each segment	CT1 = USD 1,166,667	CT2 = USD 4,526,489	CT3 = USD 164,929,976
Upper limit of carbon emissions in each stage	CTQ1= 233,333	CTQ2 = 452,648	CTQ3 = 13,194,398
Various tax rates	ctr1 = USD 150/ton	ctr2 = USD 300/ton	ctr3 = USD 375/ton
Carbon credit cost	$\theta$ = USD 250/ton
Recycling operations (use ratio of glass)
Single-period	$Re$ = 0.3
Multi-period	$R{e}_1$ = 0.3	$R{e}_2$ = 0.5	$R{e}_3$ = 0.7
Recycling glass from the previous period	$MRe$ = 0.1

is the research data.

4.2. The Optimal Solution and Analysis of the Model

After detailed data processing and analysis, we have derived the optimal solution for the model.

Table 2. Single period model profit and tax.

Model 1 (Discontinuous carbon tax)
$\pi$	259,623,667
Tax	34,999,967
Model 2 (Discontinuous carbon tax with carbon rights)
$\pi$	284,623,566
Tax	34,999,933
Carbon right	+25,000,103
Model 3 (Discontinuous carbon tax with allowance)
$\pi$	262,123,666
Tax	32,499,980
Model 4 (Discontinuous Carbon Tax Including Tax Allowance and Carbon Rights)
$\pi$	287,123,566
Tax	32,499,936
Carbon right	+25,000,103

is Model 1-4 Single period Discontinuous carbon tax profit and tax.

Model 1 (Discontinuous Carbon Tax Model): The company’s profit is USD 259,623,667, and it is required to pay a carbon tax of USD 34,999,967. This model employs a discontinuous tax rate structure, where the tax rate changes abruptly when certain emission thresholds are crossed. While this model effectively imposes a cost on carbon emissions, it does not provide any additional flexibility or incentives for companies to reduce their emissions beyond the mandated levels.

Model 2 (Discontinuous Carbon Tax Model with Carbon Rights): The company’s profit increases to USD 284,623,566 with the carbon tax amount being similar to Model 1. However, the company can earn an additional USD 34,999,933 from the sale of carbon rights. The inclusion of a carbon rights trading mechanism allows companies that emit less than their allotted quota to sell their excess carbon rights to other companies, thus creating a financial incentive for emission reduction. This model encourages companies to invest in cleaner technologies and processes to maximize their profits from carbon rights trading.

Model 3 (Discontinuous Carbon Tax Model with Tax Allowances): The company’s profit is USD 262,123,666, slightly higher than Model 1. The carbon tax is slightly lower at USD 32,499,980 due to the inclusion of tax allowances. These allowances provide a tax-free emission threshold, reducing the effective tax burden on companies. This model recognizes that some level of emissions may be unavoidable in certain industries and provides a measure of relief to help maintain their competitiveness.

Model 4 (Discontinuous Carbon Tax Model with Both Tax Allowances and Carbon Rights): The company’s profit is the highest among the four models, reaching USD 287,123,566. The carbon tax is similar to Model 3, but the company earns an additional USD 32,499,936 from the sale of carbon rights. This model combines the benefits of both tax allowances and carbon rights trading, providing the greatest flexibility and incentives for companies to reduce their emissions. By offering both a tax-free emission threshold and the opportunity to profit from unused emission allowances, this model creates a strong business case for investments in clean technology and processes.

Overall, carbon tax models that incorporate carbon rights trading and tax allowances provide companies with greater opportunities for profitability. Among these, Model 4 demonstrates the best profit performance. This suggests that under a carbon tax regime, complementary measures that offer flexibility can help balance emission reduction goals with industrial interests. By creating a system that rewards emission reductions and clean investments, policymakers can work with businesses to achieve sustainable economic growth in the face of climate change challenges.

After detailed data processing and analysis, we have derived the optimal solution for the model Multi-period data

Table 3. Model multi-period profit and tax.

Model 1 (Discontinuous carbon tax)
Phase 1		Phase 2		Phase 3
$\pi$	259,330,467	$\pi$	569,324,000	$\pi$	730,956,333
Tax	34,999,967	Tax	32,182,080	Tax	27,610,627
Model 2 (Discontinuous carbon tax with carbon rights)
Phase 1		Phase 2		Phase 3
$\pi$	284,330,467	$\pi$	599,020,667	$\pi$	768,272,000
Tax	34,999,967	Tax	32,182,080	Tax	27,610,533
Carbon right	+25,000,063	Carbon right	+29,696,533	Carbon right	+37,315,767
Model 3 (Discontinuous carbon tax with allowance)
Phase 1		Phase 2		Phase 3
$\pi$	261,830,467	$\pi$	571,824,000	$\pi$	733,456,333
Tax	32,499,967	Tax	29,682,080	Tax	25,110,627
Model 4 (Discontinuous Carbon Tax Including Tax Allowance and Carbon Rights)
Phase 1		Phase 2		Phase 3
$\pi$	286,830,267	$\pi$	601,520,667	$\pi$	770,772,000
Tax	32,499,980	Tax	29,682,070	Tax	25,110,537
Carbon right	+25,000,033	Carbon right	+29,696,550	Carbon right	+37,315,767

is Model 1-4 multi-period Discontinuous carbon tax profit and tax.

Model 1 (Discontinuous Carbon Tax Model):

In this model, the company’s profit increases from USD 259,330,467 in Phase 1 to USD 569,324,000 in Phase 2 and USD 730,956,333 in Phase 3. The carbon tax decreases from USD 34,999,967 in Phase 1 to USD 32,182,080 in Phase 2 and USD 27,610,627 in Phase 3. The increase in profits and decrease in carbon tax over the three phases can be attributed to the company’s adoption of cleaner production methods, such as increasing the proportion of recycled glass in its raw materials. By using more recycled glass, the company reduces its carbon emissions, leading to lower carbon tax liabilities. This model demonstrates that investing in sustainable practices can lead to long-term financial benefits, even in the absence of additional incentives like carbon rights trading or tax allowances.

Model 2 (Discontinuous Carbon Tax Model with Carbon Rights):

The company’s profit in this model starts at USD 284,330,467 in Phase 1, increases to USD 599,020,667 in Phase 2, and reaches USD 768,272,000 in Phase 3. The carbon tax follows the same trend as in Model 1, decreasing from USD 34,999,967 in Phase 1 to USD 32,182,080 in Phase 2 and USD 27,610,533 in Phase 3. However, this model also includes revenue from the sale of carbon rights, which increases from USD 25,000,063 in Phase 1 to USD 29,696,533 in Phase 2 and USD 37,315,766 in Phase 3. The increasing revenue from carbon rights sales can be attributed to the company’s continuous efforts to reduce emissions by using more recycled glass. As the company’s emissions fall further below its allocated quota, it can sell more carbon rights, generating additional income. This model highlights the potential for companies to turn their emission reductions into a source of revenue, creating a strong incentive for sustainable practices.

Model 3 (Discontinuous Carbon Tax Model with Tax Allowances):

In this model, the company’s profit increases from USD 261,830,467 in Phase 1 to USD 571,824,000 in Phase 2 and USD 733,456,333 in Phase 3. The carbon tax decreases from USD 32,499,967 in Phase 1 to USD 29,682,080 in Phase 2 and USD 25,110,627 in Phase 3. Compared to Model 1, the profits are slightly higher, and the carbon taxes are lower due to the inclusion of tax allowances. These allowances provide a tax-free emissions threshold, effectively reducing the company’s tax burden. As the company increases its use of recycled glass over the three phases, its emissions decrease, and the impact of the tax allowances becomes more pronounced, leading to lower tax liabilities and higher profits. This model demonstrates the potential for tax allowances to provide a measure of relief for companies as they transition to cleaner production methods.

Model 4 (Discontinuous Carbon Tax Model with Both Tax Allowances and Carbon Rights):

This model combines the benefits of tax allowances and carbon rights trading, resulting in the highest profits among the four models. The company’s profit increases from USD 286,830,267 in Phase 1 to USD 601,520,667 in Phase 2 and USD 770,772,000 in Phase 3. The carbon tax decreases from USD 32,499,980 in Phase 1 to USD 29,682,070 in Phase 2 and USD 25,110,537 in Phase 3, similar to Model 3. However, the company also earns revenue from the sale of carbon rights, which increases from USD 25,000,033 in Phase 1 to USD 29,696,550 in Phase 2 and USD 37,315,767 in Phase 3. The combination of tax allowances and carbon rights trading creates a strong incentive for the company to continuously reduce its emissions, as it benefits from both lower tax liabilities and increased revenue from the sale of unused emission allowances. This model demonstrates the potential for a well-designed carbon tax system to drive sustainable practices and create win–win situations for companies and the environment.

In conclusion, these multi-phase models illustrate the long-term benefits of investing in cleaner production methods and the potential for carbon tax policies to drive sustainable change in industries. The inclusion of flexible mechanisms like carbon rights trading and tax allowances can create strong incentives for companies to reduce their emissions while maintaining their competitiveness. As companies adopt more sustainable practices over time, they can benefit from lower tax burdens, additional revenue streams, and improved profitability, all while contributing to the global effort to combat climate change.

5. Discussion

As a research subject, exploring the impact of carbon tax policies on the glass manufacturing industry holds unique significance. Firstly, it is a key player in the global glass manufacturing industry, with a comprehensive industrial chain and technological foundation. The glass industry occupies a crucial position in the economy, and therefore, studying the impact of carbon taxes on this sector provides important reference value for policymaking and industrial transformation.

The government has proposed the “2050 Net-Zero Emission Pathway”, setting ambitious carbon reduction targets. To achieve this goal, the government plans to introduce carbon pricing mechanisms, including carbon fees and a carbon trading system. In this context, studying the application effects of different carbon tax models in the glass manufacturing industry can provide valuable empirical evidence for the design of carbon pricing policies, helping to achieve energy conservation, emission reduction, and green development goals. Moreover, as an island economy, Taiwan faces the dual challenges of energy import dependence and climate change. Promoting the low-carbon transformation of energy-intensive industries, such as glass manufacturing, is not only related to industrial competitiveness but also to energy security and climate resilience. Through researching carbon tax policies, scientific evidence can be provided for Taiwan to formulate sustainable development strategies and explore ways to achieve the low-carbon transformation of the economy and society while ensuring industrial competitiveness.

The profitability analysis presented in Table 1 underscores significant financial benefits for glass manufacturing companies that have implemented advanced technologies and optimized processes, particularly in response to evolving carbon regulations. The projected profits, ranging from USD 200 million to 700 million, stem from detailed scenario analyses that reflect current market trends and the impacts of regulatory changes on operational costs and revenue streams. These substantial figures validate the economic viability of adopting sustainable practices within the industry. To provide stakeholders with actionable insights, a deeper examination of how specific technological innovations and early compliance with carbon pricing mechanisms quantitatively affect these profit outcomes would enhance our discussion. This analysis would detail the incremental financial impacts and the competitive advantages accrued, offering a granular understanding of the economic benefits involved.

The introduction of a carbon tax, leading to rising costs, may variably weaken the competitive position of small- and medium-sized glass enterprises. For glass varieties with high product homogeneity, such as flat glass, small businesses have limited scope for price increases, and the carbon tax costs will more likely erode their already thin profit margins. For technically more complex glass types, like specialty glass, small businesses, although possessing relatively stronger bargaining power, may also face the risk of reduced demand due to price increases. Overall, the carbon tax undoubtedly introduces greater operational pressures for small- and medium-sized glass enterprises. Despite the challenges posed by the carbon tax to these enterprises, crises often come with opportunities. Proactively addressing carbon taxes and achieving green transformation development is not only a general trend but could also become a new pathway for small businesses to enhance their competitiveness. For instance, enterprises could collaborate with third-party energy-saving services, using contractual energy management models to seek external funding and technical support for energy-saving renovations; or they could form joint procurement alliances with industry peers to utilize collective bargaining advantages and reduce the procurement costs of clean production equipment; or strengthen strategic collaboration with upstream and downstream players in the supply chain through technological innovation and process re-engineering, thereby achieving cost sharing and mutual benefits while improving energy efficiency. Although these measures still require further exploration and improvement, they undoubtedly pave new developmental paths for small- and medium-sized glass enterprises.

Furthermore, this research reveals the long-term benefits of enterprises adopting clean production methods. As enterprises increase the proportion of recycled glass and other environmentally friendly raw materials, their carbon emission intensity gradually decreases. Under the incentive of carbon tax policies, they can achieve higher profitability levels. This result is expected to encourage more enterprises to accelerate the pace of green transformation and promote the sustainable development of the glass manufacturing industry and other industries.

This research, using the glass manufacturing industry as an example, evaluates the emission reduction and profitability effects of different carbon tax models, providing valuable empirical references for the design and implementation of carbon pricing policies. The research results are significant not only locally but also offer reference value for other countries and regions facing similar challenges. Through the in-depth analysis of carbon tax policies, the insights and solutions developed can contribute to global efforts in addressing climate change and achieving sustainable development.

6. Conclusions

This research paper has made significant contributions to the field of carbon pricing and sustainable manufacturing by examining the impact of different carbon tax models on the glass industry in Taiwan. By integrating activity-based costing (ABC) and the theory of constraints (TOC) with carbon tax policies, this study provides valuable insights into designing effective carbon pricing mechanisms that balance emission reduction goals with industrial competitiveness.

The findings reveal that carbon tax models incorporating carbon trading and tax allowances can create a win–win situation for companies and the environment. These models incentivize companies to invest in cleaner technologies and processes, leading to reduced emissions and increased profitability. The multi-phase analysis demonstrates the long-term benefits of adopting sustainable practices, as companies can benefit from lower tax liabilities, additional revenue streams, and improved competitiveness over time.

The results suggest that a well-designed carbon tax system should include flexible mechanisms like carbon trading and tax allowances to create strong incentives for emission reduction while maintaining industrial competitiveness. This study also highlights the potential for the glass industry to contribute to Taiwan’s “2050 Net-Zero Emission Pathway” by adopting cleaner production methods and increasing the use of recycled materials.

Moreover, this research demonstrates the value of applying advanced costing methods like ABC and the TOC in the context of sustainable manufacturing. By providing accurate cost allocation and identifying production bottlenecks, these methods can help companies optimize their operations for both environmental and economic sustainability.

Future research could expand on these findings by examining the applicability of the proposed carbon tax models in other energy-intensive industries, such as steel, cement, or petrochemicals. Additionally, researchers could explore the potential synergies between carbon pricing policies and other sustainability initiatives, such as the circular economy or renewable energy adoption.

In conclusion, the findings from our study reveal significant insights into the financial and environmental impacts of implementing carbon pricing mechanisms within the glass industry. Our data indicate that companies adapting early to carbon pricing, whether through carbon taxes or emission trading systems, not only mitigate the potential costs but also enhance their profitability substantially. For instance, the profit figures ranging from USD 200 million to USD 700 million, as highlighted in Table 1, underscore the economic feasibility of proactive environmental strategies, even under stringent regulatory environments. These profits are particularly notable in scenarios where companies leverage advanced technologies and operational efficiencies to stay competitive.

Moreover, our results demonstrate that investments in cleaner technologies and efficient processes are not merely cost-saving measures but are also significant drivers of market competitiveness in the face of evolving environmental regulations. The profitability enhanced by these strategic decisions supports the argument that sustainable practices are integral to long-term business success in the glass manufacturing sector.

Although our case studies have focused on the specific context of Taiwan, the optimization models and analytical frameworks developed in this research could potentially be adapted and applied to investigate the carbon management decisions of glass enterprises in other countries. Future studies could collect data on the production costs, energy consumption, and carbon emissions of glass manufacturers in different regions and adjust the model parameters and constraints to reflect the specific policy and market conditions in each context. Comparative analyses across countries could yield valuable insights into how the institutional, technological, and economic factors influence the effectiveness and efficiency of various carbon management strategies and policy instruments. Such international comparisons could also facilitate cross-border policy learning and knowledge sharing and inform the development of more coordinated and impactful global actions for the low-carbon transition of the glass industry.