Recognition of Longitudinal Cracks on Slab Surfaces Based on Particle Swarm Optimization and eXtreme Gradient Boosting Model
Abstract
:1. Introduction
2. Experiment and Temperature Characteristics
2.1. Caster
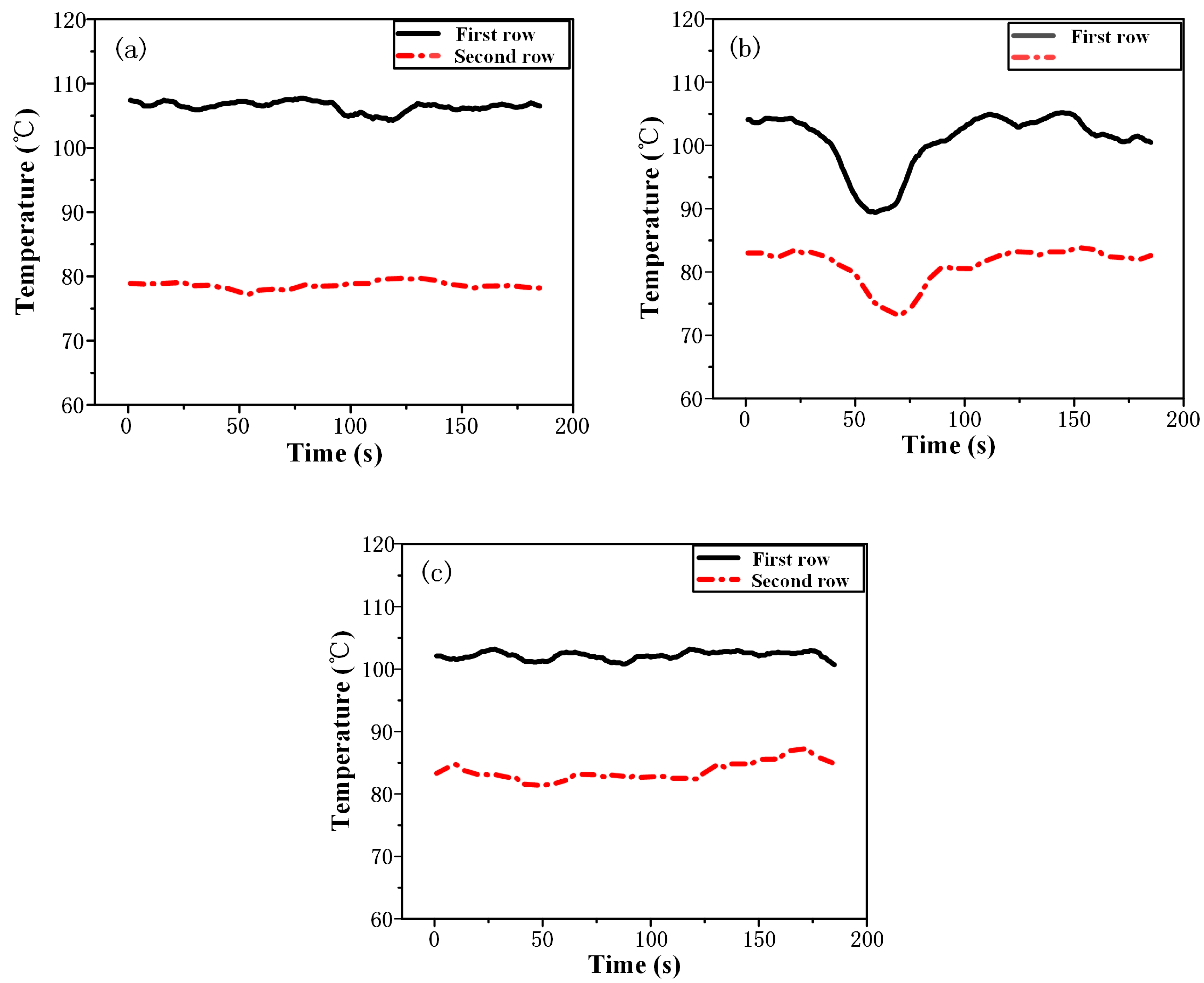
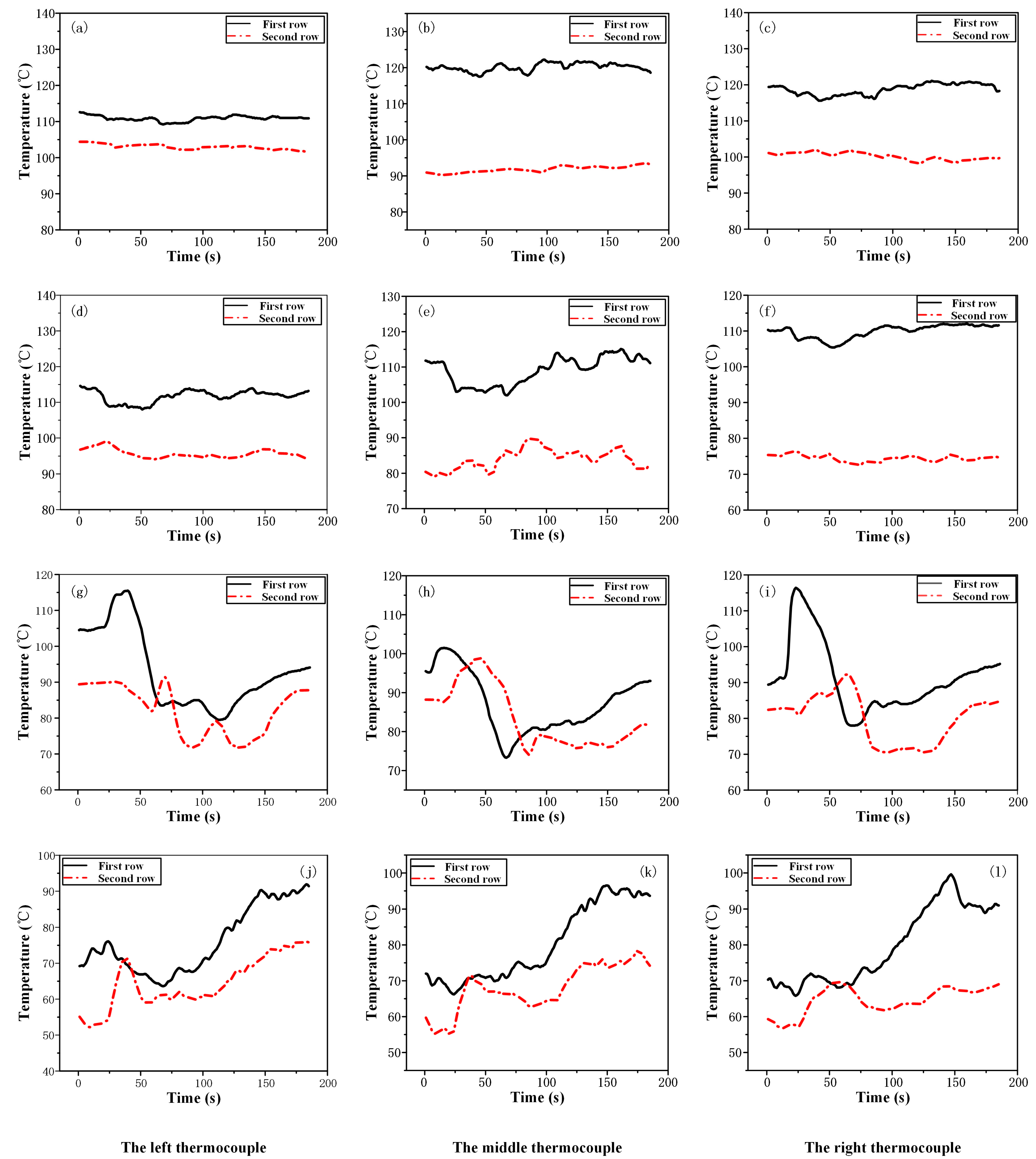
2.2. Temperature Characteristics of Surface Longitudinal Cracks
2.3. Extraction of Typical Temperature Characteristics of Longitudinal Cracks
3. Longitudinal Crack Sample Database and Dimension Reduction Using PCA
3.1. Longitudinal Crack Sample Database
3.2. Dimension Reduction of Typical Characteristics Using PCA
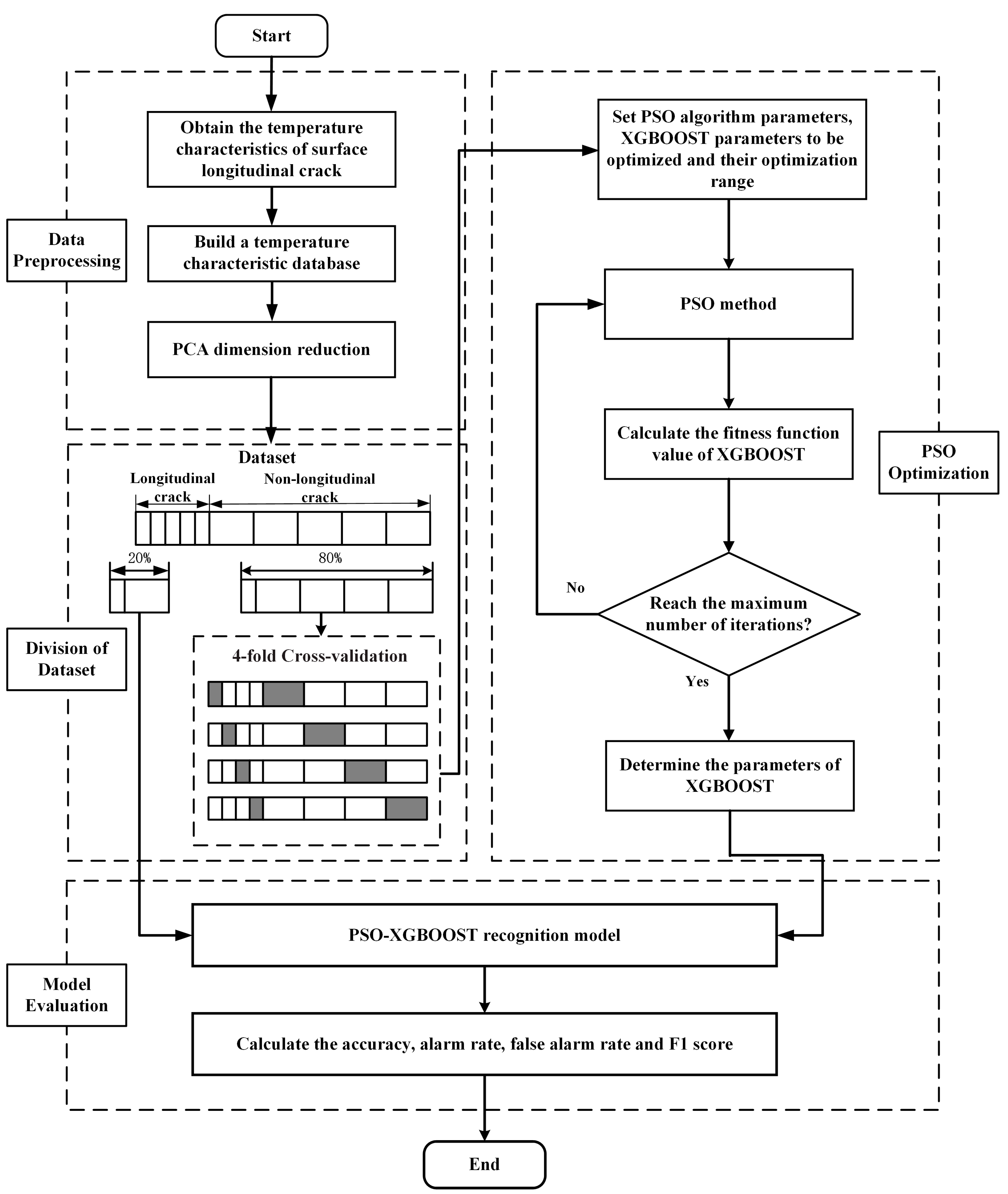
4. Methodology
5. Results and Discussion
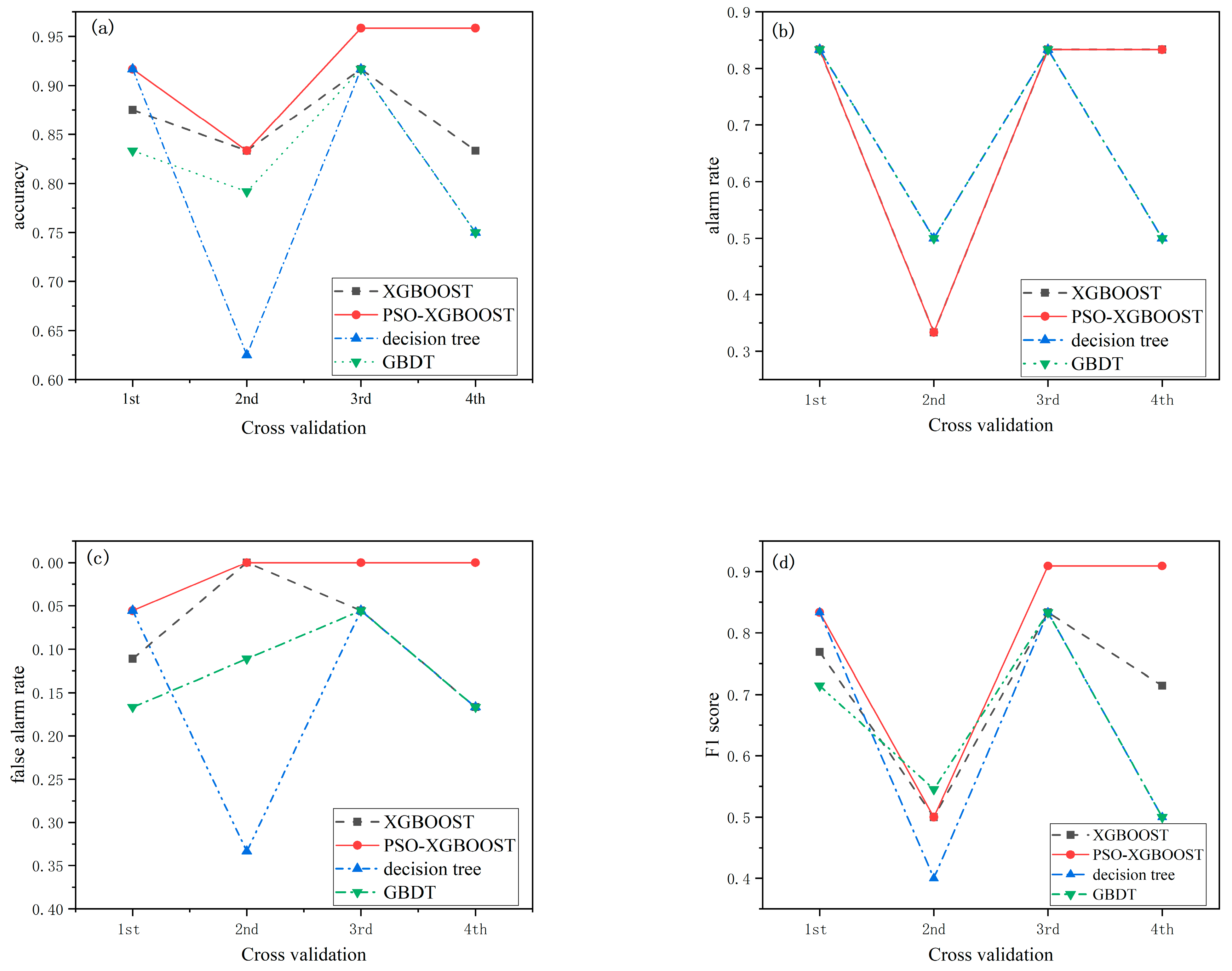
5.1. Evaluation Indexes
5.2. The Results of PSO Optimization
5.3. Discussion of Testing Results
6. Conclusions
- (1)
- In this paper, a sample database was established using all 120 samples from actual casting data of a steel plant, which consisted of longitudinal cracks and non-longitudinal cracks. The non-longitudinal crack samples contained four common conditions, which were large temperature fluctuations, small temperature fluctuations, sticker breakouts and start-up casting, and included the main large temperature fluctuation during the process of continuous casting. The 42 dimensions of the typical temperature characteristics of the middle, left and right thermocouples were extracted. The PCA method was used to reduce the original characteristic dimension from 42 to 7 on the premise of fully retaining the original information, eliminating the redundant information and reducing the complexity of the modeling operations.
- (2)
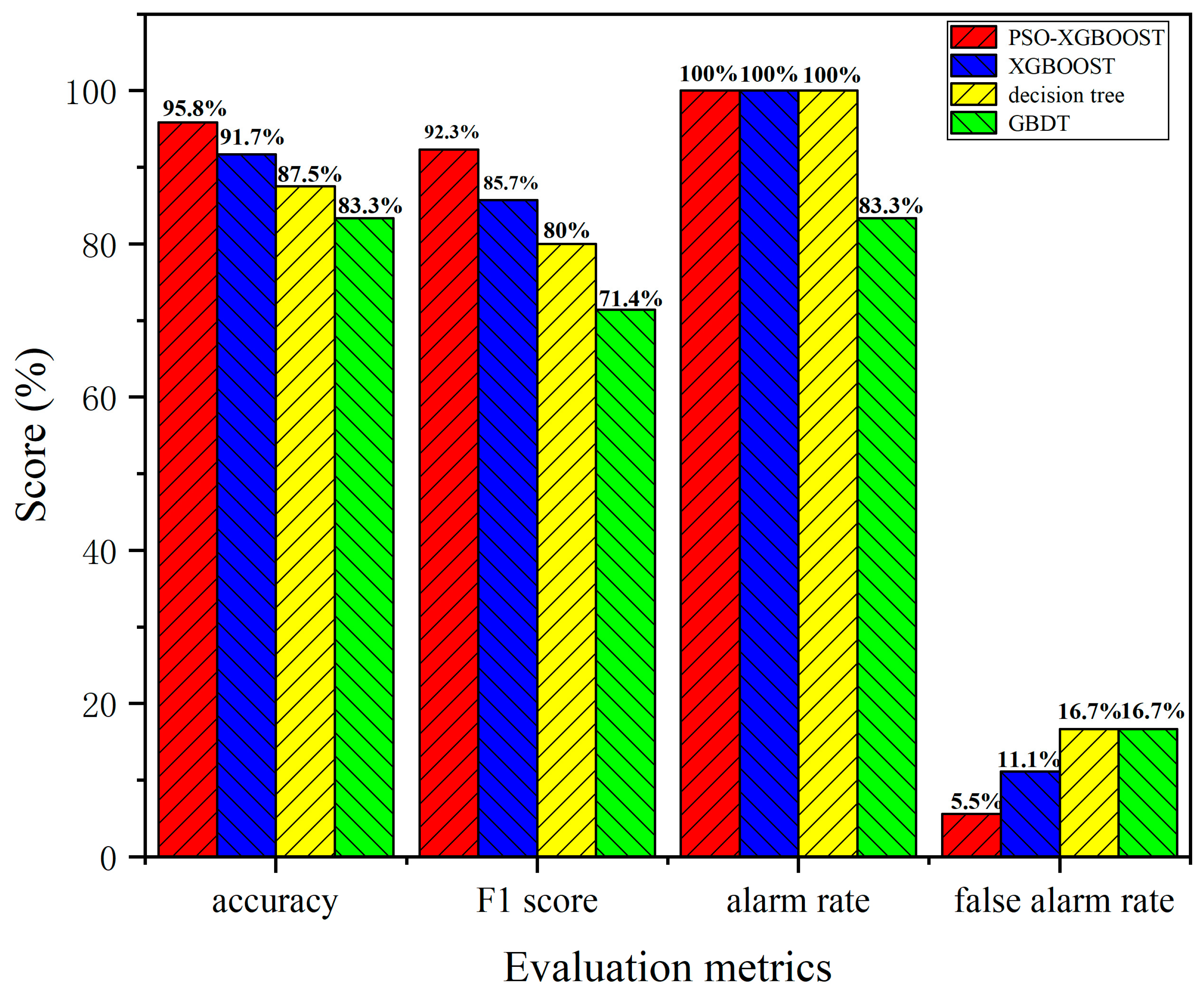
- The PSO method was used to optimize the XGBOOST model and the optimal model parameters were obtained. PSO-XGBOOST had best identification performance in all evaluation indexes, in which the accuracy reached 95.8%, the highest alarm rate was 83.3%, the F1 score reached 90.9% and the false alarm rates were as low as 0. The results revealed that the particle swarm optimization algorithm could significantly improve the identification performance of XGBOOST. The results also reflected the effectiveness of PSO in multi-parameter optimization.
- (3)
- Based on a four-fold cross-validation, PSO-XGBOOST was compared with XGBOOST, GBDT and decision tree methods on the training set. The order of the prediction accuracy of each model was PSO-XGBOOST > XGBOOST > decision tree > GBDT. Among them, PSO-XGBOOST achieved an F1 score of 95.8%, which was an improvement of 6.6%, 12.3% and 20.9% compared with XGBOOST, decision tree and GBDT, respectively. By comparison with other commonly used models, the superiority of the PSO-XGBOOST model also reflected the effectiveness of the database establishment and feature extraction methods used in this paper. The research results provide a theoretical basis and a reliable model for surface longitudinal crack identification.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Swain, A.N.S.S.; Choudhary, S.K. Effect of initial solidification characteristics on longitudinal crack formation in thin slab caster. Can. Metall. Q. 2022, 62, 372–382. [Google Scholar] [CrossRef]
- Roy, S.; Singh, R.K. Investigation of Genesis of Internal Subsurface Crack in Continuous Cast Slabs and Finding Remedial Measures. J. Fail. Anal. Prev. 2023, 23, 2633–2639. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, J. Characteristics of Inclusions and Microstructures Around Solidification Hook of Low-Carbon Steel Continuous Casting Slab. Metall. Mater. Trans. B 2023, 54, 2439–2453. [Google Scholar] [CrossRef]
- Kamaraj, A.; Haldar, N. High-temperature simulation of continuous casting mould phenomena. Trans. Indian Inst. Met. 2020, 73, 2025–2031. [Google Scholar] [CrossRef]
- Zhu, M.; Cai, Z. Formation Mechanism and Control Technology of Transverse Corner Cracks During Slab Continuous Casting of Microalloyed Steels. Steel Res. Int. 2023, 94, 2300119. [Google Scholar] [CrossRef]
- Peng, Z.; Mei, T. Cracking Behavior and High-Temperature Thermoplastic Analysis of 09CrCuSb Steel Billets. Metals 2023, 13, 1058. [Google Scholar] [CrossRef]
- Thomas, B.G. Review on modeling and simulation of continuous casting. Steel Res. Int. 2018, 89, 1700312. [Google Scholar] [CrossRef]
- Du, F.; Wang, X. Prediction of longitudinal cracks based on a full-scale finite-element model coupled inverse algorithm for a continuously cast slab. Steel Res. Int. 2017, 88, 1700013. [Google Scholar] [CrossRef]
- Fedosov, A.V.; Skrebtsov, A.M. Formation of transverse surface cracks during peritectic steel continuous casting. Metallurgist 2018, 62, 39–48. [Google Scholar] [CrossRef]
- Louhenkilpi, S.; Miettinen, J. New phenomenological quality criteria for continuous casting of steel based on solidification and microstructure tool IDS. Ironmak. Steelmak. 2021, 48, 170–179. [Google Scholar] [CrossRef]
- Klug, J.L.; Medeiros, S.L.S. Designing mould fluxes to prevent longitudinal cracking for peritectic steel slab casting. Ironmak. Steelmak. 2023, 50, 1451–1464. [Google Scholar] [CrossRef]
- Irie, S.; Tsuzumi, K. Estimation of changes in content and characteristics of mold flux during continuous casting. ISIJ Int. 2023, 63, 516–524. [Google Scholar] [CrossRef]
- Zhou, J.; Zhu, L. Analysis of the Formation Mechanism of Surface Cracks of Continuous Casting Slabs Caused by Mold Wear. Processes 2022, 10, 797. [Google Scholar] [CrossRef]
- Presoly, P.; Pierer, R. Identification of defect prone peritectic steel grades by analyzing high-temperature phase transformations. Metall. Mater. Trans. A 2013, 44, 5377–5388. [Google Scholar] [CrossRef]
- Xing, L.; Wang, M. Study on surface longitudinal crack formation of typical hypoeutectoid steel produced on a caster with billet and slab. Metals 2019, 9, 1269. [Google Scholar] [CrossRef]
- Kromhout, J.A.; Schimmel, R.C. Understanding mould powders for high-speed casting. Ironmak. Steelmak. 2018, 45, 249–256. [Google Scholar] [CrossRef]
- Furumai, K.; Zurob, H.S. Influence of mould level instability on the unevenness of solidified shell deformations during continuous casting. Ironmak. Steelmak. 2023, 50, 818–827. [Google Scholar] [CrossRef]
- Velička, M.; Pyszko, R. Research on Solid Shell Growth during Continuous Steel Casting. Materials 2023, 16, 5302. [Google Scholar] [CrossRef]
- Du, F.; Wang, X. Analysis of the non-uniform thermal behavior in slab continuous casting mold based on the inverse finite-element model. J. Mater. Process. Tech. 2014, 214, 2676–2683. [Google Scholar] [CrossRef]
- Landstrom, A.; Thurley, M.J. Morphology-based crack detection for steel slabs. IEEE J. Sel. Top. Signal Process. 2012, 6, 866. [Google Scholar] [CrossRef]
- Duan, H.; Wei, J. Longitudinal Crack Detection Approach Based on Principal Component Analysis and Support Vector Machine for Slab Continuous Casting. Steel Res. Int. 2021, 92, 2100168. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, L. Mould heat transfer and friction behavior on the surface of wide and heavy slabs in the presence of longitudinal cracks. Metall. Res. Technol. 2023, 120, 314. [Google Scholar] [CrossRef]
- Hasan, B.M.S.; Abdulazeez, A.M. A review of principal component analysis algorithm for dimensionality reduction. J. Soft Comput. Data Min. 2021, 2, 20–30. [Google Scholar]
- Emerson, R.W. A look at principal component analysis. J. Vis. Impair. Blind. 2020, 114, 240–242. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Approximating XGBoost with an interpretable decision tree. Inform. Sci. 2021, 572, 522–542. [Google Scholar] [CrossRef]
- Ogunleye, A.; Wang, Q.G. XGBoost model for chronic kidney disease diagnosis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 17, 2131–2140. [Google Scholar] [CrossRef] [PubMed]
- Jabeur, S.B.; Mefteh-Wali, S. Forecasting gold price with the XGBoost algorithm and SHAP interaction values. ANN Oper. Res. 2024, 334, 679–699. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y. An XGBoost-SHAP approach to quantifying morphological impact on urban flooding susceptibility. Ecol. Indic. 2023, 156, 111137. [Google Scholar] [CrossRef]
- Tarwidi, D.; Pudjaprasetya, S.R. An optimized XGBoost-based machine learning method for predicting wave run-up on a sloping beach. MethodsX 2023, 10, 102119. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, J. Short-term rockburst damage assessment in burst-prone mines: An explainable XGBOOST hybrid model with SCSO algorithm. Rock Mech. Rock Eng. 2023, 56, 8745–8770. [Google Scholar] [CrossRef]
- Li, Y.C. A county-level soybean yield prediction framework coupled with XGBoost and multidimensional feature engineering. Int. J. Appl. Earth Obs. 2023, 118, 103269. [Google Scholar] [CrossRef]
- Punuri, S.B.; Kuanar, S.K. Efficient net-XGBoost: An implementation for facial emotion recognition using transfer learning. Mathematics 2023, 11, 776. [Google Scholar] [CrossRef]
- Jovanovic, L.; Jovanovic, G. The explainable potential of coupling metaheuristics-optimized-xgboost and shap in revealing vocs’ environmental fate. Atmosphere 2023, 14, 109. [Google Scholar] [CrossRef]
- Li, L.; Zhao, Y. An XGBoost Algorithm Based on Molecular Structure and Molecular Specificity Parameters for Predicting Gas Adsorption. Langmuir 2023, 39, 6756–6766. [Google Scholar] [CrossRef]
- Jovanovic, G.; Perisic, M. Potential of coupling metaheuristics-optimized-XGBoost and SHAP in revealing PAHs environmental fate. Toxics 2023, 11, 394. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]


| Item | Parameters |
|---|---|
| Strand | 1 |
| Slab width | 1.8~2.7 m |
| Slab thickness | 0.22, 0.26 and 0.32 m |
| Radius | 10.75 m |
| Metallurgical length | 28.8 m |
| Mold length | 0.9 m |
| Mold level | 0.8 ± 0.003 m |
| Drive | Hydraulic drive |
| Oscillation frequency | 40~400 times·min−1 |
| Casting speed | 0.75~1.2 m·min−1 |
| Type | Location | Characteristics | |
|---|---|---|---|
| Temperature amplitude | The left thermocouple | First row | Increase amplitude |
| Decrease amplitude | |||
| Second row | Increase amplitude | ||
| Decrease amplitude | |||
| The middle thermocouple | First row | Increase amplitude | |
| Decrease amplitude | |||
| Second row | Increase amplitude | ||
| Decrease amplitude | |||
| The right thermocouple | First row | Increase amplitude | |
| Decrease amplitude | |||
| Second row | Increase amplitude | ||
| Decrease amplitude | |||
| Temperature ratio | The left thermocouple | First row | Increase ratio |
| Decrease ratio | |||
| Second row | Increase ratio | ||
| Decrease ratio | |||
| The middle thermocouple | First row | Increase ratio | |
| Decrease ratio | |||
| Second row | Increase ratio | ||
| Decrease ratio | |||
| The right thermocouple | First row | Increase ratio | |
| Decrease ratio | |||
| Second row | Increase ratio | ||
| Decrease ratio | |||
| Temperature velocity | The left thermocouple | First row | Maximum velocity |
| Minimum velocity | |||
| Second row | Maximum velocity | ||
| Minimum velocity | |||
| The middle thermocouple | First row | Maximum velocity | |
| Minimum velocity | |||
| Second row | Maximum velocity | ||
| Minimum velocity | |||
| The right thermocouple | First row | Maximum velocity | |
| Minimum velocity | |||
| Second row | Maximum velocity | ||
| Minimum velocity | |||
| Temperature standard deviation | The left thermocouple | First row | Maximum standard deviation |
| Second row | Maximum standard deviation | ||
| The middle thermocouple | First row | Maximum standard deviation | |
| Second row | Maximum standard deviation | ||
| The right thermocouple | First row | Maximum standard deviation | |
| Second row | Maximum standard deviation | ||
| Principal Component | Variance Contribution Rate (%) | Accumulated Variance Contribution Rate (%) |
|---|---|---|
| 1 | 33.98 | 33.98 |
| 2 | 18.4 | 52.38 |
| 3 | 14.09 | 66.47 |
| 4 | 5.6 | 72.07 |
| 5 | 4.94 | 77.01 |
| 6 | 4.63 | 81.64 |
| 7 | 3.56 | 85.2 |
| 8 | 2.91 | 88.11 |
| 9 | 2 | 90.11 |
| 10 | 1.89 | 92 |
| 11 | 1.75 | 93.75 |
| 12 | 1.14 | 94.89 |
| 13 | 0.97 | 95.86 |
| 14 | 0.79 | 96.65 |
| 15 | 0.62 | 97.27 |
| 16 | 0.54 | 97.81 |
| 17 | 0.4 | 98.21 |
| 18 | 0.36 | 98.57 |
| 19 | 0.36 | 98.93 |
| 20 | 0.28 | 99.21 |
| 21 | 0.21 | 99.42 |
| 22 | 0.15 | 99.57 |
| 23 | 0.1 | 99.67 |
| 24 | 0.09 | 99.76 |
| Confusion Matrix | Actual Class | ||
|---|---|---|---|
| Positive | Negative | ||
| Predicted class | Positive | TP (true-positive) | FP (false-positive) |
| Negative | FN (false-negative) | TN (true-negative) | |
| Parameters | Default Values | Optimal Range | Optimization Results |
|---|---|---|---|
| learning_rate | 0.3 | (0.01,0.2) | 0.2 |
| n_estimators | 300 | (300,1000) | 309 |
| max_depth | 6 | (3,10) | 4 |
| min_child_weight | 1 | (0.01,1) | 1 |
| gamma | 0 | (0,0.2) | 0.2 |
| reg_lambda | 1 | (0.1,1) | 0.1 |
| subsample | 1 | (0.5,1) | 0.84 |
| colsample_bytree | 1 | (0.5,1) | 0.5 |
| Confusion Matrix | Actual Class | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| PSO-XGBOOST | XGBOOST | Decision Tree | GBDT | ||||||
| Positive | Negative | Positive | Negative | Positive | Negative | Positive | Negative | ||
| Predicted class | Positive | 6 | 1 | 6 | 2 | 6 | 3 | 5 | 3 |
| Negative | 0 | 17 | 0 | 16 | 0 | 15 | 1 | 15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, L.; Shi, J.; Liu, J.; Li, G.; Wang, Z.; Zhang, Z. Recognition of Longitudinal Cracks on Slab Surfaces Based on Particle Swarm Optimization and eXtreme Gradient Boosting Model. Processes 2024, 12, 1087. https://doi.org/10.3390/pr12061087
Liu Y, Jiang L, Shi J, Liu J, Li G, Wang Z, Zhang Z. Recognition of Longitudinal Cracks on Slab Surfaces Based on Particle Swarm Optimization and eXtreme Gradient Boosting Model. Processes. 2024; 12(6):1087. https://doi.org/10.3390/pr12061087
Chicago/Turabian StyleLiu, Yu, Lai Jiang, Jing Shi, Jiabin Liu, Guohui Li, Zhaofeng Wang, and Zhi Zhang. 2024. "Recognition of Longitudinal Cracks on Slab Surfaces Based on Particle Swarm Optimization and eXtreme Gradient Boosting Model" Processes 12, no. 6: 1087. https://doi.org/10.3390/pr12061087
APA StyleLiu, Y., Jiang, L., Shi, J., Liu, J., Li, G., Wang, Z., & Zhang, Z. (2024). Recognition of Longitudinal Cracks on Slab Surfaces Based on Particle Swarm Optimization and eXtreme Gradient Boosting Model. Processes, 12(6), 1087. https://doi.org/10.3390/pr12061087







