A Semi-Global Finite-Time Dynamic Control Strategy of Stochastic Nonlinear Systems
Abstract
:1. Introduction
Can we present a new semi-global finite control method for a general stochastic nonlinear system to avoid the above problem?
- (i)
- This paper presents a new control strategy. For a general stochastic nonlinear system, we introduce the dynamic-gain-based transformation and obtain a transformed dynamic system. By providing the required conditions and adopting the idea of homogeneous domination, we present a new scheme to construct a dynamic controller, which guarantees that the whole system is SGFSP.
- (ii)
- The presented strategy is successfully applied to stabilize stochastic nonlinear systems. By imposing the assumptions and verifying all the needed conditions, we flexibly select a new Lyapunov function and provide a detailed design procedure for the studied system. Finally, a dynamic controller is designed.
2. System, Definition, and Useful Lemmas
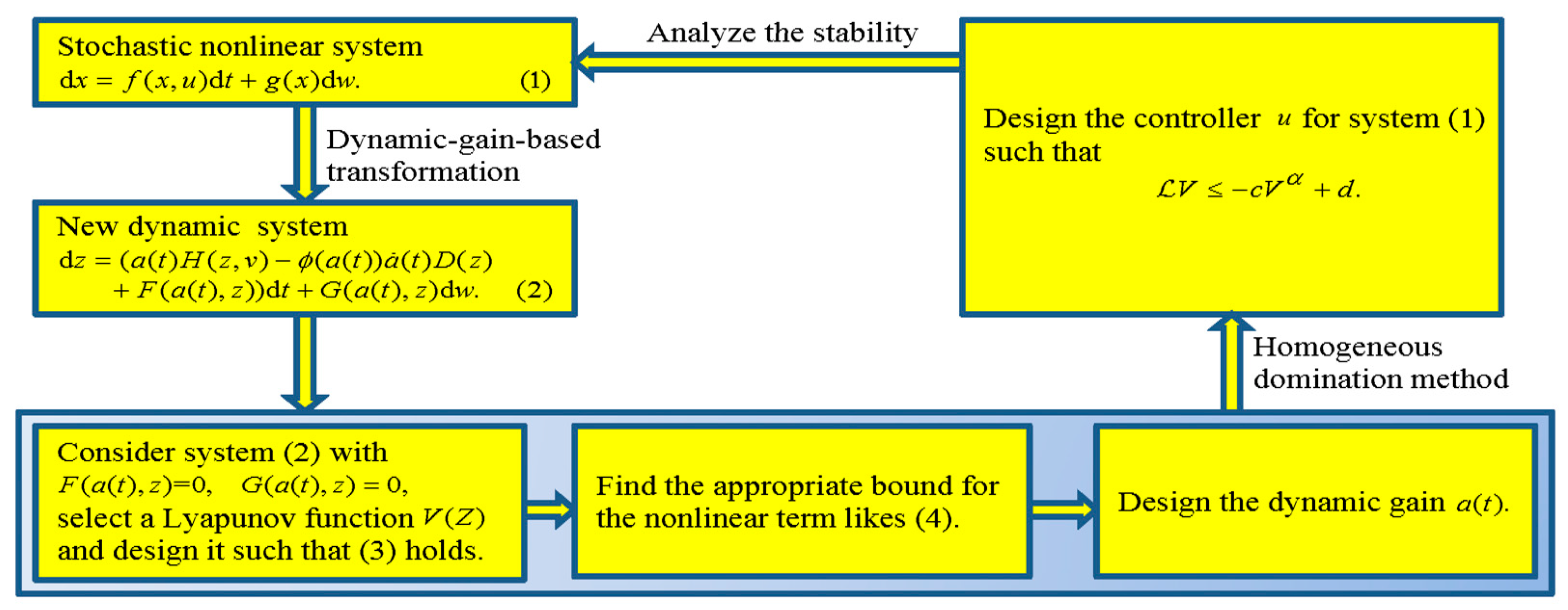
3. Dynamic-Gain-Based Homogeneous Domination Method
4. Control of Second-Order Stochastic Nonlinear System
- Step 1. By the definition choose the function then the differential operator of satisfiesChoosing the virtual controller with being a positive constant and substituting it into (8), we get
- Step 2. Noting it is deduced thatUsing Lemma 3, we have from which Lemma 1 indicateswhere Given Lemma 1 and there holdswhere and are constants. Considering and applying it yields that Thus, it follows from Lemma 1 thatwhere is a constant and satisfies Putting (10)–(12) into (9) givesIf we choose satisfying define and design then it follows thatNow, considering (6) and (13), it yields Besides, by the definition of and it is easy to deduce thatIn view of and based on Assumption 1, one can find a constant satisfyingNoting (14), (15), and Lemma 1, there are constants such thatDefining it shows that It is easy to getIn addition, there is a constant such thatBy Lemma 1, (16) and (17), there are constants and such thatThen, we can deduce that . Please refer to the appendix for detailed proofs of the above inequalities. Now, defining and it yields that (4) holds. In addition, it is not difficult to obtain where Also, there holds where Hence, all conditions of Theorem 1 are satisfied. Then, for system (5), using Theorem 1, we can construct the dynamic-gain-based controllersuch that the equilibrium of system (5) is SGFSP.◻
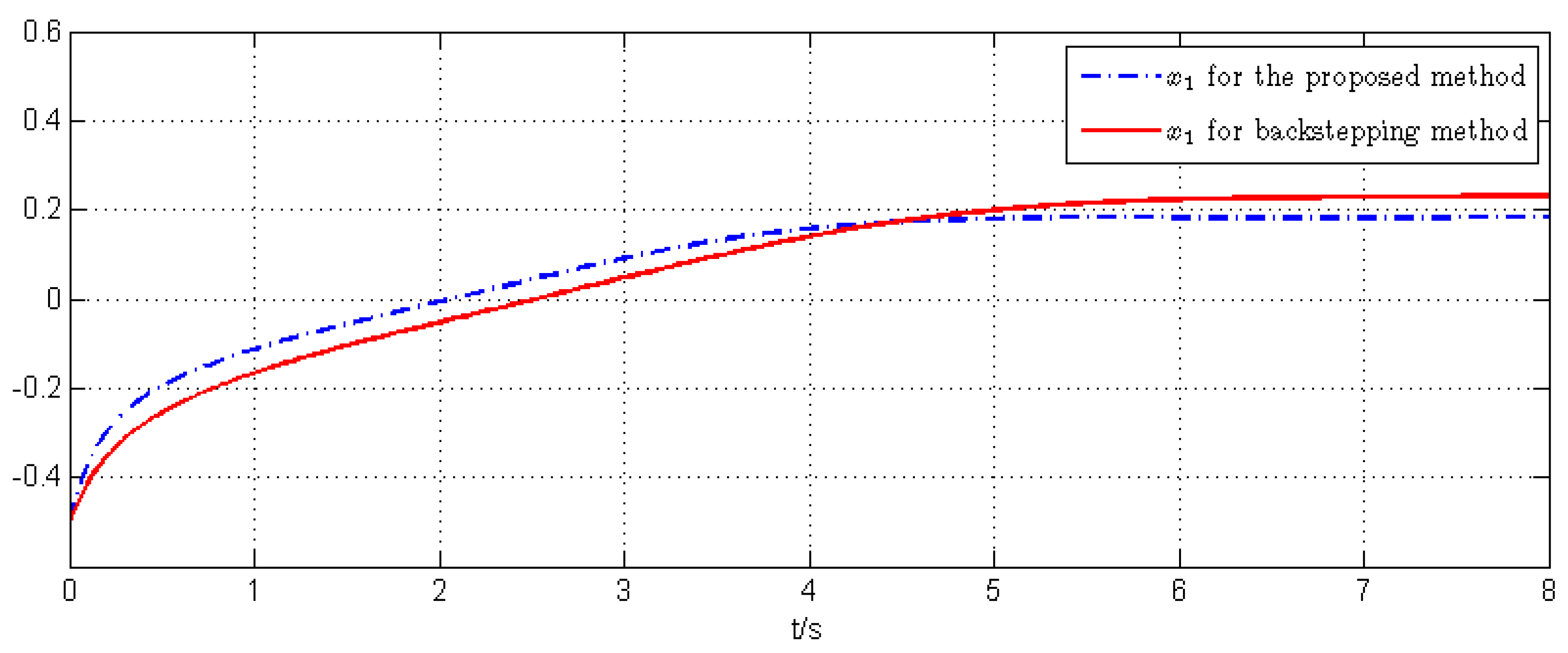
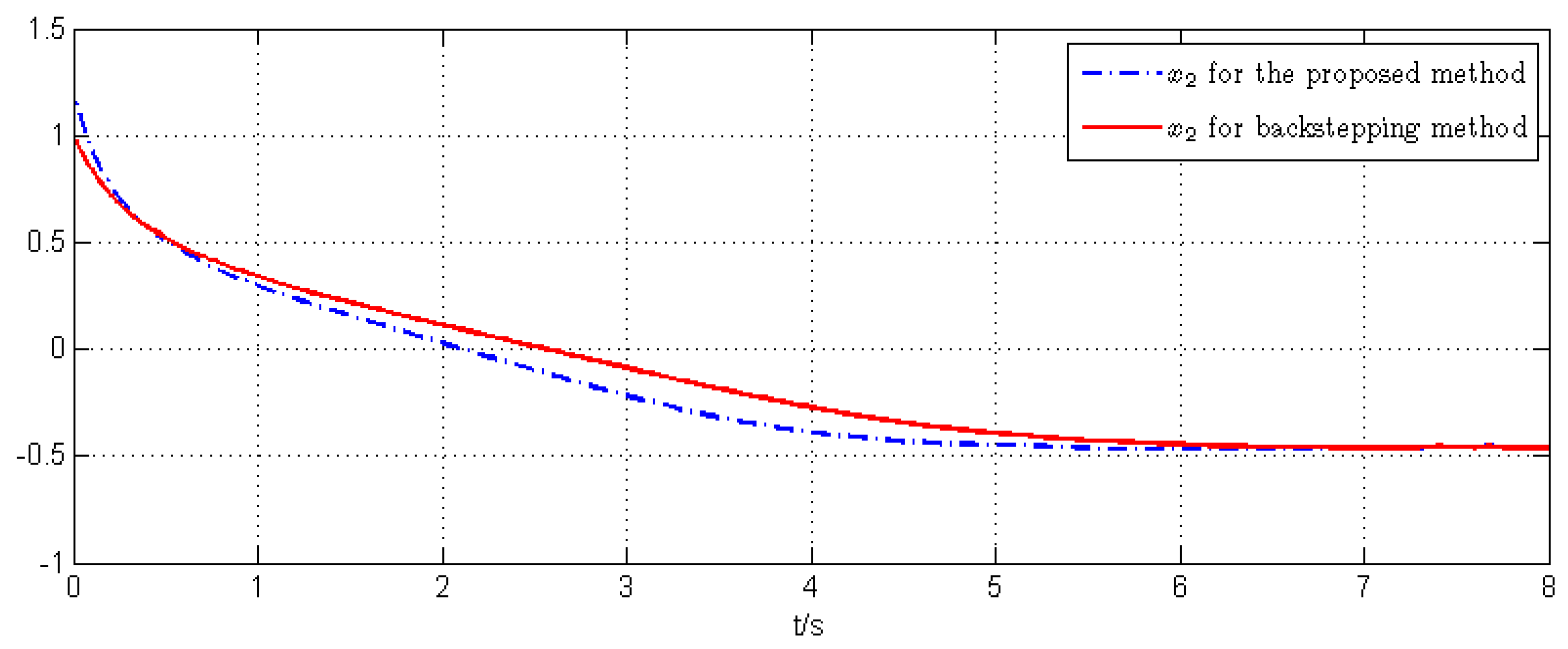
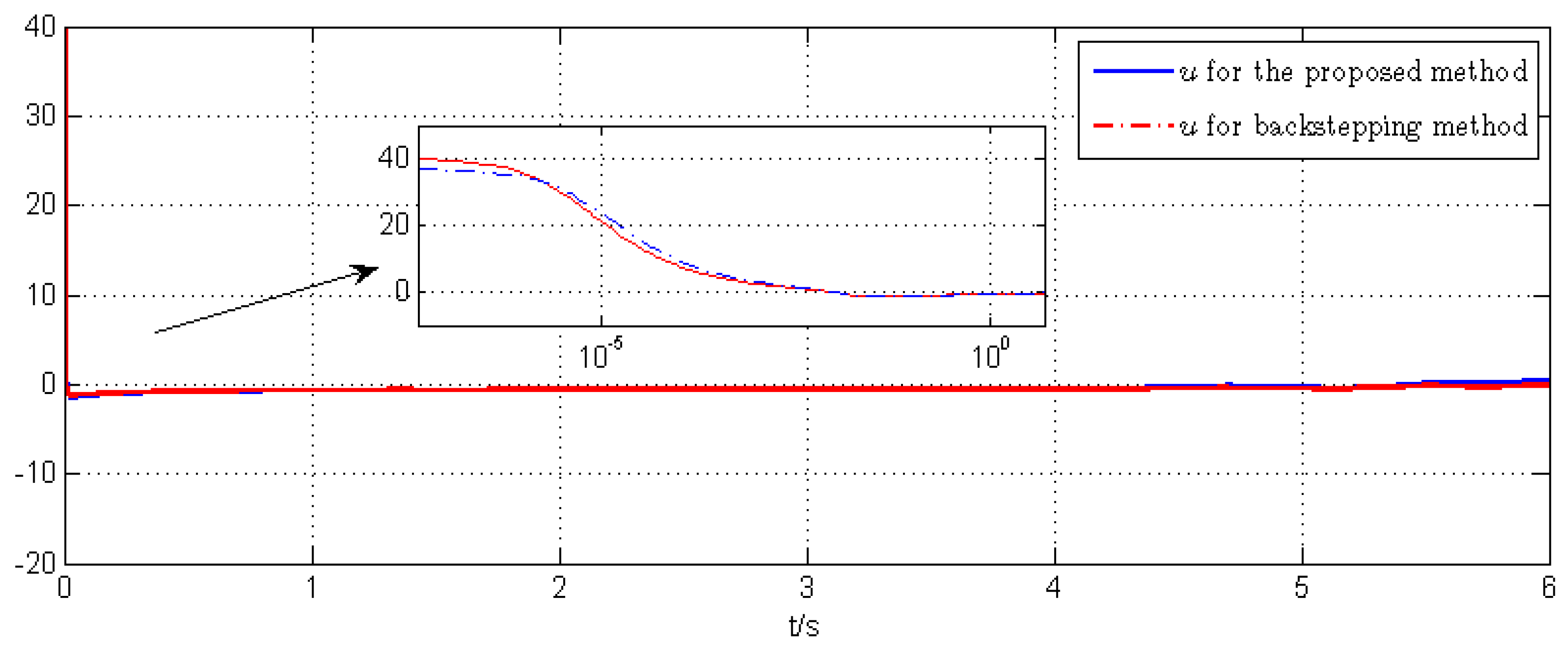
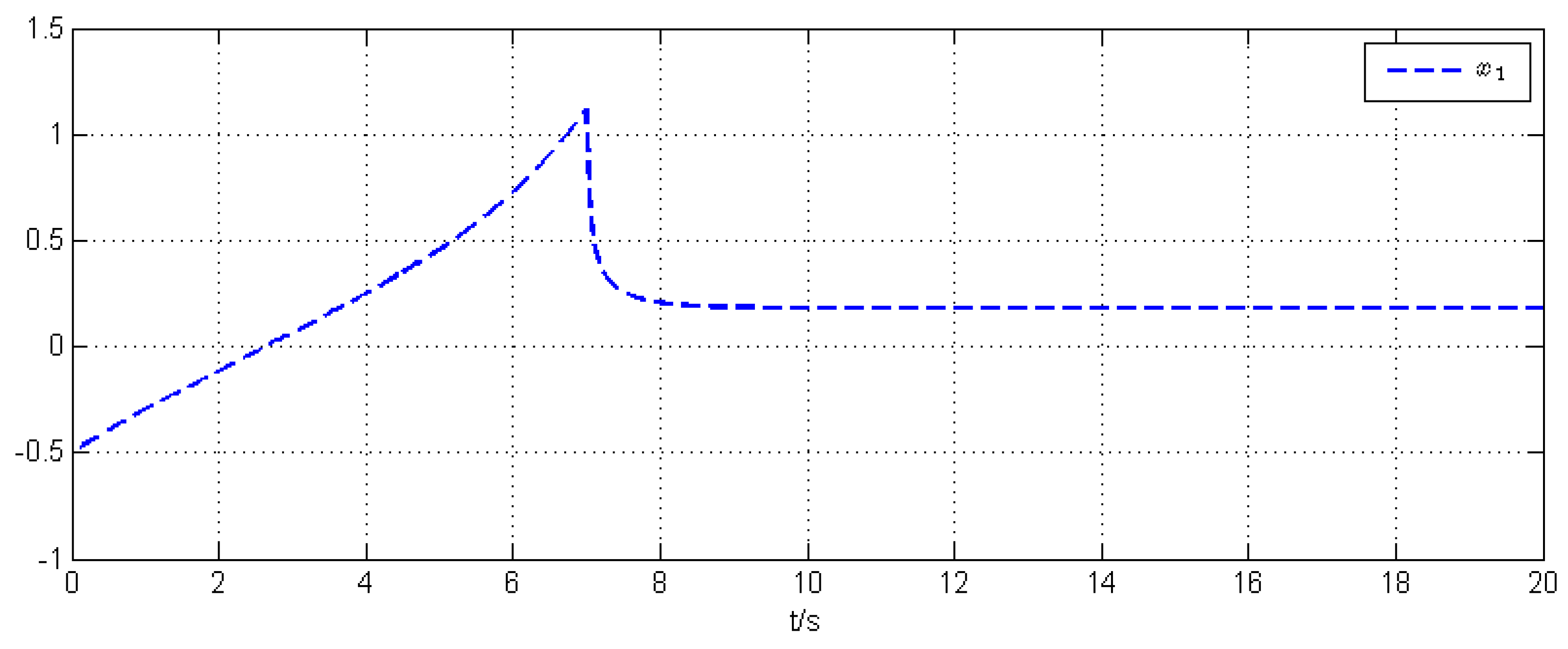
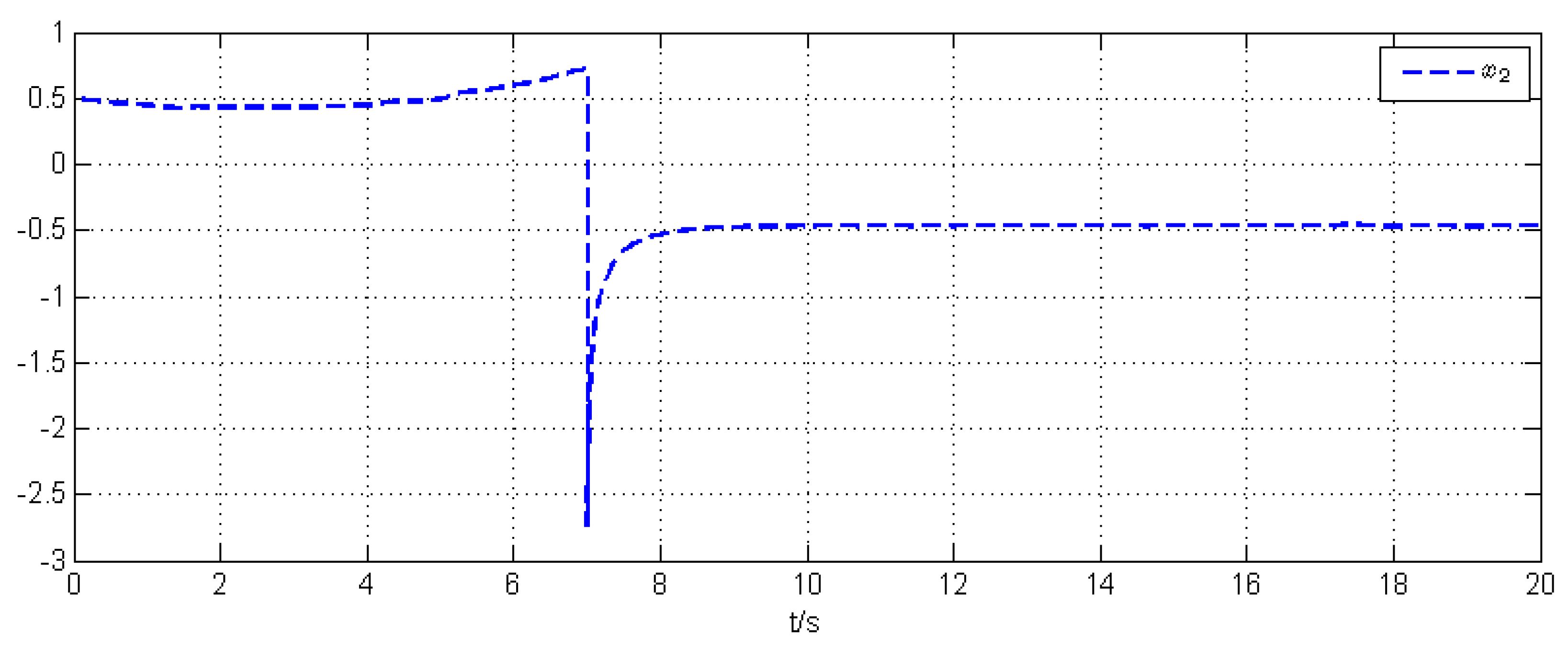
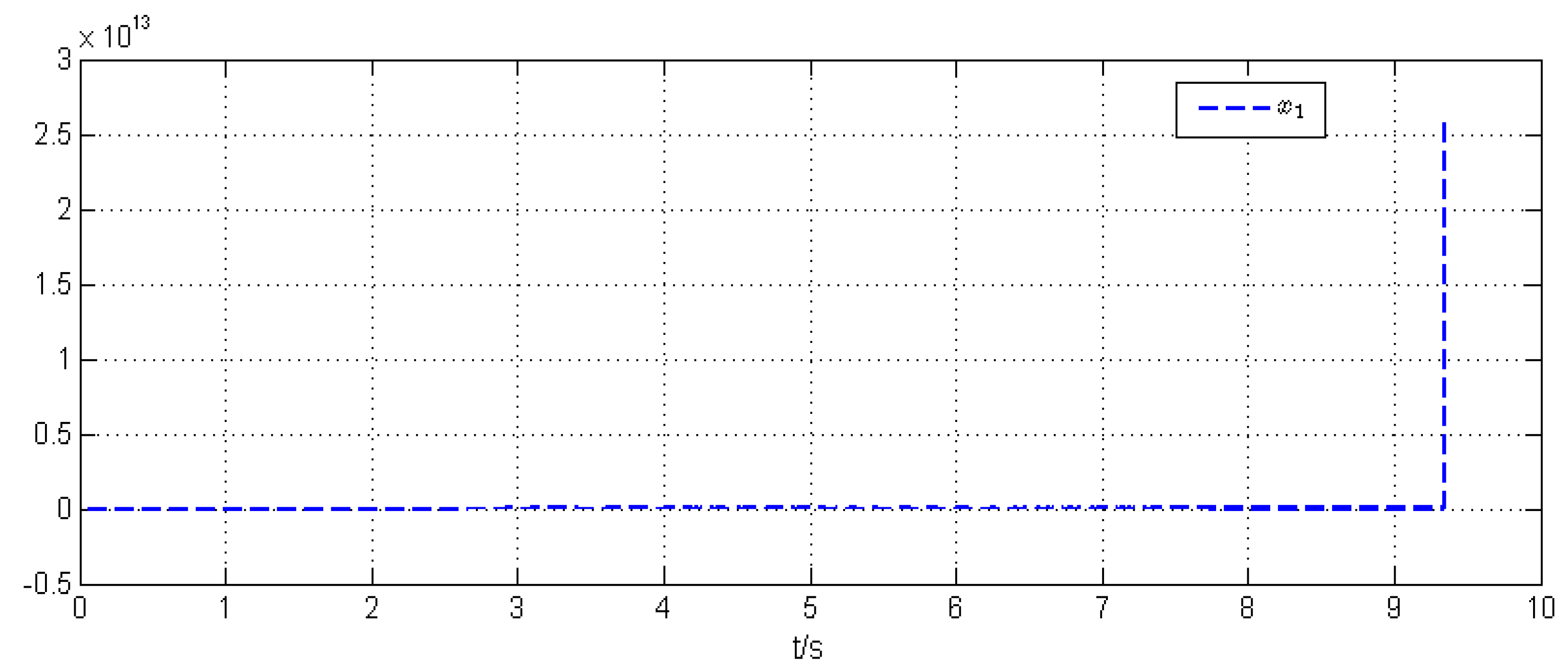
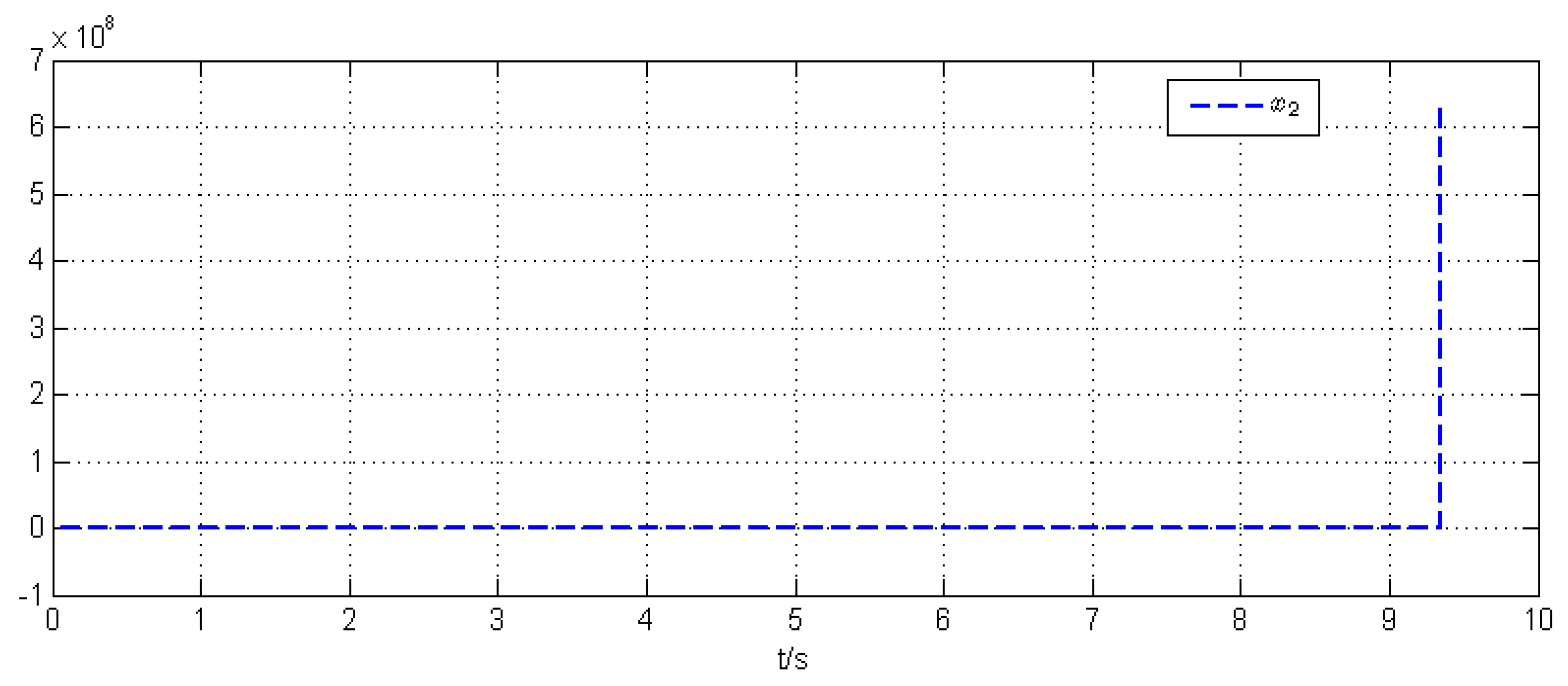
5. Simulation Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lv, L.N.; Sun, Z.Y.; Xie, X.J. Adaptive control for high-order time-delay uncertain nonlinear system and application to chemical reactor system. Int. J. Adapt. Control Signal Process. 2015, 29, 224–241. [Google Scholar] [CrossRef]
- Sun, W.; Diao, S.Z.; Su, S.F.; Wu, Y.Q. Adaptive fuzzy tracking for flexible-joint robots with random noises via command filter control. Inform. Sci. 2023, 575, 116–132. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Gao, Y.; Bian, J.S.; Wu, Y.Q. Event-triggered fixed-time tracking of state-constrained surface ships under actuation saturation with prescribed control performance. Ocean Eng. 2023, 281, 114784. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Sastry, S. Nonlinear Systems: Analysis, Stability, and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Do, K.D. Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances. Ocean Eng. 2016, 111, 267–278. [Google Scholar] [CrossRef]
- Cui, M.Y.; Wu, Z.J.; Xie, X.J. Output feedback tracking control of stochastic Lagrangian systems and its application. Automatica 2014, 50, 1424–1433. [Google Scholar] [CrossRef]
- Li, W.Q.; Krstic, M. Prescribed-time output-feedback control of stochastic nonlinear systems. IEEE Trans. Autom. Control. 2023, 68, 1431–1446. [Google Scholar] [CrossRef]
- Cui, R.H.; Xie, X.J. Adaptive state-feedback stabilization of state-constrained stochastic high-order nonlinear systems. Sci. China Inform. Sci. 2021, 64, 1–11. [Google Scholar] [CrossRef]
- Wang, H.Q.; Liu, P.X.; Bao, J.L.; Xie, X.J.; Li, S. Adaptive neural output-feedback decentralized control for largescale nonlinear systems with stochastic disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 972–983. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Shao, Y.; Chen, C.C. Fast finite-time stability and its application in adaptive control of high-order nonlinear system. Automatica 2019, 106, 339–348. [Google Scholar] [CrossRef]
- Chen, C.C.; Sun, Z.Y. A unified approach to finite-time stabilization of high-order nonlinear systems with an asymmetric output constraint. Automatica 2020, 111, 108581. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, S.Y.; Chen, X.; Zhang, B. Fast finite-time control for a class of stochastic low-order nonlinear system with uncertainties. J. Franklin Inst. 2024, 361, 106788. [Google Scholar] [CrossRef]
- Yan, Z.G.; Zhang, G.S.; Wang, J.K.; Zhang, W.H. State and output feedback finite-time guaranteed cost control of linear Itô stochastic systems. J. Syst. Sci. Complex. 2015, 28, 813–829. [Google Scholar] [CrossRef]
- You, Z.Y.; Wang, F. Adaptive fast finite-time fuzzy control of stochastic nonlinear systems. IEEE Trans. Fuzzy Syst. 2022, 30, 2279–2288. [Google Scholar] [CrossRef]
- Xia, J.W.; Li, B.M.; Su, S.F.; Sun, W.; Shen, H. Finite-time command filtered event-triggered adaptive fuzzy tracking control for stochastic nonlinear systems. IEEE Trans. Fuzzy Syst. 2021, 29, 1815–1825. [Google Scholar] [CrossRef]
- Lei, H.; Lin, W. Robust control of uncertain systems with polynomial nonlinearity by output feedback. Int. J. Robust Nonlin. Control 2009, 19, 692–723. [Google Scholar] [CrossRef]
- Wang, T.; Luo, X.; Li, W. Razumikhin-type approach on state feedback of stochastic high-order nonlinear systems with time-varying delay. Int. J. Robust Nonlin. Control 2017, 27, 3124–3134. [Google Scholar] [CrossRef]
- Min, H.; Xu, S.; Li, Y.; Chu, Y.; Wei, Y.; Zhang, Z. Adaptive finite-time control for stochastic nonlinear systems subject to unknown covariance noise. J. Franklin Inst. 2018, 355, 2645–2661. [Google Scholar] [CrossRef]
- Sui, S.; Chen, C.L.P.; Tong, S. Finite-time adaptive fuzzy prescribed performance control for high-order stochastic nonlinear systems. IEEE Trans. Fuzzy Syst. 2021, 30, 2227–2240. [Google Scholar] [CrossRef]
- Sun, J.; He, H.; Yi, J.; Pu, Z. Finite-time command-filtered composite adaptive neural control of uncertain nonlinear systems. IEEE Trans. Cybern. 2020, 52, 6809–6821. [Google Scholar] [CrossRef]
- Li, W.; Yao, X.; Krstić, M. Adaptive-gain observer-based stabilization of stochastic strict-feedback systems with sensor uncertainty. Automatica 2020, 120, 109112. [Google Scholar] [CrossRef]
- Wei, X.J.; Wu, Z.J.; Karimi, H.R. Disturbance observer-based disturbance attenuation control for a class of stochastic systems. Automatica 2016, 63, 21–25. [Google Scholar] [CrossRef]
- Su, H.; Zhang, W. Adaptive fuzzy control of stochastic nonlinear systems with fuzzy dead zones and unmodeled dynamics. IEEE Trans. Cybern. 2018, 50, 587–599. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Krstić, M. Stochastic nonlinear stabilization—I: A backstepping design. Syst. Control Lett. 1997, 32, 143–150. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, B.; Lin, C.; Wang, H.; Zhou, S. Adaptive neural control for a class of stochastic nonlinear systems by backstepping approach. Inform. Sci. 2016, 369, 748–764. [Google Scholar] [CrossRef]
- Xia, M.; Zhang, T. Adaptive neural dynamic surface control for full state constrained stochastic nonlinear systems with unmodeled dynamics. J. Franklin Inst. 2019, 356, 129–146. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, T.; Zhu, J.; Yi, Y. Adaptive output feedback dynamic surface control of stochastic nonlinear systems with state and input unmodeled dynamics. Int. J. Adapt. Control Signal Process. 2016, 30, 864–887. [Google Scholar] [CrossRef]
- Liu, S.; Niu, B.; Zong, G.; Zhao, X.; Xu, N. Adaptive neural dynamic-memory event-triggered control of high-order random nonlinear systems with deferred output constraints. IEEE Trans. Autom. Sci. Eng. 2023. [CrossRef]
- Tong, D.; Xu, C.; Chen, Q.; Zhou, W.; Xu, Y. Sliding mode control for nonlinear stochastic systems with Markovian jumping parameters and mode-dependent time-varying delays. Nonlinear Dynam. 2020, 100, 1343–1358. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Xue, X.; Wei, Y.; Li, T.; Chen, X. Backstepping control for stochastic nonlinear strict-feedback systems based on observer with incomplete measurements. Int. J. Control 2022, 95, 3211–3225. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.P.; Jing, Y.W.; Zhang, Z.Y. Semi-globally practical finite-time stability for uncertain nonlinear systems based on dynamic surface control. Int. J. Control 2021, 94, 476–485. [Google Scholar] [CrossRef]
- Spelta, A.; Pecora, N.; Pagnottoni, P. Chaos based portfolio selection: A nonlinear dynamics approach. Expert Syst. Appl. 2022, 188, 116055. [Google Scholar] [CrossRef]
- Jhangeer, A.; Almusawa, H.; Hussain, Z. Bifurcation study and pattern formation analysis of a nonlinear dynamical system for chaotic behavior in traveling wave solution. Results Phys. 2022, 37, 105492. [Google Scholar] [CrossRef]
- Song, Z.; Zhai, J. Practical output tracking control for switched nonlinear systems: A dynamic gain based approach. Nonlinear Anal. Hybrid Syst. 2018, 30, 147–162. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, Z.; Zhang, L. Small perturbations may change the sign of Lyapunov exponents for linear SDEs. Stoch. Dyn. 2022, 22, 2240038. [Google Scholar] [CrossRef]
- Luo, S.; Deng, F. Necessary and sufficient conditions for 2pth moment stability of several classes of linear stochastic systems. IEEE Trans. Autom. Control 2019, 65, 3084–3091. [Google Scholar] [CrossRef]
- Ling, Q.; Jin, X.; Wang, Y.; Li, H.F.; Huang, Z.L. Lyapunov function construction for nonlinear stochastic dynamical systems. Nonlinear Dynam. 2013, 72, 853–864. [Google Scholar] [CrossRef]
- Lin, W.; Qian, C. Adaptive control of nonlinearly parameterized systems: A nonsmooth feedback framework. IEEE Trans. Autom. Control 2002, 47, 757–774. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Xue, L.; Liu, Z.-G.; Ren, L. A Semi-Global Finite-Time Dynamic Control Strategy of Stochastic Nonlinear Systems. Processes 2024, 12, 1377. https://doi.org/10.3390/pr12071377
Luo C, Xue L, Liu Z-G, Ren L. A Semi-Global Finite-Time Dynamic Control Strategy of Stochastic Nonlinear Systems. Processes. 2024; 12(7):1377. https://doi.org/10.3390/pr12071377
Chicago/Turabian StyleLuo, Cuixian, Lingrong Xue, Zhen-Guo Liu, and Lifang Ren. 2024. "A Semi-Global Finite-Time Dynamic Control Strategy of Stochastic Nonlinear Systems" Processes 12, no. 7: 1377. https://doi.org/10.3390/pr12071377




