The Analysis of Transient Temperature in the Wellbore of a Deep Shale Gas Horizontal Well
Abstract
:1. Introduction
2. Wellbore Heat Transfer Model
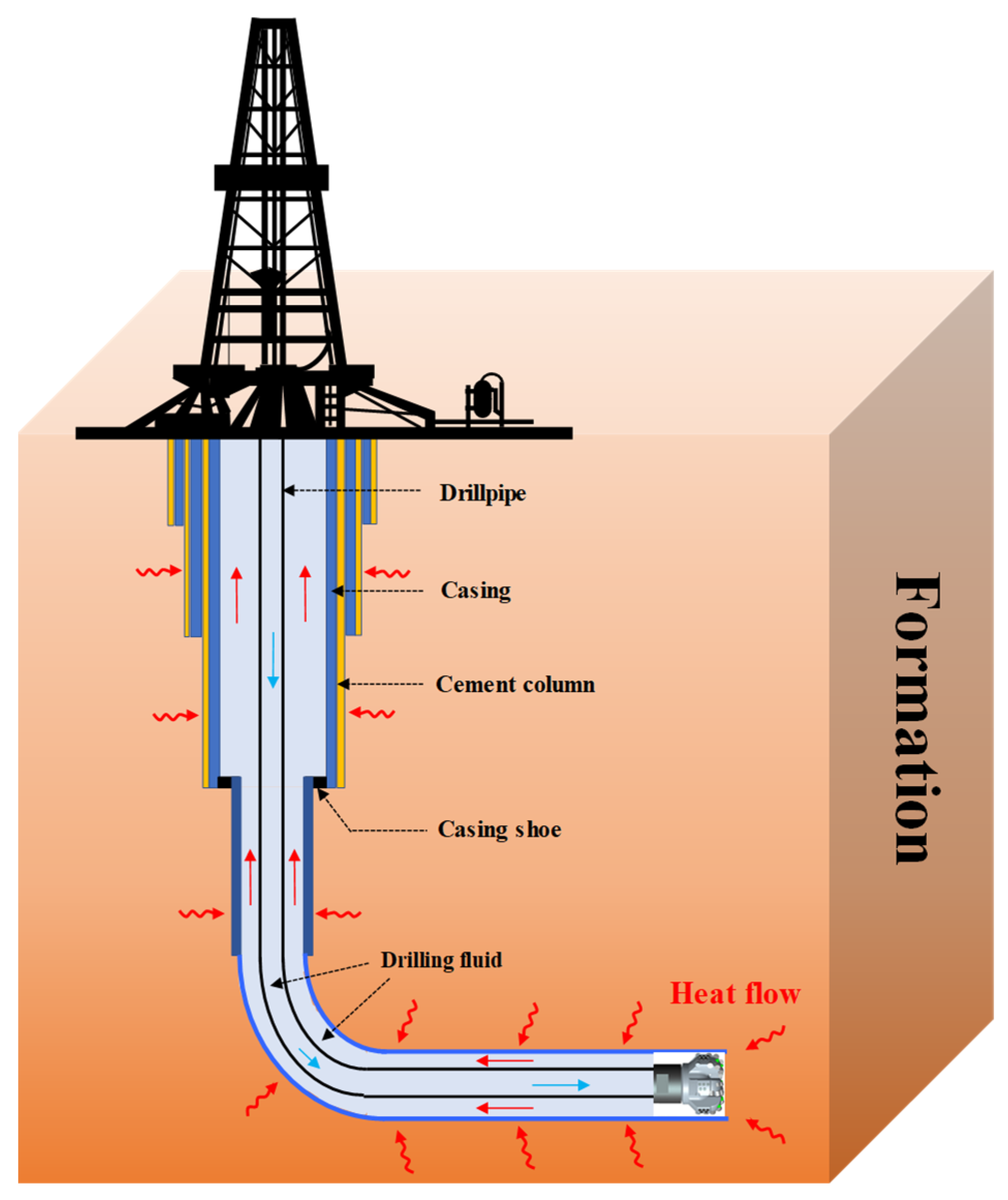
2.1. Physical Model
2.2. Model Assumes
- The formation temperature varies linearly with well depth, and the effects of overflow, loss, and fluid phase transitions during the drilling process on the wellbore temperature distribution are not considered.
- During rotary drilling, the friction heat generated by drill pipe buckling and rotation is not considered. The drill pipe is centered in the wellbore, and the wellbore trajectory has a regular geometric shape.
- Fluid conduction along the axial direction and radial temperature gradients within the fluid are neglected, while axial heat conduction of the drill pipe and convective heat transfer between the fluid and the drill pipe wall in the radial direction are considered.
- The thermophysical parameters of the fluid, formation and various heat transfer media in the wellbore remain constant, and the influence of fluid flow in the formation pores on the formation temperature distribution is neglected.
2.3. Mathematical Model
2.3.1. Temperature Model of Mud in Drill Pipe
2.3.2. Temperature Model of Drill Pipe and Drill Bit
2.3.3. Temperature Model of Annular Mud
2.3.4. Temperature Model of Formation near Well
2.4. Initial Condition and Boundary Condition
2.4.1. Initial-Boundary Condition of Vertical Section
2.4.2. Initial-Boundary Value Condition of Oblique Section
2.4.3. Initial-Boundary Condition of Horizontal Segment
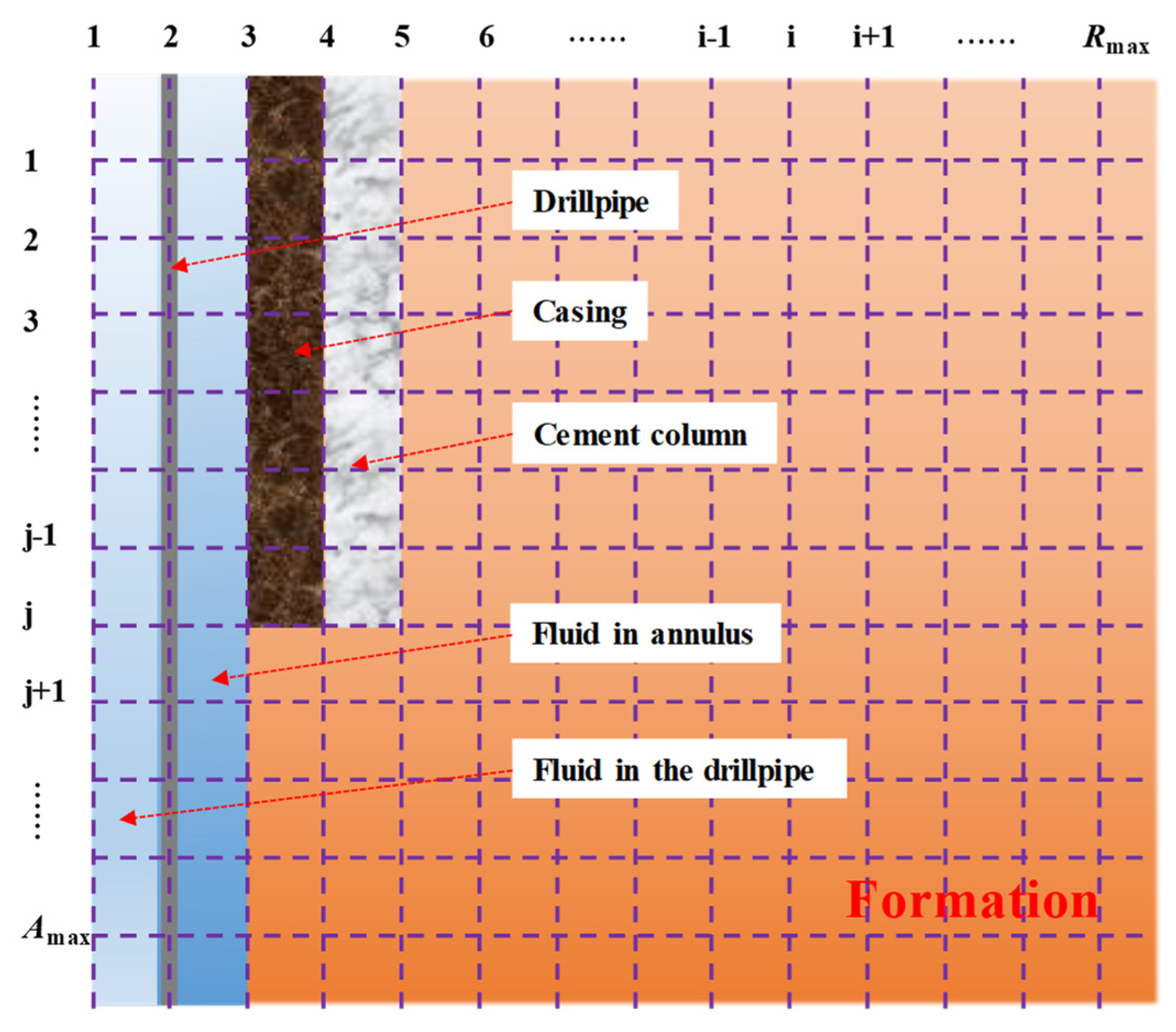
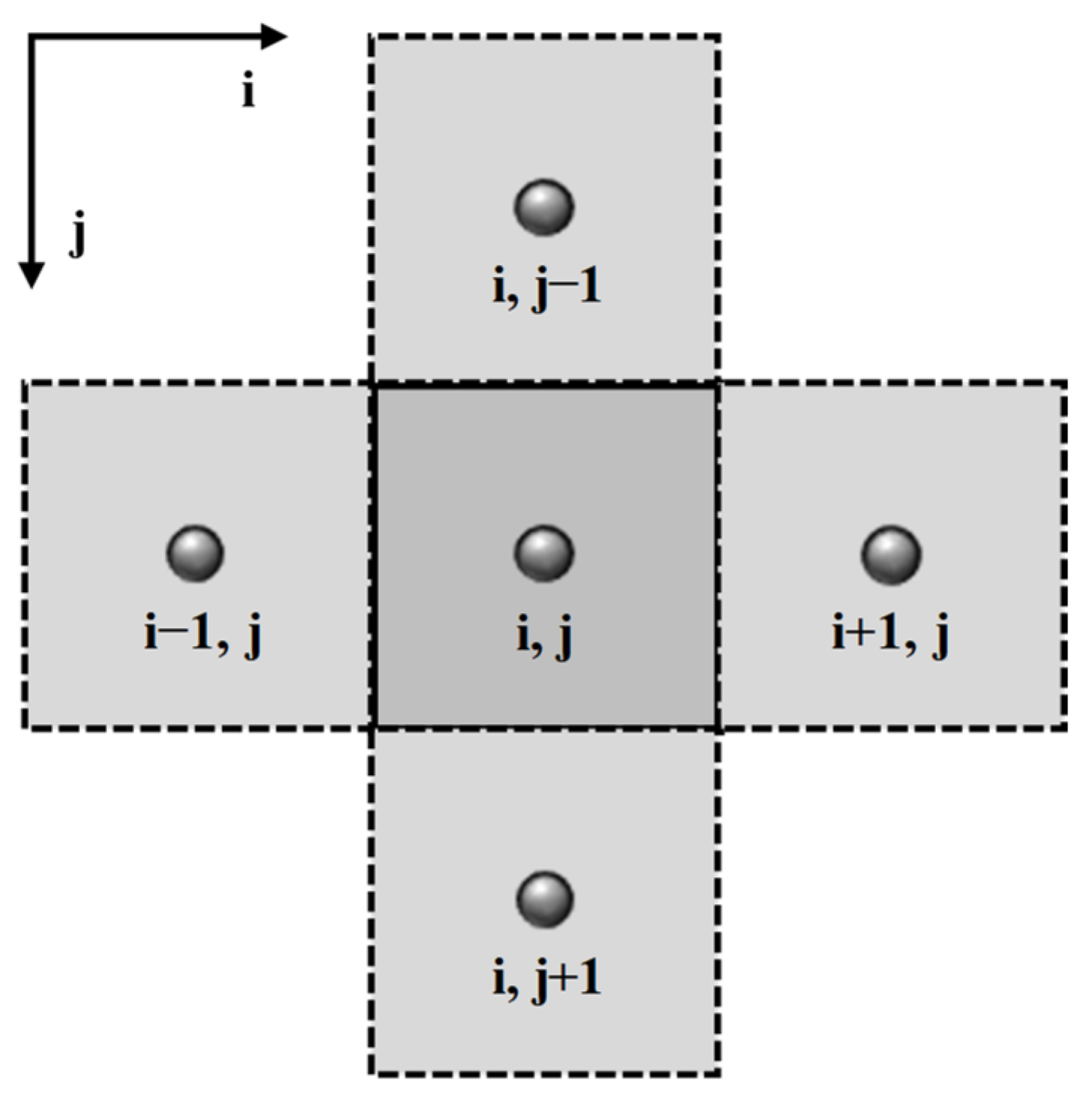
2.5. Model Discretization and Solution
3. Results and Discussion
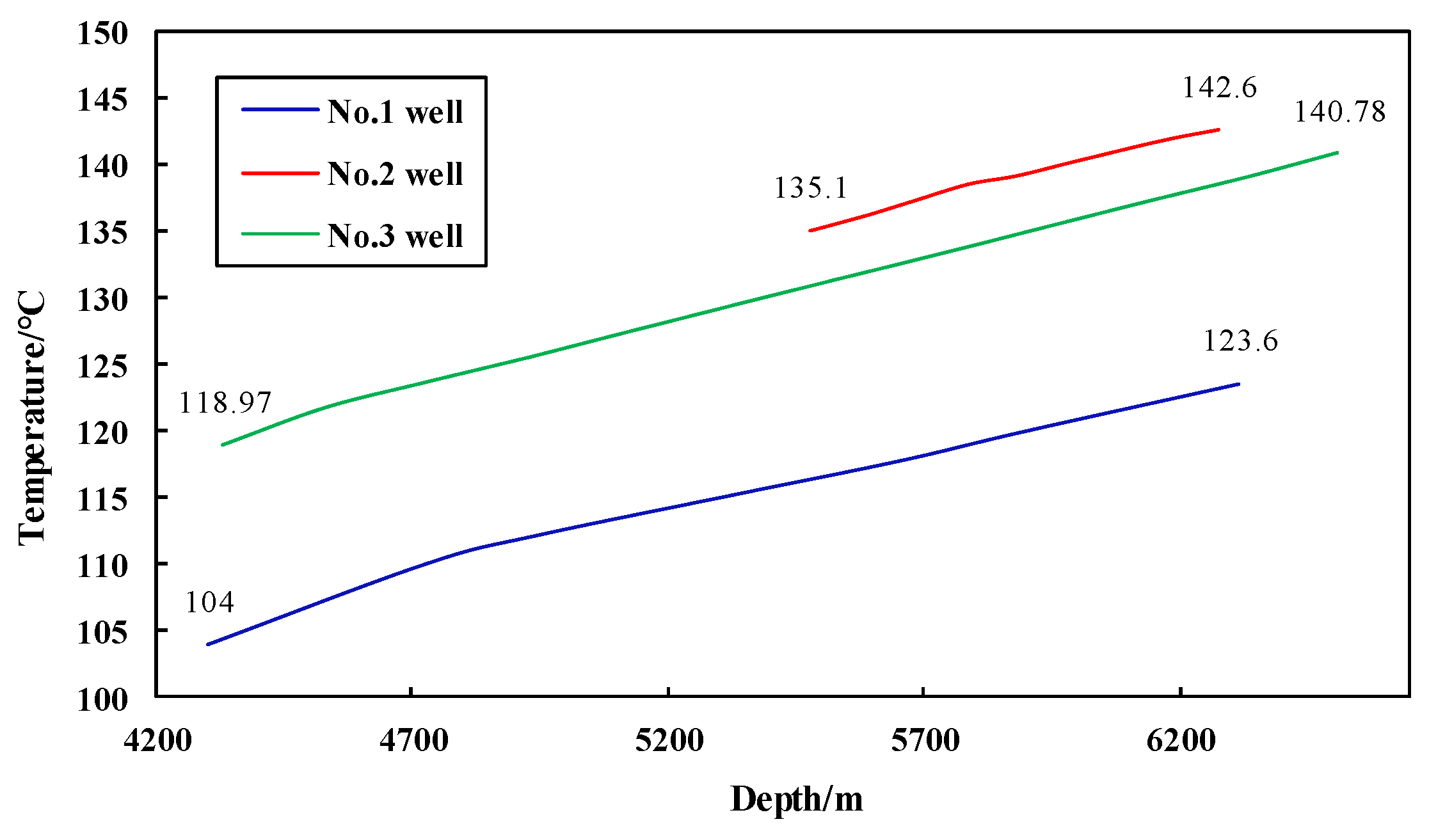
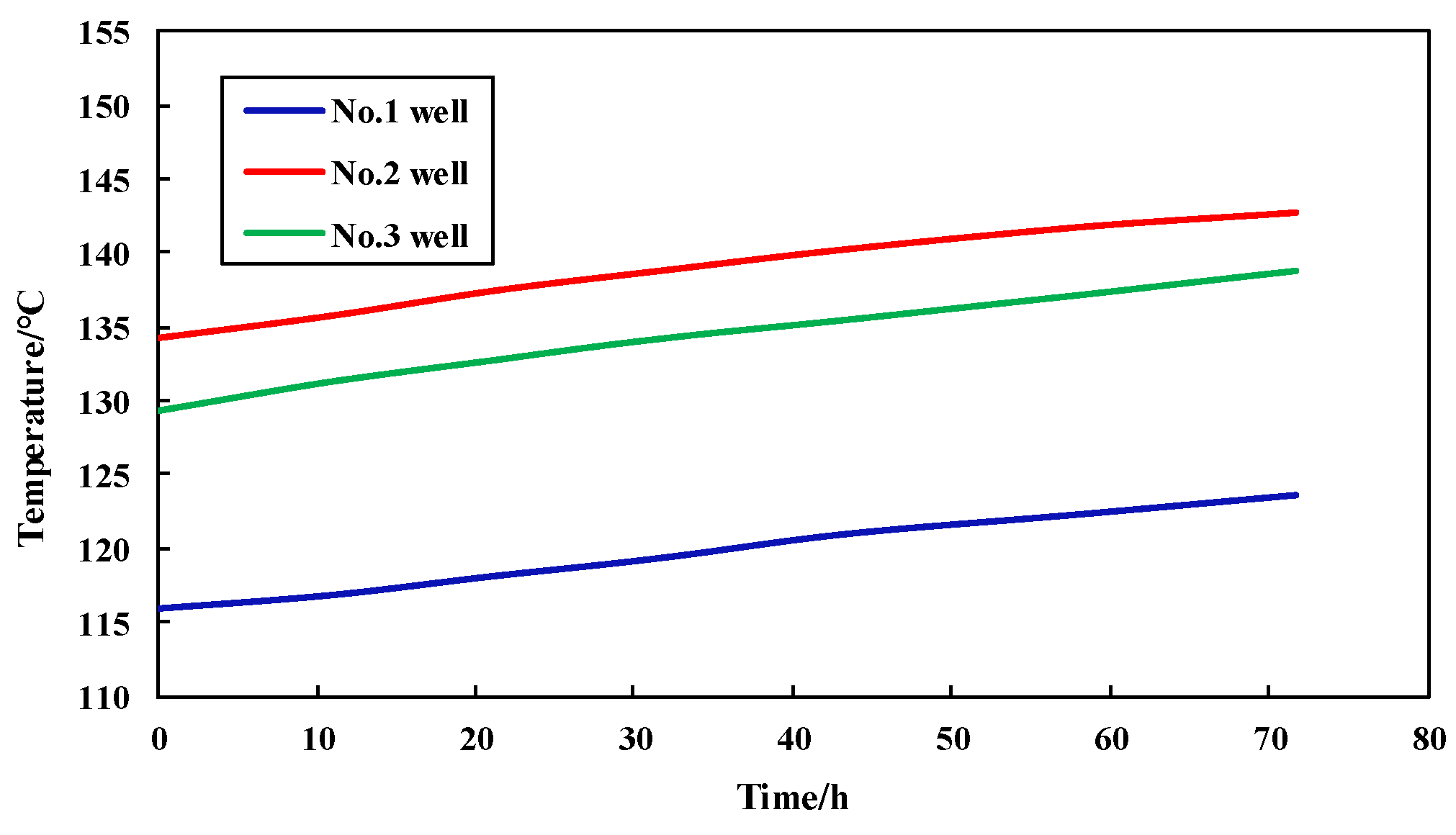
3.1. Modeling Verification
3.2. Sensitivity Analysis of Key Parameters
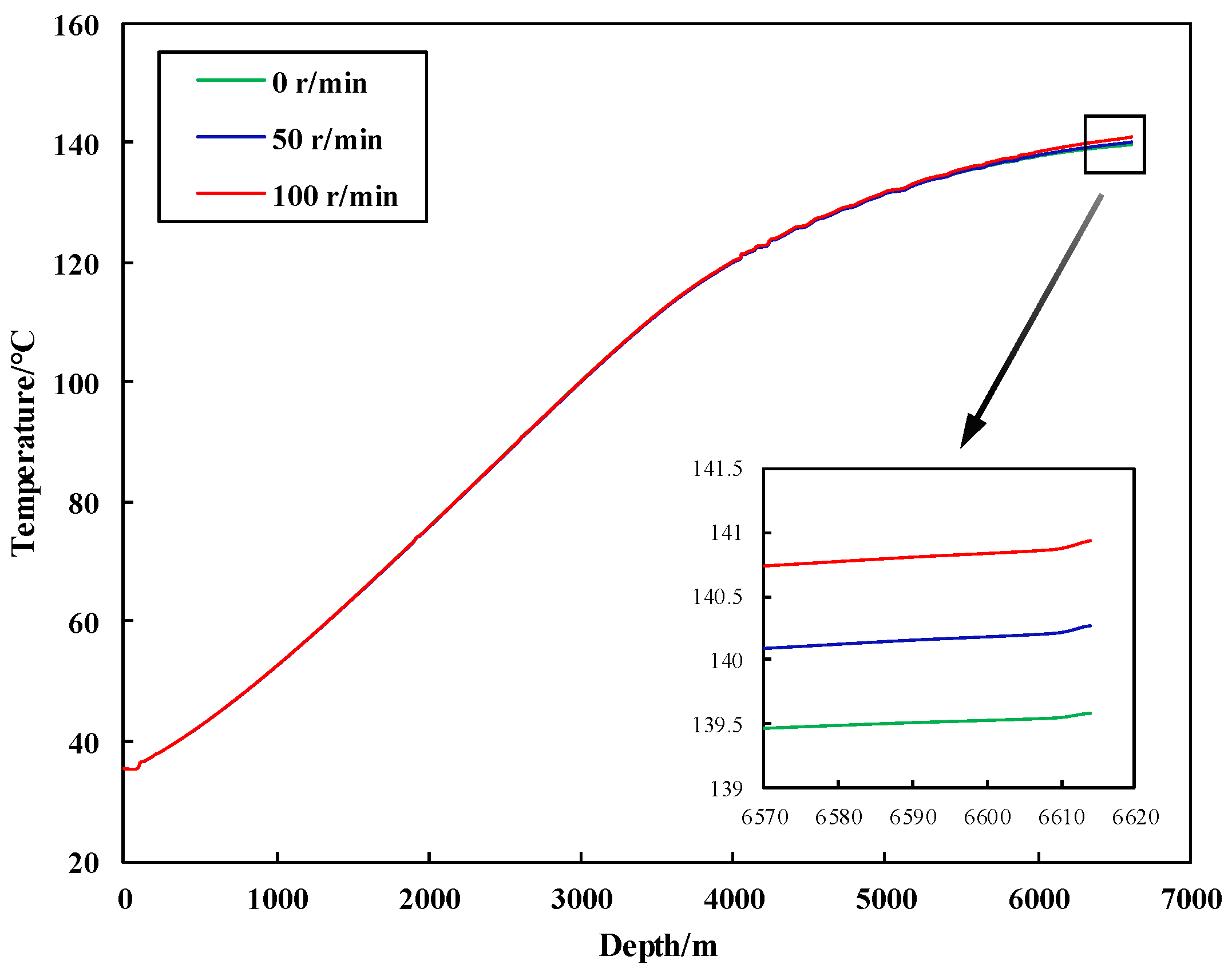
3.2.1. Influence of BHA
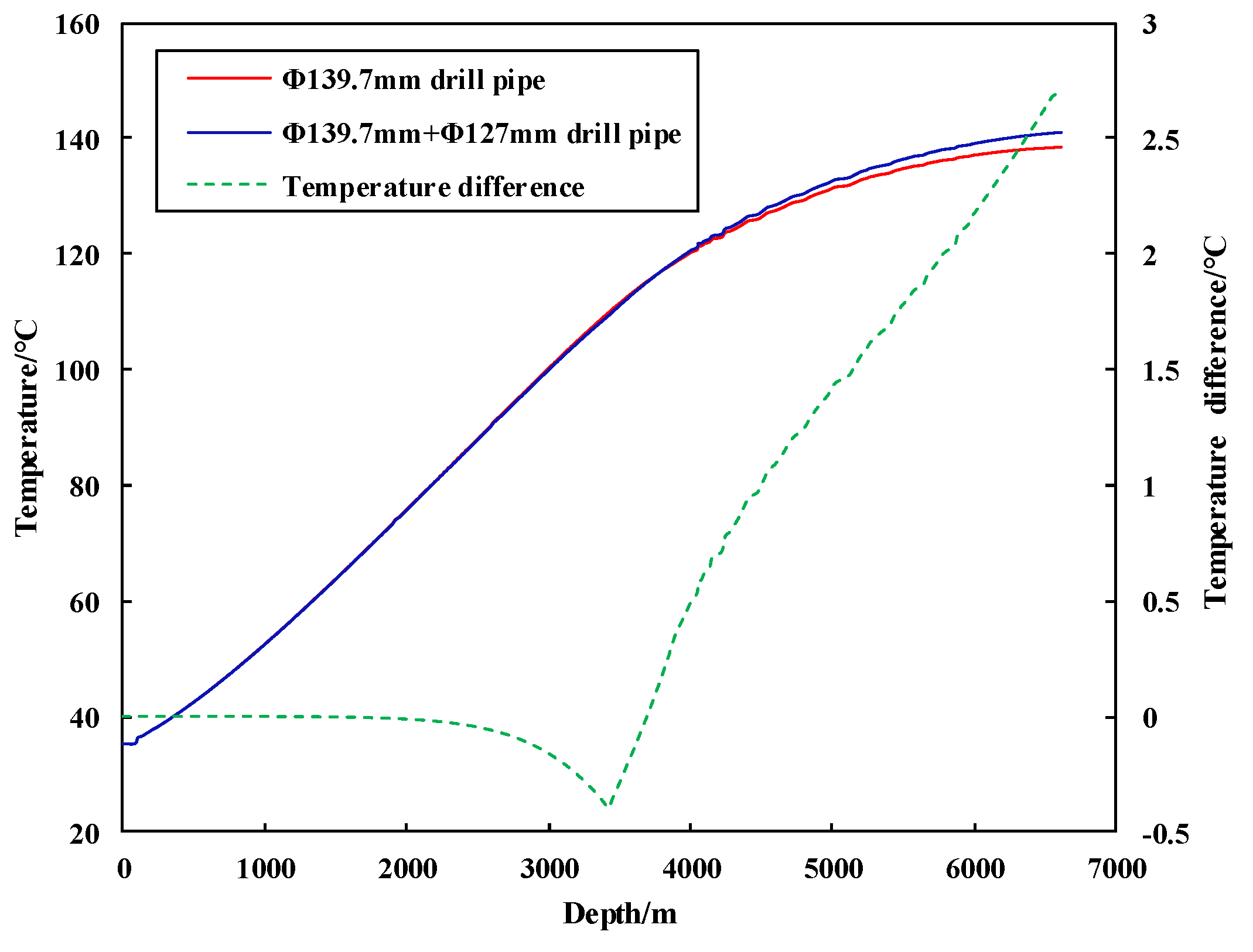
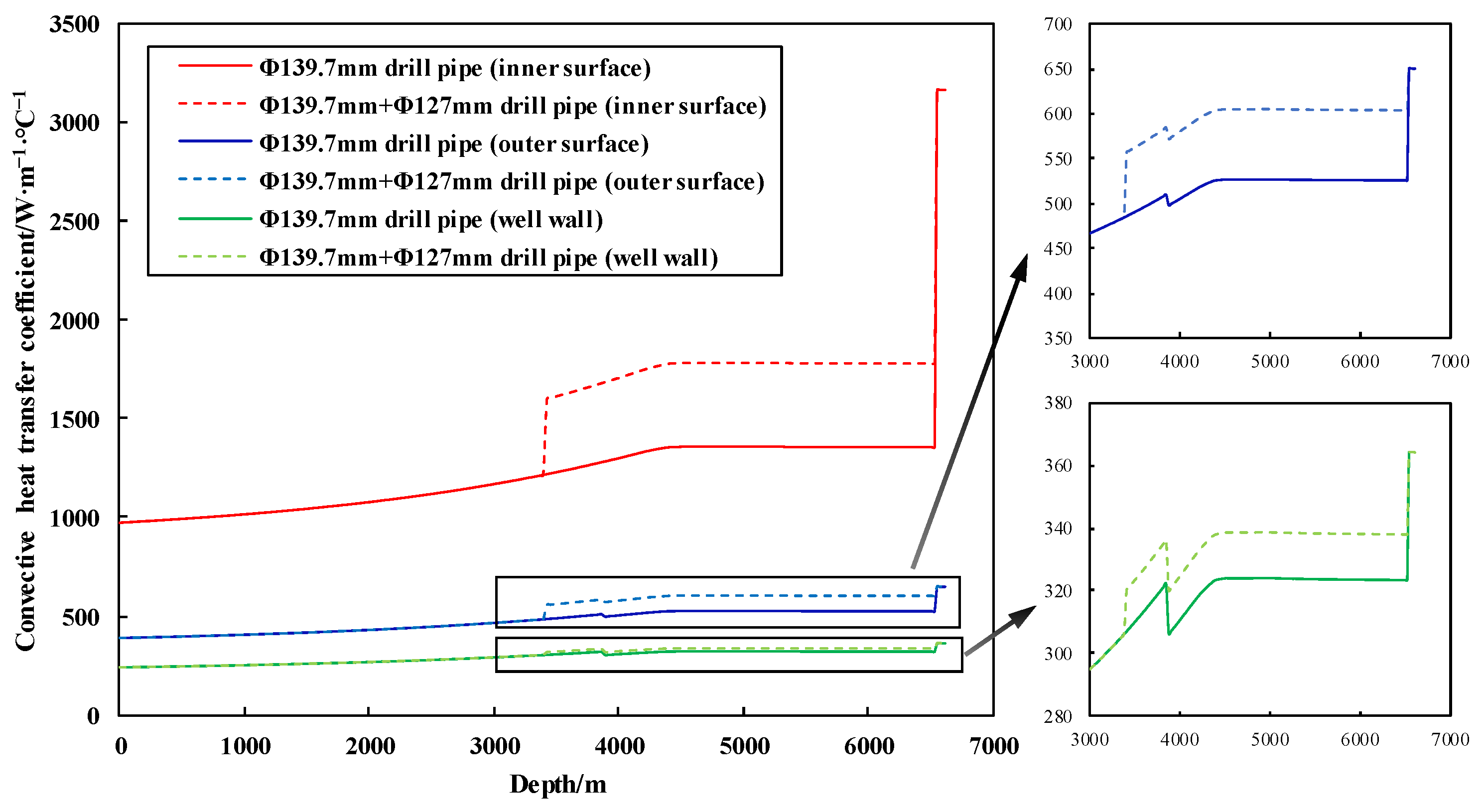
3.2.2. Influence of Drill Pipe Size
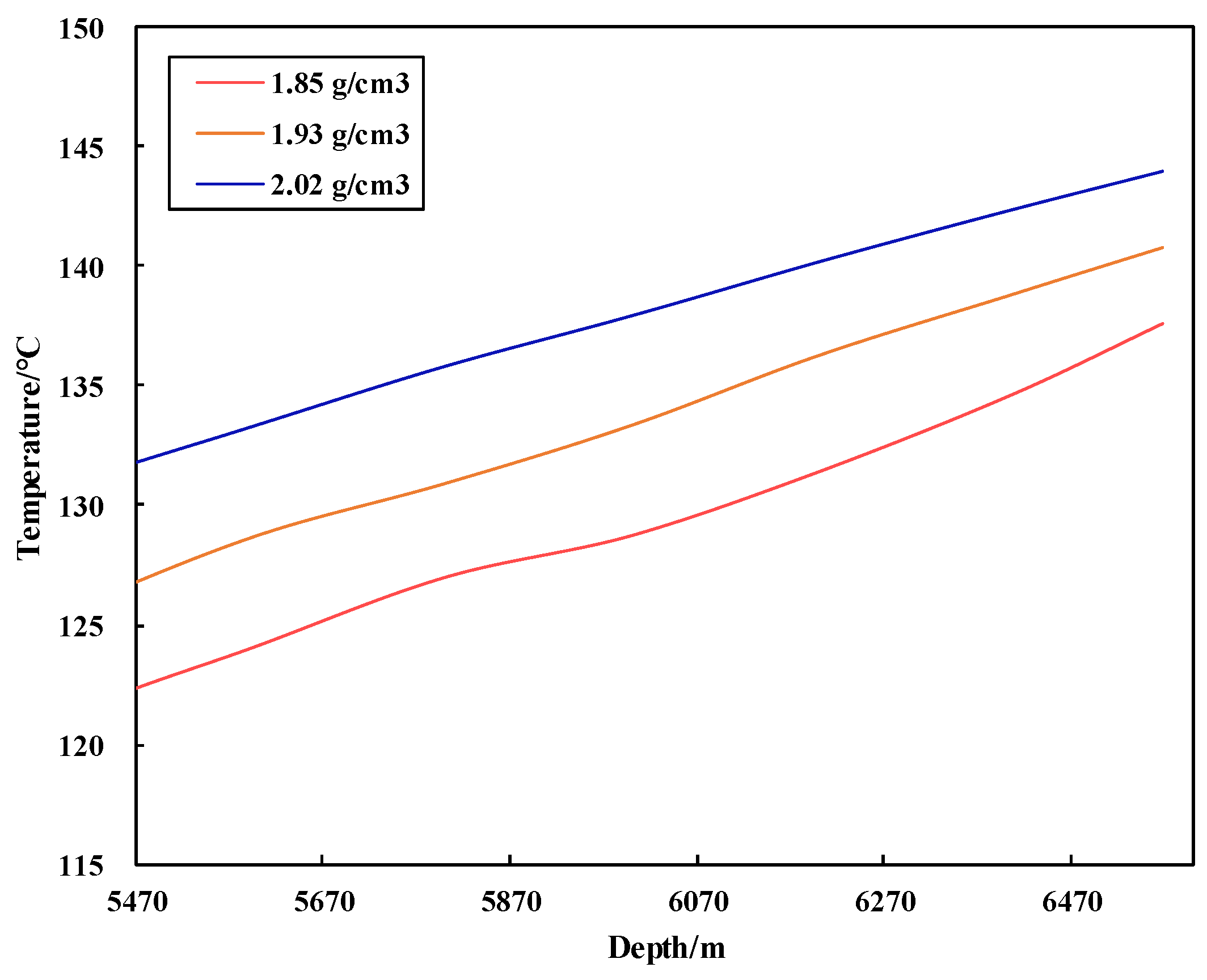
3.2.3. Influence of Drilling Fluid Density
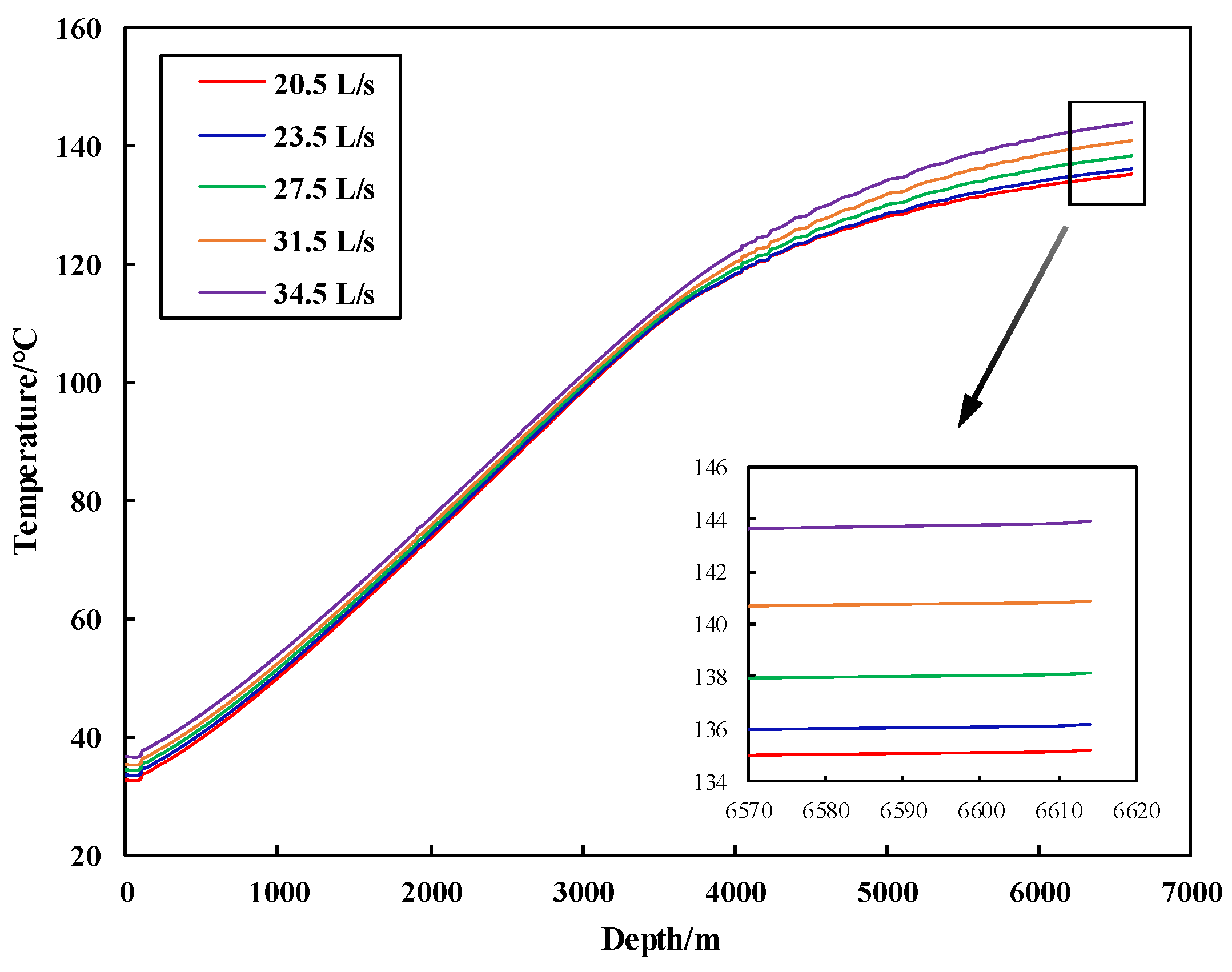
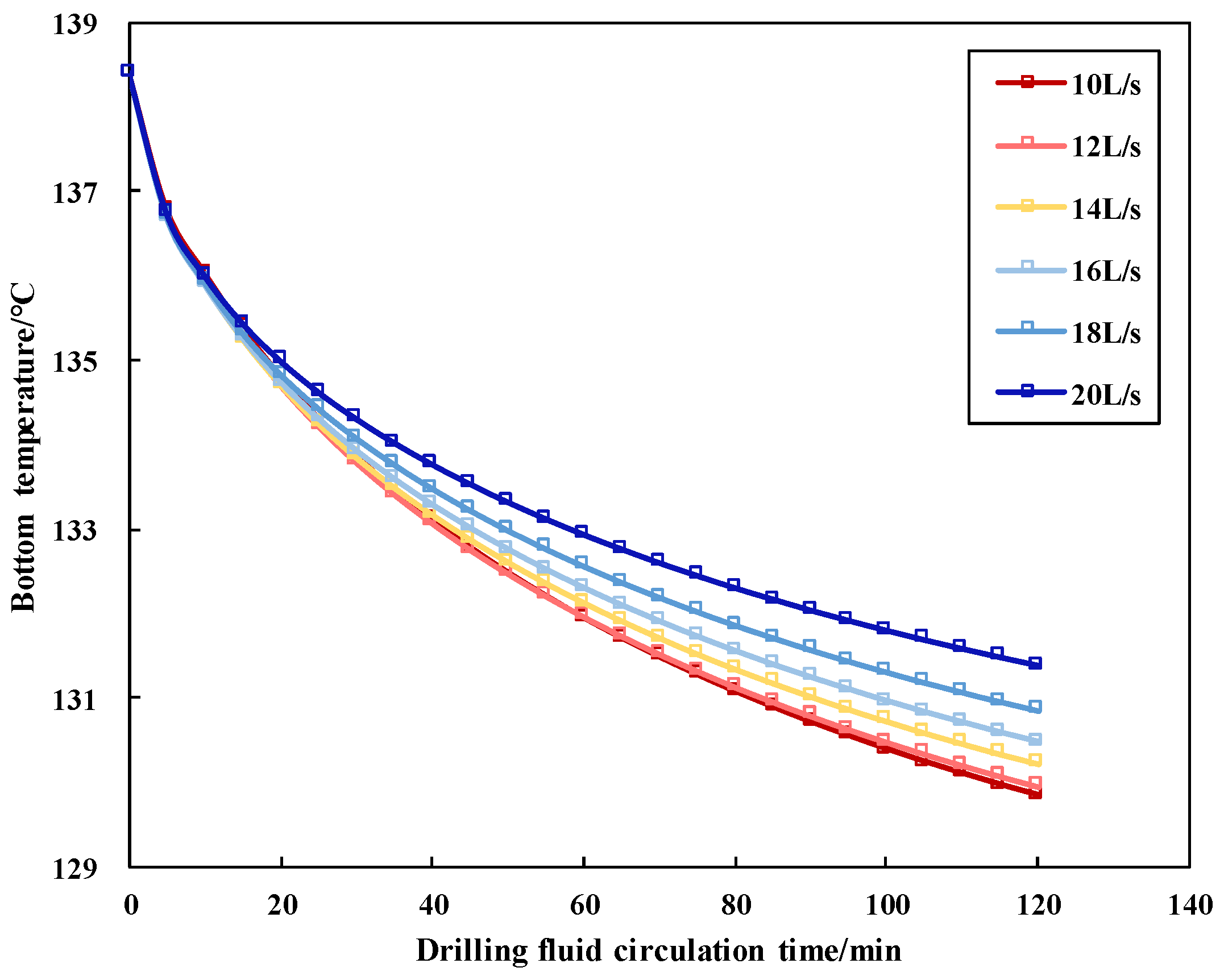
3.2.4. Influence of Drilling Fluid Flow Rate
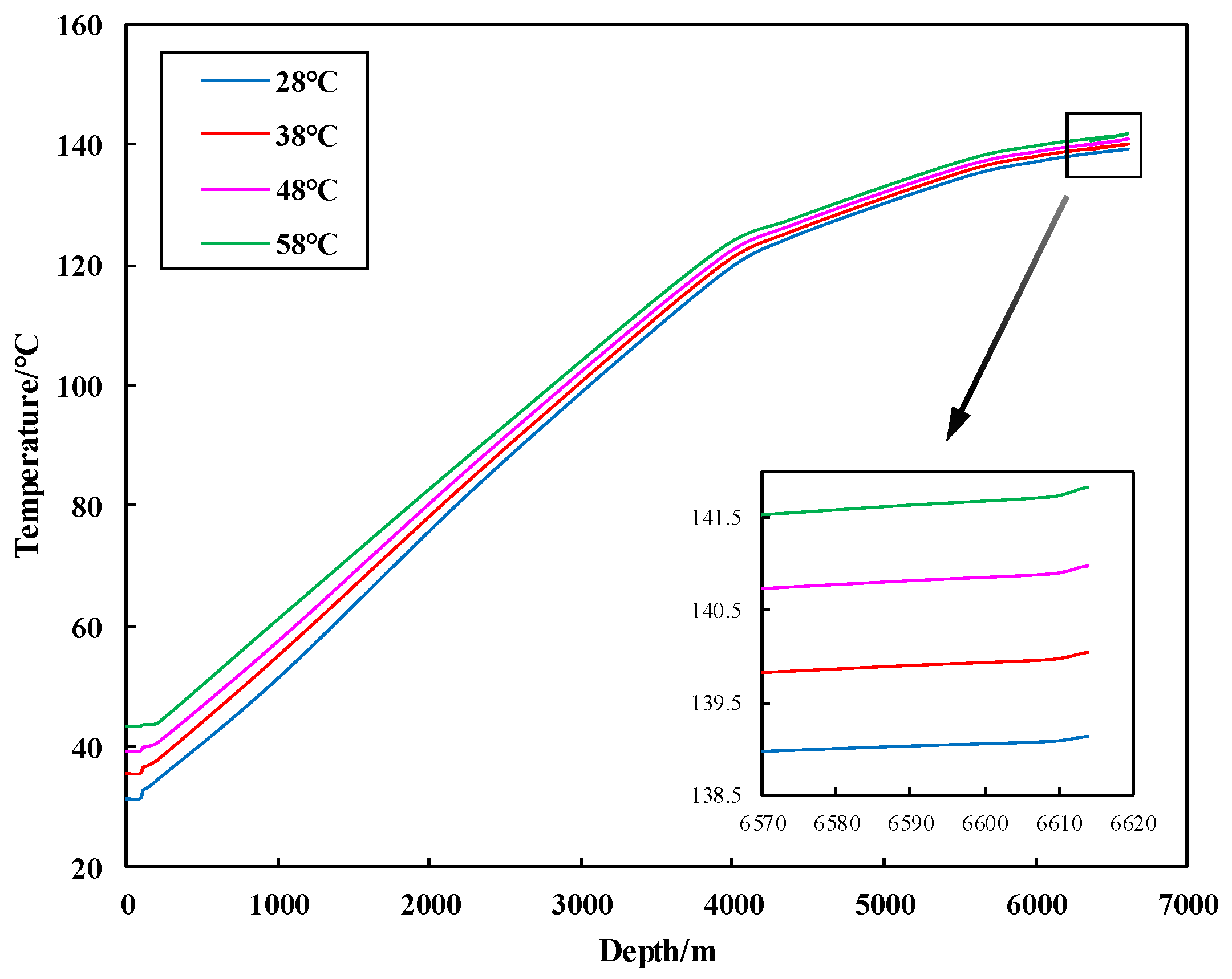
3.2.5. Influence of Inlet Temperature of Drilling Fluid
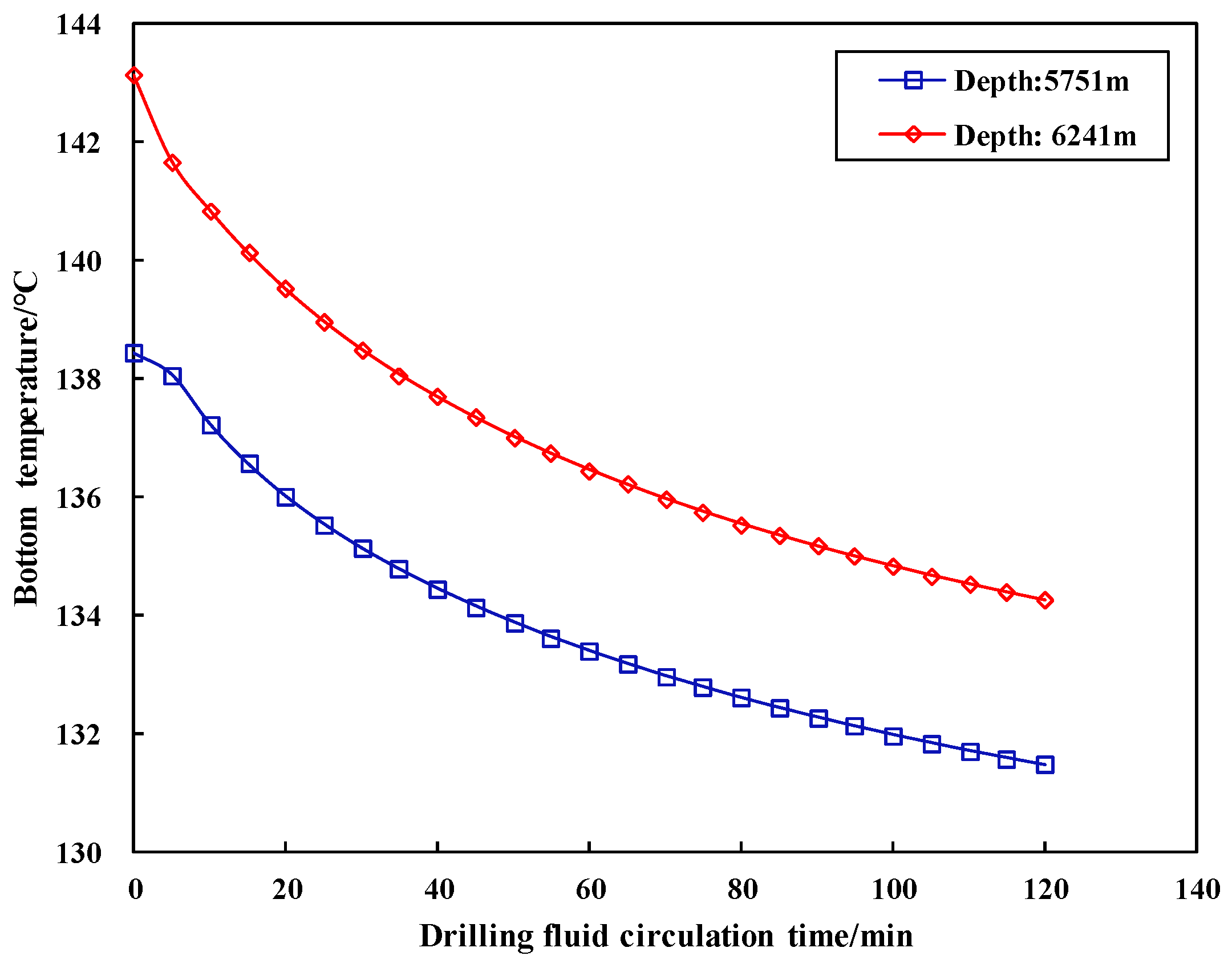
3.2.6. Influence of Drilling Fluid Circulation Time
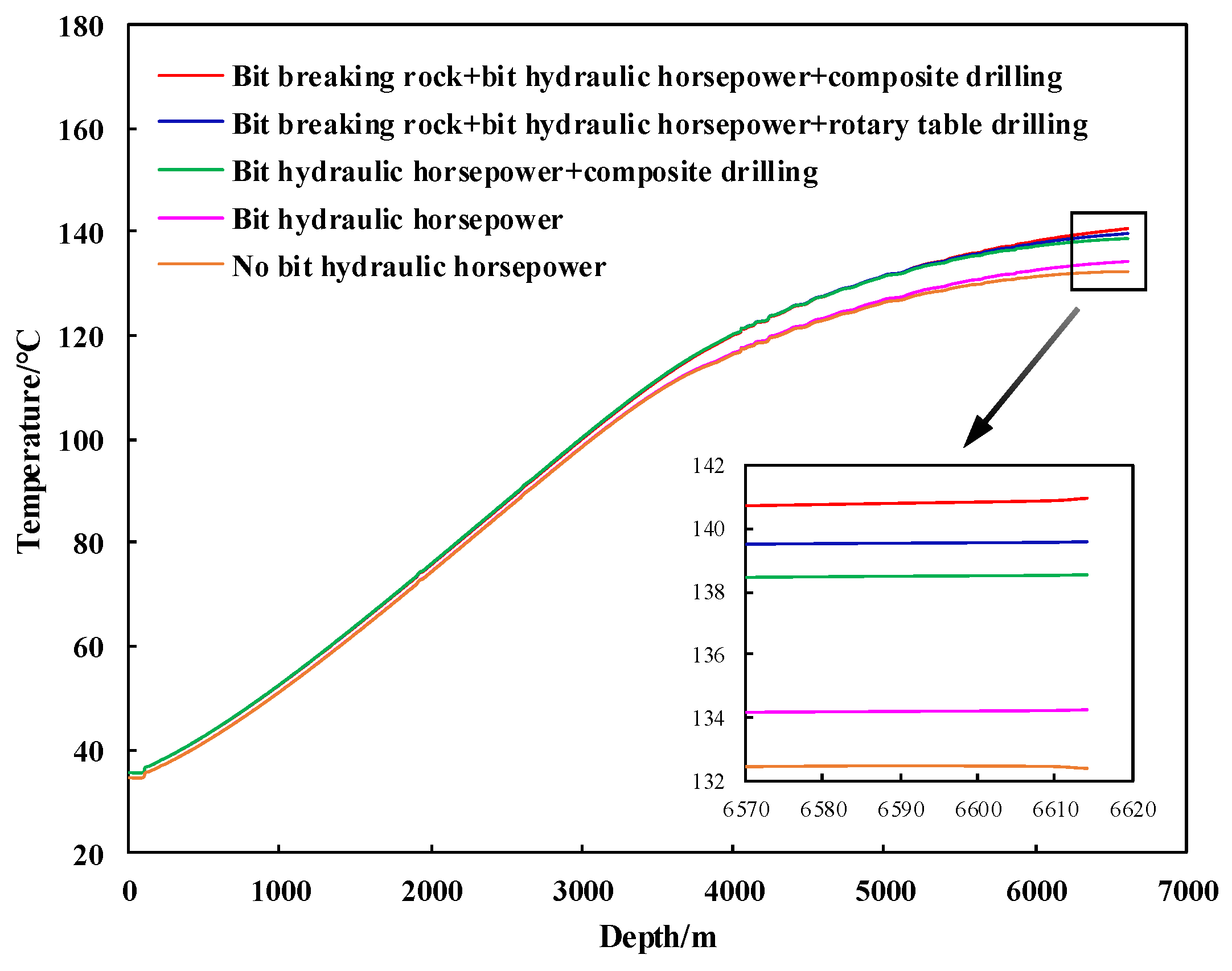
3.2.7. Influence of Heat Sources
4. Conclusions
- (1)
- Based on the established wellbore temperature field model, the RMSE of the prediction results for three wells on site are 1.05 °C, 0.54 °C, and 0.99 °C. The temperature difference between the measured data and the prediction results is less than 6 °C, and the relative error is less than 5%, indicating that the model has high accuracy.
- (2)
- When drilling in the shale gas horizontal section with a PDM, the annular temperature increases by approximately 1 °C/100 m. As the RPM of PDM decreases, the bottom hole temperature decreases. In addition, using Φ139.7 mm drill pipe is favorable for cooling than Φ139.7 mm + Φ127 mm drill pipe.
- (3)
- In the horizontal well section, when the drilling fluid density is reduced by 0.17 g/cm3, the bottom hole temperature decreases by 6.3 °C. When the drilling fluid flow rate is reduced by 14 L/s, the bottom hole temperature drops by 8.7 °C. Additionally, decreasing the drilling fluid inlet temperature by 30 °C results in a 4.3 °C reduction in the bottom hole temperature. These results show that reducing the density, flow rate, and inlet temperature of drilling fluid is beneficial for decreasing the bottom hole temperature in horizontal well sections.
- (4)
- When the drilling fluid is circulating without drilling, at a depth of 5751 m and 6251 m, the bottom hole temperature decreases by 3 °C, and the corresponding circulation times are 25 min and 15 min, respectively. The higher the temperature, the shorter the circulation time required to reduce the same degree of temperature, and the circulation flow rate should not be too large.
- (5)
- Bit-breaking rock, bit hydraulic horsepower, and drill pipe rotation affect the wellbore annular temperature. Therefore, it is recommended to reduce the downhole circulation temperature by measures such as decreasing the top drive rotation speed and removing the PDM near the critical temperature point of the rotary steering drilling tool.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Tp | thedrilling fluid temperature in the drill pipe, °C |
| Qap | the heat exchange between drilling fluid in drill pipe and annular drilling fluid in radial direction, W/m |
| QfD | the friction heat generated by drilling fluid and inner wall of drill pipe, W/m. |
| Qrd | the heat generated by the rotation of the drill pipe, W/m |
| Qrg | the friction heat generated by the bit and the formation, W |
| Qnp | the heat generated by the drilling fluid passing through the nozzle, W |
| Qla | the heat exchange between drilling fluid and formation in radial direction, W/m |
| Qfa | the heat generated by friction in annulus, W/m |
| Qp(z) | Inflow heat of drilling fluid in drill pipe in axial direction, W |
| Qp(z + dz) | Outflow heat of drilling fluid in drill pipe in axial direction, W |
| ρl | the density of drilling fluid in the drill pipe, kg/cm3 |
| cl | the specific heat capacity of drilling fluid in the drill pipe, j/(kg·°C) |
| q | the mass flow of drilling fluid, kg/s |
| z | the well depth, m |
| t | time, s |
| rpi | the inner radius of drill pipe, m |
| hpi | the convective heat transfer coefficient of the inner wall of the drill pipe, W/(m2·°C) |
| Td | the temperature of drill pipe wall, °C |
| Qfp | the heat generated by friction in the drill pipe, W/m |
| ρd | the density of drill pipe, kg/m3 |
| cd | the specific heat capacity of drill pipe, J/(kg·°C) |
| λd | the thermal conductivity of drill pipe, W/(m·°C) |
| rpo | the outer radius of drill pipe, m |
| Ta | the temperature of drilling fluid in annulus, °C |
| ξ | the correction factor |
| f | the friction coefficient between the bit and the formation |
| W | the weight on the drill bit, kN |
| N | the RPM, r/min |
| D | the outer diameter of the drill bit, m |
| d | the inner diameter of the drill bit, m |
| Qa(z) | Inflow heat of drilling fluid in the annulus in axial direction, W |
| Qa(z + dz) | Outflow heat of drilling fluid in the annulus in axial direction, W |
| hpo | the convective heat transfer coefficient of the outer wall of the drill pipe, W/(m2·°C) |
| Uw | the comprehensive heat transfer coefficient |
| r | the radial distance, m |
| λf | the formation thermal conductivity, W/(m·K) |
| cf | the specific heat capacity of rock, J/(kg·°C) |
| ρf | the rock density, kg/m3 |
| Tf | the formation temperature, °C |
| Tin | Inlet temperature of drilling fluid at wellhead, °C |
| Tout | Outlet temperature of drilling fluid at wellhead, °C |
| Hkop | The well depth of the kick-off point, m |
| Tp_kop | the drilling fluid temperature in the drill pipe at the kick-off point, °C |
| Ta_kop | the drilling fluid temperature in the annulus at the kick-off point, °C |
| Hend | the well depth at the beginning of the horizontal section, m |
| Tp_end | the drilling fluid temperature in the drill pipe at the beginning of the horizontal section, °C |
| Ta_end | the drilling fluid temperature in the annulus at the beginning of the horizontal section, °C |
| hw | the convective heat transfer coefficient between formation and wellhole, W/(m2·°C) |
| n | the time number |
| i | the radial grid number |
| j | axial grid number |
References
- Zou, C.D.; Yumanetal, W. Shale gas in China: Characteristics, challenges and prospects (Ⅱ). Pet. Explor. Dev. 2016, 43, 166–178. [Google Scholar] [CrossRef]
- Liu, P.; Feng, Y.; Zhao, L.; Li, N.; Luo, Z. Technical status and challenges of shale gas development in Sichuan Basin, China. Petroleum 2015, 1, 1–7. [Google Scholar] [CrossRef]
- Sun, J.; Xu, C.; Kang, Y.; Jing, H.; Zhang, J.; Yang, B.; You, L.; Zhang, H.; Long, Y. Formation damage mechannism and control strategy of the compound function of drilling fluid and fracturing fluid in shale reservoirs. Pet. Explor. Dev. 2024, 51, 380–388. [Google Scholar] [CrossRef]
- Nguyen, D.A.; Miska, S.Z.; Yu, M.; Saasen, A. Modeling thermal effects on wellbore stability. In Proceedings of the Trinidad and Tobago Energy Resources Conference, SPE-133428-MS, Port of Spain, Trinidad and Tobago, 27–30 June 2010. [Google Scholar] [CrossRef]
- Ramey, H.J., Jr. Wellbore Heat Transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Holmes, C.S.; Swift, S.C. Calculation of circulating mud temperatures. JPT J. Pet. Technol. 1970, 22, 670–674. [Google Scholar] [CrossRef]
- Shiu, K.C.; Beggs, H.D. Predicting temperatures in flowing oil wells. J. Energy Resour. Technol. 1980, 102, 2–11. [Google Scholar] [CrossRef]
- Kabir, C.S.; Hasan, A.R.; Kouba, G.E.; Ameen, M.M. Determining circulating fluid temperature in drilling, workover, and well control operations. SPE Drill. Complet. 1996, 11, 74–79. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.; Cheng, Y.; Li, Q.; Wang, F.; Wei, J.; Liu, Y.; Zhang, C.; Song, B.; Yan, C.; et al. Numerical simulation of fracture reorientation during hydraulic fracturing in perforated horizontal well in shale reservoirs. Energy Sources Part A Recovery Util. Environ. Eff. 2018, 40, 1807–1813. [Google Scholar] [CrossRef]
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Cheng, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical insights into factors affecting collapse behavior of horizontal wellbore in clayey silt hydrate-bearing sediments and the accompanying control strategy. Ocean Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Raymond, L. Temperature distribution in a circulating drilling fluid. J. Pet. Technol. 1969, 21, 333. [Google Scholar] [CrossRef]
- Marshall, D.W.; Bentsen, R.G. A computer-model to determine the temperature distributions in a wellbore. J. Can. Pet. Technol. 1982, 21, 63–75. [Google Scholar] [CrossRef]
- Yang, M.; Li, X.; Deng, J.; Meng, Y.; Li, G. Prediction of wellbore and formation temperatures during circulation and shut-in stages under kick conditions. Energy 2016, 94, 1018–1029. [Google Scholar] [CrossRef]
- Cai, J.; Duan, Y. Study on temperature distribution along wellbore of fracturing horizontal wells in oil reservoir. Petroleum 2015, 1, 358–365. [Google Scholar] [CrossRef]
- Hou, Z.; Yan, T.; Li, Z.; Feng, J.; Sun, S.; Yuan, Y. Temperature prediction of two phase flow in wellbore using modified heat transfer model: An experimental analysis. Appl. Therm. Eng. 2019, 149, 54–61. [Google Scholar] [CrossRef]
- Shahbazi, M.; Najafi, M.; Marji, M.F.; Rafiee, R. A thermo-mechanical simulation for the stability analysis of a horizontal wellbore in underground coal gasification. Petroleum 2023, 10, 243–253. [Google Scholar] [CrossRef]
- Kumar, A.; Samuel, R. Analytical model to predict the effect of pipe friction on downhole fluid temperatures. SPE Drill Complet. 2013, 28, 270–277. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, Y.; Wang, Z.; Chen, G.; Li, P.; Liang, W.; Gao, X.; Xu, H.; Jiang, L.; Wei, N. Wellbore temperature distribution during drilling of natural gas hydrate formation in South China sea. Petroleum 2021, 7, 451–459. [Google Scholar] [CrossRef]
- Yang, H.; Li, J.; Liu, G.; Wang, C.; Li, M.; Jiang, H. Numerical analysis of transient wellbore thermal behavior in dynamic deepwater multi-gradient drilling. Energy 2019, 179, 138–153. [Google Scholar] [CrossRef]
- Sun, W.; Pei, J.; Wei, N.; Zhao, J.; Xue, J.; Zhou, S.; Zhang, L.; Kvamme, B.; Li, Q.; Li, H.; et al. Sensitivity analysis of reservoir risk in marine gas hydrate drilling. Petroleum 2021, 7, 427–438. [Google Scholar] [CrossRef]
- Li, M.; Liu, G.; Li, J. Thermal effect on wellbore stability during drilling operation with long horizontal section. J. Nat. Gas Sci. Eng. 2015, 23, 118–126. [Google Scholar] [CrossRef]
- Yang, M.; Meng, Y.; Li, G.; Deng, J.; Zhao, X. A transient heat transfer model of wellbore and formation during the whole drilling process. Acta Pet. Sin. 2013, 34, 366–371. [Google Scholar] [CrossRef]
- Li, G.; Yang, M.; Meng, Y.; Wen, Z.; Wang, Y.; Yuan, Z. Transient heat transfer models of wellbore and formation systems during the drilling process under well kick conditions in the bottom-hole. Appl. Therm. Eng. 2016, 93, 339–347. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiong, Y.; Gao, Y.; Liu, L.; Wang, M.; Peng, G. Wellbore temperature distribution during circulation stage when well_kick occurs in a continuous formation from the bottom_hole. Energy 2018, 164, 964–977. [Google Scholar] [CrossRef]
- Al Saedi, A.; Flori, R.; Kabir, C. New analytical solutions of wellbore fluid temperature profiles during drilling, circulating, and cementing operations. J. Pet. Sci. Eng. 2018, 170, 206–217. [Google Scholar] [CrossRef]
- Yang, M.; Xie, R.; Liu, X.; Chen, Y.; Tang, D.; Meng, Y. A novel method for estimating transient thermal behavior of the wellbore with the drilling string maintaining an eccentric position in deep well operation. Appl. Therm. Eng. 2019, 163, 114346. [Google Scholar] [CrossRef]
- Abdelhafiz, M.M.; Hegele, L.A.; Oppelt, J.F. Numerical transient and steady state analytical modeling of the wellbore temperature during drilling fluid circulation. J. Pet. Sci. Eng. 2020, 186, 106775. [Google Scholar] [CrossRef]
- Song, X.C.; Guan, Z.C. Full transient analysis of heat transfer during mud circulation in deep-water wells. Acta Pet. Sin. 2011, 32, 704–708. [Google Scholar] [CrossRef]
- Khan, N.U.; May, R. A generalized mathematical model to predict transient bottomhole temperature during drilling operation. J. Pet. Sci. Eng. 2016, 147, 435–450. [Google Scholar] [CrossRef]
- Yang, H.; Li, J.; Zhang, H.; Jiang, J.; Guo, B.; Zhang, G. Numerical analysis of heat transfer rate and wellbore temperature distribution under different circulating modes of Reel-well drilling. Energy 2022, 254, 124313. [Google Scholar] [CrossRef]
- Mao, L.; Wei, C.; Jia, H.; Lu, K. Prediction model of drilling wellbore temperature considering bit heat generation and variation of mud thermophysical parameters. Energy 2023, 284, 129341. [Google Scholar] [CrossRef]
- Yang, M.; Meng, Y.; Li, G.; Li, Y.; Chen, Y.; Zhao, X.; Li, H. Estimation of wellbore and formation temperatures during the drilling process under lost circulation conditions. Math. Probl. Eng. 2013, 2013, 1943–1997. [Google Scholar] [CrossRef]
- Memarzadeh, F.; Miska, S. Numerical simulation of diamond-bit drilling with air. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, WY, USA, 21 May 1984. [Google Scholar] [CrossRef]




| Geothermal Gradient/(°C/100 m) | Wellhead Temperature/°C | |
|---|---|---|
| No.1 well | 3.0 | 31 |
| No.2 well | 3.0 | 39 |
| No.3 well | 3.0 | 38 |
| Number of Spudding | Borehole Size /mm | Well Depth /m | Casing Size /mm | Casing Depth /m |
|---|---|---|---|---|
| First-spudding | 660.4 | 200 | 508 | 198 |
| Second-spudding | 406.4 | 2609 | 339.7 | 2607 |
| Third-spudding | 311.2 | 4008 | 244.47 | 4006 |
| Four-spudding | 215.9 | 6640 | 139.7 | 6638 |
| Drilling Fluid Density/(g/cm3) | Plastic Viscosity/(mPa⋅s) | Stand Pipe Pressure/MPa | Flow Rate /(L/s) | WOB /KN | RPM /(r/min) |
|---|---|---|---|---|---|
| 1.9~2.06 | 45–57 | 36–39 | 31–32 | 80 | 75–90 |
| Drilling Tool Name | Outside Diameter /mm | Inner Diameter /mm | Length /m | Unit Weight /(N/m) |
|---|---|---|---|---|
| PDC bit | 215.9 | 0 | 0.23 | 300 |
| Drill collar | 171.5 | 57.2 | 11.5 | 1582.7 |
| Heavy-weight drill pipe | 127 | 76.2 | 10 | 720.3 |
| PDM | 172 | 57.2 | 9 | 1582.7 |
| Heavy-weight drill pipe | 127 | 76.2 | 27 | 720.3 |
| drilling jar | 172 | 78 | 10 | 1580 |
| Heavy-weight drill pipe | 127 | 76.2 | 18 | 720.3 |
| Drill pipe | 127 | 108.61 | 2600 | 284.58 |
| Drill pipe | 139.7 | 118.62 | 3954.27 | 360.47 |
| Medium | Density /(g/cm3) | Specific Heat Capacity /(J/kg·°C) | Thermal Conductivity /(W/(m·°C)) |
|---|---|---|---|
| Drilling fluid | 2.06 | 1510 | 0.75 |
| Tubular column | 7.80 | 400 | 43.75 |
| Rock | 2.64 | 837 | 2.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Fu, J.; Peng, C.; Su, Y.; Zhang, H.; Yang, M. The Analysis of Transient Temperature in the Wellbore of a Deep Shale Gas Horizontal Well. Processes 2024, 12, 1402. https://doi.org/10.3390/pr12071402
Zhang S, Fu J, Peng C, Su Y, Zhang H, Yang M. The Analysis of Transient Temperature in the Wellbore of a Deep Shale Gas Horizontal Well. Processes. 2024; 12(7):1402. https://doi.org/10.3390/pr12071402
Chicago/Turabian StyleZhang, Shilong, Jianhong Fu, Chi Peng, Yu Su, Honglin Zhang, and Mou Yang. 2024. "The Analysis of Transient Temperature in the Wellbore of a Deep Shale Gas Horizontal Well" Processes 12, no. 7: 1402. https://doi.org/10.3390/pr12071402
APA StyleZhang, S., Fu, J., Peng, C., Su, Y., Zhang, H., & Yang, M. (2024). The Analysis of Transient Temperature in the Wellbore of a Deep Shale Gas Horizontal Well. Processes, 12(7), 1402. https://doi.org/10.3390/pr12071402






