Experimental Assessment of Paper Formation Conditions and Structural Two-Sidedness and Their Impacts on Curl Phenomena
Abstract
:1. Introduction
1.1. Characterization of the Fiber Orientation in the ZD
1.2. Flow Dynamics and the Local Structure of Paper
1.3. Objectives and Organization of the Document
2. Materials and Methods
2.1. Methodology to Characterize the Variation of the Fiber Orientation Distribution Function along the Thickness Direction of Paper
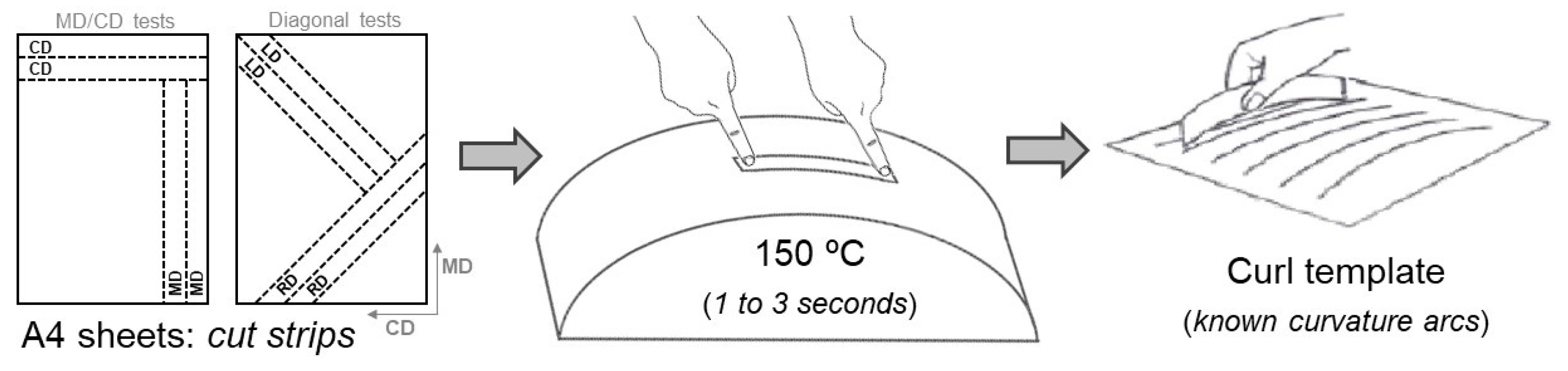
2.2. Hot Bend Method
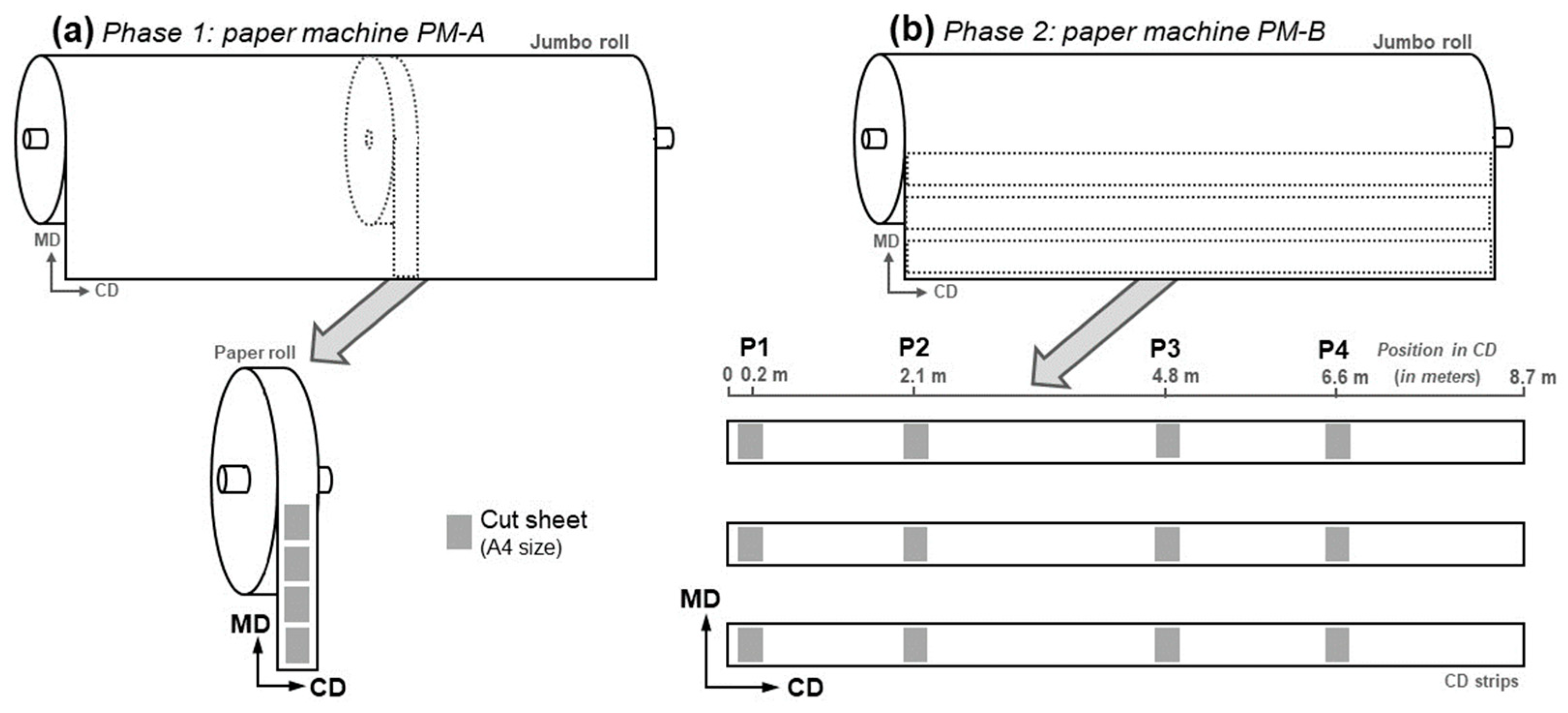
2.3. Experimental Plan
2.3.1. Phase 1: Development and Validation
2.3.2. Phase 2: Industrial Application
3. Results and Discussion for Phase 1: Methods Development and Validation
3.1. Development, Test, and Validation of SIA
3.1.1. Development of the Sheet-Splitting Technique
3.1.2. Internal Validation
3.1.3. Repeatability Analysis
3.1.4. External Validation
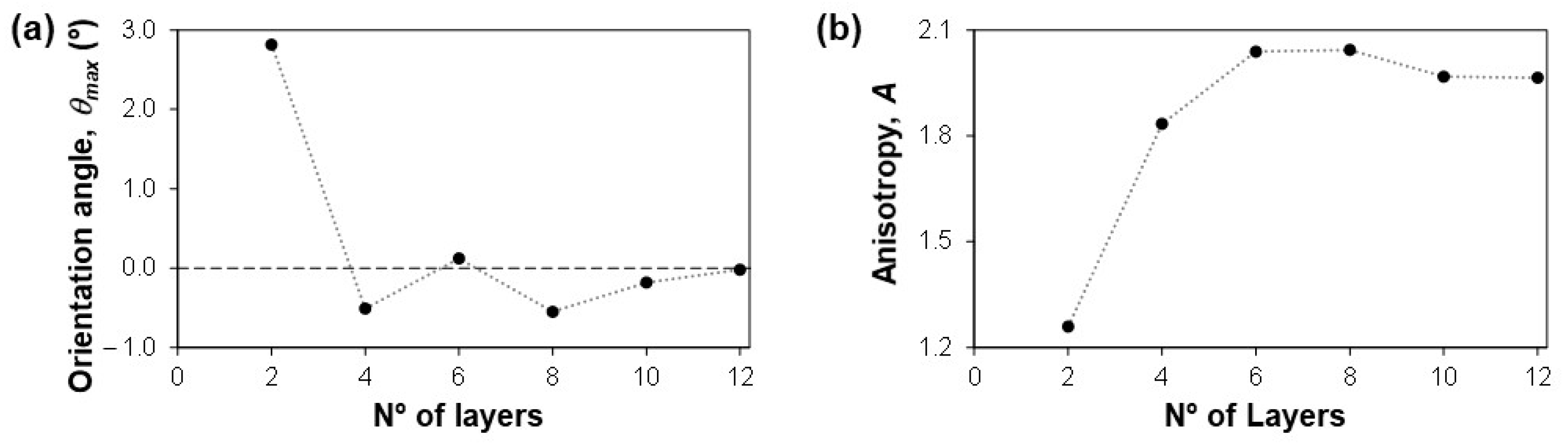
3.1.5. Analysis of the Local Structure
3.2. Repeatability of the Hot Bend Method
4. Results and Discussion for Phase 2: Industrial Application
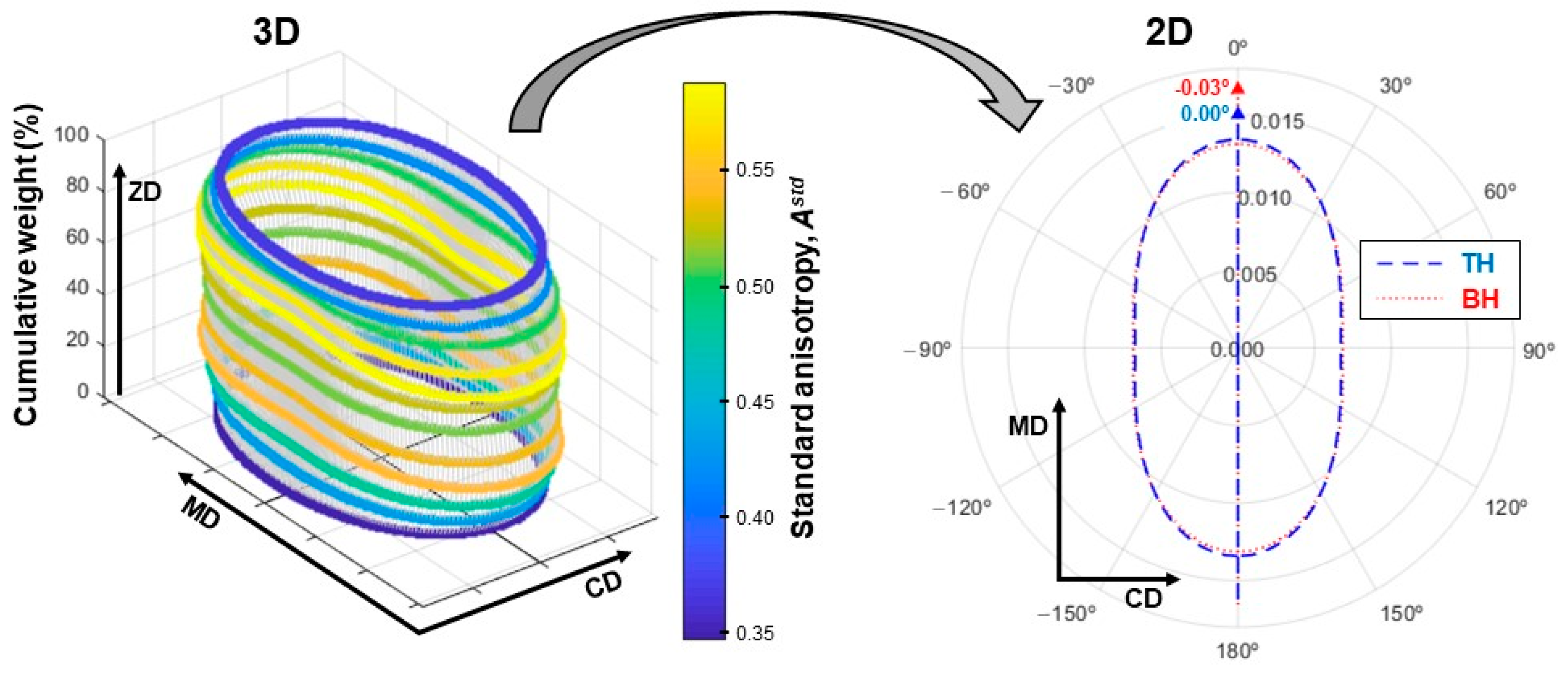
4.1. Analysis of Fiber Orientation across the ZD
4.2. In-Plane Tensile Stiffness
4.3. Potential to Develop Curl
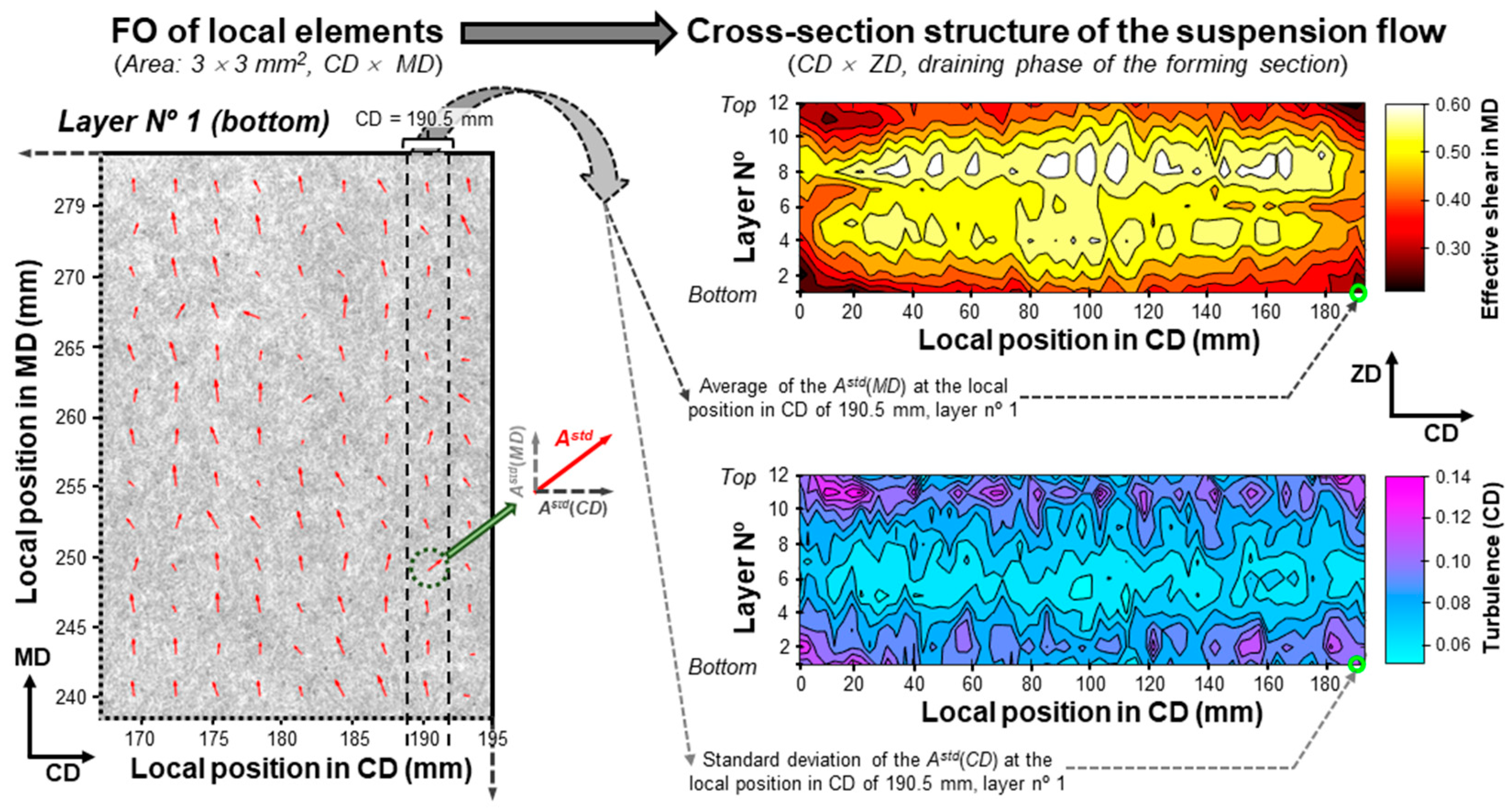
4.4. Cross-Section Structure of the Suspension Flow
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | |
| Bottom half of the paper sheet | BH |
| Bottom side of the paper sheet | BS |
| Cross-machine direction, i.e., the direction perpendicular to the MD | CD |
| Critical quality attribute | CQA |
| Diagonal (also known as angular) direction, i.e., an in-plane direction not aligned with the MD and/or CD | DD |
| Dots per inch | dpi |
| Fiber orientation | FO |
| Gradient-segmentation method | GSM |
| In-plane left diagonal direction of the paper sheet | LD |
| Machine direction, i.e., the direction parallel to the paper machine where the paper is produced | MD |
| In-plane right diagonal direction of the paper sheet | RD |
| Sheet splitting and image analysis methodology | SIA |
| Top half of the paper sheet | TH |
| Top side of the paper sheet | TS |
| Tensile stiffness orientation | TSO |
| Thickness direction of a paper sheet | ZD |
| Variables | |
| Maximum of the angular distribution function | a |
| Anisotropy, obtained using the ratio of the maximum, a, and minimum, b, values of the angular distribution function | A |
| Anisotropy MD/CD, corresponding to the ratio of the values of the angular distribution function for the MD and CD | AMD/CD |
| Standard anisotropy, being linked to the anisotropy, A, by 1 − 1/A | Astd |
| Minimum of the angular distribution function | b |
| Cosine function with three terms, a Fourier series expansion truncated in the third term, used to represent the angular distribution | fθ(θ) |
| Speed of the suspension jet at the forming section of the paper machine (m·min−1) | J |
| Difference between the speed of the suspension jet and the wire at the forming section of the paper machine (m·min−1) | J-W |
| Scale factor of the cosine function with three terms | K |
| Number of rotations tested, i.e., number of θoff introduced at an imaging step for the internal consistency assessment | n |
| Coefficient of determination | R2 |
| Average of the modulus (absolute value) of relative deviation, , for all the n considered offset angle points i, introduced at an imaging step for the internal consistency assessment | |
| Absolute value of the relative deviation of the anisotropy at a given offset angle with index i, Ai, from the standard measurement (θoff = 0°), A(0°) | |
| Relative humidity (%) | RH |
| Sample standard deviation | |
| Temperature (°C) | T |
| Wire speed at the forming section of the paper machine (m·min−1) | W |
| Sample mean | |
| Variation of the temperature (°C) | ΔT |
| First term of the cosine function with three terms | η1 |
| Second term of the cosine function with three terms | η2 |
| Third term of the cosine function with three terms | η3 |
| Orientation angle of a fiber segment, corresponding to the angle between the MD and the longitudinal direction of the fiber segment (°) | θ |
| Orientation angle, corresponding to the angle between the MD and the direction with the highest orientation level of fibers (°) | θmax |
| Offset angle, corresponding to a rotation relative to the MD introduced at an imaging step (°) | θoff |
| Density (g·cm−3) | ρ |
| Standard deviation of the mean, estimated from the sample standard deviation of the n data points, , using | |
| Subscripts | |
| Offset angle (θoff) point | i |
References
- Rutland, D.F. Dimensional Stability and Curl. In Pulp and Paper Manufacture; Kouris, M., Kocurek, M.J., Eds.; Joint Textbook Committee of the Paper Industry: Atlanta, GA, USA, 1989; Volume 9, pp. 132–151. [Google Scholar]
- Uesaka, T. Dimensional Stability and Environmental Effects on Paper Properties. In Handbook of Physical Testing of Paper—Vol. 1, 2nd ed.; Mark, R.E., Habeger, C., Jr., Borch, J., Lyne, M.B., Eds.; Marcel Dekker, Inc.: New York, NY, USA, 2002; Volume 1, pp. 115–171. [Google Scholar]
- Green, C.; Atkins, J. The Problem of Paper Curl. Tappi J. 2011, 7, 1–6. [Google Scholar]
- Reis, M.S.; Abreu, C.T.; Heitor, M.J.; Ataíde, J.; Saraiva, P.M. A New Procedure for the Routine Assessment of Paper Diagonal Curl. Tappi J. 2009, 8, 20–26. [Google Scholar] [CrossRef]
- Glynn, P.; Jones, H.W.H.; Gallay, W. The Fundamentals of Curl in Paper. Pulp Pap. Mag. Can. 1959, 60, T316–T323. [Google Scholar]
- Lloyd, M.D.; Chalmers, I.R. Use of an Image Orientation Analysis Technique to Investigate Sheet Structural Problems During Forming. In Proceedings of the 54th Appita Annual Conference, Melbourne, VIC, Australia, 3–6 April 2000; pp. 495–502. [Google Scholar]
- Lloyd, M.D.; Chalmers, I.R. Use of Fibre Orientation Analysis to Investigate Sheet Structural Problems During Forming. Appita J. 2001, 54, 15–21. [Google Scholar]
- Enomae, T.; Han, Y.; Isogai, A. Nondestructive determination of fiber orientation distribution of paper surface by image analysis. Nord. Pulp Pap. Res. J. 2006, 21, 253–259. [Google Scholar] [CrossRef]
- Mendes, A.d.O.; Fiadeiro, P.T.; Costa, A.P.; Amaral, M.E.; Belgacem, M.N. Laser Scanning for Assessment of the Fiber Anisotropy and Orientation in the Surfaces and Bulk of the Paper. Nord. Pulp Pap. Res. J. 2015, 30, 308–318. [Google Scholar] [CrossRef]
- Dias, P.A.N.; Rodrigues, R.J.; Reis, M.S. Fast characterization of in-plane fiber orientation at the surface of paper sheets through image analysis. Chemom. Intell. Lab. Syst. 2023, 234, 104761. [Google Scholar] [CrossRef]
- Gustafsson, P.-J.; Niskanen, K. 2 Paper as an engineering material. In Mechanics of Paper Products; Sören, Ö., Kaarlo, N., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2021; pp. 5–28. [Google Scholar]
- Enomae, T.; Han, Y.-H.; Isogai, A. Z-Directional Distribution of Fiber Orientation of Japanese and Western Papers Determined by Confocal Laser Scanning Microscopy. J. Wood Sci. 2008, 54, 300–307. [Google Scholar] [CrossRef]
- Kondo, Y.; Aidun, C.K. Development of Method for Analyzing Internal Properties of Coated Paper: Image Analysis Using X-ray Microtomography. Jpn. Tappi J. 2007, 61, 83–91. [Google Scholar] [CrossRef]
- Kallmes, O.J. Technique for Determining The Fiber Orientation Distribution Throughout the Thickness of a Sheet. Tappi 1969, 52, 482–485. [Google Scholar]
- Green, C.J. Curl, Expansivity, and Dimensional Stability. In Handbook of Physical and Mechanical Testing of Paper and Paperboard; Mark, R.E., Ed.; Marcel Dekker, Inc.: New York, NY, USA, 1984; Volume 2, pp. 415–443. [Google Scholar]
- Erkkilä, A.-L.; Pakarinen, P.; Odell, M. Sheet Forming Studies Using Layered Orientation Analysis. Pulp Pap. Can. 1998, 99, 81–85. [Google Scholar]
- Hirn, U.; Bauer, W. Investigating Paper Curl by Sheet Splitting. In Proceedings of the EUCEPA Conference ‘Challenges 06’, Bratislava, Slovakia, 8–9 November 2006. [Google Scholar]
- Hirn, U.; Bauer, W. Evaluating an Improved Method to Determine Layered Fibre Orientation by Sheet Splitting. In Proceedings of the 61st Appita Annual Conference and Exhibition, Gold Coast, QLD, Australia, 6–9 May 2007; pp. 71–79. [Google Scholar]
- Rosén, F.; Söderberg, D.; Lucisano, M.F.; Östlund, C. Estimation of Fibre Segment Orientation Using Steerable Filtering. In Proceedings of the PaperCon’08—Paper Conference and Trade Show, Dallas, TX, USA, 4–7 May 2008; pp. 1097–1144. [Google Scholar]
- Green, C. Curl Properties of Paper Structures. Ind. Eng. Chem. Prod. Res. Dev. 1981, 20, 147–150. [Google Scholar] [CrossRef]
- Morris, V.A.P.; Sampson, W.W. An Investigation of Heat Curl in Newsprint. Tappi J. 1998, 81, 191–194. [Google Scholar]
- Green, C. PTN318 on Analyzing Curl Problems. 2006. Available online: http://www.papercurl.com (accessed on 22 June 2024).
- Odell, M.H.; Pakarinen, P. The Compleat Fibre Orientation Control and Effects on Diverse Paper Properties. In Proceedings of the 2001 Papermakers Conference, Atlanta, GA, USA, 11–14 March 2001. [Google Scholar]
- Ono, K.; Park, C.; Aidun, C. A New Technique for Fibre Orientation Measurement Using Image Analysis. In Proceedings of the 2002 TAPPI Fall Technical Conference and Trade Fair, San Diego, CA, USA, 8–22 September 2002; pp. 1–7. [Google Scholar]
- Lucisano, M.F.; Pikulik, L. Sheet Splitting with a Heat Seal Lamination Technique; Innventia AB: Stockholm, Sweden, 2010. [Google Scholar]
- Thorpe, J.L. Exploring Fibre Orientation Within Copy Paper. In Proceedings of the 1999 International Paper Physics Conference, San Diego, CA, USA, 26–30 September 1999; pp. 447–458. [Google Scholar]
- Erkkilä, A.-L.; Leppänen, T.; Tuovinen, T. The Curl and Fluting of Paper: The Effect of Elasto-Plasticity. In Proceedings of the ECCOMAS Congress 2016: VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece, 5–10 June 2016; pp. 4752–4769. [Google Scholar]
- Lipponen, P.; Erkkilä, A.-L.; Leppänen, T.; Hämäläinen, J. On the importance of in-plane shrinkage and through-thickness moisture gradient during drying on cockling and curling phenomena. In Proceedings of the 14th Pulp and Paper Fundamental Research Symposium, Oxford, UK, 13–18 September 2009; pp. 389–436. [Google Scholar]
- Holik, H.; Moser, J.; Ruehl, T. Wire Section. In Handbook of Paper and Board, 2nd ed.; Holik, H., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; Volume 2, pp. 659–678. [Google Scholar]
- Holik, H.; Moser, J.; Ruehl, T. Headbox. In Handbook of Paper and Board, 2nd ed.; Holik, H., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; Volume 2, pp. 635–657. [Google Scholar]
- Holik, H.; Moser, J. Uniformity of Paper Web Properties. In Handbook of Paper and Board; Holik, H., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; Volume 2, pp. 879–909. [Google Scholar]
- Costa, T.G.; Gamelas, J.A.; Moutinho, I.M.; Figueiredo, M.M.; Ferreira, P.J. The Influence of Paper Surface Sizing on Inkjet Pigment Penetration. Appita J. 2010, 63, 392–398. [Google Scholar]
- Ferreira, P.J.; Gamelas, J.A.; Moutinho, I.M.; Ferreira, A.G.; Gómez, N.; Molleda, C.; Figueiredo, M.M. Application of FT-IR-ATR Spectroscopy to Evaluate the Penetration of surface Sizing Agents into the Paper Structure. Ind. Eng. Chem. Res. 2009, 48, 3867–3872. [Google Scholar] [CrossRef]
- Conn, A.; Reich, M.; Faltas, R.; Branson, T. A New, Simple, Low Cost, Paper Curl Measurement Apparatus. Appita: Technol. Innov. Manuf. Environ. 2012, 65, 352–359. [Google Scholar]
- Eriksson, L.-E.; Cavlin, S.; Fellers, C.; Carlsson, L. Curl and Twist of Paperboard-Theory and Measurement. Nord. Pulp Pap. Res. J. 1987, 2, 66–70. [Google Scholar] [CrossRef]
- Lucisano, M.F.C.; Nilsson, M.; Cochard, J. A New Instrument for Measurement of the Out-of-plane Dimensional Stability of Paperboard. In Proceedings of the 2007 International Paper Physics Conference, Gold Coast, QLD, Australia, 6–9 May 2007; pp. 349–355. [Google Scholar]
- Niskanen, K. Curl Variations in Paper and Board. Pap. Ja Puu 1996, 78, 292–297. [Google Scholar]
- Green, C.; Atkins, J. Solving Curl Problems: The Basics. Solution 2001, 84, 40–43. [Google Scholar]
- Reich, M.; Conn, A.; Faltas, R.; Liu, F.; Branson, T. Measurement of Curl Using Image Analysis. In Proceedings of the 61st Appita Annual Conference and Exhibition, Gold Coast, QLD, Australia, 6–9 May 2007; pp. 207–211. [Google Scholar]
- Green, C. PTN44 Hot Bend (or Mandrell) Curl Test-v3-4. June 2003. Available online: http://www.papercurl.com (accessed on 22 June 2024).
- Brodeur, P.; Gerhardstein, J.P. Overview of applications of ultrasonics in the pulp and paper industry. In Proceedings of the 1998 IEEE Ultrasonics Symposium, Sendai, Japan, 5–8 October 1998; pp. 809–815. [Google Scholar]
- Niskanen, K.J.; Sadowski, J.W. Evaluation of some fibre orientation measurements. J. Pulp Pap. Sci. 1989, 15, J220–J224. [Google Scholar]
- Schaffrath, H.J.; Tillmann, O. Testing of Fibers, Suspensions, and Paper and Board Grades. In Handbook of Paper and Board, 2nd ed.; Holik, H., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; Volume 2, pp. 1059–1086. [Google Scholar]
- Tan, Z. Paper: Nondestructive Evaluation. In Encyclopedia of Materials: Science and Technology; Buschow, K.H.J., Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2001; pp. 1–5. [Google Scholar]
- Hess, T.R.; Brodeur, P.H. Effects of Wet Straining and Drying on Fibre Orientation and Elastic Stiffness Orientation. J. Pulp Pap. Sci. 1996, 22, J160–J164. [Google Scholar]
- Vahey, D.W.; Considine, J.M.; Kahra, A.; Scotch, M. Comparison of fiber orientation and tensile-stiffness orientation measurements in paper. In Proceedings of the Progress in Paper Physics Seminar 2008, Espoo, Finland, 2–5 June 2008; pp. 271–273. [Google Scholar]
- Holik, H.; Mayer, R. Dryer Section. In Handbook of Paper and Board, 2nd ed.; Holik, H., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; Volume 2, pp. 713–744. [Google Scholar]
- Nordström, A.; Gudmundson, P.; Carlsson, L.A. Influence of Sheet Dimensions on Curl of Paper. J. Pulp Pap. Sci. JPPS 1998, 24, 18–25. [Google Scholar]
- Niskanen, K.J. Anisotropy of Laser Paper. Pap. Ja Puu 1993, 75, 326–328. [Google Scholar]
- Mendes, A.H.T.; Kim, H.Y.; Ferreira, P.J.T.; Park, S.W. The Importance of the Measurement of Paper Differential CD Shrinkage. O Pap. 2012, 73, 45–49. [Google Scholar]




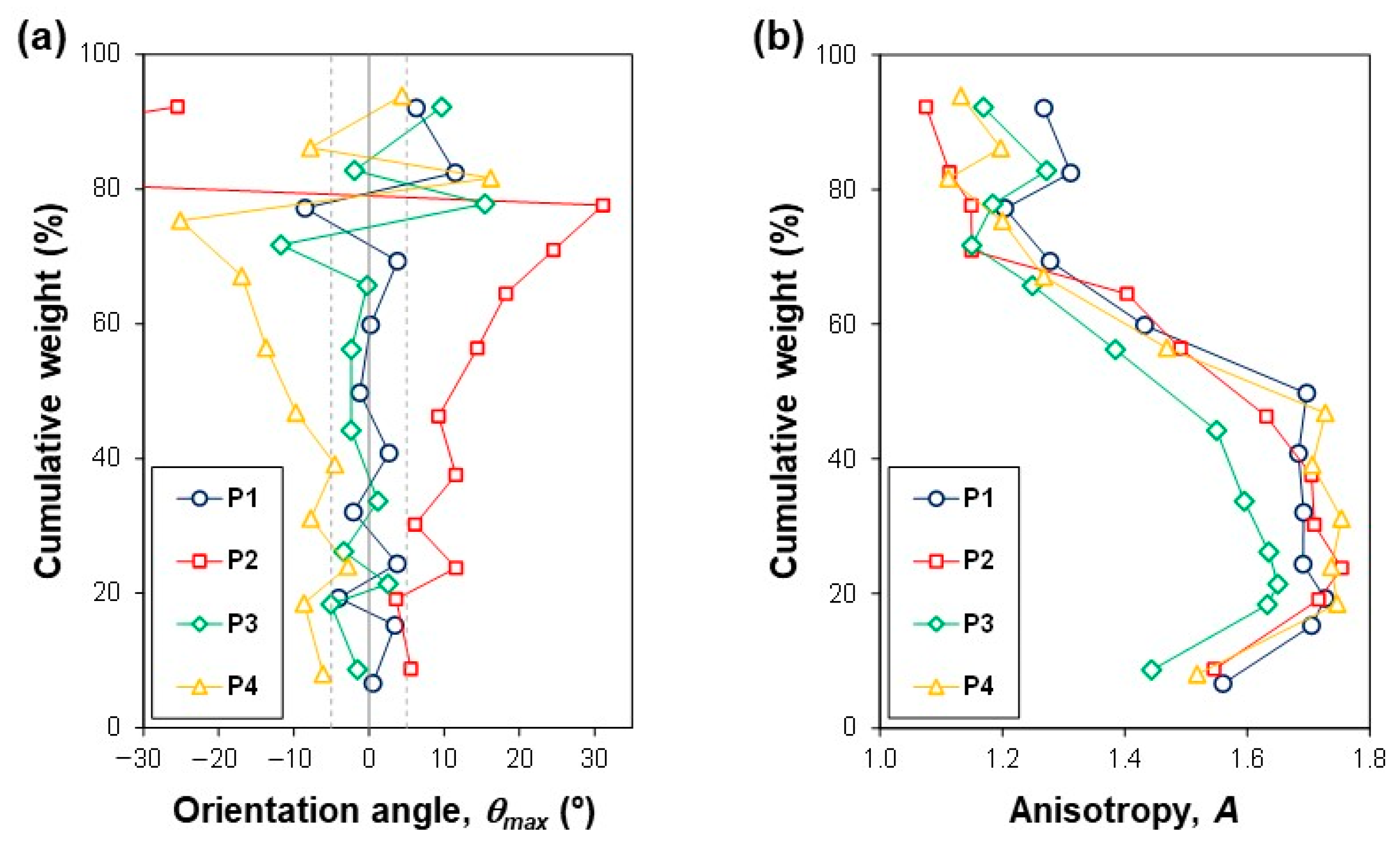

| Reference | Orientation Angle, θmax (°) | Anisotropy, A | ||||
|---|---|---|---|---|---|---|
| BH | TH | Overall | BH | TH | Overall | |
| DT1 | −0.76 | −1.28 | −1.02 | 2.04 | 2.08 | 2.06 |
| DT2 | 0.16 | −0.24 | −0.03 | 1.96 | 1.88 | 1.92 |
| DT3 | −0.03 | 0.00 | −0.02 | 1.92 | 2.01 | 1.96 |
| −0.21 | −0.51 | −0.36 | 1.97 | 1.99 | 1.98 | |
| 0.48 | 0.68 | 0.58 | 0.06 | 0.10 | 0.07 | |
| Type of Tests | Direction | Curl Magnitude (10−1 m−1) | |||||
|---|---|---|---|---|---|---|---|
| TS | BS | TS − BS | |||||
| MD/CD | MD | 13.8 | 1.4 | 13.3 | 2.6 | 0.4 | 2.9 |
| CD | 34.2 | 5.6 | 20.4 | 2.9 | 13.8 | 6.3 | |
| Diagonal 1 | LD | 5.4 | 13.2 | 8.8 | 11.9 | −3.3 | 14.6 |
| RD | 12.5 | 7.7 | 7.5 | 11.2 | 5.0 | 13.9 | |
| Property | Position in CD | SIA | TSO | |||
|---|---|---|---|---|---|---|
| BH | TH | |TH − BH| | Global | |||
| θmax (°) | P1 | 0.43 | 3.14 | 2.71 | 1.13 | −0.62 |
| P2 | 8.01 | 14.39 | 6.38 | 9.52 | 3.59 | |
| P3 | −1.41 | 0.82 | 2.23 | −0.72 | −0.54 | |
| P4 | −6.62 | −10.63 | 4.01 | −7.67 | −3.20 | |
| A | P1 | 1.67 | 1.29 | 0.39 | 1.50 | 2.77 |
| P2 | 1.67 | 1.17 | 0.50 | 1.39 | 2.31 | |
| P3 | 1.58 | 1.22 | 0.36 | 1.39 | 2.29 | |
| P4 | 1.69 | 1.20 | 0.49 | 1.42 | 2.35 | |
| Type of Tests | Direction | Side | Curl Magnitude (10−1 m−1) | |||
|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |||
| MD/CD | MD | TS | 13.8 | 18.8 | 13.8 | 16.3 |
| BS | −13.8 | −12.5 | −12.5 | −13.8 | ||
| TS − BS | 27.5 | 31.3 | 26.3 | 30.0 | ||
| CD | TS | −25.0 | −57.5 | −27.5 | −45.0 | |
| BS | 50.0 | 28.8 | 37.5 | 47.5 | ||
| TS − BS | −75.0 | −86.3 | −65.0 | −92.5 | ||
| Diagonal 1 | LD | TS | 12.5 | −10.0 | 5.0 | 5.0 |
| BS | 18.8 | 11.3 | 5.0 | 11.3 | ||
| TS − BS | −6.3 | −21.3 | 0.0 | −6.3 | ||
| RD | TS | −3.8 | 11.3 | 1.3 | −1.3 | |
| BS | 22.5 | 12.5 | 21.3 | 21.3 | ||
| TS − BS | −26.3 | −1.3 | −20.0 | −22.5 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dias, P.A.N.; Rodrigues, R.; Reis, M.S. Experimental Assessment of Paper Formation Conditions and Structural Two-Sidedness and Their Impacts on Curl Phenomena. Processes 2024, 12, 1536. https://doi.org/10.3390/pr12071536
Dias PAN, Rodrigues R, Reis MS. Experimental Assessment of Paper Formation Conditions and Structural Two-Sidedness and Their Impacts on Curl Phenomena. Processes. 2024; 12(7):1536. https://doi.org/10.3390/pr12071536
Chicago/Turabian StyleDias, Paulo A. N., Ricardo Rodrigues, and Marco S. Reis. 2024. "Experimental Assessment of Paper Formation Conditions and Structural Two-Sidedness and Their Impacts on Curl Phenomena" Processes 12, no. 7: 1536. https://doi.org/10.3390/pr12071536
APA StyleDias, P. A. N., Rodrigues, R., & Reis, M. S. (2024). Experimental Assessment of Paper Formation Conditions and Structural Two-Sidedness and Their Impacts on Curl Phenomena. Processes, 12(7), 1536. https://doi.org/10.3390/pr12071536







