Enhancing Vapor Compression Refrigeration Systems Efficiency via Two-Phase Length and Superheat Evaporator MIMO Control
Abstract
1. Introduction
2. Dynamic Model of a VCRS in Thermosys
3. Thermodynamic Analysis of the VCRS Cycle
4. Results
4.1. VCRS Operational Parameters as a Function of Actuation Variables
4.2. VCRS Operational Parameters as a Function of Control Variables
4.3. VCRS Model for Control Design
4.4. MIMO Sliding Mode Control for a VCRS
- Assumption 1. is nonsingular and such that .
- Assumption 2. .
4.5. Simulation Results
5. Concluding Remarks
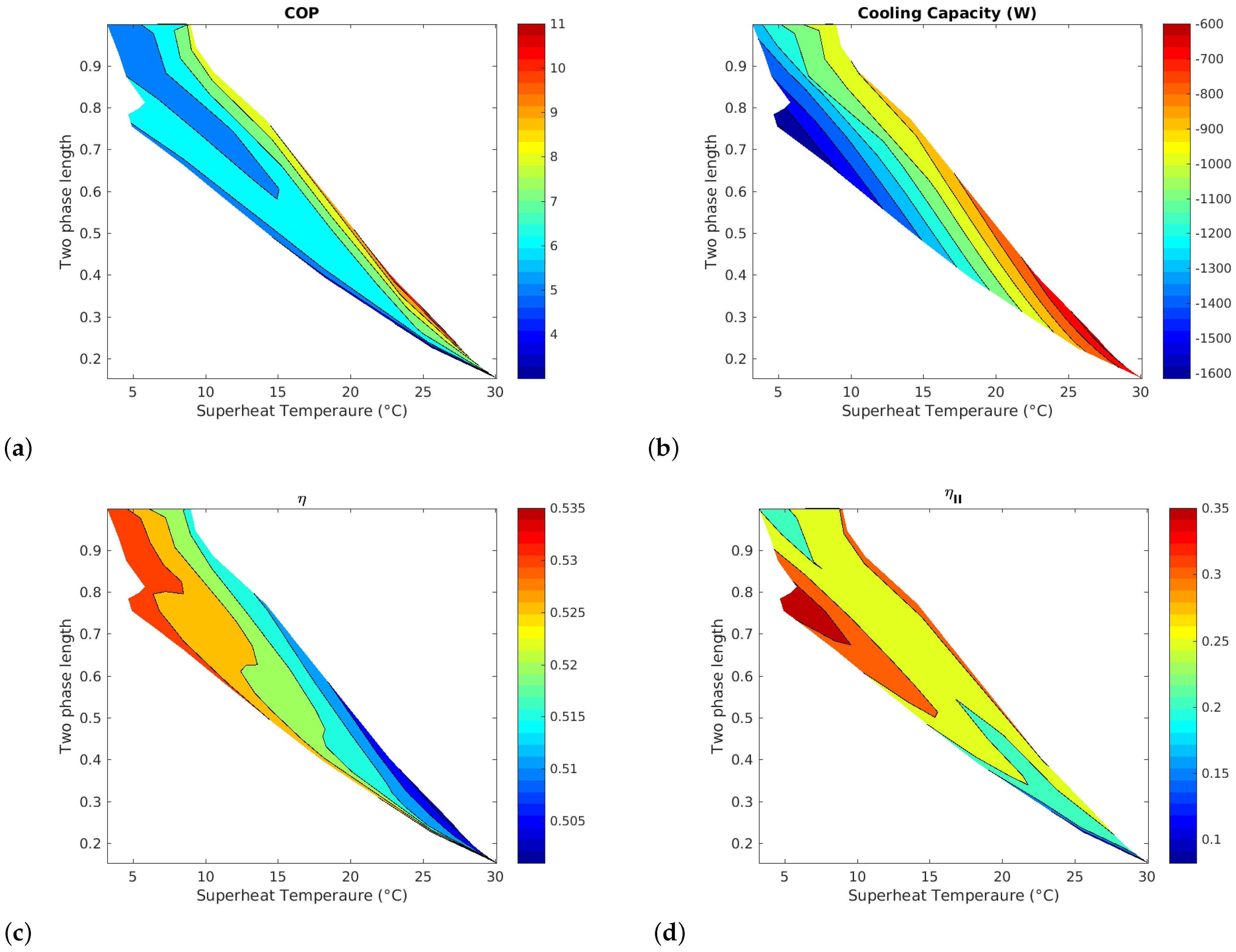
- The study revealed through parametric analysis that the combined manipulation of compressor speed and EEV opening allows the system to be brought to operating regions favorable for optimal two-phase length and cooling capacity.
- It is demonstrated that merely seeking to maximize the two-phase length is insufficient for optimizing the system’s efficiency or COP. Rather, it was found that the operating region where higher efficiency is achieved corresponds to a two-phase length between 0.7 and 0.9.
- A control system based on the two-phase length and the superheat temperature was proposed to bring the system to the high-efficiency operating points found through the performed parametric analysis. Different scenarios were used to evaluate the behavior of the control system.
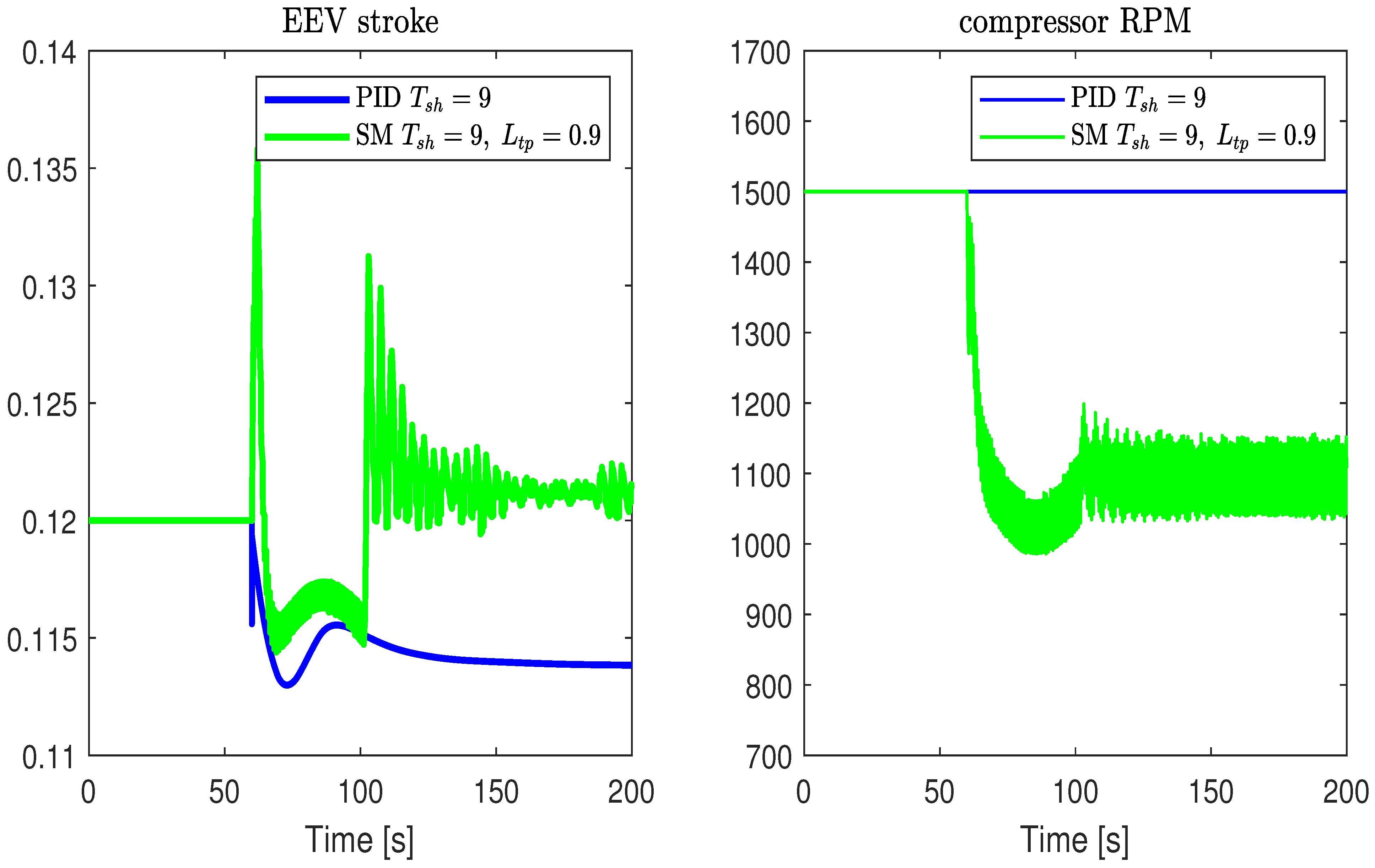
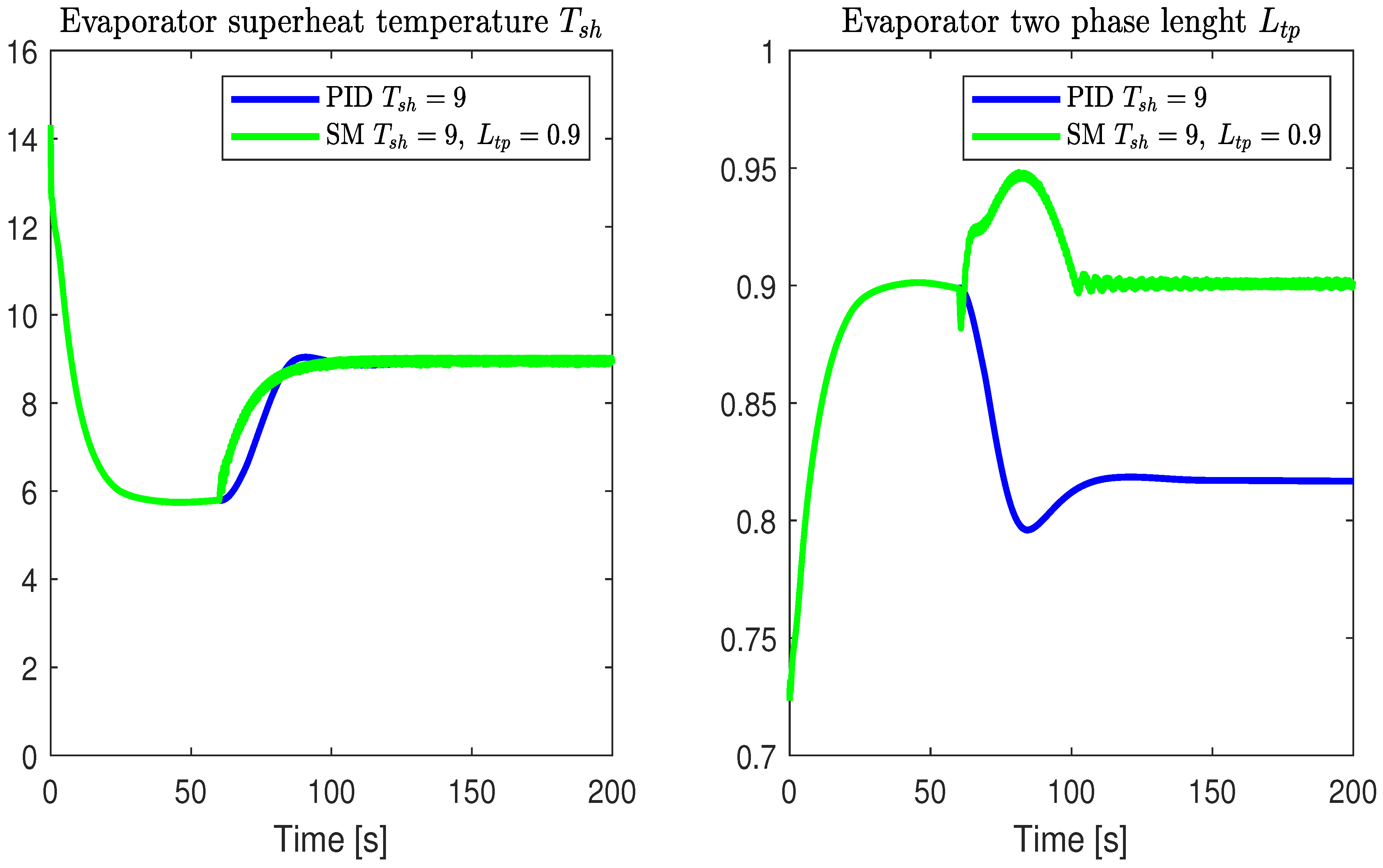
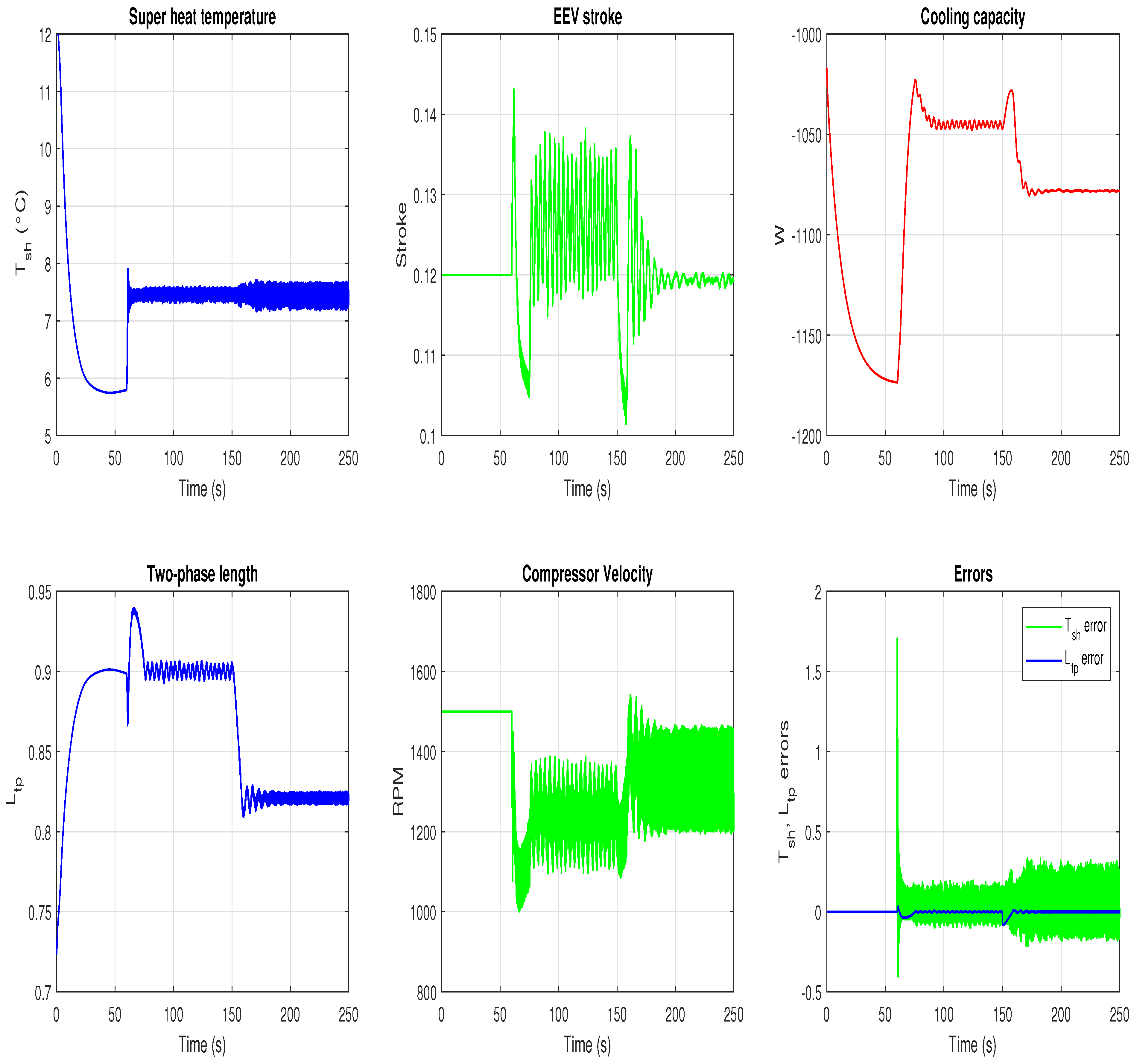
- The control system can be used to adjust the compressor speed based on the cooling capacity requirements of the VCRS. For instance, in the case presented in Figure 8, the cooling capacity of the system can be reduced, representing a decrease in compressor speed of approximately 11.5%. This reduction directly translates to energy savings for the system.
- It was found that controlling the evaporator’s two-phase length and the superheat temperature makes it possible to reduce the compressor speed maintaining the cooling capacity. To the best of the author’s knowledge, this is the first investigation in which a control for a refrigeration system is based on the two-phase length of the evaporator.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Superheat temperature in the evaporator | |
| Condenser inlet temperature | |
| Enthalpy at the inlet of the condenser | |
| Enthalpy at the outlet of the evaporator | |
| Cooling capacity of the system | |
| Refrigerant mass flow | |
| Exergy destruction in compressor | |
| Exergy destruction in condenser | |
| Exergy destruction in valve | |
| Exergy destruction in evaporator | |
| Entropy generated | |
| Energy flux to high temperature medium | |
| High temperature medium | |
| Energy flux to low temperature medium | |
| Low temperature medium | |
| First law efficiency | |
| Second law efficiency | |
| Supplied energy | |
| COP | Coefficient of Performance |
Appendix A
- = Specific heat at constant pressure of vapor refrigerant,
- = Refrigerant mass flow rate at point 4,
- = Refrigerant vapor quality at point 4,
- = Enthalpy of liquid refrigerant,
- = Mass flow rate of liquid refrigerant,
- = Convection heat transfer coefficient of refrigerant,
- = Evaporator heat exchanger area,
- = Evaporator flow length,
- = Enthalpy of the refrigerant vapor in saturation,
- = Enthalpy of liquid refrigerant at saturation,
- = Two phase length in the evaporato,
- = Refrigerant volume in the evaporator,
- = Vapor refrigerant density,
- = Density of liquid refrigerant at point 4,
- = Initial temperature,
- = Temperature at point 1,
- = Temperature of the working fluid in the evaporator at the saturation point of the pipe.
References
- Sleiti, A.K.; Al-Ammari, W.A.; Al-Khawaja, M. Review of innovative approaches of thermo-mechanical refrigeration systems using low grade heat. Int. J. Energy Res. 2020, 44, 9808–9838. [Google Scholar] [CrossRef]
- Cohen, R.; Hamilton, J.; Pearson, J. Possible Energy Conservation through Use of Variable Capacity Compressors. In Proceedings of the International Compressor Engineering Conference 1974, West Lafayette, IN, USA, 10–14 July 1974. [Google Scholar]
- Binneberg, P.; Kraus, E.; Quack, H. Reduction in Power Consumption of Household Refrigerators by Using Variable Speed Compressors. In Proceedings of the International Refrigeration and Air Conditioning Conference 2002, West Lafayette, IN, USA, 16–19 July 2002. [Google Scholar]
- Khatri, R.; Joshi, A. Energy performance comparison of inverter based variable refrigerant flow unitary AC with constant volume unitary AC. Energy Procedia 2017, 109, 18–26. [Google Scholar] [CrossRef]
- Schibuola, L.; Scarpa, M.; Tambani, C. Variable speed drive (VSD) technology applied to HVAC systems for energy saving: An experimental investigation. Energy Procedia 2018, 148, 806–813. [Google Scholar] [CrossRef]
- Liu, C.; Sang, C.; Li, G.; Li, W.; Ning, B.; Zhu, J.; Guo, Y.; Li, T. Experimental investigation on the influence of electronic expansion valve opening on the performance of miniature refrigeration system. Appl. Therm. Eng. 2024, 248, 123287. [Google Scholar] [CrossRef]
- Li, H.; Su, Z.; Zhao, C.; An, T.; Qin, X.; Chen, G.; Gao, J.; Zhang, Y. Influence of compressor speed on the performance of low pressure vapor-injected refrigeration systems. Therm. Sci. 2024, 28, 2043–2049. [Google Scholar] [CrossRef]
- Al-Hassani, A.H.; Al-Badri, A.R. Effects of compressor speed and electronic expansion valve opening on the performance of R410a water chiller system. Wasit J. Eng. Sci. 2020, 8, 12–20. [Google Scholar] [CrossRef]
- Nunes, T.; Vargas, J.; Ordonez, J.; Shah, D.; Martinho, L. Modeling, simulation and optimization of a vapor compression refrigeration system dynamic and steady state response. Appl. Energy 2015, 158, 540–555. [Google Scholar] [CrossRef]
- Roy, R.; Emani, M.S.; Mandal, B.K. Numerical simulation of vapour compression refrigeration system using refrigerant R152a, R404a and R600a. Indian J. Sci. Res. 2017, 15, 62–67. [Google Scholar]
- Catano, J.; Zhang, T.; Wen, J.T.; Jensen, M.K.; Peles, Y. Vapor compression refrigeration cycle for electronics cooling–Part I: Dynamic modeling and experimental validation. Int. J. Heat Mass Transf. 2013, 66, 911–921. [Google Scholar] [CrossRef]
- Chi, J.; Didion, D. A simulation model of the transient performance of a heat pump. Int. J. Refrig. 1982, 5, 176–184. [Google Scholar] [CrossRef]
- Jankovic, Z.; Pavkovic, B.; Sieres, J.; Zivic, M. Compressor Speed, Expansion Valve Opening and Refrigerant Charge Influences on the Propane Unit Design. In Proceedings of the International Refrigeration and Air Conditioning Conference 2022, West Lafayette, IN, USA, 10–14 July 2022. [Google Scholar]
- Koury, R.; Machado, L.; Ismail, K. Numerical simulation of a variable speed refrigeration system. Int. J. Refrig. 2001, 24, 192–200. [Google Scholar] [CrossRef]
- Tu, Q.; Zhang, L.; Cai, W.; Guo, X.; Yuan, X.; Deng, C.; Zhang, J. Control strategy of compressor and sub-cooler in variable refrigerant flow air conditioning system for high EER and comfortable indoor environment. Appl. Therm. Eng. 2018, 141, 215–225. [Google Scholar] [CrossRef]
- Rasmussen, B.P.; Alleyne, A.G. Dynamic Modeling and Advanced Control of Air Conditioning and Refrigeration Systems; Air Conditioning and Refrigeration Center TR-244; University of Illinois: Urbana, IL, USA, 2006. [Google Scholar]
- Xia, Y.; Du, J.; Deng, S. Effects of superheat nonlinearity on the operational stability of a direct expansion (DX) air conditioning (A/C) system. Energy Procedia 2017, 142, 1854–1859. [Google Scholar] [CrossRef]
- Schurt, L.C.; Hermes, C.J.; Neto, A.T. A model-driven multivariable controller for vapor compression refrigeration systems. Int. J. Refrig. 2009, 32, 1672–1682. [Google Scholar] [CrossRef]
- Yang, Z.; Pollock, D.T.; Wen, J.T. Optimization and predictive control of a vapor compression cycle under transient pulse heat load. Int. J. Refrig. 2017, 75, 14–25. [Google Scholar] [CrossRef]
- Yin, X.; Li, S. Model Predictive Control for Vapor Compression Refrigeration Cycle Process. Int. J. Autom. Comput. 2015. [Google Scholar] [CrossRef]
- Li, H.; Jeong, S.K.; You, S.S. Feedforward control of capacity and superheat for a variable speed refrigeration system. Appl. Therm. Eng. 2009, 29, 1067–1074. [Google Scholar] [CrossRef]
- Jain, N.; Alleyne, A.G. Comparison of SISO and MIMO control techniques for a diagonally dominant vapor compression system. In Proceedings of the 2009 American Control Conference, St. Louis, MI, USA, 10–12 June 2009; pp. 1580–1585. [Google Scholar] [CrossRef]
- Bejarano, G.; Alfaya, J.A.; Ortega, M.G.; Rubio, F.R. Multivariable analysis and H∞ control of a one-stage refrigeration cycle. Appl. Therm. Eng. 2015, 91, 1156–1167. [Google Scholar] [CrossRef]
- Alfaya, J.A.; Bejarano, G.; Ortega, M.G.; Rubio, F.R. Controllability analysis and robust control of a one-stage refrigeration system. Eur. J. Control 2015, 26, 53–62. [Google Scholar] [CrossRef]
- Kim, J.G.; Han, C.H.; Jeong, S.K. Disturbance observer-based robust control against model uncertainty and disturbance for a variable speed refrigeration system. Int. J. Refrig. 2020, 116, 49–58. [Google Scholar] [CrossRef]
- Goyal, A.; Staedter, M.A.; Garimella, S. A review of control methodologies for vapor compression and absorption heat pumps. Int. J. Refrig. 2019, 97, 1–20. [Google Scholar] [CrossRef]
- Ding, T.L.; Norris, S.; Subiantoro, A. Adaptive Reinforcement Learning PI Controllers for Vapor Compression Cycle Control. In Proceedings of the 19th International Refrigeration and Air Conditioning Conference, Purdue, West Lafayette, IN, USA, 10–14 July 2022. [Google Scholar]
- Christian Rosdahl, B.B.; Eisenhower, B. Model-free MIMO control tuning of a chiller process using reinforcement learning. Sci. Technol. Built Environ. 2023, 29, 782–794. [Google Scholar] [CrossRef]
- Huang, Y.; Khajepour, A.; Ding, H.; Bagheri, F.; Bahrami, M. An energy-saving set-point optimizer with a sliding mode controller for automotive air-conditioning/refrigeration systems. Appl. Energy 2017, 188, 576–585. [Google Scholar] [CrossRef]
- Jackson, S.D.; Palazotto, A.N.; Pachter, M.; Niedbalski, N. Control of Vapor Compression Cycles under Transient Thermal Loads. In Proceedings of the AIAA Scitech 2019 Forum, Online, 7–11 January 2019. [Google Scholar] [CrossRef]
- Utkin, V.I.; Guldner, J.; Shi, J. Sliding Mode Control in Electromechanical Systems; Automation and Control Engineering Series; Taylor & Francis: Abingdon, UK, 2009. [Google Scholar]
- Bejarano-Rincón, A.; Estrada, A.; Herrera-Hernández, E.; Alvarado-Orozco, J. Control design for a class of multivariable nonlinear system with uncertain control direction: A laser cladding case study. Eur. J. Control 2021, 60, 114–124. [Google Scholar] [CrossRef]
- Rubagotti, M.; Incremona, G.P.; Ferrara, A. A Discrete-Time Integral Sliding Mode Control Law for Systems With Matched and Unmatched Disturbances. IEEE Control Syst. Lett. 2024, 8, 448–453. [Google Scholar] [CrossRef]
- Ekren, O.; Sahin, S.; Isler, Y. Comparison of different controllers for variable speed compressor and electronic expansion valve. Int. J. Refrig. 2010, 33, 1161–1168. [Google Scholar] [CrossRef]
- Li, B.; Peuker, S.; Hrnjak, P.S.; Alleyne, A.G. Refrigerant mass migration modeling and simulation for air conditioning systems. Appl. Therm. Eng. 2011, 31, 1770–1779. [Google Scholar] [CrossRef]
- Pangborn, H.; Alleyne, A.G.; Wu, N. A comparison between finite volume and switched moving boundary approaches for dynamic vapor compression system modeling. Int. J. Refrig. 2015, 53, 101–114. [Google Scholar] [CrossRef]
- Wallace, M.; McBride, R.; Aumi, S.; Mhaskar, P.; House, J.; Salsbury, T. Energy efficient model predictive building temperature control. Chem. Eng. Sci. 2012, 69, 45–58. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, W.; Huang, M. A state-space dynamic model for vapor compression refrigeration system based on moving-boundary formulation. Int. J. Refrig. 2015, 60, 174–189. [Google Scholar] [CrossRef]
- Qiao, H.; Laughman, C.R.; Aute, V.; Radermacher, R. An advanced switching moving boundary heat exchanger model with pressure drop. Int. J. Refrig. 2016, 65, 154–171. [Google Scholar] [CrossRef]
- Cengel, Y. Solucionario termodinámica (vol. 7ma edicion); McGraw Hill: Mexico City, Mexico, 2012. [Google Scholar]
- Solanki, N.; Arora, A.; Singh, R. Performance enhancement and environmental analysis of vapor compression refrigeration system with dedicated mechanical subcooling. Int. J. Air-Cond. Refrig. 2023, 31, 26. [Google Scholar] [CrossRef]
- Utkin, V.; Lee, H. Chattering problem in sliding mode control systems. IFAC Proc. Vol. 2006, 39, 1. [Google Scholar] [CrossRef]
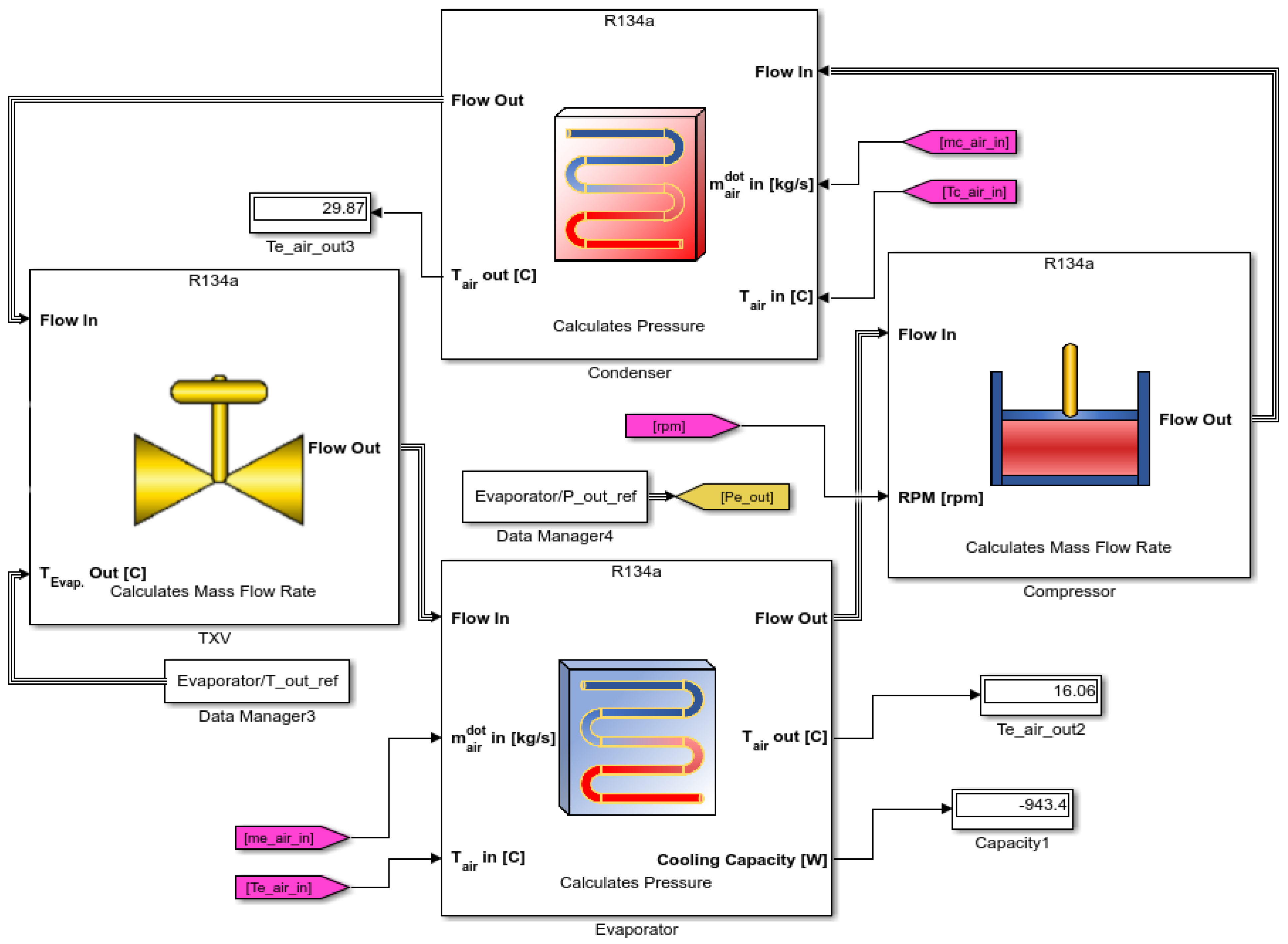




| Evaporator | |
| Hydraulic diameter (m) | 0.008163 |
| Length of a refrigerant passage (m) | 1.88 |
| Number of steps | 4 |
| Cross-sectional area of air of a side passage (m2) | 0.282 |
| Air contact surface area of one step (m2) | 0.73 |
| One pass coolant contact surface area (m2) | 0.0505 |
| Cross-sectional area of refrigerant passage (m2) | 5.156 × 10−5 |
| Coil material | stainless steel |
| Mass of one pass of heat exchanger (kg) | 1.4 |
| Condenser | |
| Hydraulic diameter (m) | 0.00856 |
| Length of a refrigerant passage (m) | 0.88 |
| Number of steps | 14 |
| Cross-sectional area of air of a side passage (m2) | 0.0260 |
| Air contact surface area of one step (m2) | 0.601 |
| One pass coolant contact surface area (m2) | 0.0236 |
| Cross-sectional area of refrigerant passage (m2) | 5.75 × 10−5 |
| Coil material | copper |
| Mass of one pass of heat exchanger (kg) | 0.255 |
| Expansion valve | |
| Cv (kPa·kg/m3) | 6 × 10−5 |
| Polynomial degree | 2 |
| Compresor | |
| Volume (m3) | 2.15 × 10−5 |
| Max. Turning speed (rpm) | 3000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estrada, A.; Córdova-Castillo, L.; Piedra, S. Enhancing Vapor Compression Refrigeration Systems Efficiency via Two-Phase Length and Superheat Evaporator MIMO Control. Processes 2024, 12, 1600. https://doi.org/10.3390/pr12081600
Estrada A, Córdova-Castillo L, Piedra S. Enhancing Vapor Compression Refrigeration Systems Efficiency via Two-Phase Length and Superheat Evaporator MIMO Control. Processes. 2024; 12(8):1600. https://doi.org/10.3390/pr12081600
Chicago/Turabian StyleEstrada, Antonio, Leonardo Córdova-Castillo, and Saúl Piedra. 2024. "Enhancing Vapor Compression Refrigeration Systems Efficiency via Two-Phase Length and Superheat Evaporator MIMO Control" Processes 12, no. 8: 1600. https://doi.org/10.3390/pr12081600
APA StyleEstrada, A., Córdova-Castillo, L., & Piedra, S. (2024). Enhancing Vapor Compression Refrigeration Systems Efficiency via Two-Phase Length and Superheat Evaporator MIMO Control. Processes, 12(8), 1600. https://doi.org/10.3390/pr12081600





