A Coupling Model of Gas–Water Two-Phase Productivity for Multilateral Horizontal Wells in a Multilayer Gas Reservoir
Abstract
:1. Introduction
2. Methodology
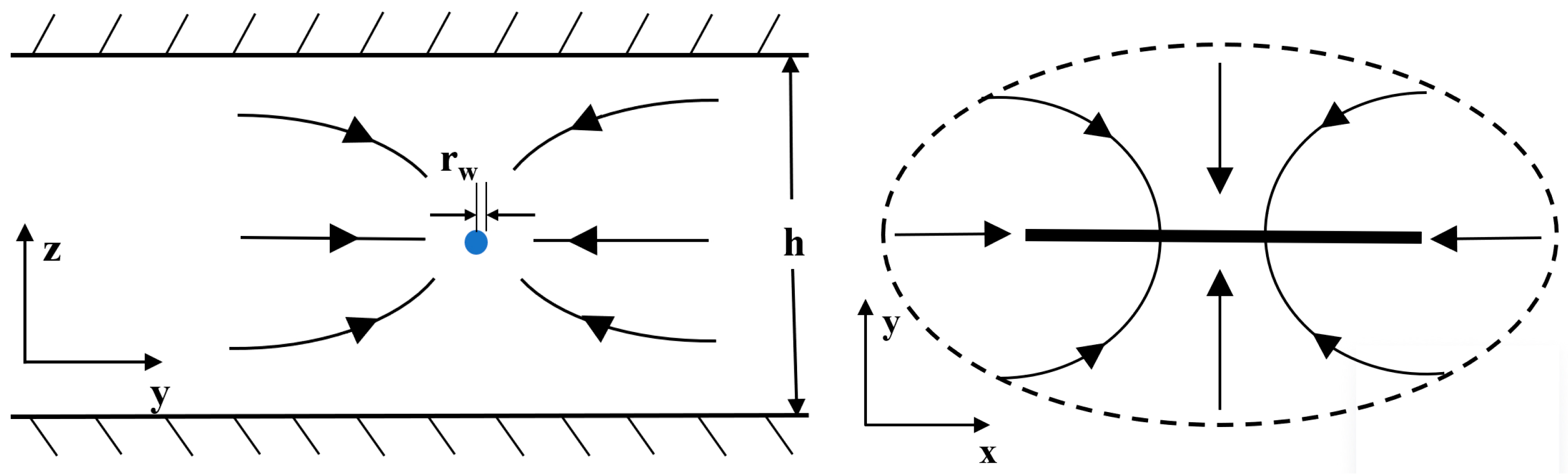
2.1. Basic Assumptions
- (1)
- The gas reservoir is horizontal with a uniform reservoir thickness h, and it has a uniform initial pressure pi;
- (2)
- The effects of gravity and capillary force are neglected;
- (3)
- The water flows steadily with a constant density and viscosity;
- (4)
- Considering two-phase steady state flow, the production process is isothermal and controlled by Darcy’s law;
- (5)
- The properties of the gas and reservoir are isotropic and homogeneous.
2.2. Coupling Modeling for Productivity of Horizontal Wells
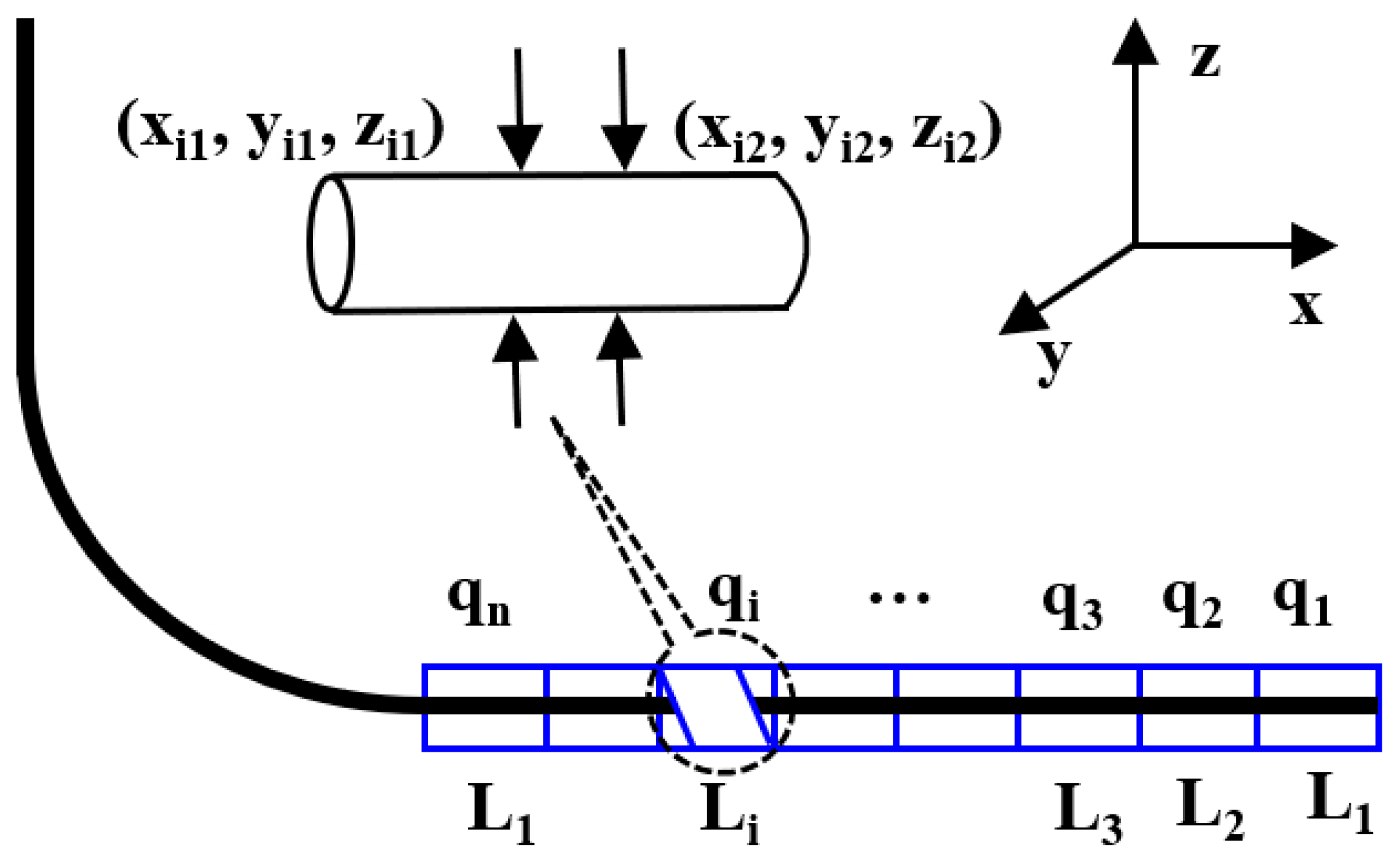
2.2.1. Reservoir Inflow Model
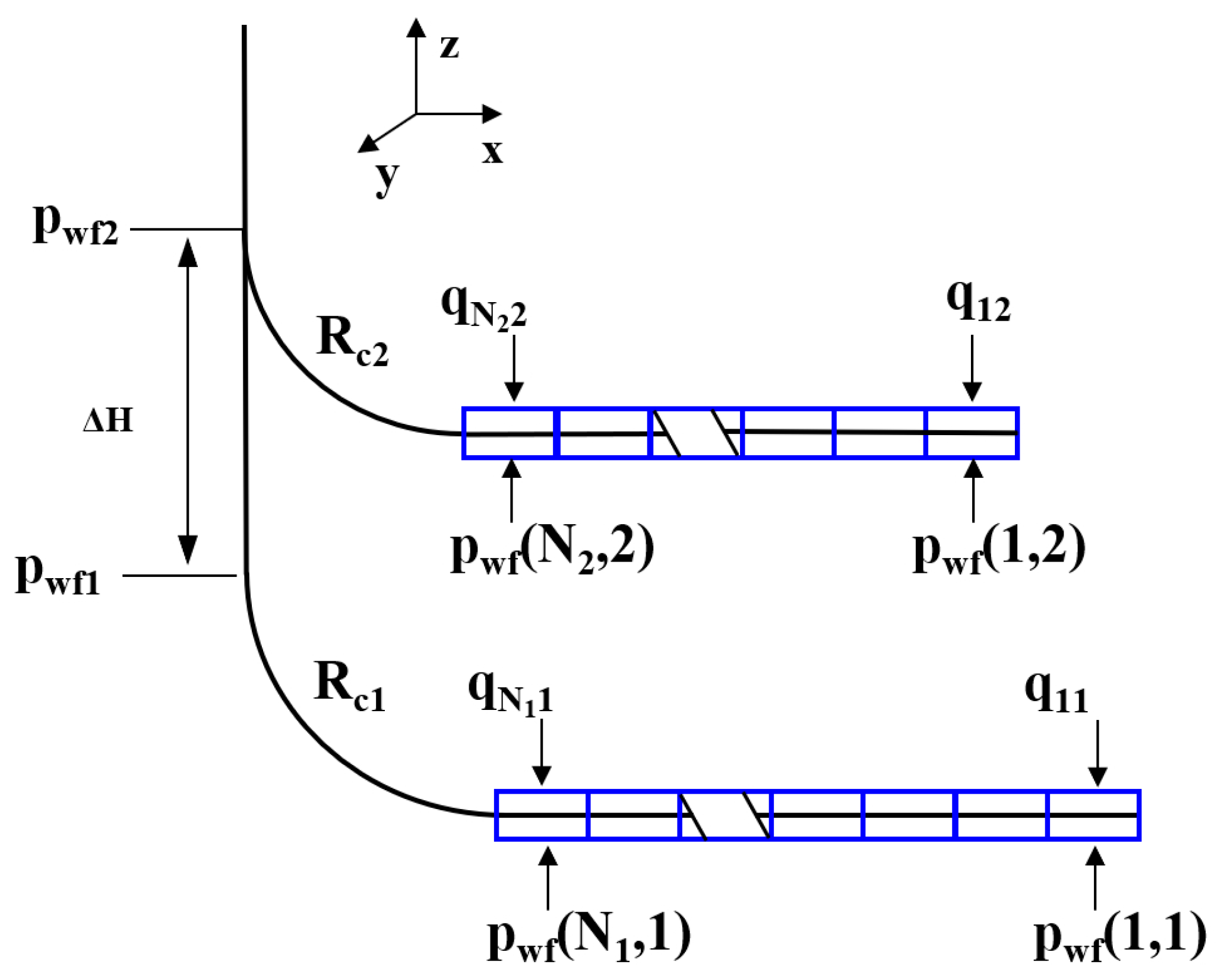
2.2.2. Wellbore Flow Model
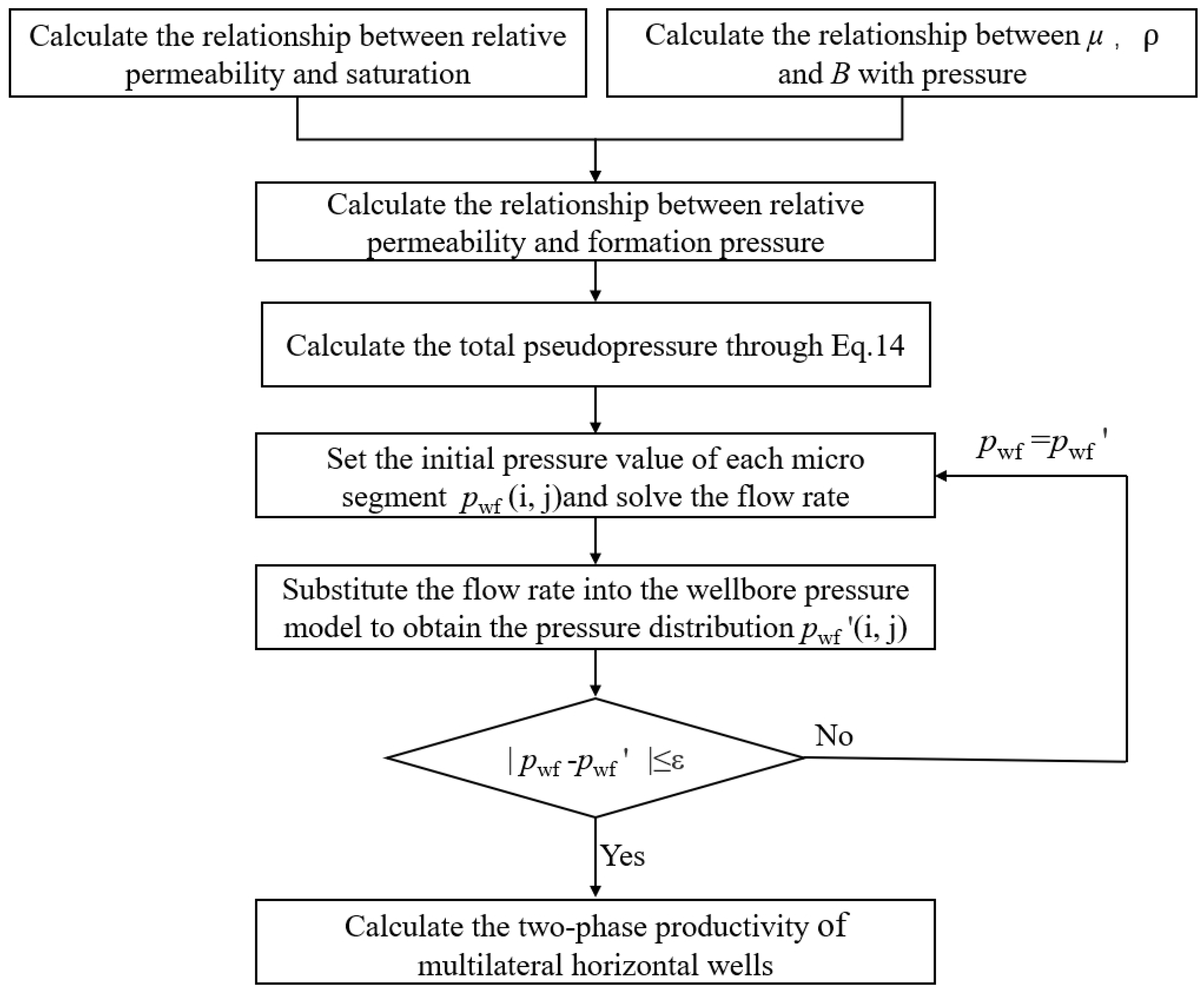
2.3. Coupling Model Solution
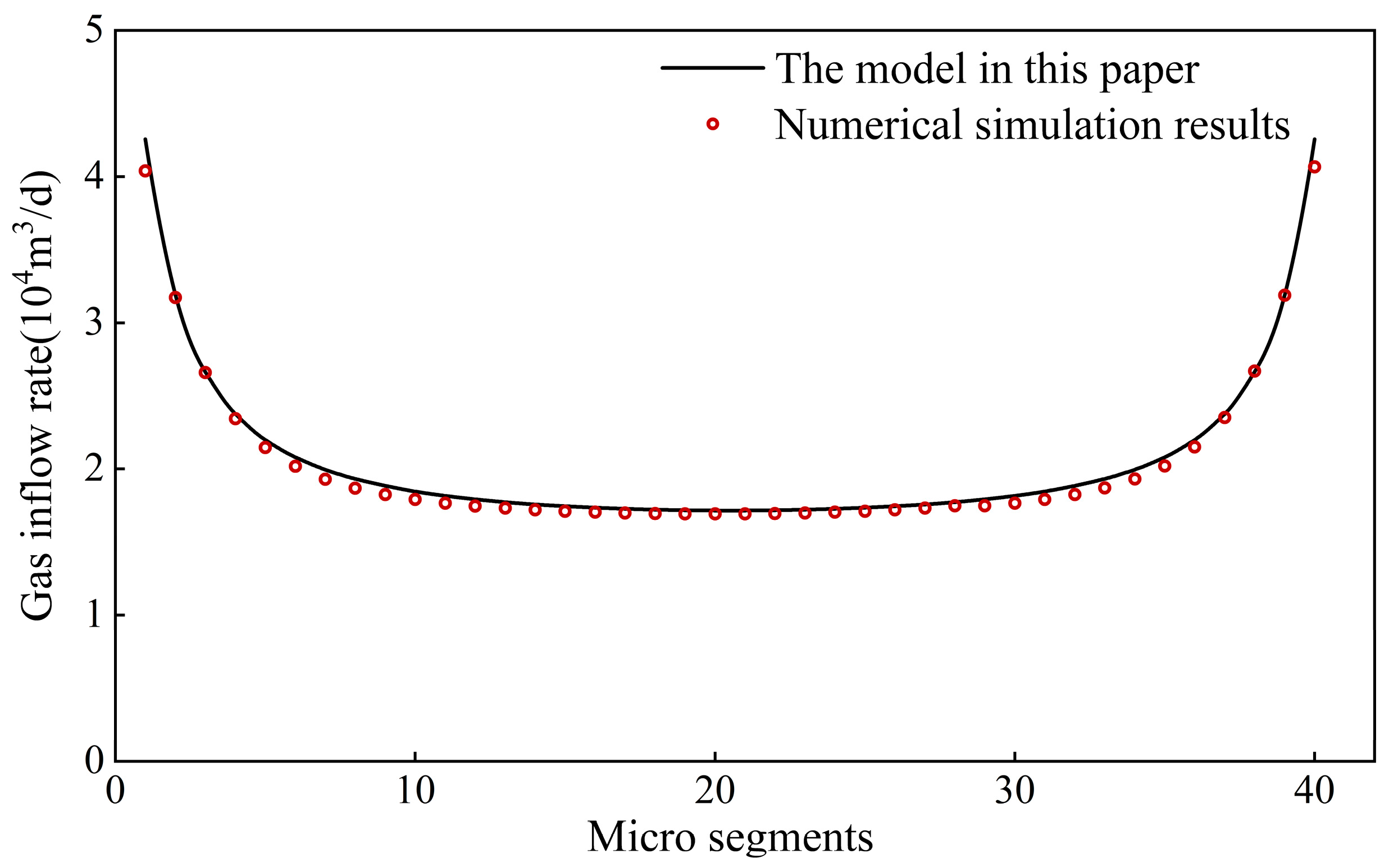
3. Results and Discussion
3.1. Coupling Model Solution
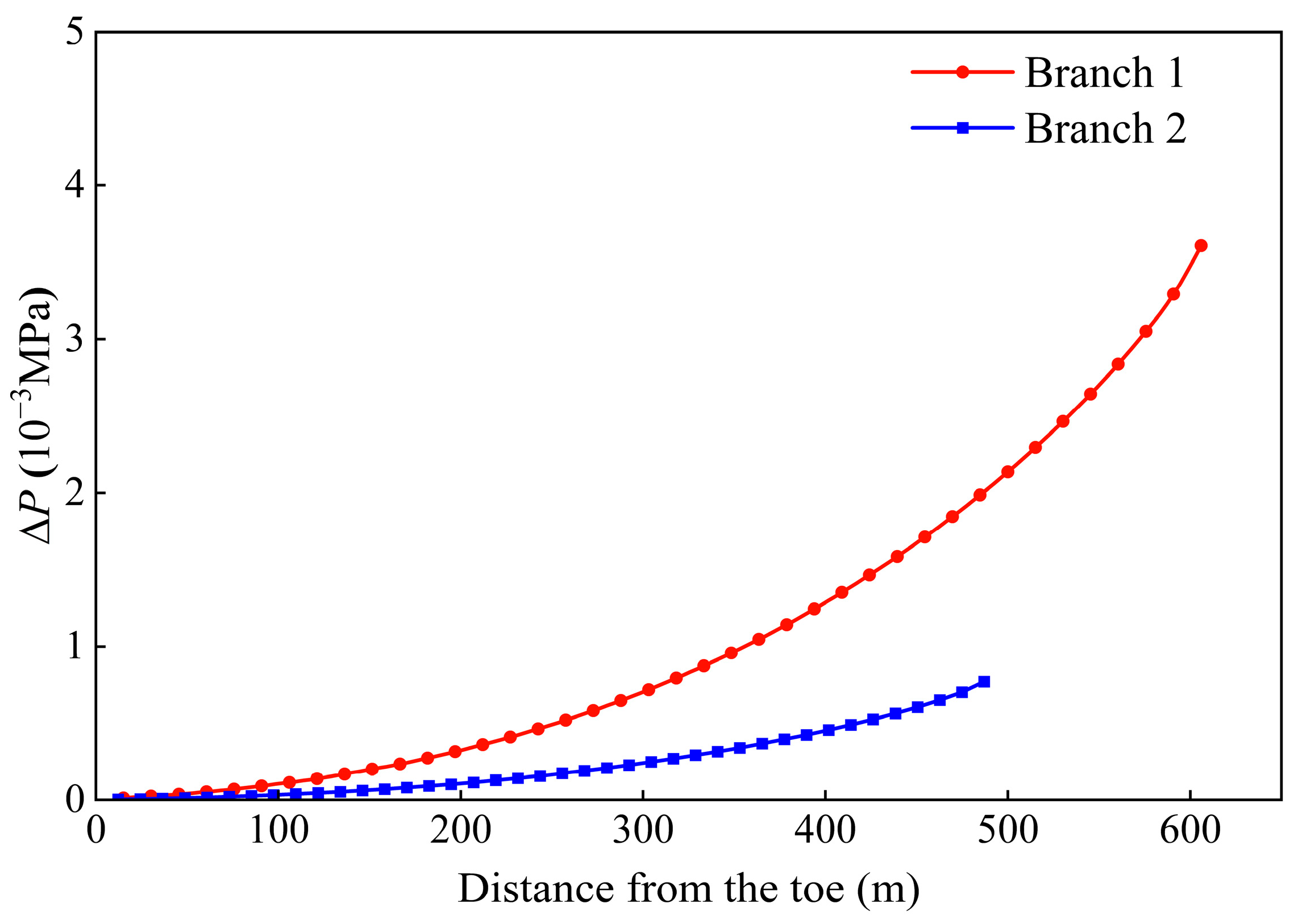
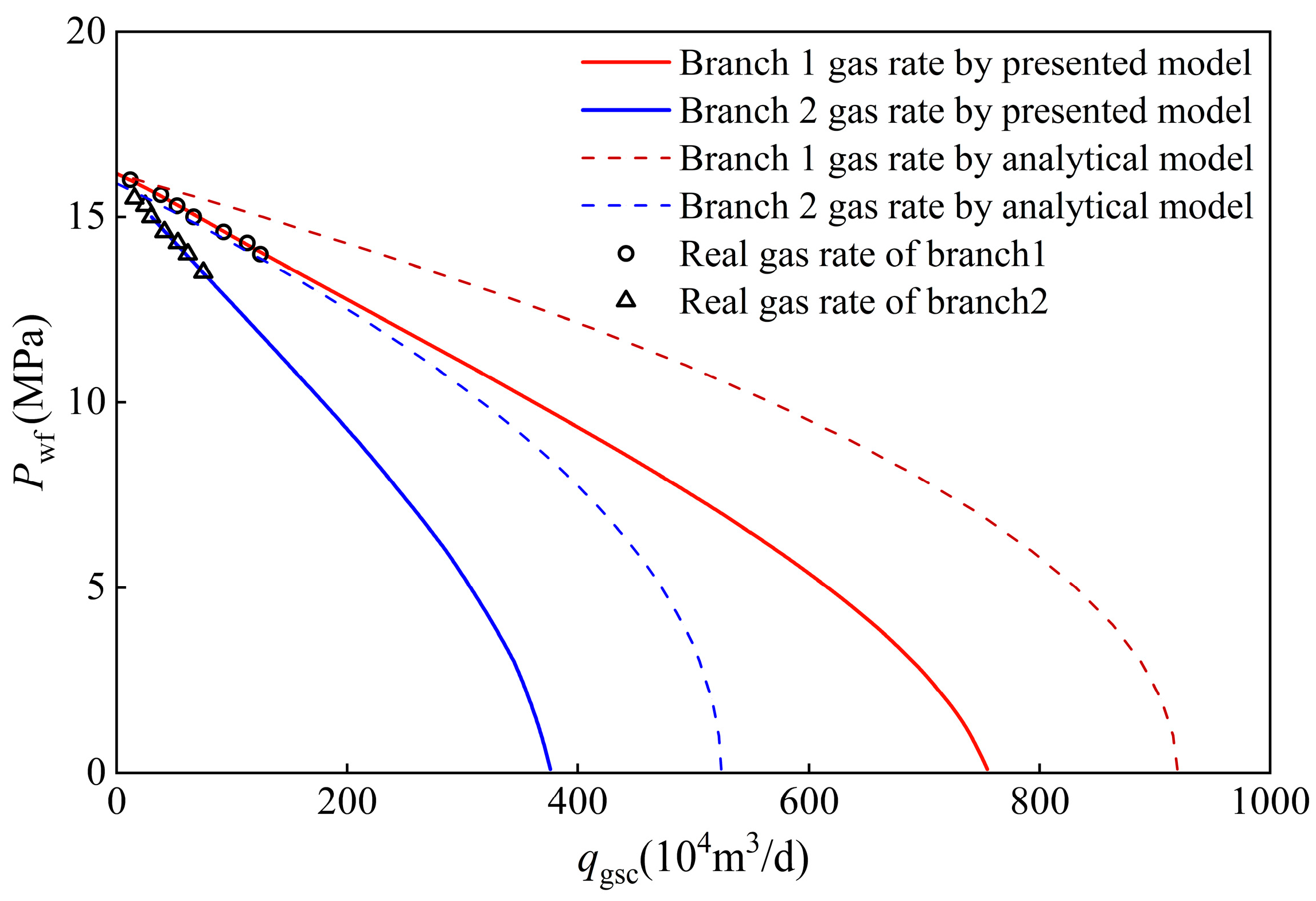
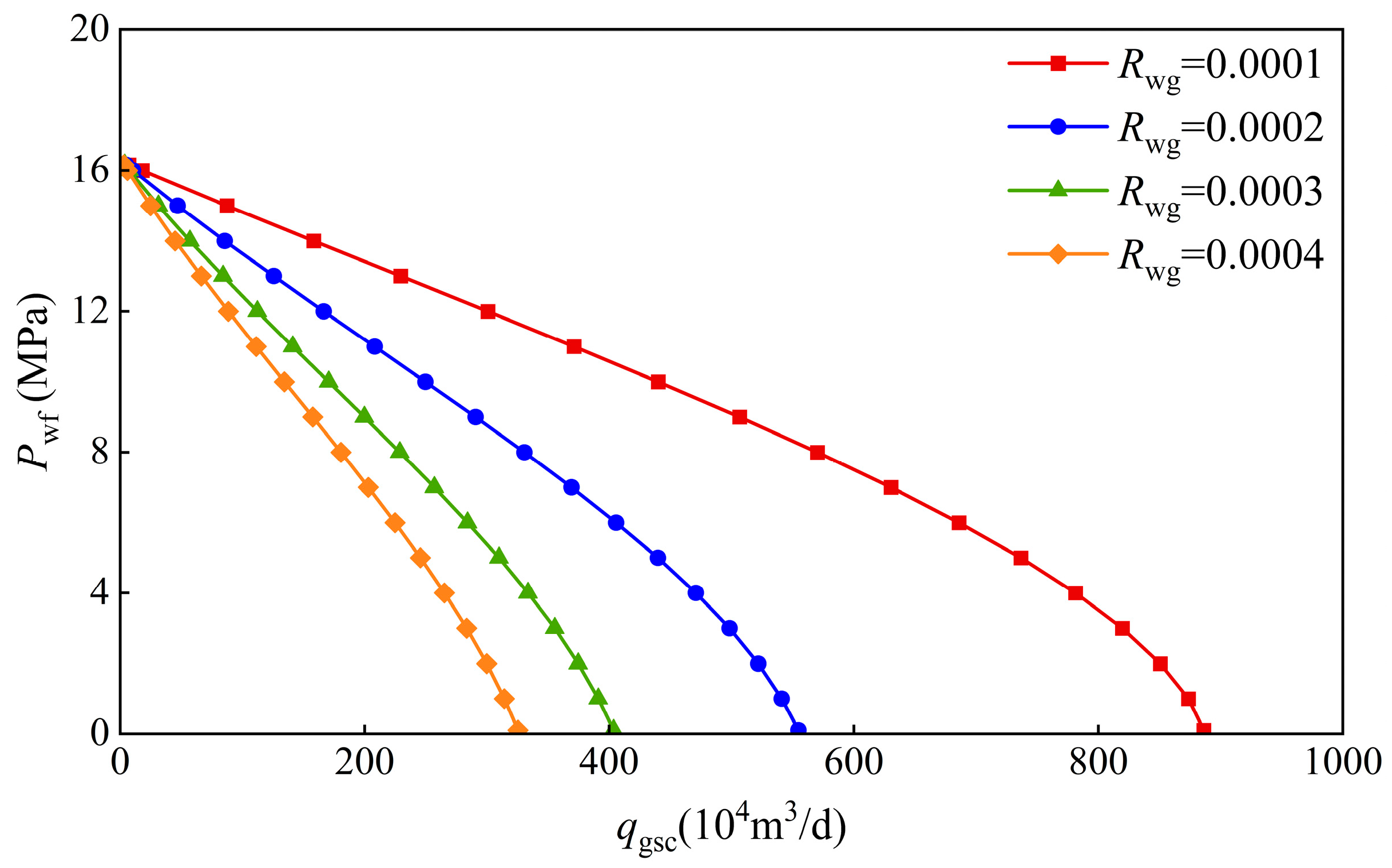
3.2. Field Application
4. Conclusions
- (1)
- The wellbore flow model utilized in the presented model accounts for both the accelerated pressure drop and friction pressure drop. The results indicate that the pressure in the wellbore was not uniform and increased nonlinearly from the toe to the heel.
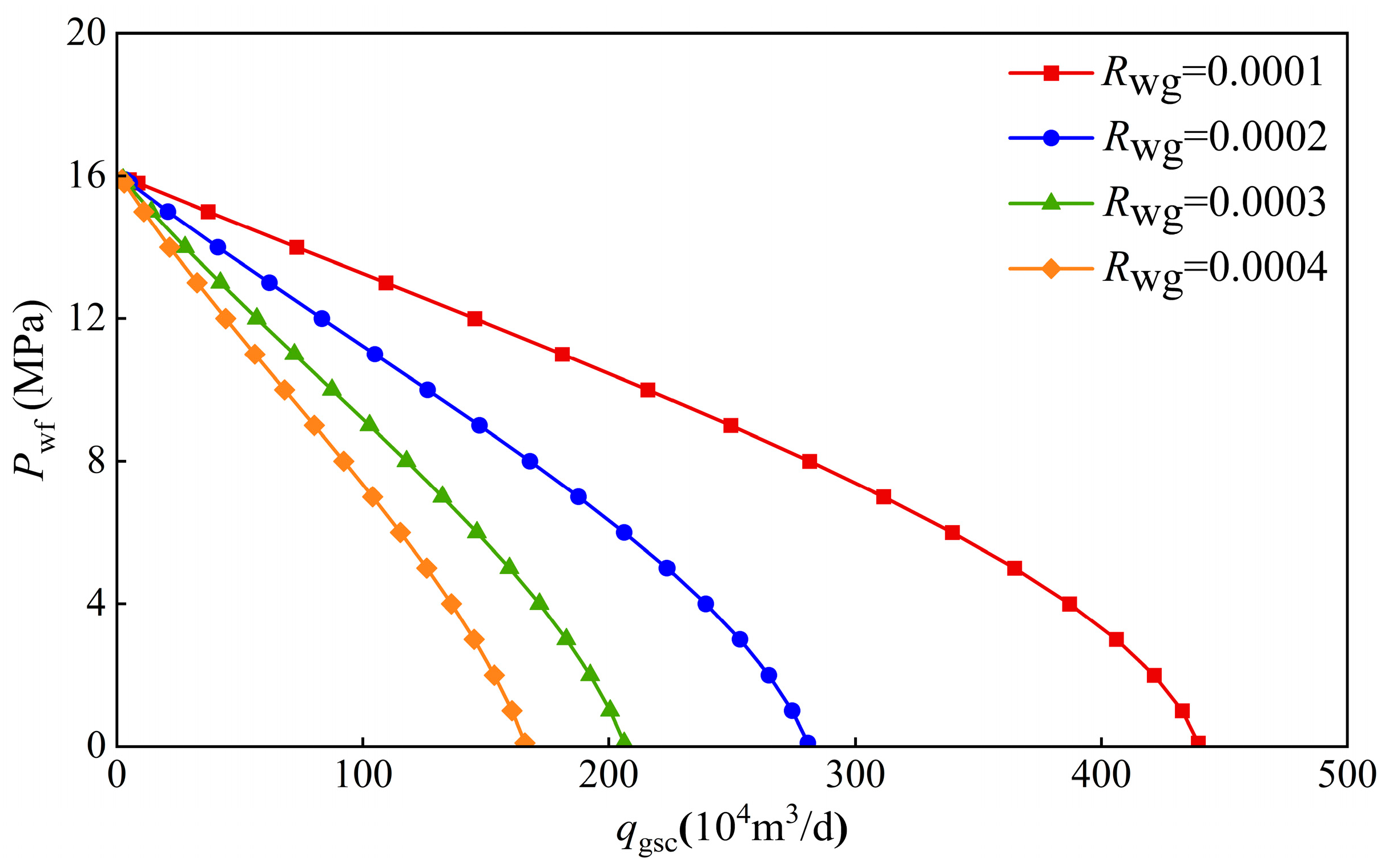
- (2)
- Well X31 in the YM gas field was presented to demonstrate the practical applicability of the proposed approach. The sensitivity analysis shows that the productivity of multilateral wells decreases as the gas-to-water volume ratio increases.
- (3)
- Compared with the analytical model of horizontal well productivity, the semi-analytical model proposed in this paper can better match the actual production data, while the calculation results of the analytical model of the horizontal well were larger. This is because the model proposed in this paper considers the influence of the wellbore pressure drop, wellbore variable flow, and water-to-gas ratio on productivity.
- (4)
- In the production process of horizontal wells, reasonable production pressure differences should be controlled to reduce the water production of gas wells and avoid a decline in productivity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | wellbore area (m2) |
| qgsc | gas flow rate at standard condition (m3/d) |
| Bg | gas volume factor |
| qwsc | water flow rate at standard condition (m3/d) |
| Bw | water volume factor |
| qi | radial flow in microsegment of reservoir (m3/d) |
| D | diameter of the horizontal wellbore (m) |
| qg | gas flow rate at reservoir condition (m3/d) |
| f | coefficient of friction |
| qw | water flow rate at reservoir condition (m3/d) |
| h | reservoir thickness (m) |
| qm | equivalent flow rate at reservoir condition (m3/d) |
| ΔH | height difference between pwf1 and pwf2 (m) |
| Qij | flow rate at inflow end of microsegment i on branch j (m3/d) |
| i | number of microsegments |
| qij | radial flow rate at inflow end of microsegment i on branch j (m3/d) |
| j | number of branch |
| qs | radial inflow of wellbore per unit length (m3/(s·m)) |
| K | permeability of reservoir (mD) |
| r | distance between certain point in reservoir and microsegment (m) |
| Krg | relative permeability of gas |
| Rwg | water-to-gas ratio (m3/m3) |
| Krw | relative permeability of water |
| Rcj | radius of inclined section of branch j (m) |
| ki | permeability at microsegment i (mD) |
| rw | horizontal wellbore radius (m) |
| Lij | length of microsegment i on branch j (m) |
| vg | seepage velocity of gas (m/s) |
| M | any point in reservoir |
| vw | seepage velocity of water (m/s) |
| m(p) | two-phase generalized pseudo-pressure (g·MPa/(cm3·mPa·s)) |
| Zw | distance from horizontal well to bottom boundary (m) |
| n | number of boundary mirrors |
| ρgsc | density of gas at standard condition (g/cm3) |
| Nj | number of microsegments on the jth branch |
| ρwsc | density of water at standard condition (g/cm3) |
| Pi | original reservoir pressure (MPa) |
| ρg | density of gas at reservoir condition (g/cm3) |
| p (i, j) | pressure of ith microsegment on branch j (MPa) |
| ρw | density of water at reservoir condition (g/cm3) |
| pwfj | pressure at junction on branch j and vertical wellbore (MPa) |
| ρm | equivalent density at reservoir condition (g/cm3) |
| Δpij | horizontal microsegment pressure drop of ith microsegment on branch j (MPa) |
| μg | viscosity of gas (mPa·s) |
| Δps | inclined wellbore pressure drop (MPa) |
| μw | viscosity of water (mPa·s) |
| Δpv | vertical wellbore pressure drop (MPa) |
| ɛ | elative roughness of pipe’s inside surface |
Appendix A

References
- Ouyang, L.B.; Aziz, K. A general single-phase wellbore/reservoir coupling model for multilateral wells. SPE Reserv. Eval. Eng. 2001, 4, 327–335. [Google Scholar] [CrossRef]
- Tabatabaei, M.; Ghalambor, A. A new method to predict performance of horizontal and multilateral wells. SPE Prod. Oper. 2011, 26, 75–87. [Google Scholar] [CrossRef]
- Hassan, A.; Abdulraheem, A.; Elkatatny, S.; Ahmed, M. New approach to quantify productivity of fishbone multilateral well. In Proceedings of the SPE Annual Technical Conference and Exhibition (D021S012R008), San Antonio, TX, USA, 9–11 October 2017; SPE: Richardson, TX, USA, 2017. [Google Scholar]
- Wang, Z.; Fu, X.; Guo, P.; Tu, H.; Wang, H.; Zhong, S. Gas-liquid flowing process in a horizontal well with premature liquid loading. J. Nat. Gas Sci. Eng. 2015, 25, 207–214. [Google Scholar] [CrossRef]
- Zhou, X.; Zeng, F.; Zhang, L. Improving Steam-Assisted Gravity Drainage performance in oil sands with a top water zone using polymer injection and the fishbone well pattern. Fuel 2016, 184, 449–465. [Google Scholar] [CrossRef]
- Joshi, S.D. Augmentation of well productivity with slant and horizontal wells (includes associated papers 24547 and 25308). J. Pet. Technol. 1988, 40, 729–739. [Google Scholar] [CrossRef]
- Babu, D.K.; Odeh, A.S. Productivity of a horizontal well. SPE Reserv. Eng. 1989, 4, 417–421. [Google Scholar] [CrossRef]
- Kong, X.Y.; Xu, X.Z.; Lu, D.T. Pressure transient analysis for horizontal well and multi-branched horizontal wells. In Proceedings of the SPE/CIM International Conference on Horizontal Well Technology, Calgary, AB, Canada, 18–20 November 1996; p. SPE-37069. [Google Scholar]
- Raghavan, R.; Ambastha, A.K. An assessment of the productivity of multilateral completions. J. Can. Pet. Technol. 1998, 37, 58–67. [Google Scholar] [CrossRef]
- Wu, J.; Liu, Y.; Yang, H. New Method of Productivity Equation for Multibranch Horizontal Well in Three-Dimensional Anisotropic Oil Reservoirs. J. Energy Resour. Technol. 2012, 134, 032801. [Google Scholar] [CrossRef]
- Meng, F.; He, D.; Yan, H.; Zhao, H.; Zhang, H.; Li, C. Production performance analysis for slanted well in multilayer commingled carbonate gas reservoir. J. Pet. Sci. Eng. 2021, 204, 108769. [Google Scholar] [CrossRef]
- Al-Rbeawi, S.; Artun, E. Fishbone type horizontal wellbore completion: A study for pressure behavior, flow regimes, and productivity index. J. Pet. Sci. Eng. 2019, 176, 172–202. [Google Scholar] [CrossRef]
- Bazitov, M.V.; Golovko, I.S.; Konosov, D.A.; Mingazov, A.N.; Nigmatullin, R.R.; Lokot, A.V.; Malyasov, V.Y. First Fishbone well drilling at Vankorskoe field. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 26–28 October 2015; p. SPE-176510. [Google Scholar]
- Cavalcante Filho, J.S.; Xu, Y.; Sepehrnoori, K. Modeling fishbones using the embedded discrete fracture model formulation: Sensitivity analysis and history matching. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015; SPE: Richardson, TX, USA, 2015; p. D011S008R006. [Google Scholar]
- Borisov, J.P. Oil Production Using Horizontal and Multiple Deviation Wells; Nedra: Moscow, Russia, 1964; p. 364. [Google Scholar]
- Giger, F.M.; Reiss, L.H.; Jourdan, A.P. The reservoir engineering aspects of horizontal drilling. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 16–19 September 1984; OnePetro: Richardson, TX, USA, 1984. [Google Scholar]
- Dikken, B.J. Pressure drop in horizontal wells and its effect on production performance. J. Pet. Technol. 1990, 42, 1426–1433. [Google Scholar] [CrossRef]
- Ozkan, E.; Sarica, C.; Haciislamoglu, M.; Raghavan, R. Effect of conductivity on horizontal-well pressure-behavior. SPE Adv. Technol. Ser. 1995, 3, 85–94. [Google Scholar] [CrossRef]
- Chen, W.; Zhu, D.; Hill, A.D. A comprehensive model of multilateral well deliverability. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 7–10 November 2000; OnePetro: Richardson, TX, USA, 2000. [Google Scholar]
- Guo, B.; Zhou, J.; Liu, Y.; Ghalambor, A. A rigorous analytical model for fluid flow in drainholes of finite conductivity applied to horizontal and multilateral wells. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium, Oklahoma City, OK, USA, 31 March–3 April 2007; p. SPE-106947. [Google Scholar]
- Penmatcha, V.R.; Aziz, K. Comprehensive reservoir/wellbore model for horizontal wells. SPE J. 1999, 4, 224–234. [Google Scholar] [CrossRef]
- Adesina, F.; Paul, A.; Oyinkepreye, O.; Adebowale, O. An improved model for estimating productivity of horizontal drain hole. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 2–4 August 2016. [Google Scholar]
- Yan, G.; Li, Z.; Bore, T.; Torres SA, G.; Scheuermann, A.; Li, L. A lattice Boltzmann exploration of two-phase displacement in 2D porous media under various pressure boundary conditions. J. Rock Mech. Geotech. Eng. 2022, 14, 1782–1798. [Google Scholar] [CrossRef]
- Yan, G.; Bore, T.; Schlaeger, S.; Scheuermann, A.; Li, L. Dynamic effects in soil water retention curves: An experimental exploration by full-scale soil column tests using spatial time-domain reflectometry and tensiometers. Acta Geotech. 2024, 1–27. [Google Scholar] [CrossRef]
- Yan, G.; Li, Z.; Galindo Torres, S.A.; Scheuermann, A.; Li, L. Transient two-phase flow in porous media: A literature review and engineering application in geotechnics. Geotechnics 2022, 2, 32–90. [Google Scholar] [CrossRef]
- Vairogs, J.; Hearn, C.L.; Dareing, D.W.; Rhoades, V.W. Effect of rock stress on gas production from low-permeability reservoirs. J. Pet. Technol. 1971, 23, 1161–1167. [Google Scholar] [CrossRef]
- Jones, F.O.; Owens, W.W. A laboratory study of low-permeability gas sands. J. Pet. Technol. 1980, 32, 1631–1640. [Google Scholar] [CrossRef]
- Warpinski, N.R. Hydraulic fracturing in tight, fissured media. J. Pet. Technol. 1991, 43, 146–209. [Google Scholar] [CrossRef]
- Farquhar, R.A.; Smart BG, D.; Todd, A.C.; Tompkins, D.E.; Tweedie, A.J. Stress sensitivity of low-permeability sandstones from the Rotliegendes sandstone. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993; p. SPE-26501. [Google Scholar]
- Texas, A.; Economides, M.J.; Buchsteiner, H.; Warpinski, N.R. Step Pressure Tests for Stress Sensitive Permeability Determination. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control, Lafayette, Louisiana, 7–10 February 1994. [Google Scholar]
- Bai, W.; Cheng, S.; Wang, Y.; Cai, D.; Guo, X.; Guo, Q. A transient production prediction method for tight condensate gas wells with multiphase flow. Pet. Explor. Dev. 2024, 51, 172–179. [Google Scholar] [CrossRef]
- Dou, X.; Liao, X.; Zhao, X.; Wang, H.; Lv, S. Quantification of permeability stress-sensitivity in tight gas reservoir based on straight-line analysis. J. Nat. Gas Sci. Eng. 2015, 22, 598–608. [Google Scholar] [CrossRef]
- Zhao, K.; Du, P. Performance of horizontal wells in composite tight gas reservoirs considering stress sensitivity. Adv. Geo-Energy Res. 2019, 3, 287–303. [Google Scholar] [CrossRef]
- Zhao, L.; Jiang, H.; Wang, H.; Yang, H.; Sun, F.; Li, J. Representation of a new physics-based non-Darcy equation for low-velocity flow in tight reservoirs. J. Pet. Sci. Eng. 2020, 184, 106518. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Zhao, W.; Ji, P.; Cheng, S.; Yu, H. Explicit Original Gas in Place Determination of Naturally Fractured Reservoirs in Gas Well Rate Decline Analysis. Adv. Geo-Energy Res. 2023, 9, 117–124. [Google Scholar] [CrossRef]
- Luo, W.; Li, H.T.; Wang, Y.Q.; Wang, J.C. A new semi-analytical model for predicting the performance of horizontal wells completed by inflow control devices in bottom-water reservoirs. J. Nat. Gas Sci. Eng. 2015, 27, 1328–1339. [Google Scholar] [CrossRef]
- Holmes, J.A.; Barkve, T.; Lund, Ø. Application of a multisegment well model to simulate flow in advanced wells. In Proceedings of the SPE Europec Featured at EAGE Conference and Exhibition, The Hague, The Netherlands, 20–22 October 1998; p. SPE-50646. [Google Scholar]
- Neylon, K.; Reiso, E.; Holmes, J.A.; Nesse, O.B. Modeling well inflow control with flow in both annulus and tubing. In Proceedings of the SPE Reservoir Simulation Conference, The Woodlands, TX, USA, 2–4 February 2009; p. SPE-118909. [Google Scholar]
- Wan, J.; Dale, B.A.; Ellison, T.K.; Benish, T.G.; Grubert, M.A. Coupled well and reservoir simulation models to optimize completion design and operations for subsurface control. In Proceedings of the SPE Europec Featured at EAGE Conference and Exhibition, Rome, Italy, 9–12 June 2008; p. SPE-113635. [Google Scholar]
- Ayesha, A.M.; Hamdy, H. Wellbore segmentation using inflow control devices: Design and optimization process. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 1–4 November 2010; Society of Petroleum Engineers: Abu Dhabi, United Arab Emirates, 2010. [Google Scholar]
- Yue, P.; Jia, B.; Sheng, J.; Lei, T.; Tang, C. A coupling model of water breakthrough time for a multilateral horizontal well in a bottom water-drive reservoir. J. Pet. Sci. Eng. 2019, 177, 317–330. [Google Scholar] [CrossRef]
- Zeng, Y.; Bian, X.Q.; Wang, L.G.; Zhang, L.M. Coupling model of gas-water two-phase productivity calculation for fractured horizontal wells in tight gas reservoirs. Geoenergy Sci. Eng. 2024, 234, 212666. [Google Scholar] [CrossRef]
- Liu, P.; Wang, Q.; Luo, Y.; He, Z.; Luo, W. Study on a new transient productivity model of horizontal well coupled with seepage and wellbore flow. Processes 2021, 9, 2257. [Google Scholar] [CrossRef]
- Zeghadnia, L.; Robert, J.L.; Achour, B. Explicit solutions for turbulent flow friction factor: A review, assessment and approaches classification. Ain Shams Eng. J. 2019, 10, 243–252. [Google Scholar] [CrossRef]
- Yang, J.; Chen, J.; Wang, Q.; Ye, C.; Yu, F. A simple and accurate model to predict pressure drop in vertical gas wells. Energy Sources Part A Recovery Util. Environ. Eff. 2024, 46, 1245–1259. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Initial reservoir pressure (MPa) | 16 |
| Initial reservoir temperature (K) | 313 |
| Reservoir thickness (m) | 10 |
| Reservoir permeability (mD) | 50 |
| Initial gas saturation | 0.7 |
| Index of gas relative permeability curve | 2 |
| Index of water relative permeability curve | 3 |
| Water-to-gas volume ratio | 0.0001 |
| Initial gas viscosity (mPa·s) | 0.02 |
| Initial gas density at standard condition (g/cm3) | 0.000732 |
| Initial water density at standard condition (g/cm3) | 1 |
| Length of horizontal well (m) | 400 |
| Radius of horizontal wellbore (m) | 0.108 |
| Curvature radius of horizontal wellbore (m) | 15 |
| Parameters | Branch 1 | Branch 2 |
|---|---|---|
| Initial reservoir pressure (MPa) | 16.16 | 15.9 |
| Initial reservoir temperature (K) | 313 | 311 |
| Reservoir thickness (m) | 9.72 | 8.73 |
| Reservoir permeability (mD) | 50 | 43 |
| Initial gas saturation | 0.71 | 0.63 |
| Index of gas relative permeability curve | 2 | 3 |
| Index of water relative permeability curve | 3 | 3 |
| Water-to-gas volume ratio | 0.00013 | 0.00012 |
| Initial gas viscosity (mPa·s) | 0.0178 | 0.0183 |
| Initial gas density at standard condition (g/cm3) | 0.000678 | 0.000679 |
| Initial water density at standard condition (g/cm3) | 1 | 1 |
| Length of horizontal well (m) | 606 | 487 |
| Radius of horizontal wellbore (m) | 0.108 | 0.108 |
| Curvature radius of horizontal wellbore (m) | 15 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Zhang, Y.; Luo, E.; Xu, A.; Chen, Y.; Liu, Y.; Zeng, X.; Jiang, L. A Coupling Model of Gas–Water Two-Phase Productivity for Multilateral Horizontal Wells in a Multilayer Gas Reservoir. Processes 2024, 12, 1643. https://doi.org/10.3390/pr12081643
He J, Zhang Y, Luo E, Xu A, Chen Y, Liu Y, Zeng X, Jiang L. A Coupling Model of Gas–Water Two-Phase Productivity for Multilateral Horizontal Wells in a Multilayer Gas Reservoir. Processes. 2024; 12(8):1643. https://doi.org/10.3390/pr12081643
Chicago/Turabian StyleHe, Jun, Yufeng Zhang, Erhui Luo, Anzhu Xu, Yefei Chen, Yunyang Liu, Xing Zeng, and Luyang Jiang. 2024. "A Coupling Model of Gas–Water Two-Phase Productivity for Multilateral Horizontal Wells in a Multilayer Gas Reservoir" Processes 12, no. 8: 1643. https://doi.org/10.3390/pr12081643
APA StyleHe, J., Zhang, Y., Luo, E., Xu, A., Chen, Y., Liu, Y., Zeng, X., & Jiang, L. (2024). A Coupling Model of Gas–Water Two-Phase Productivity for Multilateral Horizontal Wells in a Multilayer Gas Reservoir. Processes, 12(8), 1643. https://doi.org/10.3390/pr12081643





