Parameter Optimization of an Absorption Heat Exchanger with Large Temperature Difference
Abstract
:1. Introduction
2. Absorption Heat Exchanger System
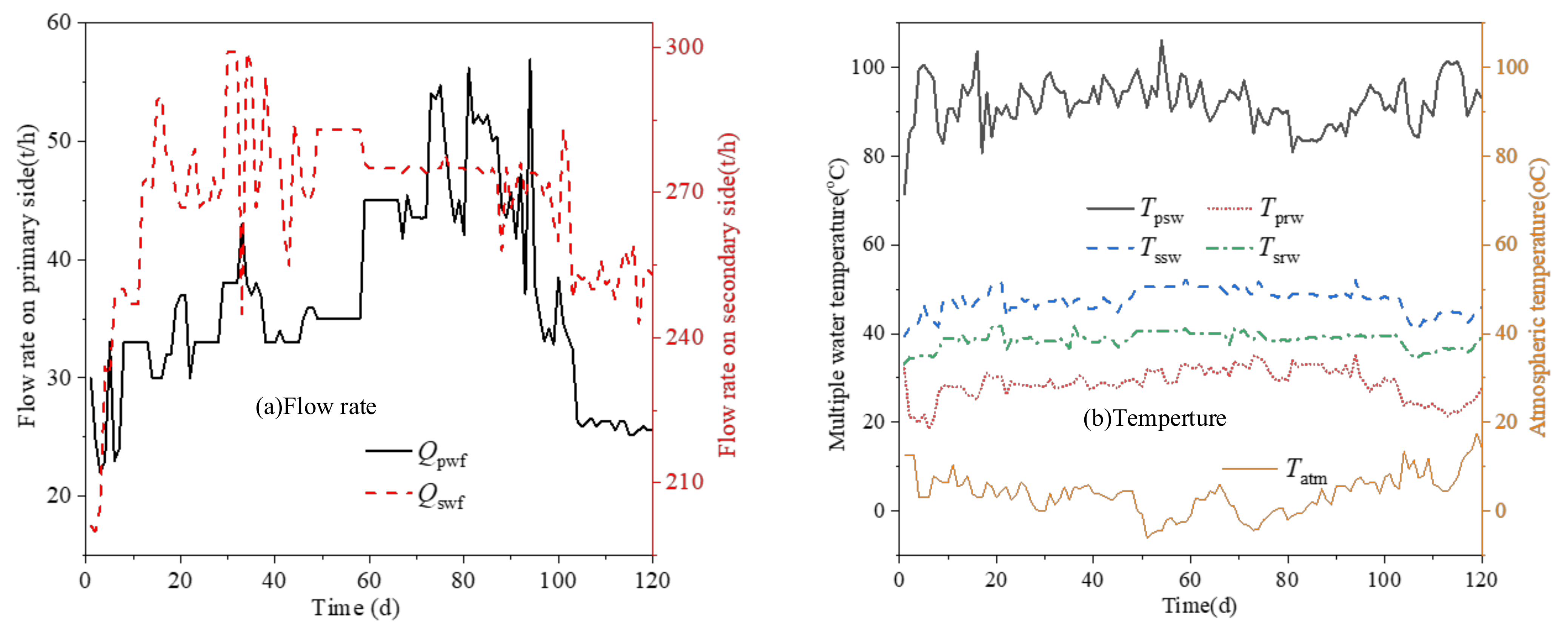
2.1. Operating Parameters
2.2. Operating Characteristics
3. Modelling
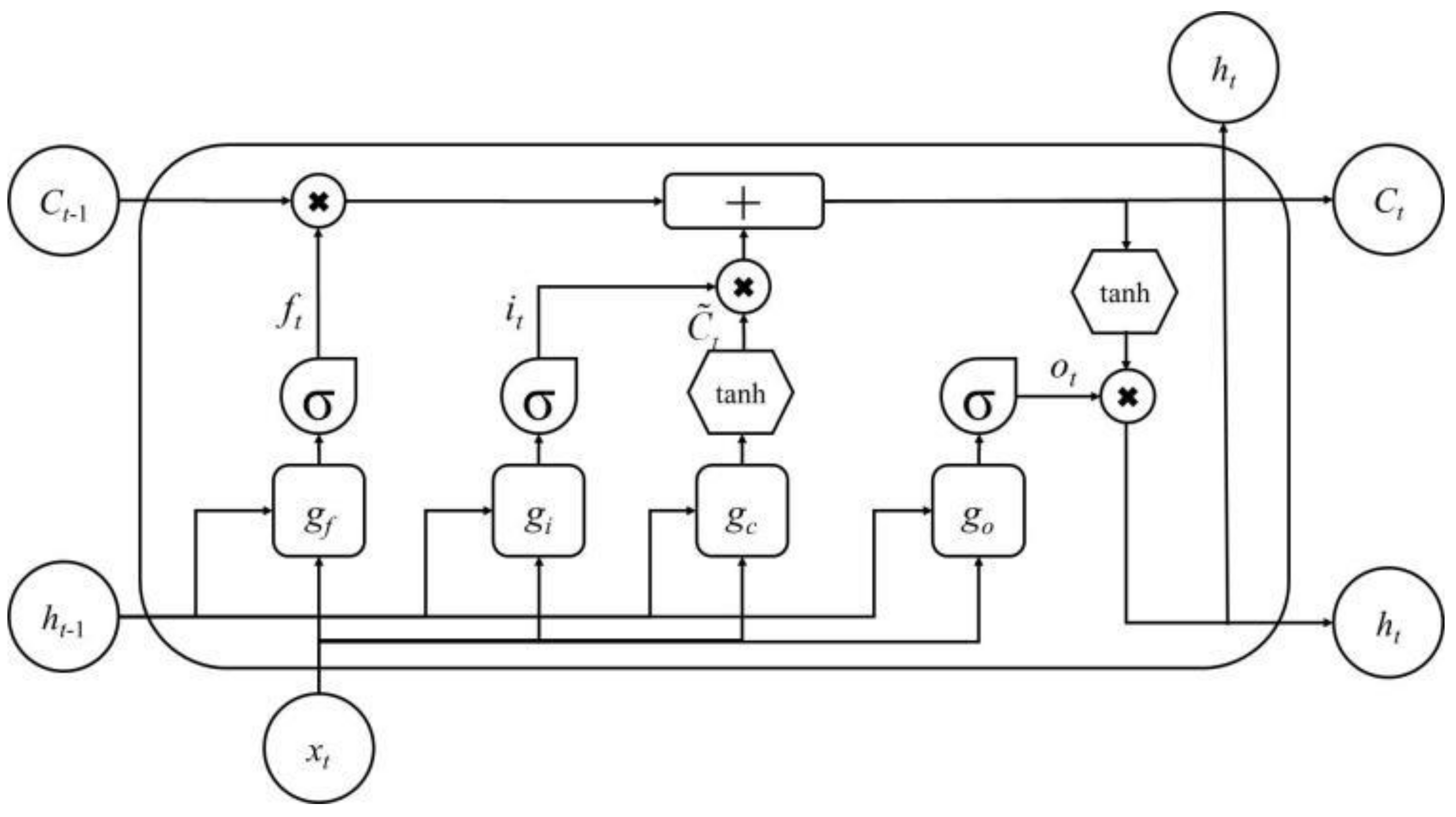
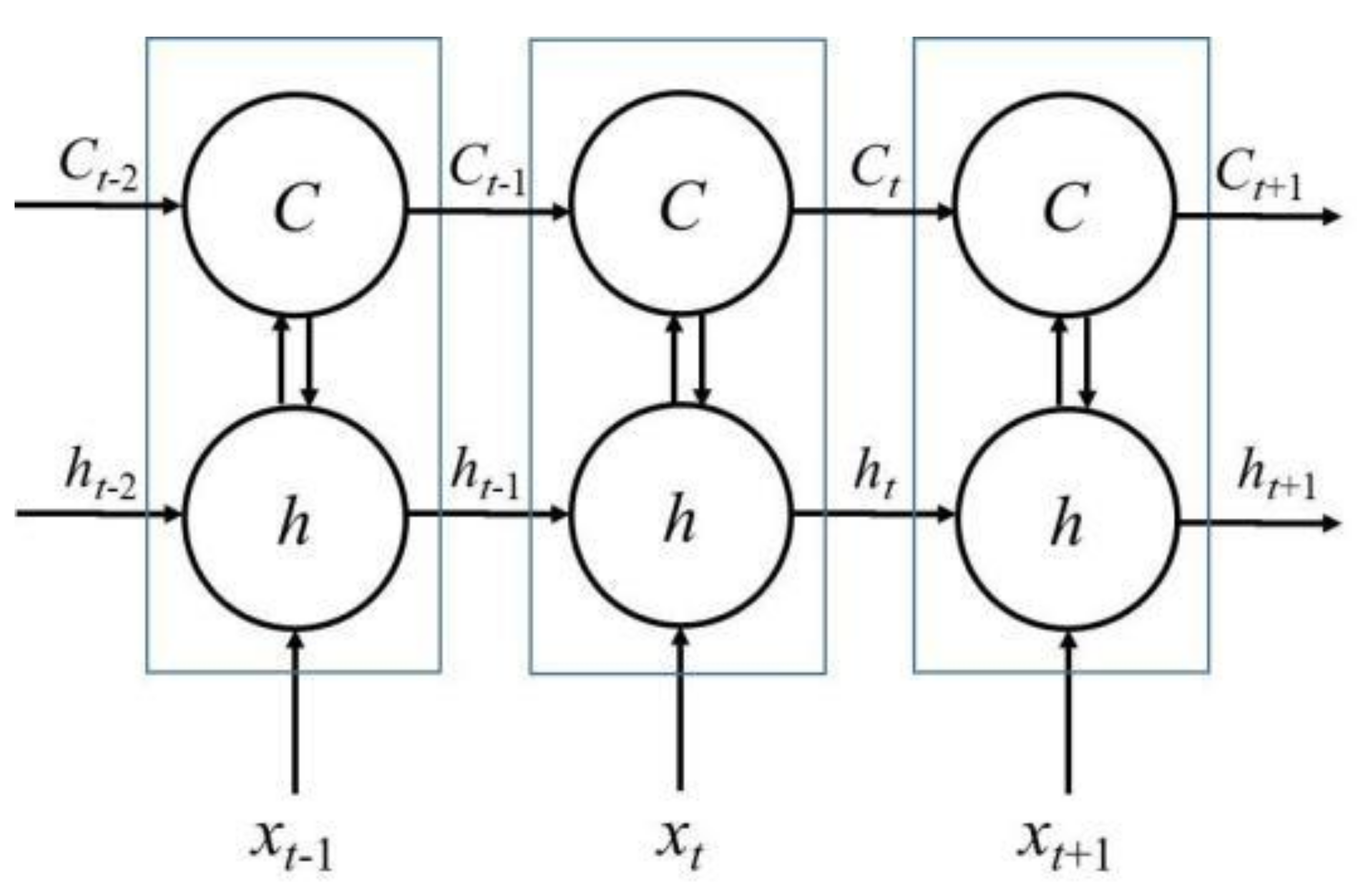
3.1. Prediction Model
3.2. Model Optimization
3.3. Evaluation Criteria
4. Results and Discussion
4.1. Scheme Contrast
4.2. Performance Indices of Predictive Model
4.3. Analysis of Prediction Results
4.4. Analysis of Optimization Results
4.5. Sensitivity Assessment
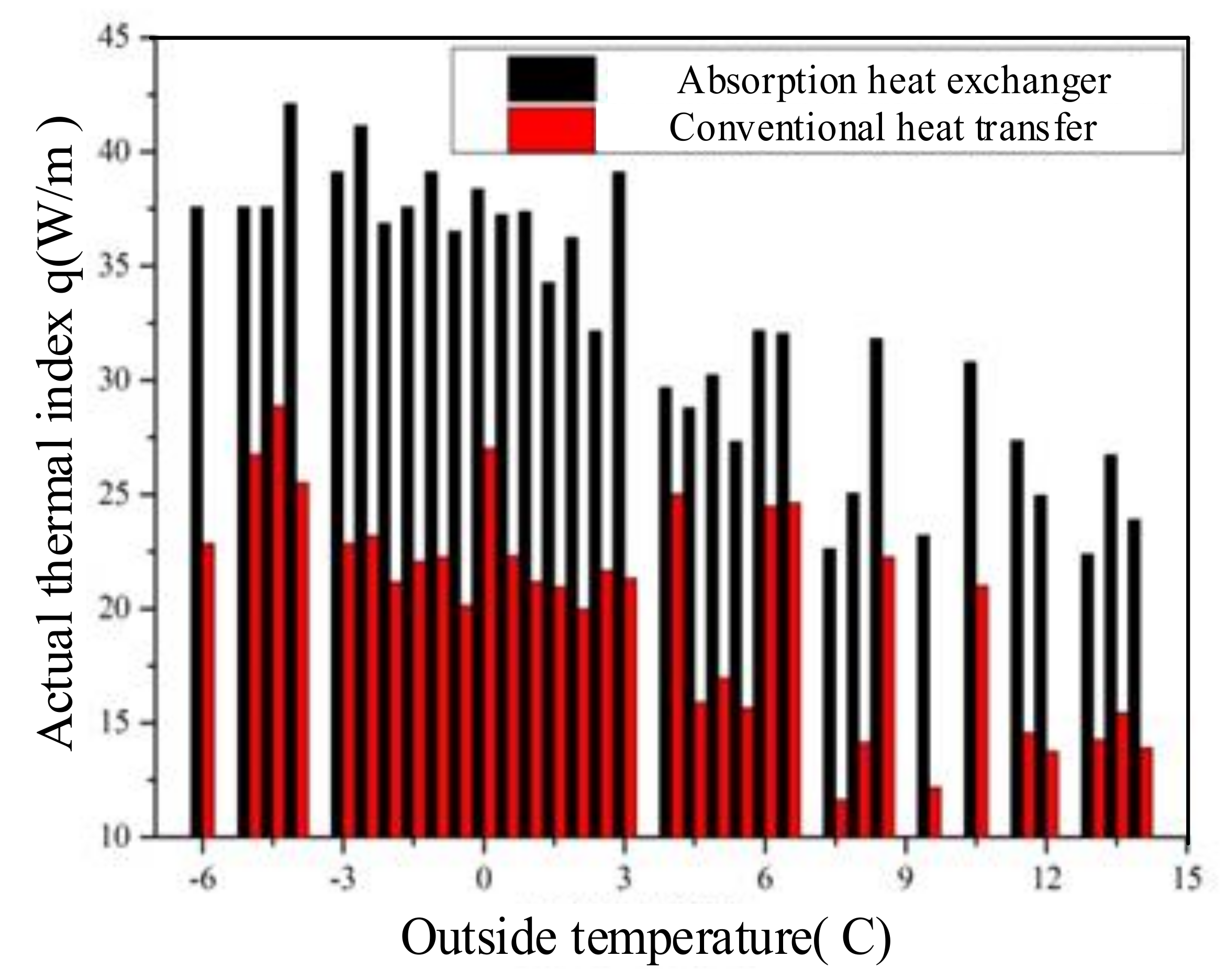
4.6. Large Temperature Difference Heat Exchange Station Running Vacuum
5. Conclusions
- (1)
- Compared to the performance indices of predictions for the return water temperatures of the primary side and secondary side based on the SVM model, RF model, and XGboost model, the values of three performance indices evaluated for the LSTM model were the smallest, and the LSTM model had a better fitting and generalization capability than the other models, indicating that the LSTM model could accurately simulate the operating conditions of an absorption heat exchange unit.
- (2)
- After the optimization, the return water temperature of the primary side decreased from 29.6 °C to 28.2 °C, while the return water temperature of the secondary side decreased from 39.8 °C to 38.6 °C, and the water flow rate of primary side was reduced from 39 t/h to 35.2 t/h.
- (3)
- The relationship between the water flow rate of secondary side and the supply water temperature of the primary side was close to linear, and for every 1 °C increase in the latter, the former increased by about 3.18 t/h. The linear fitting degree of the relationship between the water flow rate of the secondary side and the supply water temperature of the secondary side was a little lower; for every 1 °C increase in the latter, the former decreased by about 36.43 t/h, and the variation amplitude was much larger.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| LSTM | Long short-term memory; |
| SVM | Support vector machine; |
| RF | Random forest; |
| XGBoost | Extreme gradient boosting; |
| COP | Coefficient of performance; |
| RNN | Recurrent neural network; |
| PSO | Particle swarm optimization; |
| RMSE | Root mean square error; |
| MAE | Mean absolute error; |
| MAPE | Mean absolute percentage error; |
| Qpwf | Flow rate of primary heat supply network; |
| Qswf | Flow rate of secondary heat supply network; |
| Tatm | Atmospheric temperature; |
| Tprw | Return water temperature on primary side; |
| Tpsw | Supply water temperature on primary side; |
| Tssw | Supply water temperature on secondary side; |
| Tsrw | Return water temperature on secondary side. |
References
- Wang, Y.; Wang, X.; Zheng, L.; Gao, X.; Wang, Z.; You, S.; Zhang, H.; Wei, S. Thermo-hydraulic coupled analysis of long-distance district heating systems based on a fully-dynamic model. Appl. Therm. Eng. 2023, 222, 119912. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Xu, K.; Zhang, S.; Zheng, H.; Dong, X. Optimization study of a novel district heating system based on large temperature-difference heat exchange. Energy Convers. Manag. 2022, 258, 115517. [Google Scholar] [CrossRef]
- Cao, F.; Wang, Y.; Ye, Z. Theoretical analysis of internal heat exchanger in transcritical CO2 heat pump systems and its experimental verification. Int. J. Refrig. 2019, 106, 506–516. [Google Scholar] [CrossRef]
- Ramadan, M.; Murr, R.; Khaled, M.; Olabi, A.G. Mixed numerical—Experimental approach to enhance the heat pump performance by drain water heat recovery. Energy 2018, 149, 1010–1021. [Google Scholar] [CrossRef]
- Wang, J.; Hua, J.; Fu, L.; Wang, Z.; Zhang, S. A theoretical fundamental investigation on boilers equipped with vapor-pump system for Flue-Gas Heat and Moisture Recovery. Energy 2019, 171, 956–970. [Google Scholar] [CrossRef]
- Li, F.; Duanmu, L.; Fu, L.; Zhao, X. Application of absorption heat pump and direct-contact total heat exchanger to advanced-recovery flue-gas waste heat for gas boiler. Sci. Technol. Built Environ. 2019, 25, 149–155. [Google Scholar] [CrossRef]
- Cao, J.; Zheng, L.; Peng, J.; Wang, W.; Leung, M.K.; Zheng, Z.; Hu, M.; Wang, Q.; Cai, J.; Pei, G.; et al. Advances in coupled use of renewable energy sources for performance enhancement of vapour compression heat pump: A systematic review of applications to buildings. Appl. Energy 2023, 332, 120571. [Google Scholar] [CrossRef]
- Song, M.; Deng, S.; Dang, C.; Mao, N.; Wang, Z. Review on improvement for air source heat pump units during frosting and Defrosting. Appl. Energy 2018, 211, 1150–1170. [Google Scholar] [CrossRef]
- Qu, M.; Fan, Y.; Chen, J.; Li, T.; Li, Z.; Li, H. Experimental study of a control strategy for a cascade air source heat pump water heater. Appl. Therm. Eng. 2017, 110, 835–843. [Google Scholar] [CrossRef]
- Mao, N.; Hao, J.; He, T.; Xu, Y.; Song, M.; Tang, J. Unsteady heat transfer properties of spray falling over a horizontal tube in an oily sewage source heat pump. Appl. Therm. Eng. 2020, 179, 115675. [Google Scholar] [CrossRef]
- Ma, L.; Ren, T.; Zhang, T.; Zhao, T.; Zhang, J. Experimental study on effect of operating parameters on performance of serially cascaded wastewater source heat pump. J. Build. Eng. 2020, 32, 101458. [Google Scholar] [CrossRef]
- Ma, L.; Zhen, X.; Zhang, J. The Performance Simulation Analysis of the Sewage-source Heat Pump Heater Unit Dealing with Large Temperature Difference. Procedia Eng. 2017, 205, 1769–1776. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.; Cao, F. Extremum seeking control for efficient operation of an air-source heat pump water heater with internal heat exchanger cycle vapor injection. Int. J. Refrig. 2019, 99, 153–165. [Google Scholar] [CrossRef]
- Dai, B.; Qi, H.; Liu, S.; Ma, M.; Zhong, Z.; Li, H.; Sun, Z. Evaluation of transcritical CO2 heat pump system integrated with mechanical subcooling by utilizing energy, exergy and economic methodologies for residential heating. Energy Convers. Manag. 2019, 192, 202–220. [Google Scholar] [CrossRef]
- Amir, F.M.; Yusoff, M.Z.; Abu Hassan, S.H. Fluid film characteristics over horizontal multi-faceted tube and the augmentation of thermal performance. Appl. Therm. Eng. 2022, 201, 117795. [Google Scholar] [CrossRef]
- Fan, X.; Pu, J.; Wu, Z.; Wang, Y.; You, S.; Zhang, H.; Liu, J.; Jiang, Y.; Liu, S.; Wan, Z. Thermodynamic performance and heat and mass transfer analysis of air source absorption heat pump for heating. J. Build. Eng. 2023, 76, 107390. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, L.; Zhang, S.; Tang, D. Study on a novel co-operated heat and power system for improving energy efficiency and flexibility of cogeneration plants. Appl. Therm. Eng. 2019, 163, 114429. [Google Scholar] [CrossRef]
- Xie, X.; Yi, Y.; Zhang, H.; Jiang, Y. Theoretical model of absorption heat pump from ideal solution to real solution: Temperature lift factor model. Energy Convers. Manag. 2022, 271, 116328. [Google Scholar] [CrossRef]
- Li, Y.; Bi, Y.; Lin, Y.; Wang, H.; Sun, R. Analysis of the soil heat balance of a solar-ground source absorption heat pump with the soil-based energy storage in the transition season. Energy 2023, 264, 126394. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, E.; Liu, L.; Qi, C. Machine learning-based performance prediction for ground source heat pump systems. Geothermics 2022, 105, 102509. [Google Scholar] [CrossRef]
- Song, Z. Reexamining CO generation from the Perspective of Sustainable Development. Proc. CSEE 1998, 18, 225–230. [Google Scholar]
- Sun, F.; Zhao, X.; Chen, X.; Fu, L.; Liu, L. New configurations of district heating system based on natural gas and deep geothermal energy for higher energy efficiency in northern China. Appl. Therm. Eng. 2019, 151, 439–450. [Google Scholar] [CrossRef]
- Fu, L.; Li, Y.; Wu, Y.; Wang, X.; Jiang, Y. Low carbon district heating in China in 2025- a district heating mode with low grade waste heat as heat source. Energy 2021, 230, 120765. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Nasouri, M.; Bidhendi, G.N.; Hoveidi, H.; Amiri, M.J. Parametric study and performance-based multi-criteria optimization of the indirect-expansion solar-assisted heat pump through the integration of Analytic Network process (ANP) decision-making with MOPSO algorithm. Sol. Energy 2021, 225, 814–830. [Google Scholar] [CrossRef]
- Qian, J.; Sun, X.; Zhong, X.; Zeng, J.; Xu, F.; Zhou, T.; Shi, K.; Li, Q. Multi-objective optimization design of the wind-to-heat system blades based on the Particle Swarm Optimization algorithm. Appl. Energy 2024, 355, 122186. [Google Scholar] [CrossRef]
- Wang, W.; Wu, L.; Zhang, H.; Li, J. Optimal Dispatch of Water Source Heat Pump Regional Energy Systems Based on Neighborhood Adaptive Particle Swarm Optimization. Energy Technol. 2022, 10, 2200049. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, H.; Sun, X.; Lu, H.; Wang, T. Optimizing the solar-air hybrid source heat pump heating system based on the particle swarm algorithm. Energy Rep. 2022, 8, 379–393. [Google Scholar] [CrossRef]



| Heating Area (m2) | Flowrate for 10,000 m2 of Heating Area (t/h) | The Primary Side | The Secondary Side | ||||
|---|---|---|---|---|---|---|---|
| Water Supply Temperature (°C) | Return Water Temperature (°C) | Flow Rate (t/h) | Water Supply Temperature (°C) | Return Water Temperature (°C) | Flow Rate (t/h) | ||
| 83,327 | 5.19 | 97.2 | 29.6 | 39.0 | 45.8 | 39.8 | 214.0 |
| Model | MAPE | RMSE | MAE | |
|---|---|---|---|---|
| Return water temperature of primary side | SVM | 3.52% | 1.38 | 1.16 |
| RF | 5.28% | 2.07 | 1.86 | |
| XGboost | 4.87% | 1.8 | 1.45 | |
| LSTM | 2.89% | 1.14 | 0.82 | |
| Return water temperature of secondary side | SVM | 2.10% | 1.1 | 0.89 |
| RF | 3.62% | 1.56 | 1.23 | |
| XGboost | 4.48% | 1.93 | 1.75 | |
| LSTM | 1.85% | 1.04 | 0.71 |
| Parameters | Original Operating Data | Optimized Results | |
|---|---|---|---|
| Atmospheric temperature | °C | 3.5 | 3.5 |
| Flow rate of primary side | t/h | 39 | 35.2 |
| Flow rate of secondary side | t/h | 214 | 214 |
| Supply water temperature of primary side | °C | 97.2 | 97.2 |
| Supply water temperature of secondary side | °C | 45.8 | 45.8 |
| Return water temperature of primary side | °C | 29.6 | 28.2 |
| Return water temperature of secondary side | °C | 39.8 | 38.6 |
| Serial Number | Unit Running Time (Date) | Number of Vacuuming |
|---|---|---|
| 1 | 11.15–2.19 | 0 |
| 2 | 2.20 | 1 |
| 3 | 2.21–3.15 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Wang, J.; Jiang, H.; Yang, X.; Zuo, X.; Yuan, M. Parameter Optimization of an Absorption Heat Exchanger with Large Temperature Difference. Processes 2024, 12, 1669. https://doi.org/10.3390/pr12081669
Chen J, Wang J, Jiang H, Yang X, Zuo X, Yuan M. Parameter Optimization of an Absorption Heat Exchanger with Large Temperature Difference. Processes. 2024; 12(8):1669. https://doi.org/10.3390/pr12081669
Chicago/Turabian StyleChen, Jiangtao, Jinxing Wang, Huawei Jiang, Xin Yang, Xiangli Zuo, and Miao Yuan. 2024. "Parameter Optimization of an Absorption Heat Exchanger with Large Temperature Difference" Processes 12, no. 8: 1669. https://doi.org/10.3390/pr12081669
APA StyleChen, J., Wang, J., Jiang, H., Yang, X., Zuo, X., & Yuan, M. (2024). Parameter Optimization of an Absorption Heat Exchanger with Large Temperature Difference. Processes, 12(8), 1669. https://doi.org/10.3390/pr12081669





