Adaptive Finite-Time Constrained Attitude Stabilization for an Unmanned Helicopter System under Input Delay and Saturation
Abstract
:1. Introduction
- (1)
- In this paper, the problem of attitude stabilization control with output constraints, actuator saturation, input delay and external disturbance is considered. The dependence on precise input delay and the upper bound of disturbance is relaxed; thus, the control scheme is more concise.
- (2)
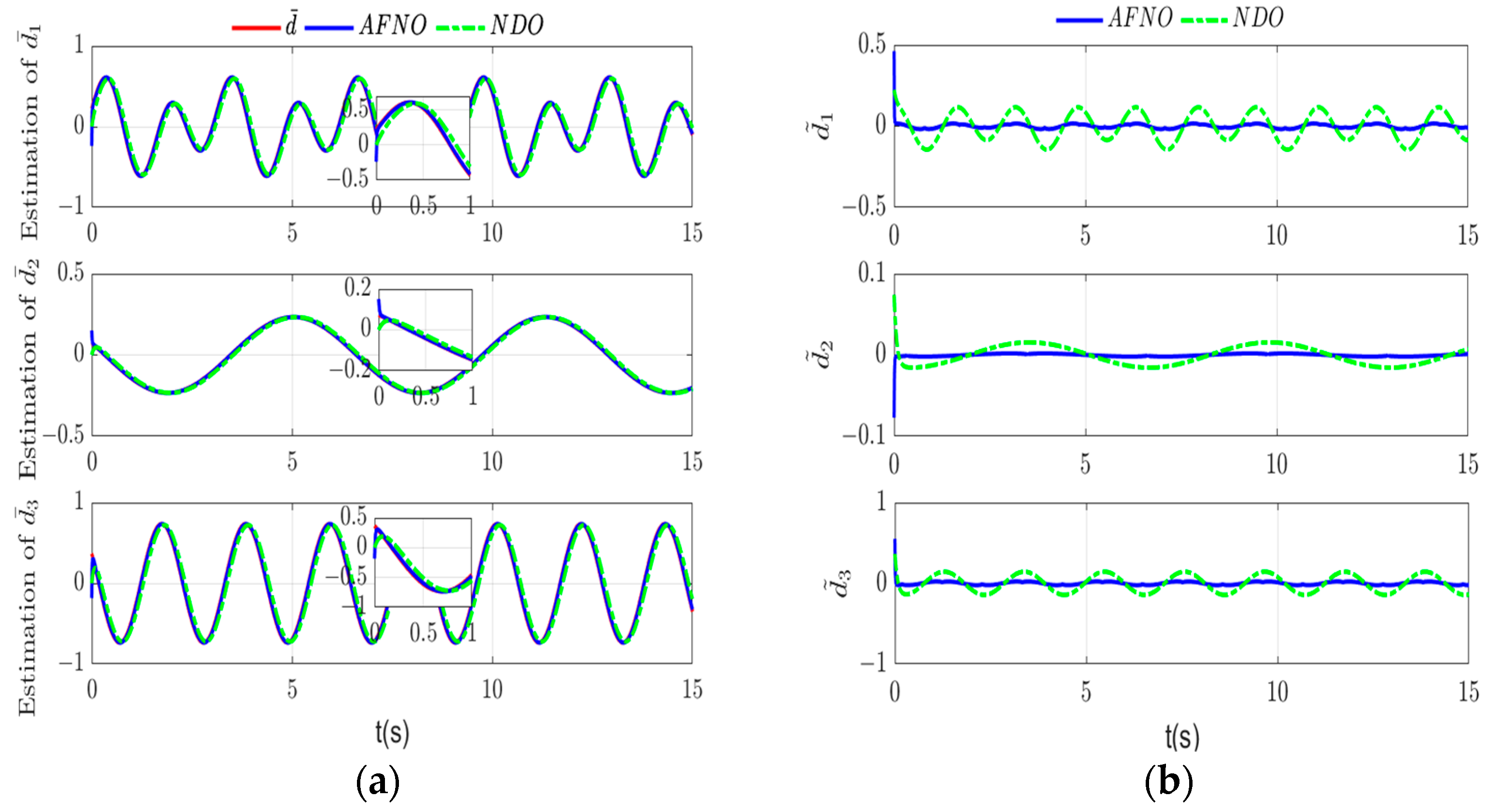
- By integrating the BLF and input memory compensation, a novel constrained memory sliding mode (CMSM) is designed to handle the input delay and attitude constraints. On this basis, an adaptive finite-time nonlinear observer (AFNO) is designed for quickly estimating the external interference and unknown delay deviation.
- (3)
- Based on CMSM and AFNO, a saturated finite-time attitude stabilization controller (SFASC) is designed to tackle the input saturation problem via the adaptive laws. By using Lyapunov analysis, the constrained attitude can converge to zero in finite time despite the disturbance, input delay and actuator saturation.
2. Problem Formulation and Preliminaries
2.1. Attitude Dynamics
- All the signals of the closed-loop control system are finite-time stable, and the states of system (1) converge to zero in finite time.
- The attitude angles are always within the prescribed constraint intervals, and the control input constraints are never violated despite the disturbances and input delay.
2.2. Mathematical Preliminaries
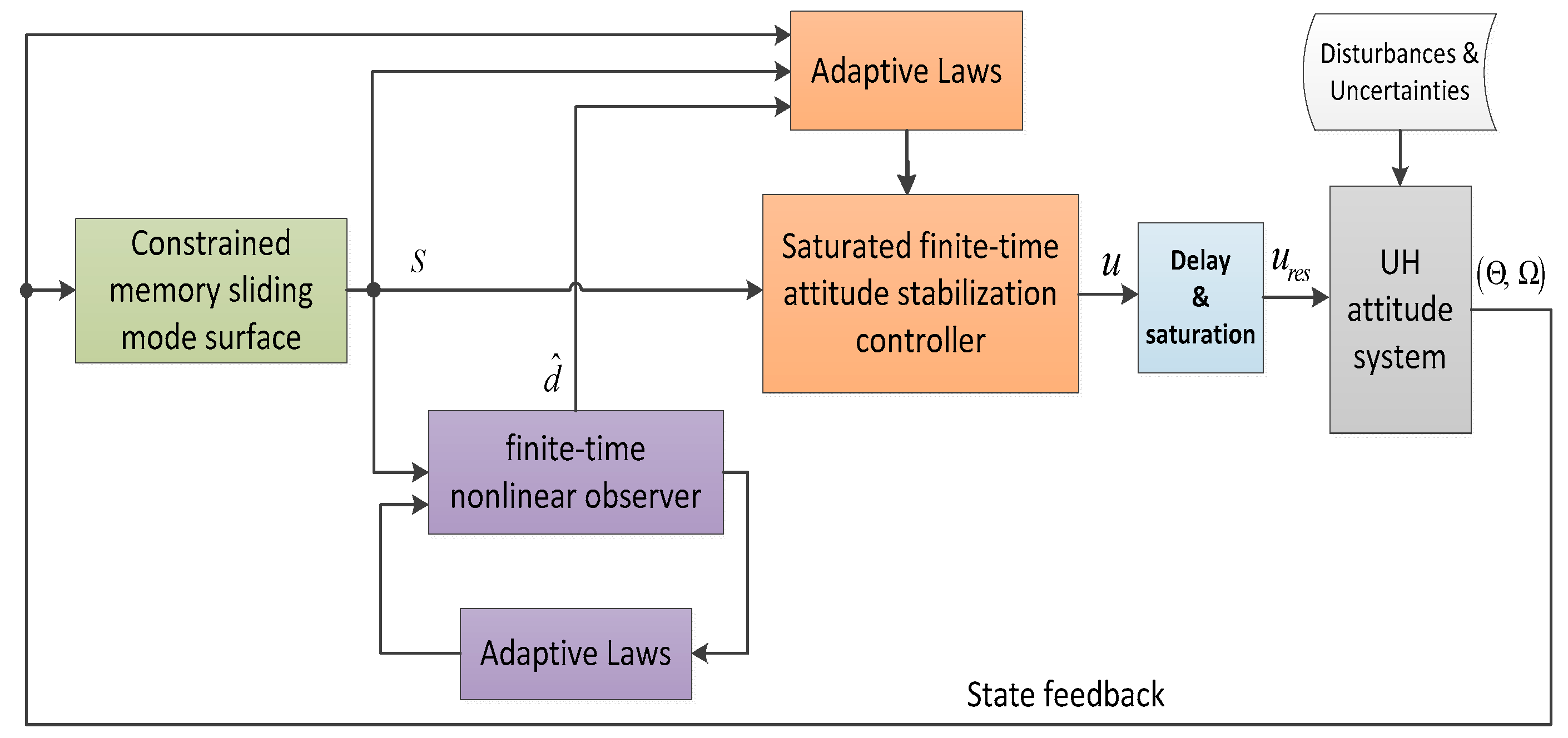
3. Main Results and Analysis
3.1. Constrained Memory Sliding Mode Surface Design
3.2. Adaptive Finite-Time Nonlinear Observer Design
3.3. Saturated Finite-Time Attitude Stabilization Controller
- (1)
- All the signals of the closed-loop attitude control system are stable and bounded in finite time despite the attitude constraints, actuator saturation, input delay and external disturbance.
- (2)
- The system states converge to zero in finite time.
- (3)
- The attitudes remain within the constrained set.
- (4)
- The control inputs never violate the saturation constraints.
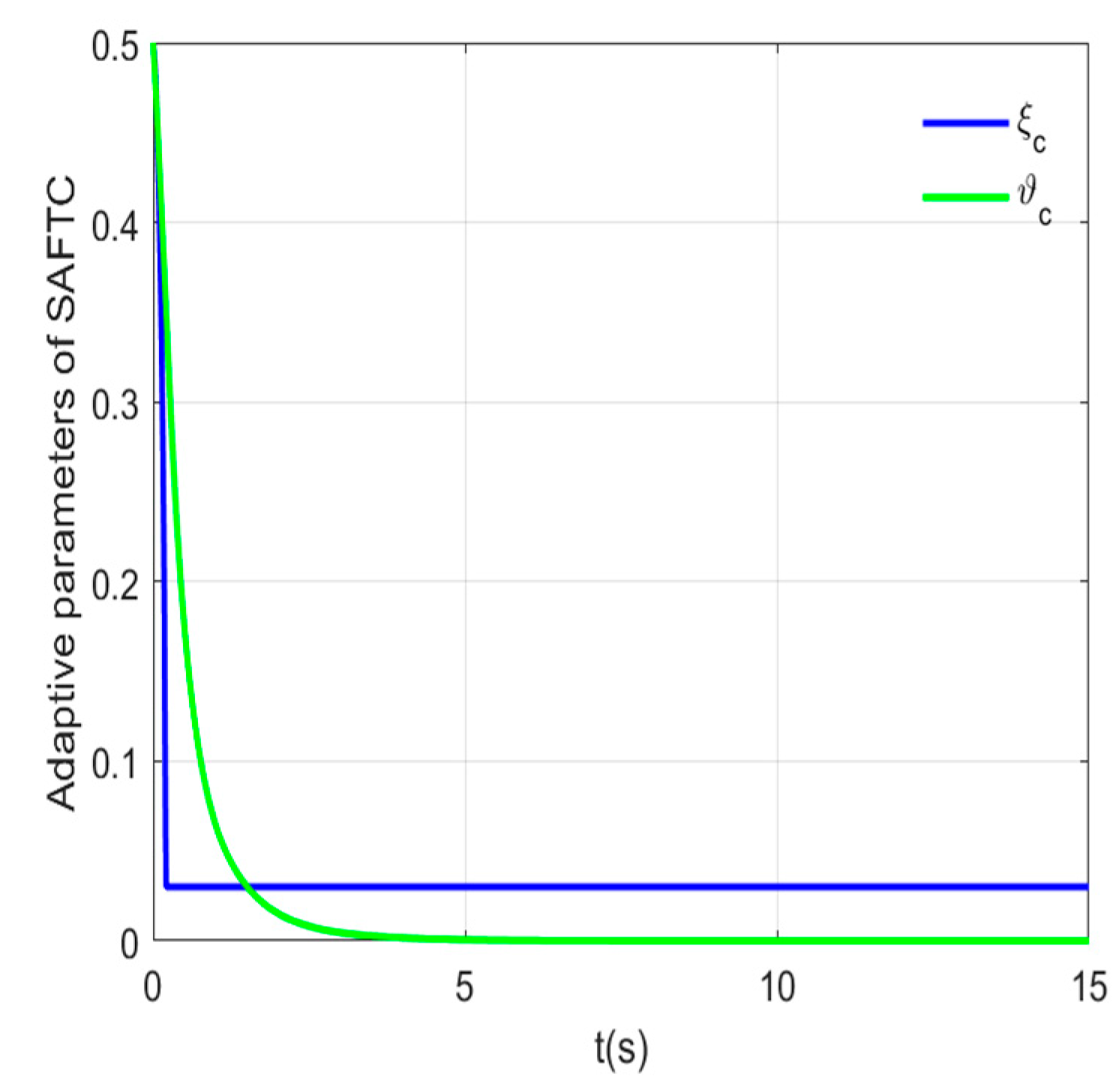
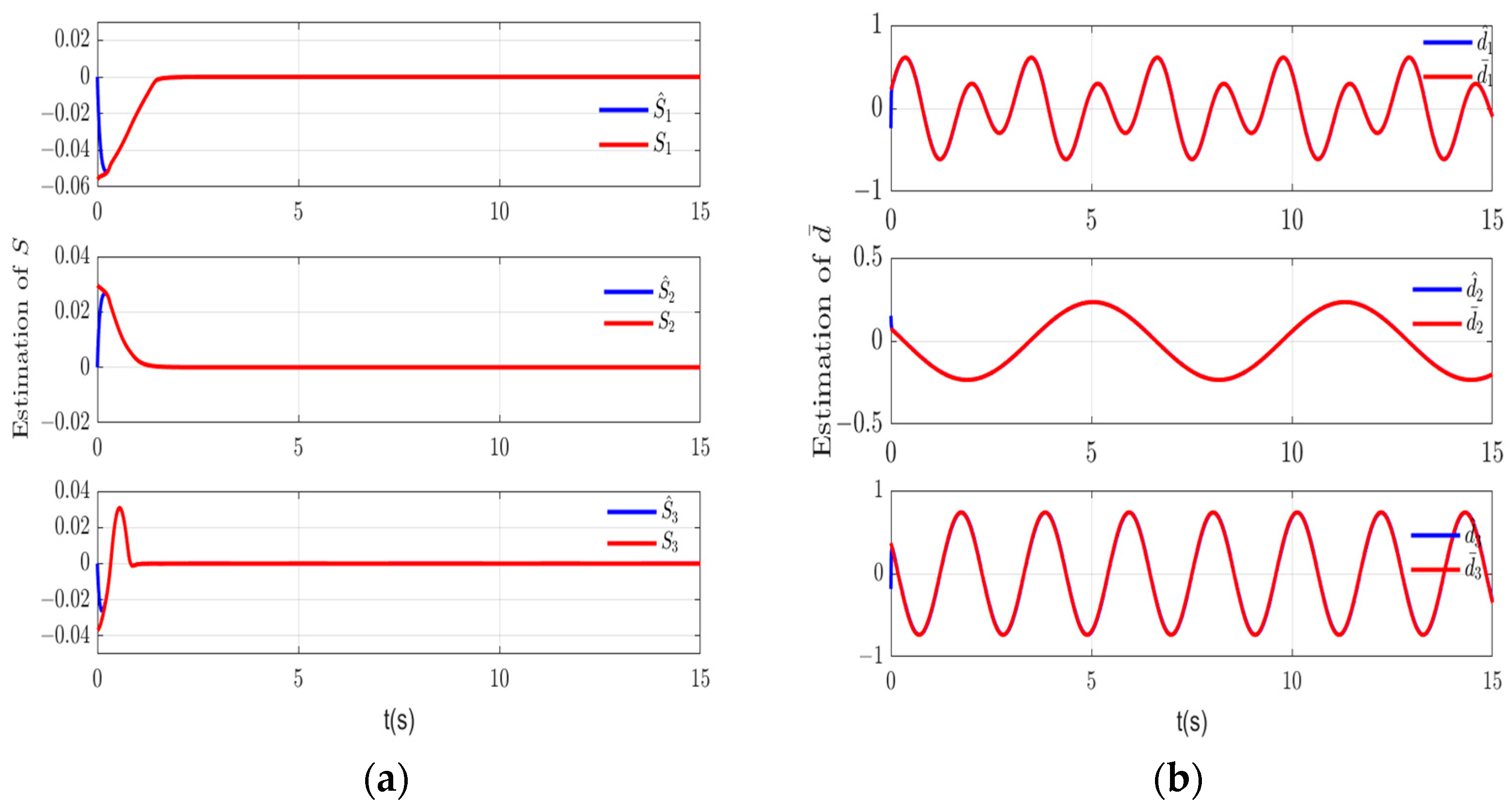
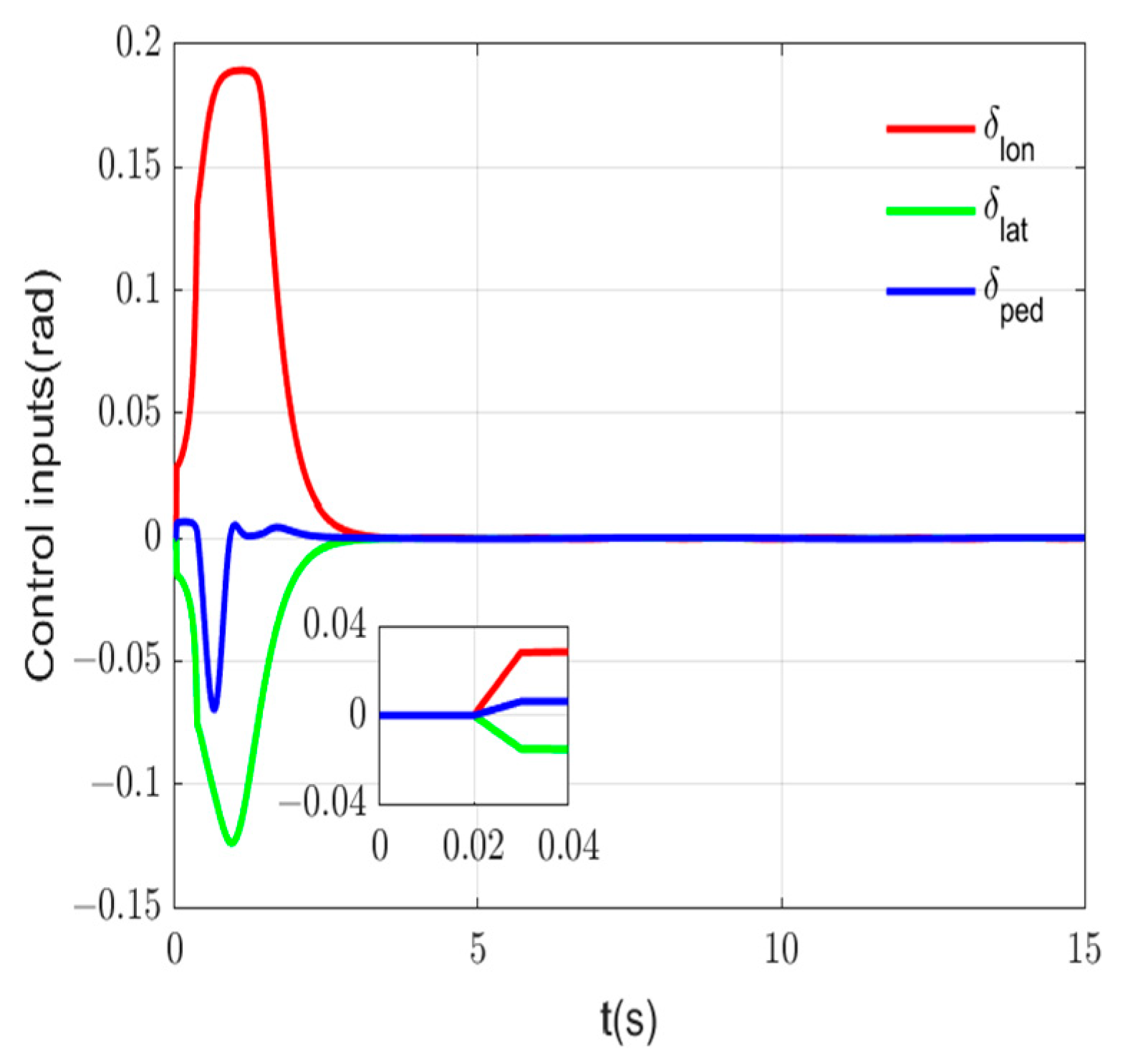
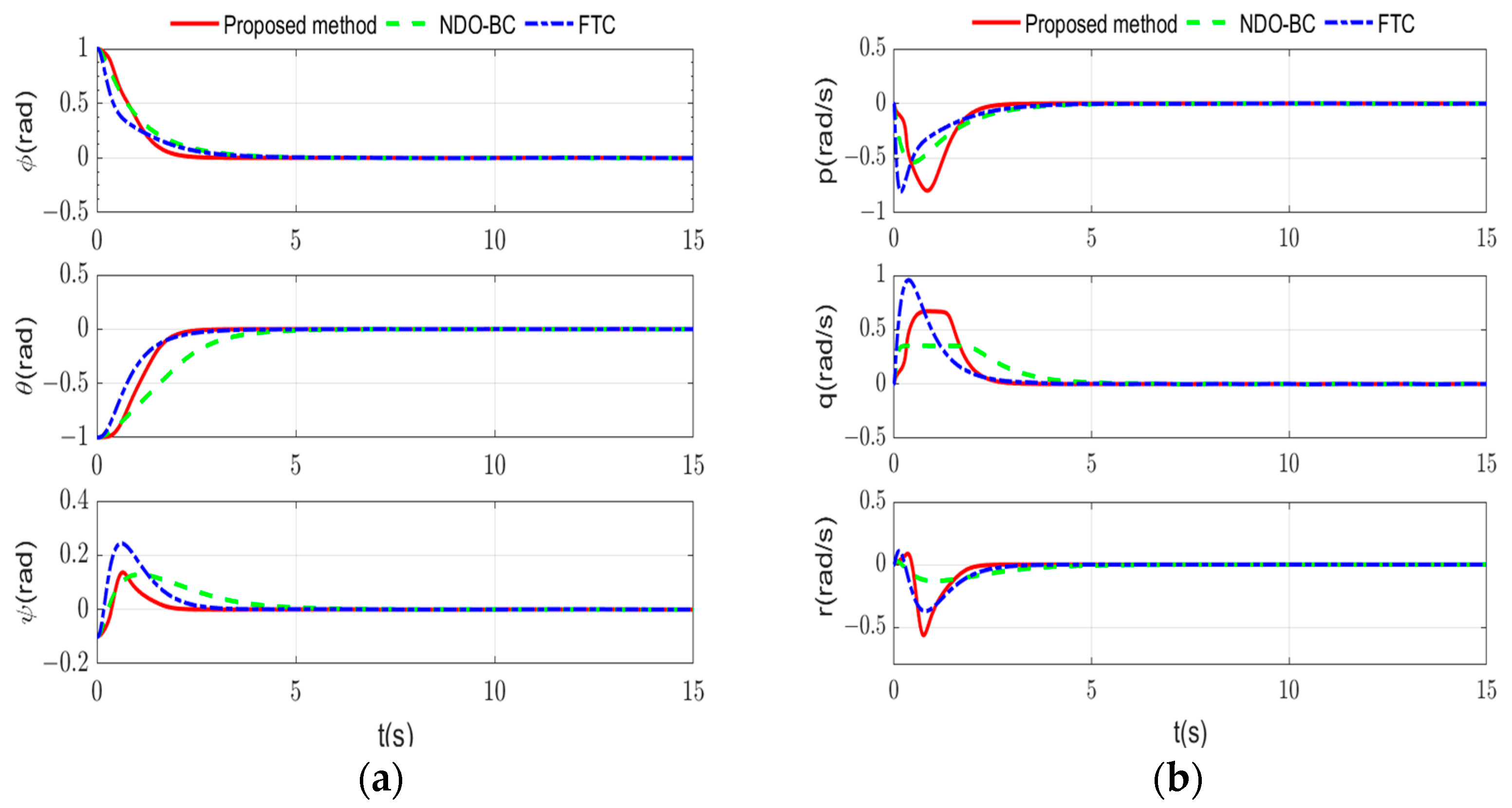
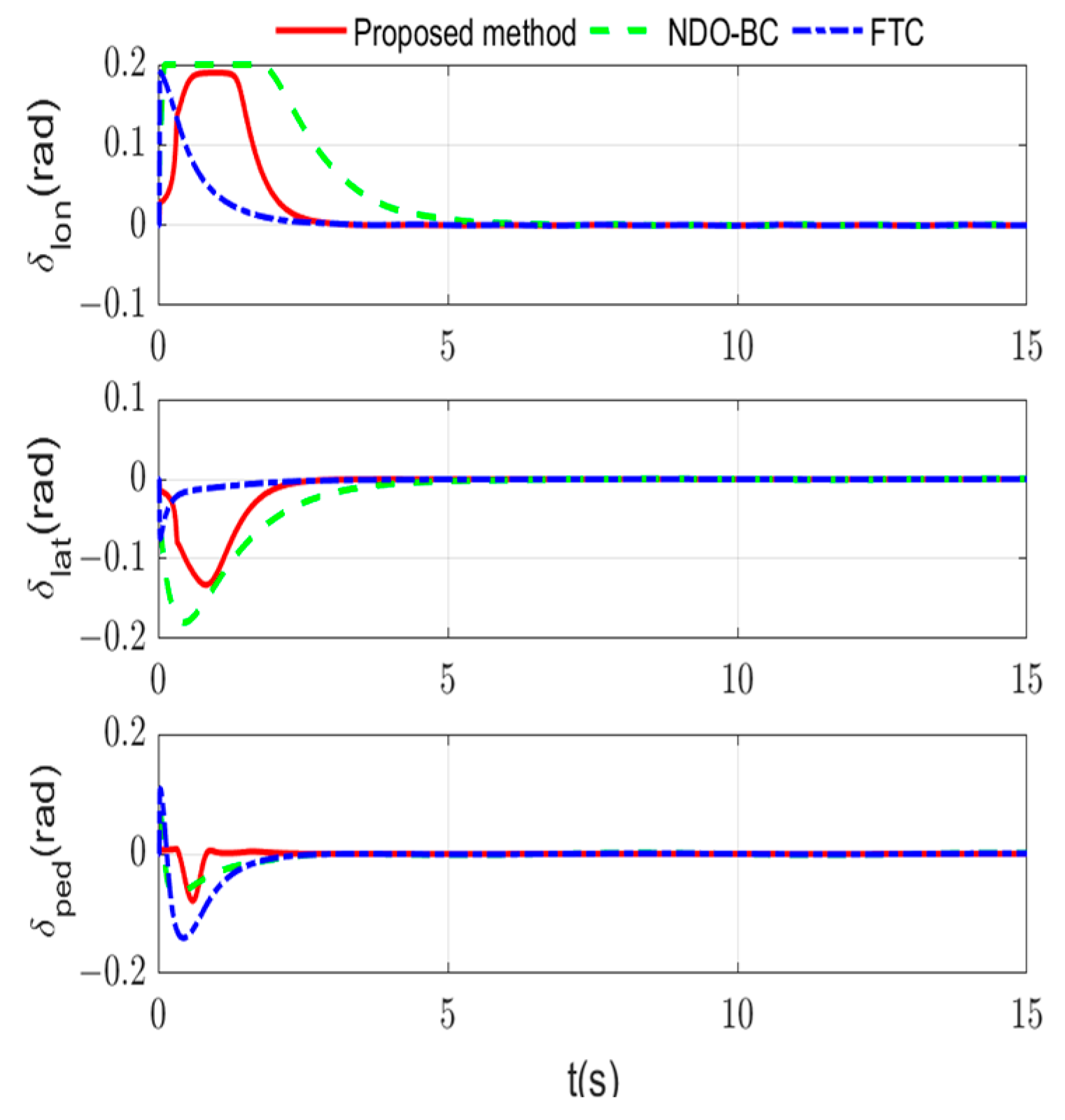
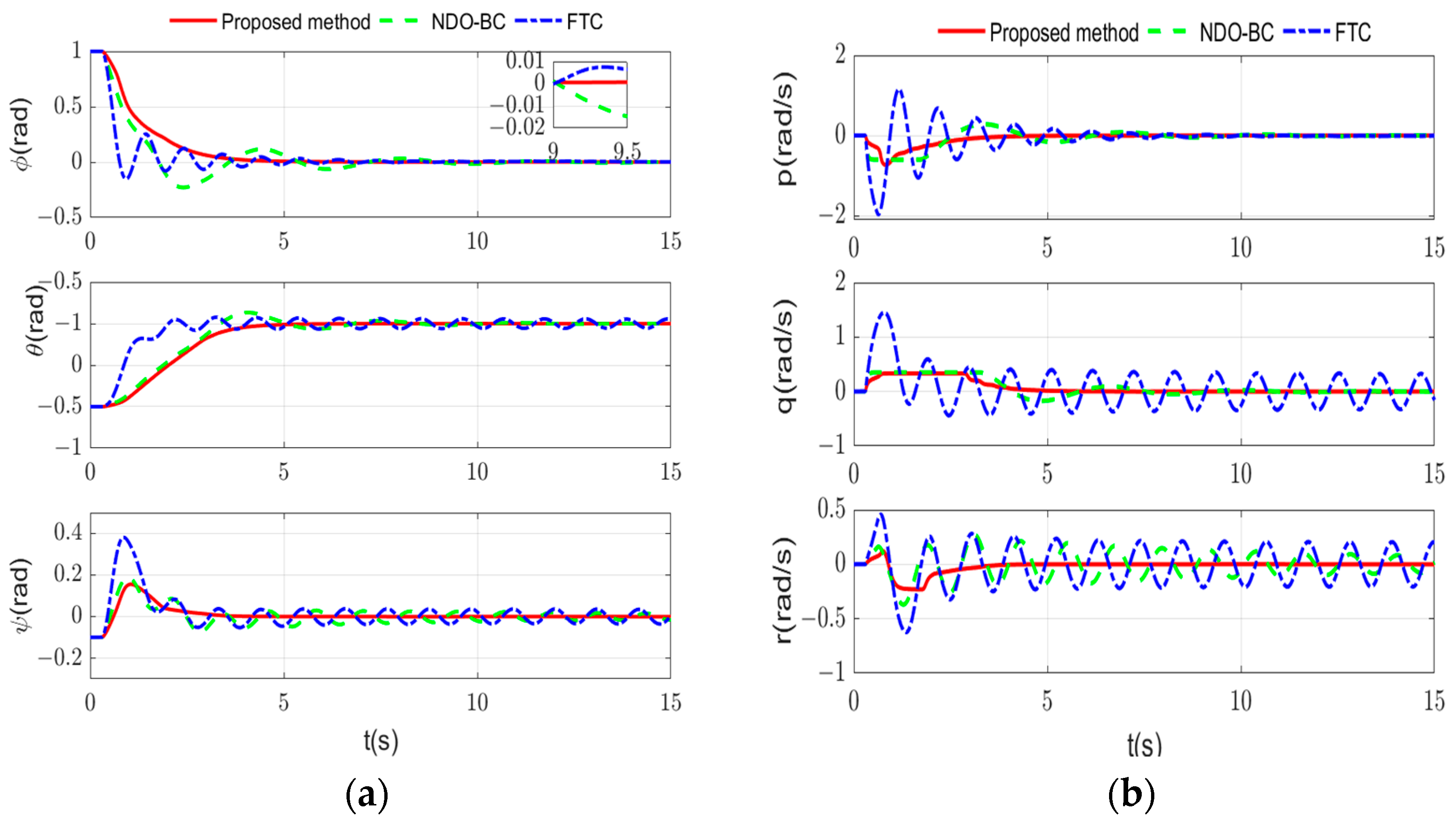
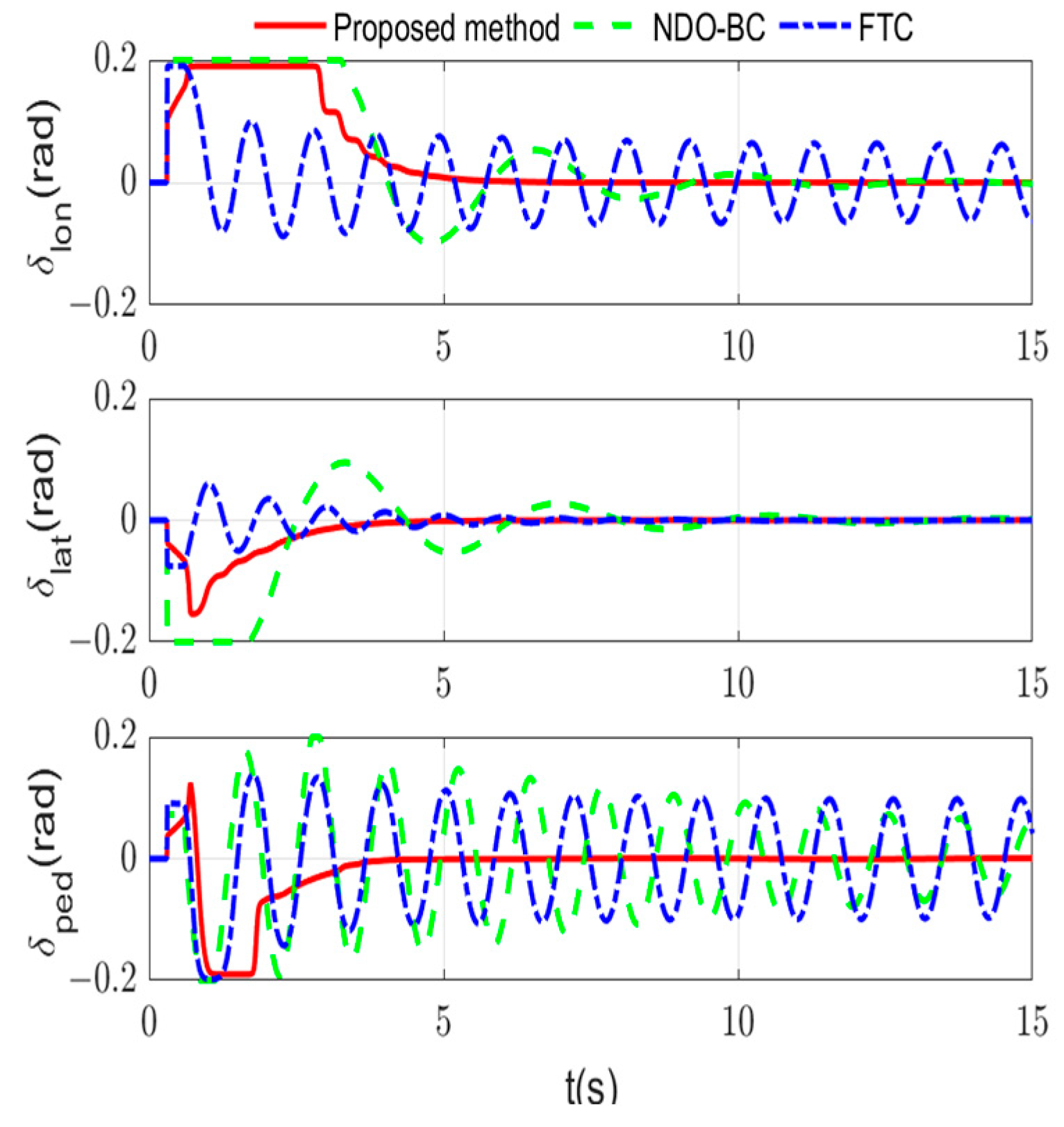
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aslam, F.; Haydar, M.F. H∞ inverse optimal attitude tracking on the special orthogonal group SO (3). Int. J. Control. 2023, 96, 3155–3167. [Google Scholar] [CrossRef]
- Xie, S.; Chen, Q.; He, X.; Tao, M.; Tao, L. Finite-time command-filtered approximation-free attitude tracking control of rigid spacecraft. Nonlinear Dyn. 2022, 107, 2391–2405. [Google Scholar] [CrossRef]
- Fang, X.; Wu, A.; Shang, Y.; Dong, N. A novel sliding mode controller for small-scale unmanned helicopters with mismatched disturbance. Nonlinear Dyn. 2016, 83, 1053–1068. [Google Scholar] [CrossRef]
- Zheng, F.; Xiong, B.; Zhang, J.; Zhen, Z.; Wang, F. Improved neural network adaptive control for compound helicopter with uncertain cross-coupling in multimodal maneuver. Nonlinear Dyn. 2022, 108, 3505–3528. [Google Scholar] [CrossRef]
- Gao, J.; Min, B.; Chen, Y.; Jing, A.; Wang, J.; Pan, G. Compound learning based event-triggered adaptive attitude control for underwater gliders with actuator saturation and faults. Ocean Eng. 2023, 280, 114651. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, T.; Yang, J.; Liu, J. Neuro-adaptive finite time composite fault tolerant control for attitude control systems of satellites. Radio Sci. 2024, 59, e2023RS007744. [Google Scholar] [CrossRef]
- Canciello, G.; Cavallo, A.; D’Amato, E.; Mattei, M. Attitude and velocity high-gain control of a tilt-trirotor UAV. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017. [Google Scholar] [CrossRef]
- Canciello, G.; Cavallo, A.; Schiavo, A.L.; Russo, A. Multi-objective adaptive sliding manifold control for More Electric Aircraft. ISA Trans. 2020, 107, 316–328. [Google Scholar] [CrossRef]
- Islam, S.; Liu, P.X.; El Saddik, A. Robust control of four-rotor unmanned aerial vehicle with disturbance uncertainty. IEEE Trans. Ind. Electron. 2014, 62, 1563–1571. [Google Scholar] [CrossRef]
- Zhou, B. Multi-variable adaptive high-order sliding mode quasi-optimal control with adjustable convergence rate for unmanned helicopters subject to parametric and external uncertainties. Nonlinear Dyn. 2022, 108, 3671–3692. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- He, W.; Yan, Z.; Sun, C.; Chen, Y. Adaptive neural network control of a flapping wing micro aerial vehicle with disturbance observer. IEEE Trans. Cybern. 2017, 47, 3452–3465. [Google Scholar] [CrossRef]
- Wang, D.; Zong, Q.; Tian, B.; Shao, S.; Zhang, X.; Zhao, X. Neural network disturbance observer-based distributed finite-time formation tracking control for multiple unmanned helicopters. ISA Trans. 2018, 73, 208–226. [Google Scholar] [CrossRef]
- Sabbghian-Bidgoli, F.; Farrokhi, M. Polynomial fuzzy observer-based integrated fault estimation and fault-tolerant control with uncertainty and disturbance. IEEE Trans. Fuzzy Syst. 2020, 30, 741–754. [Google Scholar] [CrossRef]
- Chen, M.; Chen, W.H. Sliding mode control for a class of uncertain nonlinear system based on disturbance observer. Int. J. Adapt. Control Signal Process. 2010, 24, 51–64. [Google Scholar] [CrossRef]
- Wu, S.N.; Sun, X.Y.; Sun, Z.W.; Wu, X.D. Sliding mode control for staring mode space craft using a disturbance observer. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 215–224. [Google Scholar] [CrossRef]
- Hu, Q.; Li, B.; Qi, J. Disturbance observer based finite-time attitude control for rigid spacecraft under input saturation. Aerosp. Sci. Technol. 2014, 39, 13–21. [Google Scholar] [CrossRef]
- Cui, R.H.; Xue, X.J. Output feedback stabilization of stochastic planar nonlinear systems with output constraint. Automatica 2022, 143, 110471. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, H.; Yu, X.; Zhang, W.; Chen, J. Attitude constraint-based recovery for under-actuated AUVs under vertical plane control during the capture stage. Ocean Eng. 2023, 281, 115012. [Google Scholar] [CrossRef]
- Mirshamsi, A.; Nobakhti, A. Uncertainty disturbance estimator control for delayed linear systems with input constraint. Automatica 2024, 167, 111763. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S.; Tay, E.H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S. Control of nonlinear systems with partial state constraints using a barrier Lyapunov function. Int. J. Control. 2011, 84, 2008–2023. [Google Scholar] [CrossRef]
- Li, R.; Chen, M.; Wu, Q. Adaptive neural tracking control for uncertain nonlinear systems with input and output constraints using disturbance observer. Neurocomputing 2017, 235, 27–37. [Google Scholar] [CrossRef]
- Yan, K.; Chen, M.; Wu, Q.; Zhu, R. Robust adaptive compensation control for unmanned autonomous helicopter with input saturation and actuator faults. Chin. J. Aeronaut. 2019, 32, 2299–2310. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, Y.; Guo, W.W. Robust tracking control for uncertain MIMO nonlinear systems with input saturation using RWNNDO. Neurocomputing 2014, 144, 436–447. [Google Scholar] [CrossRef]
- Chu, Z.; Xiang, X.; Zhu, D.; Luo, C.; Xie, D. Adaptive fuzzy sliding mode diving control for autonomous underwater vehicle with input constraint. Int. J. Fuzzy Syst. 2018, 20, 1460–1469. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, T. Leader-following formation control of second-order nonlinear systems with time-varying communication delay. Int. J. Control Autom. Syst. 2021, 19, 1729–1739. [Google Scholar] [CrossRef]
- Yang, H.L.; Ruby, R.; Wu, K.S. Delay performance of priority-queue equipped UAV-based mobile relay networks: Exploring the impact of trajectories. Comput. Netw. 2022, 210, 108856. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Wang, W. Adaptive backstepping control of uncertain systems with unknown input time-delay. Automatica 2009, 45, 1415–1422. [Google Scholar] [CrossRef]
- Li, S.; Duan, N.; Min, H. Trajectory tracking control for quadrotor unmanned aerial vehicle with input delay and disturbances. Asian J. Control. 2024, 26, 150–161. [Google Scholar] [CrossRef]
- Li, D.P.; Liu, Y.J.; Tong, S.; Chen, C.P.; Li, D.J. Neural networks-based adaptive control for nonlinear state constrained systems with input delay. IEEE Trans. Cybern. 2018, 49, 1249–1258. [Google Scholar] [CrossRef]
- You, F.; Chen, N.; Zhu, Z.; Cheng, S.; Yang, H.; Jia, M. Adaptive fuzzy control for nonlinear state constrained systems with input delay and unknown control coefficients. IEEE Access 2019, 7, 53718–53730. [Google Scholar] [CrossRef]
- Luo, R.C.; Chung, L.Y. Stabilization for linear uncertain system with time latency. IEEE Trans. Ind. Electron. 2002, 49, 905–910. [Google Scholar] [CrossRef]
- Yue, D.; Han, Q.L. Delayed feedback control of uncertain systems with time-varying input delay. Automatica 2005, 41, 233–240. [Google Scholar] [CrossRef]
- Tong, S.; Sui, S.; Li, Y. Fuzzy adaptive output feedback control of MIMO nonlinear systems with partial tracking errors constrained. IEEE Trans. Fuzzy Syst. 2015, 23, 729–742. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Zhao, L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica 2018, 92, 173–180. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Q.; Sun, C. Adaptive tracking control of high-order MIMO nonlinear systems with prescribed performance. Front. Inf. Technol. Electron. Eng. 2021, 22, 986–1001. [Google Scholar] [CrossRef]
- Ye, D.; Xiao, Y.; Sun, Z.; Xiao, B. Neural network based finite-time attitude tracking control of spacecraft with angular velocity sensor failures and actuator saturation. IEEE Trans. Ind. Electron. 2021, 69, 4129–4136. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Attitude stabilization of rigid spacecraft with finite-time convergence. Int. J. Robust Nonlinear Control. 2011, 21, 686–702. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yang, T. Adaptive Finite-Time Constrained Attitude Stabilization for an Unmanned Helicopter System under Input Delay and Saturation. Processes 2024, 12, 1787. https://doi.org/10.3390/pr12091787
Li Y, Yang T. Adaptive Finite-Time Constrained Attitude Stabilization for an Unmanned Helicopter System under Input Delay and Saturation. Processes. 2024; 12(9):1787. https://doi.org/10.3390/pr12091787
Chicago/Turabian StyleLi, Yang, and Ting Yang. 2024. "Adaptive Finite-Time Constrained Attitude Stabilization for an Unmanned Helicopter System under Input Delay and Saturation" Processes 12, no. 9: 1787. https://doi.org/10.3390/pr12091787




