Analysis of the Impact of Multiple Explosion Source Layouts on the Kinetic Characteristics of Gas Explosions in Blind Roadways
Abstract
1. Introduction
2. Mathematical Model
2.1. Basic Equations
- —Cartesian coordinate parameters;
- —Fluid density, kg/m3;
- —Pressure, Pa;
- —Velocity components for x, y, and z coordinate directions, respectively, m/s;
- —Time coordinates;
- —Temperature, °C;
- —Gas constant;
- —Specific energy, J/kg.
- —Reaction rate constant;
- —Frequency factor;
- —Temperature index;
- —Activation energy, J/kmol.
2.2. Physical Model
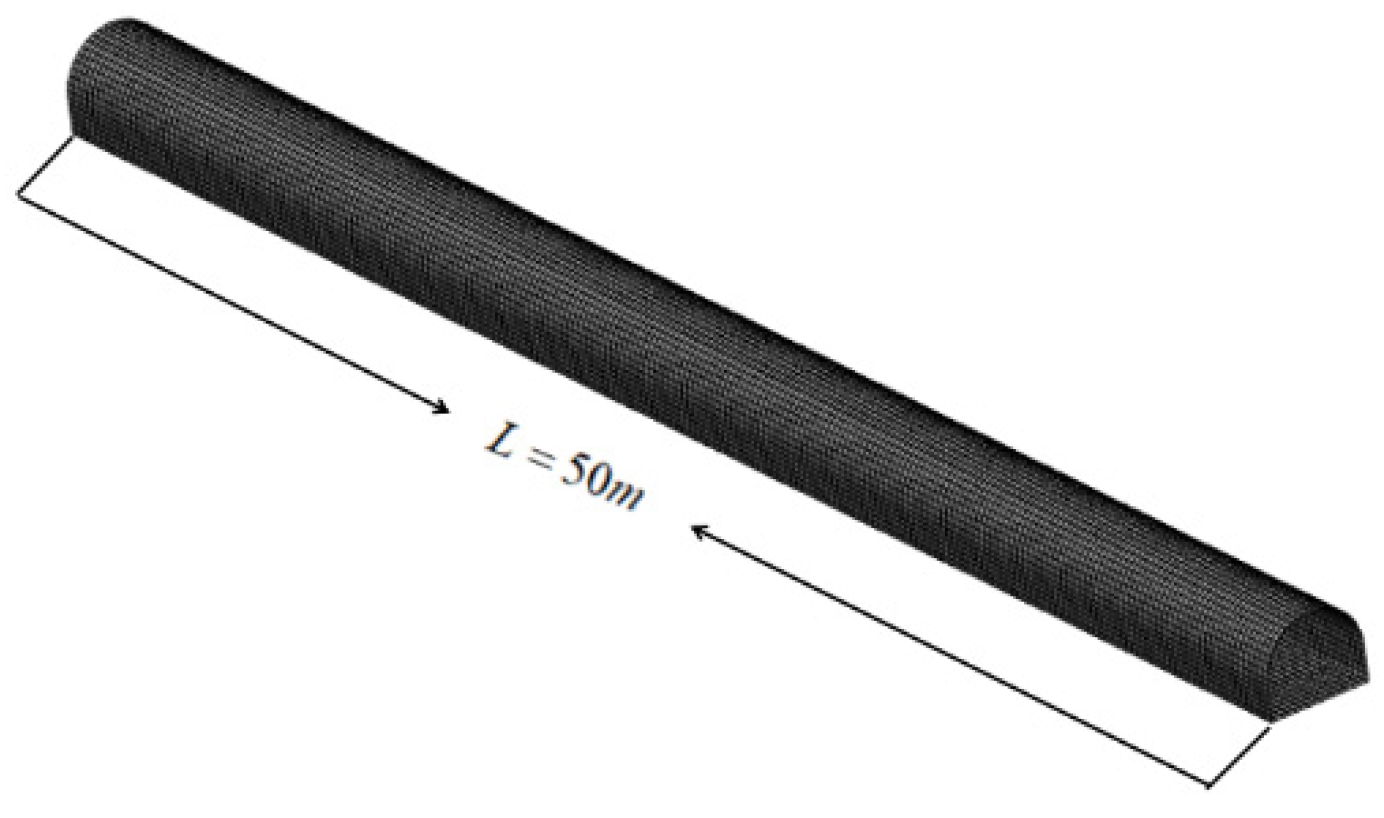
2.2.1. Numerical Modeling
2.2.2. Simulation Assumptions and Boundary Condition Setup
- (1)
- An electric spark ignition method is used, and the gas accumulation area is ignited within the tunnel.
- (2)
- The explosion process is a rapid, irreversible chemical reaction.
- (3)
- During the simulation, all gases are considered compressible, and the effect of gravity is neglected.
- (4)
- All wall surfaces in the simulation are assumed to be adiabatic and rigid. During the explosion, wall surfaces do not undergo relative displacement nor exchange energy with the external environment.
- (5)
- The explosion process is considered a single-step reaction, with the products being CO2 and H2O.
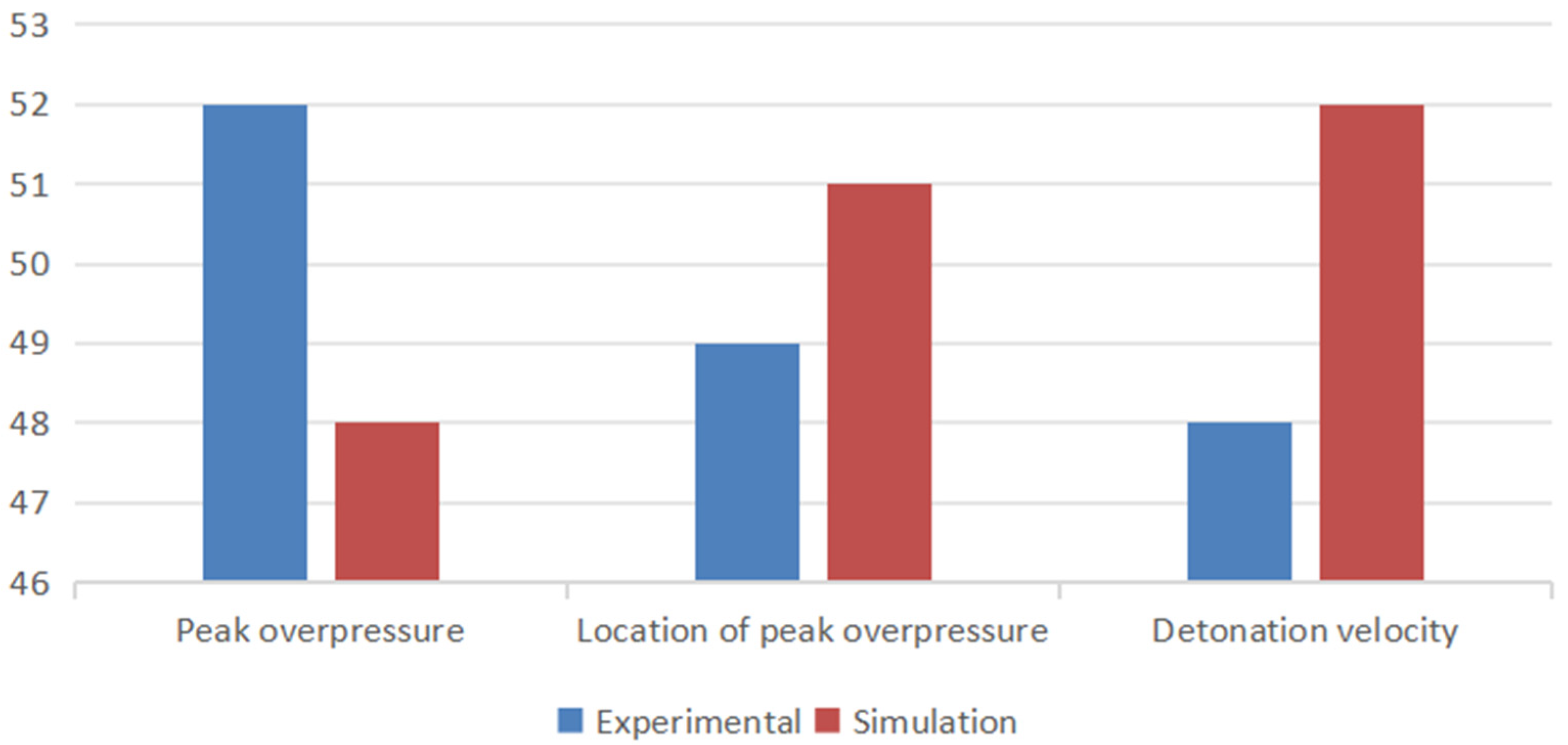
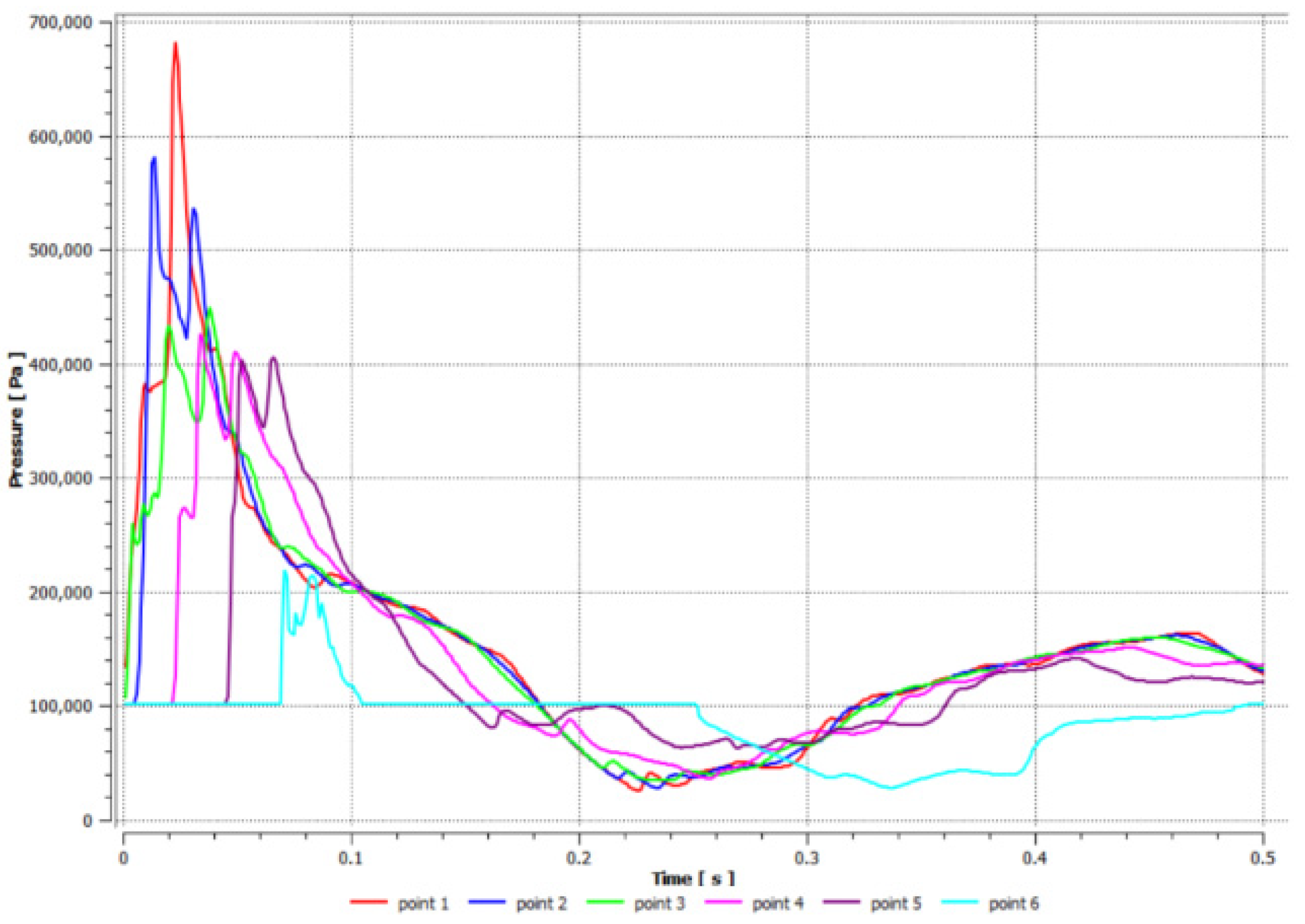
2.3. Validation of Numerical Simulation Reasonableness
3. Numerical Simulation Results
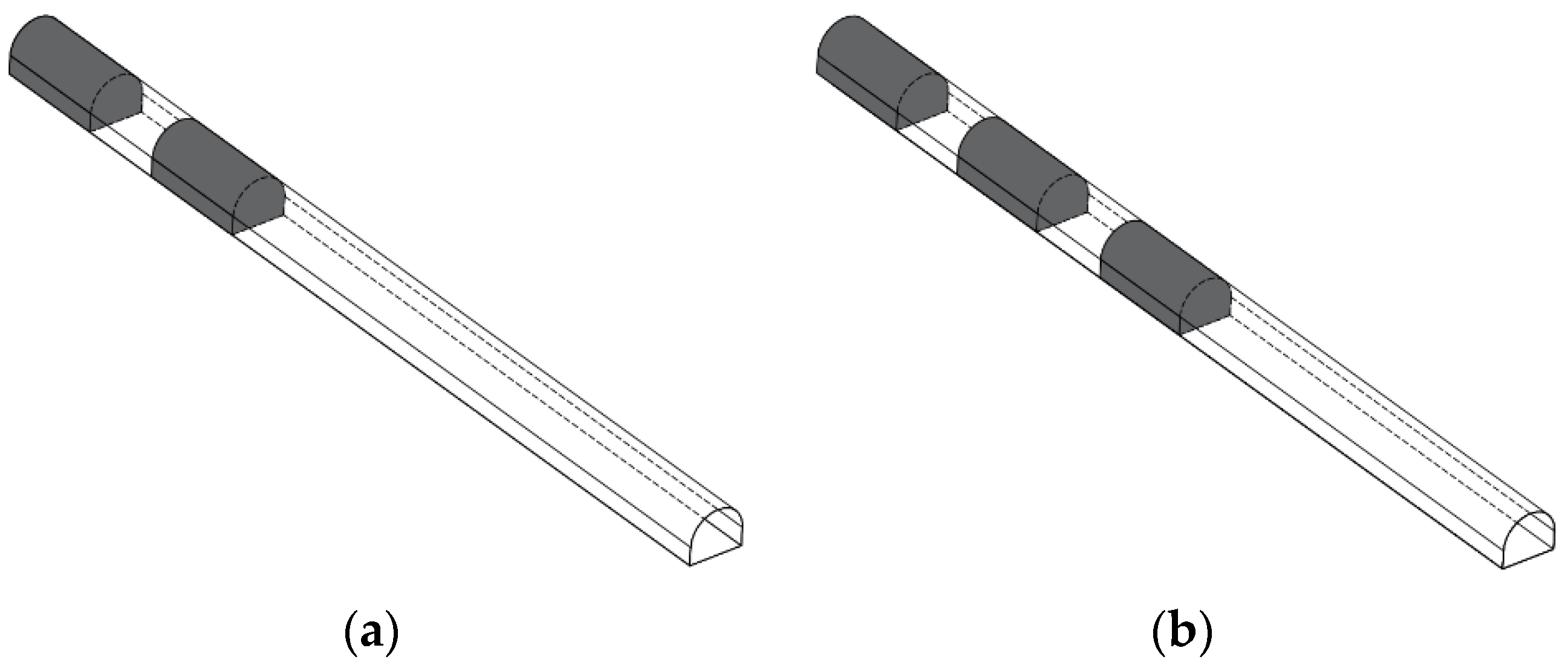
3.1. Models with Different Numbers of Explosion Sources
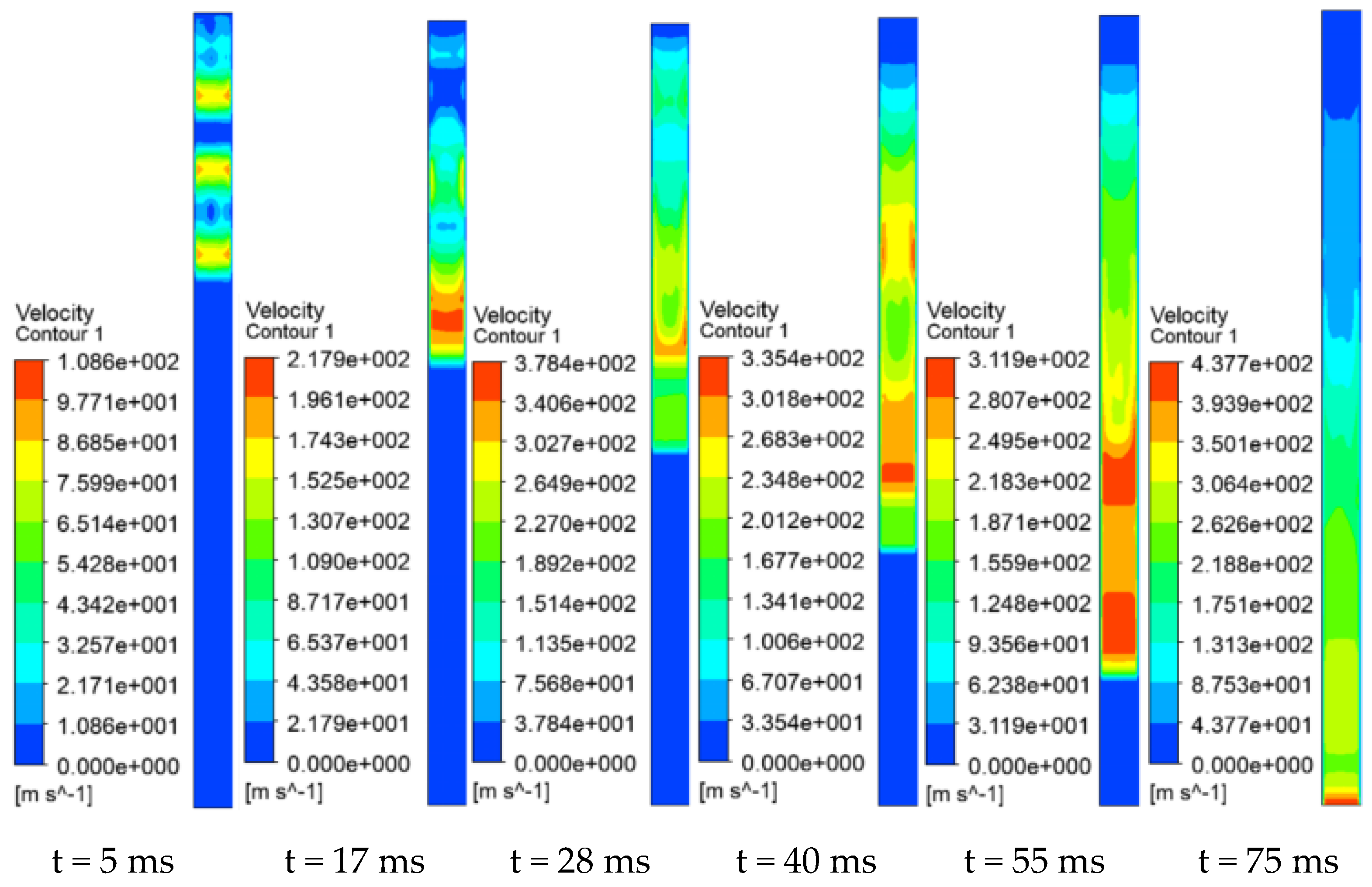
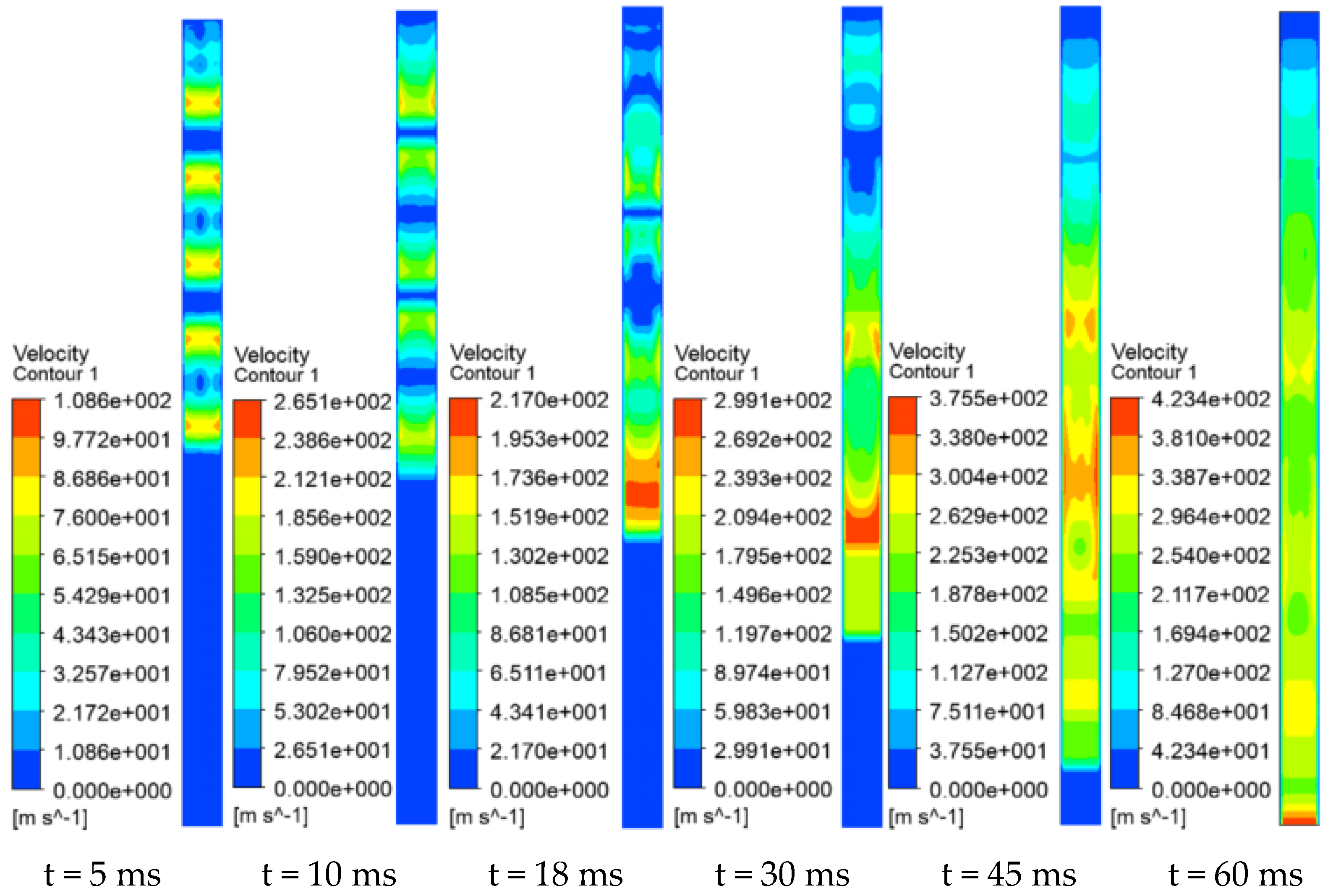
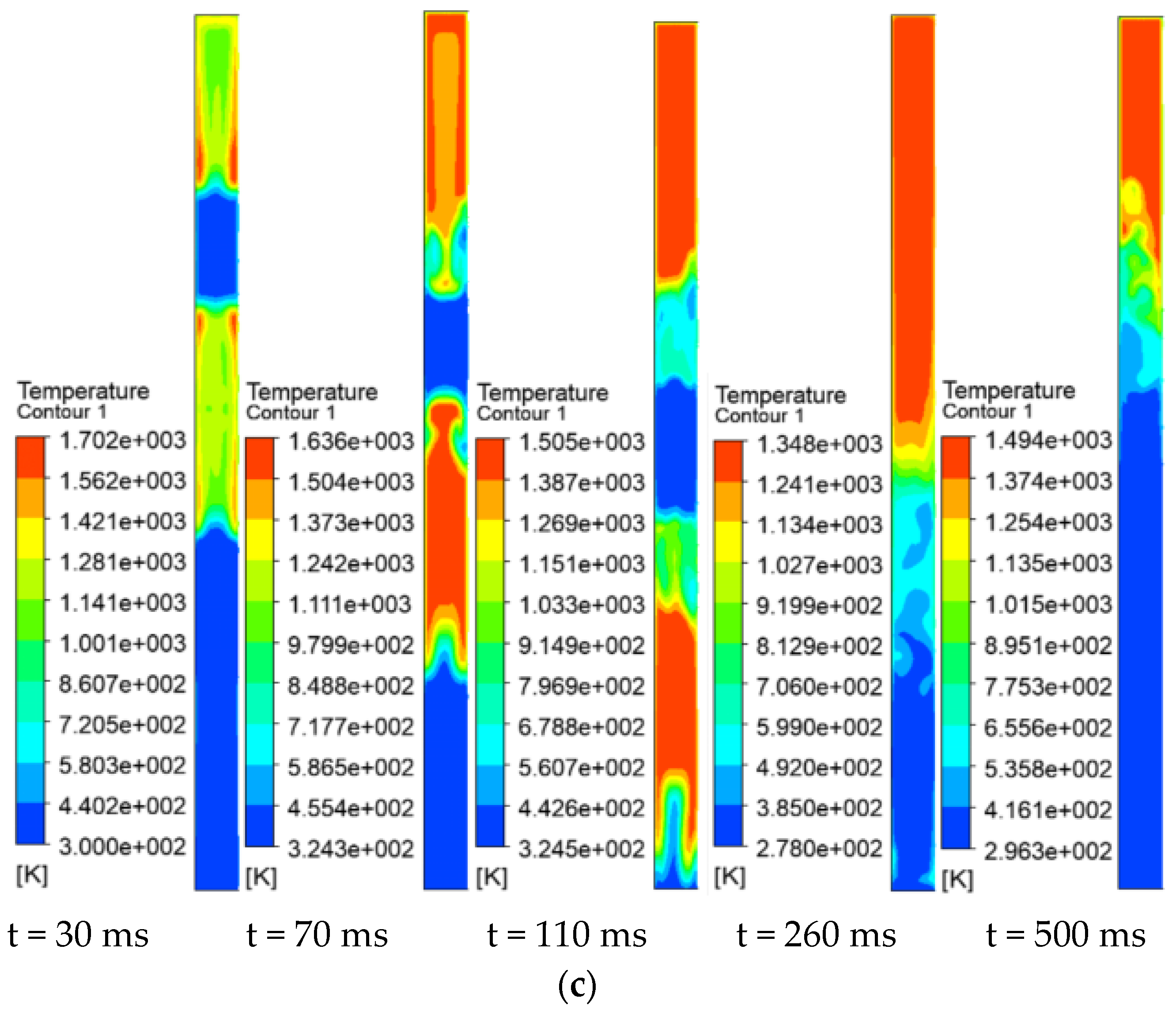
3.1.1. Shock Wave Propagation Process
3.1.2. Analysis of the Formation Pattern of Pressure Overlap Zones in Multiple Explosion Sources
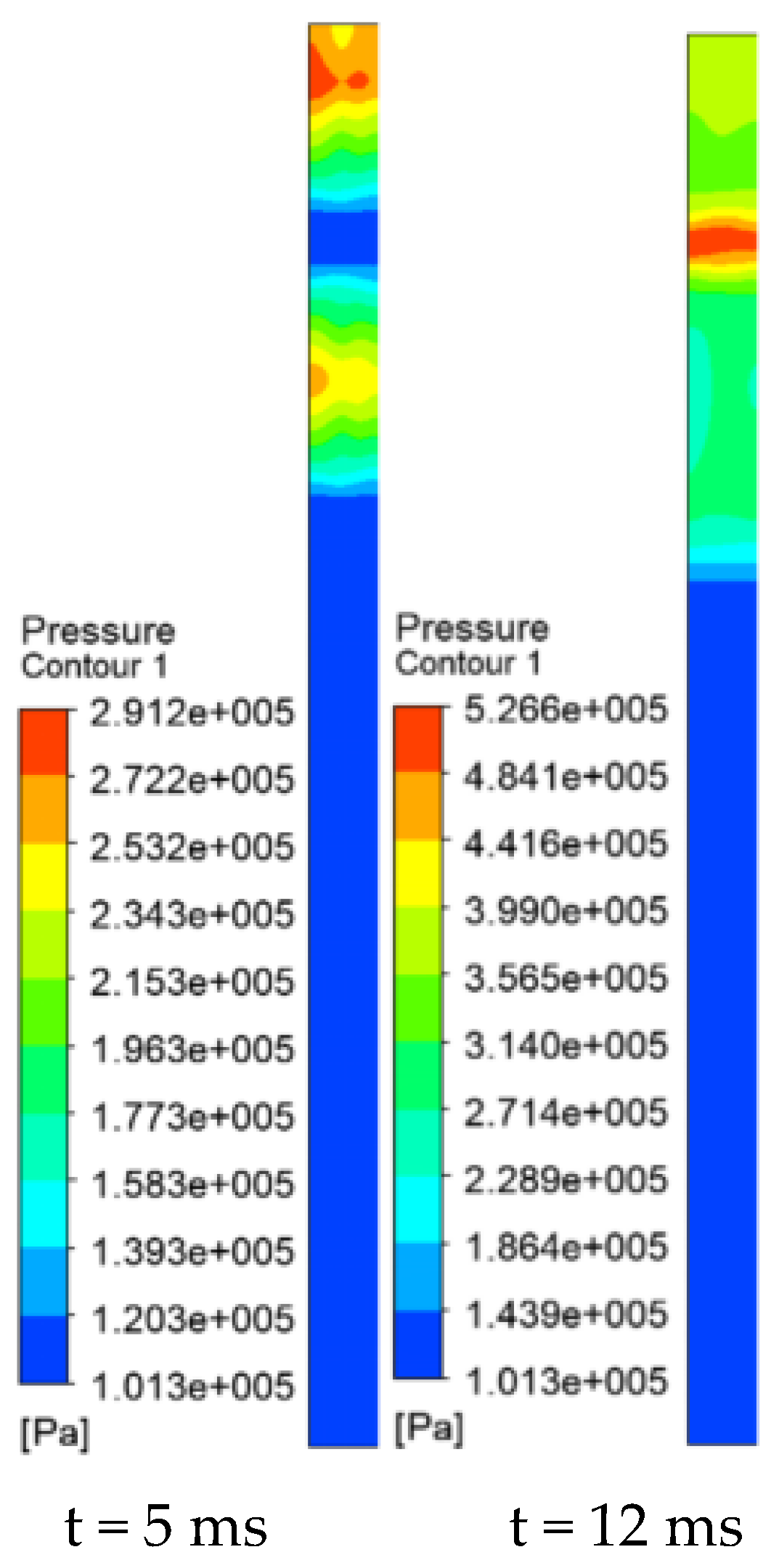
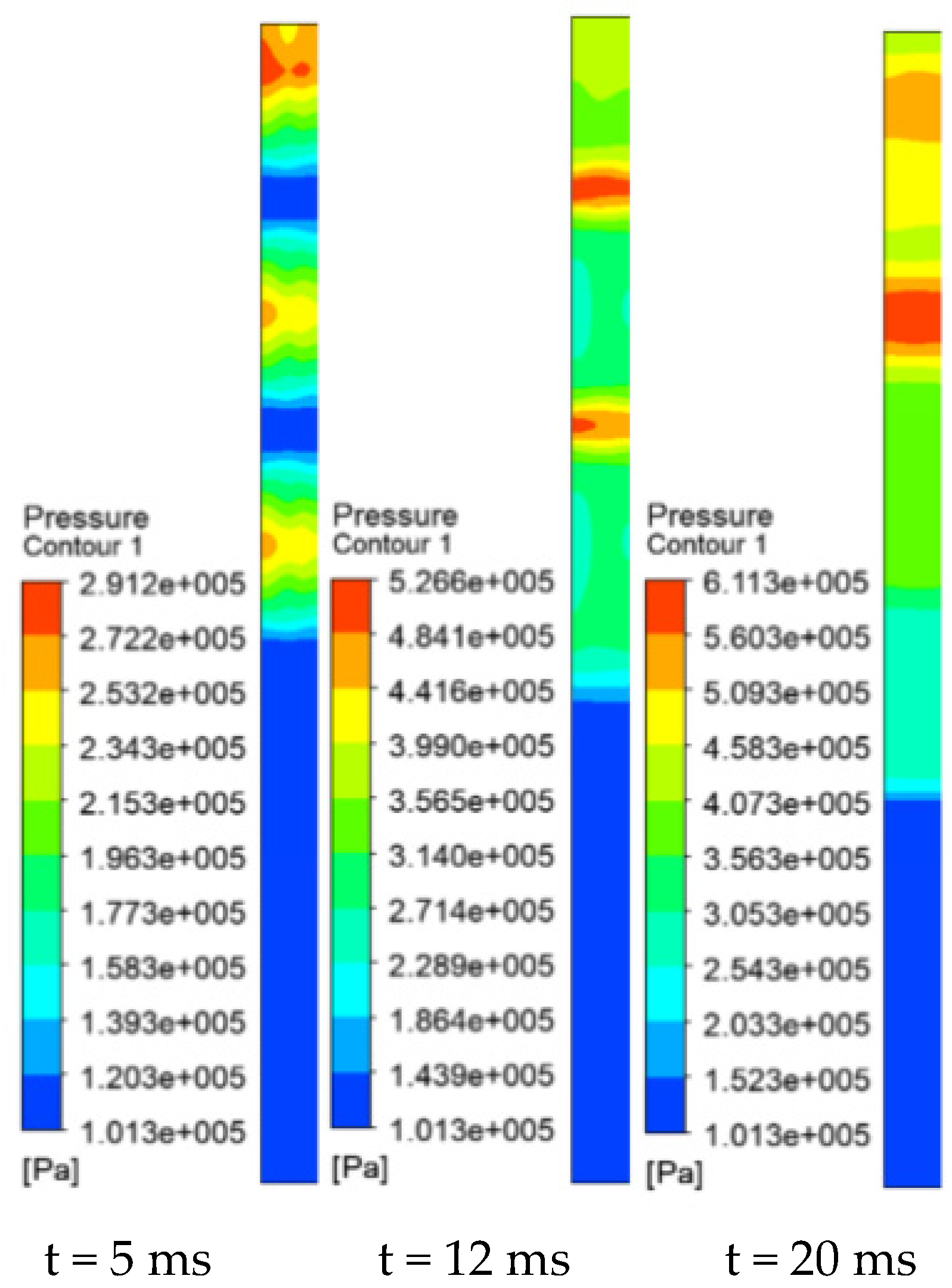
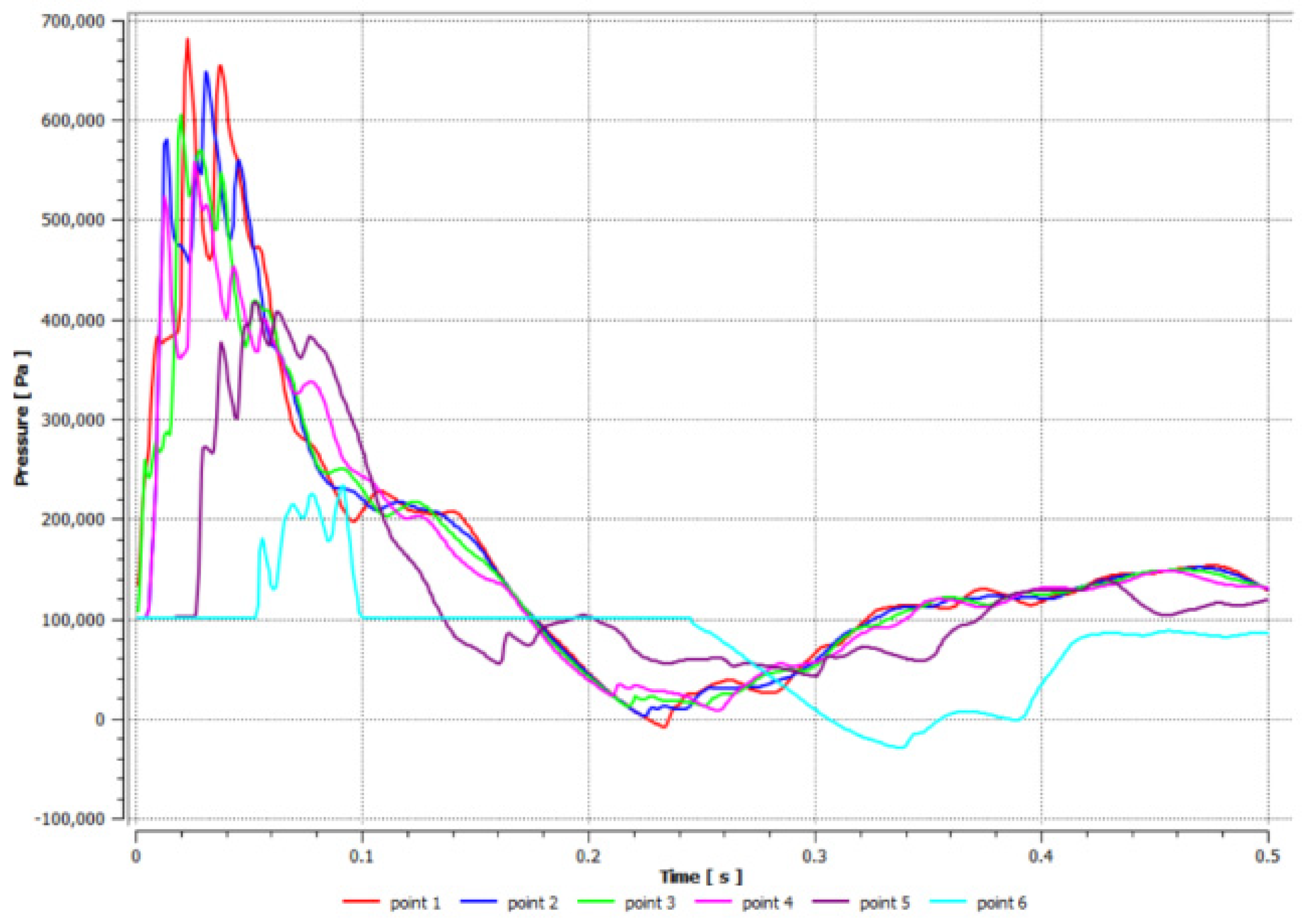
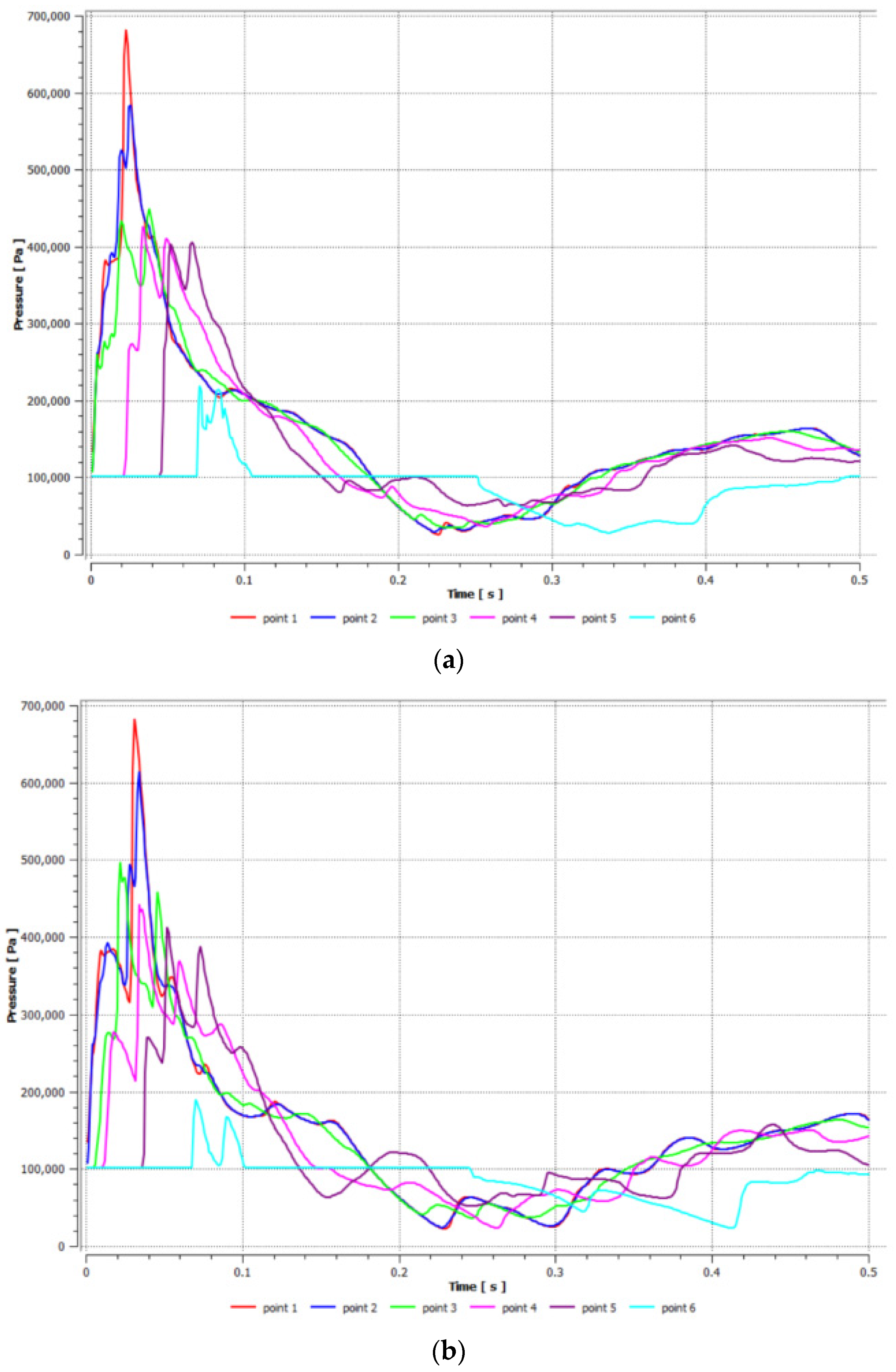
3.1.3. Analysis of Pressure from Different Numbers of Explosion Sources
- (1)
- Double-Explosion Source Model
- (2)
- Three-Explosion Source Model
3.1.4. Analysis of Regional Pressure Extremes
3.2. Models with Different Intervals between Explosion Sources
3.2.1. Effects of Different Intervals on Flame Propagation
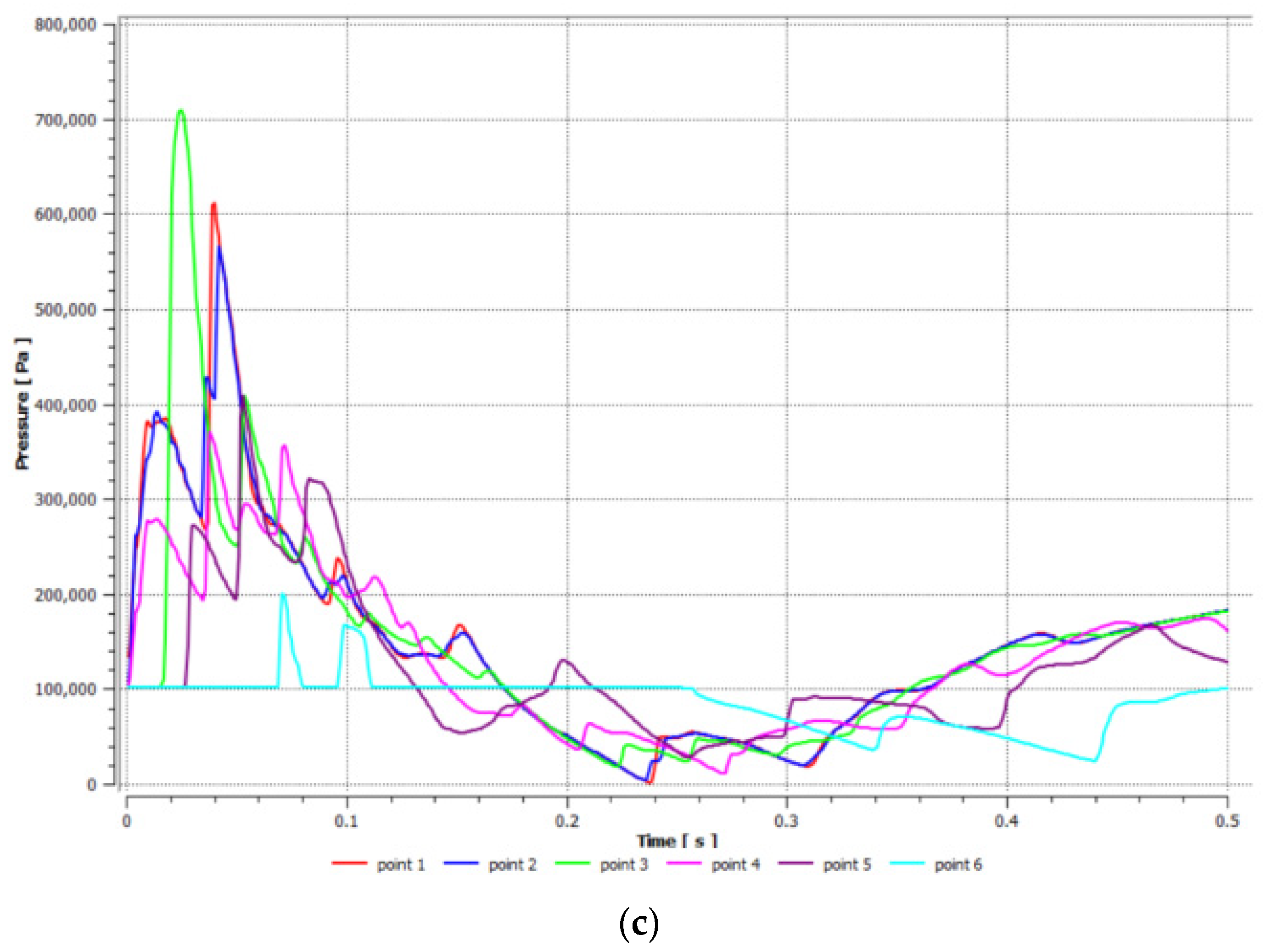
3.2.2. Effects of Different Intervals on Pressure Distribution
4. Conclusions
- (1)
- During a multi-source gas explosion, counter-propagating shock waves create pressure overlap zones within the tunnel. The pressure waves in these overlap zones coupled with the explosion shock waves in the tunnel, resulting in multiple segments of low-velocity regions (where shock waves meet) and high-velocity regions (generated by explosion waves, wall-reflected waves, and overlap zone pressure waves) within the tunnel at different times.
- (2)
- The number of pressure overlap zones formed by multiple explosion sources in the tunnel dynamically changes as the shock waves propagate. For n explosion sources, the number of pressure overlap zones decreases incrementally over time because each encounter of adjacent shock waves eliminates one overlap zone.
- (3)
- The pressure distribution from a multi-source gas explosion within the tunnel differs from that of a single-source model, exhibiting multiple pressure oscillations over time. Overall, the pressure decreases gradually as the distance from the explosion source increases. Locations with significantly higher pressures are the closed end and the pressure overlap zones formed by counter-propagating shock waves.
- (4)
- Simulation results indicate that the interval distance between explosion sources has a minor impact on the propagation patterns of shock waves and flames within the tunnel. However, the meeting time, the velocity at the meeting point, and pressure of the shock waves all increase with the increase in the interval distance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, B. Analysis on the current situation of coal mine safety in China. Energy Technol. Manag. 2006, 3, I0001. [Google Scholar]
- Si, R.; Li, R.; Su, D. Experimental study on the influence of coal dust cloud mass concentration on gas explosion pressure. J. Saf. Environ. 2018, 18, 1796–1798. [Google Scholar]
- Li, Z.; Wang, T.; Wang, S.; Wang, Y. Simulation study on disaster evolution of ventilation system in coal and gas outburst mine. J. Coal Ind. 2017, 42, 929–934. [Google Scholar]
- Wang, D. Thermal power disaster and characteristics of coal mine. J. Coal Ind. 2018, 43, 137–142. [Google Scholar]
- Savinko, C.K. Downhole Air Shock Wave; Ding, A.; Long, W., Translators; Metallurgical Industry Press: Beijing, China, 1979. [Google Scholar]
- Dunn-Rankin, D.; Barr, P.K.; Sawyer, R.F. Numerical and experimental study of tulip flame formation in aclosed vessel. In Proceedings of the 21st Symposium (International) on Combustion, Munich, Germany, 3–8 August 1986; Pergamon: Pittsburgh, PA, USA, 1986; pp. 1291–1301. [Google Scholar]
- Strehlow, R.A. Combustion Fundamentals; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Gonzalez, M.; Borghi, R.; Saouab, A. Interaction of aflame front with its self-generated flow in an enclosure: The “tulip flame” phenomenon. Combust. Flame 1992, 88, 201–220. [Google Scholar] [CrossRef]
- Catlin, C.A.; Fairweather, M. Predictions of turbulent, premixed flame propagation in explosion tubes. Combust. Flame 1995, 102, 115–128. [Google Scholar] [CrossRef]
- Kristoffersen, K.; Vaagsaether, K.; Bjerketvedt, D.; Thomas, G.O. Propane–air pipe explosion experiments. Data for estimation of 1-D burning velocity in slow regimes. Exp. Therm. Fluid Sci. 2004, 28, 723–728. [Google Scholar] [CrossRef]
- Feng, C.; Chen, L.; Qian, X. Influence of ignition position on the overpressure of gas explosion in a solitary headway. J. Saf. Environ. 2001, 1, 56–59. [Google Scholar]
- Bartknecht, W. Explosion Process and the Protective Measures; He, H., Translator; Chemical Industry Press: Beijing, China, 1985. (In Chinese) [Google Scholar]
- Yang, S.; Jing, G.; Jia, Z. Injury study on impact current of gas explosion in coal mine. J. China Coal Soc. 2009, 34, 1354–1358. [Google Scholar]
- Li, Z.; Liu, H.; Dun, Z.; Ren, L.; Fang, J. Grouting effect on rock fracture using shear and seepage assessment. Constr. Build. Mater. 2020, 242, 118131. [Google Scholar] [CrossRef]
- Zheng, D.; Li, X.; Guo, Z.; Liu, K. Experimental and Numerical Simulation of Flame Propagation Mechanism in Methane Explosion. Res. Fire Prot. Theory 2014, 33, 725–728. [Google Scholar]
- Cheng, F.; Deng, J.; Cai, Z.; Luo, Z.; Xiao, Y. The influence of gas accumulation range on the damage characteristics and propagation rules of gas explosion shock waves in single ended roadways. Min. Saf. Environ. Prot. 2016, 43, 1–5. [Google Scholar]
- Xu, J.; Xu, S.; Yang, G. Experimental study on the propagation of mine gas explosion. J. Coal Sci. 2004, 33, 55–57. [Google Scholar]
- Nie, B.; He, X.; Li, X. Study on the Dynamic Change Law of Gas Explosion Flame Based on Image Correlation Coefficient. In Proceedings of the Fifth National Symposium on Strong Dynamic Load Effects and Protection and the Innovative Research Group Symposium on Dynamic Mechanical Behavior of Complex Media/Structures, Hohhot, China, 15–19 July 2013. [Google Scholar]
- Sun, J.; Chen, D. Structural characteristics of methane/air premixed flames with different concentrations. In Proceedings of the 2009 Academic Annual Meeting of the China Occupational Safety and Health Association, Xiamen, China, 11–14 November 2009. [Google Scholar]
- Chen, D.; Sun, J.; Liu, Y.; Ma, Y.; Han, X. Propagation characteristics of methane/air premixed gas flames. Explos. Shock 2008, 28, 385–390. [Google Scholar]
- Liu, Y.; Sun, J.; Chen, D. Experimental study on the structure of methane coal dust composite flames in pipelines. J. China Univ. Sci. Technol. 2006, 36, 65–68. [Google Scholar]
- Chen, X.; Sun, J.; Yao, L.; Liu, Y. Microstructural characteristics during Tulip flame formation. Combust. Sci. Technol. 2008, 14, 350–354. [Google Scholar]
- He, X.; Sun, J.; Chen, X.; Yuan, G. Experimental and numerical simulation study on the propagation characteristics of methane-air premixed flames in pipelines. J. China Univ. Sci. Technol. 2009, 39, 419–423. [Google Scholar]
- Ma, H.; Chen, X.; Jing, D. Simulation of gas explosion and explosion discharge process in H-type ventilation roadway. Chin. J. Saf. Sci. 2021, 31, 45–51. [Google Scholar]
- Liu, R.; Zhu, Y. Full scale simulation of gas explosion in long wall face of coal mine. Chin. J. Saf. Sci. 2018, 28, 62–68. [Google Scholar]
- Chen, X.; Guo, L.; Cheng, F. Numerical simulation of gas explosion in single head roadway. Coal Mine Saf. 2012, 43, 20–22. [Google Scholar]
- Ye, Q.; Wang, W.; Jia, Z.; Liu, J. Characteristics of gas explosion propagation in H-type tunnel with different arrangement of dual explosive sources. J. High Press. Phys. 2024, 38, 150–162. [Google Scholar]
- Wang, W.; Ye, Q.; Jia, Z. Numerical simulation study of gas explosion model with different accumulation ranges in H-type roadway. Min. Saf. Environ. Prot. 2023, 50, 13–18. [Google Scholar]
- Yang, K.; Si, R.; Huang, Z.; Jia, Q.; Zhao, J.; Niu, Y. Experimental study of gas explosion pressure and flame wave propagation in different pipe diameters. Eng. Blasting 2024. [Google Scholar] [CrossRef]
- Lin, B.; Ye, Q.; Zhai, C.; Jian, C. Propagation Law and Analysis of Gas Explosions in Branched Pipelines. J. China Coal Soc. 2008, 33, 136–139. [Google Scholar]
- Lin, B.; Zhang, R.; Lv, H. Study on the Flame Propagation Law and Acceleration Mechanism in Gas Explosions. J. China Coal Soc. 1999, 24, 56–58. [Google Scholar]
- Zhai, C.; Lin, B.; Ye, Q.; Li, X.; Zhu, C. Influence of geometry shape on gas explosion propagation laws in bend roadways. Procedia Earth Planet. Sci. 2009, 1, 193–198. [Google Scholar]
- Ye, Q.; Lin, B.; Jia, Z.; Jia, Z.; Zhu, C. Propaga tion law and analysis of gas explosion in bend duct. Procedia Earth Planet. Sci. 2009, 1, 316–321. [Google Scholar]
- Zhu, C.; Lin, B.; Lu, Z.; Jiang, B.; Liu, Y. Ex-periments on flame and shock wave propagation in a par-allel tunnel in underground coal mines. In Progress in Safety Science and Technology; Science Press: Beijing, China, 2010; pp. 1204–1208. [Google Scholar]
- Deng, Z. Numerical simulation of damage and failure of roadway wall caused by gas explosion. Sci. Technol. Eng. 2020, 20, 1792–1798. [Google Scholar]
- Ning, Y. Derivation and application of a simple calculation formula for the cross-section of an arch roadway. In Proceedings of the 2012 National Coal Mine Safety Academic Annual Conference, Guangzhou, China, 28 October 2012. [Google Scholar]
- Yang, S.; Jing, G. Propagation of gas explosion in semi-enclosed restricted space. J. Liaoning Univ. Eng. Technol. 2014, 33, 28–32. [Google Scholar]



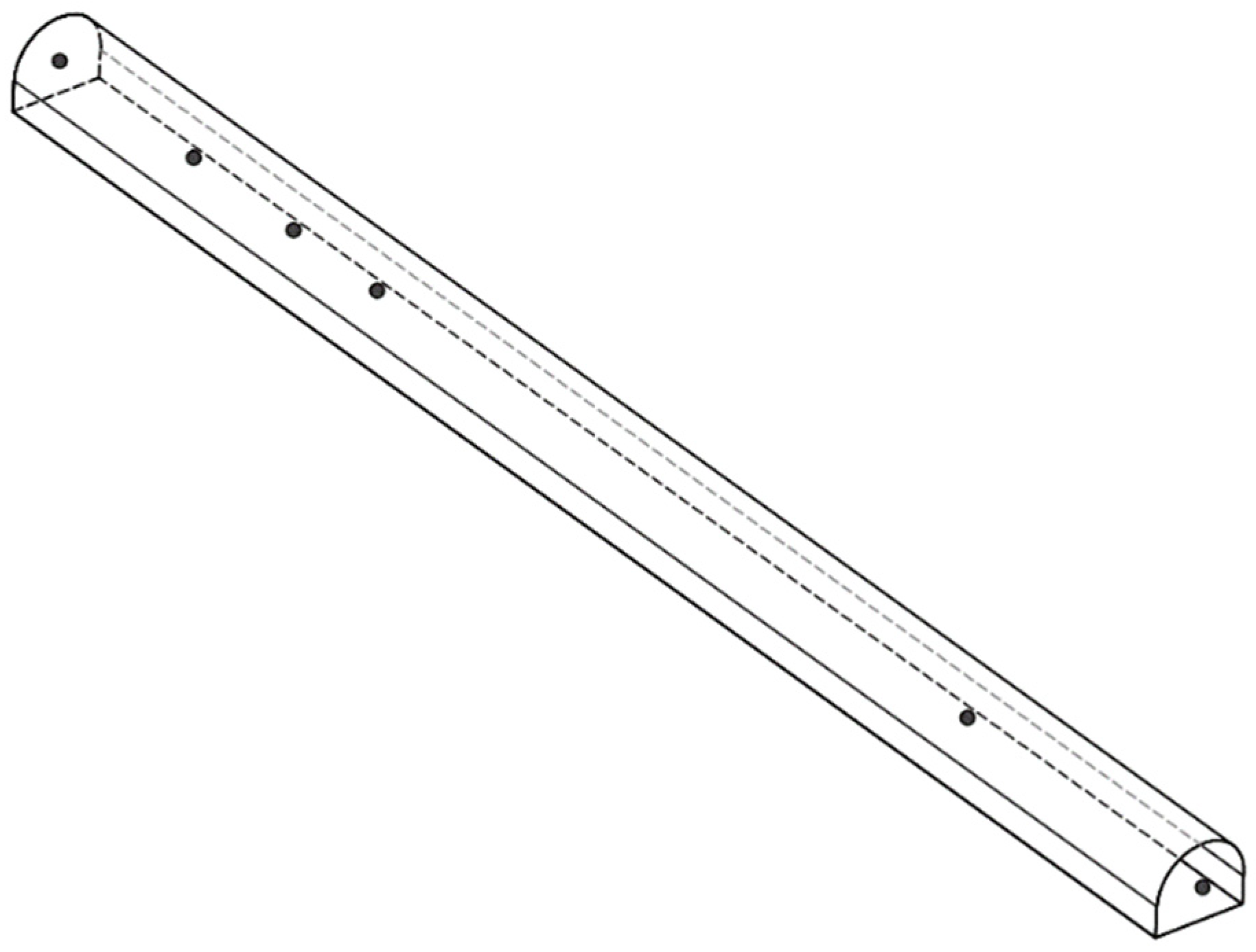

| Parameters | Value |
|---|---|
| Entrance | Wall |
| Exit pressure P (Pa) | 101,325 |
| Wall roughness height L (m) | 0 |
| Initial temperature T (°C) | 298 K |
| Volume fraction of CH4 in gas explosion zone p (%) | 9.5 |
| Volume fraction of O2 in gas explosion zone p (%) | 21 |
| Ignition energy E (j) | 0.1 |
| Ignition time t (ms) | 1 |
| Total duration t (ms) | 500 |
| Types | Gas Accumulation Length (m) | Peak Overpressure (MPa) | Location of Peak Overpressure (m) | Detonation Velocity (m/s) |
|---|---|---|---|---|
| Experiment | 5 | 0.49 | 9.8 | 302 |
| Simulation | 5 | 0.452 | 10.1 | 329 |
| Error rate% | 7.8 | 3.1 | 8.9 |
| Position | Pressure Extremes (MPa) |
|---|---|
| Closed end | 0.681 |
| Pressure overlap zone by explosion sources 1 and 2 | 0.581 |
| Center of the explosion from explosion source 2 | 0.449 |
| Center point of the tunnel | 0.426 |
| Middle of the rear half of the tunnel | 0.406 |
| Tunnel exit | 0.220 |
| Position | Pressure Extremes (MPa) | Note |
|---|---|---|
| Closed end | 0.681 | |
| Pressure overlap zone by explosion sources 1 and 2 | 0.649 | |
| Center of the explosion from explosion source 2 (Secondly formed pressure overlap zone) | 0.606 | The pressure extremes in the secondly formed pressure overlap zone is 0.548, with a time interval of 0.018 s from the initial peak pressure. |
| Pressure overlap zone by explosion sources 2 and 3 | 0.559 | |
| Middle of the rear half of the tunnel | 0.418 | |
| Tunnel exit | 0.233 |
| Interval (m) | Overpressure in the Pressure Overlap Zone (MPa) | Meeting Position | Meeting Time (ms) | Velocity (m/s) |
|---|---|---|---|---|
| 5 | 0.5836 | Middle of the explosion source interval zone | 7 | 169 |
| 10 | 0.7077 | Middle of the explosion source interval zone | 15 | 325 |
| 15 | 0.7137 | Middle of the explosion source interval zone | 18 | 337 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Ye, Q.; Jia, Z. Analysis of the Impact of Multiple Explosion Source Layouts on the Kinetic Characteristics of Gas Explosions in Blind Roadways. Processes 2024, 12, 1980. https://doi.org/10.3390/pr12091980
Wang W, Ye Q, Jia Z. Analysis of the Impact of Multiple Explosion Source Layouts on the Kinetic Characteristics of Gas Explosions in Blind Roadways. Processes. 2024; 12(9):1980. https://doi.org/10.3390/pr12091980
Chicago/Turabian StyleWang, Weijian, Qing Ye, and Zhenzhen Jia. 2024. "Analysis of the Impact of Multiple Explosion Source Layouts on the Kinetic Characteristics of Gas Explosions in Blind Roadways" Processes 12, no. 9: 1980. https://doi.org/10.3390/pr12091980
APA StyleWang, W., Ye, Q., & Jia, Z. (2024). Analysis of the Impact of Multiple Explosion Source Layouts on the Kinetic Characteristics of Gas Explosions in Blind Roadways. Processes, 12(9), 1980. https://doi.org/10.3390/pr12091980





