The Influence of Pre-Lift Gate Opening on the Internal and External Flow Characteristics During the Startup Process of an Axial Flow Pump
Abstract
1. Introduction
2. Model and Methods
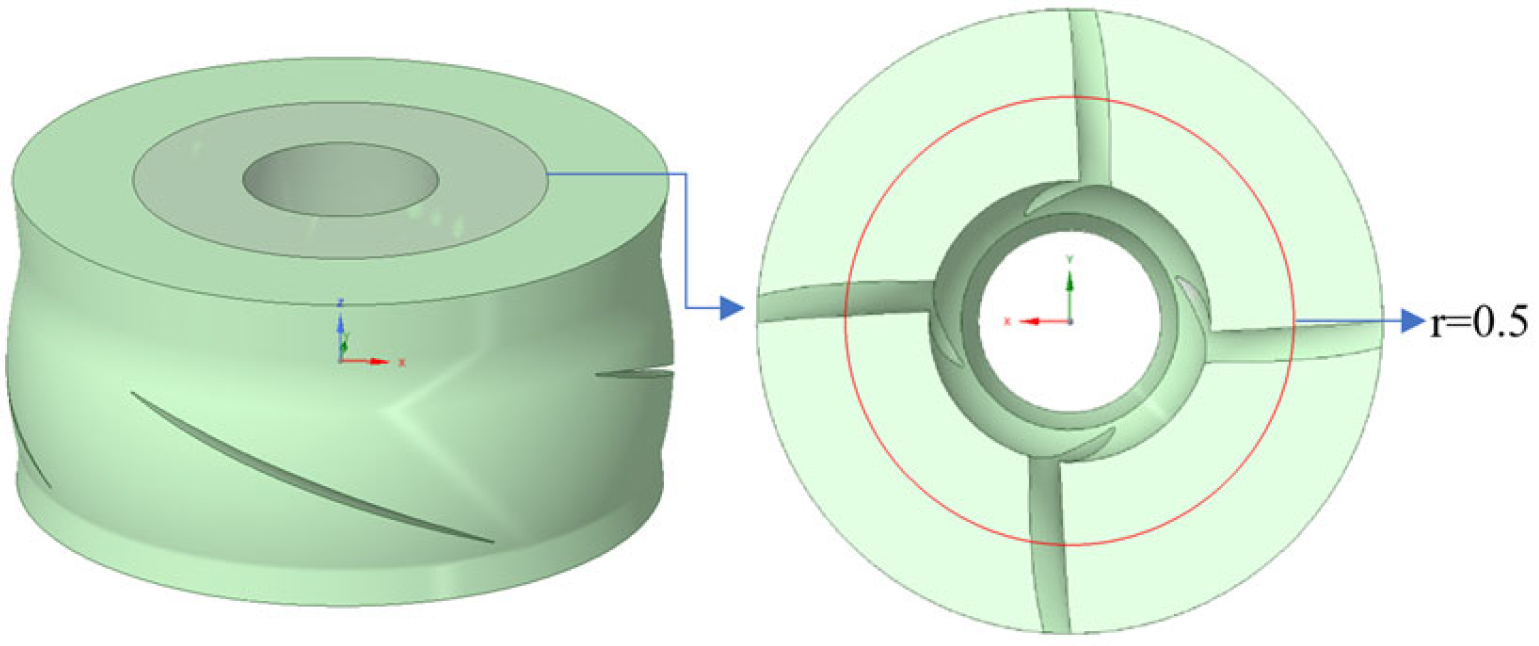
2.1. Model Parameters
2.2. Numerical Computation Methods and Boundary Conditions
2.2.1. Numerical Computation Methods
2.2.2. Boundary Conditions
2.3. Mesh Generation
3. Numerical Computation and Results Analysis
3.1. Experimental Validation
3.2. Effect of the Gate Pre-Opening Angle on Performance
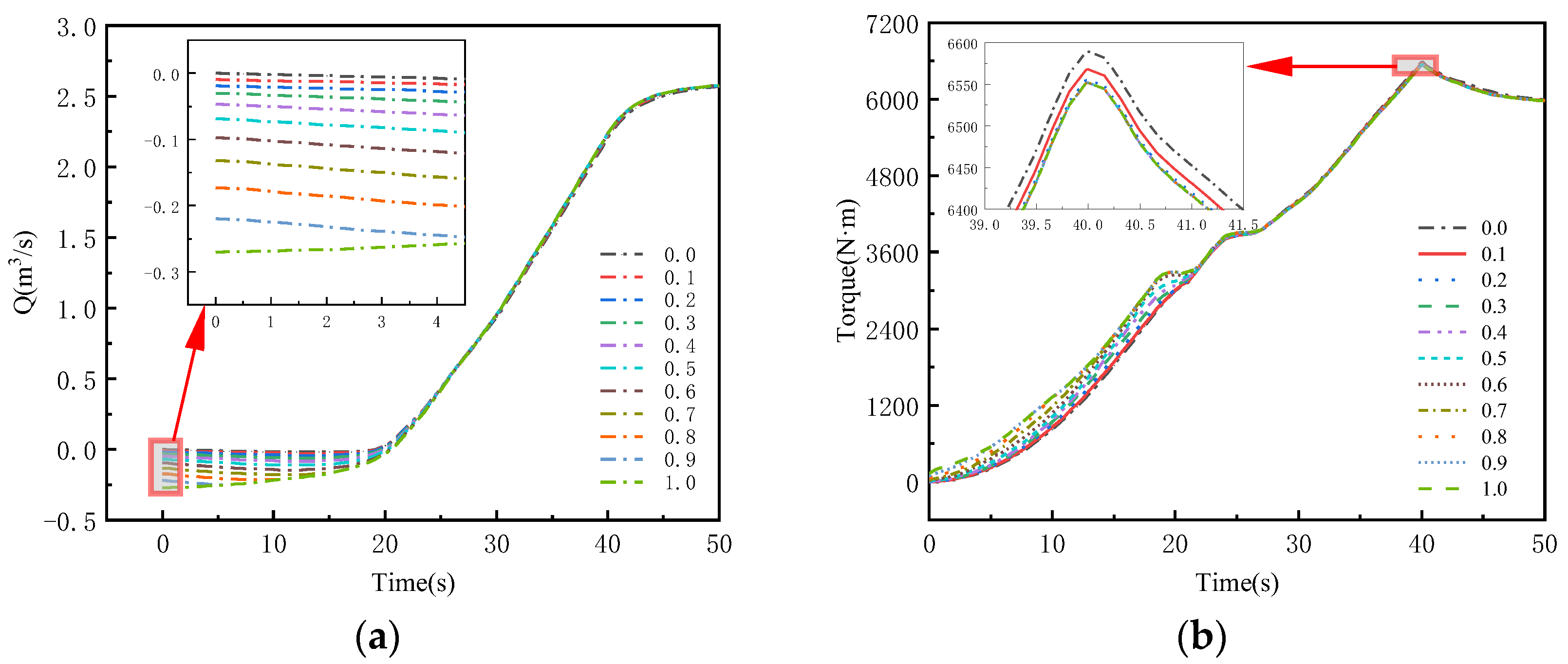
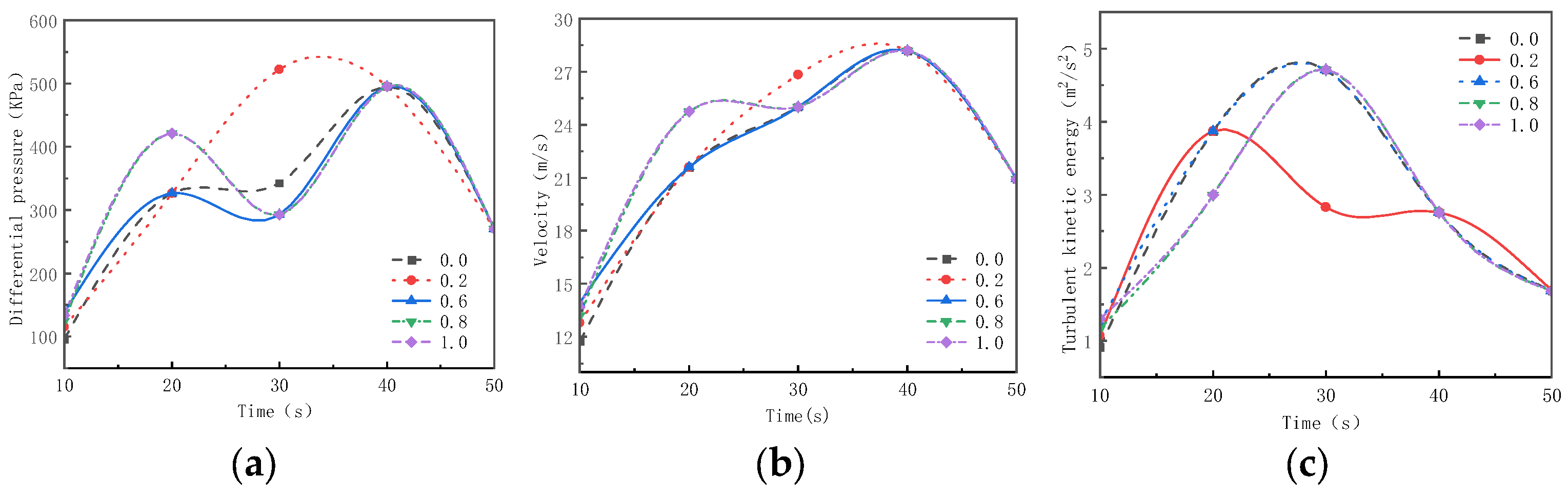
3.2.1. Flow Rate, Torque Calculation, and Analysis
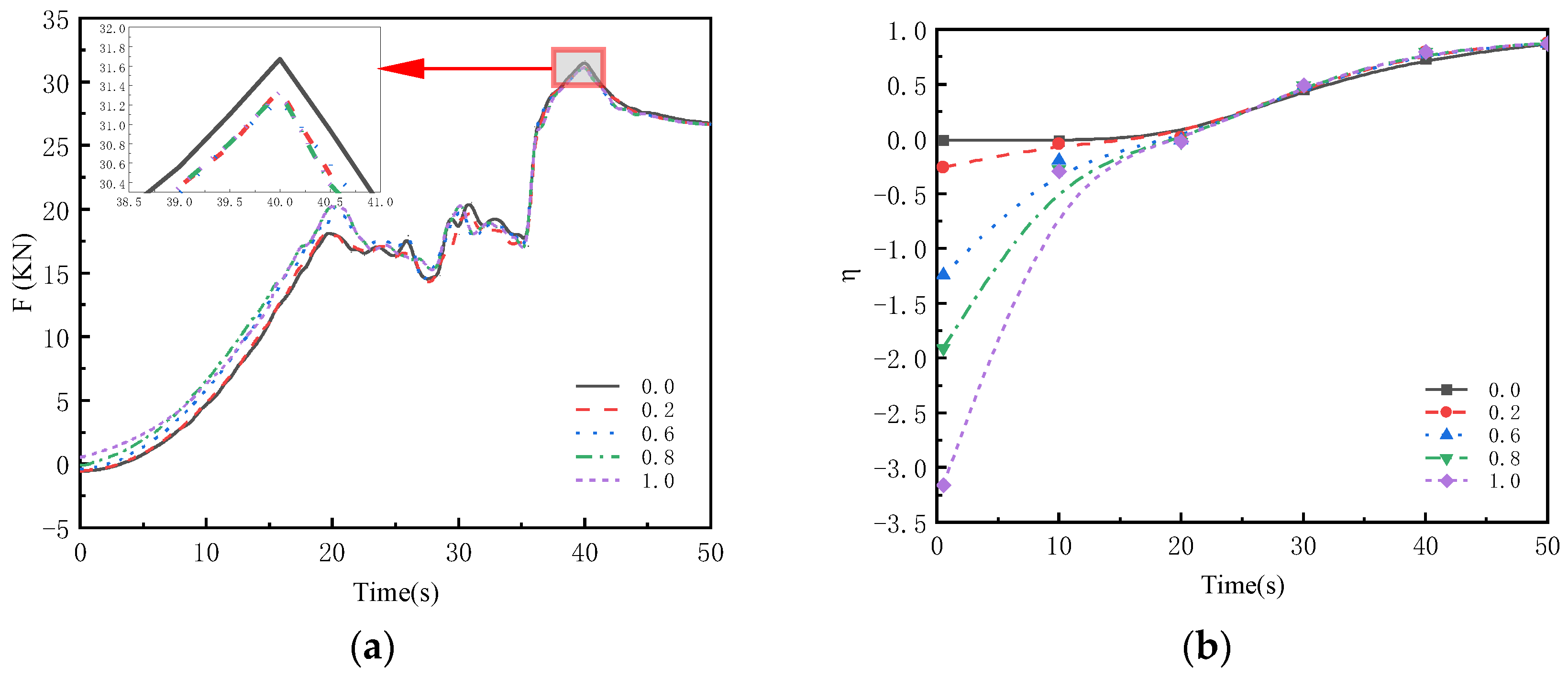
3.2.2. Axial Force, Efficiency Calculation, and Analysis
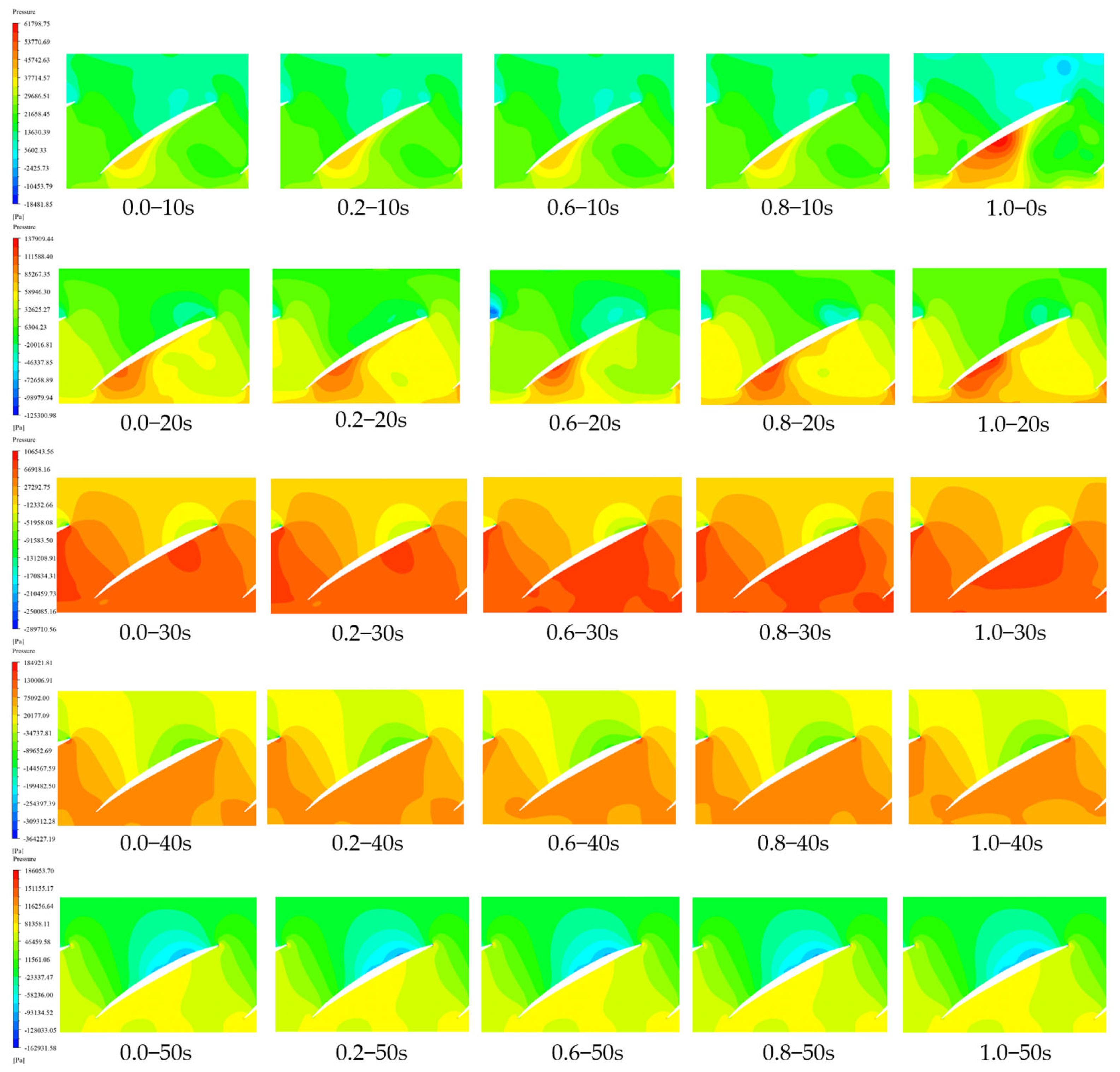
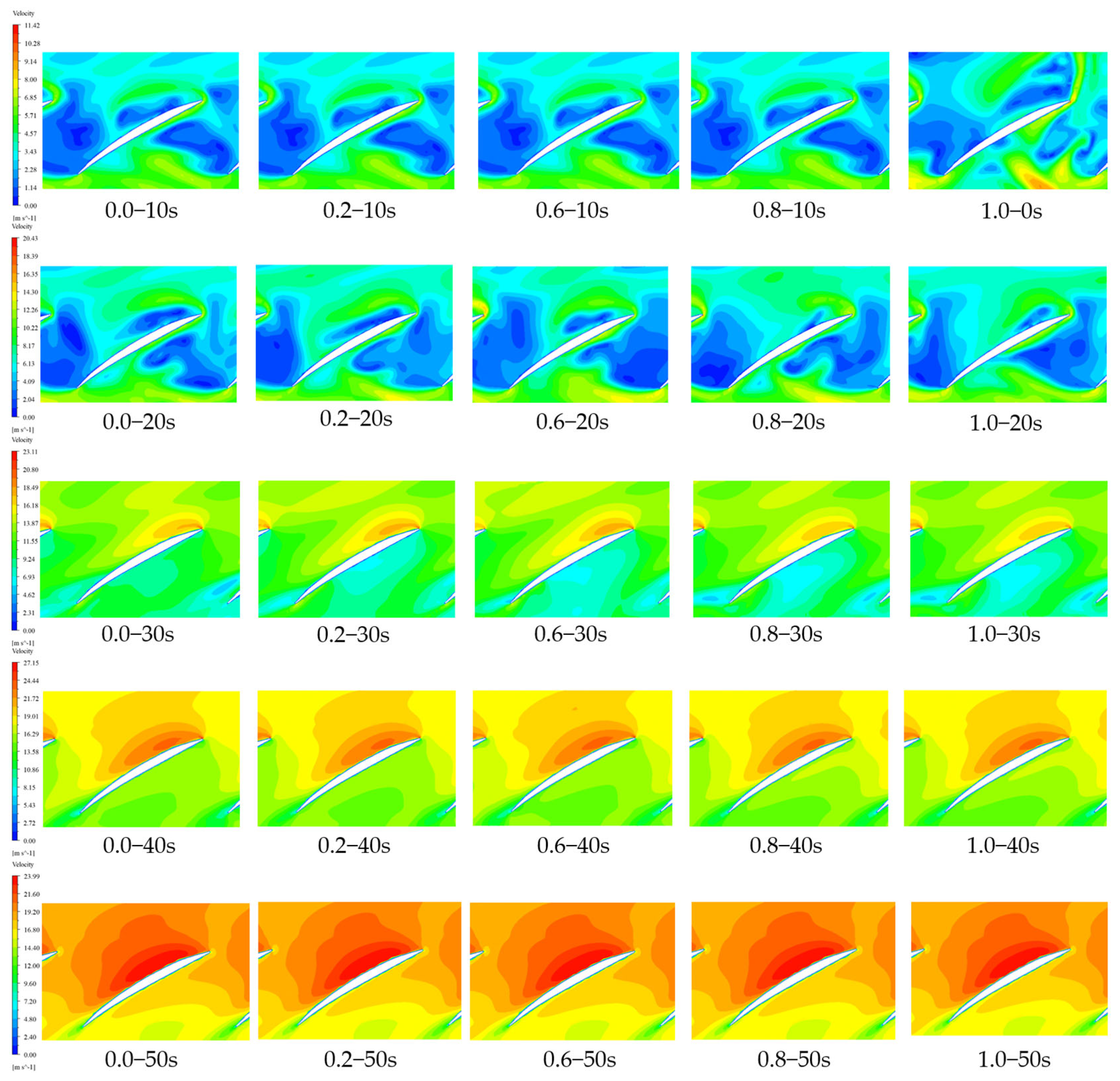
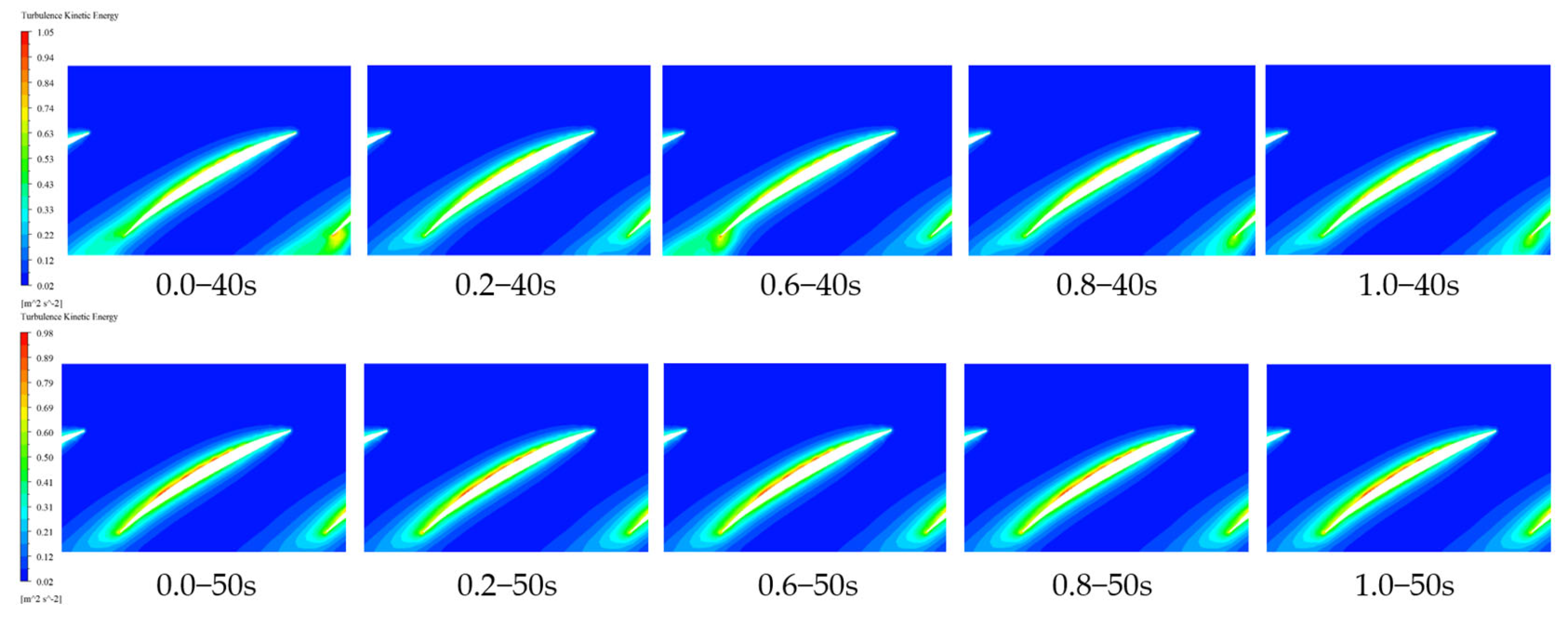
3.2.3. Internal Flow Field Calculation and Analysis
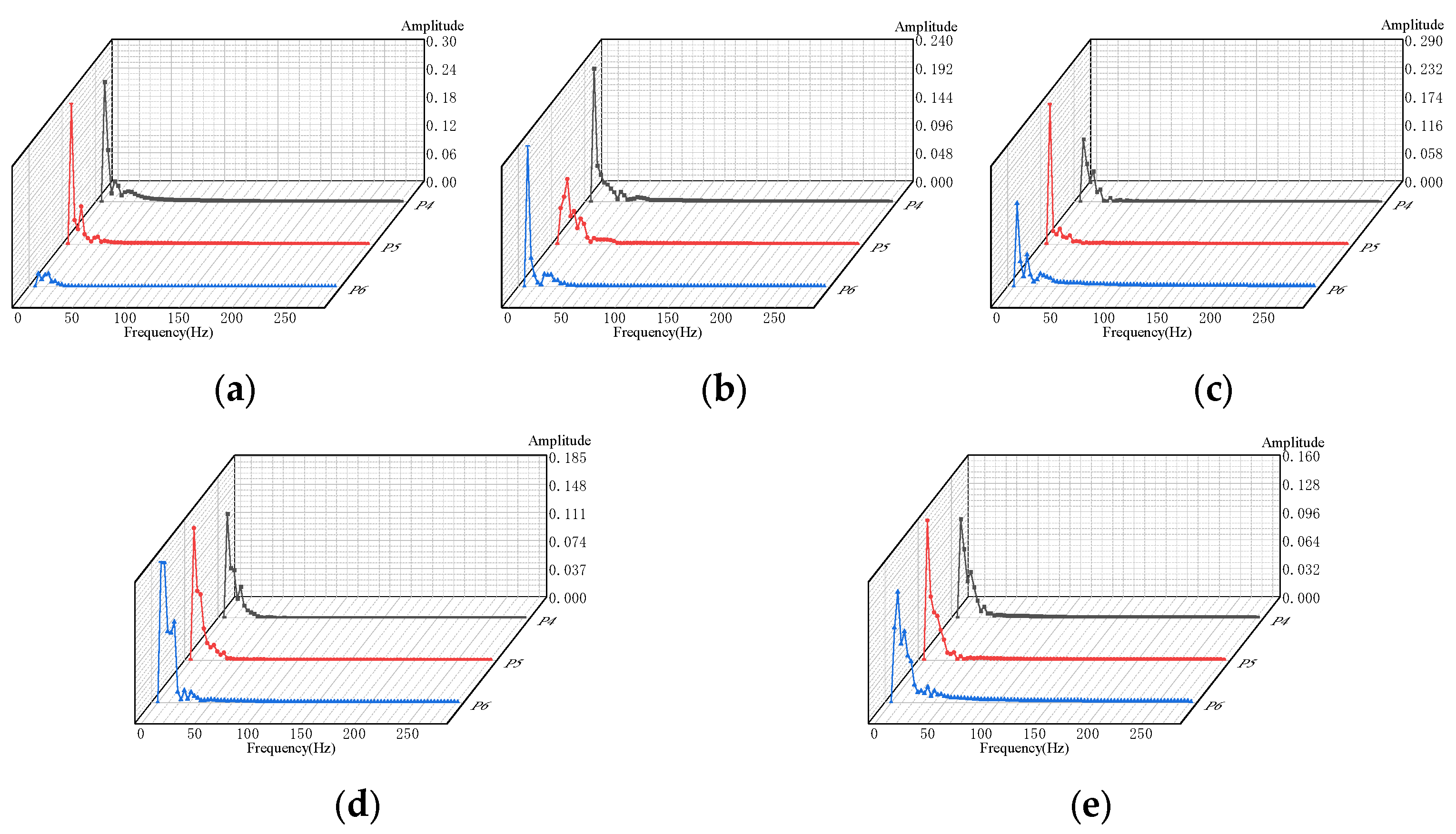
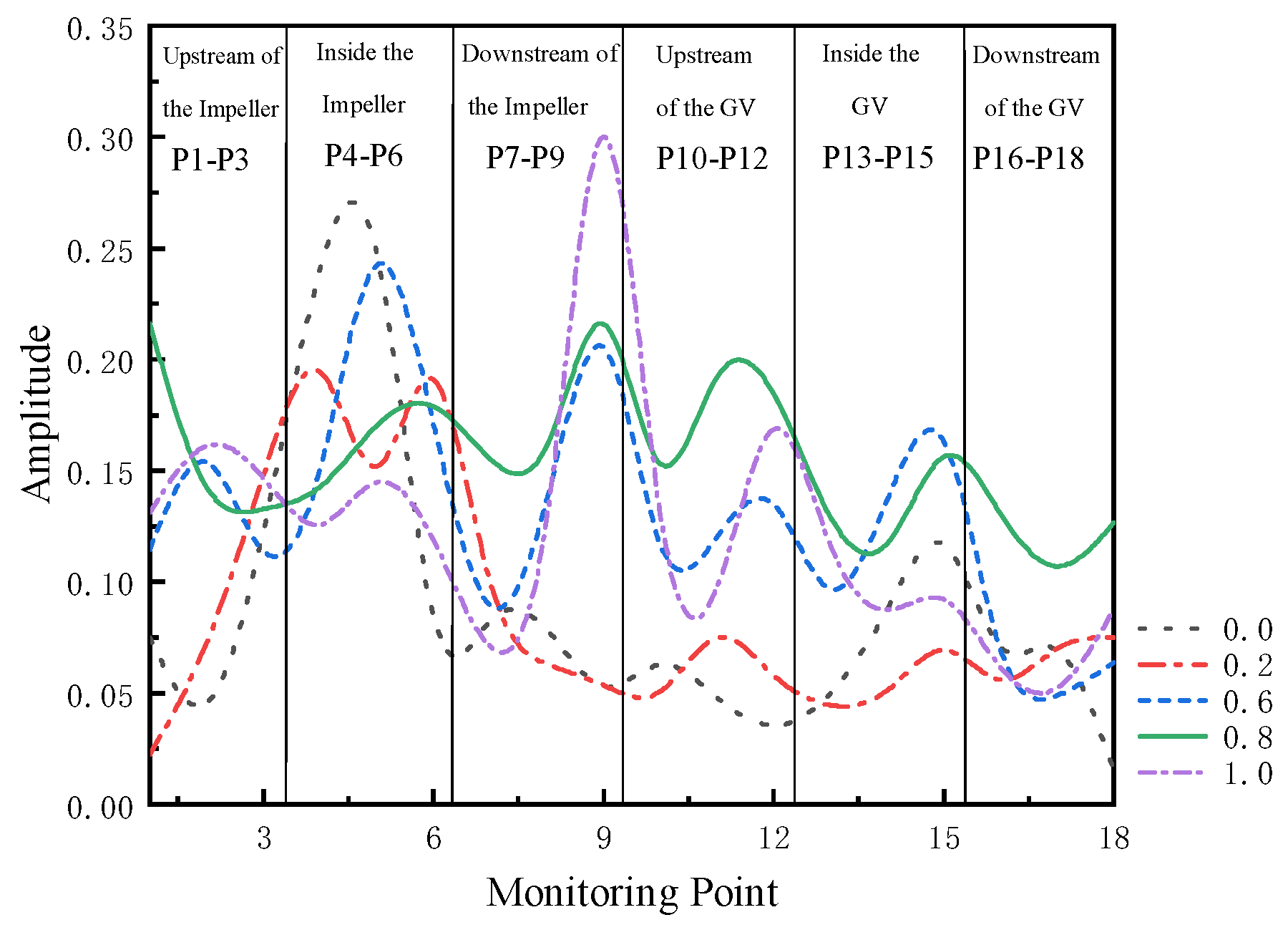
3.3. Analysis of the Effect of Gate Pre-Lift on Pressure Fluctuation Characteristics
4. Conclusions
- (1)
- During the startup of the axial flow pump at different gate pre-opening degrees, backflow persists for the first 20 s, and the backflow rate within the pump increases with the gate pre-opening degree. When the gate pre-opening degree is 0.6, it is 5.89% of the pump’s rated flow rate. When the valve is fully open and the pump is restarted, the maximum backflow rate reaches 10.98% of the rated flow rate. This results in poor fluid stability within the pump, and the efficiency changes negatively due to the influence of the backflow rate.
- (2)
- At the moment the axial flow pump reaches its rated speed during startup, the axial force peaks. However, the gate pre-opening degree has little impact on the axial force during startup, as the curves of axial force versus time are almost identical.
- (3)
- During the pump startup process, when starting with a gate pre-opening degree of 0.6, the internal pressure difference of the pump is minimized. Within the first 20 s of startup, the internal pressure difference in the impeller is greatest with gate pre-opening degrees of 0.8 and 1.0, which is 28.96% higher than at 0.6. The flow velocity is also 14.62% higher compared to that of the 0.6 degree opening. Therefore, the internal flow conditions of the pump are relatively better when starting with a gate pre-opening degree of 0.6 compared to other degrees.
- (4)
- During the pump startup process, with gate pre-opening degrees of 0.8 and 1.0, the initial pressure fluctuation amplitude within the pump is minimal. The relative amplitudes are only 0.621 and 0.525, respectively, which are 41.00% and 28.51% lower than the maximum amplitudes corresponding to 0 and 0.2 degrees. In summary, the peak pressure inside the pump is minimized when the valve pre-opening degree is around 0.8, while the pressure difference and flow velocity are relatively lower at a pre-opening degree of 0.6. It is recommended to start the pump with a valve pre-opening degree of around 0.6 to 0.8.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meng, F.; Qin, Z.J.; Li, Y.J.; Chen, J. Investigation of Transient Characteristics of a Vertical Axial-Flow Pump with Non-Uniform Suction Flow. Machines 2022, 10, 855. [Google Scholar] [CrossRef]
- Jing, R.; He, X.J. Overview of axial flow pump and its application. Gen. Mach. 2014, 147, 86–89. [Google Scholar]
- Fu, S.F.; Zheng, Y.; Kan, K.; Chen, H.X.; Han, X.X.; Liang, X.L.; Liu, H.W.; Tian, X.Q. Numerical simulation and experimental study of transient characteristics in an axial flow pump during start-up. Renew. Energy 2020, 146, 1879–1887. [Google Scholar] [CrossRef]
- Hu, C.Y.; Zhang, X.W.; Tang, F.P.; Xv, X.D.; Huang, C.B.; Jin, L. Influence of Overflow Orifice Diameter on the Transient Process of Axial Flow Pump System. J. Trans. Chin. Soc. Agric. Mach. 2023, 54, 181–191. [Google Scholar]
- Liu, Y.F.; Zhou, D.Q.; Zheng, Y.; Zhang, H.S.; Xu, J.Y. Numerical simulation of starting process of axial flow pump with quick-stop gate. J. South North Water Divers. Water Sci. Technol. 2017, 15, 167–172. [Google Scholar]
- Zhang, L.J.; Wang, S.; Yin, G.J.; Guan, C.N. Fluid–structure interaction analysis of fluid pressure pulsation and structural vibration features in a vertical axial pump. Adv. Mech. Eng. 2019, 11, 168781401982858. [Google Scholar] [CrossRef]
- Guo, Y.L.; Yang, C.X.; Wang, Y.; Lv, T.Z.; Zhao, S. Study on Inlet Flow Field Structure and End-Wall Effect of Axial Flow Pump Impeller under Design Condition. Energies 2022, 15, 4969. [Google Scholar] [CrossRef]
- Zhang, X.W.; Tang, F.P.; Liu, C.; Shi, L.J.; Liu, H.Y.; Sun, Z.Z.; Hu, W.Z. Numerical Simulation of Transient Characteristics of Start-Up Transition Process of Large Vertical Siphon Axial Flow Pump Station. Front. Energy Res. 2021, 9, 706975. [Google Scholar] [CrossRef]
- Song, Y.C. Research on Flow Mechanism of Transition Process of Pumped Storage Unit Based on Three-Dimensional Coupling. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2022. [Google Scholar]
- Liu, Y.Z. Three-Dimensional Coupling Simulation Analysis of Multi-Cylinder Diesel Engine Intake and Exhaust System. Master’s Thesis, Harbin Engineering University, Harbin, China, 2020. [Google Scholar]
- Fu, X.L.; Li, D.Y.; Wang, H.J.; Li, Z.G.; Zhao, Q.; Wei, X.Z. One- and three-dimensional coupling flow simulations of pumped-storage power stations with complex long-distance water conveyance pipeline system. J. Clean. Prod. 2021, 315, 128–228. [Google Scholar] [CrossRef]
- Wang, S. Flow Field Analysis and Performance Optimization of Airflow Transmission Pipeline of Five-Stroke Engine. Master’s Thesis, Chongqing University of Technology, Chongqing, China, 2023. [Google Scholar]
- Liu, D.M.; Zhang, X.X.; Yang, Z.Y.; Liu, K.; Cheng, Y.G. Evaluating the pressure fluctuations during load rejection of two pump-turbines in a prototype pumped-storage system by using 1D-3D coupled simulation. Renew. Energy 2021, 171, 1276–1289. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Z.R.; Yang, Z.Y.; Zhang, X.X.; Tai, R.; Cheng, Y.G. Evolution and influence of pump-turbine cavitation during load rejection transients of a pumped-storage plant. J. Hydraul. Res. 2022, 60, 527–542. [Google Scholar] [CrossRef]
- Lv, J.W.; Fu, X.L.; Li, D.Y.; Wang, H.J.; Wei, X.Z. Instability mechanism of pump power-trip of ultra-high head pump turbines. J. Hydroelectr. Eng. 2023, 11, 11–20. [Google Scholar]
- Tang, M.J.; Cheng, Y.G.; Liu, D.M.; Chen, H.; Liu, K. FSI simulation of a high-head pump-turbine during load rejection process. J. Phys. Conf. Ser. 2024, 2752, 012198. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, K.Y.; Zhang, Y.L.; Jia, X.Q. Effect on Starting Modes on Centrifugal Pump Performance. Processes 2022, 10, 2362. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Y.; Song, X.; Tang, F.; Dai, J.; Yang, F.; Wang, H.; Shi, L. Investigation on the Influence of Flap Valve Area on Transition Process of Large Axial Flow Pump System. J. Mar. Sci. Eng. 2023, 11, 326. [Google Scholar] [CrossRef]
- Zheng, F.C.; Zhang, X.P.; Chen, T.R.; Huang, B.; Xu, J.; Wang, G.Y. Strong transient characteristics in axial flow waterjet pump during rapid starting period with special emphasis on saddle zone. Ocean Eng. 2023, 269, 113506. [Google Scholar] [CrossRef]
- Xuan, Y.F.; Zhu, G.J.; Luo, X.Q.; Wang, Y.; Wang, L.K. Experimental Study on the Stability of Mixed-Flow Pump During Segmented Start-Up Process. Arab. J. Sci. Eng. 2024. prepublish. [Google Scholar] [CrossRef]
- Zhang, X. Study on Flow-Induced Vibration of Low-Specific-Speed Centrifugal Pump Based on Fluid-Structure Interaction. Master’s Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2016. [Google Scholar]
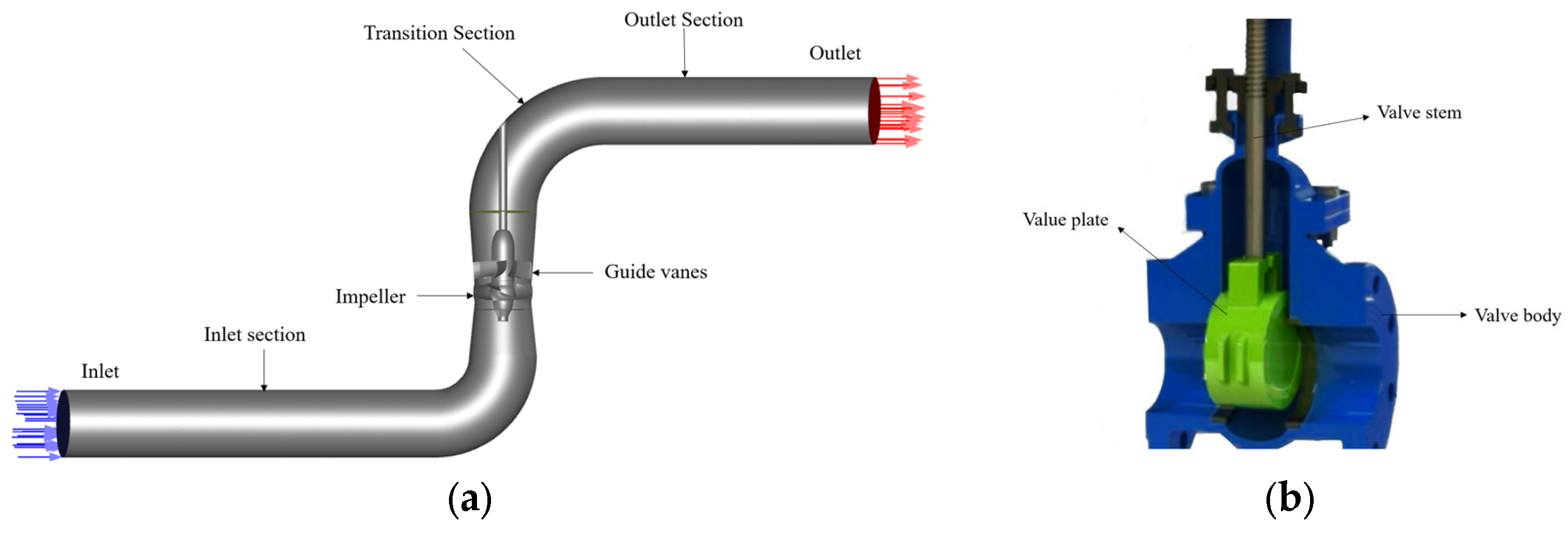
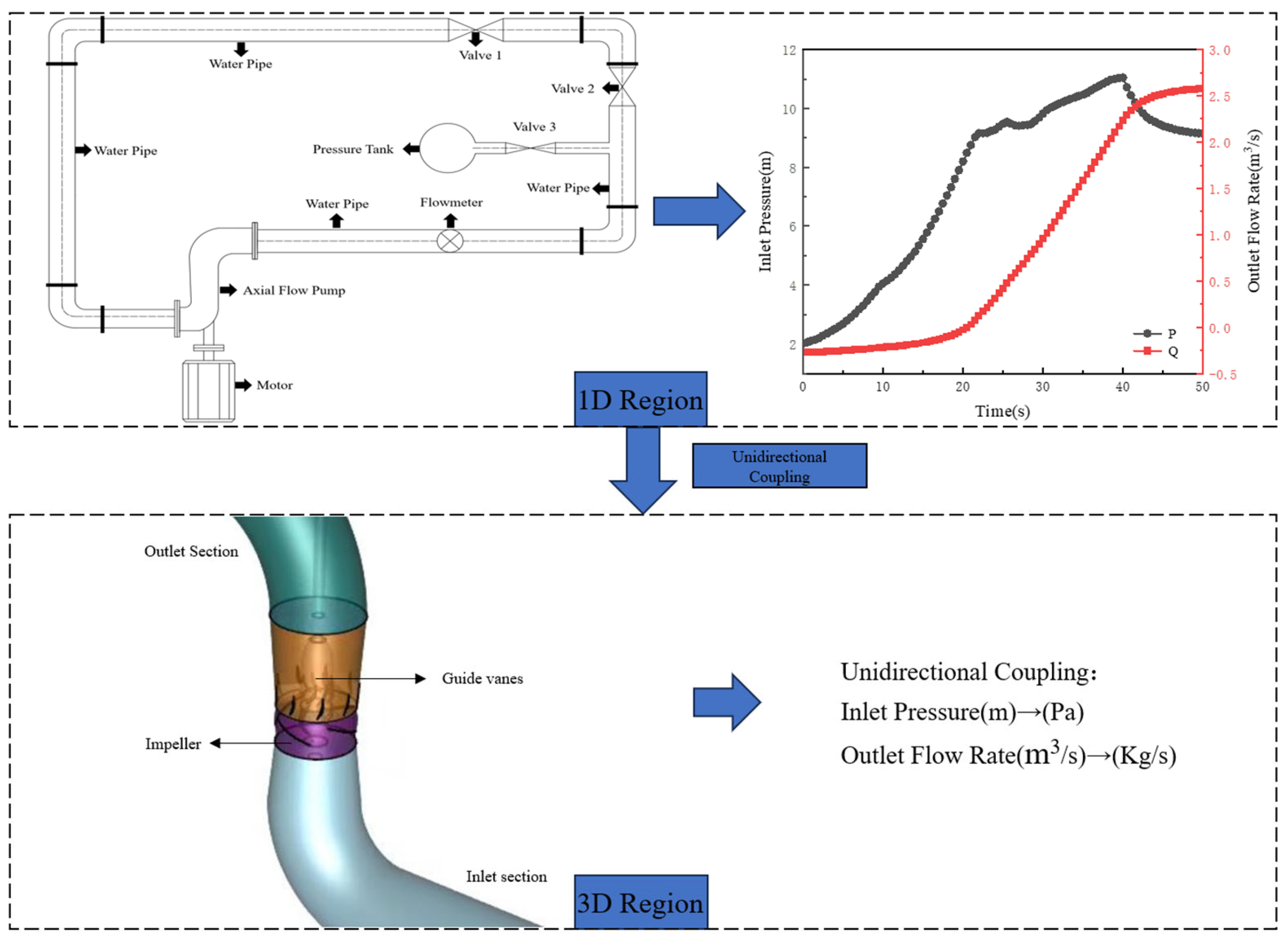
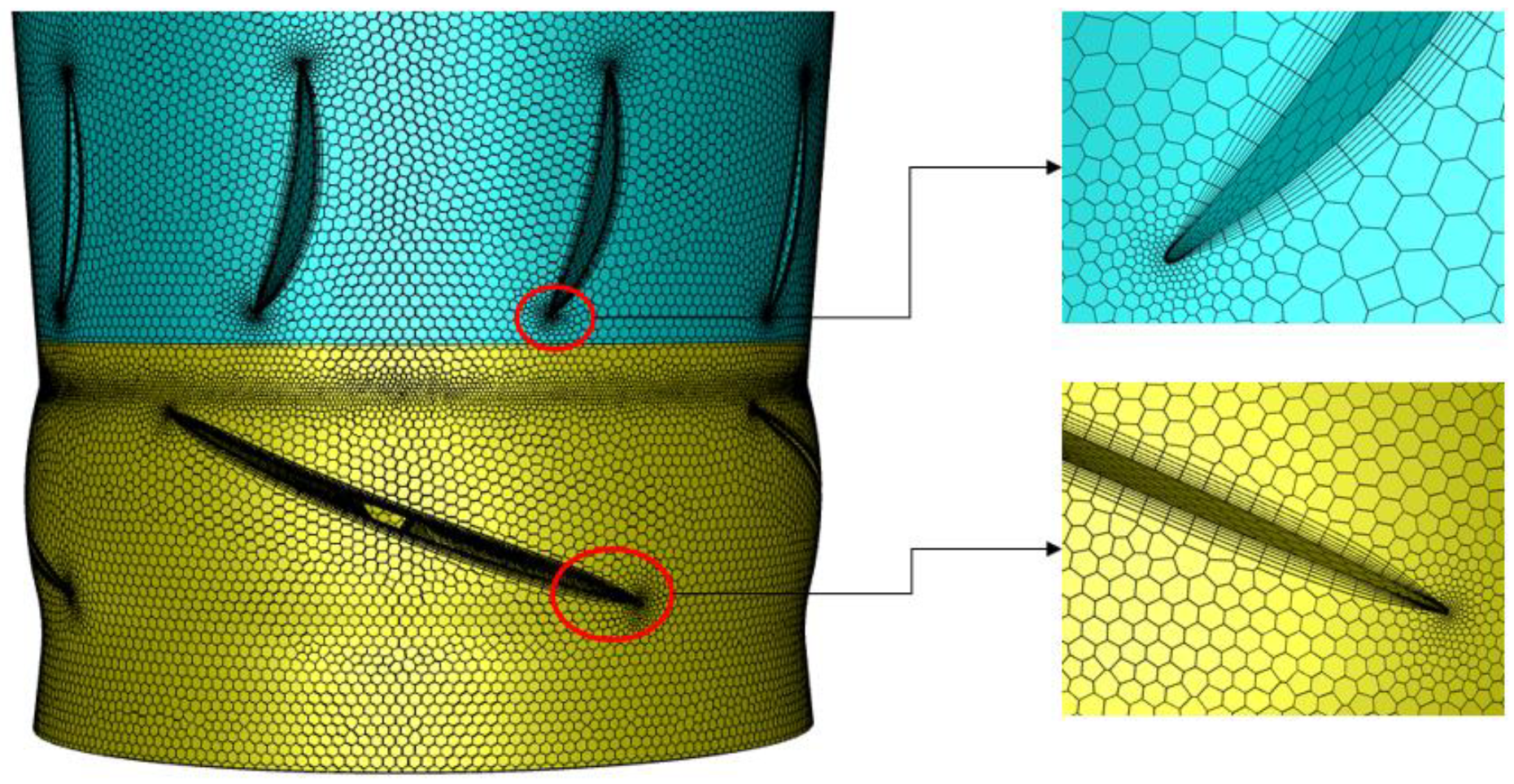
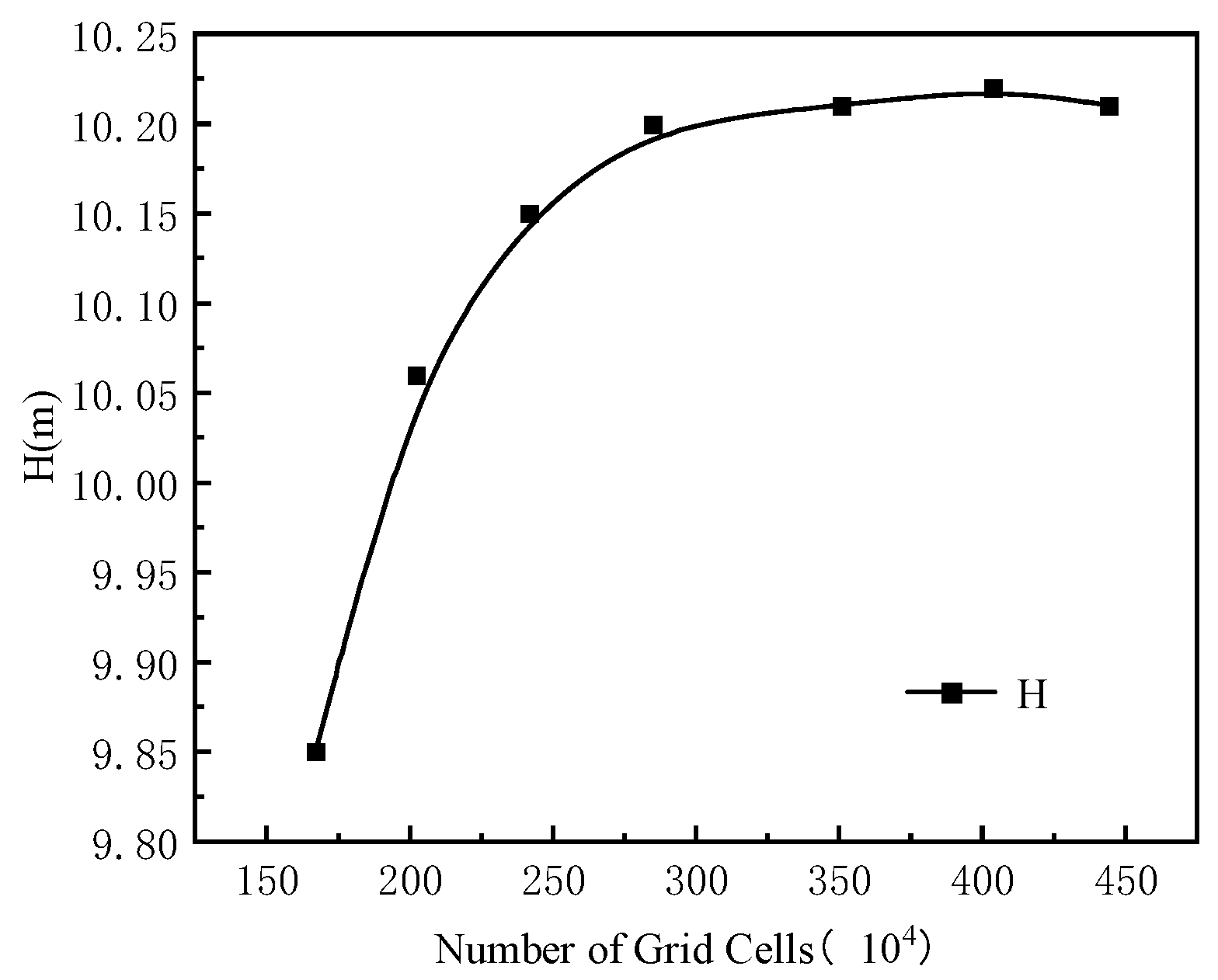




| Parameters Name | Symbols | Values |
|---|---|---|
| Impeller Outer Diameter | D2 (mm) | 350 |
| Number of Impeller Blades | Zimp | 4 |
| Number of GV Blades | Zgui | 9 |
| Rotating Speed | n (rpm) | 750 |
| Flow Rate | Q (m3/s) | 2.46 |
| Head | H (m) | 10.2 |
| Opening Degree | 0 | 0.2 | 0.6 | 0.8 | 1.0 | |
|---|---|---|---|---|---|---|
| Time | ||||||
| 10 s | −0.5795 | −0.5753 | −0.4336 | −0.3787 | −0.3811 | |
| 20 s | 0.1372 | 0.2442 | 0.2049 | 0.3731 | 0.3811 | |
| 30 s | 0.0497 | 0.0427 | 0.0670 | 0.0515 | 0.0515 | |
| 40 s | 0.8520 | 0.7934 | 0.8378 | 0.7590 | 0.7590 | |
| 50 s | 0.8652 | 0.8635 | 0.8638 | 0.8633 | 0.8633 | |
| Opening Degree | 0 | 0.2 | 0.6 | 0.8 | 1.0 | |
|---|---|---|---|---|---|---|
| Time | ||||||
| 10 s | −0.8714 | −0.9010 | −0.9094 | −0.8478 | −0.8149 | |
| 20 s | −0.2991 | −0.1980 | 0.2549 | 0.0910 | −0.2069 | |
| 30 s | 1.6998 | 1.9014 | 1.7051 | 1.8653 | 1.8653 | |
| 40 s | 2.6343 | 2.5752 | 2.6477 | 2.5894 | 2.5894 | |
| 50 s | 0.6822 | 0.6407 | 0.6523 | 0.6317 | 0.6317 | |
| Opening Degree | 0 | 0.2 | 0.6 | 0.8 | 1.0 | |
|---|---|---|---|---|---|---|
| Time | ||||||
| 10 s | 0.2343 | 0.3647 | 0.4574 | 0.5742 | 0.6624 | |
| 20 s | 0.1536 | 0.1941 | 0.4866 | 0.3450 | 0.3539 | |
| 30 s | 0.1210 | 0.0935 | 0.0914 | 0.0715 | 0.0715 | |
| 40 s | −0.0122 | −0.0251 | −0.0137 | −0.0257 | −0.0257 | |
| 50 s | −0.1270 | −0.1270 | −0.1268 | −0.1271 | −0.1271 | |
| Opening Degree | 0 | 0.2 | 0.6 | 0.8 | 1.0 | |
|---|---|---|---|---|---|---|
| Time | ||||||
| 10 s | 0.4252 | 0.4300 | 0.5413 | 0.6564 | 0.9470 | |
| 20 s | 1.7640 | 2.0214 | 1.7903 | 1.5897 | 1.6991 | |
| 30 s | 1.0212 | 1.0632 | 0.9904 | 1.0667 | 1.0667 | |
| 40 s | 0.8944 | 0.8916 | 1.0237 | 1.0464 | 1.0464 | |
| 50 s | 0.9792 | 0.9815 | 0.9803 | 0.9813 | 0.9813 | |
| Pre-Opening Degree | Monitoring Point | Fundamental Frequency | Amplitude | Relative Amplitude | Subharmonic Frequency | Amplitude | Relative Amplitude |
|---|---|---|---|---|---|---|---|
| 0.0 | P4 | 3.125 | 0.256 | 0.850 | 12.500 | 0.044 | 0.415 |
| P5 | 3.125 | 0.301 | 1.000 | 12.500 | 0.081 | 0.764 | |
| P6 | 3.125 | 0.028 | 0.093 | 12.500 | 0.027 | 0.255 | |
| 0.2 | P4 | 3.125 | 0.227 | 0.754 | 28.125 | 0.018 | 0.170 |
| P5 | 9.375 | 0.111 | 0.369 | 15.625 | 0.056 | 0.528 | |
| P6 | 3.125 | 0.240 | 0.797 | 18.750 | 0.021 | 0.198 | |
| 0.6 | P4 | 3.125 | 0.129 | 0.429 | 12.500 | 0.064 | 0.604 |
| P5 | 3.125 | 0.288 | 0.957 | 12.500 | 0.032 | 0.302 | |
| P6 | 3.125 | 0.171 | 0.568 | 12.500 | 0.065 | 0.613 | |
| 0.8 | P4 | 3.125 | 0.137 | 0.455 | 15.625 | 0.041 | 0.387 |
| P5 | 3.125 | 0.174 | 0.578 | 21.875 | 0.020 | 0.189 | |
| P6 | 3.125 | 0.187 | 0.621 | 15.625 | 0.106 | 1.000 | |
| 1.0 | P4 | 3.125 | 0.112 | 0.372 | 12.500 | 0.052 | 0.491 |
| P5 | 3.125 | 0.158 | 0.525 | 28.125 | 0.009 | 0.085 | |
| P6 | 6.250 | 0.125 | 0.415 | 12.500 | 0.081 | 0.764 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Deng, L. The Influence of Pre-Lift Gate Opening on the Internal and External Flow Characteristics During the Startup Process of an Axial Flow Pump. Processes 2024, 12, 1984. https://doi.org/10.3390/pr12091984
Fu Y, Deng L. The Influence of Pre-Lift Gate Opening on the Internal and External Flow Characteristics During the Startup Process of an Axial Flow Pump. Processes. 2024; 12(9):1984. https://doi.org/10.3390/pr12091984
Chicago/Turabian StyleFu, You, and Lingling Deng. 2024. "The Influence of Pre-Lift Gate Opening on the Internal and External Flow Characteristics During the Startup Process of an Axial Flow Pump" Processes 12, no. 9: 1984. https://doi.org/10.3390/pr12091984
APA StyleFu, Y., & Deng, L. (2024). The Influence of Pre-Lift Gate Opening on the Internal and External Flow Characteristics During the Startup Process of an Axial Flow Pump. Processes, 12(9), 1984. https://doi.org/10.3390/pr12091984






