Simulation and Local Parametric Sensitivity Analysis of a Computational Model of Fructose Metabolism
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Recommendations for Menu Planning
2.1.2. Mathematical Model of Hepatic Fructose Metabolism
2.2. Methods
2.2.1. Simulation of Mathematical Model of Hepatic Fructose Metabolism
2.2.2. Local Sensitivity Analysis of the Kinetic Parameters of the Mathematical Model of Hepatic Fructose Metabolism
3. Results and Discussion
3.1. Analysis of the Meal Plans
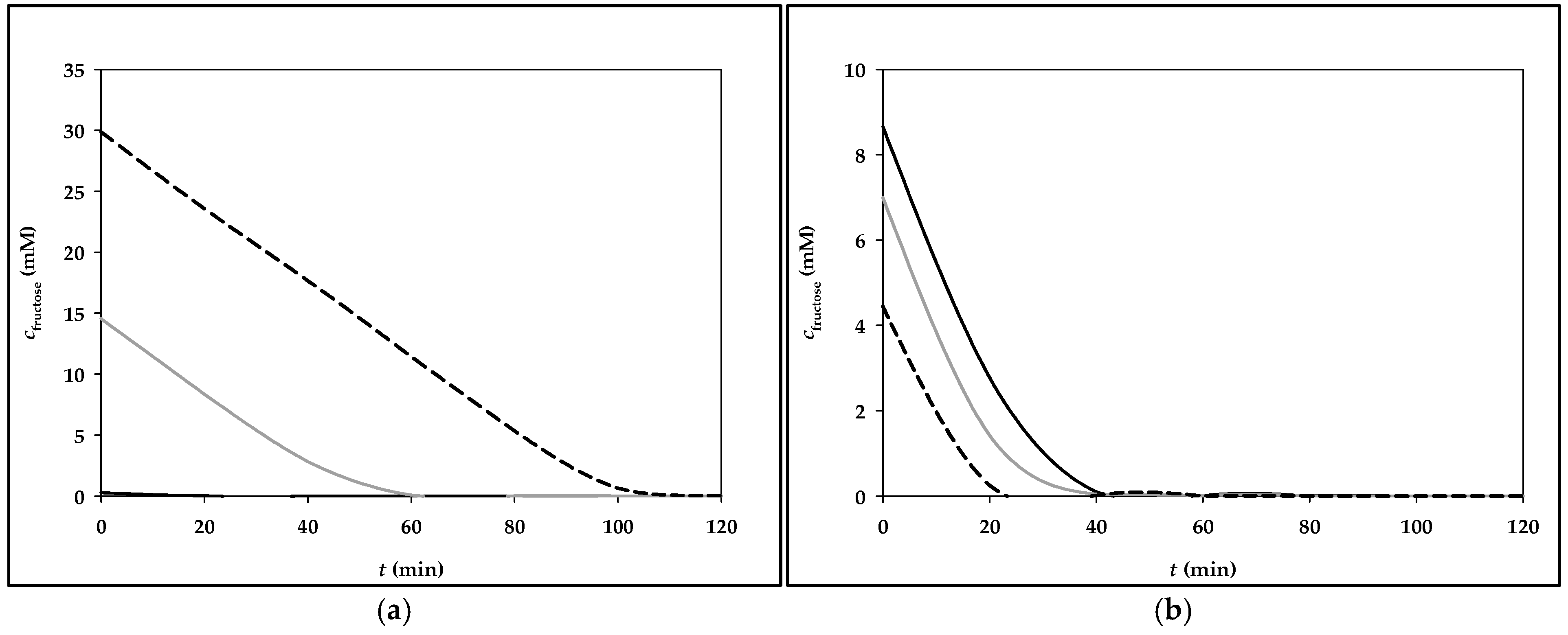
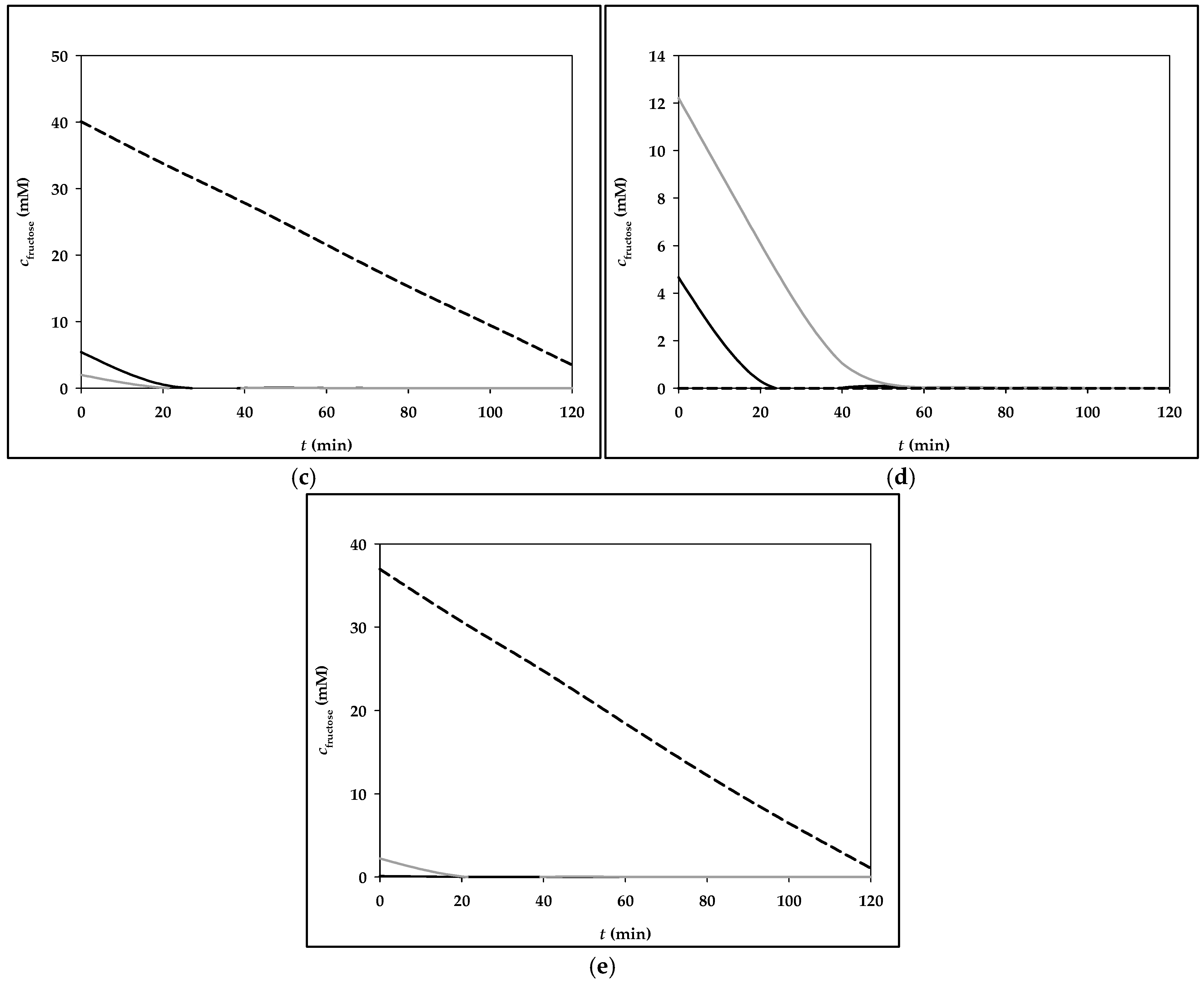
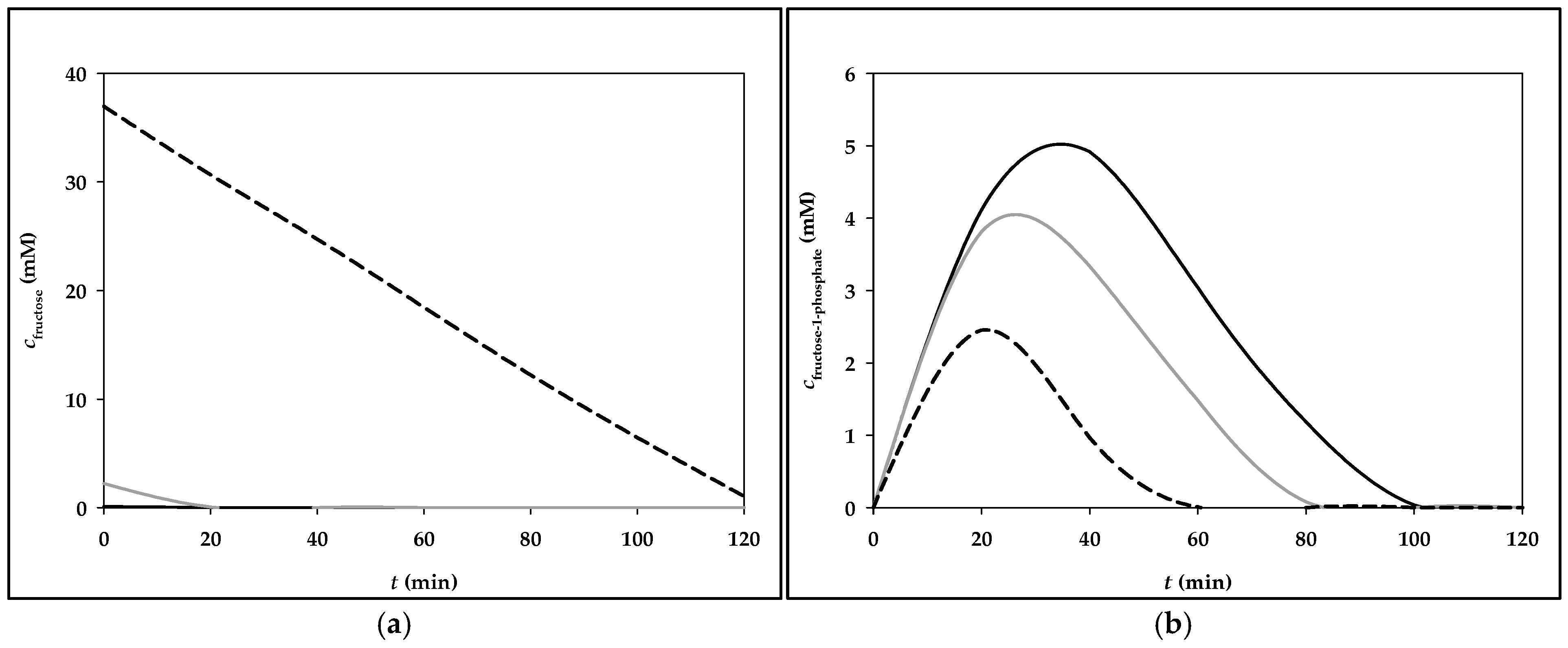
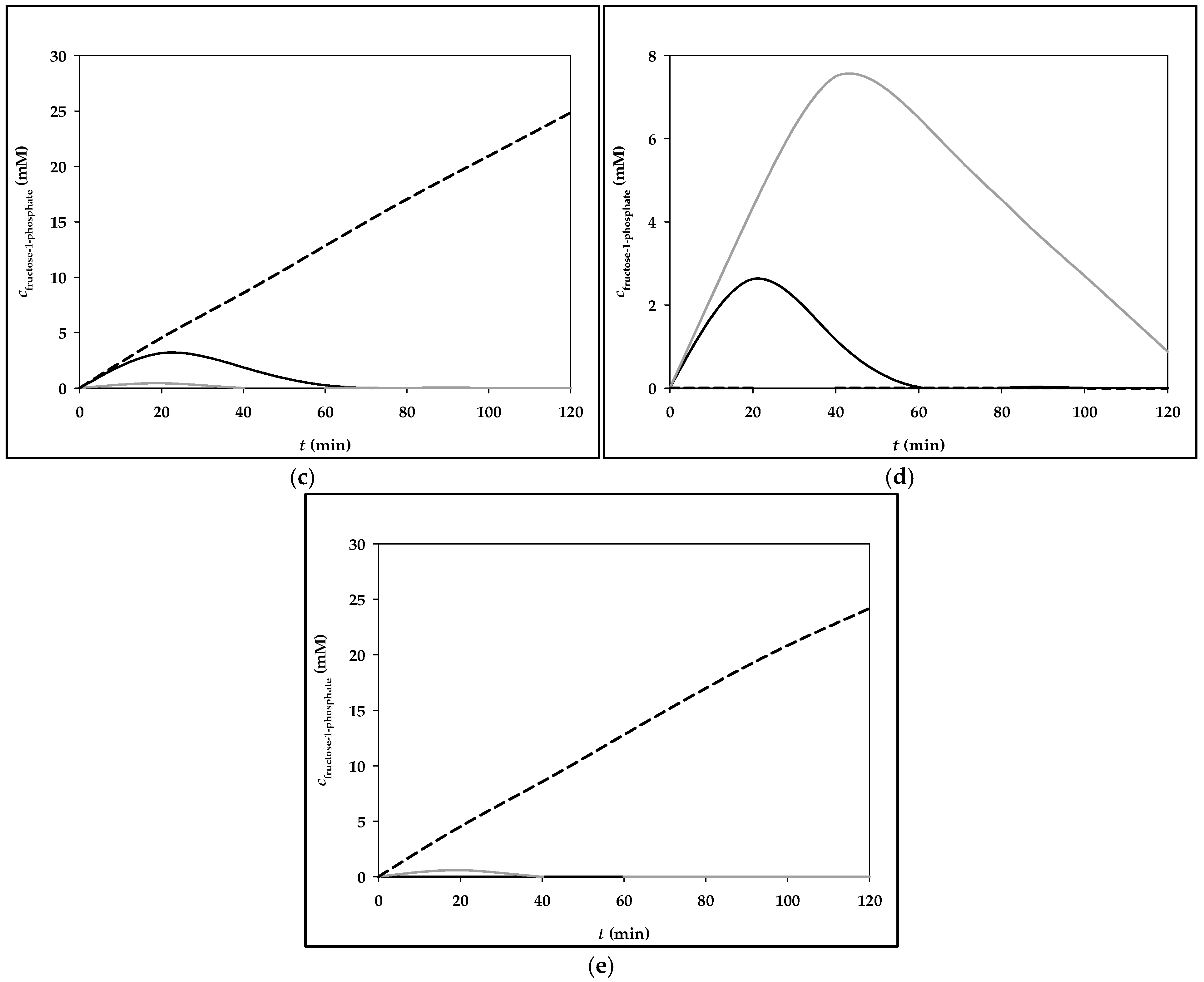
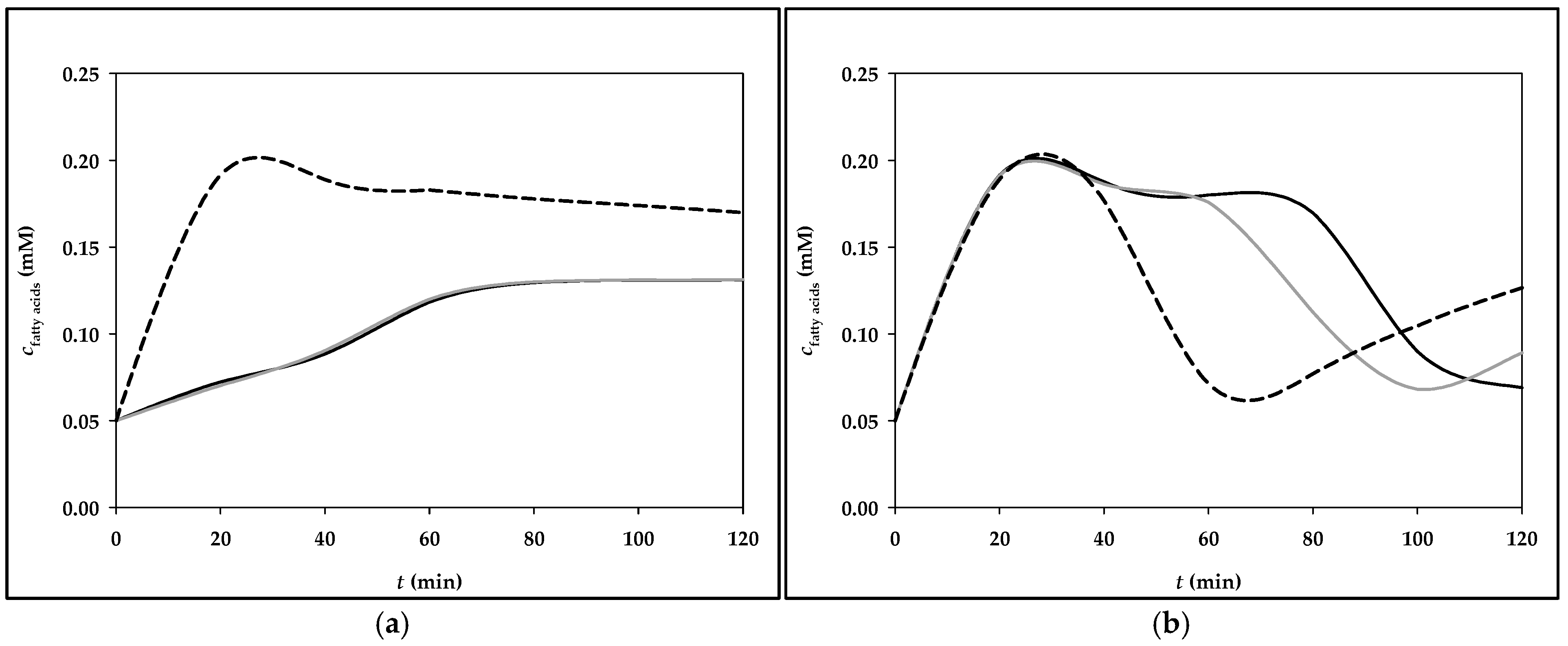
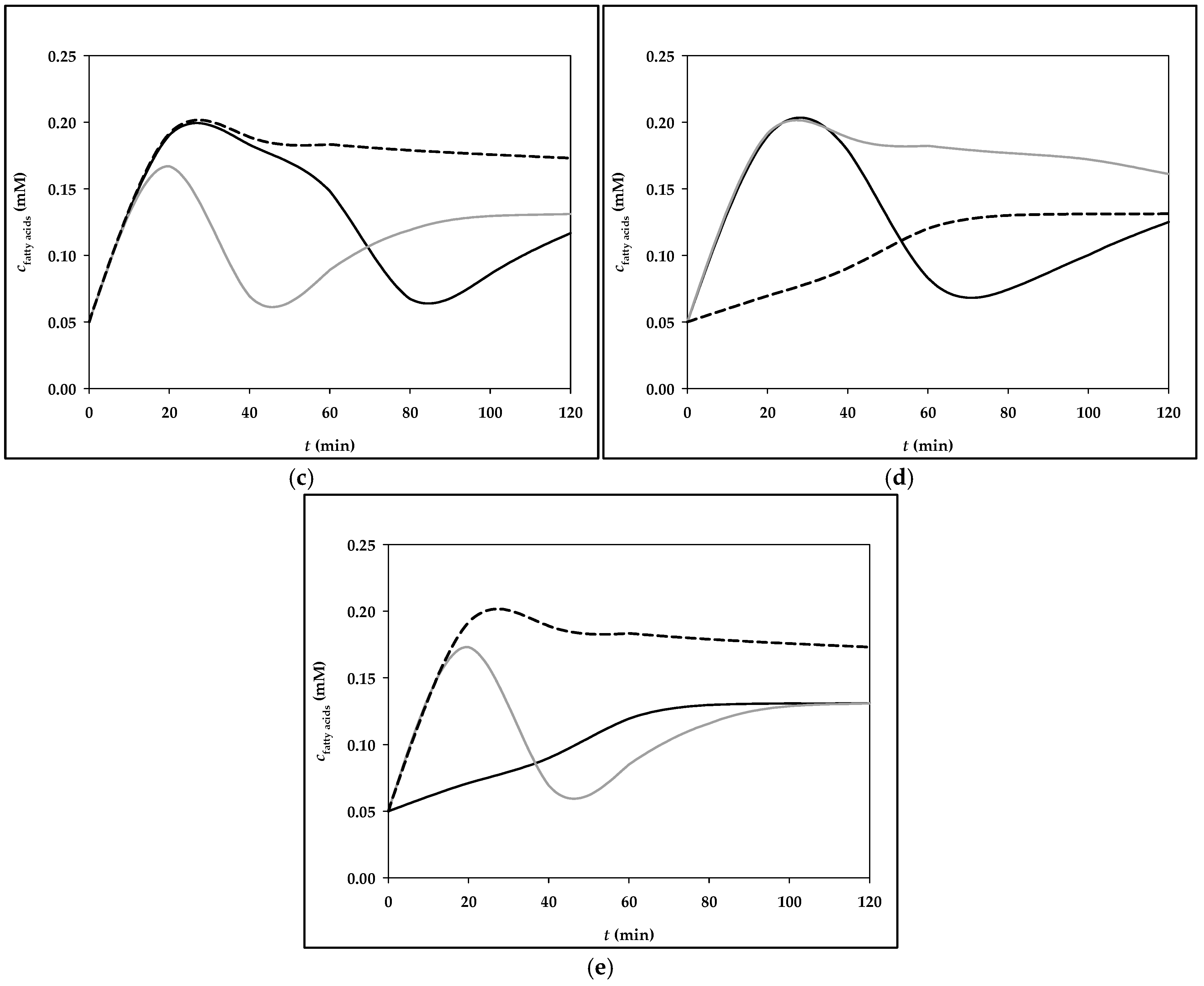
3.2. Simulation of Fructose Metabolism Model
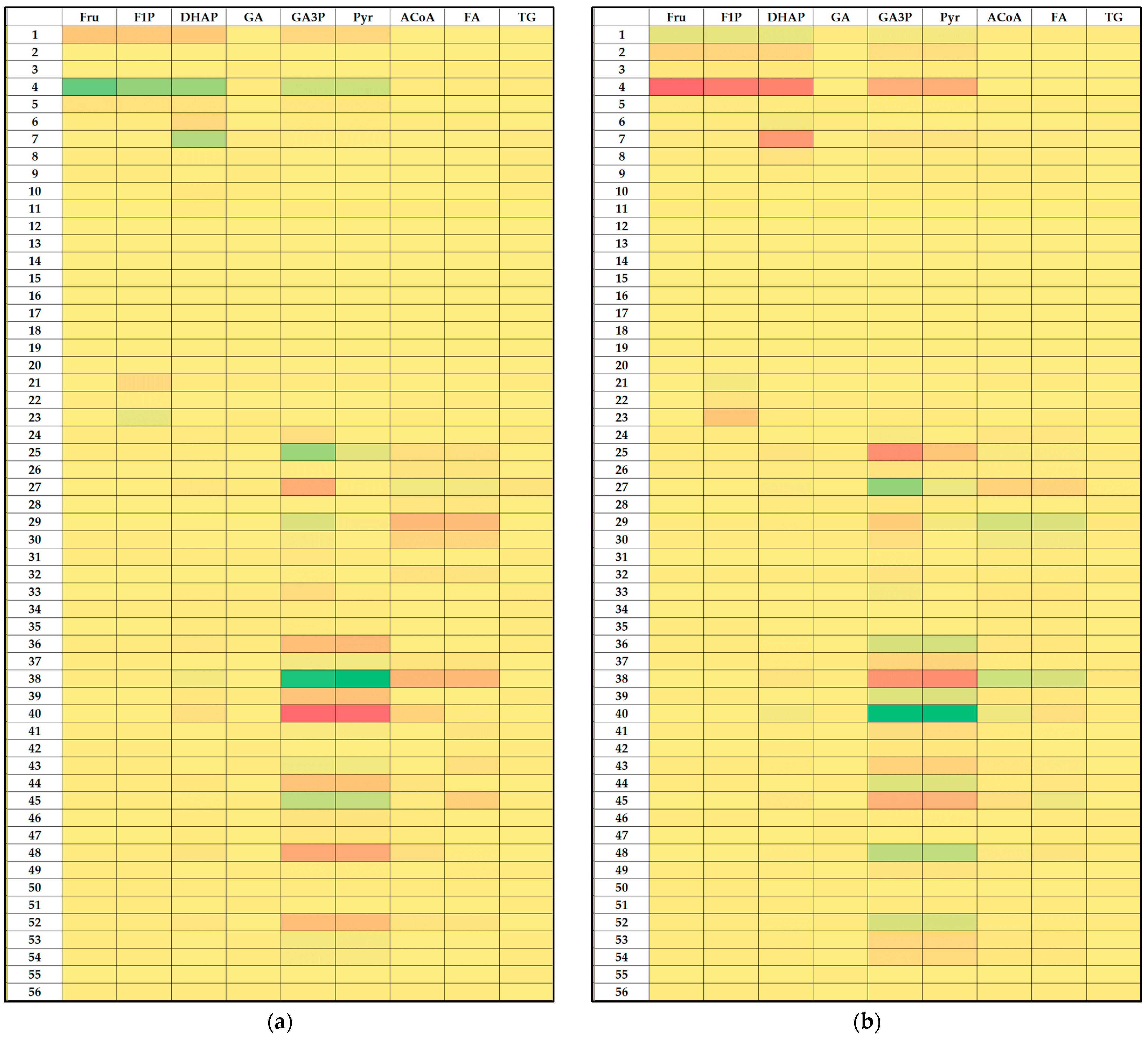
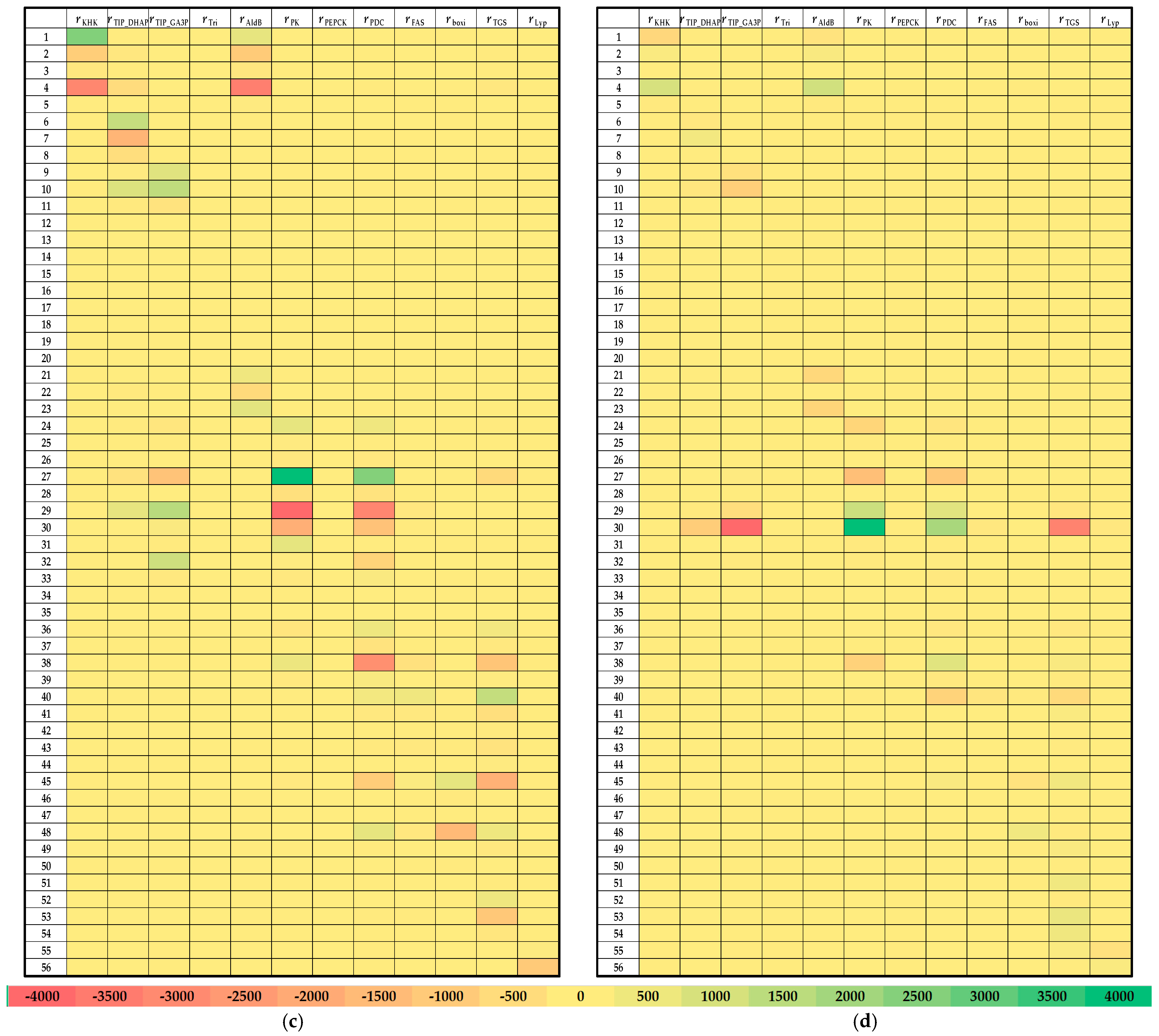
3.3. Local Sensitivity Analysis of the Fructose Metabolism Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Funahashi, A.; Morohashi, M.; Kitano, H.; Tanimura, N. CellDesigner: A process diagram editor for gene-regulatory and biochemical networks. BioSilico 2003, 1, 159–162. [Google Scholar] [CrossRef]
- Diaz-Beltran, L.; Cano, C.; Wall, D.P.; Esteban, F.J. Systems Biology as a Comparative Approach to Understand Complex Gene Expression in Neurological Diseases. Behav. Sci. 2013, 3, 253. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Laubichler, M.D. From systems to biology: A computational analysis of the research articles on systems biology from 1992 to 2013. PLoS ONE 2018, 13, e0200929. [Google Scholar] [CrossRef] [PubMed]
- Oulas, A.; Minadakis, G.; Zachariou, M.; Sokratous, K.; Bourdakou, M.M.; Spyrou, G.M. Systems Bioinformatics: Increasing precision of computational diagnostics and therapeutics through network-based approaches. Brief. Bioinform. 2019, 20, 806. [Google Scholar] [CrossRef]
- Pinu, F.R.; Beale, D.J.; Paten, A.M.; Kouremenos, K.; Swarup, S.; Schirra, H.J.; Wishart, D. Systems Biology and Multi-Omics Integration: Viewpoints from the Metabolomics Research Community. Metabolites 2019, 9, 76. [Google Scholar] [CrossRef]
- Coskun, A.; Ertaylan, G.; Pusparum, M.; Van Hoof, R.; Kaya, Z.Z.; Khosravi, A.; Zarrabi, A. Advancing personalized medicine: Integrating statistical algorithms with omics and nano-omics for enhanced diagnostic accuracy and treatment efficacy. Biochim. Biophys. Acta—Mol. Basis Dis. 2024, 1870, 167339. [Google Scholar] [CrossRef]
- Chi, J.; Shu, J.; Li, M.; Mudappathi, R.; Jin, Y.; Lewis, F.; Boon, A.; Qin, X.; Liu, L.; Gu, H. Artificial intelligence in metabolomics: A current review. TrAC Trends Anal. Chem. 2024, 178, 117852. [Google Scholar] [CrossRef]
- Puniya, B.L.; Verma, M.; Damiani, C.; Bakr, S.; Dräger, A. Perspectives on computational modeling of biological systems and the significance of the SysMod community. Bioinform. Adv. 2024, 4, vbae090. [Google Scholar] [CrossRef]
- Funahashi, A.; Matsuoka, Y.; Jouraku, A.; Morohashi, M.; Kikuchi, N.; Kitano, H. CellDesigner 3.5: A versatile modeling tool for biochemical networks. Proc. IEEE 2008, 96, 1254–1265. [Google Scholar] [CrossRef]
- Kitano, H. Systems Biology: A Brief Overview. Science 2002, 295, 1662–1664. [Google Scholar] [CrossRef]
- Bruggeman, F.J.; Westerhoff, H.V. The nature of systems biology. Trends Microbiol. 2007, 15, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Madhavan, M.; Mustafa, S. Systems biology-the transformative approach to integrate sciences across disciplines Systems Biology: Integrating Biological Sciences. Phys. Sci. Rev. 2023, 8, 2523–2545. [Google Scholar] [CrossRef]
- Bartlett, A.; Lewis, J.; Williams, M.L. Generations of interdisciplinarity in bioinformatics. New Genet. Soc. 2016, 35, 186–209. [Google Scholar] [CrossRef]
- Tavassoly, I.; Goldfarb, J.; Iyengar, R. Systems biology primer: The basic methods and approaches. Essays Biochem. 2018, 62, 487–500. [Google Scholar] [CrossRef]
- Badimon, L.; Vilahur, G.; Padro, T. Systems biology approaches to understand the effects of nutrition and promote health. Br. J. Clin. Pharmacol. 2017, 83, 38. [Google Scholar] [CrossRef]
- Kosić, M.; Benković, M.; Jurina, T.; Valinger, D.; Gajdoš Kljusurić, J.; Jurinjak Tušek, A. Analysis of Hepatic Lipid Metabolism Model: Simulation and Non-Stationary Global Sensitivity Analysis. Nutrients 2022, 14, 4992. [Google Scholar] [CrossRef]
- Lee, B.Y.; Ordovás, J.M.; Parks, E.J.; Anderson, C.A.M.; Barabási, A.L.; Clinton, S.K.; de la Haye, K.; Duffy, V.B.; Franks, P.W.; Ginexi, E.M.; et al. Research gaps and opportunities in precision nutrition: An NIH workshop report. Am. J. Clin. Nutr. 2022, 116, 1877–1900. [Google Scholar] [CrossRef]
- de Hoogh, I.M.; Winters, B.L.; Nieman, K.M.; Bijlsma, S.; Krone, T.; van den Broek, T.J.; Anderson, B.D.; Caspers, M.P.M.; Anthony, J.C.; Wopereis, S. A novel personalized systems nutrition program improves dietary patterns, lifestyle behaviors and health-related outcomes: Results from the habit study. Nutrients 2021, 13, 1763. [Google Scholar] [CrossRef]
- Clemente-Suárez, V.J.; Peris-Ramos, H.C.; Redondo-Flórez, L.; Beltrán-Velasco, A.I.; Martín-Rodríguez, A.; David-Fernandez, S.; Yáñez-Sepúlveda, R.; Tornero-Aguilera, J.F. Personalizing Nutrition Strategies: Bridging Research and Public Health. J. Pers. Med. 2024, 14, 305. [Google Scholar] [CrossRef]
- Ma, C.; Gurkan-Cavusoglu, E. A comprehensive review of computational cell cycle models in guiding cancer treatment strategies. NPJ Syst. Biol. Appl. 2024, 10, 1234567890. [Google Scholar] [CrossRef]
- Martins, M.L.; Pacza, T.; Müller, K.; Baranyi, J. A computational approach to nutrition science reveals the dynamics of the protein content of human milk. Innov. Food Sci. Emerg. Technol. 2022, 82, 103167. [Google Scholar] [CrossRef]
- Nunes, C.A.; Alvarenga, V.O.; de Souza Sant’Ana, A.; Santos, J.S.; Granato, D. The use of statistical software in food science and technology: Advantages, limitations and misuses. Food Res. Int. 2015, 75, 270–280. [Google Scholar] [CrossRef] [PubMed]
- Knights, V.; Kolak, M.; Markovikj, G.; Gajdoš Kljusurić, J. Modeling and Optimization with Artificial Intelligence in Nutrition. Appl. Sci. 2023, 13, 7835. [Google Scholar] [CrossRef]
- Langellier, B.A.; Bilal, U.; Montes, F.; Meisel, J.D.; de Cardoso, L.O.; Hammond, R.A. Complex Systems Approaches to Diet: A Systematic Review. Am. J. Prev. Med. 2019, 57, 273. [Google Scholar] [CrossRef]
- Ahmed, S.; de la Parra, J.; Elouafi, I.; German, B.; Jarvis, A.; Lal, V.; Lartey, A.; Longvah, T.; Malpica, C.; Vázquez-Manjarrez, N.; et al. Foodomics: A Data-Driven Approach to Revolutionize Nutrition and Sustainable Diets. Front. Nutr. 2022, 9, 874312. [Google Scholar] [CrossRef]
- Brodland, G.W. How computational models can help unlock biological systems. Semin. Cell Dev. Biol. 2015, 47–48, 62–73. [Google Scholar] [CrossRef]
- Atwell, K.; Dunn, S.J.; Osborne, J.M.; Kugler, H.; Hubbard, E.J.A. How computational models contribute to our understanding of the germ line. Mol. Reprod. Dev. 2016, 83, 944. [Google Scholar] [CrossRef]
- Sordo Vieira, L.; Laubenbacher, R.C. Computational models in systems biology: Standards, dissemination, and best practices. Curr. Opin. Biotechnol. 2022, 75, 102702. [Google Scholar] [CrossRef]
- Roman, M.; Olaru, S. Model-Based Design for Biosystems. Control Opportunities and Discrete-Time Modelling Challenges. IFAC-Pap. 2018, 51, 666–671. [Google Scholar] [CrossRef]
- Liu, C.; Ma, Y.; Zhao, J.; Nussinov, R.; Zhang, Y.C.; Cheng, F.; Zhang, Z.K. Computational network biology: Data, models, and applications. Phys. Rep. 2020, 846, 1–66. [Google Scholar] [CrossRef]
- Douard, V.; Ferraris, R.P. The role of fructose transporters in diseases linked to excessive fructose intake. J. Physiol. 2013, 591, 401–414. [Google Scholar] [CrossRef] [PubMed]
- Tappy, L.; Lê, K.A.; Tran, C.; Paquot, N. Fructose and metabolic diseases: New findings, new questions. Nutrition 2010, 26, 1044–1049. [Google Scholar] [CrossRef] [PubMed]
- Tappy, L.; Le, K.A. Metabolic effects of fructose and the worldwide increase in obesity. Physiol. Rev. 2010, 90, 23–46. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Li, Y.; Guo, X.; Zhong, L.; Tang, S. Food groups and the likelihood of non-alcoholic fatty liver disease: A systematic review and meta-analysis. Br. J. Nutr. 2020, 124, 1–13. [Google Scholar] [CrossRef]
- Inci, M.K.; Park, S.H.; Helsley, R.N.; Attia, S.L.; Softic, S. Fructose impairs fat oxidation: Implications for the mechanism of western diet-induced NAFLD. J. Nutr. Biochem. 2023, 114, 109224. [Google Scholar] [CrossRef]
- Hengist, A.; Koumanov, F.; Gonzalez, J.T. Fructose and metabolic health: Governed by hepatic glycogen status? J. Physiol. 2019, 597, 3573–3585. [Google Scholar] [CrossRef]
- Rippe, J.M.; Angelopoulos, T.J. Sucrose, High-Fructose Corn Syrup, and Fructose, Their Metabolism and Potential Health Effects: What Do We Really Know? Adv. Nutr. 2013, 4, 236–245. [Google Scholar] [CrossRef]
- Koene, E.; Schrauwen-Hinderling, V.B.; Schrauwen, P.; Brouwers, M.C.G.J. Novel insights in intestinal and hepatic fructose metabolism: From mice to men. Curr. Opin. Clin. Nutr. Metab. Care 2022, 25, 354–359. [Google Scholar] [CrossRef]
- Roeb, E.; Weiskirchen, R. Fructose and Non-Alcoholic Steatohepatitis. Front. Pharmacol. 2021, 12, 634344. [Google Scholar] [CrossRef]
- Wang, D.D.; Li, Y.; Bhupathiraju, S.N.; Rosner, B.A.; Sun, Q.; Giovannucci, E.L.; Rimm, E.B.; Manson, J.A.E.; Willett, W.C.; Stampfer, M.J.; et al. Fruit and Vegetable Intake and Mortality Results From 2 Prospective Cohort Studies of US Men and Women and a Meta-Analysis of 26 Cohort Studies. Circulation 2021, 143, 1642–1654. [Google Scholar] [CrossRef]
- Aune, D.; Giovannucci, E.; Boffetta, P.; Fadnes, L.T.; Keum, N.N.; Norat, T.; Greenwood, D.C.; Riboli, E.; Vatten, L.J.; Tonstad, S. Fruit and vegetable intake and the risk of cardiovascular disease, total cancer and all-cause mortality—A systematic review and dose-response meta-analysis of prospective studies. Int. J. Epidemiol. 2017, 46, 1029–1056. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Davies, N.A.; Bogle, I.D.L. Computational Modeling of Fructose Metabolism and Development in NAFLD. Front. Bioeng. Biotechnol. 2020, 8, 537669. [Google Scholar] [CrossRef] [PubMed]
- Zi, Z. Sensitivity analysis approaches applied to systems biology models. IET Syst. Biol. 2011, 5, 336–346. [Google Scholar] [CrossRef]
- Qian, G.; Mahdi, A. Sensitivity analysis methods in the biomedical sciences. Math. Biosci. 2020, 323, 108306. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Hartley, L.; Igbinedion, E.; Holmes, J.; Flowers, N.; Thorogood, M.; Clarke, A.; Stranges, S.; Hooper, L.; Rees, K. Increased consumption of fruit and vegetables for the primary prevention of cardiovascular diseases. Cochrane Database Syst. Rev. 2013, 2013, CD009874. [Google Scholar]
- Rakhra, V.; Galappaththy, S.L.; Bulchandani, S.; Cabandugama, P.K. Obesity and the Western Diet: How We Got Here. Mo. Med. 2020, 117, 536. [Google Scholar]
- López-Taboada, I.; González-Pardo, H.; Conejo, N.M. Western Diet: Implications for Brain Function and Behavior. Front. Psychol. 2020, 11, 564413. [Google Scholar] [CrossRef]
- Zhang, H.; Li, M.; Mo, L.; Luo, J.; Shen, Q.; Quan, W. Association between Western Dietary Patterns, Typical Food Groups, and Behavioral Health Disorders: An Updated Systematic Review and Meta-Analysis of Observational Studies. Nutrients 2024, 16, 125. [Google Scholar] [CrossRef]
- Kris-Etherton, P.M.; Petersen, K.S.; Hibbeln, J.R.; Hurley, D.; Kolick, V.; Peoples, S.; Rodriguez, N.; Woodward-Lopez, G. Nutrition and behavioral health disorders: Depression and anxiety. Nutr. Rev. 2021, 79, 247–260. [Google Scholar] [CrossRef]
- Bermudez, B.; Ortega-Gomez, A.; Varela, L.M.; Villar, J.; Abia, R.; Muriana, F.J.G.; Lopez, S. Clustering effects on postprandial insulin secretion and sensitivity in response to meals with different fatty acid compositions. Food Funct. 2014, 5, 1374–1380. [Google Scholar] [CrossRef] [PubMed]
- Dholariya, S.J.; Orrick, J.A. Biochemistry, Fructose Metabolism. In StatPearls [Internet]; StatPearls Publishing, 2022. Available online: https://www.ncbi.nlm.nih.gov/sites/books/NBK576428/ (accessed on 18 November 2024).
- Skenderian, S.; Park, G.; Jang, C. Organismal Fructose Metabolism in Health and Non-Alcoholic Fatty Liver Disease. Biology 2020, 9, 405. [Google Scholar] [CrossRef] [PubMed]
- Parry, S.A.; Turner, M.C.; Hodson, L. Lifestyle interventions affecting hepatic fatty acid metabolism. Curr. Opin. Clin. Nutr. Metab. Care 2020, 23, 373–379. [Google Scholar] [CrossRef]
- Bizeau, M.E.; Pagliassotti, M.J. Hepatic adaptations to sucrose and fructose. Metabolism. 2005, 54, 1189–1201. [Google Scholar] [CrossRef]
- Brouwers, M.C.G.J. Fructose 1-phosphate, an evolutionary signaling molecule of abundancy. Trends Endocrinol. Metab. 2022, 33, 680–689. [Google Scholar] [CrossRef]
- Aldámiz-Echevarría, L.; de las Heras, J.; Couce, M.L.; Alcalde, C.; Vitoria, I.; Bueno, M.; Blasco-Alonso, J.; Concepción García, M.; Ruiz, M.; Suárez, R.; et al. Non-alcoholic fatty liver in hereditary fructose intolerance. Clin. Nutr. 2020, 39, 455–459. [Google Scholar] [CrossRef]
- Simons, N.; Debray, F.G.; Schaper, N.C.; Kooi, M.E.; Feskens, E.J.M.; Hollak, C.E.M.; Lindeboom, L.; Koek, G.H.; Bons, J.A.P.; Lefeber, D.J.; et al. Patients With Aldolase B Deficiency Are Characterized by Increased Intrahepatic Triglyceride Content. J. Clin. Endocrinol. Metab. 2019, 104, 5056–5064. [Google Scholar] [CrossRef]
- Geidl-Flueck, B.; Hochuli, M.; Németh, Á.; Eberl, A.; Derron, N.; Köfeler, H.C.; Tappy, L.; Berneis, K.; Spinas, G.A.; Gerber, P.A. Fructose- and sucrose- but not glucose-sweetened beverages promote hepatic de novo lipogenesis: A randomized controlled trial. J. Hepatol. 2021, 75, 46–54. [Google Scholar] [CrossRef]
- Lodge, M.; Dykes, R.; Kennedy, A. Regulation of Fructose Metabolism in Nonalcoholic Fatty Liver Disease. Biomolecules 2024, 14, 845. [Google Scholar] [CrossRef]
- Simons, N.; Veeraiah, P.; Simons, P.I.H.G.; Schaper, N.C.; Kooi, M.E.; Schrauwen-Hinderling, V.B.; Feskens, E.J.M.; Van Der Ploeg, E.M.C.; Van Den Eynde, M.D.G.; Schalkwijk, C.G.; et al. Effects of fructose restriction on liver steatosis (FRUITLESS); a double-blind randomized controlled trial. Am. J. Clin. Nutr. 2021, 113, 391–400. [Google Scholar] [CrossRef]
- Sysoev, A. Sensitivity Analysis of Mathematical Models. Computation 2023, 11, 159. [Google Scholar] [CrossRef]
- Savatorova, V. Exploring Parameter Sensitivity Analysis in Mathematical Modeling with Ordinary Differential Equations. CODEE J. 2023, 16, 4. [Google Scholar] [CrossRef]
- Nguyen Quang, M.; Rogers, T.; Hofman, J.; Lanham, A.B. Global Sensitivity Analysis of Metabolic Models for Phosphorus Accumulating Organisms in Enhanced Biological Phosphorus Removal. Front. Bioeng. Biotechnol. 2019, 7, 234. [Google Scholar] [CrossRef]
- Carta, J.A.; Díaz, S.; Castañeda, A. A global sensitivity analysis method applied to wind farm power output estimation models. Appl. Energy 2020, 280, 115968. [Google Scholar] [CrossRef]
- Link, K.G.; Stobb, M.T.; Paola, J.D.; Neeves, K.B.; Fogelson, A.L.; Sindi, S.S.; Leiderman, K. A local and global sensitivity analysis of a mathematical model of coagulation and platelet deposition under flow. PLoS ONE 2018, 13, e0200917. [Google Scholar] [CrossRef]
- McDonald, A.G.; Tipton, K.F. Parameter Reliability and Understanding Enzyme Function. Molecules 2022, 27, 263. [Google Scholar] [CrossRef]
- Manheim, D.C.; Detwiler, R.L. Accurate and reliable estimation of kinetic parameters for environmental engineering applications: A global, multi objective, Bayesian optimization approach. MethodsX 2019, 6, 1398–1414. [Google Scholar] [CrossRef]
- Lagrotta, C.E.; Barbet, M.C.; Lei, L.; Burke, M.P. Towards a high-accuracy kinetic database informed by theoretical and experimental data: CH3 + HO2 as a case study. Proc. Combust. Inst. 2021, 38, 1043–1051. [Google Scholar] [CrossRef]
- Miskovic, L.; Béal, J.; Moret, M.; Hatzimanikatis, V. Uncertainty reduction in biochemical kinetic models: Enforcing desired model properties. PLoS Comput. Biol. 2019, 15, e1007242. [Google Scholar] [CrossRef]
- Bechmann, L.P.; Hannivoort, R.A.; Gerken, G.; Hotamisligil, G.S.; Trauner, M.; Canbay, A. The interaction of hepatic lipid and glucose metabolism in liver diseases. J. Hepatol. 2012, 56, 952–964. [Google Scholar] [CrossRef]

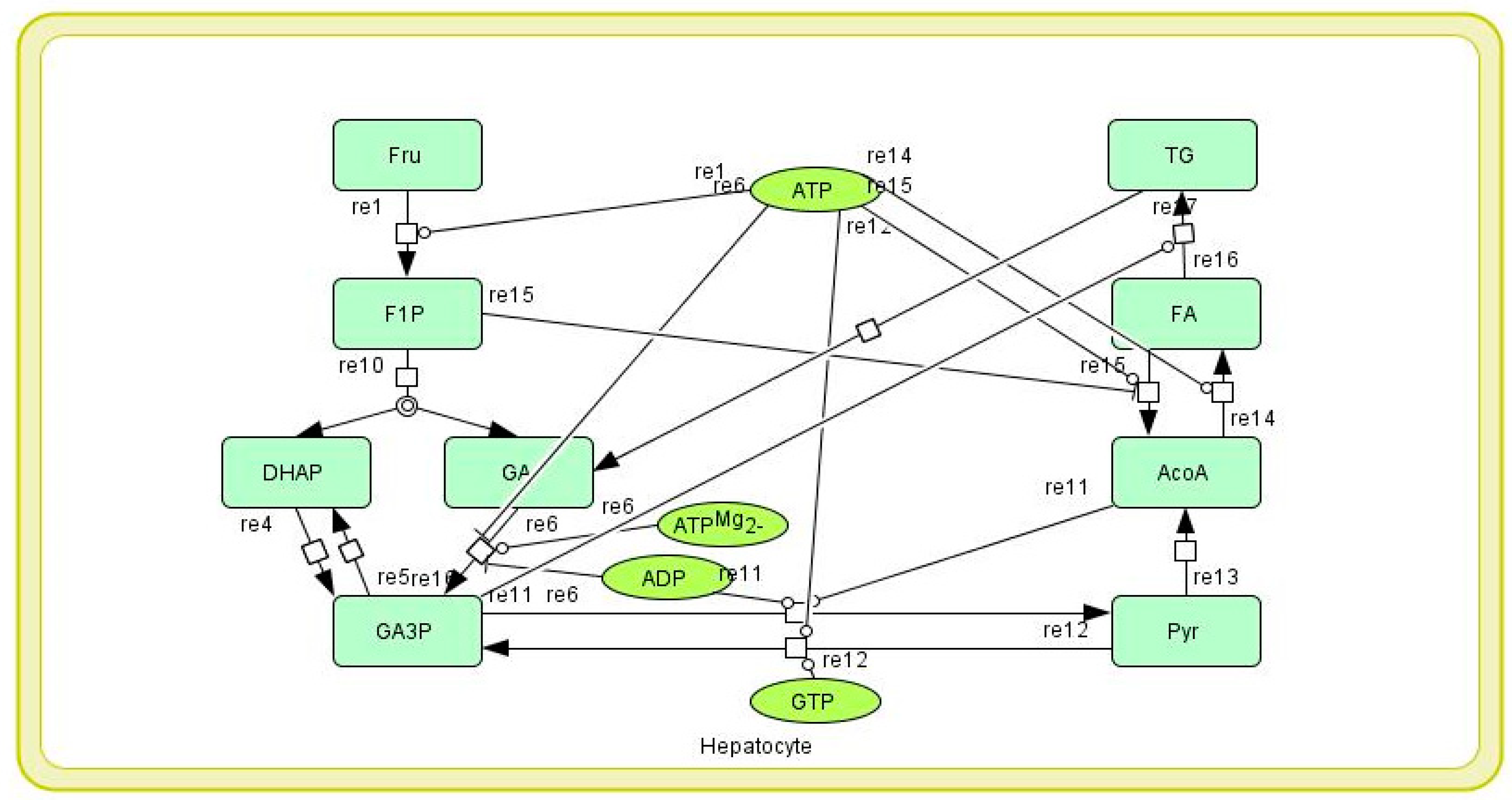


| Model Variable | Mass Balance | Initial Value |
|---|---|---|
| Fructose (Fru) | According to menu | |
| Fructose-1-phosphate (F1P) | 0.2 µM | |
| Dihydroxyacetone phosphate (DHAP) | 15 µM | |
| Glyceraldehyde (GA) | 1500 µM | |
| Glyceraldehyde-3-phosphate (GA3P) | 480 µM | |
| Pyruvate/Lactate (Pyr) | 1200 µM | |
| Acetyl-CoA (ACoA) | 40 µM | |
| Fatty acids (FA) | 50 µM | |
| Triglycerides (TG) | 1050 µM |
| Num. | Kinetic Parametar | Value | Num. | Kinetic Parametar | Value |
|---|---|---|---|---|---|
| 1 | 4.5 µ | 29 | |||
| 2 | 800 µ | 30 | 0.8 | ||
| 3 | 1430 µ | 31 | 30 | ||
| 4 | nFru | 32 | 35 µ | ||
| 5 | nATP | 33 | 500 µ | ||
| 6 | 2.7 µ | 34 | 10 µ | ||
| 7 | nDHAP | 35 | 64 µ | ||
| 8 | 590 µ | 36 | 15 µ | ||
| 9 | 0.05 µ | 37 | 540 µ | ||
| 10 | nGA3P | 1 | 38 | 1 | |
| 11 | 400 µ | 39 | 35 | ||
| 12 | 16.7 µ | 40 | |||
| 13 | nGA | 1 | 41 | 58 µ | |
| 14 | 18 µ | 42 | 120 µ | ||
| 15 | 1 | 43 | 1 | ||
| 16 | 770 µ | 44 | 300 | ||
| 17 | 1 | 45 | 3.3 µ | ||
| 18 | 380 | 46 | 5 µ | ||
| 19 | 1 | 47 | 87 µ | ||
| 20 | 1100 | 48 | 0.4 | ||
| 21 | 1.7 µ | 49 | 47.8 | ||
| 22 | 230 µ | 50 | 1 | ||
| 23 | 1 | 51 | 100 | ||
| 24 | 87 µ | 52 | |||
| 25 | 1 | 53 | 645 µ | ||
| 26 | 250 µ | 54 | 460 µ | ||
| 27 | 1 | 55 | 0.085 µ | ||
| 28 | 240 µ | 56 | 50715 µ |
| Menu | Meals Components with Corresponding Masses | Fructose Mass (g) |
|---|---|---|
| Menu 1 | Breakfast: whole grain tortilla, (45 g), whole egg, (94 g), butter (5 g), spinach (50 g), fresh reduced fat cheese (30 g), yogurt (200 g) | 0.25 g |
| Brunch: integral toast (25 g), peanut butter (13.3 g), banana (154 g) | 7.8 g | |
| Lunch: integral pasta (60 g), chicken white meat (150 g), champignons (250 g), cooking cream, 10% m.m. (200 g), olive oil (10 g) | 0.49 g | |
| Snack: almonds (13.5 g), orange (176 g) | 4.2 g | |
| Dinner: hake (150 g), white rice (60 g), peas (100 g), olive oil(5 g) | 0.1 g | |
| Menu 2 | Breakfast: granola (40 g), Greek yogurt (150 g), raspberries (100 g), honey (8 g), flax seeds (9 g), squeezed orange juice (200 g) | 13.1 g |
| Brunch: wholemeal toast (50 g), marmalade (40 g), | 6.3 g | |
| Lunch: cream spinach soup (250 g), salmon (150 g), kale (150 g), potatoes (150 g), olive oil (10 g) | 1.8 g | |
| Snack: vanilla ice cream (100 g), chocolate milk (200 g) | 11 g | |
| Dinner: turkey white meat (150 g), quinoa (50 g), paprika (50 g), carrot (50 g), zucchini (50 g), red onion (50 g), olive oil (10 g) | 2 g | |
| Menu 3 | Breakfast: corn flakes (40 g), milk (200 g), pear (130 g), grape juice, 100% (200 g) | 26.9 g |
| Brunch: croissant (50 g), mango (100 g) | 4 g | |
| Lunch: Whopper burger (270 g), Burger King side salad (98 g), yogurt sauce (250 g), cooking cream, 10% m.m. (15.4 g), Coca-Cola (475 g) | 36.1 g | |
| Snack: peanuts (20 g) | 0 g | |
| Dinner: bottle of Sprite (500 g), drained canned tuna (100 g), canned chickpeas (150 g), paprika (100 g), cucumber (150 g), onion, red (50 g), honey (8 g), mustard (8 g), lemon juice (10 g) | 33.3 g |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buljan, I.; Benković, M.; Jurina, T.; Sokač Cvetnić, T.; Valinger, D.; Gajdoš Kljusurić, J.; Jurinjak Tušek, A. Simulation and Local Parametric Sensitivity Analysis of a Computational Model of Fructose Metabolism. Processes 2025, 13, 125. https://doi.org/10.3390/pr13010125
Buljan I, Benković M, Jurina T, Sokač Cvetnić T, Valinger D, Gajdoš Kljusurić J, Jurinjak Tušek A. Simulation and Local Parametric Sensitivity Analysis of a Computational Model of Fructose Metabolism. Processes. 2025; 13(1):125. https://doi.org/10.3390/pr13010125
Chicago/Turabian StyleBuljan, Ivona, Maja Benković, Tamara Jurina, Tea Sokač Cvetnić, Davor Valinger, Jasenka Gajdoš Kljusurić, and Ana Jurinjak Tušek. 2025. "Simulation and Local Parametric Sensitivity Analysis of a Computational Model of Fructose Metabolism" Processes 13, no. 1: 125. https://doi.org/10.3390/pr13010125
APA StyleBuljan, I., Benković, M., Jurina, T., Sokač Cvetnić, T., Valinger, D., Gajdoš Kljusurić, J., & Jurinjak Tušek, A. (2025). Simulation and Local Parametric Sensitivity Analysis of a Computational Model of Fructose Metabolism. Processes, 13(1), 125. https://doi.org/10.3390/pr13010125










