Performance Simulation and Experimental Verification of a Low-Temperature Differential Free-Piston Stirling Air Conditioner Under Multi-Harmonic Drive
Abstract
:1. Introduction
2. Derivation of the Numerical Model
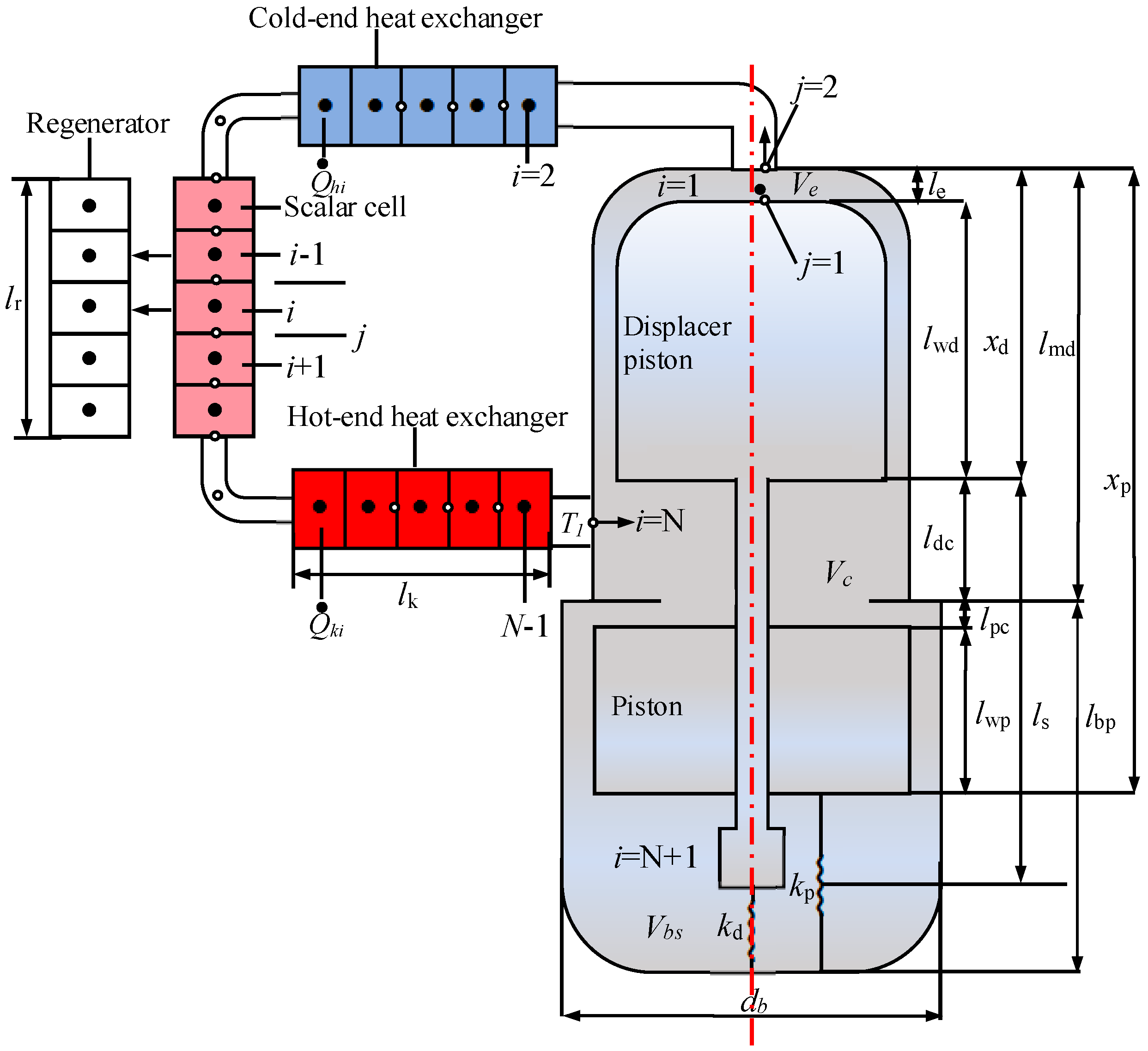
2.1. Physical Model of the FPSAC
2.2. Physical Model of the FPSAC Derivation of the Numerical Model
2.3. Governing Transport Equations
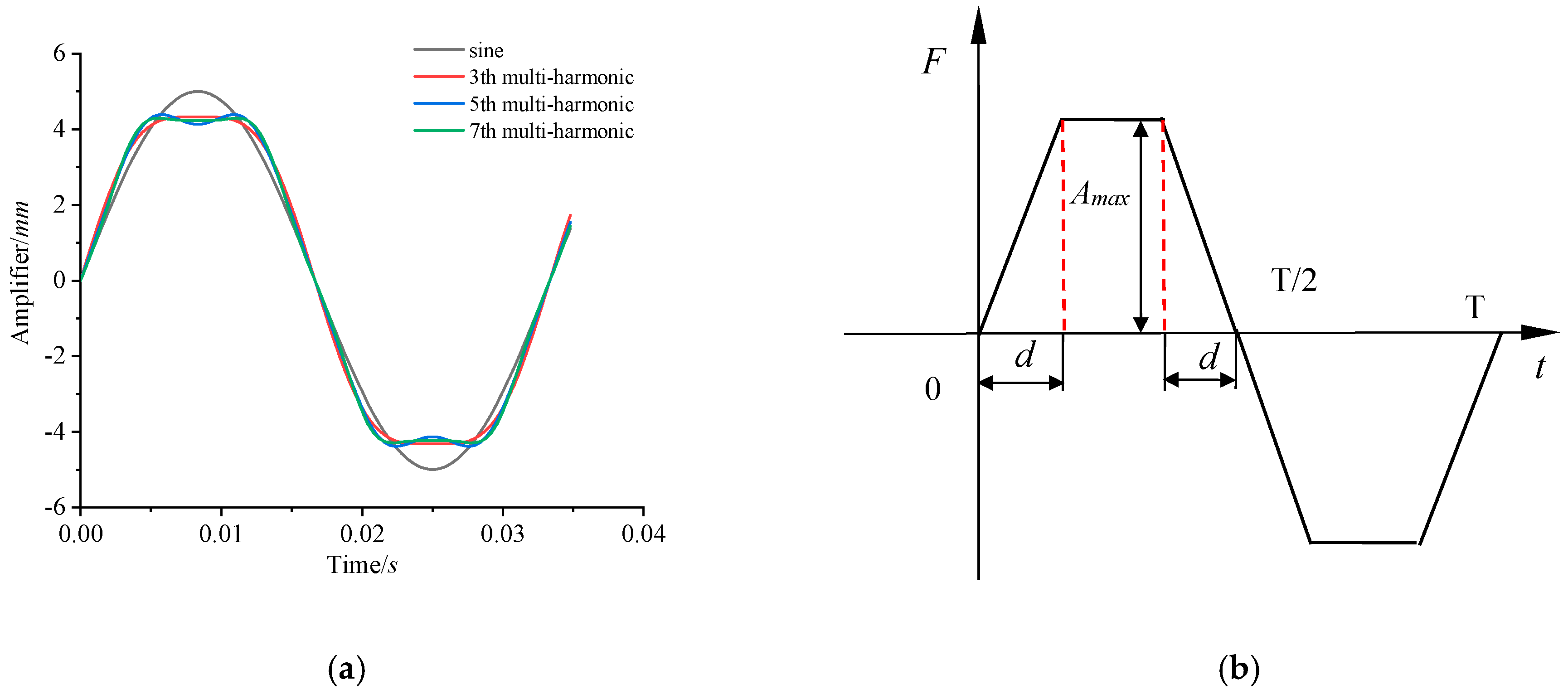
2.3.1. The Electromagnetic Thrust of a Permanent Magnet Linear Oscillation Motor Under Multi-Harmonic Drive
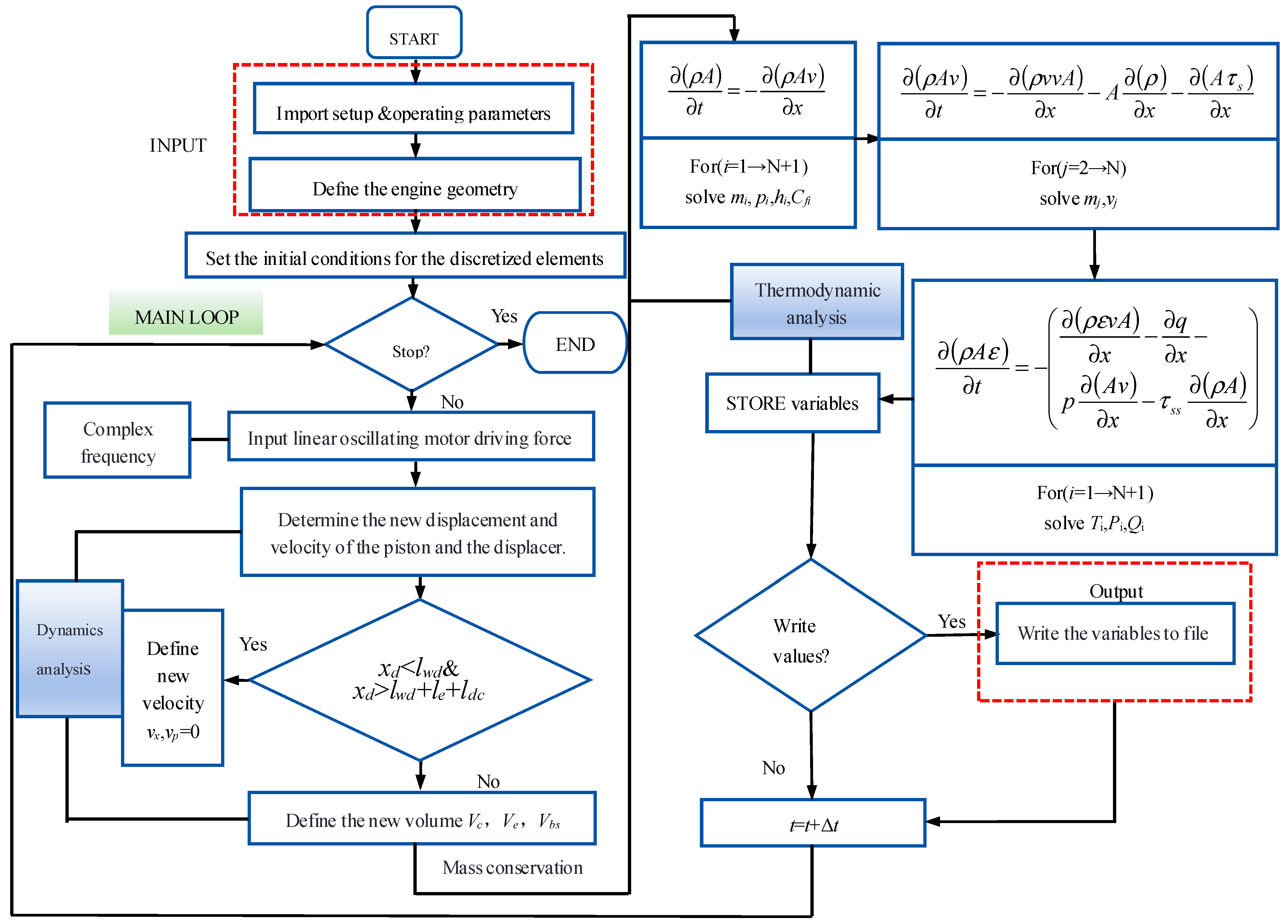
2.3.2. Discretization of the Thermodynamic-Dynamic Control Equations by the Finite Differences
- (1)
- Conservation of mass
- (2)
- Conservation of momentum
- (3)
- Conservation of energy
2.3.3. Calculation of Heat Transfer and Fluid Friction Coefficient in the Heat Exchanger
- (1)
- Heat transfer in cold-end heat exchangers and hot-end heat exchangers
- (2)
- The friction factor Cf of the fluid within the heat exchanger
- (3)
- The heat transfer rate Q of the regenerator
- (4)
- Iterative formula for temperature change in the regenerator matrix
- (5)
- Boundary temperature of the control volume
- (6)
- Fluid Friction Factor Cf in the Capillary Tubes of the Regenerator
2.3.4. Discretization of Two-Dimensional Nonlinear Dynamics Equations
2.4. Simulation of the FPSAC
3. Results and Discussion
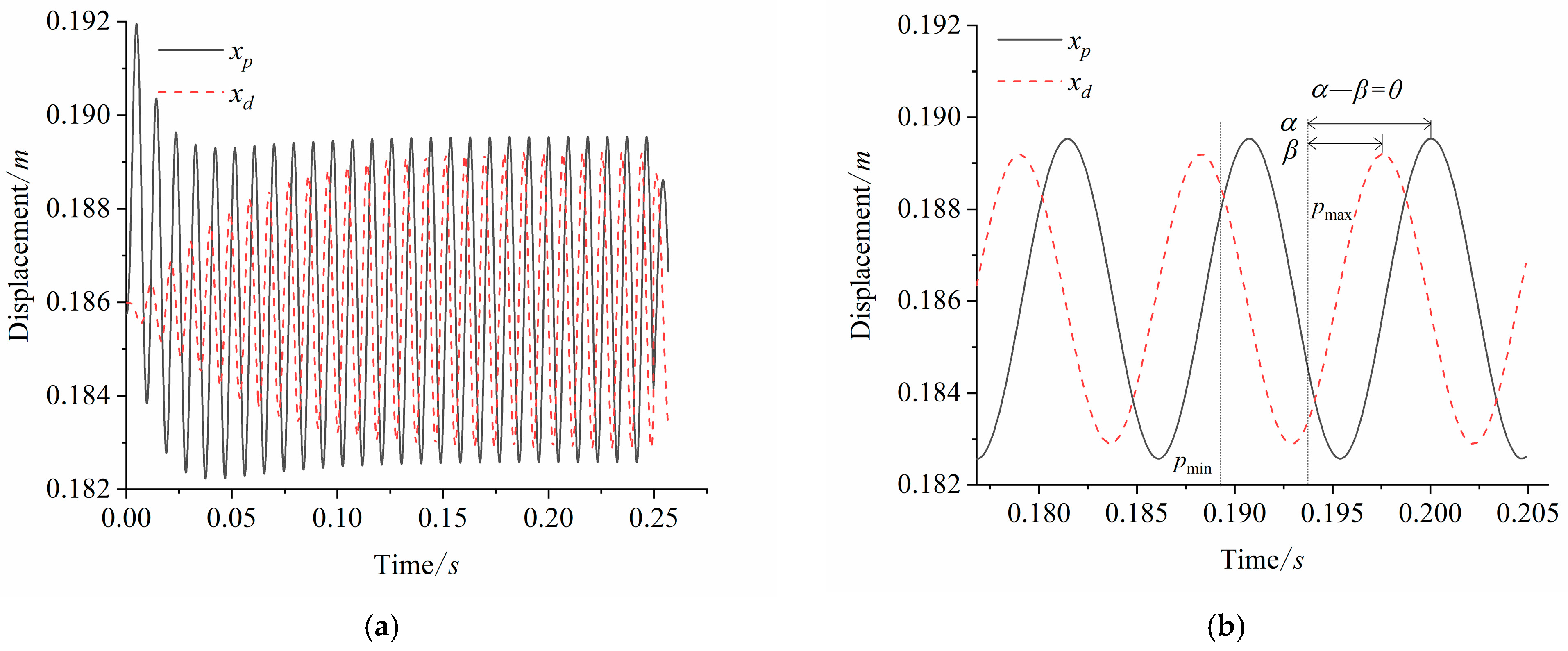
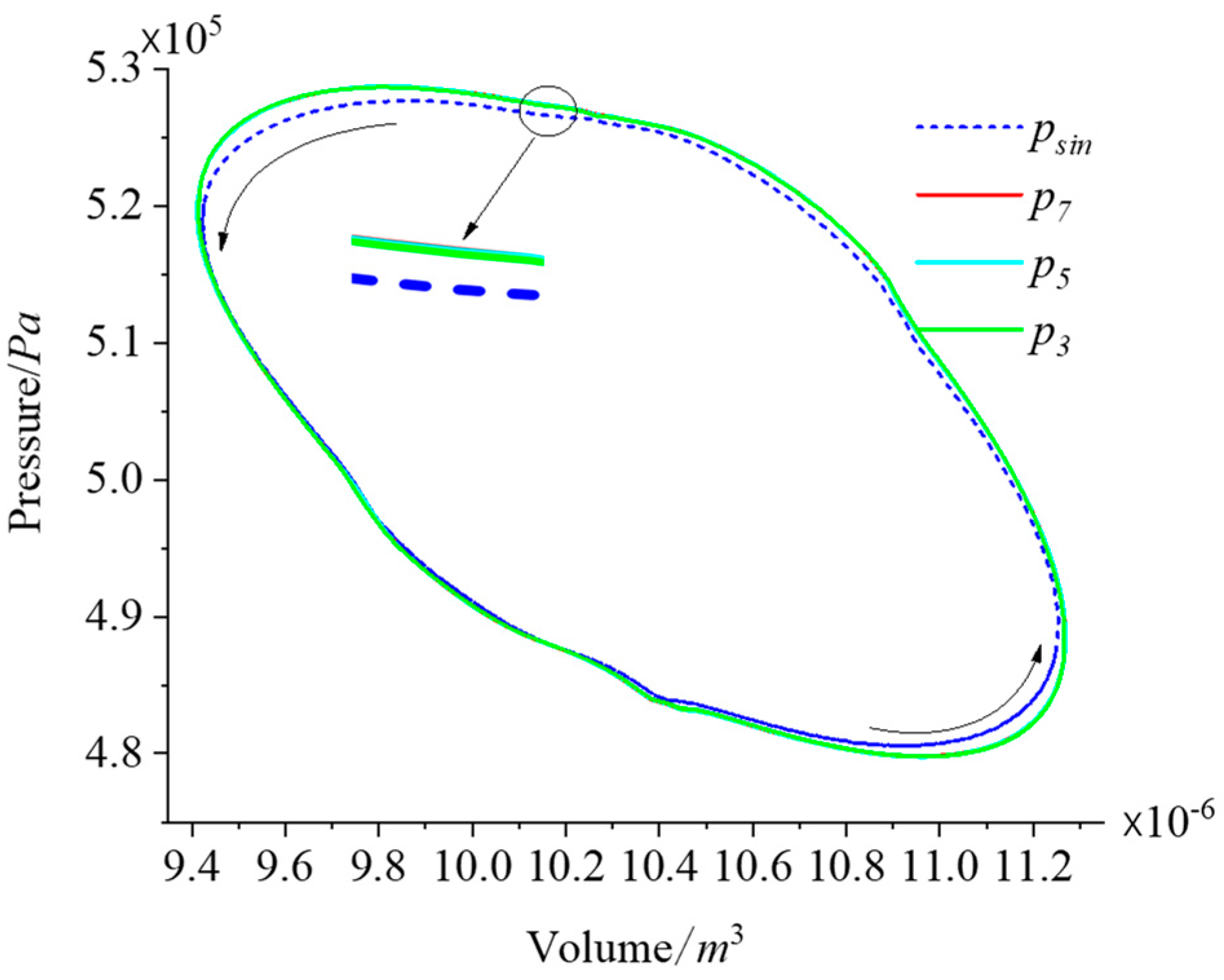
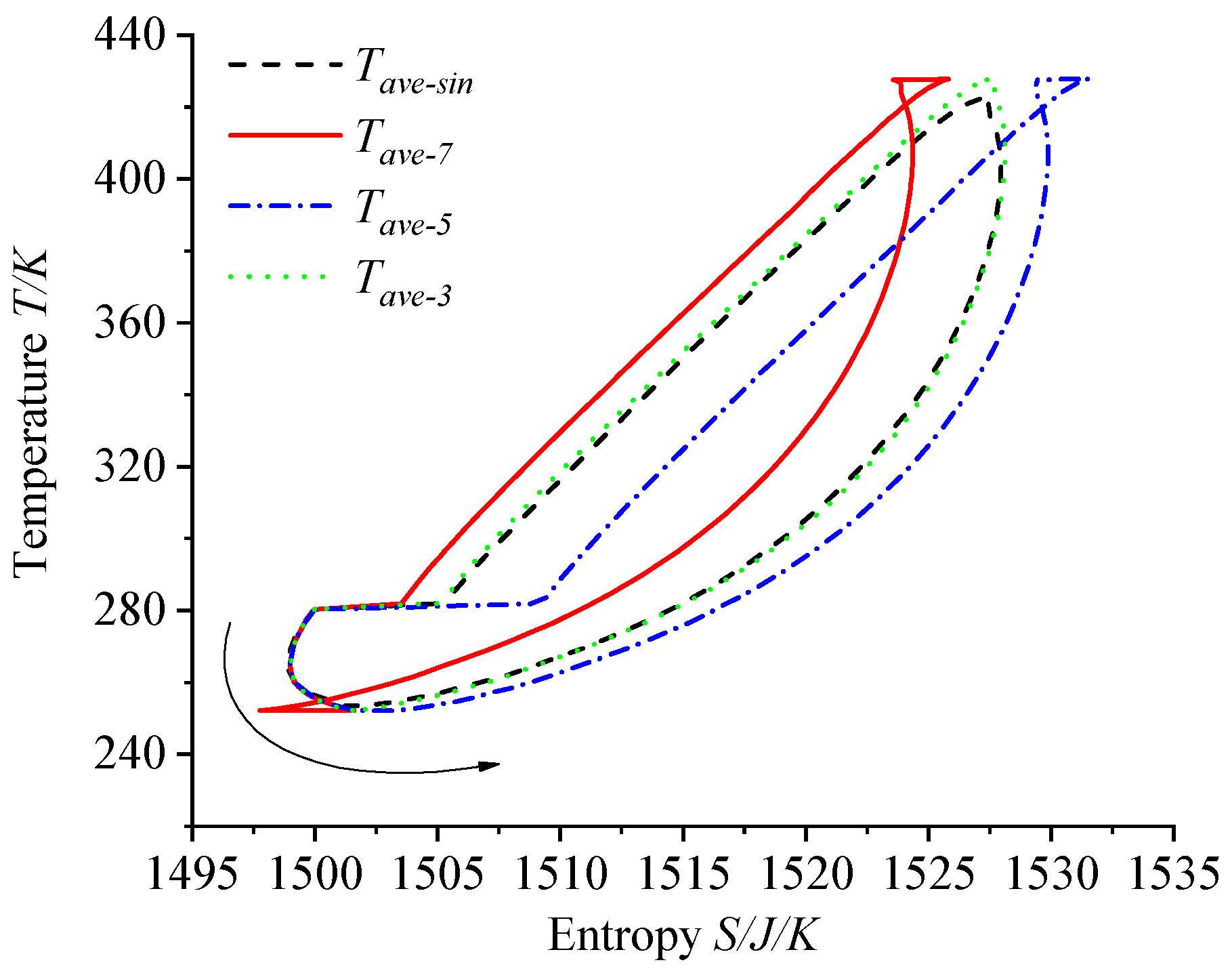
3.1. Impact of Different Drives on the Thermodynamic and Kinematic Parameters of the FPSAC in Cooling Mode
3.1.1. The Impact of Harmonic Drive on Thermodynamic-Dynamic Parameters
3.1.2. Comparison Between Harmonic Drive and Multi-Harmonic Drive
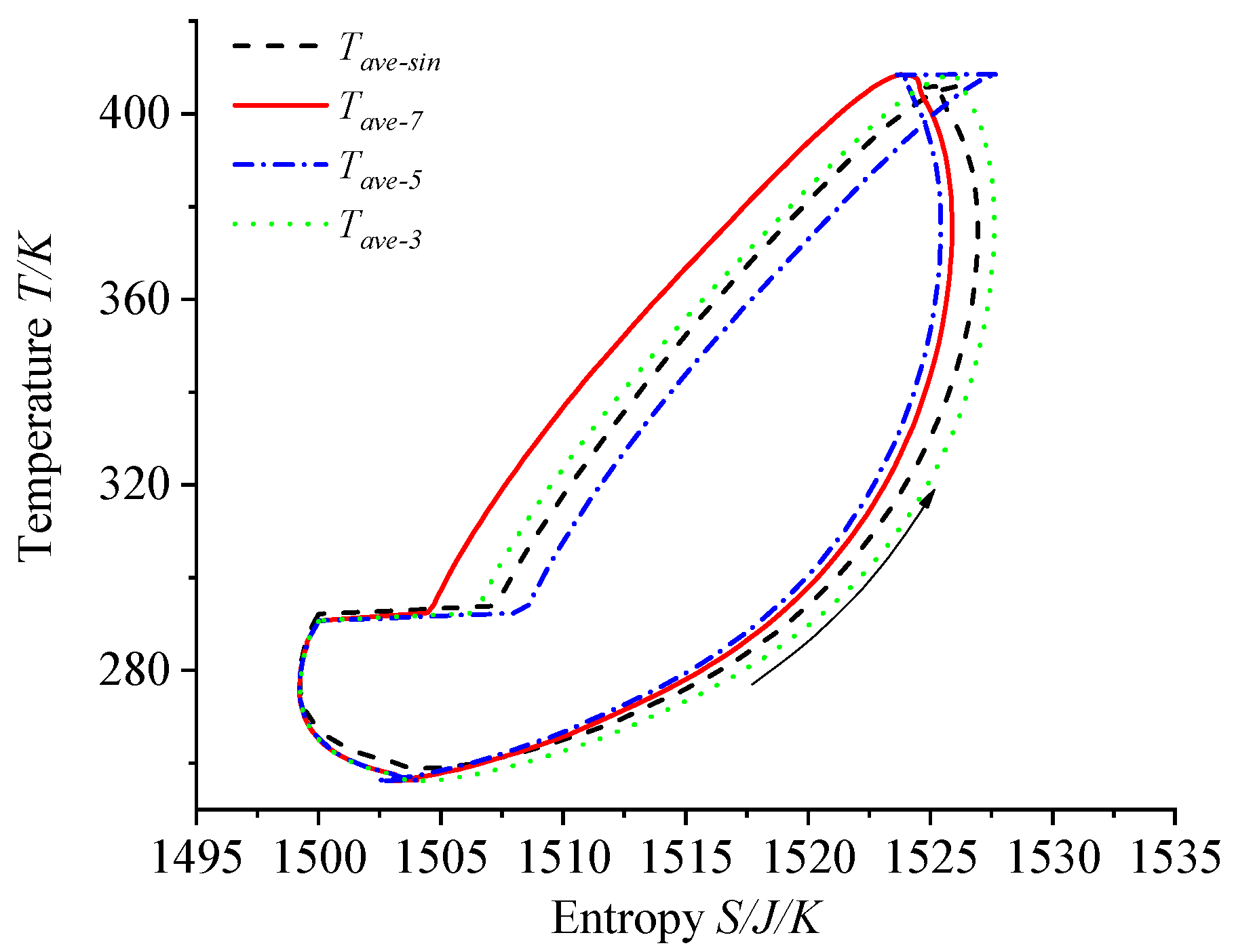
3.2. Impact of Different Drives on Thermodynamic and Kinetic Parameters of FPSAC in Heating Mode
4. Performance Testing Experimental Study of FPSAC
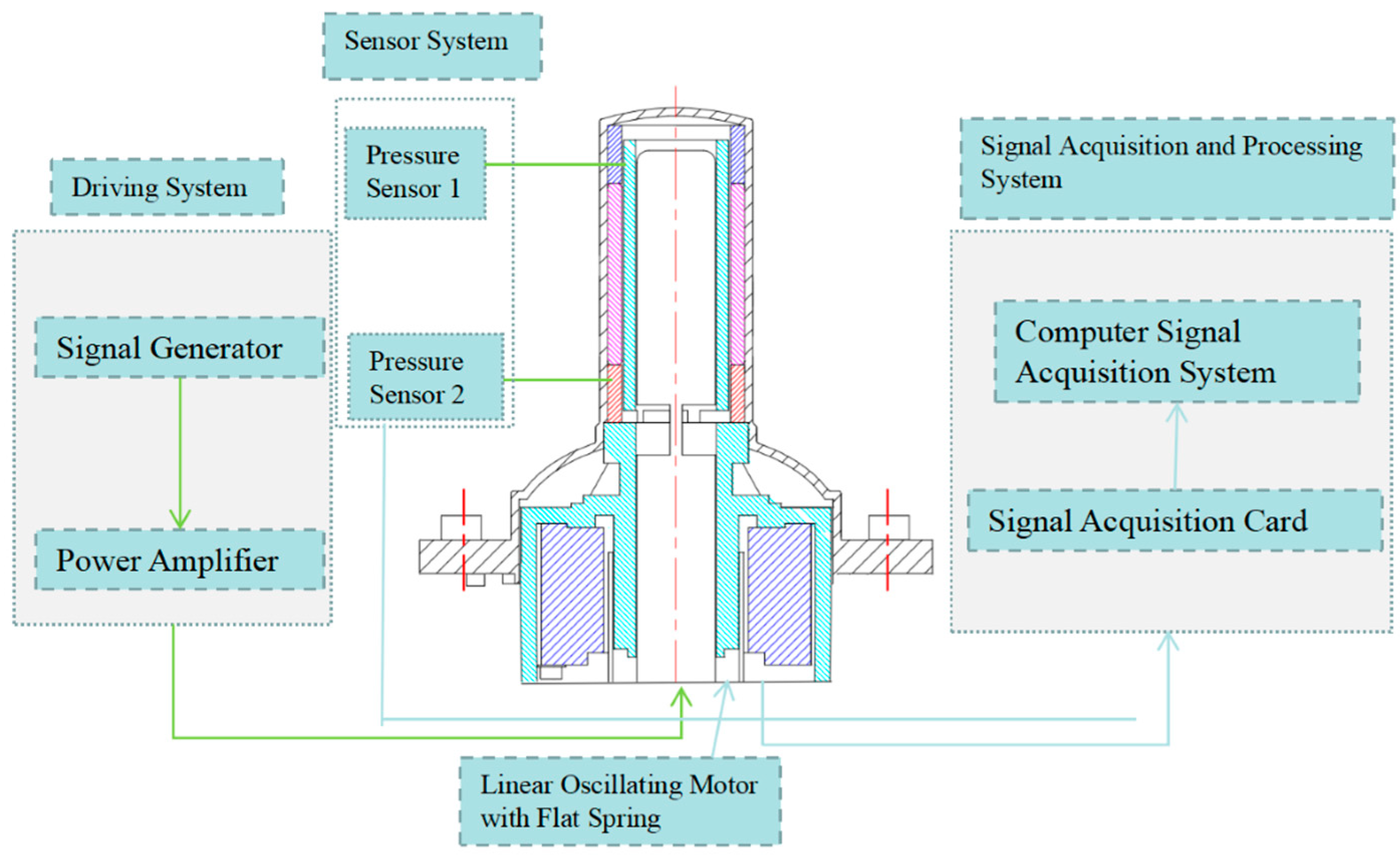
4.1. Experimental Setup
4.2. Test Bench
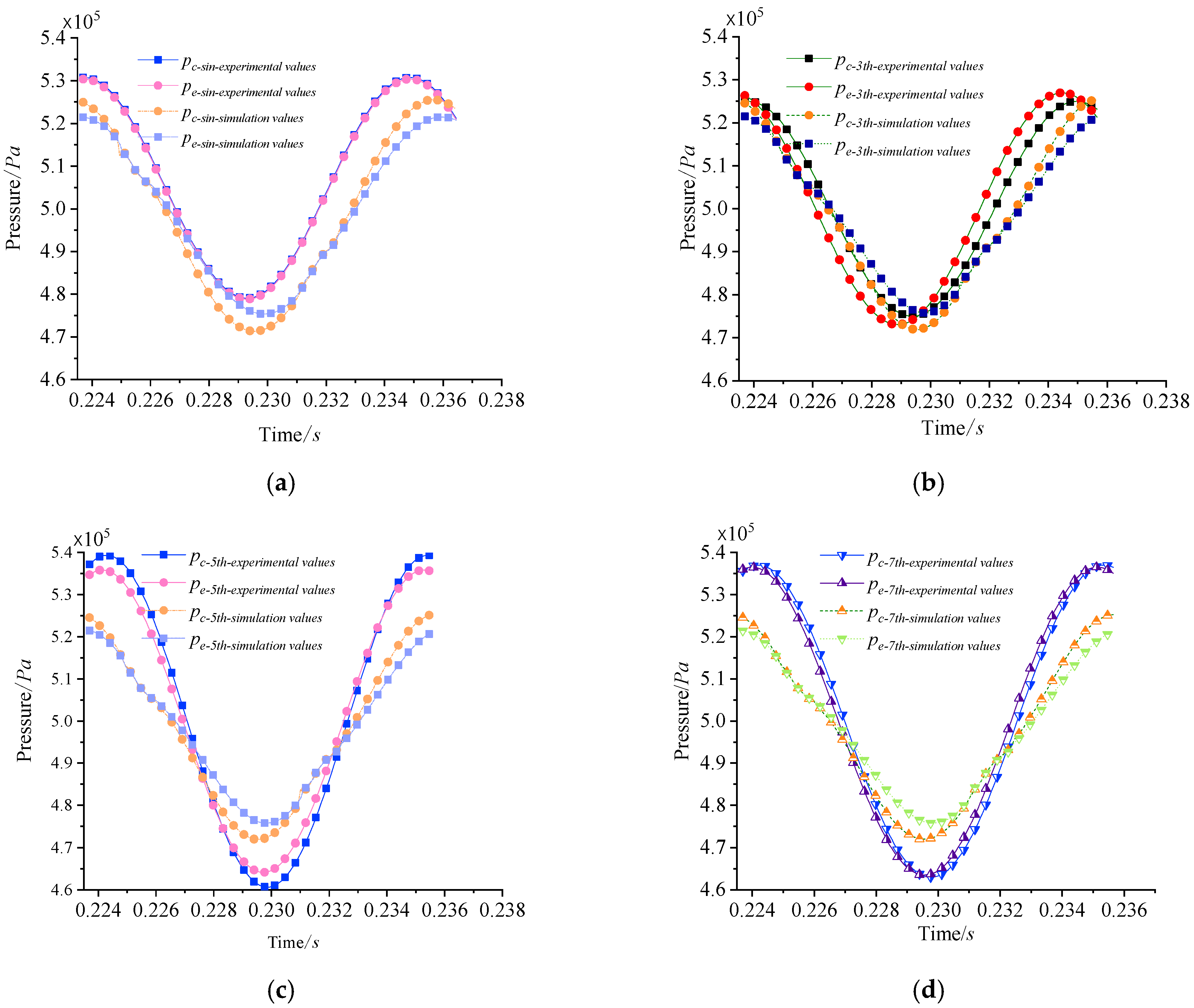
4.3. Analysis of Experimental Results
- (1)
- Inflation pressure error. The Stirling air conditioner utilized a vacuum evacuation process, followed by the injection of air. During operation, any variations in the vacuum level, if it does not reach the desired value, could affect the final pressure readings. Furthermore, the removal of the gas nozzle after inflation could result in slight leakage, leading to deviations in the inflation pressure and contributing to measurement errors.
- (2)
- Modeling error. In developing the fundamental equations to simulate the operation of the Stirling air conditioner, several assumptions were made, including the consideration of axial heat conduction within the gas and the assumption of constant wall temperatures for the heat exchangers. These assumptions inevitably led to minor deviations in the simulation model.
- (3)
- Measurement error in experiments. Due to the structural constraints of the free-piston Stirling air conditioner, the pressure sensors could not be fully inserted into the compression and expansion chambers during the experimental tests. As a result, the measured data may deviate from the actual pressures. Although multiple measurements were taken and averaged, this process still introduces a degree of experimental measurement error.
- (1)
- During the development of the FPSAC system model, discrepancies between the actual performance and theoretical predictions may occur due to inaccuracies or limitations in the reference data.
- (2)
- Assumptions made while deriving the fundamental equations to simulate the FPSAC operating process can introduce biases into the model.
- (3)
- Errors resulting from the precision limitations of the chosen sensors, environmental fluctuations, and variations in the operating conditions further contribute to the overall uncertainty in the system performance experiments. Despite these factors, the cumulative effect of these uncertainties remains within an acceptable range, thereby ensuring the reliability of the experimental results.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| F | force | N |
| B | magnetic flux density | T |
| x | displacement | m |
| acceleration | m2/s | |
| l | length | m |
| C | friction factor | N/m2 |
| Re | Reynolds number | |
| P | pressure | Pa |
| V | volume | mm3 |
| A | area | mm2 |
| N | number | |
| m | mass | g |
| velocity | m/s | |
| c | specific heat capacity | J/kg·K |
| T | temperature | K |
| R | thermodynamic constant | J/mol·K |
| μ | dynamic viscosity | N·s/m2 |
| px | pressure gradient | Pa/m |
| Q | heat | J |
| ρ | density | kg/m3 |
References
- Wong, W.A.; Wilson, K.; Smith, E.; Collins, J. Path Finding the Flight Advanced Stirling Convertor Design with the ASCE3. In Proceedings of the Tenth International Energy Conversion Engineering Conference (IECEC-2012), Atlanta, GA, USA, 30 July–1 August 2012. NASA TM-2014-21775. [Google Scholar]
- Jang, K.H.; Kim, H.S.; Lee, S.H. Numerical analysis of free-piston stirling cooler systems for improving cooling performance. Case Stud. Therm. Eng. 2022, 37, 102272. [Google Scholar] [CrossRef]
- Onwuemezie, L. Numerical study of H2-fuelled micro-free piston CHP system, coupled with thermophotovoltaic (TPV) and battolyser units. Process Saf. Environ. Prot. 2024, 192, 13–25. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Liu, B.; Dong, H.; Liu, X. Progress in Applications of Reverse Stirling Cycle Technology in Air Conditioning System of Pure Electric Vehicles. J. Xi’an Technol. Univ. 2021, 6, 609–620. [Google Scholar]
- Corporation, I. High-Efficiency Stirling Air Conditioning: Office of Scientific & Technical Information Technical Reports; Advanced Research Projects Agency: Ballston, VA, USA, 2012. [Google Scholar]
- Mraz, S.J. Stirling Cycle for Solar Power and Air Conditioning. Mach. Des. 2011, 83, 19. [Google Scholar]
- Hachem, H.; Gheith, R.; Aloui, F.; Nasrallah, S.B.; Dincer, I. Exergy Assessment of Heat Transfer inside a Beta Type Stirling Engine. Int. J. Exergy 2016, 20, 186–202. [Google Scholar]
- Hachem, H.; Gheith, R.; Nasrallah, S.B.; Aloui, F. Impact of Operating Parameters on Beta Type Regenerative Stirling Machine Performances. In Proceedings of the ASME-JSME-KSME 2015, Joint Fluids Engineering Conference, Seoul, Republic of Korea, 26–31 July 2015; p. 22088. [Google Scholar]
- Hachem, H.; Gheith, R.; Aloui, F.; Ben Nasrallah, S. Numerical characterization of a γ-Stirling engine considering losses and interaction between functioning parameters. Energy Convers. Manag. 2015, 96, 532–543. [Google Scholar] [CrossRef]
- Luo, K.; Sun, Y.; Luo, E.; Hu, J.; Wu, Z.; Zhang, L.; Jia, Z.; Jiang, Z.; Zhou, Y. Investigation on the Electric-Driven High Power Free-Piston Stirling Cooler at Air-Conditioning Temperature Range. J. Eng. Therm. 2022, 43, 2623–2630. [Google Scholar]
- Mou, J.; Hong, G. Startup mechanism and power distribution of free piston Stirling engine. Energy 2017, 123, 655–663. [Google Scholar] [CrossRef]
- Valenti, G.; Bischi, A.; Campanari, S.; Silva, P.; Ravida, A.; Macchi, E. Experimental and Numerical Study of a Microcogeneration Stirling Unit under On–Off Cycling Operatio. Energies 2021, 14, 801. [Google Scholar] [CrossRef]
- Minale, T.; Lanzetta, F.; Bégot, S.; Getie, M.Z. Review on the technological advancement of Stirling cycle heat pumps. Energy Rep. 2024, 12, 3504–3518. [Google Scholar] [CrossRef]
- Regalado-Rodríguez, N.; Militello, C. Comparative study of the effects of increasing heat transfer area within compression and expansion chambers in combination with modified pistons in Stirling engines. A simulation approach based on CFD and a numerical thermodynamic model. Energy Convers. Manag. 2022, 268, 115930. [Google Scholar] [CrossRef]
- Wang, K.; Dubey, S.; Choo, F.H.; Duan, F.A. A transient One-dimensional Numerical Model for Kinetic Stirling Engine. Appl. Energy 2016, 183, 775–790. [Google Scholar] [CrossRef]
- Chi, C.; Li, R.; Mou, J.; Lin, M.; Jiao, K.; Yang, M.; Liu, H.; Hong, G. Theoretical and Experimental Study of Free Piston Stirling Generator for High Cold End Temperatures. Energy 2024, 289, 129841. [Google Scholar] [CrossRef]
- Yang, H.S.; Zhu, H.Q.; Xiao, X.Z. Comparison of the Dynamic Characteristics and Performance of Beta-type Stirling Engines Operating with Different Driving Mechanisms. Energy 2023, 275, 127535. [Google Scholar] [CrossRef]
- Ukan, R.; Yakn, A.; Behet, R. Second law analysis of an internal combustion engine for different fuels consisting of NaBH4, ethanol and methanol mixtures. Int. J. Hydrogen Energy 2024, 49, 1257–1267. [Google Scholar] [CrossRef]
- Cabir, B.; Yakin, A. Evaluation of gasoline-phthalocyanines fuel blends in terms of engine performance and emissions in gasoline engines. J. Energy Inst. 2024, 112, 101483. [Google Scholar] [CrossRef]
- Yakin, A.; Mehmet, G.; Celebi, S.; Demir, U.; Yilmaz, E. Investigation of the performance and emission effects of ammonia-borane as a B–N-based amine-borane adduct in gasoline engines. Int. J. Hydrogen Energy 2024, 87, 1129–1139. [Google Scholar] [CrossRef]
- Finkelstein, T. Thermodynamic Analysis of Stirling Engines. J. Spacecr. Rockets 2012, 4, 1184–1189. [Google Scholar] [CrossRef]
- Urieli, I.; Berchowitz, D.M. Stirling Cycle Engine Analysis; Adam Hilger: Bristol, UK, 1984. [Google Scholar]
- Schock, A. Stirling Engine Nodal Analysis Program. J. Energy 1978, 2, 354–362. [Google Scholar] [CrossRef]
- Goldberg, L.F. One and Two-Dimensional Stirling Machine Simulation Using Experimentally Generated Reversing Flow Turbulence Models; NASA-CR-185285; NASA: Washington, DC, USA, 1990.
- Andersen, S.K. Numerical Simulation of Cyclic Thermodynamic Processes; Technical University of Denmark: Kongens Lyngby, Denmark, 2006. [Google Scholar]
- Deetlefs, I.N. Design, Simulation, Manufacture and Testing of a Free-Piston Stirling Engine; University of Stellenbosch: Stellenbosch, South Africa, 2014. [Google Scholar]
- Mohammadi, M.A.; Jafarian, A. CFD Simulation to Investigate Hydrodynamics of Oscillating Flow in a Beta-type Stirling Engine. Energy 2018, 153, 287–300. [Google Scholar] [CrossRef]
- Kropiwnicki, J. Low temperature rotary Stirling engine: Conceptual design and theoretical analysis. Appl. Therm. Eng. 2024, 257, 124276. [Google Scholar] [CrossRef]
- Yang, D.; Gschwendtner, M.; Waleed, Z.; Protheroe, M. The pressure-volume relationship in an ideal Stirling refrigerator. Cryogenics 2024, 141, 103882. [Google Scholar] [CrossRef]
- Ye, W.; Wang, W.; Long, H.; Sun, S.; Kong, L. Effect of thermodynamic-dynamic parameters on the oscillation and performance of a free piston Stirling engine. Appl. Ther. Eng. 2024, 253, 123845. [Google Scholar] [CrossRef]
- Bert, J.; Chrenko, D.; Sophy, T.; Moyne, L.; Sirot, F. Simulation, experimental validation and kinematic optimization of a Stirling engine using air and helium. Energy 2014, 78, 701–712. [Google Scholar] [CrossRef]
- Masser, R.; Khodja, A.; Scheunert, M.; Schwalbe, K.; Fischer, A. Optimized piston motion for an alpha-type Stirling engine. Entropy 2020, 22, 700. [Google Scholar] [CrossRef] [PubMed]
- Paul, R.; Khodja, A.; Fischer, A.; Masser, R.; Hoffmann, H. Power-optimal control of a Stirling engine’s frictional piston motion. Entropy 2022, 24, 362. [Google Scholar] [CrossRef] [PubMed]
- Zainudin, M.; Bakar, R.; Ming, G. Kinematic and thermodynamic operational analysis of rhombic-drive Stirling engine prototype. IOP Conf. Ser. Mater. Sci. Eng. 2020, 788, 012070. [Google Scholar] [CrossRef]
- Briggs, M. Improving power density of free-piston stirling engines. In Proceedings of the 14th International Energy Conversion Engineering Conference, Salt Lake City, UT, USA, 25–27 July 2016; p. 5016. [Google Scholar]
- Craun, M.; Bamieh, B. Optimal periodic control of an ideal stirling engine model. J. Dyn. Syst. Meas. Control 2015, 137, 071002. [Google Scholar] [CrossRef]
- Wong, H.; Goh, S. Experimental comparison of sinusoidal motion and non-sinusoidal motion of rise-dwell-fall-dwell in a Stirling engine. J. Mech. Eng. Sci. 2020, 14, 6971–6981. [Google Scholar] [CrossRef]
- Karabulut, H.; Okur, M.; Cinar, C. Mechanical Configuration and Thermodynamic Analysis of an Alpha-Type Stirling Engine with Crank-Shifted Driving Mechanism. Iran. J. Sci. Technol. Trans. Mech. Eng. 2022, 46, 431–448. [Google Scholar] [CrossRef]
- Öztürk, E. Optimization of a novel drive mechanism approaching the ideal cycle for beta type Stirling engines. Eng. Sci. Technol. Int. J. 2023, 47, 101555. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, K.; Zhang, J. Study on the Thermodynamic–Kinetic Coupling Characteristics of Free-Piston Stirling Air Conditioning. Energies 2024, 17, 5795. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Lu, Z.; Liu, B.; Dong, H. Analysis of Radial Heat Transfer Characteristics of Oscillating Flow in Regenerator with Normal Hexagonal Bundle. Energies 2023, 16, 6411. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Lu, Z.; Liu, J.; Liu, B.; Dong, H. Analytical Solution of Heat Transfer Performance of Grid Regenerator in Inverse Stirling Cycle. Energies 2022, 15, 7024. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Zhang, T.; Lu, Z.; Dong, H. Analysis and experiment of heat transfer performance of straight-channel grid regenerator. Int. J. Heat Technol. 2022, 40, 781–791. [Google Scholar] [CrossRef]
- Jin, D. Technologies of Stirling Engine; Harbin Engineering University Press: Harbin, China, 2009. [Google Scholar]
- De La Bat, J.G. Theoretical Simulation, Manufacture and Experimental Evaluation of a Free-Piston Stirling Engine Electric Generator. Ph.D. Thesis, Faculty of Engineering, University of Stellenbosch, Stellenbosch, South Africa, 2019. [Google Scholar]
- De la Bat, B.; Harms, T.; Dobson, R.; Bell, A. Derivation and numerical case study of a one-dimensional, compressible-flow model of a novel free-piston Stirling engine. Energy 2020, 199, 117404. [Google Scholar] [CrossRef]
- Bird, R.; Stewart, W.; Lightfoot, E. Transport Phenomena, 2nd ed.; John Wiley and Sons Inc.: New York, NY, USA, 2002. [Google Scholar]
- Sari, M.; Ouazir, Y.; Mezani, S. New 2-D Quasi-Analytical Computation of Eddy Currents in Axisymmetrical Problems: Application to Tubular Linear Induction Motor. IEEE Trans. Magn. 2023, 3, 1–13. [Google Scholar] [CrossRef]
- Sun, Z.; Jia, G.; Huang, C.; Zhou, W.; Mao, Y.; Lei, Z. Accurate Modeling and Optimization of Electromagnetic Forces in an Ironless Halbach-Type Permanent Magnet Synchronous Linear Motor. Energies 2023, 16, 5785. [Google Scholar] [CrossRef]
- Ranieri, S.; Prado, G.; MacDonald, B. Efficiency Reduction in Stirling Engines Resulting from Sinusoidal Motion. Energies 2018, 11, 2887. [Google Scholar] [CrossRef]
- Muzzo, L.E.; Matoba, G.K.; Ribeiro, L.F. Uncertainty of pipe flow friction factor equations. Mech. Res. Commun. 2021, 116, 103764. [Google Scholar] [CrossRef]
- Gedeon, D.; Wood, J. Oscillating-Flow Regenerator Test Rig: Hardware and Theory with Derived Correlations for Screens and Felts; NASA-CR-198442; NASA: Washington, DC, USA, 1996.




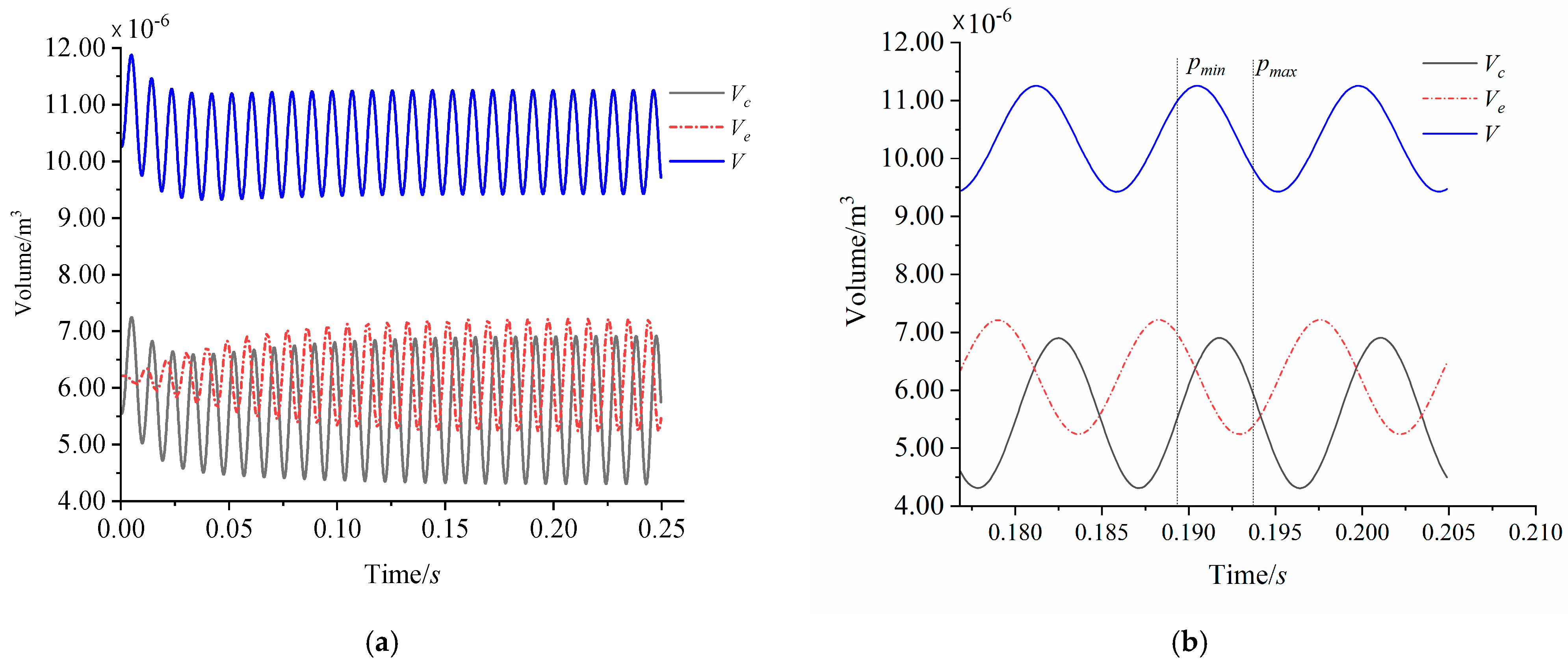
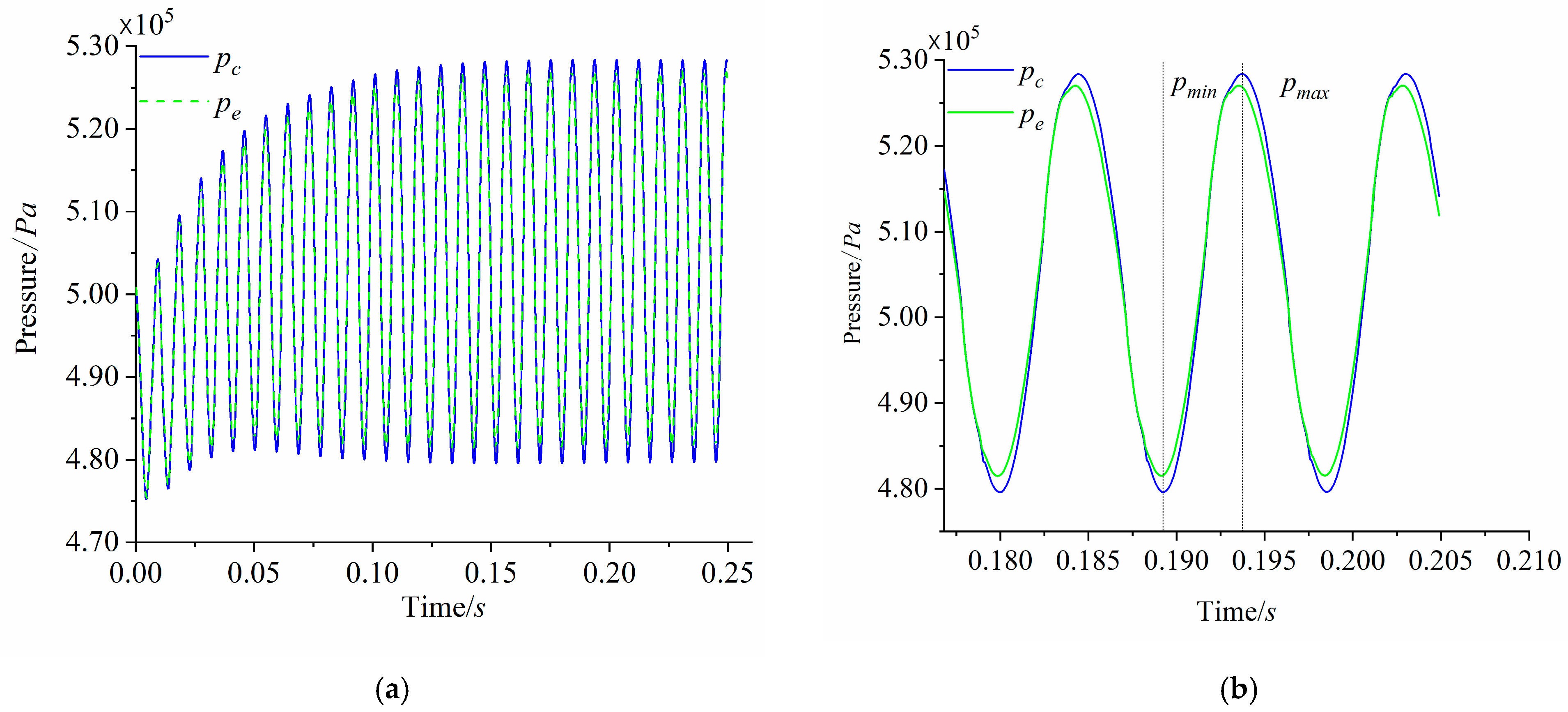
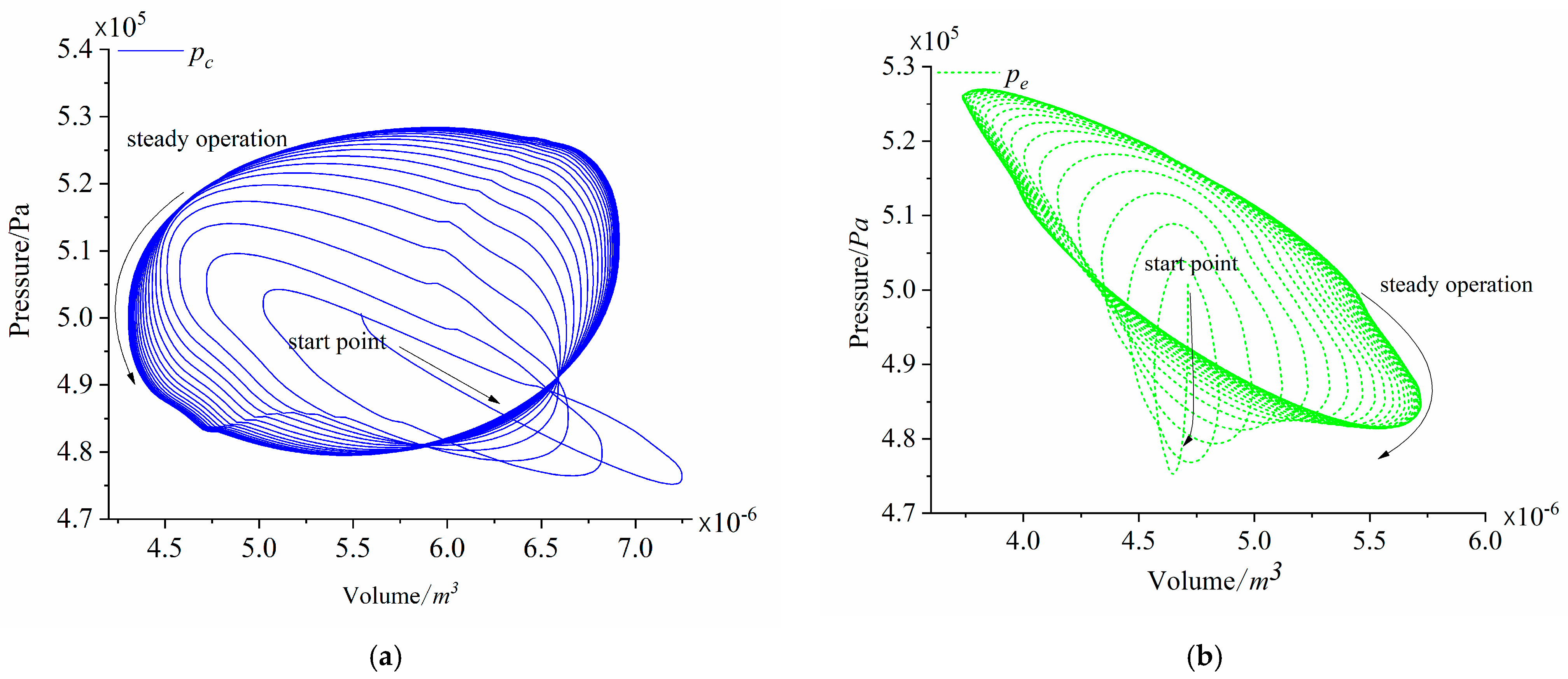
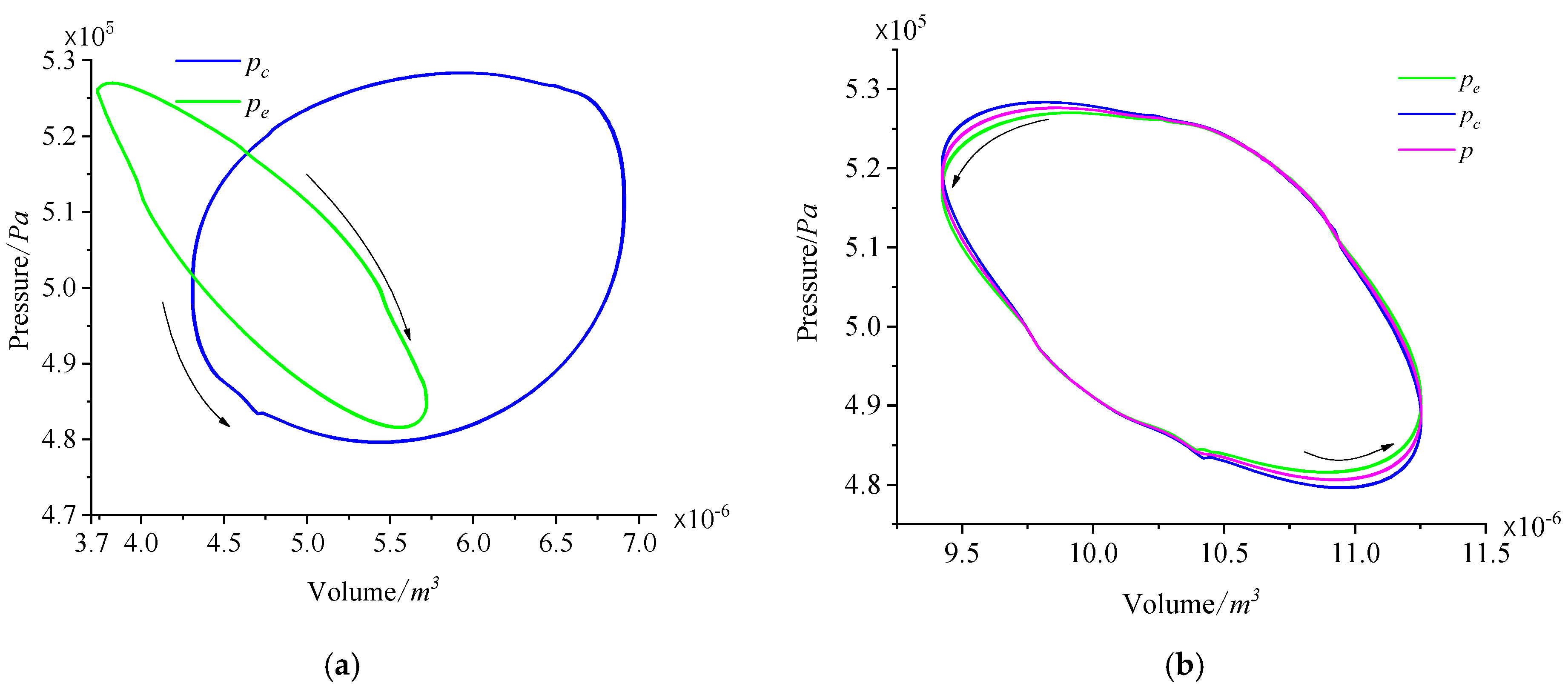
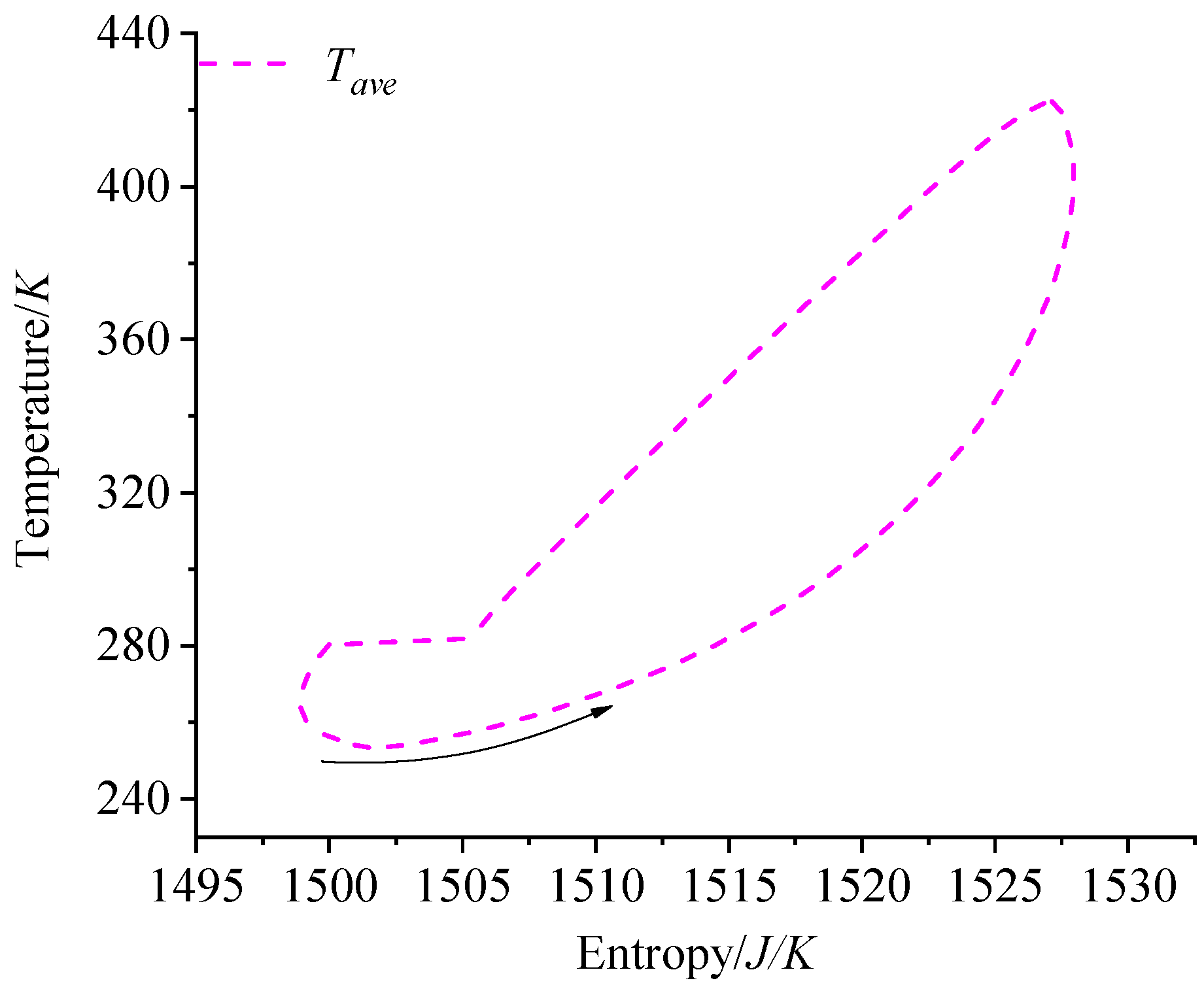

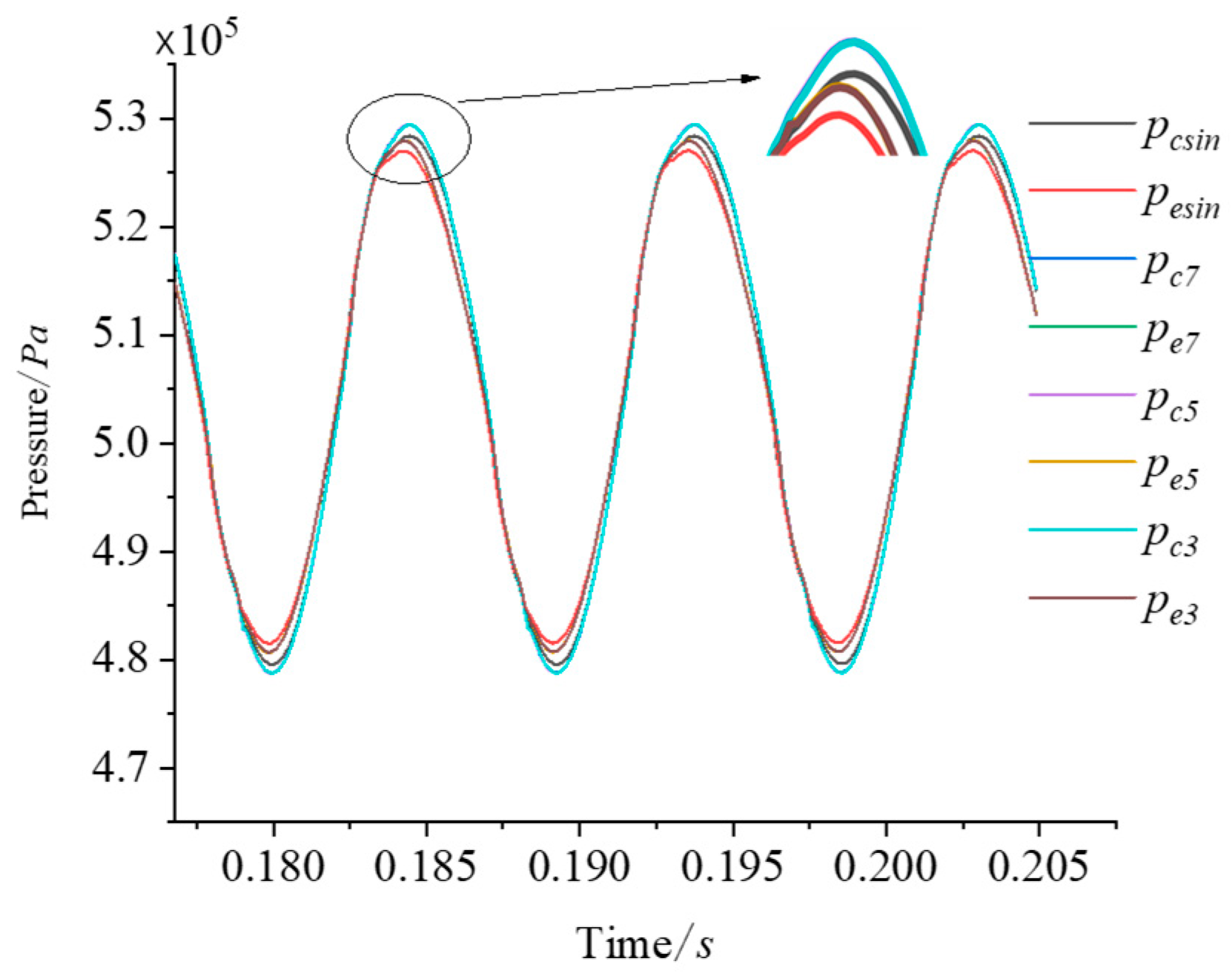
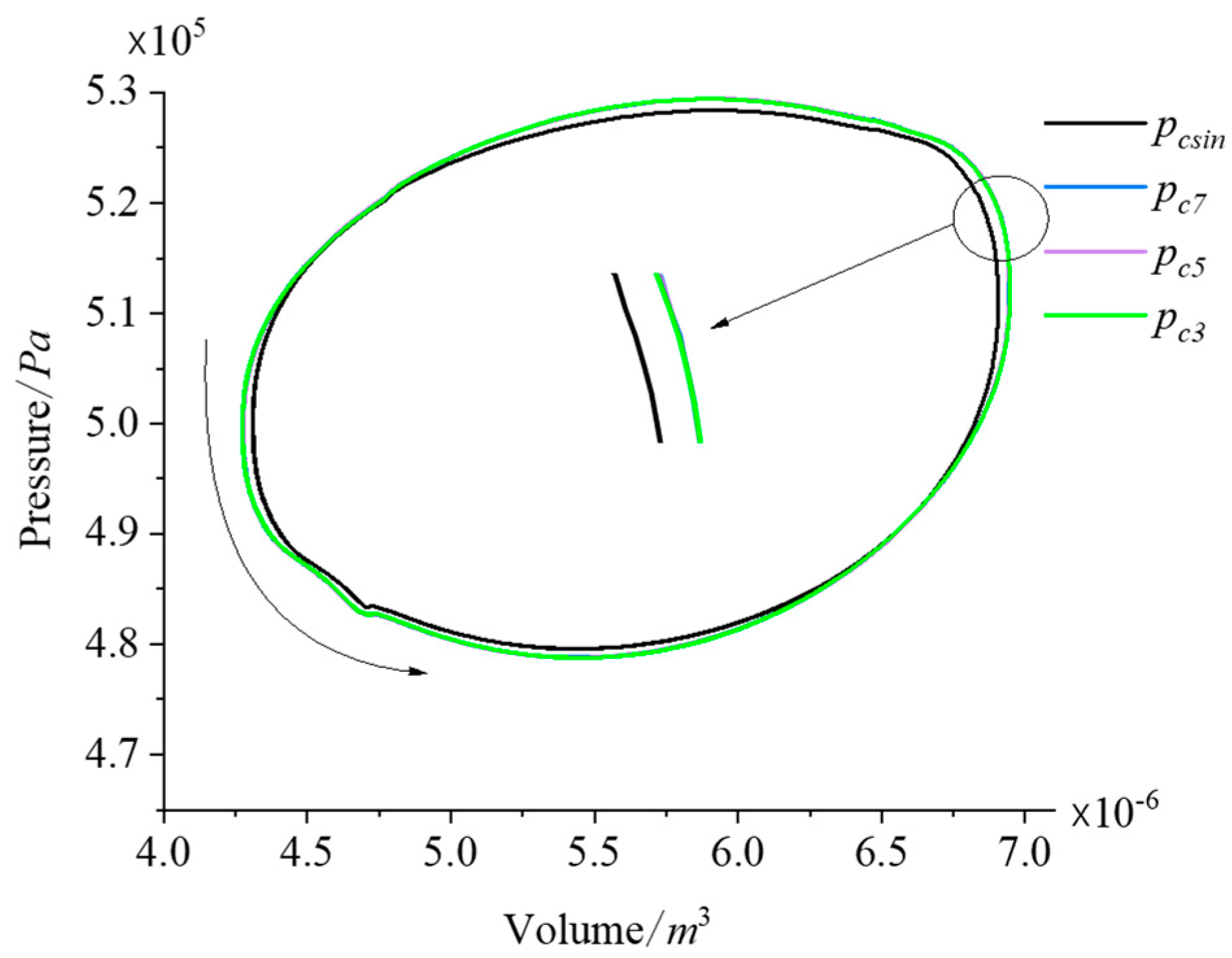
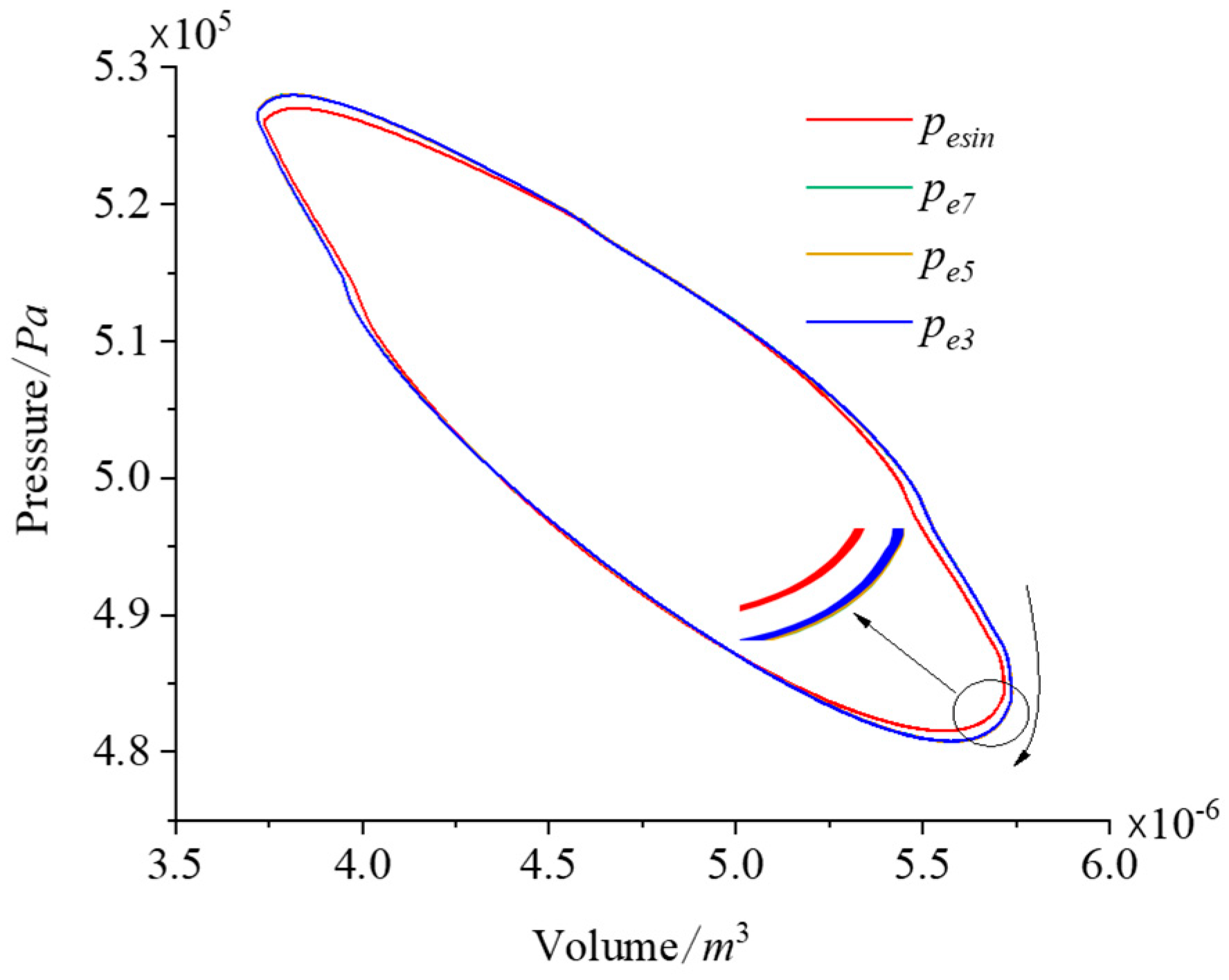



| Simulation Parameters | Value | Unit |
|---|---|---|
| Time step | dt = 17 × 10−10 | s |
| No. of heater cells | Nh = 50 | |
| No. of cooler cells | Nc = 50 | |
| No. of regenerator cells | Nr = 50 | |
| Working fluid | He | |
| Average charge pressure | p0 = 5 × 105 | Pa |
| Total engine gas mass | mt = 0.03 | g |
| Hot-end temperature | Th = 320 | K |
| Cold-end temperature | Tc = 290 | K |
| Structural Parameters and Dynamic Parameters | Value | Unit |
|---|---|---|
| Heater length | Lh = 14.2 | mm |
| Cooler length | Lc = 14.2 | mm |
| Regenerator length | Lr = 45.0 | mm |
| Regenerator inner diameter | r = 0.7 | mm |
| Regenerator outer diameter | R = 1 | mm |
| Displacer diameter | D1 = 19.343 | mm |
| Displacer shaft diameter | D2 = 3.2791 | mm |
| Power piston diameter | D3 = 19.4602 | mm |
| Heater/cooler length | Lrl = 4.4 | mm |
| Heater/cooler width | Lrw = 0.3 | mm |
| Heater/cooler height | Lrh = 12.5 | mm |
| Displacer length | L1 = 63.62 | mm |
| Power piston length | L3 = 65.05 | mm |
| Distance between the power piston and the upper chamber | LE = 6.18 | mm |
| Distance between the displacer and the upper chamber | Lc = 6.18 | mm |
| Displacer mass | md = 18.2 | g |
| Power piston mass | mp = 60.4 | g |
| Displacer spring stiffness | kd = 4.7 | N/mm |
| Power piston spring stiffness | kp = 6.2 | N/mm |
| Linear motor operating frequency | f = 80 | Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, J.; Guo, J.; Zhang, G.; Zhang, J. Performance Simulation and Experimental Verification of a Low-Temperature Differential Free-Piston Stirling Air Conditioner Under Multi-Harmonic Drive. Processes 2025, 13, 134. https://doi.org/10.3390/pr13010134
Wang Y, Zhang J, Guo J, Zhang G, Zhang J. Performance Simulation and Experimental Verification of a Low-Temperature Differential Free-Piston Stirling Air Conditioner Under Multi-Harmonic Drive. Processes. 2025; 13(1):134. https://doi.org/10.3390/pr13010134
Chicago/Turabian StyleWang, Yajuan, Junan Zhang, Junde Guo, Gao Zhang, and Jianhua Zhang. 2025. "Performance Simulation and Experimental Verification of a Low-Temperature Differential Free-Piston Stirling Air Conditioner Under Multi-Harmonic Drive" Processes 13, no. 1: 134. https://doi.org/10.3390/pr13010134
APA StyleWang, Y., Zhang, J., Guo, J., Zhang, G., & Zhang, J. (2025). Performance Simulation and Experimental Verification of a Low-Temperature Differential Free-Piston Stirling Air Conditioner Under Multi-Harmonic Drive. Processes, 13(1), 134. https://doi.org/10.3390/pr13010134






