Structural Design Analysis of Substrate with Honeycomb Core Under Normal Pressure, Using RSM and ANN
Abstract
:1. Introduction
2. Method
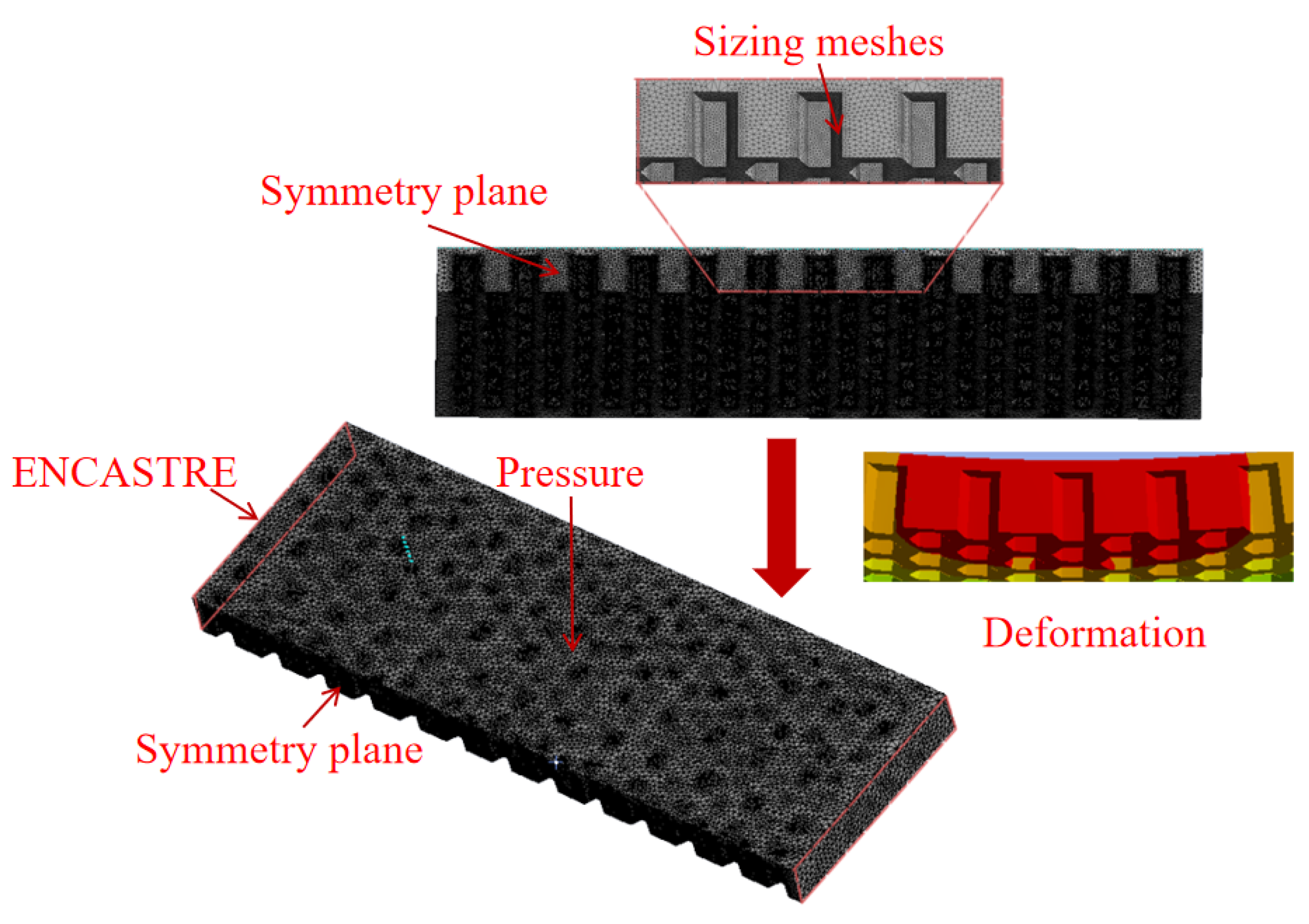
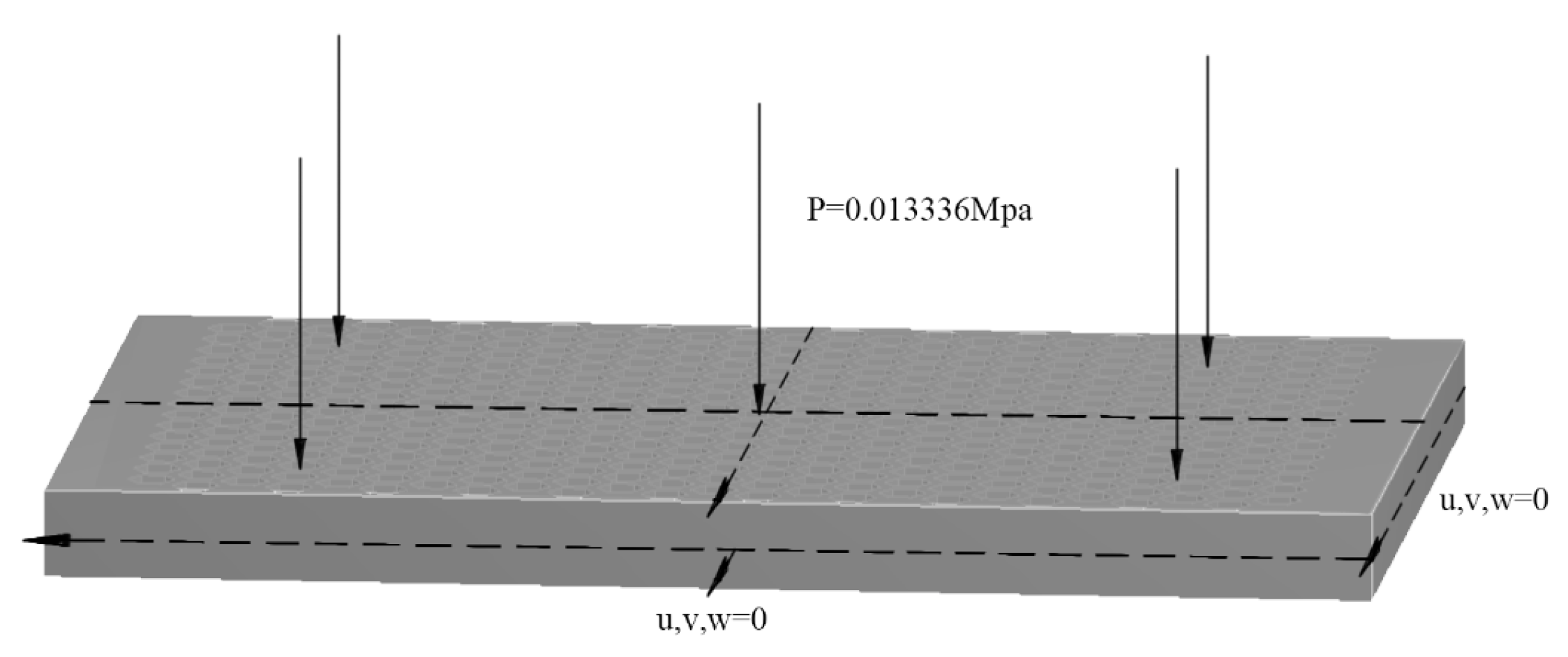
2.1. Problem Description
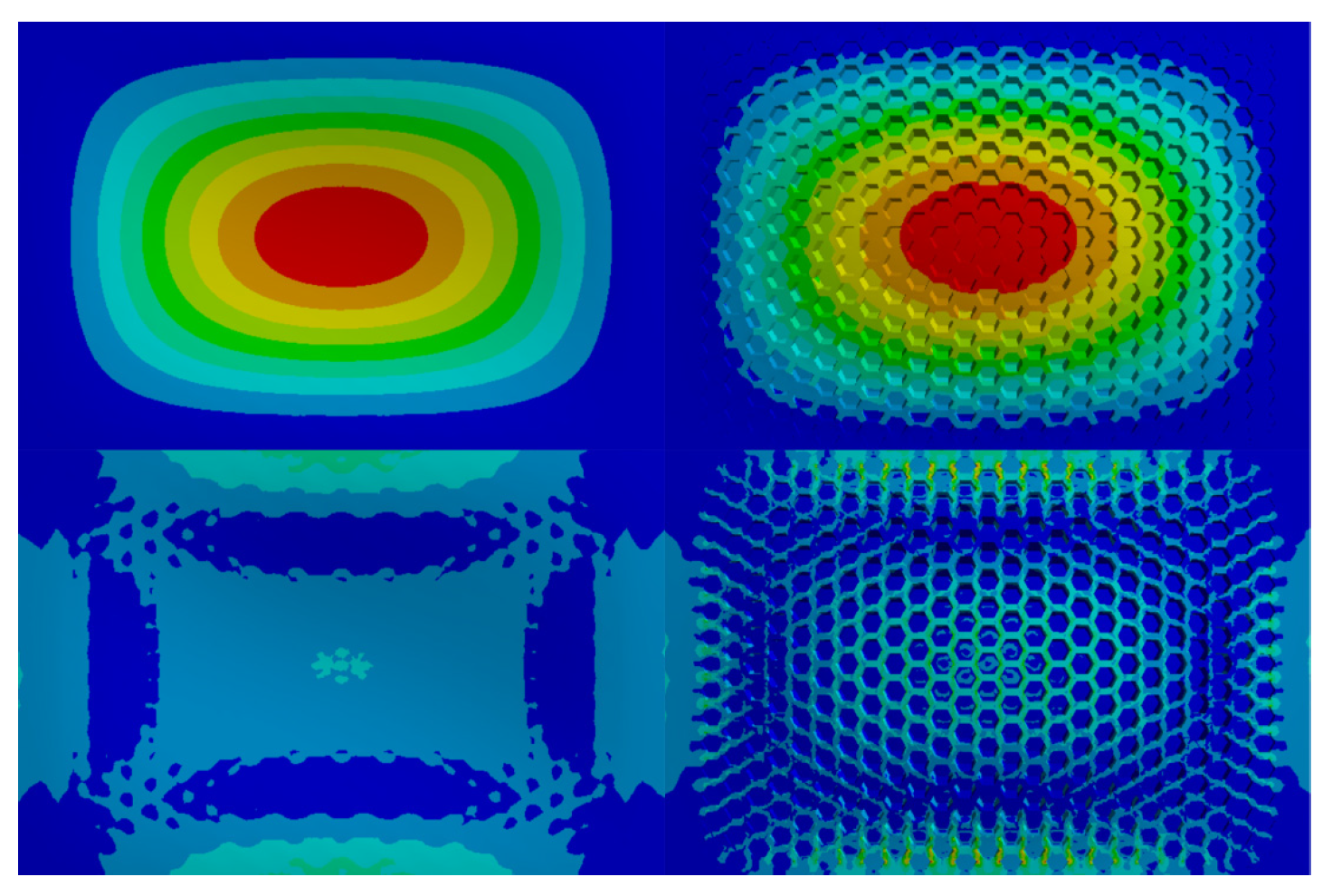
2.2. Finite Elemental Method
2.3. Mesh Convergence Study
2.4. Response-Surface Method
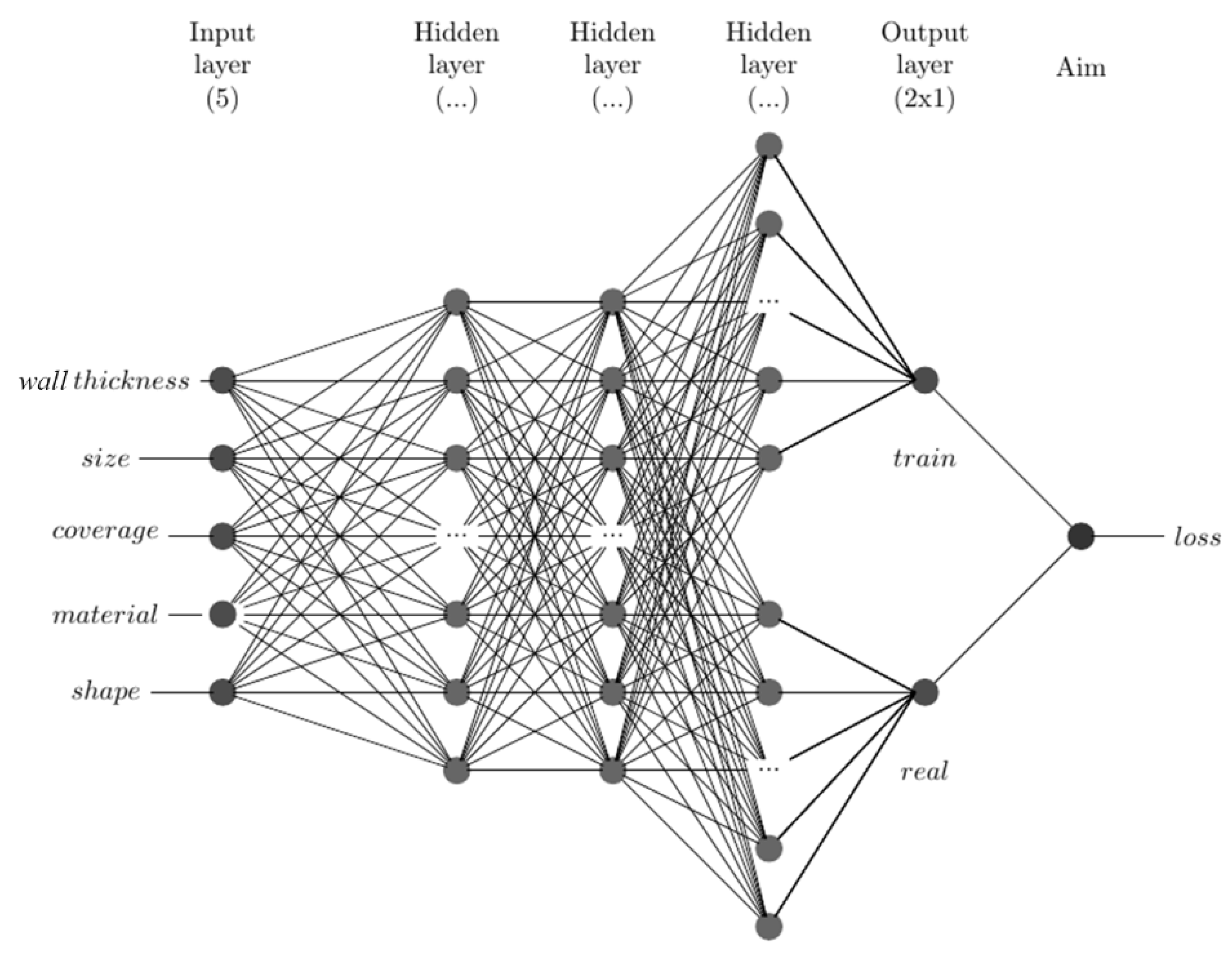
2.5. Artificial Neural Network Method
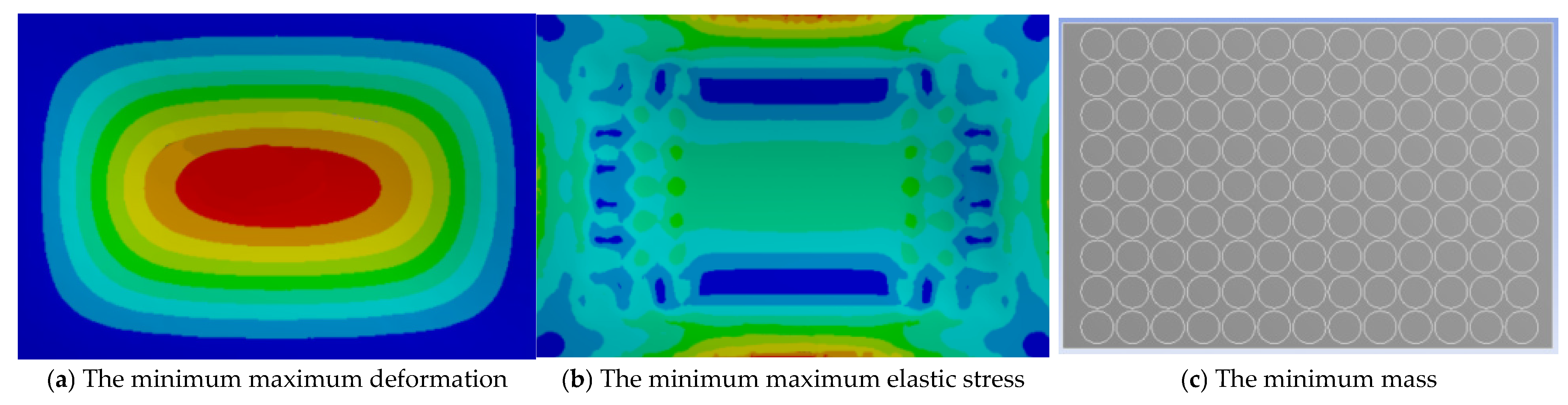
3. Results and Discussions
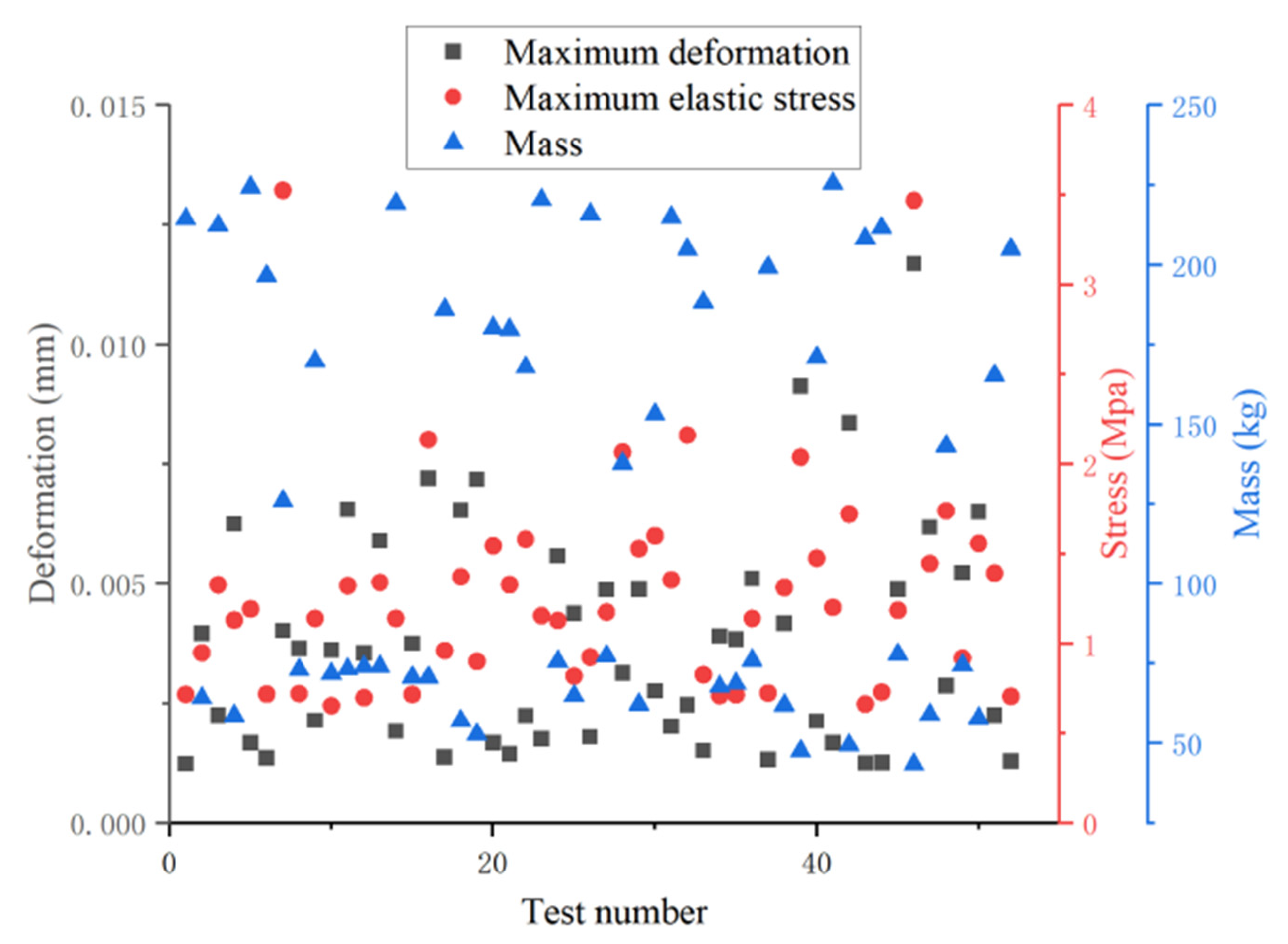
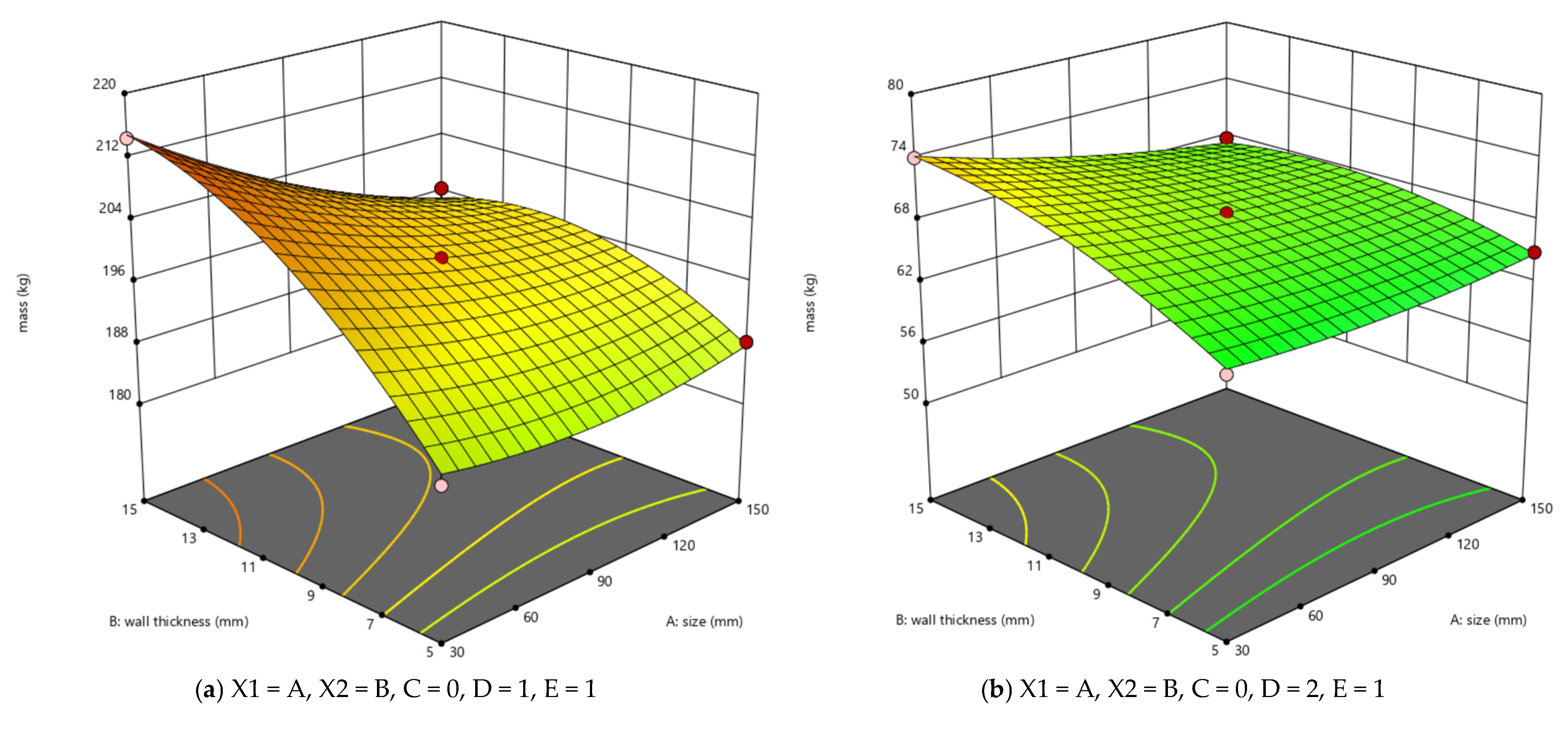
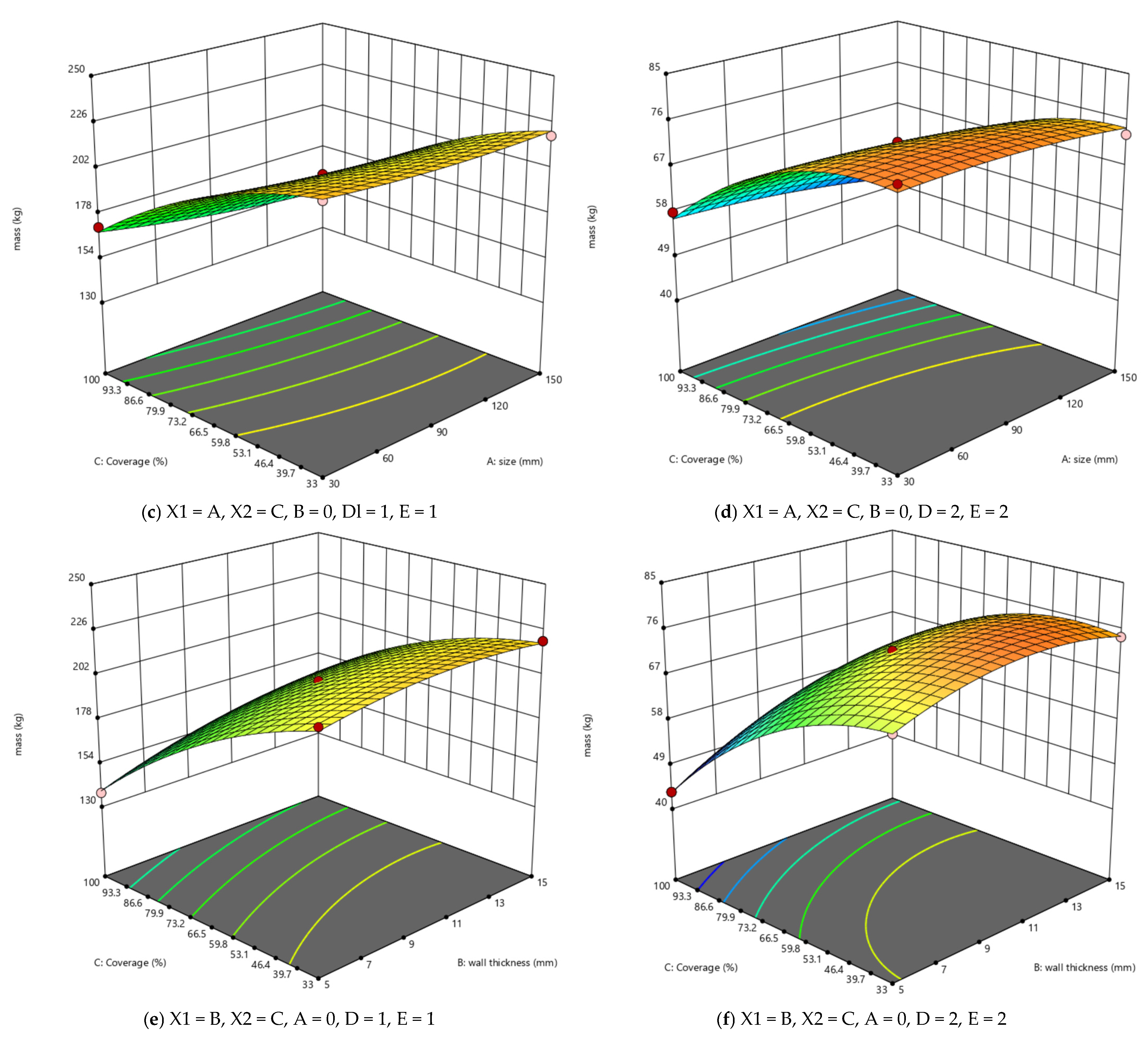
3.1. RSM Results Analysis
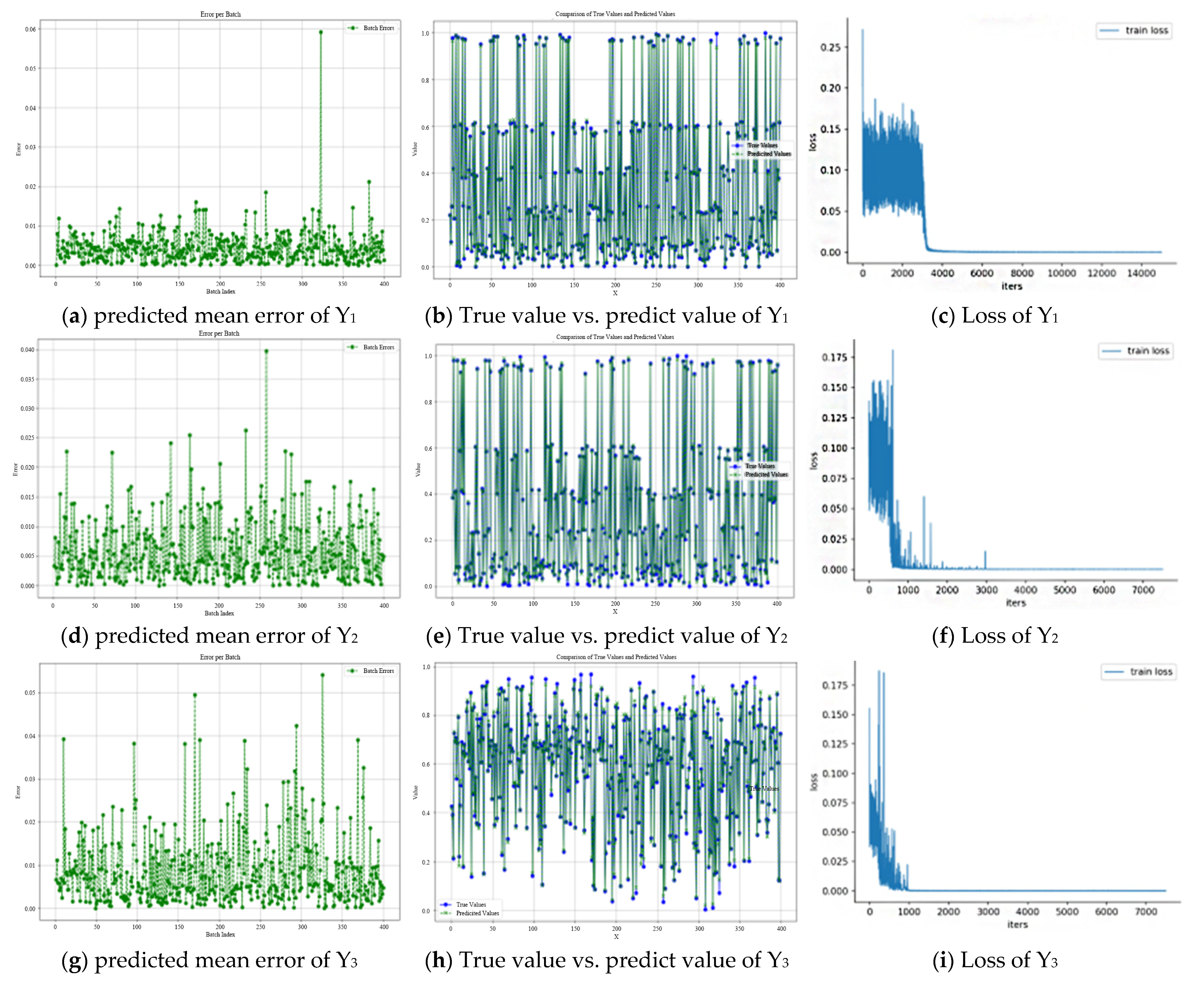
3.2. ANN Results
3.3. Discussions
4. Conclusions
5. Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Replication of Results
Appendix A.1. Data Generated
| import random |
| c_values = [0, 13, 26, 33, 39, 52, 65, 79, 100] |
| d_values = [0.1, 0.11] |
| e_values =[0.1, 0.11] |
| data = [] |
| count = 0 |
| while count < 2000: |
| a = round(random.uniform(30, 90), 3) |
| b = round(random.uniform(5, 15), 3) |
| c = random.choice(c_values) |
| d = random.choice(d_values) |
| e = random.choice(e_values) |
| x = 0.0025 + (0.0003) * a - (0.0006) * b + (0.0007) *c + (0.0018) * d + (0.0002)*e - (0.0001) * a * b + (0.0001) * a * c + (0.0001) * a * d + (0.0001) * a * e - (0.0004) * b * c - (0.0003) * b * d - (0.0002) * b * e + (0.0003) * c * d + (0) * c * e + (0.0001) * d * e - (0.0002) * a * a + (0.0004) * b * b + (0.0019) * c * c |
| x = 0.0025 + (0.0003 + bias_x_a) * a -(0.0006 + bias_x_b) * b + (0.0007 + bias_x_c) *c + (0.0018 + bias_x_d) * d + (0.0002)*e - (0.0001) * a * b + (0.0001) * a * c + (0.0001) * a * d + (0.0001) * a * e - (0.0004 + bias_x_bc) * b * c - (0.0003 + bias_x_bd) * b * d - (0.0002) * b * e + (0.0003 + bias_x_cd) * c * d + (0) * c * e + (0.0001) * d * e - (0.0002) * a * a + (0.0004) * b * b + (0.0019 + bias_x_cc) * c * c |
| z = 0.6896 + 0.0071 * a - 0.39 * b + 0.2298 * c - 0.021 * d + 0.1384 * e - 0.0117 * a * b -0.0164 * a * c - 0.0192 * a * d + 0.055 * a * e - 0.2004 * b * c + 0.0031 * b * d - 0.2364 * b * e - 0.024 * c * d + 0.0633 * c * e + 0.0133 * d * e - 0.0501 * a * a + 0.2981 * b * b + 0.7176 * c * c |
| x = z * 0.000001 |
| data.append((a, b, c, d, e, x)) |
| count += 1 |
| with open('data2.txt', 'w') as file: |
| for item in data: |
| file.write(f"{item[0]} {item[1]} {item[2]} {item[3]} {item[4]} {item[5]}\n") |
Appendix A.2. ANN for Train
| import torch |
| import torch.nn as nn |
| import torch.optim as optim |
| import numpy as np |
| from torch.utils.data import Dataset, DataLoader |
| import matplotlib.pyplot as plt |
| from sklearn.preprocessing import MinMaxScaler |
| def read_data_file(file_path): |
| with open(file_path, 'r') as file: |
| lines = file.readlines() |
| data_list = [] |
| labels_list = [] |
| for line in lines: |
| parts = line.strip().split() |
| features = torch.tensor([float(x) for x in parts[:5]], dtype=torch.float32) |
| labels = torch.tensor([float(y) for y in parts[5:]], dtype=torch.float32) |
| data_list.append(features) |
| labels_list.append(labels) |
| return torch.stack(data_list), torch.stack(labels_list) |
| file_path = 'C:\\Users\\lpy\\Desktop\\ultralytics-main\\data2.txt' |
| data, labels = read_data_file(file_path) |
| class CustomDataset(Dataset): |
| def __init__(self, data, labels): |
| self.data = data |
| self.labels = labels |
| self.scaler = MinMaxScaler(feature_range=(0, 1)) |
| self.data = self.scaler.fit_transform(data.numpy()) |
| self.data = torch.tensor(self.data, dtype=torch.float32) |
| self.scaler1 = MinMaxScaler(feature_range=(0, 1)) |
| self.labels = self.scaler1.fit_transform(labels.numpy()) |
| self.labels = torch.tensor(self.labels, dtype=torch.float32) |
| def __len__(self): |
| return len(self.labels) |
| def __getitem__(self, idx): |
| data_item = self.data[idx] |
| labels_item = self.labels[idx] |
| return data_item, labels_item |
| if __name__ == "__main__": |
| dataset = CustomDataset(data, labels) |
| dataset_size = len(dataset) |
| train_size = int(0.8 * dataset_size) |
| train_dataset = torch.utils.data.Subset(dataset, list(range(train_size))) |
| val_dataset = torch.utils.data.Subset(dataset, list(range(train_size, dataset_size))) |
| dataloader = DataLoader(train_dataset, batch_size=32, shuffle=True, num_workers=8) |
| dataloader1 = DataLoader(val_dataset, batch_size=1, shuffle=False, num_workers=8) |
| device = torch.device("cuda" if torch.cuda.is_available() else "cpu") |
| X = data.to(device) |
| Y = labels.to(device) |
| class Net(nn.Module): |
| def __init__(self): |
| super(Net, self).__init__() |
| self.linear1 = nn.Linear(5, 32) |
| self.relu1 = nn.ReLU() |
| self.linear2 = nn.Linear(32, 64) |
| self.relu2 = nn.ReLU() |
| self.linear3 = nn.Linear(64, 128) |
| self.relu3 = nn.ReLU() |
| self.linear4 = nn.Linear(128, 256) |
| self.relu4 = nn.ReLU() |
| self.linear5 = nn.Linear(256,128) |
| self.relu5 = nn.ReLU() |
| self.linear6 = nn.Linear(128, 64) |
| self.relu6 = nn.ReLU() |
| self.linear7 = nn.Linear(64, 32) |
| self.relu7 = nn.ReLU() |
| self.linear11 = nn.Linear(32, 1) |
| def forward(self, X): |
| X = self.linear1(X) |
| X = self.relu1(X) |
| X = self.linear2(X) |
| X = self.relu2(X) |
| X = self.linear3(X) |
| X = self.relu3(X) |
| X = self.linear4(X) |
| X = self.relu4(X) |
| X = self.linear5(X) |
| X = self.relu5(X) |
| X = self.linear6(X) |
| X = self.relu6(X) |
| X = self.linear7(X) |
| X = self.relu7(X) |
| X = self.linear11(X) |
| return X |
| model = Net() |
| model.to(device) |
| sgdd = optim.SGD(model.parameters(), lr=0.2) |
| sched= optim.lr_scheduler.StepLR(sgdd,60,0.1) |
| epoch = 150 |
| loss1 = nn.MSELoss(reduction='mean') |
| train_loss = [] |
| for i in range(epoch): |
| model.train() |
| running_loss = 0.0 |
| for data_batch, labels_batch in dataloader: |
| data_batch, labels_batch = data_batch.to(device), labels_batch.to(device) |
| sgdd.zero_grad() |
| predict = model(data_batch) |
| loss = loss1(predict, labels_batch) |
| train_loss.append(loss.item()) |
| loss.backward() |
| sgdd.step() |
| running_loss += loss.item() * data_batch.size(0) |
| sched.step() |
| with open("./train_loss.txt", 'w') as train_los: |
| train_los.write(str(train_loss)) |
| epoch_loss = running_loss / len(dataloader1.dataset) |
| print(f"Epoch {i+1}/150, Loss: {epoch_loss}") |
| with torch.no_grad(): |
| s=0 |
| all_label1 = [] |
| all_predict = [] |
| all_err = [] |
| for data_batch, label1 in dataloader1: |
| data_batch = data_batch.to(device) |
| predict = model(data_batch) |
| label1_flattened = label1.cpu().numpy().flatten() |
| predict_flattened = predict.squeeze().cpu().numpy().flatten() |
| all_label1.extend(label1_flattened) |
| all_predict.extend(predict_flattened) |
| s = np.abs(predict_flattened - label1_flattened).mean() |
| all_err.append(s) |
| #m = s / len(dataloader1) |
| m = s / len(dataloader1)# |
| #print (len(dataloader1)) |
| print(m) |
| plt.figure(figsize=(12, 8)) |
| plt.plot(range(1, len(all_err) + 1), all_err, marker='o', linestyle='--', color='green', label='Batch Errors') |
| plt.legend() |
| plt.title('Error per Batch') |
| plt.xlabel('Batch Index') |
| plt.ylabel('Error') |
| plt.grid(True) |
| plt.show() |
| plt.figure(figsize=(12, 8)) |
| plt.plot(range(len(dataloader1)), all_label1, marker='o', linestyle='-', color='blue', label='True Values') |
| plt.plot(range(len(dataloader1)), all_predict, marker='x', linestyle='--', color='green', label='Predicted Values') |
| plt.legend() |
| plt.title('Comparison of True Values and Predicted Values') |
| plt.xlabel('X') |
| plt.ylabel('Values') |
| plt.grid(True) |
| plt.show() |
| def data_read(dir_path): |
| with open(dir_path, "r") as f: |
| raw_data = f.read() |
| data = raw_data[1:-1].split(", ") |
| return np.asfarray(data, float) |
| if __name__ == "__main__": |
| train_loss_path = 'C:\\Users\\lpy\\Desktop\\ultralytics-main\\train_loss.txt' |
| y_train_loss = data_read(train_loss_path) |
| x_train_loss = range(len(y_train_loss)) |
| plt.figure() |
| ax = plt.axes() |
| ax.spines['top'].set_visible(False) |
| ax.spines['right'].set_visible(False) |
| plt.xlabel('iters') |
| plt.ylabel('loss') |
| plt.plot(x_train_loss, y_train_loss, linewidth=1, linestyle="solid", label="train loss") |
| plt.legend() |
| plt.title('Loss curve') |
| plt.show() |
Appendix A.3. ANN for Robustness
| import numpy as np |
| import random |
| from keras.models import Sequential |
| from keras.layers import Dense |
| import matplotlib.pyplot as plt |
| import math |
| import random |
| import torch |
| input_size = 3 |
| hidden_size1 = 64 |
| hidden_size2 = 32 |
| output_size = 2 |
| epochs = 1000 |
| learning_rate = 0.01 |
| data = ('generated_data.txt') |
| X = np.array([d[:-2] for d in data]) |
| y = np.array([d[-2:] for d in data]) |
| def initialize_parameters(input_size, hidden_size1, hidden_size2, output_size): |
| W1 = np.random.randn(input_size, hidden_size1) * 0.01 |
| b1 = np.zeros((1, hidden_size1)) |
| W2 = np.random.randn(hidden_size1, hidden_size2) * 0.01 |
| b2 = np.zeros((1, hidden_size2)) |
| W3 = np.random.randn(hidden_size2, output_size) * 0.01 |
| b3 = np.zeros((1, output_size)) |
| parameters = { |
| "W1": W1, |
| "b1": b1, |
| "W2": W2, |
| "b2": b2, |
| "W3": W3, |
| "b3": b3 |
| } |
| return parameters |
| def sigmoid(x): |
| return 1 / (1 + np.exp(-x)) |
| def sigmoid_derivative(x): |
| return x * (1 - x) |
| def relu(x): |
| return np.maximum(0, x) |
| def relu_derivative(x): |
| return (x > 0)* 1 |
| def forward_propagation(X, parameters): |
| W1 = parameters["W1"] |
| b1 = parameters["b1"] |
| W2 = parameters["W2"] |
| b2 = parameters["b2"] |
| W3 = parameters["W3"] |
| b3 = parameters["b3"] |
| Z1 = np.dot(X, W1) + b1 |
| A1 = relu(Z1) |
| Z2 = np.dot(A1, W2) + b2 |
| A2 = relu(Z2) |
| Z3 = np.dot(A2, W3) + b3 |
| A3 = sigmoid(Z3) |
| cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) |
| return A3, cache |
| def mean_squared_error(y_true, y_pred): |
| mse_loss = np.mean((y_true - y_pred)** 2) |
| return mse_loss |
| def root_mean_squared_error(y_true, y_pred): |
| mse = mean_squared_error(y_true, y_pred) |
| rmse_loss = np.sqrt(mse) |
| return rmse_loss |
| def backward_propagation(parameters, cache, X, Y): |
| m = X.shape[1] |
| (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache |
| delta3 = A3 - Y |
| delta2 = np.dot(delta3, W3.T) * relu_derivative(A2) |
| dW3 = np.dot(A2.T, delta3) / m |
| db3 = np.sum(delta3) / m |
| dW2 = np.dot(A1.T, delta2) / m |
| db2 = np.sum(delta2) / m |
| dW1 = np.dot(X.T, delta2) / m |
| db1 = np.sum(delta2) / m |
| grads = { |
| "dW1": dW1, |
| "db1": db1, |
| "dW2": dW2, |
| "db2": db2, |
| "dW3": dW3, |
| "db3": db3 |
| } |
| return grads |
| def update_parameters(parameters, grads, learning_rate): |
| parameters["W1"] -= learning_rate * grads["dW1"] |
| parameters["b1"] -= learning_rate * grads["db1"] |
| parameters["W2"] -= learning_rate * grads["dW2"] |
| parameters["b2"] -= learning_rate * grads["db2"] |
| parameters["W3"] -= learning_rate * grads["dW3"] |
| parameters["b3"] -= learning_rate * grads["db3"] |
| return parameters |
| def train(X, Y, epochs, learning_rate, input_size, hidden_size1, hidden_size2, output_size): |
| parameters = initialize_parameters(input_size, hidden_size1, hidden_size2, output_size) |
| for epoch in range(epochs): |
| AL, cache = forward_propagation(X, parameters) |
| loss = mse_loss(AL, Y) |
| grads = backward_propagation(parameters, cache, X, Y) |
| parameters = update_parameters(parameters, grads, learning_rate) |
| if epoch % 100 == 0: |
| print(f"Epoch {epoch}, Loss: {loss}") |
| return parameters |
| parameters = train(X, y, epochs, learning_rate, input_size, hidden_size1, hidden_size2, output_size) |
| def predict(X, parameters): |
| AL, _ = forward_propagation(X, parameters) |
| return AL#activation layer |
| c_values = [0, 13, 26, 33, 39, 52, 66, 79, 100] |
| data_matrix = np.empty((100, 3)) |
| for i in range(100): |
| a = round(random.uniform(20, 100), 2) |
| b = round(random.uniform(1, 20), 2) |
| c = random.choice(c_values) |
| data_matrix[i] = [a, b, c] |
| X_pre = data_matrix[i] |
| predictions = predict(X_pre, parameters) |
| print("Predictions:", predictions) |
| plt.scatter(y[:, 0], predictions[:, 0], color='blue') |
| plt.scatter(y[:, 1], predictions[:, 1], color='green') |
| plt.xlabel('Actual') |
| plt.ylabel('Predicted') |
| plt.title('Prediction vs Actual') |
| plt.show() |
| min_x = min_y = float('inf') |
| min_x_index = min_y_index = -1 |
| for index, (x, y) in enumerate(predictions): |
| min_x = x |
| min_x_index = index |
| if y < min_y: |
| min_y = y |
| min_y_index = index |
| if min_x_index == min_y_index: |
| min_a, min_b, min_c = a[min_x_index] [0] |
| print(f"Min x and y: x={min_x}, y={min_y}, a={min_a}, b={min_b}, c={min_c}") |
| else: |
| print("No single point found where both x and y are simultaneously minimized.") |
| epochs = list(range(1, len(train_losses) + 1)) |
| plt.figure(figsize=(10, 6)) |
| plt.plot(epochs, train_losses, label='Training Loss') |
| plt.plot(epochs, test_losses, label='Test Loss') |
| plt.title('Loss Function Convergence for Training and Test Data') |
| plt.xlabel('Epochs') |
| plt.ylabel('Loss') |
| plt.legend() |
| plt.show() |
Appendix A.4
| Size/mm | Wall Thickness/mm | Coverage/% | Material | Shape | Deformation/mm | Elastic Stress/Map | Mass/kg |
|---|---|---|---|---|---|---|---|
| 90 | 10 | 33 | 1 | 0 | 0.00224840 | 0.00000664 | 212.37 |
| 60 | 5 | 100 | 1 | 0 | 0.00402450 | 0.00001764 | 125.98 |
| 60 | 15 | 100 | 1 | 0 | 0.00215420 | 0.00000571 | 169.86 |
| 90 | 5 | 67 | 1 | 0 | 0.00168160 | 0.00000773 | 180.28 |
| 30 | 5 | 67 | 1 | 0 | 0.00144240 | 0.00000668 | 179.73 |
| 30 | 10 | 100 | 1 | 0 | 0.00224320 | 0.00000801 | 167.94 |
| 60 | 15 | 33 | 1 | 0 | 0.00179950 | 0.00000463 | 215.94 |
| 60 | 5 | 33 | 1 | 0 | 0.00247110 | 0.00001082 | 204.97 |
| 30 | 10 | 33 | 1 | 0 | 0.00168260 | 0.00000609 | 225.54 |
| 60 | 10 | 67 | 1 | 0 | 0.00125970 | 0.00000337 | 208.26 |
| 30 | 15 | 67 | 1 | 0 | 0.00126860 | 0.00000367 | 211.55 |
| 90 | 10 | 100 | 1 | 0 | 0.00287370 | 0.00000871 | 143.26 |
| 90 | 15 | 67 | 1 | 0 | 0.00130360 | 0.00000354 | 204.97 |
| 60 | 15 | 100 | 2 | 0 | 0.00625420 | 0.00001659 | 58.64 |
| 30 | 15 | 67 | 2 | 0 | 0.00364840 | 0.00001061 | 73.03 |
| 60 | 10 | 67 | 2 | 0 | 0.00362290 | 0.00000975 | 71.90 |
| 90 | 10 | 33 | 2 | 0 | 0.00656050 | 0.00001938 | 73.32 |
| 90 | 15 | 67 | 2 | 0 | 0.00375270 | 0.00001051 | 70.76 |
| 60 | 5 | 33 | 2 | 0 | 0.00720840 | 0.00003132 | 70.76 |
| 90 | 5 | 67 | 2 | 0 | 0.00488650 | 0.00002242 | 62.24 |
| 30 | 5 | 67 | 2 | 0 | 0.00417170 | 0.00001931 | 62.05 |
| 90 | 10 | 100 | 2 | 0 | 0.00836510 | 0.00002523 | 49.46 |
| 30 | 10 | 33 | 2 | 0 | 0.00488850 | 0.00001759 | 77.86 |
| 60 | 5 | 100 | 2 | 0 | 0.01172700 | 0.00005081 | 43.49 |
| 60 | 15 | 33 | 2 | 0 | 0.00523110 | 0.00001347 | 74.55 |
| 30 | 10 | 100 | 2 | 0 | 0.00650860 | 0.00002312 | 57.98 |
| 30 | 15 | 67 | 1 | 6 | 0.00123610 | 0.00000371 | 214.42 |
| 30 | 10 | 33 | 1 | 6 | 0.00168010 | 0.00000641 | 224.28 |
| 90 | 15 | 67 | 1 | 6 | 0.00135580 | 0.00000366 | 196.52 |
| 90 | 10 | 33 | 1 | 6 | 0.00191800 | 0.00000598 | 219.24 |
| 30 | 5 | 67 | 1 | 6 | 0.00137910 | 0.00000495 | 185.97 |
| 60 | 15 | 33 | 1 | 6 | 0.00175930 | 0.00000606 | 220.38 |
| 60 | 5 | 100 | 1 | 6 | 0.00314250 | 0.00001065 | 137.78 |
| 90 | 10 | 100 | 1 | 6 | 0.00276660 | 0.00000837 | 153.16 |
| 60 | 5 | 33 | 1 | 6 | 0.00202470 | 0.00000693 | 214.88 |
| 90 | 5 | 67 | 1 | 6 | 0.00151040 | 0.00000429 | 188.26 |
| 60 | 10 | 67 | 1 | 6 | 0.00133450 | 0.00000366 | 199.27 |
| 30 | 10 | 100 | 1 | 6 | 0.00213180 | 0.00000776 | 171.05 |
| 60 | 15 | 100 | 1 | 6 | 0.00225220 | 0.00000722 | 165.32 |
| 30 | 5 | 67 | 2 | 6 | 0.00396700 | 0.00001429 | 64.20 |
| 30 | 15 | 67 | 2 | 6 | 0.00355380 | 0.00001063 | 74.02 |
| 60 | 5 | 33 | 2 | 6 | 0.00589780 | 0.00002006 | 74.18 |
| 60 | 15 | 100 | 2 | 6 | 0.00653510 | 0.00002084 | 57.07 |
| 90 | 10 | 100 | 2 | 6 | 0.00717970 | 0.00001439 | 52.87 |
| 90 | 10 | 33 | 2 | 6 | 0.00558440 | 0.00001731 | 75.69 |
| 90 | 5 | 67 | 2 | 6 | 0.00437670 | 0.00001243 | 64.99 |
| 30 | 10 | 33 | 2 | 6 | 0.00487620 | 0.00001845 | 77.43 |
| 90 | 15 | 67 | 2 | 6 | 0.00390640 | 0.00001058 | 67.84 |
| 60 | 10 | 67 | 2 | 6 | 0.00384070 | 0.00001061 | 68.79 |
| 60 | 15 | 33 | 2 | 6 | 0.00511220 | 0.00001750 | 76.08 |
| 60 | 5 | 100 | 2 | 6 | 0.00913460 | 0.00003080 | 47.57 |
| 30 | 10 | 100 | 2 | 6 | 0.00617620 | 0.00002226 | 59.05 |
References
- Espalin, D.; Muse, D.W.; MacDonald, E.; Wicker, R.B. 3d printing multifunctionality: Structures with electronics. Int. J. Adv. Manuf. Technol. 2014, 72, 963–978. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3d printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Wen, S.; Shen, Q.; Wei, Q.; Yan, C.; Zhu, W.; Shi, Y.; Yang, J.; Shi, Y. Material optimization and post-processing of sand moulds manufactured by the selective laser sintering of binder-coated al2o3 sands. J. Mater. Process. Technol. 2015, 225, 93–102. [Google Scholar] [CrossRef]
- Shirzad, M.; Zolfagharian, A.; Bodaghi, M.; Nam, S.Y. Auxetic metamaterials for bone-implanted medical devices: Recent advances and new perspectives. Eur. J. Mech.-A/Solids 2023, 98, 104905. [Google Scholar] [CrossRef]
- Jiang, W.; Ren, X.; Wang, S.L.; Zhang, X.G.; Zhang, X.Y.; Luo, C.; Xie, Y.M.; Scarpa, F.; Alderson, A.; Evans, K.E. Manufacturing, characteristics and applications of auxetic foams: A state-of-the-art review. Compos. Part B Eng. 2022, 235, 109733. [Google Scholar] [CrossRef]
- Sadikbasha, S.; Pandurangan, V. High velocity impact response of sandwich structures with auxetic tetrachiral cores: Analytical model, finite element simulations and experiments. Compos. Struct. 2023, 317, 117064. [Google Scholar] [CrossRef]
- Novak, N.; Al-Rifaie, H.; Airoldi, A.; Krstulovi´c-Opara, L.; Lodygowski, T.; Ren, Z.; Vesenjak, M. Quasi-static and impact behaviour of foam-filled graded auxetic panel. Int. J. Impact Eng. 2023, 178, 104606. [Google Scholar] [CrossRef]
- Huang, J.; Gong, X.; Zhang, Q.; Scarpa, F.; Liu, Y.; Leng, J. In-plane mechanics of a novel zero poisson's ratio honeycomb core. Compos. Part B Eng. 2016, 89, 67–76. [Google Scholar] [CrossRef]
- He, Q.; Ma, D.; Zhang, Z.; Yao, L. Crushing analysis and crashworthiness optimization design of reinforced regular hexagon honeycomb sandwich panel. Sci. Eng. Compos. Mater. 2016, 23, 625–639. [Google Scholar] [CrossRef]
- Sun, G.; Chen, D.; Wang, H.; Hazell, P.J.; Li, Q. High-velocity impact behaviour of aluminium honeycomb sandwich panels with different structural configurations. Int. J. Impact Eng. 2018, 122, 119–136. [Google Scholar] [CrossRef]
- Li, D.; Chen, Z.; Li, J.; Yi, J. Ultimate strength assessment of ship hull plate with multiple cracks under axial compression using artificial neural networks. Ocean Eng. 2022, 263, 112438. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B.; Karaboga, N. A survey on the studies employing machine learning (ml) for enhancing artificial bee colony (abc) optimization algorithm. Cogent Eng. 2020, 7, 1855741. [Google Scholar] [CrossRef]
- Mehta, V.; Bawa, S.; Singh, J. Analytical review of clustering techniques and proximity measures. Artif. Intell. Rev. 2020, 53, 5995–6023. [Google Scholar] [CrossRef]
- Telikani, A.; Tahmassebi, A.; Banzhaf, W.; Gandomi, A.H. Evolutionary machine learning: A survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Wu, Y.; Fang, J.; He, Y.; Li, W. Crashworthiness of hierarchical circular-joint quadrangular honeycombs. Thin-Walled Struct. 2018, 133, 180–191. [Google Scholar] [CrossRef]
- Quan, T.Q.; Anh, V.M.; Duc, N.D. Natural frequency analysis of sandwich plate with auxetic honeycomb core and cntrc face sheets using analytical approach and artificial neural network. Aerosp. Sci. Technol. 2024, 144, 108806. [Google Scholar] [CrossRef]
- Gupta, A.; Pradyumna, S. Nonlinear dynamic analysis of sandwich shell panels with auxetic honeycomb core and curvilinear fibre reinforced facesheets. Eur. J. Mech.-A/Solids 2022, 95, 104640. [Google Scholar] [CrossRef]
- Pham, Q.-H.; Tran, V.K.; Tran, T.T. Vibration characteristics of sandwich plates with an auxetic honeycomb core and laminated three-phase skin layers under blast load. Def. Technol. 2023, 24, 148–163. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, H.; Ma, J.; Yang, X.; Yang, J. Deformation behaviors and energy absorption characteristics of a hollow re-entrant auxetic lattice metamaterial. Aerosp. Sci. Technol. 2023, 142, 108583. [Google Scholar] [CrossRef]
- Sarafraz, M.; Seidi, H.; Kakavand, F.; Viliani, N.S. Free vibration and bucklinganalyses of a rectangular sandwich plate with an auxetic honeycomb core and laminated three-phase polymer/gnp/fiber face sheets. Thin-Walled Struct. 2023, 183, 110331. [Google Scholar] [CrossRef]
- Anh, V.T.T.; Khoa, N.D.; Ngo, T.; Duc, N.D. Vibration of hybrid eccentrically stiffened sandwich auxetic double curved shallow shells in thermal environment. Aerosp. Sci. Technol. 2023, 137, 108277. [Google Scholar] [CrossRef]
- Liu, B.; Li, S.; Li, Y. Bending of fgm sandwich plates with tunable auxetic core using dqm. Eur. J. Mech.-A/Solids 2023, 97, 104838. [Google Scholar] [CrossRef]
- Topal, U.; Goodarzimehr, V.; Bardhan, A.; Vo-Duy, T.; Shojaee, S. Maximization of the fundamental frequency of the fg-cntrc quadrilateral plates using a new hybrid psog algorithm. Compos. Struct. 2022, 295, 115823. [Google Scholar] [CrossRef]
- Cho, J. Nonlinear bending analysis of fg-cntrc plate resting on elastic foundation by natural element method. Eng. Anal. Bound. Elem. 2022, 141, 65–74. [Google Scholar] [CrossRef]
- Zhu, P.; Lei, Z.; Liew, K.M. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos. Struct. 2012, 94, 1450–1460. [Google Scholar] [CrossRef]
- Tahir, Z.u.R.; Mandal, P.; Adil, M.T.; Naz, F. Application of artificial neural network to predict buckling load of thin cylindrical shells under axial compression. Eng. Struct. 2021, 248, 113221. [Google Scholar] [CrossRef]
- Pham, Q.-H.; Nguyen, P.-C.; Tran, T.T. Free vibration response of auxetic honeycomb sandwich plates using an improved higher-order es-mitc3 element and artificial neural network. Thin-Walled Struct. 2022, 175, 109203. [Google Scholar] [CrossRef]
- Wang, L.; Wang, C.; Wang, S.; Sun, G.; You, B.; Hu, Y. A novel ann-based boundary strategy for modeling micro/nanopatterns on airfoil with improved aerodynamic performances. Aerosp. Sci. Technol. 2022, 121, 107347. [Google Scholar] [CrossRef]
- Mahesh, V. Artificial neural network (ann) based investigation on the static behaviour of piezo-magneto-thermo-elastic nanocomposite sandwich plate with cnt agglomeration and porosity. Int. J. Non-Linear Mech. 2023, 153, 104406. [Google Scholar] [CrossRef]
- Thompson, M.L.; Kramer, M.A. Modeling chemical processes using prior knowledge and neural networks. AIChE J. 1994, 40, 1328–1340. [Google Scholar] [CrossRef]
- McFarland, R., Jr. Hexagonal cell structures under post-buckling axial load. AIAA J. 1963, 1, 1380–1385. [Google Scholar] [CrossRef]
- Wierzbicki, T. Crushing analysis of metal honeycombs. Int. J. Impact Eng. 1983, 1, 157–174. [Google Scholar] [CrossRef]
- Liaghat, G.; Alavinia, A. A comment on the axial crush of metallic honeycombs by wu and jiang. Int. J. Impact Eng. 2003, 28, 1143–1146. [Google Scholar] [CrossRef]
- Yin, H.; Wen, G. Theoretical prediction and numerical simulation of honeycomb structures with various cell specifications under axial loading. Int. J. Mech. Mater. Des. 2011, 7, 253–263. [Google Scholar] [CrossRef]
- Becker, W. The in-plane stiffnesses of a honeycomb core including the thickness effect. Arch. Appl. Mech. 1998, 68, 334–341. [Google Scholar] [CrossRef]
- Wang, A.-J.; McDowell, D. In-plane stiffness and yield strength of periodic metal honeycombs. J. Eng. Mater. Technol. 2004, 126, 137–156. [Google Scholar] [CrossRef]
- Abd El-Sayed, F.; Jones, R.; Burgess, I. A theoretical approach to the deformation of honeycomb based composite materials. Composites 1979, 10, 209–214. [Google Scholar] [CrossRef]
- Li, Y.; Abbès, F.; Hoang, M.; Abbès, B.; Guo, Y. Analytical homogenization for in-plane shear, torsion and transverse shear of honeycomb core with skin and thickness effects. Compos. Struct. 2016, 140, 453–462. [Google Scholar] [CrossRef]
- Sorohan, S.¸.; Sandu, M.; Sandu, A.; Constantinescu, D.M. Finite element models used to determine the equivalent in-plane properties of honeycombs. Mater. Today Proc. 2016, 3, 1161–1166. [Google Scholar] [CrossRef]
- Asemi, K.; Salehi, M.; Akhlaghi, M. Three dimensional graded finite element elasticity shear buckling analysis of FGM annular sector plates. Aerosp. Sci. Technol. 2015, 43, 1–13. [Google Scholar] [CrossRef]









| Level | A Size/mm | B Wall Thickness/mm | C Coverage/% | D Material | E Shape |
|---|---|---|---|---|---|
| −1 | 30 | 5 | 100 | steel | hexagonal |
| 0 | 60 | 10 | 66.5 | ||
| 1 | 90 | 15 | 33 | aluminum | circular |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 0.000263178 | 18 | 1.46 × 10−5 | 23.1 | <0.0001 | significant |
| A—size | 2.77 × 10−6 | 1 | 2.77 × 10−6 | 4.38 | 0.0441 | ** |
| B—wall thickness | 1.00 × 10−5 | 1 | 1.00 × 10−5 | 15.8 | 0.0004 | ** |
| C—Coverage | 1.58 × 10−5 | 1 | 1.58 × 10−5 | 24.97 | <0.0001 | ** |
| D—material | 0.000177342 | 1 | 0.000177342 | 280.17 | <0.0001 | ** |
| E—shape | 1.42 × 10−6 | 1 | 1.42 × 10−6 | 2.24 | 0.1438 | |
| AB | 4.95 × 10−8 | 1 | 4.95 × 10−8 | 0.0782 | 0.7815 | |
| AC | 5.64 × 10−8 | 1 | 5.64 × 10−8 | 0.0891 | 0.7672 | |
| AD | 5.57 × 10−7 | 1 | 5.57 × 10−7 | 0.8792 | 0.3552 | |
| AE | 1.54 × 10−7 | 1 | 1.54 × 10−7 | 0.2433 | 0.6251 | |
| BC | 3.15 × 10−6 | 1 | 3.15 × 10−6 | 4.98 | 0.0326 | ** |
| BD | 2.44 × 10−6 | 1 | 2.44 × 10−6 | 3.85 | 0.0582 | * |
| BE | 1.31 × 10−6 | 1 | 1.31 × 10−6 | 2.07 | 0.16 | |
| CD | 3.45 × 10−6 | 1 | 3.45 × 10−6 | 5.45 | 0.0258 | ** |
| CE | 7.51 × 10−8 | 1 | 7.51 × 10−8 | 0.1186 | 0.7327 | |
| DE | 4.27 × 10−7 | 1 | 4.27 × 10−7 | 0.674 | 0.4176 | |
| A2 | 2.94 × 10−7 | 1 | 2.94 × 10−7 | 0.4648 | 0.5002 | |
| B2 | 1.34 × 10−6 | 1 | 1.34 × 10−6 | 2.11 | 0.1555 | |
| C2 | 3.29 × 10−5 | 1 | 3.29 × 10−5 | 52.01 | <0.0001 | ** |
| Residual | 2.09 × 10−5 | 33 | 6.33 × 10−7 | |||
| Cor Total | 0.0002 | 51 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 16.5389 | 18 | 0.9188 | 14.6809 | 0.0000 | significant |
| A—size | 0.0016 | 1 | 0.0016 | 0.0256 | 0.8739 | |
| B—wall thickness | 4.8678 | 1 | 4.8678 | 77.7768 | 0.0000 | ** |
| C—Coverage | 1.6893 | 1 | 1.6893 | 26.9916 | 0.0000 | ** |
| D—material | 0.0230 | 1 | 0.0230 | 0.3679 | 0.5483 | |
| E—shape | 0.9959 | 1 | 0.9959 | 15.9117 | 0.0003 | ** |
| AB | 0.0022 | 1 | 0.0022 | 0.0350 | 0.8527 | |
| AC | 0.0043 | 1 | 0.0043 | 0.0690 | 0.7944 | |
| AD | 0.0118 | 1 | 0.0118 | 0.1881 | 0.6673 | |
| AE | 0.0968 | 1 | 0.0968 | 1.5459 | 0.2225 | |
| BC | 0.6424 | 1 | 0.6424 | 10.2645 | 0.0030 | ** |
| BD | 0.0003 | 1 | 0.0003 | 0.0049 | 0.9444 | |
| BE | 1.7888 | 1 | 1.7888 | 28.5810 | 0.0000 | ** |
| CD | 0.0185 | 1 | 0.0185 | 0.2948 | 0.5908 | |
| CE | 0.1283 | 1 | 0.1283 | 2.0497 | 0.1616 | |
| DE | 0.0092 | 1 | 0.0092 | 0.1467 | 0.7042 | |
| A2 | 0.0230 | 1 | 0.0230 | 0.3673 | 0.5486 | |
| B2 | 0.8124 | 1 | 0.8124 | 12.9801 | 0.0010 | ** |
| C2 | 4.7081 | 1 | 4.7081 | 75.2260 | 0.0000 | ** |
| Residual | 18.608 | 51 | ||||
| Cor Total | 0.00165 | 1 | 0.0016 | 0.0255 | 0.8739 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 223,986.04 | 39 | 5743.2319 | 394.0750 | 0.0000 | significant |
| A—size | 384.1923 | 1 | 384.1923 | 26.3616 | 0.0002 | ** |
| B—wall thickness | 1854.9075 | 1 | 1854.9075 | 127.2755 | 0.0000 | ** |
| C—Coverage | 14,322.27 | 1 | 14,322.2735 | 982.7307 | 0.0000 | ** |
| D—material | 17,800.89 | 1 | 17,800.8964 | 1221.4183 | 0.0000 | ** |
| E—shape | 36.5541 | 1 | 36.5541 | 2.5082 | 0.1392 | |
| AB | 84.4239 | 1 | 84.4239 | 5.7928 | 0.0331 | * |
| AC | 67.1252 | 1 | 67.1252 | 4.6058 | 0.0530 | * |
| AD | 90.9934 | 1 | 90.9934 | 6.2436 | 0.0280 | * |
| AE | 1.6124 | 1 | 1.6124 | 0.1106 | 0.7452 | |
| BC | 341.4734 | 1 | 341.4734 | 23.4304 | 0.0004 | ** |
| BD | 439.4649 | 1 | 439.4649 | 30.1541 | 0.0001 | ** |
| BE | 97.9125 | 1 | 97.9125 | 6.7183 | 0.0236 | ** |
| CD | 3393.0674 | 1 | 3393.0674 | 232.8172 | 0.0000 | ** |
| CE | 0.0056 | 1 | 0.0056 | 0.0004 | 0.9847 | |
| DE | 8.6671 | 1 | 8.6671 | 0.5947 | 0.4555 | |
| A2 | 0.7234 | 1 | 0.7234 | 0.0496 | 0.8274 | |
| B2 | 273.7032 | 1 | 273.7032 | 18.7803 | 0.0010 | ** |
| C2 | 781.1391 | 1 | 781.1391 | 53.5983 | 0.0000 | ** |
| BCD | 80.9280 | 1 | 80.9280 | 5.5529 | 0.0363 | * |
| B2D | 64.8357 | 1 | 64.8357 | 4.4487 | 0.0566 | * |
| C2D | 185.0323 | 1 | 185.0323 | 12.6961 | 0.0039 | ** |
| C2E | 73.7215 | 1 | 73.7215 | 5.0584 | 0.0441 | * |
| Residual | 174.8874 | 12 | 14.5739 | |||
| Cor Total | 224,160.93 | 51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Xing, F. Structural Design Analysis of Substrate with Honeycomb Core Under Normal Pressure, Using RSM and ANN. Processes 2025, 13, 189. https://doi.org/10.3390/pr13010189
Li P, Xing F. Structural Design Analysis of Substrate with Honeycomb Core Under Normal Pressure, Using RSM and ANN. Processes. 2025; 13(1):189. https://doi.org/10.3390/pr13010189
Chicago/Turabian StyleLi, Peiyuan, and Fei Xing. 2025. "Structural Design Analysis of Substrate with Honeycomb Core Under Normal Pressure, Using RSM and ANN" Processes 13, no. 1: 189. https://doi.org/10.3390/pr13010189
APA StyleLi, P., & Xing, F. (2025). Structural Design Analysis of Substrate with Honeycomb Core Under Normal Pressure, Using RSM and ANN. Processes, 13(1), 189. https://doi.org/10.3390/pr13010189






