Transfer Learning for Thickener Control
Abstract
:1. Introduction
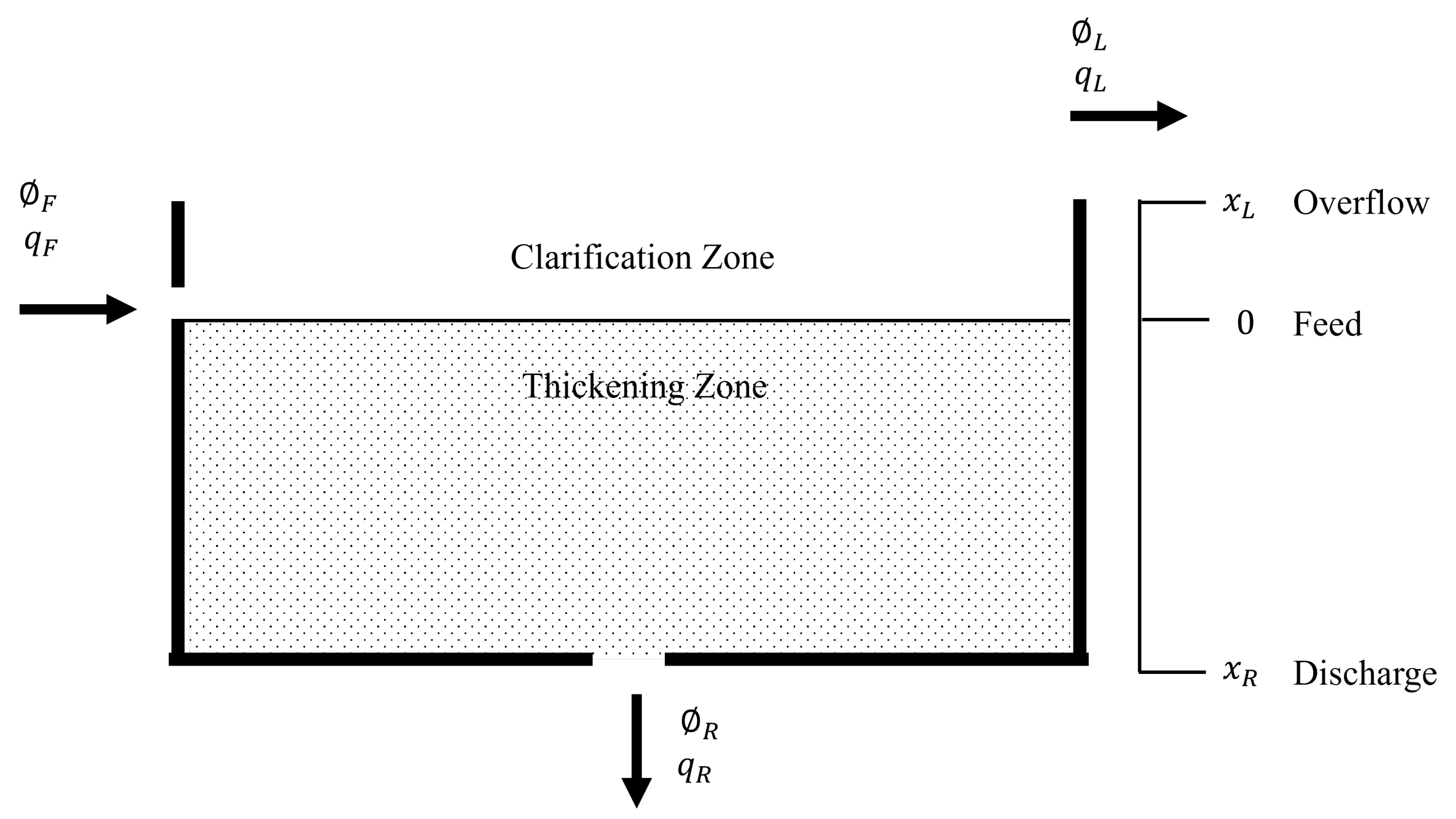
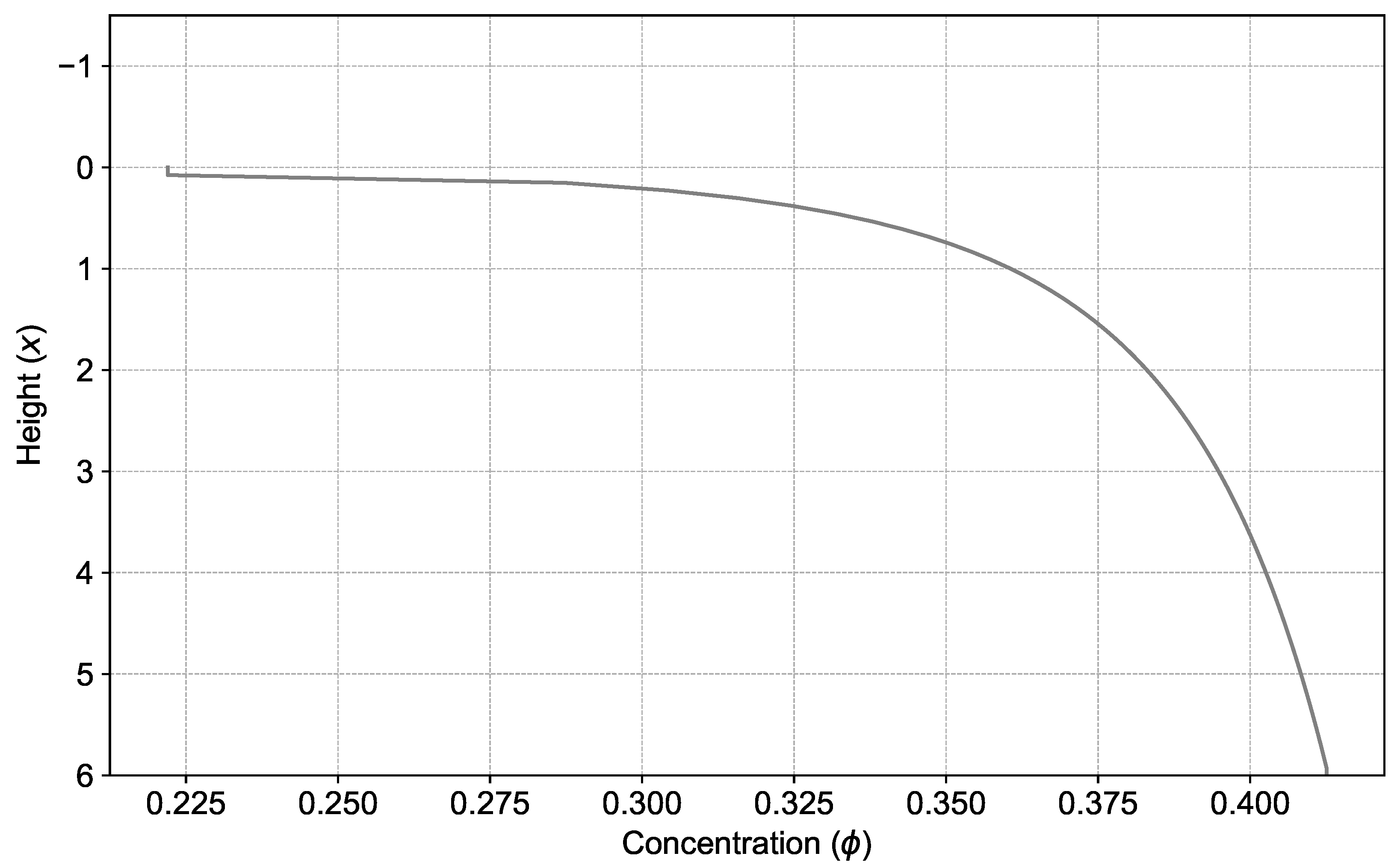
1.1. Continuous Thickener Modeling
1.2. Thickener Simulation and Control
1.3. Thickener Simulation and Control with Data-Driven Methods
1.4. Transfer Learning in Process Control
2. Methodology
2.1. Thickener Modeling
2.2. Transfer Learning
2.2.1. Transformer Model
2.2.2. Transfer Learning Models
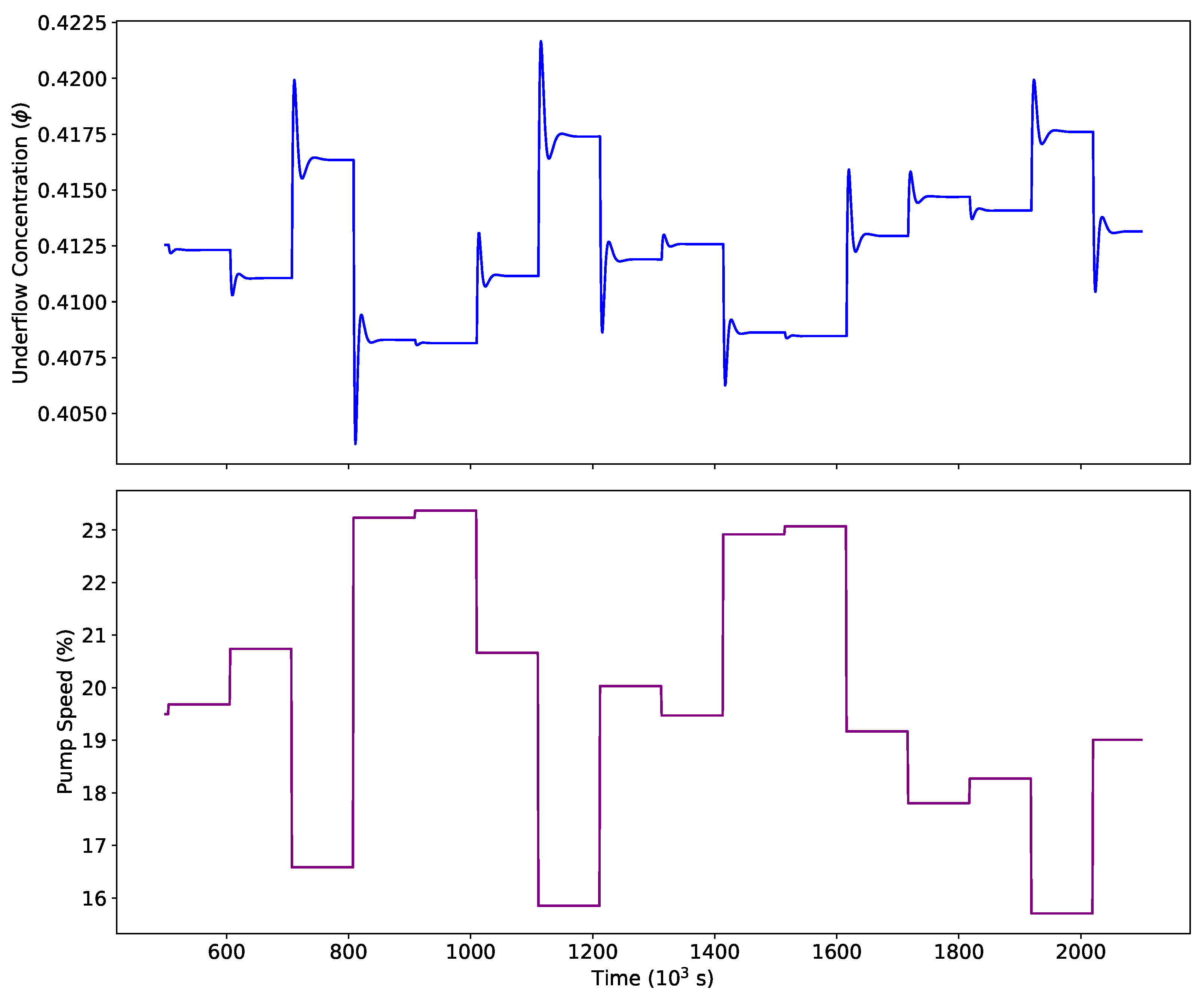
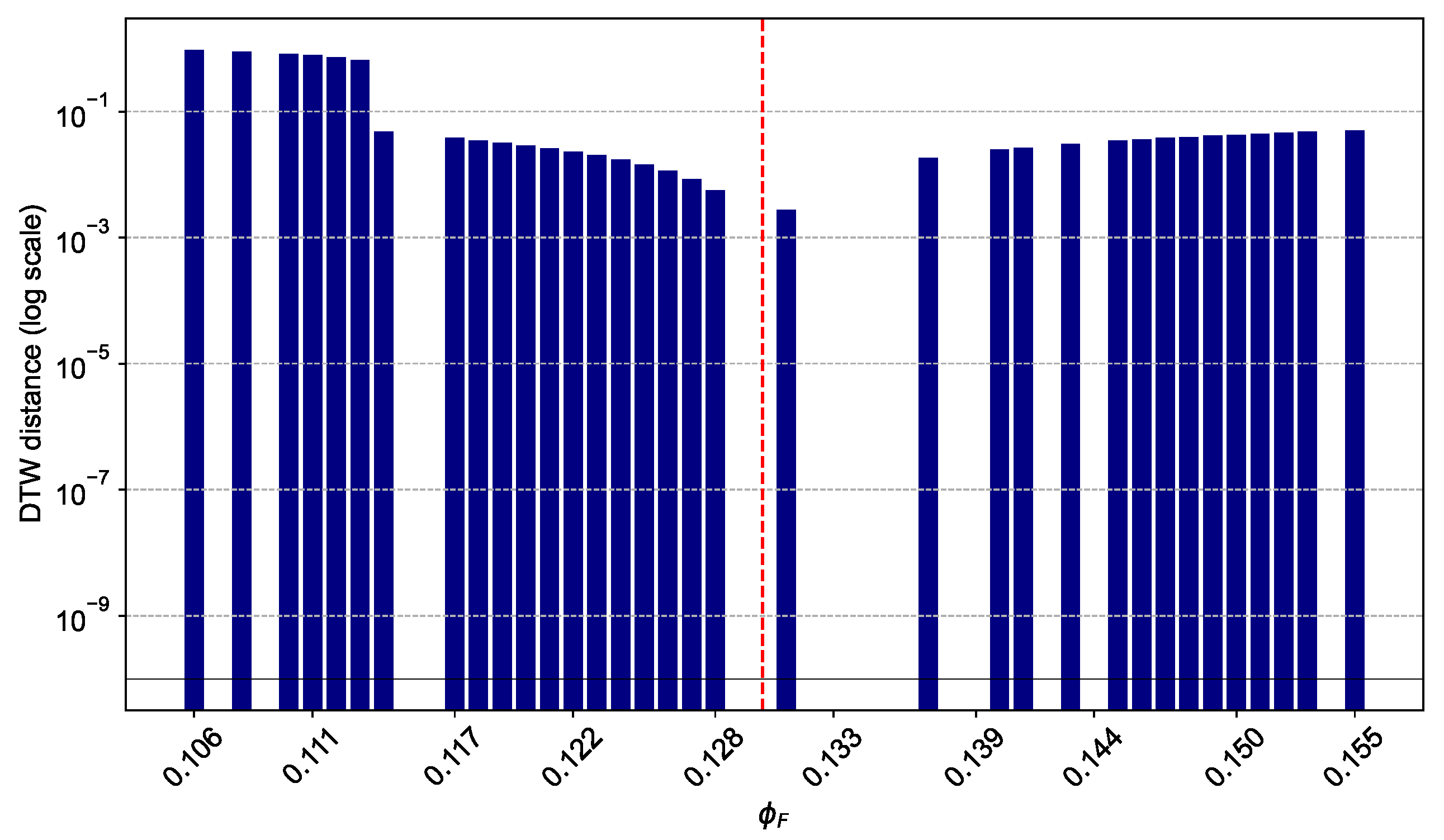
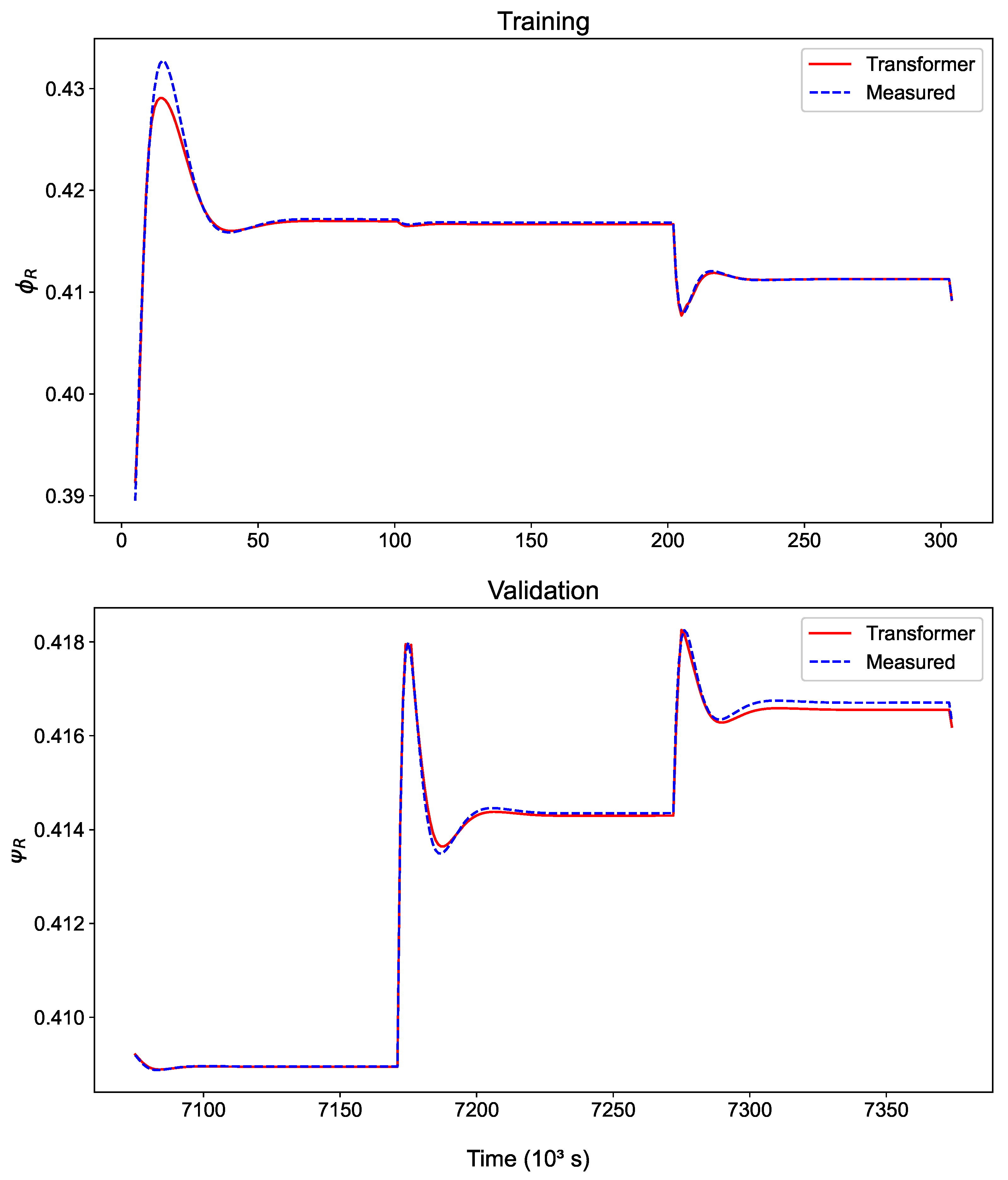
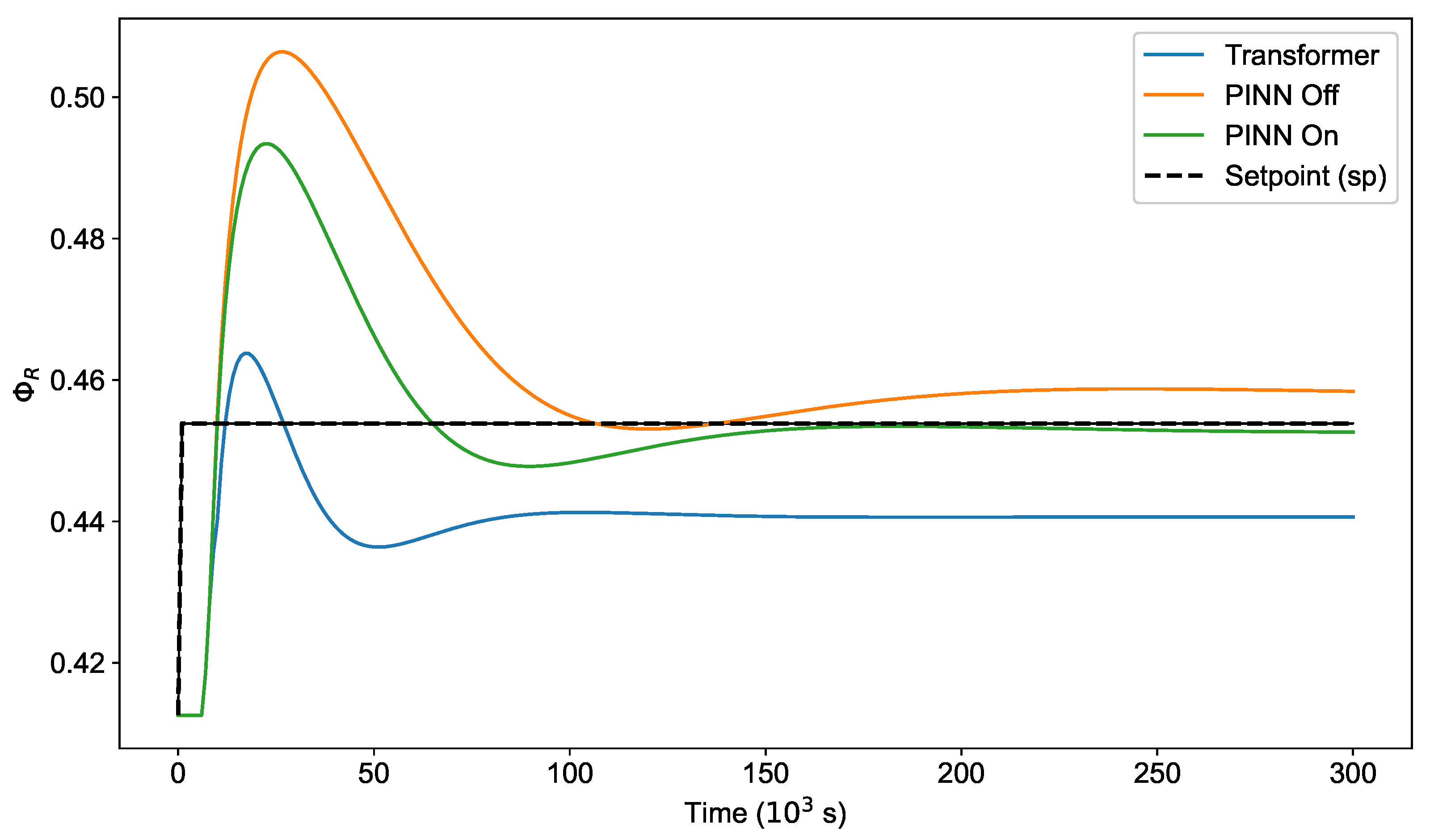
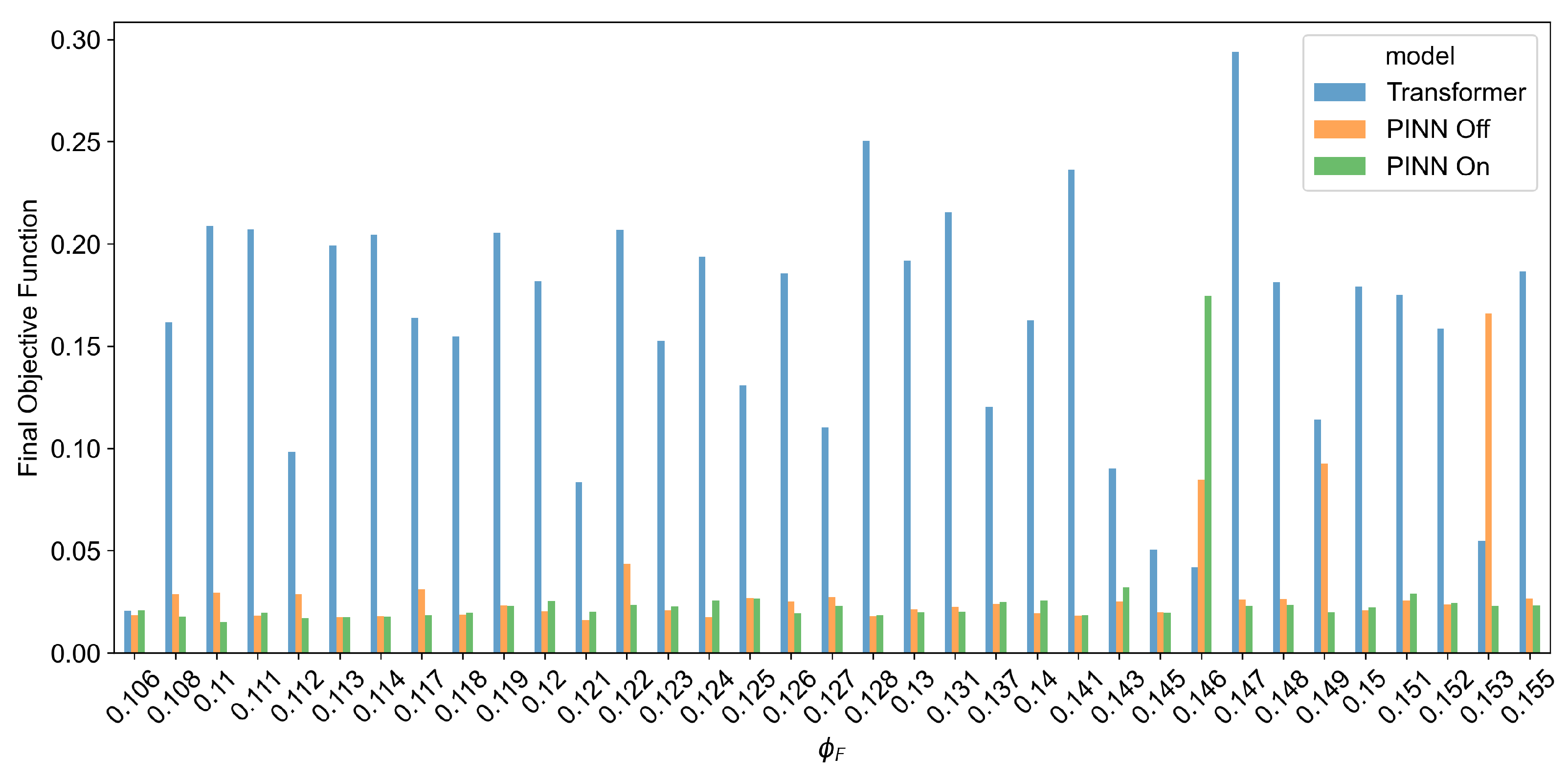
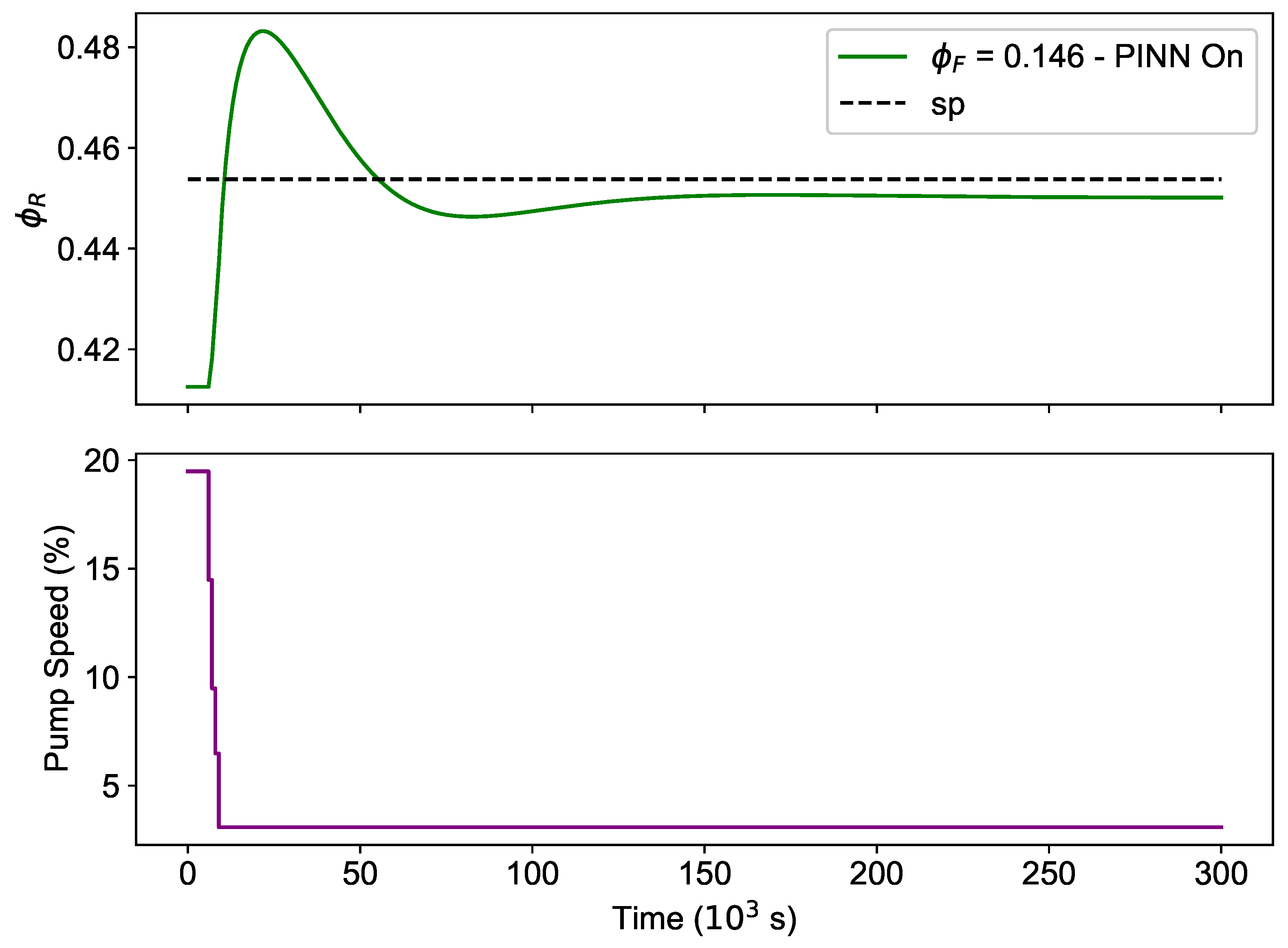
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wills, B.; Finch, J. Wills’ Mineral Processing Technology: An Introduction to the Practical Aspects of Ore Treatment and Mineral Recovery; Butterworth-Heinemann: Waltham, MA, USA, 2016. [Google Scholar]
- Concha, F.; Bürger, R. Thickening in the 20 th century: A historical perspective. Min. Metall. Explor. 2003, 20, 57–67. [Google Scholar]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 48, 166–176. [Google Scholar] [CrossRef]
- Diehl, S. A conservation Law with Point Source and Discontinuous Flux Function Modelling Continuous Sedimentation. SIAM J. Appl. Math. 1996, 56, 388–419. [Google Scholar] [CrossRef]
- Bürger, R.; Concha, F. Mathematical model and numerical simulation of the settling of flocculated suspensions. Int. J. Multiph. Flow 1998, 24, 1005–1023. [Google Scholar] [CrossRef]
- Gao, R.; Zhou, K.; Zhang, J.; Guo, H.; Ren, Q. Research on the dynamic characteristics in the flocculation process of mineral processing tailings. IEEE Access Pract. Innov. Open Solut. 2019, 7, 129244–129259. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Wu, A.; Yang, K.; Zhang, X.; Guo, J. Effect of flocculant dosage on the settling properties and underflow concentration of thickener for flocculated tailing suspensions. Water Sci. Technol. 2023, 88, 304–320. [Google Scholar] [CrossRef]
- Bürger, R.; Narváez, A. Steady-state, control, and capacity calculations for flocculated suspensions in clarifier-thickeners. Int. J. Miner. Process. 2007, 84, 274–298. [Google Scholar] [CrossRef]
- Bustos, M.C.; Concha, F.; Bürger, R.; Tory, E.M.; Bustos, M.C.; Concha, F.; Bürger, R.; Tory, E.M. Theory of sedimentation of ideal suspensions. In Sedimentation and Thickening: Phenomenological Foundation and Mathematical Theory; Springer: Berlin/Heidelberg, Germany, 1999; pp. 27–34. [Google Scholar]
- Berres, S.; Bürger, R.; Tory, E.M. Applications of polydisperse sedimentation models. Chem. Eng. J. 2005, 111, 105–117. [Google Scholar] [CrossRef]
- Betancourt, F.; Concha, F.; Sbarbaro-Hofer, D. Simple mass balance controllers for continuous sedimentation. Comput. Chem. Eng. 2013, 54, 34–43. [Google Scholar] [CrossRef]
- Bürger, R.; Karlsen, K.; Towers, J.D. A Model of Continuous Sedimentation of Flocculated Suspensions in Clarifier-Thickener Units. SIAM J. Appl. Math. 2005, 65, 882–940. [Google Scholar] [CrossRef]
- Xu, N.; Wang, X.; Zhou, J.; Wang, Q.; Fang, W.; Peng, X. An intelligent control strategy for thickening process. Int. J. Miner. Process. 2015, 142, 56–62. [Google Scholar] [CrossRef]
- Yao, Y.; Tippett, M.; Bao, J.; Bickert, G. Dynamic Modeling of Industrial Thickener for Control Design; Engineers Australia: Barton, Australia, 2012. [Google Scholar]
- Oulhiq, R.; Benjelloun, K.; Kali, Y.; Saad, M.; Griguer, H. Constrained model predictive control of an industrial high-rate thickener. J. Process Control 2024, 133, 103147. [Google Scholar] [CrossRef]
- Tan, C.K.; Bao, J.; Bickert, G. A study on model predictive control in paste thickeners with rake torque constraint. Miner. Eng. 2017, 105, 52–62. [Google Scholar] [CrossRef]
- Richardson, J.; Zaki, W. The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem. Eng. Sci. 1954, 3, 65–73. [Google Scholar] [CrossRef]
- Diaz, P.; Salas, J.C.; Cipriano, A.; Núñez, F. Random forest model predictive control for paste thickening. Miner. Eng. 2021, 163, 106760. [Google Scholar] [CrossRef]
- Jia, R.; You, F. Application of Robust Model Predictive Control Using Principal Component Analysis to an Industrial Thickener. IEEE Trans. Control Syst. Technol. 2024, 32, 1090–1097. [Google Scholar] [CrossRef]
- Yuan, Z.; Hu, J.; Wu, D.; Ban, X. A Dual-Attention Recurrent Neural Network Method for Deep Cone Thickener Underflow Concentration Prediction. Sensors 2020, 20, 1260. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Karimi, H.R. Underflow concentration prediction based on improved dual bidirectional LSTM for hierarchical cone thickener system. Int. J. Adv. Manuf. Technol. 2023, 127, 1651–1662. [Google Scholar] [CrossRef]
- Yuan, Z.; Li, X.; Wu, D.; Ban, X.; Wu, N.Q.; Dai, H.N.; Wang, H. Continuous-Time Prediction of Industrial Paste Thickener System with Differential ODE-Net. IEEE/CAA J. Autom. Sin. 2022, 9, 686–698. [Google Scholar] [CrossRef]
- Xu, J.N.; Zhao, Z.B.; Wang, F.Q. Data driven control of underflow slurry concentration in deep cone thickener. In Proceedings of the 2017 6th Data Driven Control and Learning Systems (DDCLS), Chongqing, China, 26–27 May 2017; IEEE: Beijing, China, 2017; pp. 690–693. [Google Scholar]
- Jia, R.; Zhang, S.; Li, Z.; Li, K. Data-driven tube-based model predictive control of an industrial thickener. In Proceedings of the 2022 4th International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 24–27 August 2022; IEEE: Beijing, China, 2022; pp. 1–6. [Google Scholar]
- Yuan, Z.; Zhang, Z.; Li, X.; Cui, Y.; Li, M.; Ban, X. Controlling Partially Observed Industrial System Based on Offline Reinforcement Learning—A Case Study of Paste Thickener. In Proceedings of the IEEE Transactions on Industrial Informatics, Beijing, China, 17–20 August 2024; pp. 1–11. [Google Scholar] [CrossRef]
- Arce Munoz, S.; Pershing, J.; Hedengren, J.D. Physics-informed transfer learning for process control applications. Ind. Eng. Chem. Res. 2024, 63, 21432–21443. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, Y.; Dai, W.; Pan, S.J. Transfer Learning; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Núñez, F.; Langarica, S.; Díaz, P.; Torres, M.; Salas, J.C. Neural Network-Based Model Predictive Control of a Paste Thickener Over an Industrial Internet Platform. IEEE Trans. Ind. Inform. 2020, 16, 2859–2867. [Google Scholar] [CrossRef]
- Cordiano, F. Physics-Informed Neural Network based Model Predictive Control for Constrained Stochastic Systems. Master’s Thesis, ETH Zurich, Zürich, Switzerland, 2022. [Google Scholar] [CrossRef]


| Layer Type | Details |
|---|---|
| Input Layer | Shape: (window = 5, features: 2) |
| Multi-Head Attention (1st block) | 10 heads, key_dim = 2; Residual connection with input |
| Dense Layer | 100 units, tanh activation |
| Dropout | 0.2 dropout rate |
| Dense Layer | Output units: n_feature, no activation |
| Multi-Head Attention (2nd block) | 10 heads, key_dim = 2; Residual connection with input |
| Dense Layer | 100 units, tanh activation |
| Dropout | 0.2 dropout rate |
| Dense Layer | Output units: features: 2, no activation |
| Flatten | Flatten the output |
| Output Layer | Dense layer, units: n_label, linear activation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arce Munoz, S.; Hedengren, J.D. Transfer Learning for Thickener Control. Processes 2025, 13, 223. https://doi.org/10.3390/pr13010223
Arce Munoz S, Hedengren JD. Transfer Learning for Thickener Control. Processes. 2025; 13(1):223. https://doi.org/10.3390/pr13010223
Chicago/Turabian StyleArce Munoz, Samuel, and John D. Hedengren. 2025. "Transfer Learning for Thickener Control" Processes 13, no. 1: 223. https://doi.org/10.3390/pr13010223
APA StyleArce Munoz, S., & Hedengren, J. D. (2025). Transfer Learning for Thickener Control. Processes, 13(1), 223. https://doi.org/10.3390/pr13010223







