Effect of Pellet Proportion and Charging Sequence on Burden Distribution in Blast Furnaces According to Discrete Element Method Simulation
Abstract
:1. Introduction
2. Model Establishment
2.1. Discrete Element Method
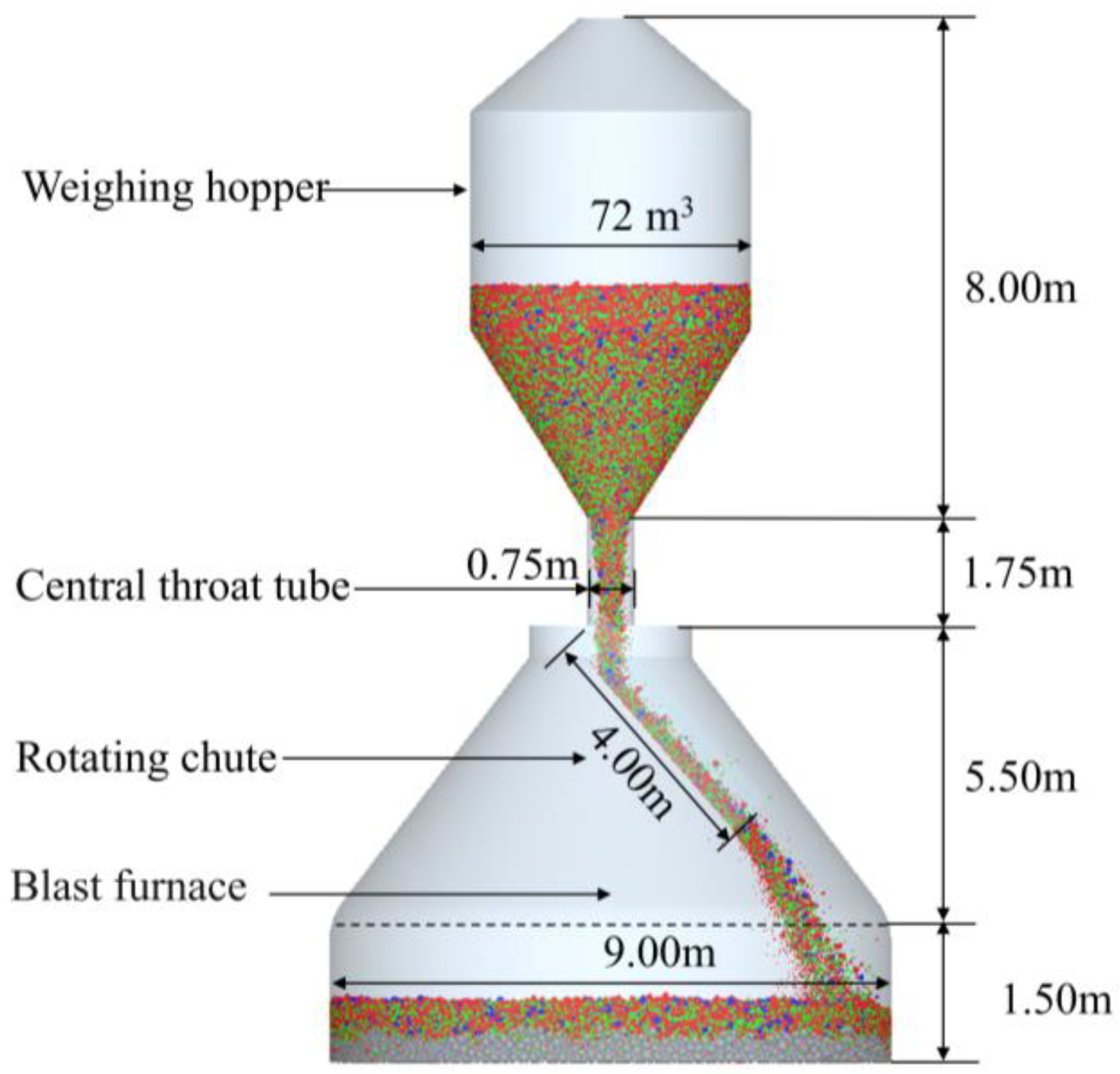
2.2. Simulation Conditions
3. Results and Discussion
3.1. Model Validation
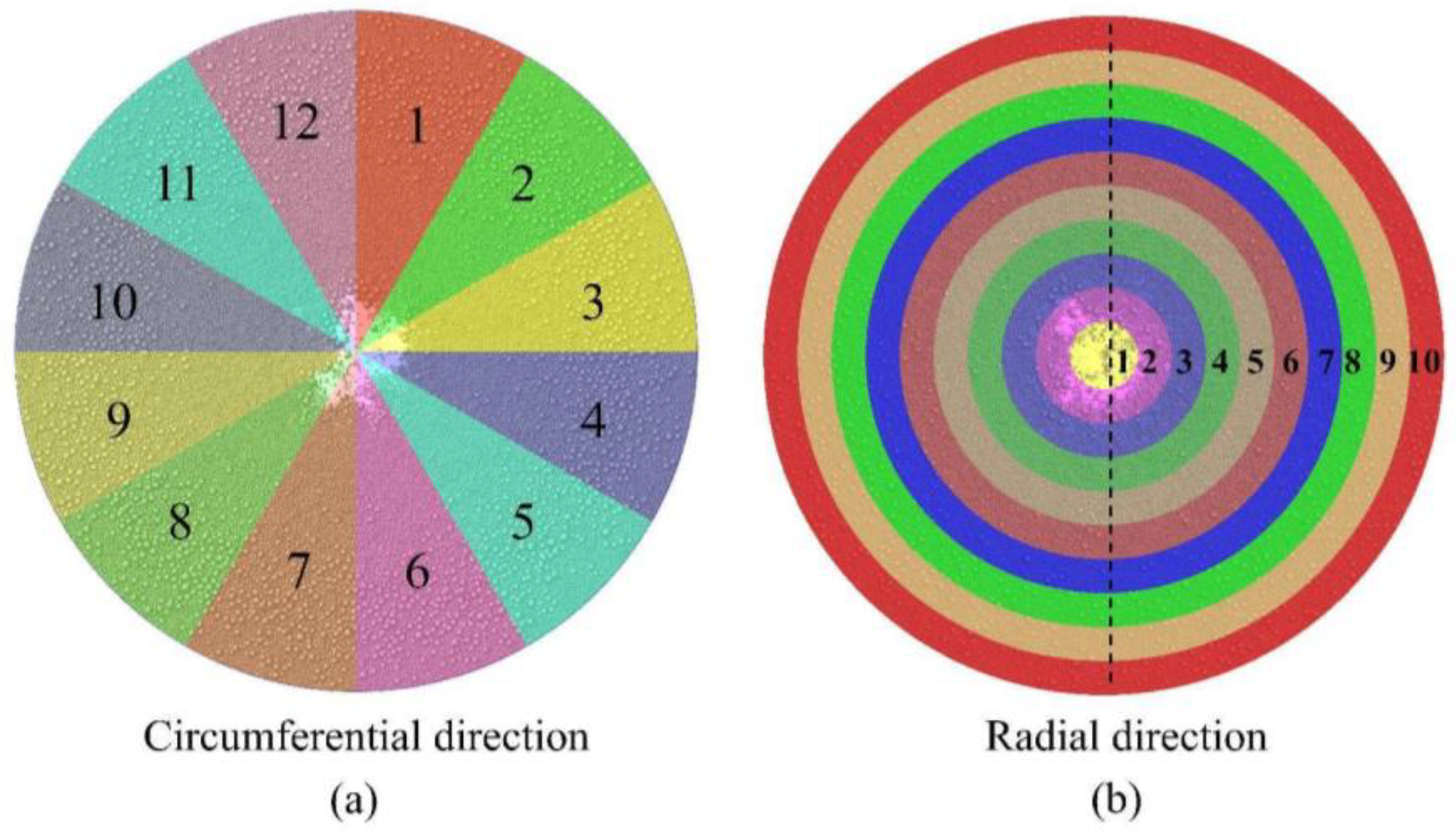
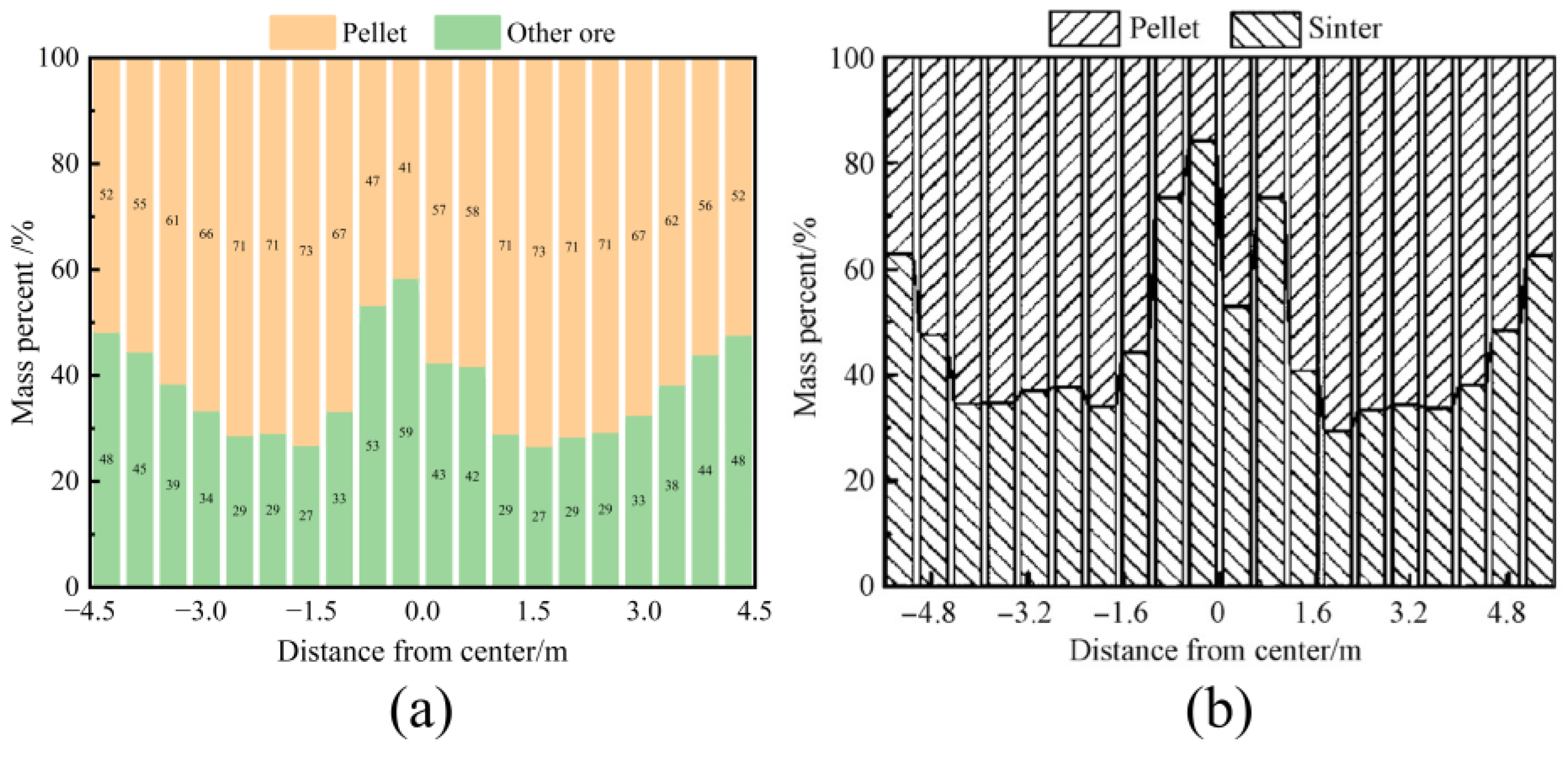
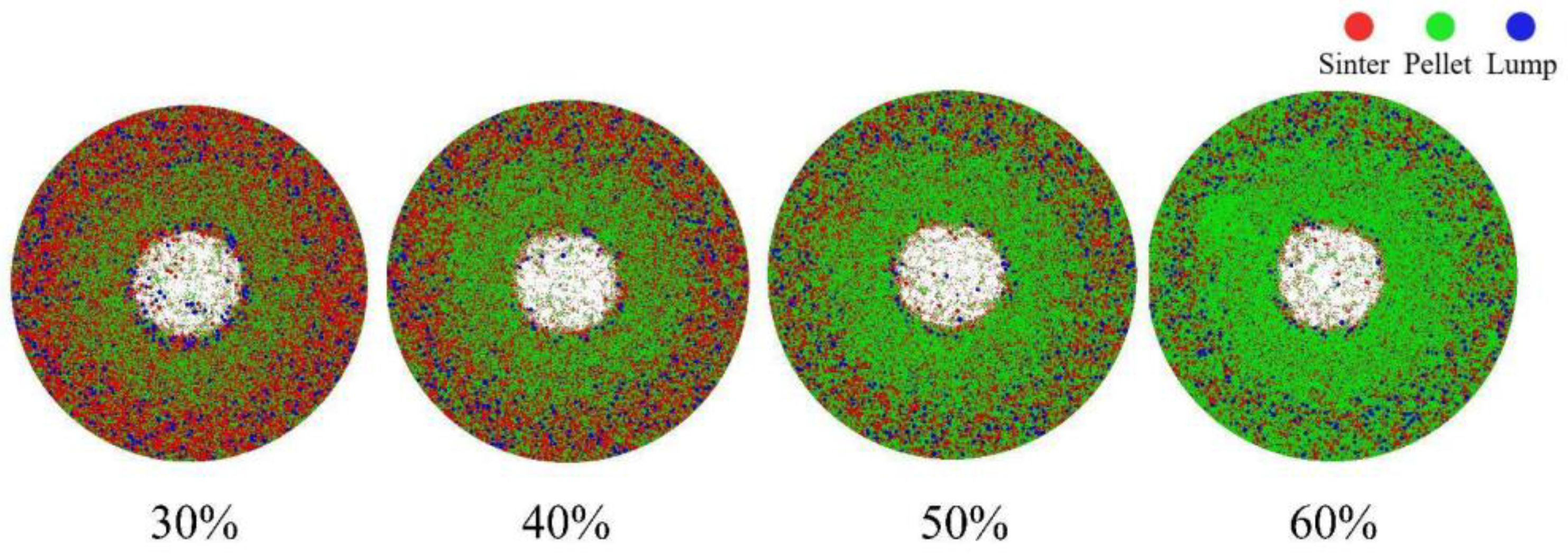
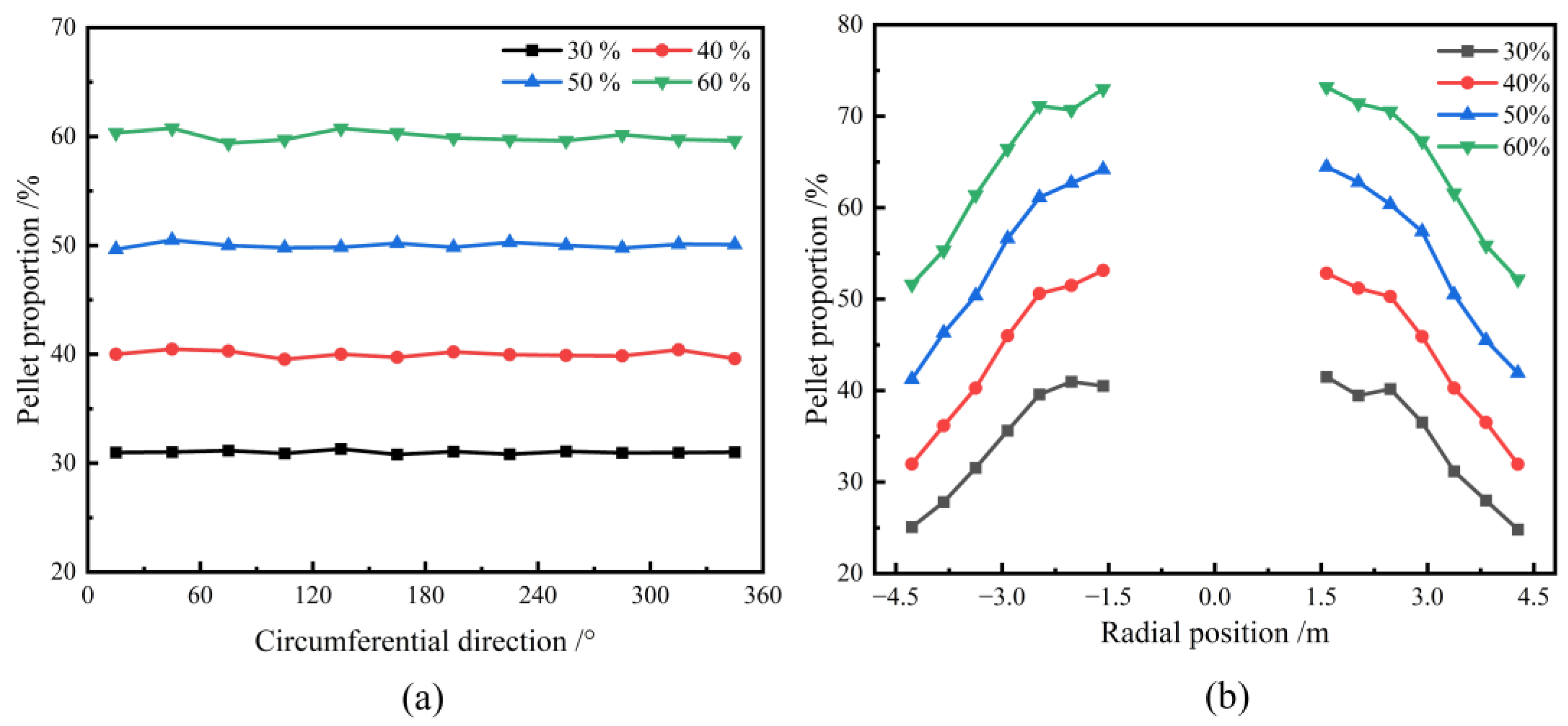
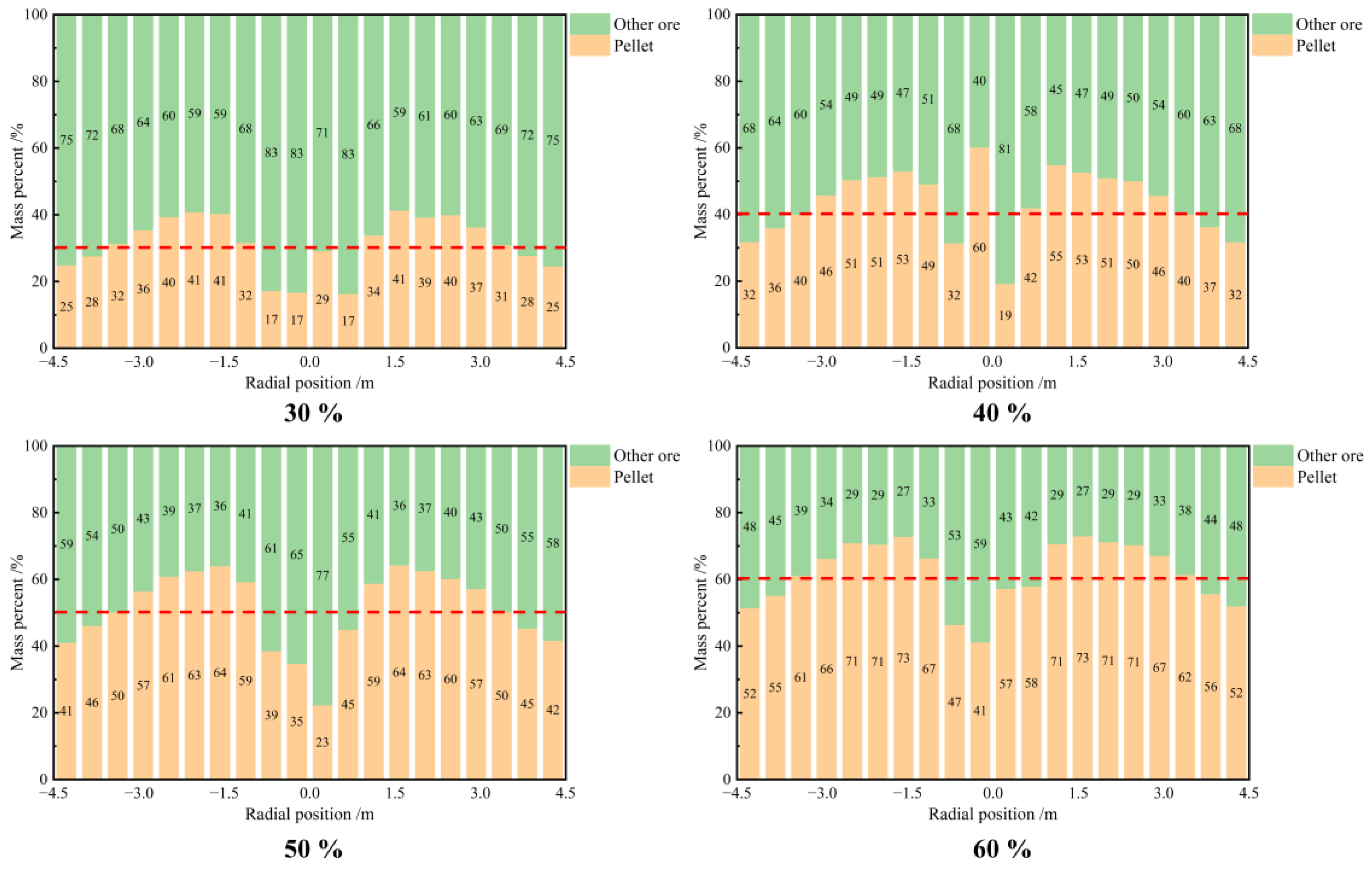
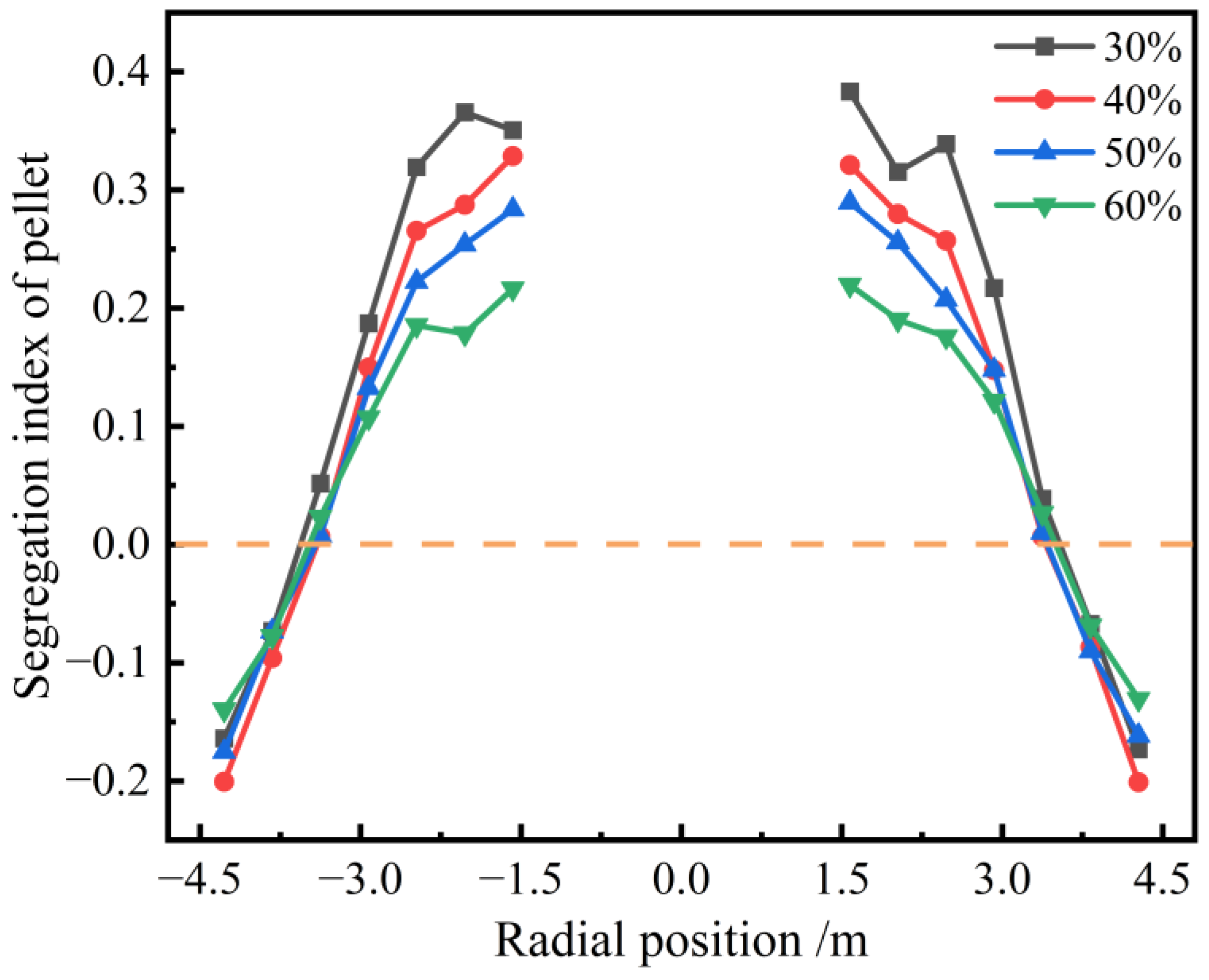
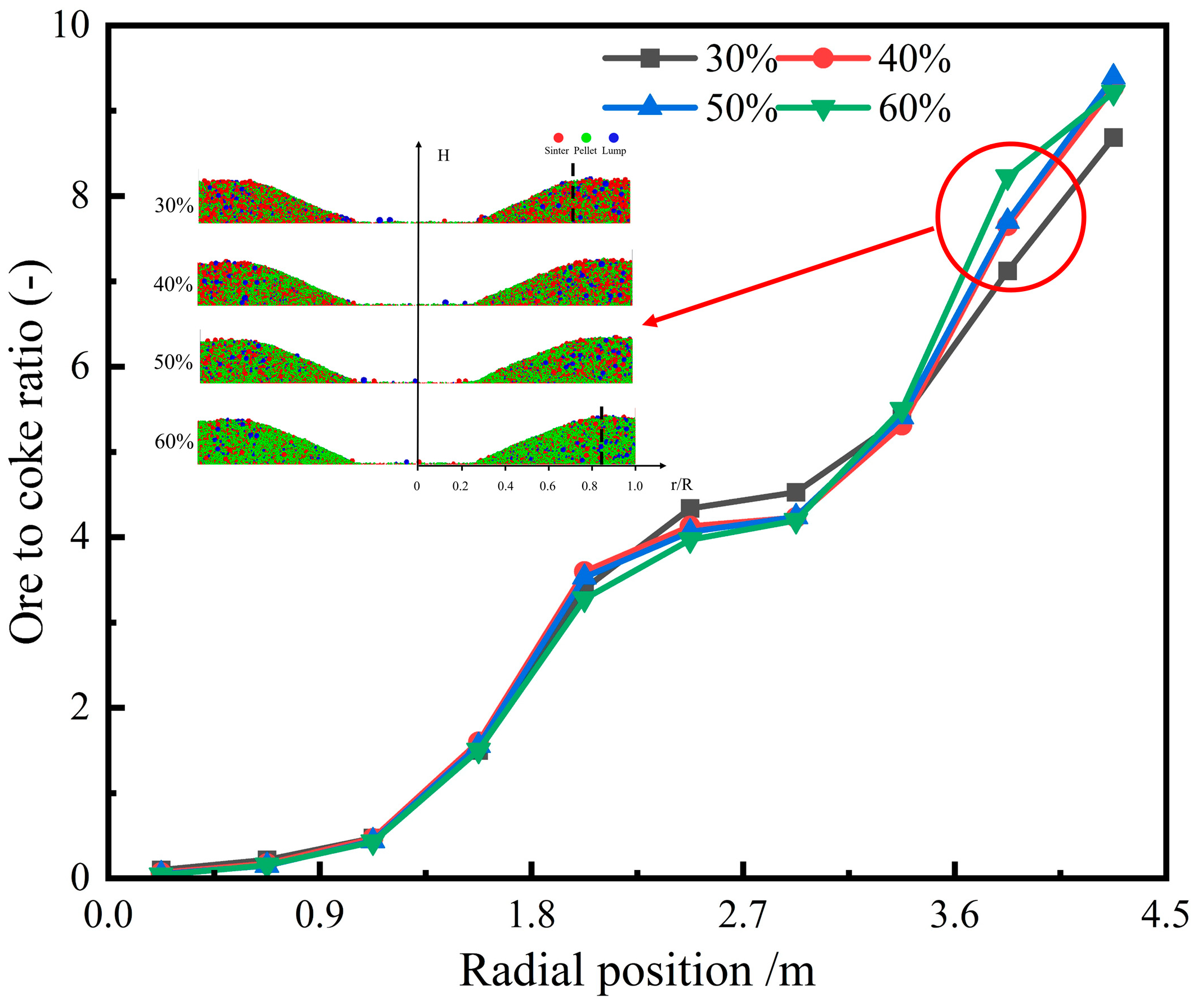
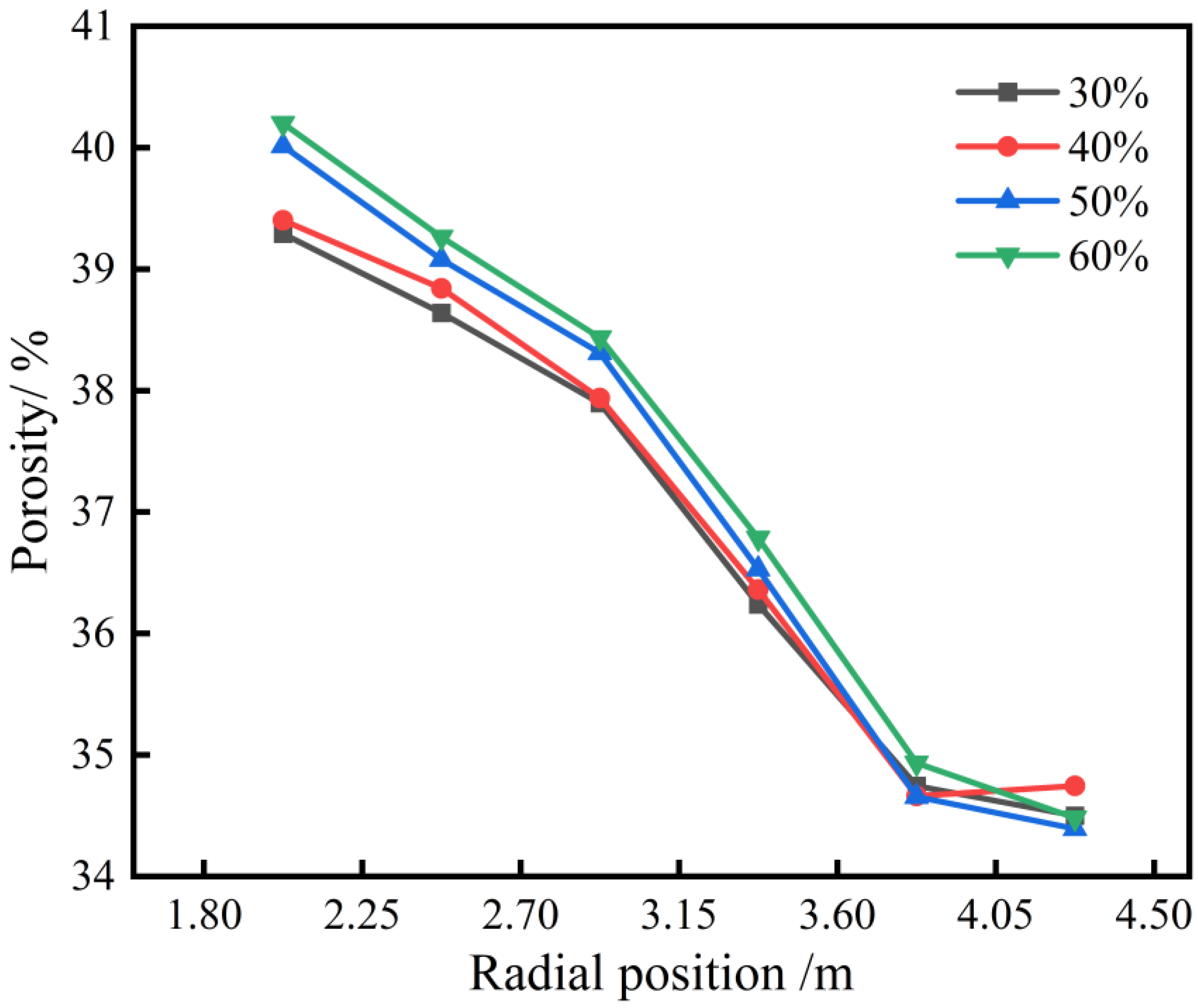
3.2. Effect of Pellet Proportion on Burden Distribution
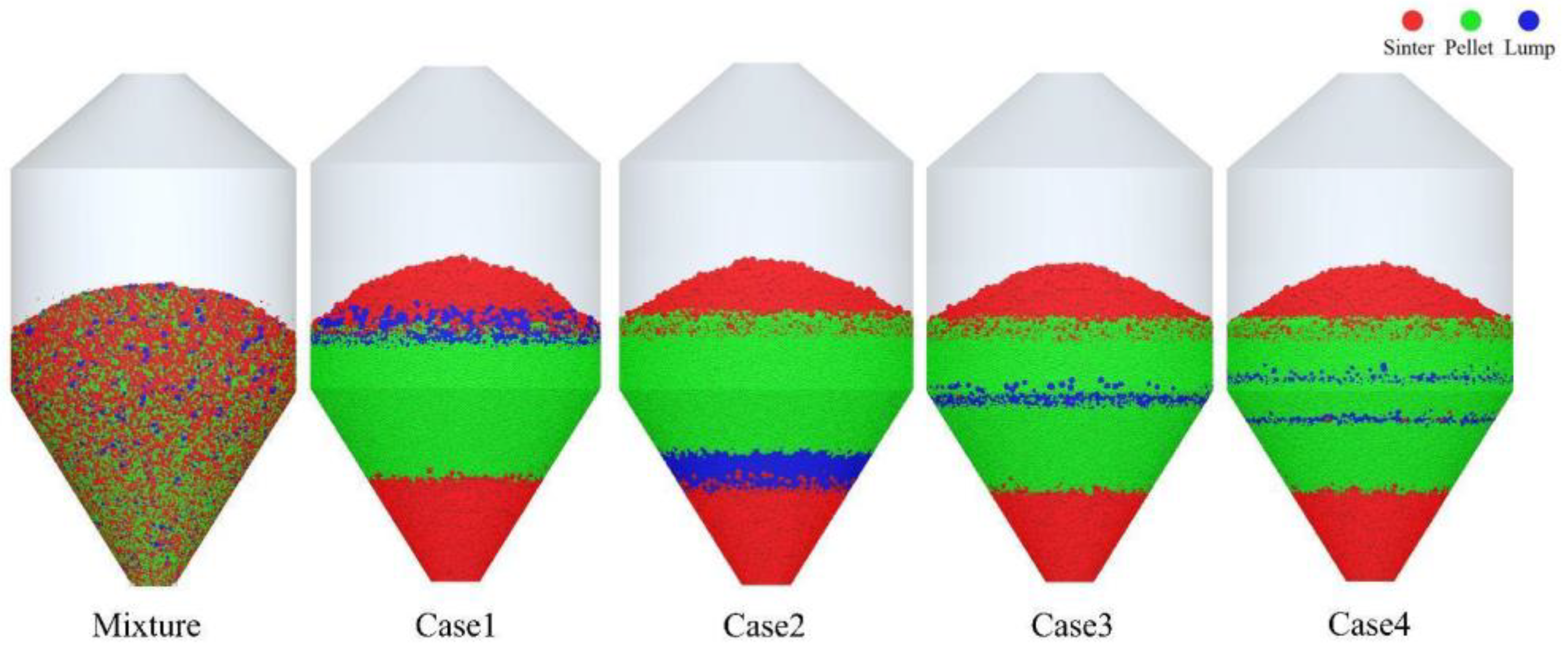
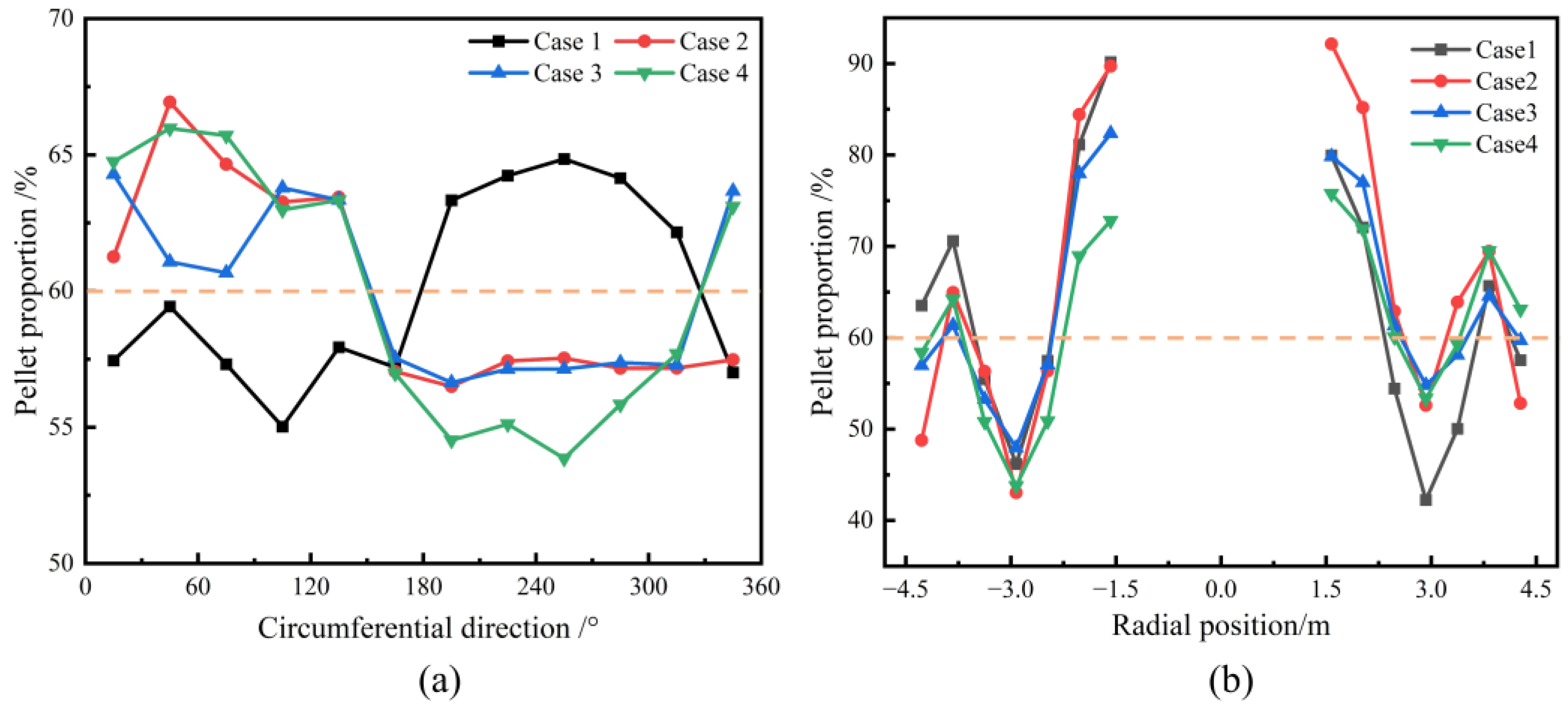
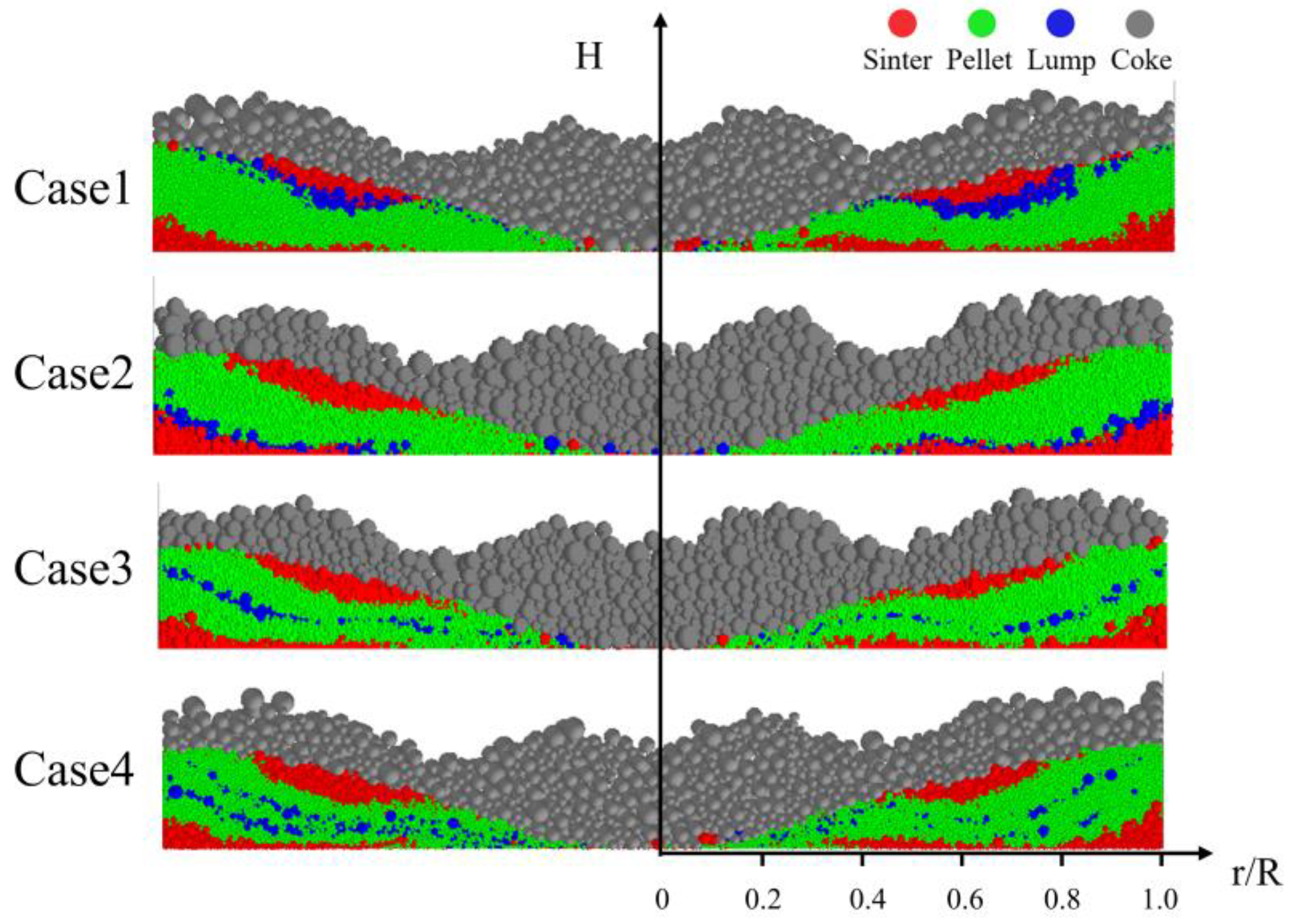
3.3. Effect of Charging Sequence on Burden Distribution
4. Conclusions
- (1)
- Under different pellet proportion conditions, the pellet mass fraction gradually increases from the furnace wall towards the center. With a higher pellet proportion, the radial segregation index of the pellets diminishes. However, the pellet proportion has a minimal impact on the circumferential mass distribution of the burden.
- (2)
- The porosity of the ore layer increases progressively from the furnace wall to the center. Additionally, with a higher pellet proportion, the porosity tends to increase.
- (3)
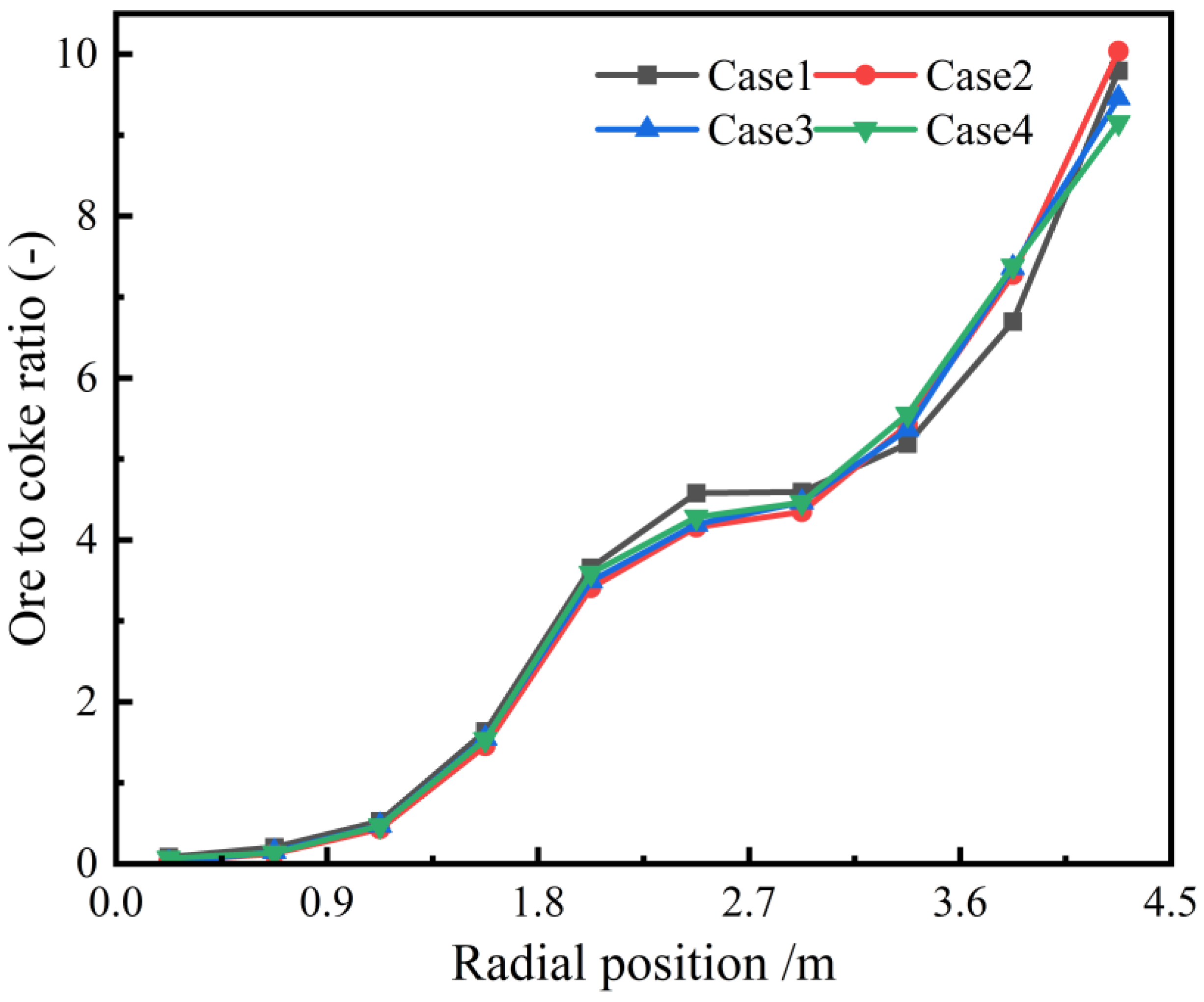
- The radial ore-to-coke ratio is minimally affected by variations in pellet proportion and charging sequence.
- (4)
- As the pellet proportion increases, alternating charging can reduce pellet rolling, thereby lowering the flowability of the furnace burden and enhancing the stability of the gas flow distribution.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, C.; Guo, Z.; Pan, J.; Zhu, D.; Li, S.; Yang, C.; Tian, H. Current situation of carbon emissions and countermeasures in China’s ironmaking industry. Int. J. Miner. Metall. Mater. 2023, 30, 1633–1650. [Google Scholar] [CrossRef]
- Wei, H.; Saxén, H.; Yu, Y. Numerical Analysis of Factors Affecting the Burden Surface and Porosity Distribution in the Upper Part of the Blast Furnace. Metals 2023, 13, 292. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Liu, Z.; Wang, T.; Wang, Y.; Li, K.; Wang, G.; Xu, T.; Zhang, Y. Isothermal kinetic analysis on reduction of solid/liquid wustite by hydrogen. Int. J. Miner. Metall. Mater. 2022, 29, 1830–1838. [Google Scholar] [CrossRef]
- He, L.; Jiang, X.; An, H.; Zheng, H.; Gao, Q.; Shen, F. Effects of pellet ratio on the burden movement and distribution characteristics in the BF throat. Powder Technol. 2024, 432, 119130. [Google Scholar] [CrossRef]
- Agrawal, A. Blast furnace performance under varying pellet proportion. Trans. Indian Inst. Met. 2019, 72, 777–787. [Google Scholar] [CrossRef]
- Mio, H.; Narita, Y.; Nakano, K.; Nomura, S. Validation of the burden distribution of the 1/3-scale of a blast furnace simulated by the discrete element method. Processes 2019, 8, 6. [Google Scholar] [CrossRef]
- Chen, J.; Zuo, H.; Xue, Q.; Wang, J. A review of burden distribution models of blast furnace. Powder Technol. 2022, 398, 117055. [Google Scholar] [CrossRef]
- Li, C.; Dong, K.; Liu, S.; Chandratilleke, G.R.; Zhou, Z.; Shen, Y. DEM study of particle segregation in the throat region of a blast furnace. Powder Technol. 2022, 407, 117660. [Google Scholar] [CrossRef]
- Roeplal, R.; Pang, Y.; Adema, A.; van der Stel, J.; Schott, D. Modelling of phenomena affecting blast furnace burden permeability using the Discrete Element Method (DEM)—A review. Powder Technol. 2023, 415, 118161. [Google Scholar] [CrossRef]
- Mitra, T.; Saxén, H. Discrete element simulation of charging and mixed layer formation in the ironmaking blast furnace. Comput. Part. Mech. 2016, 3, 541–555. [Google Scholar] [CrossRef]
- Mitra, T.; Saxén, H. Investigation of coke collapse in the blast furnace using mathematical modeling and small scale experiments. ISIJ Int. 2016, 56, 1570–1579. [Google Scholar] [CrossRef]
- Chen, J.-S.; Zuo, H.-B.; Wang, J.-X.; Xue, Q.-G.; Wang, J.-S. Mathematical model of burden distribution in bell-less top blast furnace. J. Iron Steel Res. Int. 2023, 30, 216–226. [Google Scholar] [CrossRef]
- Li, H.; Saxén, H.; Liu, W.; Zou, Z.; Shao, L. Model-based analysis of factors affecting the burden layer structure in the blast furnace shaft. Metals 2019, 9, 1003. [Google Scholar] [CrossRef]
- Li, M.; Wei, H.; Ge, Y.; Xiao, G.; Yu, Y. A Mathematical Model Combined with Radar Data for Bell-Less Charging of a Blast Furnace. Processes 2020, 8, 239. [Google Scholar] [CrossRef]
- Wu, D.; Yao, F.; Zhang, D.; Zu, E.; Zhou, P.; Chen, W. A self-adaption growth model for the burden packing process in a bell-less blast furnace. Processes 2024, 12, 1523. [Google Scholar] [CrossRef]
- Chibwe, D.K.; Evans, G.M.; Doroodchi, E.; Monaghan, B.J.; Pinson, D.J.; Chew, S.J. Charge material distribution behaviour in blast furnace charging system. Powder Technol. 2020, 366, 22–35. [Google Scholar] [CrossRef]
- Chen, J.; Zuo, H.; Zhao, H.; Xue, Q.; Wang, J. Burden circumferential mass segregation at the blast furnace with parallel hoppers. Powder Technol. 2022, 409, 117845. [Google Scholar] [CrossRef]
- Wei, H.; Ding, W.; Li, Y.; Nie, H.; Saxén, H.; Long, H.; Yu, Y. Porosity distribution of moving burden layers in the blast furnace throat. Granul. Matter 2021, 23, 10. [Google Scholar] [CrossRef]
- Zhou, K.; Jiang, Z.; Pan, D.; Gui, W.; Huang, J.; Xu, C. Research on the velocity distribution law of the coke in the chute of blast furnace based on discrete element method. Comput. Part. Mech. 2023, 10, 303–311. [Google Scholar] [CrossRef]
- Li, Q.; Guo, S.; Wang, S.; Zou, Z. CFD-DEM investigation on pressure drops of heterogeneous alternative-layer particle beds for low-carbon operating blast furnaces. Metals 2022, 12, 1507. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y.; Li, C.; Guo, H.; Yan, B. Research on the factors affecting the formation of ore-free zone at blast furnace throat based on DEM. Processes 2023, 11, 967. [Google Scholar] [CrossRef]
- Zhou, H.; Wu, J.; Hong, Z.; Wang, L.P.; Wu, S.; Kou, M.; Wang, G.; Luo, Y. Numerical simulation of coke collapse and its optimization during burden charging at the top of bell-less blast furnace. Powder Technol. 2021, 389, 155–162. [Google Scholar] [CrossRef]
- Zhao, Z.; Saxén, H.; Liu, Y.; She, X.; Xue, Q. Numerical study on the influence of pellet proportion on burden distribution in blast furnace. Ironmak. Steelmak. 2023, 50, 613–620. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Raju, A.B.; Pani, S.; Ghosh, U.; Nag, S.; GSR, M.; Pal, P.; Singh, U. Effect of Selective Pellet Loading on Burden Distribution and Blast Furnace Operations. ISIJ Int. 2023, 63, 271–281. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, N.; Zhou, Z.; Ning, Z.; Chen, M. Effect of combined ferrous burden composition and ore-coke interaction on blast furnace burden distribution. Powder Technol. 2025, 449, 120416. [Google Scholar] [CrossRef]
- Kou, M.; Xu, J.; Wu, S.; Zhou, H.; Gu, K.; Yao, S.; Wen, B. Effect of cross-section shape of rotating chute on particle movement and distribution at the throat of a bell-less top blast furnace. Particuology 2019, 44, 194–206. [Google Scholar] [CrossRef]
- Si, R.; Wang, Z.; Zhang, J.; Dai, J.; Zhang, S.; Jiang, D.; Wei, H. DEM study of the porosity distribution of sinter and coke layers in the throat region of a blast furnace. Powder Technol. 2023, 427, 118755. [Google Scholar] [CrossRef]
- Terui, K.; Kashihara, Y.; Hirosawa, T.; Nouchi, T. Optimization of coke mixed charging based on discrete element method. ISIJ Int. 2017, 57, 1804–1810. [Google Scholar] [CrossRef]
- Mio, H.; Nakauchi, T.; Kawaguchi, Y.; Enaka, T.; Narita, Y.; Inayoshi, A.; Matsuzaki, S.; Orimoto, T.; Nomura, S. High-speed video recording of particle trajectory via rotating chute of Nagoya No. 3 blast furnace and its comparison with simulated behavior using DEM. ISIJ Int. 2017, 57, 272–278. [Google Scholar] [CrossRef]
- Mio, H.; Narita, Y.; Matsuzaki, S.; Nishioka, K.; Nomura, S. Measurement of particle charging trajectory via rotating chute of 1/3-scale blast furnace and its comparing with numerical analysis using Discrete Element Method. Powder Technol. 2019, 344, 797–803. [Google Scholar] [CrossRef]
- Hong, Z.; Zhou, H.; Wu, J.; Zhan, L.; Fan, Y.; Zhang, Z.; Wu, S.; Xu, H.; Wang, L.P.; Kou, M. Effects of Operational Parameters on Particle Movement and Distribution at the Top of a Bell-Less Blast Furnace Based on Discrete Element Method. Steel Res. Int. 2021, 92, 2000262. [Google Scholar] [CrossRef]
- Xu, W.; Cheng, S.; Li, C. Effect of the charging sequence of iron-bearing burden on burden distribution during the charging process of blast furnace based on discrete element method. Ironmak. Steelmak. 2022, 49, 208–216. [Google Scholar] [CrossRef]
- Kou, M.; Zeng, W.; Zhang, Z.; She, X.; Zhang, T.; Zhao, B.; Ma, X.; Zhou, H. Central coke charging and its effect on coke collapse at the throat of blast furnace by DEM simulation. Powder Technol. 2022, 408, 117784. [Google Scholar] [CrossRef]
- Wei, H.; Nie, H.; Li, Y.; Saxén, H.; He, Z.; Yu, Y. Measurement and simulation validation of DEM parameters of pellet, sinter and coke particles. Powder Technol. 2020, 364, 593–603. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Biswas, R.; Basu, S.; Nag, S. Characterisation of binary mixtures of pellets and sinter for DEM simulations. Adv. Powder Technol. 2022, 33, 103358. [Google Scholar] [CrossRef]
- Wei, H.; Li, M.; Li, Y.; Ge, Y.; Saxén, H.; Yu, Y. Discrete element method (DEM) and experimental studies of the angle of repose and porosity distribution of pellet pile. Processes 2019, 7, 561. [Google Scholar] [CrossRef]
- Di, Z.; Yan, B.; Cheng, B.; Wang, S.; Fan, C. Effects of particle size composition and burden ratio on burden segregation in the blast furnace throat based on DEM. Powder Technol. 2024, 448, 120319. [Google Scholar] [CrossRef]
- Xu, W. Investigation on Burden Distribution Segregation Optimization of Blast Furnace and Gas Solid Flow Characteristics in Blast Furnace. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2020. [Google Scholar]
- Xu, W.; Cheng, S.; Niu, Q.; Hu, W.; Bang, J. The DEM study of segregation phenomena of burden distribution during the charging process of blast furnace with two parallel hoppers. Ironmak. Steelmak. 2020, 47, 337–343. [Google Scholar] [CrossRef]
- Zhang, F.; Xu, W.; Cheng, X.; Chen, Y. Analysis on key process and technology of blast furnace ironmaking on high charging proportion of pellet ore. Iron Steel 2024, 59, 32–45. [Google Scholar]

| Forces and Torques | Symbols | Equations |
|---|---|---|
| Normal elastic force | ||
| Normal damping force | ||
| Tangential elastic force | ||
| Tangential damping force | ||
| Torque by tangential forces | ||
| Rolling friction torque | ||
| where, , , , , , , , , , . Note that the tangential forces () should be replaced by the maximum friction force when they are larger than the later force. | ||
| Type | Diameter/mm | Mass Ratio/wt% | Mass/kg |
|---|---|---|---|
| Coke-1 | 90 | 27 | 5273 |
| Coke-2 | 150 | 56 | 10,937 |
| Coke-3 | 210 | 17 | 3320 |
| Sinter-1 | 21 | 19 | 8926 |
| Sinter-2 | 39 | 22 | 10,335 |
| Sinter-3 | 60 | 27 | 12,685 |
| Sinter-4 | 105 | 32 | 15,034 |
| Pellet-1 | 33 | 23 | 6203 |
| Pellet-2 | 42 | 71 | 19,149 |
| Pellet-3 | 54 | 6 | 1618 |
| Lump ore-1 | 36 | 20 | 2610 |
| Lump ore-2 | 60 | 22 | 2871 |
| Lump ore-3 | 105 | 46 | 6003 |
| Lump ore-4 | 135 | 12 | 1566 |
| Parameters | Sinter | Pellet | Lump Ore | Coke | Wall | |
|---|---|---|---|---|---|---|
| Density ρ/kg·m−3 | 3382 | 3015 | 4230 | 1050 | 7850 | |
| Shear modulus G/MPa | 10 | 10 | 10 | 2.2 | 79,000 | |
| Poisson’s ratio υ/- | 0.25 | 0.25 | 0.21 | 0.22 | 0.30 | |
| Static friction coefficient μs/- | Sinter | 0.84 | 0.40 | 0.41 | 0.79 | 0.61 |
| Pellet | 0.25 | 0.27 | 0.42 | 0.48 | ||
| Lump ore | 0.60 | 0.71 | 0.69 | |||
| Coke | 0.87 | 0.71 | ||||
| Rolling friction coefficient μr/- | Sinter | 0.17 | 0.07 | 0.10 | 0.12 | 0.09 |
| Pellet | 0.02 | 0.03 | 0.05 | 0.06 | ||
| Lump ore | 0.07 | 0.09 | 0.09 | |||
| Coke | 0.20 | 0.09 | ||||
| Restitution coefficient e/- | Sinter | 0.36 | 0.43 | 0.39 | 0.31 | 0.35 |
| Pellet | 0.30 | 0.48 | 0.34 | 0.54 | ||
| Lump ore | 0.41 | 0.32 | 0.43 | |||
| Coke | 0.35 | 0.31 | ||||
| Time step/s | 1 × 10−5 | |||||
| Chute Angle/° | 41 | 39 | 37 | 35 | 33 | 30 | 14 |
|---|---|---|---|---|---|---|---|
| Number of revolutions (Ore) | 4 | 4 | 3 | 2 | 1 | ||
| Number of revolutions (Coke) | 3 | 3 | 2 | 2 | 2 | 1 | 5 |
| Simulation Scheme | |
|---|---|
| Case1 | S, S, P, P, P, P, L, L, S |
| Case2 | S, L, L, P, P, P, P, S |
| Case3 | S, P, P, L, L, P, P, S |
| Case4 | S, P, L, P, L, P, S |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Zhang, C.; Han, J.; Wang, Z.; Ren, W.; Zhang, J.; Chen, Z.; Lu, P. Effect of Pellet Proportion and Charging Sequence on Burden Distribution in Blast Furnaces According to Discrete Element Method Simulation. Processes 2025, 13, 237. https://doi.org/10.3390/pr13010237
Wei H, Zhang C, Han J, Wang Z, Ren W, Zhang J, Chen Z, Lu P. Effect of Pellet Proportion and Charging Sequence on Burden Distribution in Blast Furnaces According to Discrete Element Method Simulation. Processes. 2025; 13(1):237. https://doi.org/10.3390/pr13010237
Chicago/Turabian StyleWei, Haoyuan, Chi Zhang, Jixiang Han, Zhenyang Wang, Wei Ren, Jianliang Zhang, Ziluo Chen, and Peiyuan Lu. 2025. "Effect of Pellet Proportion and Charging Sequence on Burden Distribution in Blast Furnaces According to Discrete Element Method Simulation" Processes 13, no. 1: 237. https://doi.org/10.3390/pr13010237
APA StyleWei, H., Zhang, C., Han, J., Wang, Z., Ren, W., Zhang, J., Chen, Z., & Lu, P. (2025). Effect of Pellet Proportion and Charging Sequence on Burden Distribution in Blast Furnaces According to Discrete Element Method Simulation. Processes, 13(1), 237. https://doi.org/10.3390/pr13010237





