Optimization of Copper Recovery from Cyanide Leaching Solutions Used in Gold–Copper Ore Processing Using Probabilistic–Deterministic Experimental Design
Abstract
:1. Introduction
- -
- The AVR (acidification–volatilization–regeneration) method designed for the regeneration of cyanide and its modifications, namely, the AuGMENT (resin with a quarter naryamino group) and Vitrokele (cross-linked polystyrene structure-based resin) processes;
- -
- The modified Newton–Raphson MNR method, which includes cyanide regeneration and copper sulphide production;
- -
- Methods based on absorbent carbon use;
- -
- Methods based on ion-exchange resin use;
- -
- Other less common methods [6].
2. Materials and Methods
- -
- ≥98% sodium cyanide (NaCN) tablets for ore leaching;
- -
- Sulphuric acid (H2SO4) to maintain the pH value;
- -
- Adsorbent carbon Norit RO 3515-B for gold extraction from the cyanide solutions;
- -
- Lime milk to thicken the pulps.
2.1. Collection of the Solutions to Run Copper Precipitation Experiments
2.2. Flowsheet for the Copper Precipitation Experiment
2.3. Copper Precipitation from Cyanide Solutions
- n—the number of the dots described;
- k—the number of operative factors (which equals 1 for specific dependences);
- yei—the experimental result value;
- yTi—the theoretical (calculated) result value;
- yav—the average experimental value.
3. Results
3.1. Results of the Experiments on Copper Precipitation with Na2S Supplement
3.2. Results of the Experiments on Copper Precipitation with No Na2S Supplement
- -
- A sulphuric acid-specific consumption of 1.48 g/L;
- -
- A consumption of Magnafloc 351 flocculating agent at 0.5 g/L m3 of pulp;
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Gold Council Gold Demand Trends Full Year 2022. Available online: https://www.gold.org/goldhub/research/gold-demand-trends/gold-demand-trends-full-year-2022/supply (accessed on 21 August 2024).
- Medina, D.; Anderson, C.G. A Review of the Cyanidation Treatment of Copper-Gold Ores and Concentrates. Metals 2020, 10, 897. [Google Scholar] [CrossRef]
- Sceresini, B. Gold-Copper Ores. In Developments in Mineral Processing; Mike, D., Adams, B.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 15, pp. 789–824. [Google Scholar] [CrossRef]
- Estay, H. Designing the SART process—A review. Hydrometallurgy 2018, 176, 147–165. [Google Scholar] [CrossRef]
- La Brooy, S.R.; Linge, H.G.; Walker, G.S. Review of gold extraction from ores. Miner. Eng. 1994, 7, 1213–1241. [Google Scholar] [CrossRef]
- Xie, F.; Dreisinger, D.; Doyle, F. A Review on Recovery of Copper and Cyanide from Waste Cyanide Solutions. Miner. Process. Extr. Metall. Rev. 2013, 34, 387–411. [Google Scholar] [CrossRef]
- Yilmaz, E.; Yazici, E.Y.; Ahlatci, F.; Celep, O.; Deveci, H. Precipitation of copper from cyanide leach solutions using sodium dimethyldithiocarbamate (SDDC). Hydrometallurgy 2021, 202, 105610. [Google Scholar] [CrossRef]
- Liu, W.; Li, W.; Liu, W.; Shen, Y.; Zhou, S.; Cui, B. A new strategy for extraction of copper cyanide complex ions from cyanide leach solutions by ionic liquids. J. Mol. Liq. 2023, 383, 122108. [Google Scholar] [CrossRef]
- Li, W.; Liu, W.; Liu, W.; Kou, W. Removal of copper and iron cyanide complex from cyanide solution by polymer-surfactant aggregates. Colloids Surf. A Physicochem. Eng. Asp. 2024, 700, 134788. [Google Scholar] [CrossRef]
- Alonso-González, O.; Nava-Alonso, F.; Uribe-Salas, A. Copper removal from cyanide solutions by acidification. Miner. Eng. 2009, 22, 324–329. [Google Scholar] [CrossRef]
- Li, M.; Li, B.; Chen, J.; Shen, X.; Cui, S.; Liu, K.; Han, Q. A novel green method for copper recovery from cuprous thiocyanate-containing acidified sediments in the gold industry. J. Clean. Prod. 2021, 329, 129729. [Google Scholar] [CrossRef]
- Karppinen, A.; Seisko, S.; Nevatalo, L.; Wilson, B.P.; Yliniemi, K.; Lundström, M. Gold recovery from cyanidation residue by chloride leaching and carbon adsorption—Preliminary results from CICL process. Hydrometallurgy 2024, 226, 106304. [Google Scholar] [CrossRef]
- Botz, M.; Guzman, G.; Sevilla, L. Campaign testing the yanacocha sart plant with high-copper feed solution. In Proceedings of the Society for Mining, Metallurgy, and Exploration, Inc. (SME), Denver, CO, USA, 15–18 February 2015. [Google Scholar]
- Baker, B.; Rodriguez, F.; Littlejohn, P. SART implementation at Gold Mines in Latin America. In World Gold 2017; CIM/ICM: Vancouver, BC, Canada, 2017; Available online: https://onemine.org/documents/sart-implementation-at-gold-mines-in-latin-america (accessed on 21 August 2024).
- Kratochvil, D.; Salari, D.; Avilez, T. SART implementation at heap leach operations in Mexico, 2018. In Proceedings of the 50th Canadian Minerals Processors Conference in Ottawa, Ottawa, ON, Canada, 24 January 2018. [Google Scholar]
- MacPhail, P.K.; Fleming, C.; Sarbutt, K. Cyanide Recovery by the SART Process for the Lobo-Marte Project, Chile. In Randol Gold and Silver Forum, Society for Mining; Metallurgy & Exploration: Denver, CO, USA, 1998. [Google Scholar]
- Estay, H.; Gim-Krumm, M.; Quilaqueo, M. Two-Stage SART Process: A Feasible Alternative for Gold Cyanidation Plants with High Zinc and Copper Contents. Minerals 2018, 8, 392. [Google Scholar] [CrossRef]
- Fleming, C.A.; Melashvili, M. The SART process: Killing the sacred cows. In Proceedings of the XXVIII International Mineral Processing Congress (IMPC 2016), Quebec, QC, Canada, 11–15 September 2016; pp. 2107–2120. [Google Scholar]
- Estay, H.; Gim-Krumm, M.; Seriche, G.; Quilaqueo, M.; Barros, L.; Ruby-Figueroa, R.; Romero, J.; Troncoso, E. Optimizing the SART process: A critical assessment of its design criteria. Miner. Eng. 2020, 146, 106116. [Google Scholar] [CrossRef]
- Estay, H.; Ruby-Figueroa, R.; Quilaqueo, M.; Seriche, G.; Cortés, I.; Gim-Krumm, M.; Barros, L. Enhancing the effectiveness of copper and cyanide recovery in gold cyanidation: A new integrated membrane process. Hydrometallurgy 2021, 202, 105606. [Google Scholar] [CrossRef]
- Lu, D.; Chang, Y.; Wang, W.; Xie, F.; Asselin, E.; Dreisinger, D. Copper and Cyanide Extraction with Emulsion Liquid Membrane with LIX 7950 as the Mobile Carrier: Part 1, Emulsion Stability. Metals 2015, 5, 2034–2047. [Google Scholar] [CrossRef]
- Xie, F.; Wang, W. Recovery of copper and cyanide from waste cyanide solutions using emulsion liquid membrane with LIX 7950 as the carrier. Environ. Technol. 2017, 38, 1961–1968. [Google Scholar] [CrossRef] [PubMed]
- Seriche, G.; Quilaqueo, M.; Barros, L.; Gim-Krumm, M.; Cortés, I.; Troncoso, E.; Ruby-Figueroa, R.; Estay, H. Integrated Membrane Process Coupled with Metal Sulfide Precipitation to Recover Zinc and Cyanide. Minerals 2022, 12, 229. [Google Scholar] [CrossRef]
- Sceresini, B.; Breuer, P. Chapter 43-Gold-Copper Ores. In Adams Gold Ore Processing, 2nd ed.; Mike, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 771–801. [Google Scholar] [CrossRef]
- Das, A.K.; Saikat, D. Chapter 3-Optimization of Extraction Using Mathematical Models and Computation. In Computational Phytochemistry; Satyajit, D., Sarker, L.N., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 75–106. ISBN 9780128123645. [Google Scholar] [CrossRef]
- Liu, P.-j.; Liu, Z.-g.; Chu, M.-s.; Yan, R.-j.; Li, F.; Tang, J. Multiobjective collaborative optimization of novel carbothermal reduction process of stainless steel dust and laterite nickel ore. Trans. Nonferrous Met. Soc. China 2023, 33, 1919–1931. [Google Scholar] [CrossRef]
- Gürkan, E.H.; Tibet, Y.; Çoruh, S. Application of Full Factorial Design Method for Optimization of Heavy Metal Release from Lead Smelting Slag. Sustainability 2021, 13, 4890. [Google Scholar] [CrossRef]
- Mihăilescu, M.; Negrea, A.; Ciopec, M.; Negrea, P.; Duțeanu, N.; Grozav, I.; Svera, P.; Vancea, C.; Bărbulescu, A.; Dumitriu, C.Ș. Full Factorial Design for Gold Recovery from Industrial Solutions. Toxics 2021, 9, 111. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Teo, P.T.; Zakaria, S.K.; Mohd Sharif, N.; Abu Seman, A.; Taib, M.A.A.; Mohamed, J.J.; Yusoff, M.; Yusoff, A.H.; Mohamad, M.; Ali, A.; et al. Application of General Full Factorial Statistical Experimental Design’s Approach for the Development of Sustainable Clay-Based Ceramics Incorporated with Malaysia’s Electric Arc Furnace Steel Slag Waste. Crystals 2021, 11, 442. [Google Scholar] [CrossRef]
- Hanrahan, G.; Zhu, J.; Gibani, S.; Patil, D.G. Chemometrics and Statistics|Experimental Design. In Encyclopedia of Analytical Science, 2nd ed.; Worsfold, P., Townshend, A., Poole, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 8–13. [Google Scholar] [CrossRef]
- Malyshev, V.P. Probabilistic-deterministic planning of the experiment. Alma-Ata Sci. 1981, 116, 116. [Google Scholar]

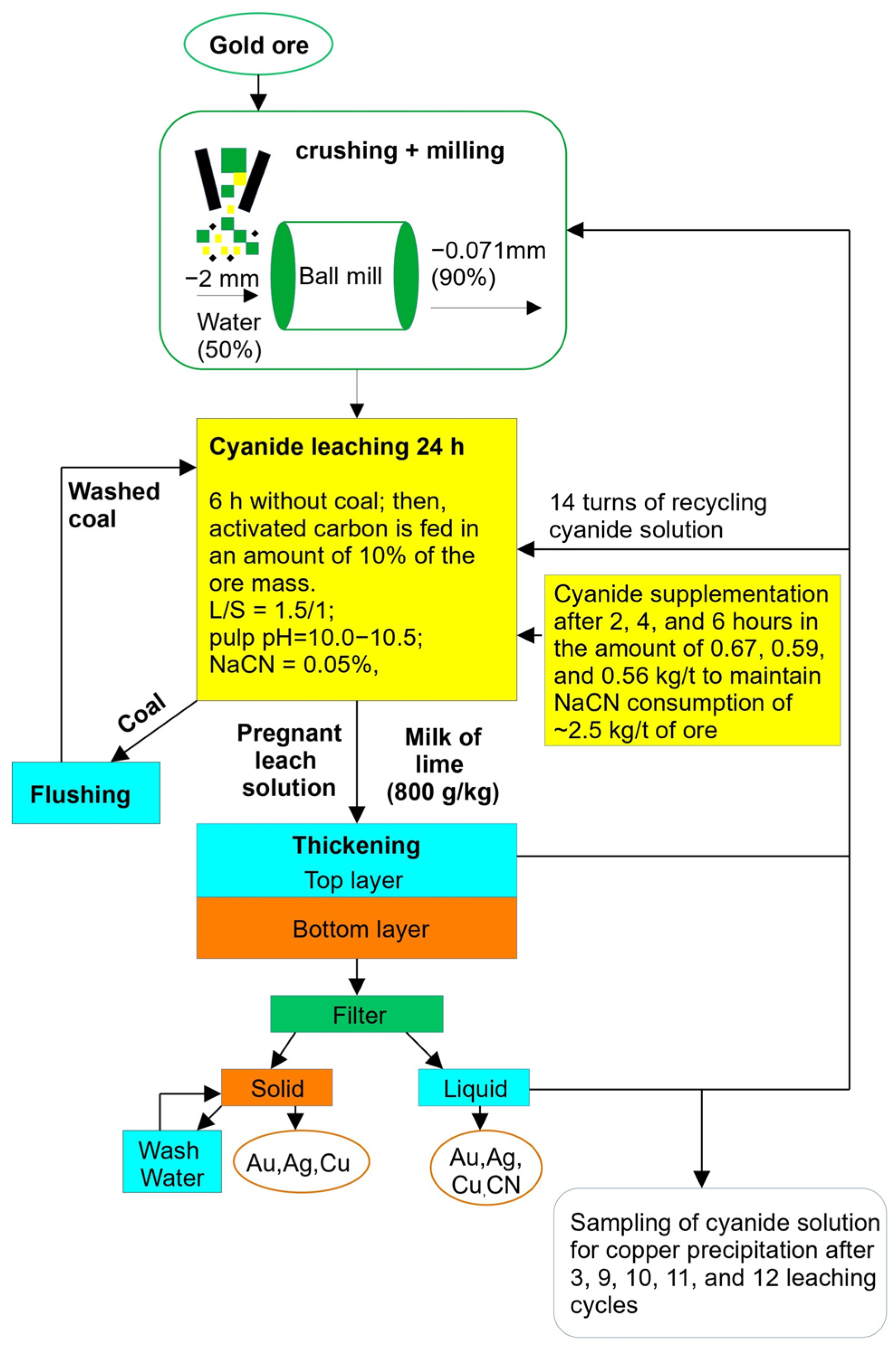



| No. | Ore Size | Coal | Composition of the Cake | Leaching Rate, % | NaCN Consumption, kg/t Ore | ||||
|---|---|---|---|---|---|---|---|---|---|
| Au, g/t | Ag, g/t | Cu, % | Au | Ag | Cu | ||||
| 1 | P80 = 0.071 mm | − | 0.26 | 0.75 | 0.1088 | 78.3 | 37.5 | 27.5 | 1.98 |
| 2 | + | 0.18 | 0.44 | 0.1138 | 85.0 | 63.3 | 24.1 | 2.40 | |
| 3 | P80 = 0.067 mm (85%) | − | 0.19 | 0.60 | 0.1086 | 84.2 | 50.0 | 27.6 | 2.16 |
| 4 | + | 0.17 | 0.48 | 0.1102 | 85.8 | 60.0 | 26.5 | 2.53 | |
| 5 | P80 = 0.057 mm (90%) | − | 0.20 | 0.72 | 0.1096 | 83.3 | 40.0 | 26.9 | 2.44 |
| 6 | + | 0.16 | 0.46 | 0.1084 | 86.7 | 61.7 | 27.7 | 2.57 | |
| 7 | + * | 0.15 | 0.49 | 0.1104 | 87.5 | 59.2 | 26.4 | 2.45 | |
| No. | NaCN Feed, kg/t | NaCN Composition of the Final Solution, % | Composition of the Cake | Leaching Rate, % | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 min | 120 min | 240 min | 360 min | Total | Au, g/t | Ag, g/t | Cu, % | Au | Ag | Cu | ||
| 1 | 0.75 | - | - | - | 0.75 | <0.01 | 1.00 | 1.2 | 0.12 | 16.7 | 20.0 | |
| 2 | 0.75 | 0.67 | - | - | 1.42 | <0.01 | 0.66 | 1.0 | 0.12 | 45.0 | 16.7 | 20.0 |
| 3 | 0.75 | 0.67 | 0.59 | - | 2.01 | <0.01 | 0.40 | 0.76 | 0.11 | 66.7 | 36.7 | 26.7 |
| 4 | 0.75 | 0.67 | 0.59 | 0.56 | 2.57 | 0.01 | 0.20 | 0.72 | 0.11 | 83.3 | 40.0 | 26.7 |
| Turnover No. | Composition of Cake | Composition of the Solution | Leaching Rate, % | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Au, g/t | Ag, g/t | Cu, % | Au, mg/L | Cu, g/L | Ca, g/L | Fe, g/L | NaCN, % | Au | Ag | Cu | |
| 1 | 0.19 | 0.50 | 0.12 | <0.02 | 0.16 | - | - | 0.005 | 84.2 | 58.3 | 20.0 |
| 2 | 0.26 | 0.30 | 0.11 | <0.02 | 0.25 | - | - | 0.030 | 78.3 | 75.0 | 26.7 |
| 3 | 0.26 | 0.30 | 0.12 | <0.02 | 0.34 | - | - | 0.022 | 78.3 | 75.0 | 20.0 |
| 4 | 0.26 | 0.30 | 0.11 | <0.02 | 0.64 | - | - | 0.042 | 78.3 | 75.0 | 26.7 |
| 5 | 0.17 | 0.32 | 0.10 | <0.02 | 0.80 | - | - | 0.043 | 85.8 | 73.3 | 33.0 |
| 6 | 0.14 | 0.34 | 0.12 | <0.02 | 0.82 | - | - | 0.045 | 88.3 | 71.6 | 20.0 |
| 7 | 0.17 | 0.48 | 0.12 | <0.02 | 1.03 | - | 0.085 | 0.045 | 85.8 | 60.0 | 20.0 |
| 8 | 0.16 | 0.48 | 0.12 | <0.02 | 1.05 | - | 0.066 | 0.048 | 86.7 | 60.0 | 20.0 |
| 9 | 0.19 | 0.48 | 0.12 | <0.02 | 1.35 | <0.01 | 0.071 | 0.049 | 84.2 | 60.0 | 20.0 |
| 10 | 0.18 | 0.48 | 0.11 | <0.02 | 1.55 | <0.01 | 0.060 | 0.049 | 85.0 | 60.0 | 26.7 |
| 11 | 0.19 | 0.72 | 0.11 | 0.029 | 1.15 | 0.011 | 0.090 | 0.042 | 84.2 | 40.0 | 26.7 |
| 12 | 0.22 | 0.60 | 0.11 | <0.02 | 1.10 | 0.014 | 0.083 | 0.041 | 81.7 | 50.0 | 26.7 |
| 13 | 0.22 | 0.60 | 0.11 | 0.024 | 1.19 | <0.01 | 0.075 | 0.040 | 81.7 | 50.0 | 26.7 |
| 14 | 0.20 | 0.42 | 0.11 | <0.02 | 1.09 | 0.013 | 0.080 | 0.034 | 83.3 | 65.0 | 26.7 |
| General | 0.20 | 0.45 | 0.114 | 83.3 | 62.5 | 24.0 | |||||
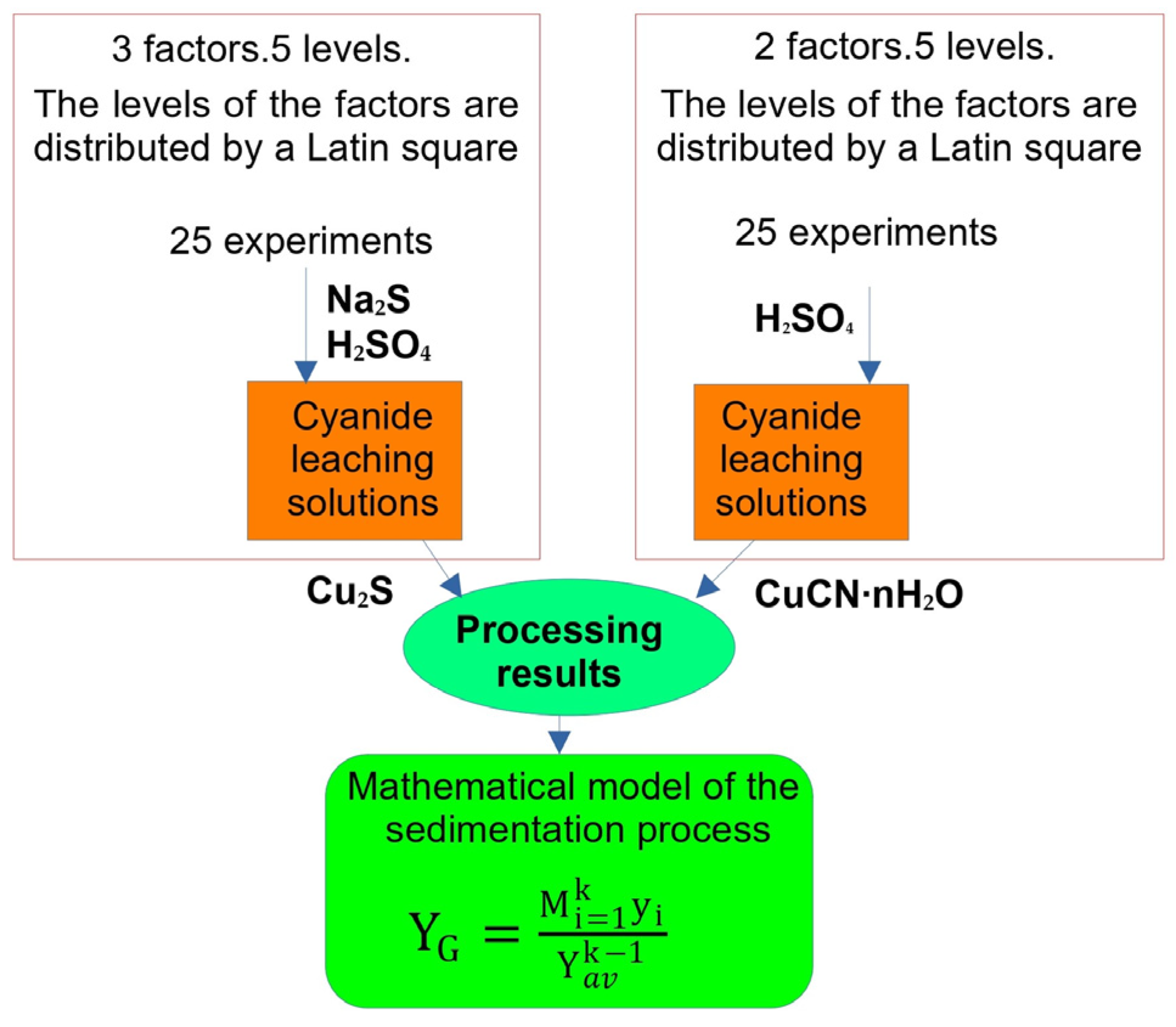
| Factors | Levels | |||||
|---|---|---|---|---|---|---|
| With Na2S | ||||||
| X1 | Consumption of sulphidizer by stoichiometry, % Na2S | 80 | 83.3 | 90 | 117 | 156 |
| X2 | pH of the solution after acidification | 3 | 3.5 | 4 | 4.5 | 5 |
| X3 | Initial Cu concentration in the solution, g/L | 0.34 | 1.1 | 1.15 | 1.35 | 1.55 |
| Without Na2S | ||||||
| X4 | Initial Cu concentration in the solution, g/L | 0.34 | 1.1 | 1.15 | 1.35 | 1.55 |
| X5 | pH of the solution after acidification | 3 | 3.5 | 4 | 4.5 | 5 |
| No. | With Na2S | No. | Without Na2S | |||||
|---|---|---|---|---|---|---|---|---|
| Na2S Consump. by Stoichiometry, % | Solution pH After Acidification | Initial Cu Grade in Solution, g/L | Copper Grade in Solution After Precipitation, g/L | Initial Cu Grade in Solution, g/L | Solution pH After Acidification | Copper Grade in Solution After Precipitation, g/L | ||
| 1 | 80 | 3 | 0.34 | 0.165 | 26 | 0.34 | 3 | 0.046 |
| 2 | 80 | 4 | 1.15 | 0.806 | 27 | 0.34 | 4 | 0.087 |
| 3 | 80 | 3.5 | 1.10 | 0.653 | 28 | 0.34 | 3.5 | 0.052 |
| 4 | 80 | 5 | 1.55 | 1.211 | 29 | 0.34 | 5 | 0.34 |
| 5 | 80 | 4.5 | 1.35 | 1.041 | 30 | 0.34 | 4.5 | 0.33 |
| 6 | 90 | 3 | 1.15 | 0.587 | 31 | 1.15 | 3 | 0.172 |
| 7 | 90 | 4 | 1.10 | 0.703 | 32 | 1.15 | 4 | 0.393 |
| 8 | 90 | 3.5 | 1.55 | 1.003 | 33 | 1.15 | 3.5 | 0.194 |
| 9 | 90 | 5 | 1.35 | 1.162 | 34 | 1.15 | 5 | 1.15 |
| 10 | 90 | 4.5 | 0.34 | 0.206 | 35 | 1.15 | 4.5 | 1.09 |
| 11 | 83.3 | 3 | 1.10 | 0.638 | 36 | 1.1 | 3 | 0.165 |
| 12 | 83.3 | 4 | 1.55 | 1.192 | 37 | 1.1 | 4 | 0.382 |
| 13 | 83.3 | 3.5 | 1.35 | 0.898 | 38 | 1.1 | 3.5 | 0.234 |
| 14 | 83.3 | 5 | 0.34 | 0.192 | 39 | 1.1 | 5 | 1.1 |
| 15 | 83.3 | 4.5 | 1.15 | 0.889 | 40 | 1.1 | 4.5 | 1.07 |
| 16 | 156 | 3 | 1.55 | 0.966 | 41 | 1.55 | 3 | 0.232 |
| 17 | 156 | 4 | 1.35 | 0.901 | 42 | 1.55 | 4 | 0.487 |
| 18 | 156 | 3.5 | 0.34 | 0.176 | 43 | 1.55 | 3.5 | 0.371 |
| 19 | 156 | 5 | 1.15 | 0.878 | 44 | 1.55 | 5 | 1.55 |
| 20 | 156 | 4.5 | 1.10 | 0.832 | 45 | 1.55 | 4.5 | 1.49 |
| 21 | 117 | 3 | 1.35 | 0.675 | 46 | 1.35 | 3 | 0.202 |
| 22 | 117 | 4 | 0.34 | 0.187 | 47 | 1.35 | 4 | 0.437 |
| 23 | 117 | 3.5 | 1.15 | 0.732 | 48 | 1.35 | 3.5 | 0.265 |
| 24 | 117 | 5 | 1.10 | 0.871 | 49 | 1.35 | 5 | 1.35 |
| 25 | 117 | 4.5 | 1.55 | 1.204 | 50 | 1.35 | 4.5 | 1.32 |
| Factors | Levels | Total | Private Averages | Total Averages | ||||
|---|---|---|---|---|---|---|---|---|
| Y1 | 0.7752 | 0.7618 | 0.7322 | 0.7338 | 0.7506 | 3.7536 | 0.75 | 0.75 |
| Y2 | 0.6062 | 0.6924 | 0.7578 | 0.8344 | 0.8628 | 3.7536 | 0.75 | |
| Y3 | 0.19 | 0.74 | 0.78 | 0.94 | 1.12 | 3.75 | 0.75 | |
| Factors | Levels | Total | Private Averages | Total Averages | ||||
|---|---|---|---|---|---|---|---|---|
| Y1 | 0.1714 | 0.5902 | 0.5998 | 0.7148 | 0.826 | 2.9022 | 0.58 | 0.58 |
| Y2 | 0.1634 | 0.2236 | 0.3572 | 1.06 | 1.098 | 2.9022 | 0.58 | |
| Factors | Calculated Value | Experimental Value | |||||||
|---|---|---|---|---|---|---|---|---|---|
| X2 | pH | 3 | 4 | 4.5 | 3.5 | 3 | 4 | 4.5 | 3.5 |
| X3 | Initial Cu, g/L | 0.34 | 1.1 | 1.15 | 1.15 | 0.34 | 1.1 | 1.15 | 1.15 |
| YG | 0.153 | 0.756 | 0.859 | 0.720 | 0.165 | 0.703 | 0.889 | 0.732 | |
| Precipitation Cu, % | 55 | 31.3 | 25.3 | 36.3 | 51.5 | 35.1 | 22.7 | 36.4 | |
| Factors | Calculated Value | Experimental Value | |||||||
|---|---|---|---|---|---|---|---|---|---|
| X4 | pH | 3 | 3.5 | 4 | 3.5 | 3 | 3.5 | 4 | 3.5 |
| X5 | Initial Cu, g/L | 0.34 | 1.55 | 1.1 | 1.35 | 0.34 | 1.55 | 1.1 | 1.35 |
| YG | 0.031 | 0.368 | 0.488 | 0.32 | 0.046 | 0.371 | 0.382 | 0.265 | |
| Precipitation Cu, % | 89.8 | 76.2 | 55.6 | 79.3 | 86.5 | 76.1 | 65.3 | 83 | |
| Component | Content, % | Component | Content, % |
|---|---|---|---|
| Cu | 52.1 | Si | <0.001 |
| (CN) | 17.1 | Mg | 0.066 |
| Au, g/t | 29.4 | Al | 0.14 |
| Ag, g/t | 220.0 | Cd | <0.001 |
| Fe | 2.80 | Mn | 0.0041 |
| S | 0.90 | Zn | 0.074 |
| Sb | <0.030 | Pb | <0.001 |
| Sn | <0.00065 | Se | 0.0099 |
| Te | <0.002 | Sr | <0.001 |
| In | <0.00065 | Na | 0.29 |
| Ge | <0.0012 | K | 0.083 |
| Ga | <0.0007 | Li | <0.001 |
| Tl | <0.0011 | Rb | 0.0058 |
| Mo | 0.00062 | Cr | 0.0021 |
| Ni | 0.053 | V | 0.0029 |
| Co | 0.012 | W | <0.0096 |
| As | <0.030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kassymova, D.; Sapinov, R.; Kushakova, L.; Kulenova, N.; Shoshay, Z.; Adylkanova, M. Optimization of Copper Recovery from Cyanide Leaching Solutions Used in Gold–Copper Ore Processing Using Probabilistic–Deterministic Experimental Design. Processes 2025, 13, 61. https://doi.org/10.3390/pr13010061
Kassymova D, Sapinov R, Kushakova L, Kulenova N, Shoshay Z, Adylkanova M. Optimization of Copper Recovery from Cyanide Leaching Solutions Used in Gold–Copper Ore Processing Using Probabilistic–Deterministic Experimental Design. Processes. 2025; 13(1):61. https://doi.org/10.3390/pr13010061
Chicago/Turabian StyleKassymova, Dinara, Ruslan Sapinov, Larissa Kushakova, Natalya Kulenova, Zhanserik Shoshay, and Meruert Adylkanova. 2025. "Optimization of Copper Recovery from Cyanide Leaching Solutions Used in Gold–Copper Ore Processing Using Probabilistic–Deterministic Experimental Design" Processes 13, no. 1: 61. https://doi.org/10.3390/pr13010061
APA StyleKassymova, D., Sapinov, R., Kushakova, L., Kulenova, N., Shoshay, Z., & Adylkanova, M. (2025). Optimization of Copper Recovery from Cyanide Leaching Solutions Used in Gold–Copper Ore Processing Using Probabilistic–Deterministic Experimental Design. Processes, 13(1), 61. https://doi.org/10.3390/pr13010061








