Data-Driven Perovskite Design via High-Throughput Simulation and Machine Learning

Abstract

Perovskites (ABX₃) exhibit remarkable potential in optoelectronic conversion, catalysis, and diverse energy-related fields. However, the tunability of A, B, and X-site compositions renders conventional screening methods labor-intensive and inefficient. This review systematically synthesizes the roles of physical simulations and machine learning (ML) in accelerating perovskite discovery. By harnessing existing experimental datasets and high-throughput computational results, ML models elucidate structure-property relationships and predict performance metrics for solar cells, (photo)electrocatalysts, oxygen carriers, and energy-storage materials, with experimental validation confirming their predictive reliability. While data scarcity and heterogeneity inherently limit ML-based prediction of material property, integrating high-throughput computational methods as external mechanistic constraints—supplementing standardized, large-scale training data and imposing loss penalties—can improve accuracy and efficiency in bandgap prediction and defect engineering. Moreover, although embedding high-throughput simulations into ML architectures remains nascent, physics-embedded approaches (e.g., symmetry-aware networks) show increasing promise for enhancing physical consistency. This dual-driven paradigm, integrating data and physics, provides a versatile framework for perovskite design, achieving both high predictive accuracy and interpretability—key milestones toward a rational design strategy for functional materials discovery.

1. Introduction

Perovskite (ABX₃) has both performance and cost advantages in optoelectronics, catalysis, and energy storage, due to the highly tunable crystal structure and high defect tolerance [1]. Component regulation of perovskite is achievable through multi-element doping strategies at A/B/X sites. Synergistic effects of multidimensional sites result in a discrete distribution of material properties, and multiple doping combinations lead to an increased computational complexity for optimal material screening due to explosive growth of combinations.

The performance optimization of perovskite is highly dependent on precise design of the composition and structure. The traditional experimental trial-and-error method manually adjusts the element composition of A/B/X sites, but the method is limited by low efficiency and long period. First-principles calculations based on density functional theory (DFT) have revealed micro-mechanisms such as formation energy and defect states with the rise of computational materials science [2]. However, DFT optimization is time-consuming and makes it difficult to cover complex component spaces. Machine learning (ML) learns and identifies the complex relationship between material properties and structural features by training algorithms on partially known or simulation calculation data, and then predicts properties of unknown materials. The integration of machine learning and simulation calculation significantly reduces the demand for simulation calculation, and greatly expands the scope and depth of material searches [3].

This study reviewed a practical workflow that integrates machine learning and physical simulations for materials screening. The integration of ML with databases or high-throughput simulations has advanced rapidly in materials stability, optoelectronics, catalysis, and energy storage. Development trends are synthesized to offer a new route for predicting and discovering high performance perovskites.

2. Methods for Perovskite Material Screening

Beyond conventional experimental screening, perovskite materials can also be screened using materials databases, molecular simulations, and DFT. Furthermore, high-throughput simulations that integrate automated workflows and parallel computing enable batch evaluation and selection across vast candidate spaces.

2.1. Current Databases for Perovskite Materials

Perovskite databases integrate information from the literature and/or in-house experimental results, coupled with standardized processing and validation mechanisms, to build comprehensive platforms for materials properties and performance data. The Helmholtz-Zentrum Berlin Perovskite Database Project [4] systematically curates global perovskite data—key materials parameters (composition, crystal structure, optoelectronic properties) and detailed experimental conditions, fabrication processes, and measurement methods. Zhang et al. [5] analyzed 7419 PSC entries from the Perovskite Database Project and introduced TS80m—a stability metric defined as the tensile strength deviation after 80 m of coiling, incorporating acceleration factors for temperature, humidity, and irradiance to standardize test conditions. Their work identified synergistic optimization pathways via tolerance-factor control, 2D/3D device design, and carbon electrodes. However, existing materials databases remain non-application-specific and are predominantly used for early-stage structural screening or high-level trend analysis.

2.2. Applications of Molecular Simulation in Perovskites

Molecular simulation relies on classical mechanics and empirical potentials, with Molecular Dynamics and Monte Carlo being the most used. Molecular dynamics simulation provides critical insights into the dynamic behavior and stability of perovskite materials under varying temperatures and pressures [6]. Kholmurodov et al. [7] employed molecular dynamics simulations to investigate the dynamic behavior and structural properties of CaTiO₃ under ambient conditions. The influence of interatomic potential modifications on atomic pair correlations and structural reorganization was systematically elucidated. The Monte Carlo method is a numerical technique centered on random sampling, widely used in statistical physics and condensed matter research. It proves particularly effective for studying phase transitions, critical phenomena, and estimating thermodynamic properties. Zhang et al. [8] employed Monte Carlo simulations and other methods to investigate the lattice dynamics, ground-state structure, and magnetic properties of Sr₂RuO₄ under electric field modulation. This distorted structure hosts ferromagnetic half-metallic behavior with dominant out-of-plane magnetization, while remaining tunable under external electric fields without phase transition. In summary, molecular simulation proves effective for investigating large-scale molecular systems and dynamic processes, particularly suitable for studying perovskite structural evolution, thermal stability, and interfacial behavior.

DFT calculations play an irreplaceable role in characterizing electronic defects and trap states, which is essential for a deep understanding of the performance-limiting mechanisms in perovskite optoelectronic devices. By calculating the formation energy of point defects (such as vacancies, interstitials, and substitutional impurities), one can determine their likelihood of formation and concentration under specific growth conditions (e.g., Pb-rich, I-rich environments). Further analysis of the position of defect energy levels within the bandgap can identify those “deep-level traps” located deep in the bandgap. These deep-level trap states act as non-radiative recombination centers, significantly shortening carrier lifetime and reducing the photoelectric conversion efficiency of solar cells or the radiative efficiency of light-emitting diodes. For instance, calculations on common defects in lead-based perovskites, such as lead vacancies (V_Pb), iodine vacancies (V_I), or interstitial iodine (I_i), have successfully revealed their key role as non-radiative recombination centers, corroborating experimentally observed carrier dynamics. Therefore, systematic defect calculations can provide direct theoretical guidance for tracing performance degradation to its microscopic origins and for designing material passivation strategies. By computing the interactions between different passivation molecules (e.g., passivators, additives) and defect states, it is possible to pre-evaluate their passivation effects (such as eliminating defect levels or increasing defect formation energy), thereby accelerating the rational design of high-performance and high-stability perovskite materials.

2.3. Application of DFT in Perovskite

DFT, rooted in quantum mechanics and electron density analysis, evaluates perovskite stability and microscopic properties by computing energy profiles, crystal structures, and phase transitions [9]. The methodology further characterizes band structures, point defects, interface properties, and photocarrier dynamics, elucidating fundamental mechanisms including electronic transitions, defect formation, and interfacial charge transfer. Yin et al. [10] employed DFT calculations to investigate defect formation energies in α-MAPbI3 under varying growth conditions. Their study revealed tunable conductivity from p-type to n-type behavior, demonstrating the exceptional defect property adjustability in perovskite materials. Through systematic growth condition optimization, the conductivity was precisely tuned across the p-type to n-type spectrum, revealing the exceptional defect property tunability inherent to perovskite systems. DFT calculations are particularly suitable for small to medium-scale systems. This method delivers high accuracy at the cost of substantial computational requirements. It has now become the predominant technique in perovskite material design.

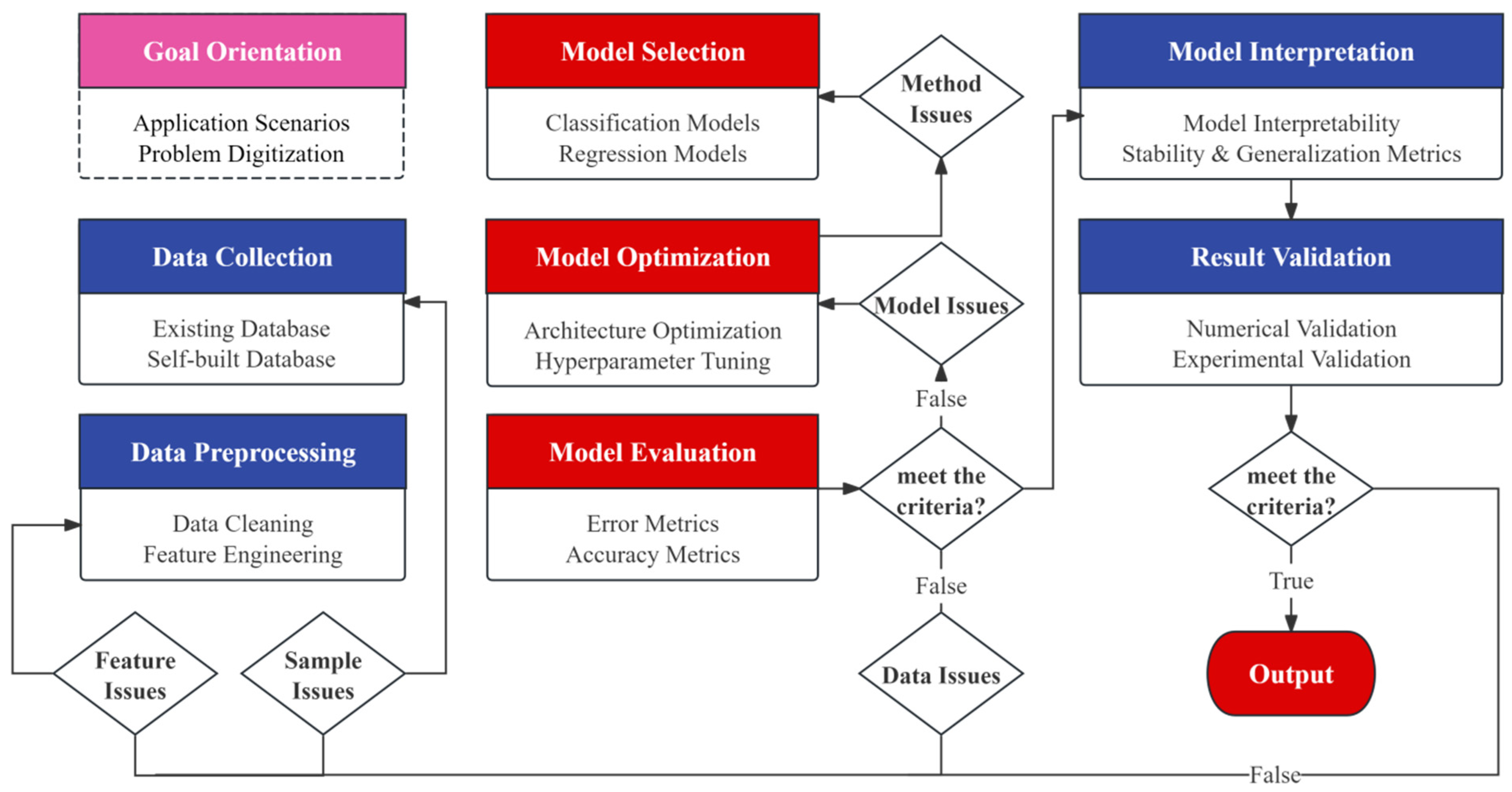
3. ML–Assisted Screening of Perovskite Materials

A forementioned material screening methods still lack sufficient coverage and accuracy. Researchers are now building specialized datasets through computational modeling, combining active learning strategies to iteratively improve prediction models. This approach breaks through the limitations of traditional trial-and-error methods, enabling targeted design of high-performance perovskite materials. Figure 1 illustrates the fundamental ML workflow for perovskite material screening, with key components analyzed below.

3.1. Data Collection and Preprocessing

High-dimensional feature modeling for perovskite is complicated by multi-scale coupling effects. Traditional semi-empirical models and feature-driven machine learning methods suffer from sparse feature spaces and insufficient valid samples due to high dimensionality and redundancy, leading to instability and overfitting [11]. Data preprocessing directly determines model performance and result reliability. Feature filtering and selection during modeling can effectively reduce dimensions, improve accuracy, and enhance generalization capability. Hu et al. [12] processed data collected from the Perovskite Database Project through missing-value treatment, stability screening, and standardization, enabling rapid high-accuracy prediction of halide double perovskite bandgaps and relative stability. Molecular feature importance rankings for passivation materials were generated and screening criteria were quantified, leading to the identification of perovskite solar cells with device efficiencies of 22.36% and 24.47%. On the other hand, molecular descriptors should be transferable, experimentally measurable, and quality-controllable, while balancing performance goals with physical interpretability. Iterative optimization through error analysis and importance evaluation is recommended.

3.2. Model Selection and Evaluation

Materials design requires differentiated use of classification (for categorical sorting) and regression (for continuous value prediction) algorithms. For classification tasks, Zhu et al. [13] developed a gradient boosting classification model that achieved 92.3% accuracy in predicting the stability of 2877 perovskites by utilizing key features like A/B-site ionic radius ratio and formation energy, significantly outperforming traditional tolerance factor empirical criteria. For regression tasks, Wan et al. [14] addressed the complex nonlinear relationships in bandgap prediction by designing a gradient boosting regression (GBR) model combined with a “last elimination” feature selection strategy. Their approach achieved a mean absolute error of 0.0287 eV across 5158 candidates while improving computational efficiency by three orders of magnitude compared to DFT calculations. The model also successfully identified the regulatory threshold of Pb²⁺/I⁻ element ratio on bandgap. The key to improving model performance is a well-designed hyperparameter search combined with effective regularization, which together suppress overfitting and enhance generalization. Evaluation and tuning should be guided by the task objective, using a mix of metrics—such as accuracy and recall—for comparative assessment. For regression, consider both MSE and RMSE rather than relying on a single metric. Applying cross-validation with multiple splits and repeated train–test cycles helps stabilize estimates, reduce randomness, and support more reliable choices of models and configurations.

3.3. Model Interpretation and Validation

Model interpretability is essential in data-driven materials design. While traditional “black-box” models can deliver high-accuracy predictions, they struggle to illuminate structure–property relationships and underlying physics, which undermines their contribution to knowledge building and, in turn, narrows their scope of application. Yang et al. [15] used symbolic regression to obtain an explicit formula that links the band gap to physical descriptors, directly quantifying how input features influence (or determine) Eg. The analysis points to the B–X electronegativity difference as the dominant factor, and the resulting compact expression achieves a test error (RMSE ≈ 0.08–0.09 eV) comparable to DFT-level uncertainty.

In the final stage of ML-based property prediction for perovskites, validate model-selected candidates via experiments or high-accuracy calculations. If results diverge from predictions, trace back to revise the model and features; if they align, confirm the findings and deliver the final conclusions and candidate list. Pritish et al. [16] trained a random-forest model on samples extracted from 182 papers to predict optical band gaps for 10,920 halide perovskite compositions, achieving RMSE ≈ 0.146 eV—on par with DFT accuracy. They synthesized Cs₂PbSnI₆ nanocrystals, whose measured photoluminescence peak at 794 nm matched the prediction, validating the model.

4. Applications of High-Throughput Simulation and ML in Perovskite Design

4.1. Structural Formability and Stability of Perovskite Design

The structural formability of perovskite lattice is the basis for material screening. Not all elements can occupy the A, B, or X sites in an ABX₃ perovskite, and the choice of ions directly determines whether the phase forms and what structure results. The tolerance factor (t) first proposed by Goldschmidt [17] and now the most widely used stability descriptor:

$$\mathrm{t}={\displaystyle \frac{{\mathrm{r}}_{\mathrm{A}}+{\mathrm{r}}_{\mathrm{X}}}{\sqrt{2}({\mathrm{r}}_{\mathrm{B}}+{\mathrm{r}}_{\mathrm{X}})}}$$

where r_A, r_B, and r_X are the ionic radii of the A-site cation, B-site cation, and X-site anion, respectively.

This t considers only ionic radii. By introducing the octahedral factor (μ) and the atomic packing ratio (ρ) to jointly refine t, the predictive accuracy for structural formability improves markedly. Sun et al. [18] built a stability–radius mapping from a high-throughput DFT database using kernel ridge regression, tuning regularization via five-fold cross-validation. They further proposed a composite descriptor (μ + t)^η, where the octahedral factor (μ) enables the quantification of the intrinsic stability of BX₆ octahedra, while the exponent η—positively correlated with ρ—serves to balance the synergistic contributions of μ and t. This descriptor modestly improved the prediction accuracy (Figure 2).

Perovskite stability depends on cation lattice parameters, bond strength and anisotropy, as well as anion selection and doping ratios. For multicomponent solid solutions, building high-dimensional compositional supercells makes DFT cost scale roughly cubically with atom count. Machine learning can effectively overcome this computational bottleneck. Shetty et al. [19] trained ML models on DFT data to predict hull energies E_hull for screening thermodynamically stable perovskites. Among six classifiers including RF, NN, and AdaBoost, AdaBoost delivered the best performance across four evaluation metrics for perovskite oxides. Krishnaraj et al. [20] noted that E_hull alone tends to overestimate stability and emphasized the need to include vibrational free energy. A polynomial–ML scheme (GPR/RF + SISSO) on 80 perovskites learned the coefficients of FH(T) and reduced the ZPE error from 18.9 to 8 meV/atom, which markedly improved thermodynamic stability assessment.

4.2. Applications of Perovskites in Photoelectric Effects

Perovskites, with high absorption, broad spectral response, excellent carrier transport, and low exciton binding energy, are valuable for solar cells, LEDs, and photodetectors. Even as lab efficiencies approach theoretical limits, screening materials for photoelectric performance remains a central focus in perovskite research.

4.2.1. Halide and Oxide Perovskite Solar Cells

The photovoltaic performance of perovskite solar cells is governed by light absorption, carrier transport and recombination, and interfacial stability [21]. In the ABX₃ lattice, corner-sharing [BX₆]⁴⁻ octahedra formed by B-site cations (e.g., Pb²⁺, Sn²⁺) and halides (e.g., I⁻, Br⁻) give rise to direct bandgaps and large absorption coefficients, supporting effective spectral utilization [22]. The A-site cations regulate tolerance factors and lattice dynamics, stabilizing the perovskite framework through hydrogen-bonding interactions in hybrid compositions and predominantly ionic/steric effects in all-inorganic compositions. These structural and chemical controls lower defect densities, suppress nonradiative recombination [23], and extend carrier diffusion lengths, collectively improving device efficiency and operational robustness [24].

Given the wealth of data in the solar-cell field, key performance metrics for perovskite solar cells (e.g., bandgap, short-circuit current density, open-circuit voltage) can be taken directly from published literature. Notably, when the dataset is sufficiently large, missing values for some parameters have only a limited impact on training machine-learning models [25]. Yan et al. [26] built a dataset from 248 papers and trained predictive models with Extreme Gradient Boosting and Random Forest (Figure 3). Descriptors included bandgap, short-circuit current density, open-circuit voltage, elemental ratios, and A-site cation type. The workflow predicted five previously unexplored low-bandgap perovskites of the form (FAPbI₃)_X(MAPbBr_2.8Cl_0.2)_1−X (X = 0.90, 0.92, 0.95, 0.97, 0.99). Experiments reported a best (FAPbI₃)_0.95(MAPbBr_2.8Cl_0.2)_0.05 power conversion efficiency of 22.5% with a relative error below 2% versus the ML result. Li et al. [27] cleaned and curated bandgap data for 300 (Cs_aFA₆MA_(1−a−6)Pb(Cl_XBr_YI_(1−X−Y))₃, where the A-site is occupied by Cs⁺, FA⁺, or MA⁺, and the X-site is occupied by Cl⁻, Br⁻, or I⁻.) lead-halide perovskites and retained 109 valid entries. Three machine-learning models were trained on four input features (the mole fractions of Cs, FA, Cl, and Br) with five-fold cross-validation. The neural network achieved the lowest RMSE on the test set.

On the other hand, the literature data alone cannot support accurate prediction. First-principles calculations and related simulations are needed to re-evaluate the optoelectronic properties of perovskites and to supply more reliable training sets for machine-learning models [28]. Talapatra et al. [29] used high-throughput DFT to assemble bandgap data for 5152 perovskite oxides (ABO₃, A₂BB′O₆, AA′B₂O₆ and AA′BB′O₆) and built a staged pipeline with Random Forest classification and regression. The workflow first separates wide- and narrow-bandgap materials, then predicts bandgaps for the wide-bandgap set. The study flagged 13,589 potential wide-bandgap candidates (e.g., Ba₂TaInO₆, LaCsTaDyO₆), with 310 high-confidence new compounds (e.g., DyCsTaInO₆, Sr₂AuErO₆) showing a DFT-validated prediction error of 0.21 eV, and delivered a design map for how elemental substitution (e.g., alkaline earth or rare earth metals on the A/A′ sites and transition metals on the B/B′ sites) affects bandgaps. Zhu et al. [30] performed high-throughput DFT and computed 488 bandgap-related entries along with decomposition energy and spectroscopic-limit efficiency. Recursive feature elimination identified 10 key descriptors such as ionic radius and electronegativity. From 177,264 entries, the workflow retained 434 candidates and ultimately predicted four lead-free perovskites (MABa_0.125Sn_0.875I₃, K_0.25FA_0.75Ba_0.125Sn_0.875I₃, FA_0.25MA_0.75Ba_0.125Sn_0.875I₃ and Cs_0.375FA_0.625Ba_0.125Sn_0.875I₃) with high efficiency and strong stability (Figure 4). Xu et al. developed a machine learning-assisted pseudohalide anion screening method, selecting 168 candidate structures from 5 million molecules in the PubChem database through DFT—using Cs_0.05FA_0.9MA_0.05Pb(I_0.95Br_0.05)₃ perovskite as a model system. Key descriptors such as topological polar surface area were used to construct a predictive model. Experimental validation ultimately confirmed that sodium thioglycolate enhanced the perovskite solar cell efficiency to 24.56% and significantly improved device stability. Kim et al. significantly enhanced the performance of perovskite solar cells by developing a methoxyphenethylammonium iodide (M-PEAI)/cyclohexylammonium bromide (CHA)Br composite additive. This additive forms a quasi-2D intermediate layer on the perovskite surface, suppressing ion migration through strong intermolecular interactions and optimizing energy level alignment. Using a SnO₂/perovskite/additive/Spiro-OMeTAD device architecture, a power conversion efficiency of 26.28% was achieved, with 88% efficiency retention after 440 h of illumination. The study confirmed that the additive operates through a dual mechanism of interface modification and defect passivation, reducing trap density by an order of magnitude while endowing the device with 9000 h of environmental stability.

4.2.2. Formamidinium Lead Triiodide Perovskite Light-Emitting Diodes

Perovskite light-emitting diode performance is governed by the interplay of exciton recombination, carrier balance, and defect control [31]. In the ABX₃ lattice, B–X quantum confinement enables narrowband emission with a very small full width at half maximum [32]. The A-site tunes carrier transport, yielding electron-to-hole mobility ratios on the same order of magnitude [33]. Zhang et al. [34] combined literature and in-house data to assemble a 132-additive database, merging MACCS, ECFP, and FP2 fingerprints with 208 RDKit descriptors to build an enriched molecular model. Joint feature integration with neural-network tuning mitigated small-sample bias and fingerprint redundancy, reaching 96% prediction accuracy. The workflow identified new additives, raising FAPbI₃ external quantum efficiency to 22.7%.

4.2.3. Two-Dimensional Metal Halide Perovskite Single-Crystal Photodetectors

Perovskite photodetectors benefit from the ABX₃ lattice, where strong B–X covalent hybridization yields a direct bandgap and high absorption [35]. Low defect density with strong dielectric screening suppresses nonradiative recombination [36]. Intrinsic ambipolar transport improves carrier dynamics [37]. Pandey et al. [38] compiled a 225-sample dataset (2D metal halide perovskites, e.g., BA₂PbI₄, BA₂MAPb₂I₇, BA₂MA₃Pb₄I₁₃, BA₂PbBr₄ and BA₂MAPb₂Br₇) from over 150 studies, covering nitrogen content, layer shift factor, bandgap, and related properties. Among four ML models, a decision tree gave the lowest errors for material responsivity and detectivity. Experiments on five photodetector types showed close agreement between predictions and measurements.

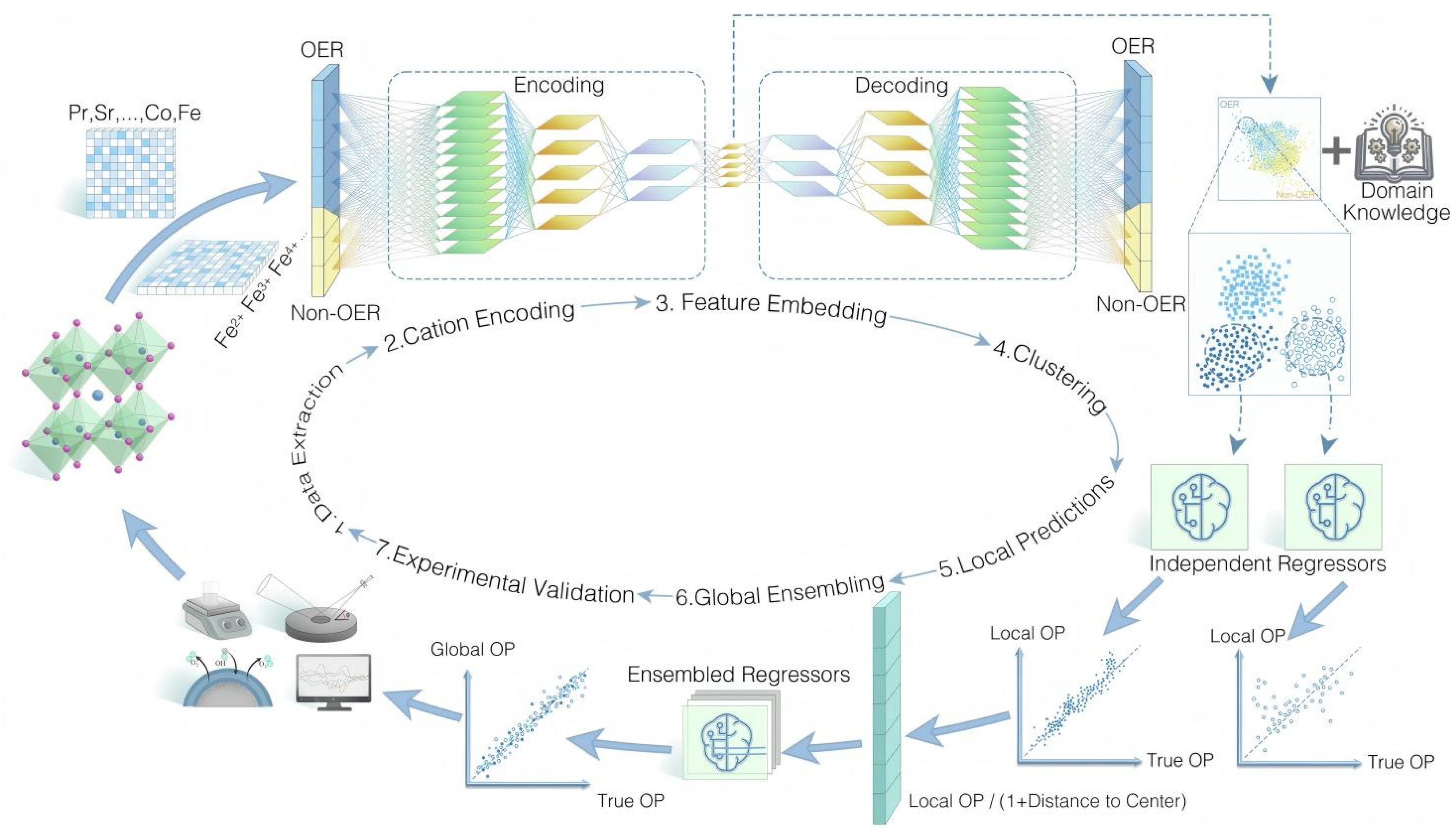
4.3. Perovskites as Catalytic Materials

Perovskites, with tunable crystal structures, strong redox activity, and intrinsic conductivity, have emerged as standout catalysts for green energy conversion and carbon neutrality [39]. A-site rare-earth/alkaline-earth cations (e.g., La³⁺, Sr²⁺) tune lattice distortion and oxygen-vacancy concentration, while B-site transition metals (e.g., Fe³⁺, Co³⁺) govern redox activity. Catalytic activity, selectivity, and stability of perovskite oxides are enhanced via A/B-site doping, oxygen-vacancy engineering, heterostructure construction, and double-perovskite design [40].

4.3.1. Perovskite Halide Photocatalyst

In perovskite halides photocatalysis, light generates electron–hole pairs that separate and migrate to the surface for redox reactions. Compared with conventional semiconductors, metal halide perovskites offer high absorption and strong tunability. Adjusting the halide composition tailors the bandgap to the visible range and improves photon-to-carrier conversion efficiency [41]. Typical applications include photocatalytic water splitting for H₂ [42], CO₂ photoreduction [43], and degradation of organic pollutants [44]. Zhai et al. [28] built a multi-parameter literature dataset and used support vector regression with an RBF kernel plus forward–backward stepwise selection to identify features governing perovskite halides specific surface area, yielding a high-accuracy model that speeds the design and screening of high-SSA photocatalysts. Biswas et al. [45] assembled a DFT-based dataset, added tree-structured regularization, and applied a fully corrected regularized greedy algorithm to predict decomposition energy and bandgap, outperforming ensemble baselines with broader generality. After hyperparameter tuning and evaluation using RMSE, the study selected 3043 halide perovskites from 151,140 compounds (Figure 5). Among these, the A-site contains inorganic cations (Cs, Rb) or organic cations (MA, FA), the B-site consists of alloyed divalent metals of Ge/Sn/Pb and Ca/Sr, the X-site is Br/I, and a typical example is CsCa_0.25Ge_0.75Br₃.

4.3.2. Perovskite Oxide Electrocatalyst

In electrocatalysis, perovskite oxides activity arises from the synergy of crystal structure, electronic states, and surface chemistry. Structural tuning enables precise optimization of the electronic structure, mainly via A/B-site doping and oxygen-vacancy engineering. This approach co-modulates intermediate adsorption, electron transfer efficiency, and reaction pathways. Perovskite oxide electrocatalysts are used in solid oxide fuel cells [46], water electrolysis for hydrogen [47], and CO₂ electroreduction [48].

The oxygen evolution reaction (OER) is a key anodic half-reaction in electrocatalysis. Perovskite oxides doped with selected transition metals, such as LaCuO₃ with B-site Co or Ni, have emerged as efficient OER catalysts. Li et al. [49] combined DFT-augmented datasets with Gaussian process regression to predict high-OER perovskite oxides, using composition and bulk-electronic descriptors with recursive feature elimination and an adaptive, uncertainty-aware learning strategy, yielding 10 stable and active double perovskite oxides such as KRbCo₂O₆ and BaSrCo₂O₆ from 4000 candidates. Chang et al. [50] introduced a transfer-learning framework for alkaline OER, building OER and non-OER datasets from literature, encoding cations with an autoencoder, clustering by K-Means and phase ranking, and using a tuned gradient boosting regressor with global ensembling and active learning, which identified high-performance compositions such as Pr_0.1Sr_0.9Co_0.5Fe_0.3Mn_0.3O₃ (Figure 6).

Besides using intrinsic elemental properties as features, some studies take external conditions as the primary descriptors. Li et al. [51] used machine learning to design perovskite OER catalysts operable across temperatures. A literature-based dataset included oxygen-vacancy concentrations at different temperatures, with operating temperature as a key variable to predict equilibrium lattice vacancies. After benchmarking 36 models, a gradient boosting regressor performed best, then SHAP, DFT, and extensive experiments validated the model, yielding high-performance compositions at multiple temperatures, such as SrCo_0.8Ta_0.15V_0.05O_3−δ and SrCo_0.8Ta_0.16W_0.04O_3−δ. Jacobs et al. [52] built a random-forest high-throughput framework to couple perovskite area-specific resistance with high-temperature operation, accelerating SOFC and electrolyzer catalyst discovery. A 749-entry database captured oxygen surface-exchange coefficients, diffusion, and area-specific resistance. Random-forest models for 500 °C and 800 °C mapped vacancy formation energy and active-site density to quantitative features, with SHAP and experiments confirming the approach, leading to low-ASR perovskite oxides at target temperatures.

4.3.3. Perovskite Oxide Chemical Looping Oxygen Carrier

Chemical looping splits complex reactions into multiple elementary steps via chemical intermediates. The oxygen carrier acts as the oxygen shuttle, typically a metal oxide, and reactions proceed through reversible lattice-oxygen release and uptake [53]. Perovskites offer high oxygen storage activity and synergistic catalysis, while precise A/B-site doping tunes equilibrium oxygen partial pressure and lattice-oxygen mechanisms, highlighting strong oxygen-carrier potential [54]. Perovskite carriers show promise in chemical looping air separation [55], CO₂ splitting [56], and oxygen uncoupling [57]. Oxygen-vacancy formation energy is the most common descriptor. Li et al. [58] used high-throughput DFT to build a perovskite oxide dataset, screened by oxygen-vacancy formation energy ΔG at fixed vacancy concentration, then trained a random forest with cation ratios as inputs and target ΔG under given conditions, yielding ~20,000 candidates from 227,273 high-entropy quinary-plus perovskites for chemical looping air separation and CO₂ splitting, Such as Sr_0.875Ba_0.125Fe_0.5Co_0.5O_3−δ for chemical looping air separation, and Sr_0.5Y_0.5Fe_0.125Ti_0.875O_3−δ for CO₂ splitting. Ramazani et al. [59] compiled a DFT thermodynamic set for SrFeO_3−δ with single and co-doping on A/B sites, used ΔG as the key descriptor to assess oxygen release from 298–1200 K, and trained a k-nearest neighbors model with composition ratios as inputs and temperature-specific ΔG as targets, identifying two key families: Sr_1−xCa_xFe_1−γNi_γO_3−δ and the newly proposed Sr_1−xBa_xFe_1−γCu_γO_3−δ.

To develop high-performance Chemical Looping with Oxygen Uncoupling materials, Duell et al. [60] constructed a DFT thermodynamic dataset for the SrFeO_3−δ-based perovskite system. Using the Gibbs free energy of oxygen release (ΔG_O2) as the key descriptor, they evaluated the thermodynamic feasibility and kinetic potential of oxygen release for this system over the temperature range of 100–1200 K. In parallel, they trained a random forest regression model, with the characteristics of 39 substituent elements as inputs and the absolute value of ΔG_O2 at a given temperature as the prediction objective. This model was then coupled with a genetic algorithm to iteratively optimize population composition, ultimately identifying two categories of key perovskite families: one is Sr_1−xCa_xFe_1−γNi_γO_3−δ (whose low-temperature performance advantages have been verified), and the other is the newly proposed Sr_1−xA_xFe_1−γB_γO_3−δ (where A = K; B = Mg, Bi, Co, Cu, Zn). To accelerate the development of perovskite oxides for thermochemical energy storage (TCES), Cai et al. [61] combined high-throughput DFT calculations with experimental methods. Based on a dataset of over 2000 SrFeO_3−δ materials doped at the A/B sites, they screened the materials using thermodynamic descriptors (e.g., formation energy and reaction enthalpy). Eventually, they demonstrated that Sr_0.875Ba_0.125FeO_3−δ and Sr_0.125Ca_0.875Fe_0.25Mn_0.75O_3−δ achieved energy densities of 85 kJ·kg⁻¹ and 157 kJ·kg⁻¹, respectively. This result confirms the effectiveness of high-throughput methods in accelerating the development of high-performance TCES materials.

4.4. Applications of Perovskites in Energy Storage

Perovskites offer high ionic conductivity and about 5% lattice strain tolerance [62]. Their strong defect tolerance broadens the electrochemical stability window from 0.5 to 4.5 V and suppresses side reactions [63]. Solution processing can form 2–50 nm hierarchical pores, increasing surface area and interfacial kinetics, which enables high specific capacity and durable cycling [64]. Current work largely focuses on antiperovskite solid electrolytes for solid-state batteries. Kim et al. [65] compiled over 600 DFT migration barriers for 36 alkali metal thiohalides based on X₃AZ antiperovskites, selected 20 key descriptors across five categories, and with AdaBoost plus extremely randomized trees (ERT) showed that channel width and hop distance govern vacancy migration, while interstitial formation energy strongly affects interstitial migration, highlighting synergy between anion polarizability and defect-formation features. Xiang et al. [66] aggregated room-temperature ionic conductivities for 403 electrolytes, built descriptors from Magpie and site-specific ion properties, used an extremely randomized trees model, and expanded virtual samples from 168 to 150,000 via ion substitution, identifying A-site electronegativity, density, and ionic radius as primary factors for conductivity. Zhang et al. [67] mined descriptors from 106 experimental samples, proposed the ratio of tolerance factor to atomic packing factor as a key descriptor, and combined classification with symbolic regression to pinpoint candidates with high ionic conductivity such as Li₆NClBr₂, informing solid-state electrolyte design.

Table 1. Summary of Machine Learning Models, Descriptors, and Datasets Used in Perovskite-Based Energy Storage Studies.

Descriptor	Model	Dataset	Metric	Found Candidates
CCD PW Anion polarizability	AdaBoost ERTR	603 DFT migration barriers	Vacancy RMSE (71 meV) Interstitial RMSE (46 meV)	Decreasing path distance Increasing width Highly polarizable anions
A-site electronegativity A-site density A-site ionic radius	ERT	403 sets of experimental SSE data 149,652 types of virtual AP materials	Classification accuracy (94%) MAE (0.57) R2 (0.76) ROC_AUC (0.946)	16,807 superionic conductors
The ratio of tolerance factor to atomic packing factor (t/η)	Symbolic regression	106 experimental samples	RMSP (0.8)	Li6NClBr2 Li6NBrBr2 Li6NBrI2

summarizes the content of the previous paragraph.

5. Challenges and Future Directions for Applying ML to Perovskite Design

5.1. Bottlenecks and Challenges

Machine learning is emerging as a key driver for accelerating materials development, sharply shortening the discovery cycle for new materials. Current challenges center on three dimensions: data, process modeling, and model interpretability.

(1)

Data Scarcity and Low Quality

Data standardization remains the main bottleneck for applying machine learning to materials development. Perovskite research lacks large, standardized experimental databases, and heterogeneity across groups causes feature distribution shift that degrades structure prediction and model training. Most studies still rely on few-shot or transfer learning, with data cleaning and standardization used to improve compatibility. The problem is acute in emerging areas such as perovskite LEDs and catalysis, where sparse data in high-dimensional spaces drives overfitting [68], while cross-lab variation in synthesis protocols and characterization methods introduces distribution shift and environmental noise that skew stability prediction. Even advanced models such as graph neural networks suffer when inputs are not standardized, showing poor cross-dataset generalization and reduced interpretability. Although data-standardization initiatives are underway worldwide, progress still trails algorithmic advances. Furthermore, perovskite materials and device performance are highly sensitive to micro-environmental conditions. Parameters often considered secondary or not systematically recorded—such as laboratory humidity during experiments, ambient temperature, and even the exposure time of precursor solutions to air—can significantly impact the performance and stability of the final product. This high dependency on hidden variables makes the standardization and comparability of datasets exceptionally difficult, greatly aggravating the issues of data scarcity and low quality.

(2)

Model Generalization and Interpretability Gaps

Inherent limitations in model architecture, training strategies, and optimization methods can affect the accuracy of machine learning predictions. There is often a natural trade-off between the generalization capability and interpretability of AI algorithms. Traditional linear models or shallow neural networks struggle to capture the complex nonlinear relationships between perovskite composition, structure, and properties, limiting their generalization. Purely data-driven black-box models often lack explicit integration of prior scientific knowledge, reducing interpretability and sometimes leading to unphysical predictions. Deep models handle complex process–structure relations yet still fall short on mechanisms: kGNNs cannot quantify how GBLD relates to device stability T₈₀ [5]; SHAP showed I⁻ contributes 42% to bandgap yet explains interface recombination poorly [69]; lab-trained models lose about 30% on slot-die lines due to distribution shift [70]. These challenges stem from the unique ABX₃ octahedral structure of perovskites, and involve issues such as the data dependency of supervised learning (restricting generalization), the absence of physical constraints in unsupervised learning (affecting interpretability and consistency), and the large action space in reinforcement learning (hindering policy efficiency and generalization).

(3)

Emphasis on Structure Prediction, Neglect of Fabrication and Application

Processing parameters (e.g., spin-coating speed, annealing curves) are often scattered in supplementary materials of research papers or kept as confidential industrial data, lacking standardized databases. Before 2020, most studies focused only on “predicting performance → recommending compositions” without addressing the full manufacturing process, leading to significant gaps between lab efficiency and industrial performance. This has pushed machine learning toward solving practical production challenges. As a representative example, Whitaker et al. [71] demonstrated that tuning drying/crystallization windows—via controlled wet film residence and coordinated flow rate, web speed, and die gap—enables slot die translation while preserving film morphology and device metrics during process transfer. On the other hand, fabrication processes involve multiphysics coupling (fluid dynamics, thermodynamics, crystallization kinetics), requiring temporal modeling and real-time feedback—far more complex than static structure prediction. Traditional models struggle to capture these dynamic correlations, necessitating deep learning to model nonlinear reactions. Examples include the nonlinear relationship between spin-coating speed (ω) and film thickness (d) [72], threshold effects in vapor-assisted crystallization [73], and the Arrhenius-type relationship between film crystallinity and annealing conditions [74]. These challenges require multimodal integration of process parameters for effective modeling.

5.2. Future Directions: Multimodal-Coupled Perovskite Design

In data generation, high-throughput computational methods have become an efficient approach for expanding datasets. Through high-throughput DFT and molecular dynamics simulations, vast amounts of material characteristic data can be systematically generated. High-throughput calculations enable continuous scanning of broader chemical spaces, increasing data volume by orders of magnitude while significantly accelerating exploration progress. Yao et al. [75] constructed the MatHub-2D database using high-throughput DFT, screening 1900 2D materials for carrier mobility and identifying 19 high-mobility semiconductors through deformation potential and elastic modulus analysis, achieving a data throughput 50 times greater than experimental synthesis. While experimental characterization provides localized information, high-throughput simulations can systematically compute all possible configurations to fill global data gaps. Thomas et al. [76] screened over 700 substitutional defect configurations in WS2 via high-throughput DFT, discovering that sulfur-site substitutions create ideal quantum defect energy levels, later confirmed by scanning tunneling microscopy experiments—covering defect chemical spaces far beyond experimental reach. Whereas experiments face limitations in multi-parameter control, high-throughput simulations can simultaneously scan multidimensional property spaces to establish comprehensive structure-property relationships. Li et al. [77] employed generative adversarial networks to create 50,000 virtual perovskites while calculating bandgap, defect tolerance, and carrier effective mass to guide targeted experimental validation. Multimodal data fusion techniques enable effective integration of cross-scale, multi-source data through advanced machine learning methods. Data standardization serves as the bridge connecting experimental data with machine learning models, providing a stable and efficient foundation for intelligent full-process R&D. On the other hand, data standardization requires a minimal, machine-readable process metadata schema that the community can readily adopt, centered on universally accessible records; for halide perovskite solar cells this means recording formulation with precursor identities, purity and lot, solvent volume fraction and concentration, substrate and treatment, time-aligned coating and annealing profiles, clear XRD in 2θ with FWHM and film thickness, all provided in unified CSV or NetCDF with a JSON dictionary and SI units. For perovskite catalysts this means documenting synthesis or deposition history including route, stoichiometry and dopants, the thermal program with ramp, peak, dwell and cooling, gas partial pressure and flow, film deposition rate, clear XRD with scan parameters and optional XPS or BET, using the same unified CSV or NetCDF with JSON and SI units, and reporting electrochemical data in volts versus a stated reference and current density.

The integration of multiscale physical theories with data science enables high-performance predictions while preserving physical interpretability. Architecturally embedded physics approaches achieve this by coupling high-throughput screening with machine learning, where physical laws are mathematically transformed into model inductive biases to facilitate knowledge transfer in data-scarce scenarios. Li et al. [78] developed a multimodal material property prediction model incorporating physical constraints and graph neural networks (GNNs), along with a physics-guided generative optimization strategy, enabling efficient digital material design and performance prediction. Batzner et al. [79] created an equivariant GNN model for molecular dynamics simulations by embedding E(3) equivariance (including physical symmetries like rotation and reflection) into the network architecture, achieving efficient machine learning predictions for molecules and materials while supporting high-throughput screening. These architecturally embedded physics methods transform physical principles like molecular symmetry and topological properties into machine learning model biases. Some researchers have also embedded first-principles calculations as physical constraints. Lan et al. [80] proposed a framework combining high-throughput deep reinforcement learning with first-principles calculations, where potential energy surfaces derived from first principles were incorporated as internal constraints. This approach enabled thousands of parallel simulations on a single GPU for high-throughput screening, providing an efficient and general method for complex catalytic reaction pathway prediction. Current architecturally embedded physics methods face limitations in numerical stability and high implementation costs for scalable physical constraints. Although research remains limited in this area, the approach shows clear potential for deeply integrating physical priors with data-driven methods, representing a crucial development direction for intelligent material design.

Materials design is shifting from single-point trial-and-error to full-chain intelligent development. Most studies integrate physical constraints into simulation workflows. For instance, Lu et al. [81] incorporated the Goldschmidt tolerance factor (Tf = 0.8–1.2) and the octahedral factor (Of = 0.44–0.9) to assess structural stability, while also constraining the electronegativity of B-site metals (χ = 1.4–2.2 Pauling units) and the polarization of organic molecules (PA = 1–5 × 10⁻⁴⁰ C·m²·V⁻¹) to optimize electronic properties. The application of these constraints reduced the rate of false-positive predictions in initial candidate screening from 35% to 12%, improved the mean squared error of bandgap predictions from 0.15 eV to 0.09 eV, and increased the coefficient of determination R² from 0.87 to 0.93. These results clearly demonstrate the substantial contribution of physical constraints in accelerating the discovery of stable lead-free perovskites. Researchers are building closed-loop optimization that links high-throughput experiments with computation and real-time feedback, while coupling process modeling with dynamic, data-driven control to boost model performance, prediction accuracy, and process stability. MIT’s platform [82,83] runs on the order of a hundred perovskite synthesis trials per day, adjusts annealing temperature and additive ratios on the fly, and tightly integrates an automated lab with machine learning for continuous process optimization. Ultrafast electron microscopy and other in situ probes feed degradation dynamics back into physics-informed neural networks to recalibrate diffusion and related parameters, which iteratively improves interface defect prediction. Li et al. [84] used LSTM models to parse in situ photoluminescence in real time, identified a critical threshold in vapor-assisted crystallization, and actively steered crystallization kinetics, cutting film defect density by three orders of magnitude. Graupner et al. [85] combined ML force fields with molecular dynamics in a multiscale framework to capture precursor clustering and film-scale morphology evolution, then designed graded 2D/3D architectures that enabled devices beyond 30% efficiency. Specifically, for single-junction solar cells based on (BA)₂(MA)₃Pb₄I₁₃, their work identified a complete energy funneling mechanism that suppresses non-radiative recombination and enhances exciton lifetime, suggesting a theoretical PCE exceeding 30% under ideal conditions. The USTC autonomous lab [86] integrates AI, robotics, and high-throughput experimentation into a self-driving pipeline that progresses from automated execution to closed-loop decide–experiment–optimize, and incorporates quantum computing with AI to accelerate materials discovery. This system shortens material discovery and optimization from years to weeks, improves candidate identification success rates by orders of magnitude, reduces R&D manpower by over 90%, and employs intelligent algorithms to screen stable material configurations. Similarly, the self-driving laboratory at MIT performs over 100 perovskite syntheses per day, reducing R&D duration from months to days. It achieves a three-order-of-magnitude reduction in defect density, a tenfold improvement in device stability, and enables solar cells with over 30% efficiency, while saving more than 95% of manual operational effort. Together these advances form an intelligent loop of real-time data capture, mechanism learning, and adaptive optimization, moving perovskite R&D from isolated automation toward fully integrated, end-to-end autonomy.

6. Conclusions

ML is becoming the core engine of data-driven perovskite design, especially in integration with high-throughput simulation. This pairing speeds stability evaluation, bandgap and emission tuning, defect and dopant optimization, and catalysis-relevant property discovery, moving candidates to validated leads more quickly. Open databases support rapid large-scale triage, and tight coupling with high-throughput DFT and molecular dynamics improves accuracy and robustness beyond the training domain. Future progress depends on standardized data and the explicit inclusion of physics in model architectures and in loss functions to enhance interpretability and reliability. With active learning and self-driving experimentation in the loop, the simulation-ML workflow closes the cycle from data acquisition and mechanism inference to process optimization, enabling trustworthy predictions and faster translation to devices.

A 24-month feasible roadmap

• Months 0–6—Strengthen HT simulations as reliable ML data

Focus on scaling and validating high-throughput DFT/MD to provide consistent, high-quality labels for ML. Harmonize simulation protocols, units, and metadata; prioritize stability indicators (e.g., Ehull with finite-T corrections where available), bandgaps, and process-relevant properties.

• Months 6–12—Embed physics for interpretability and reliability

Introduce symmetry-aware/equivariant architectures and lightweight physical constraints (charge neutrality, tolerance-factor bounds, defect thermodynamics) to limit unphysical extrapolation. Couple HT calculations with uncertainty-aware active learning and conduct small-batch validations.

• Months 12–24—Multimodal, process-aware, end-to-end workflows

Develop multimodal models that fuse composition/structure descriptors, microstructural images, and key process variables to predict device metrics and stability under operating conditions. Deploy closed-loop optimization with self-driving or partner labs, integrate in-situ signals.