Numerical Simulation Study on Internal Flow Law and Efficiency of Gas-Liquid Mixed Jet Pump
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Jet Pump Parameters
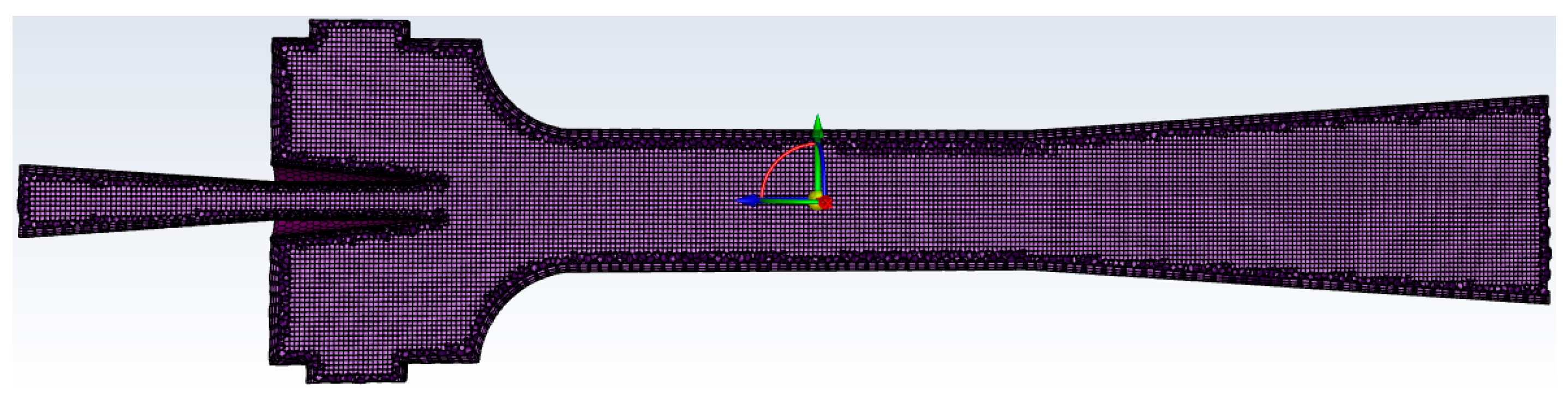
2.2. Modeling and Meshing
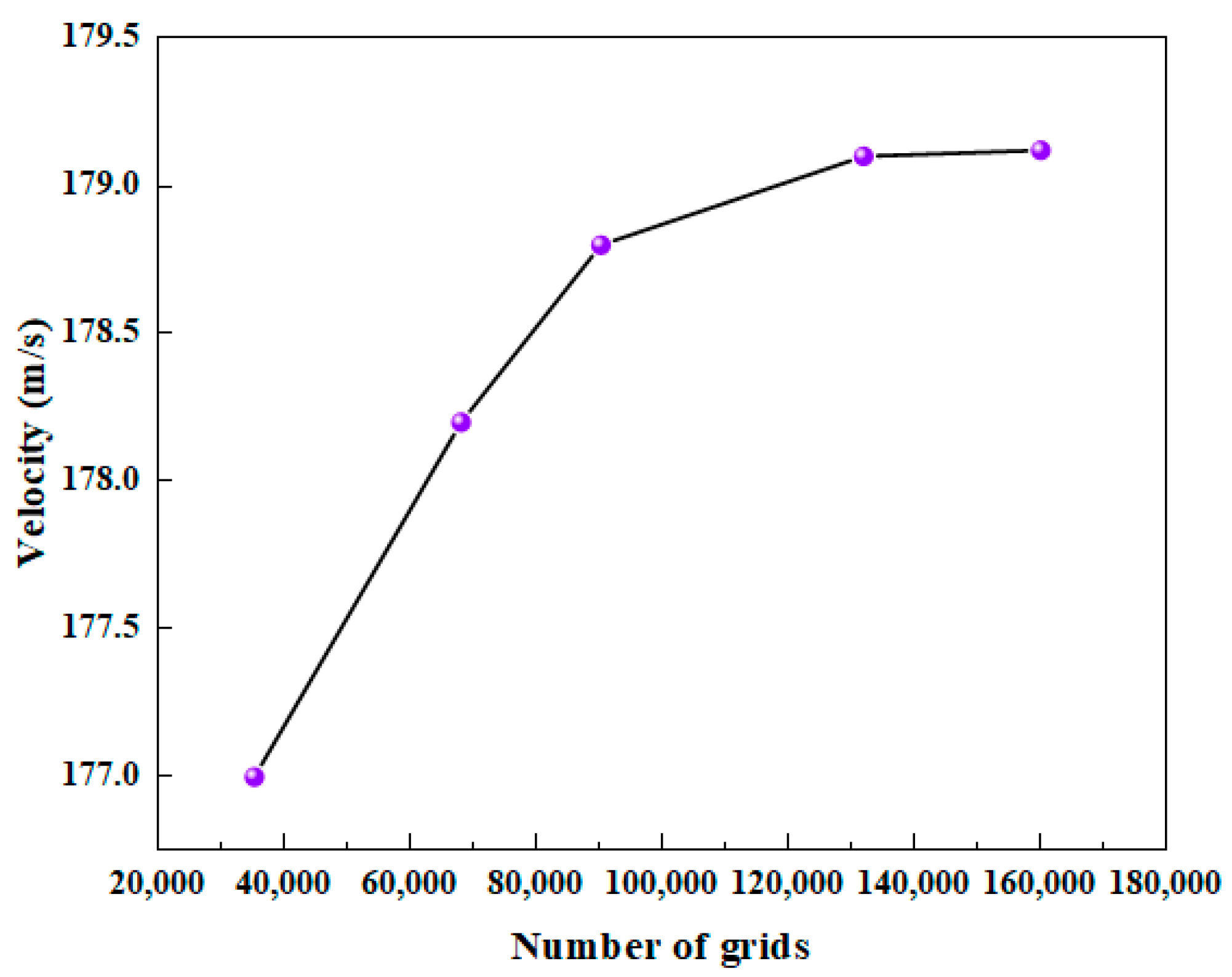
2.3. Mesh Independence Verification
2.4. Governing Equations and Turbulence Models
2.5. Accurate Validation of the Simulation Results
3. Results and Discussion
3.1. Flow Field Analysis of the Jet Pump
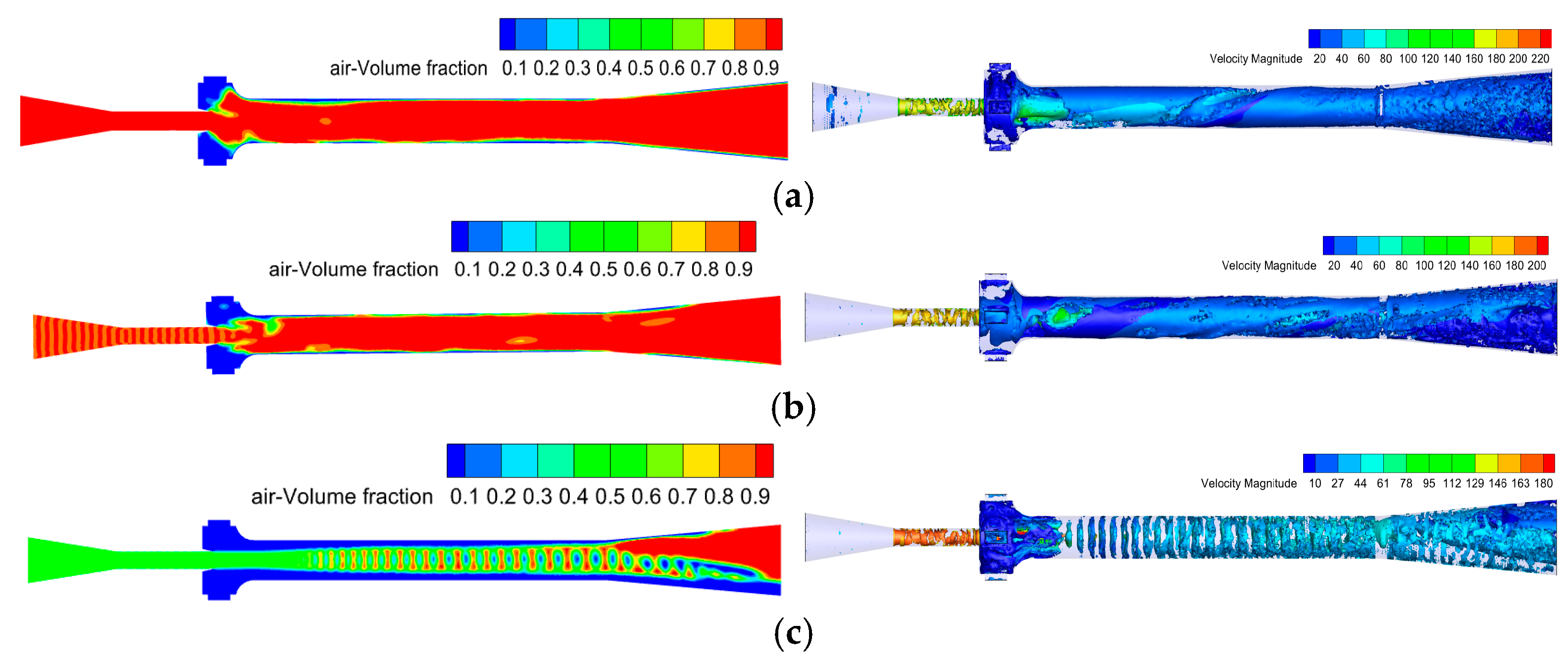
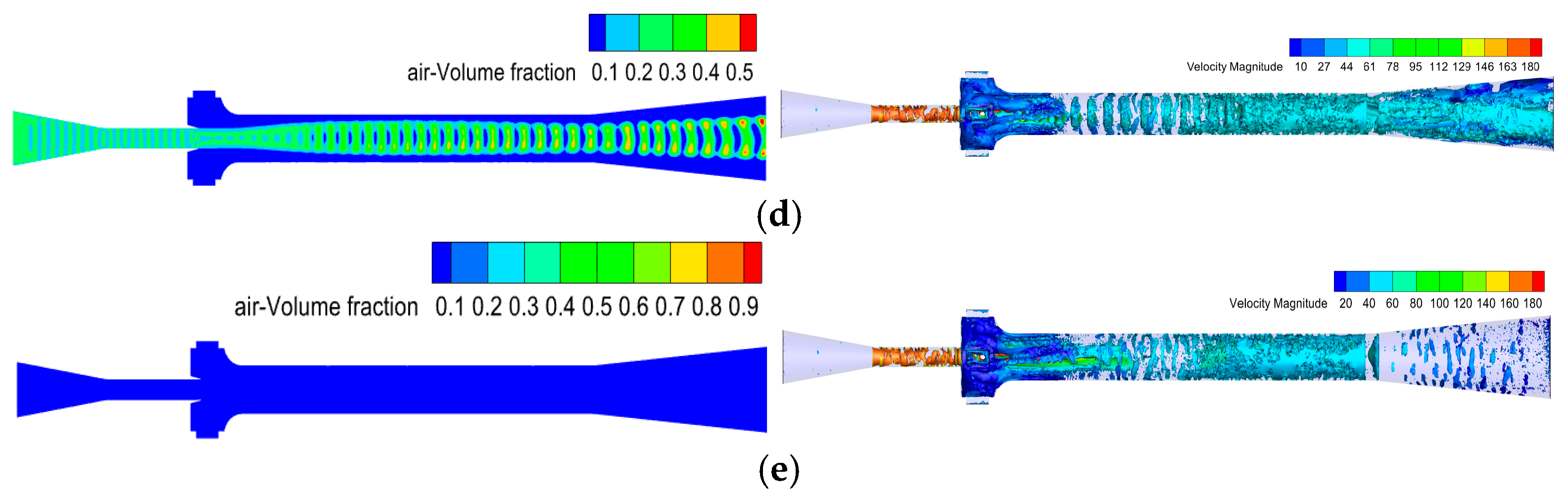
3.1.1. Phase Distribution
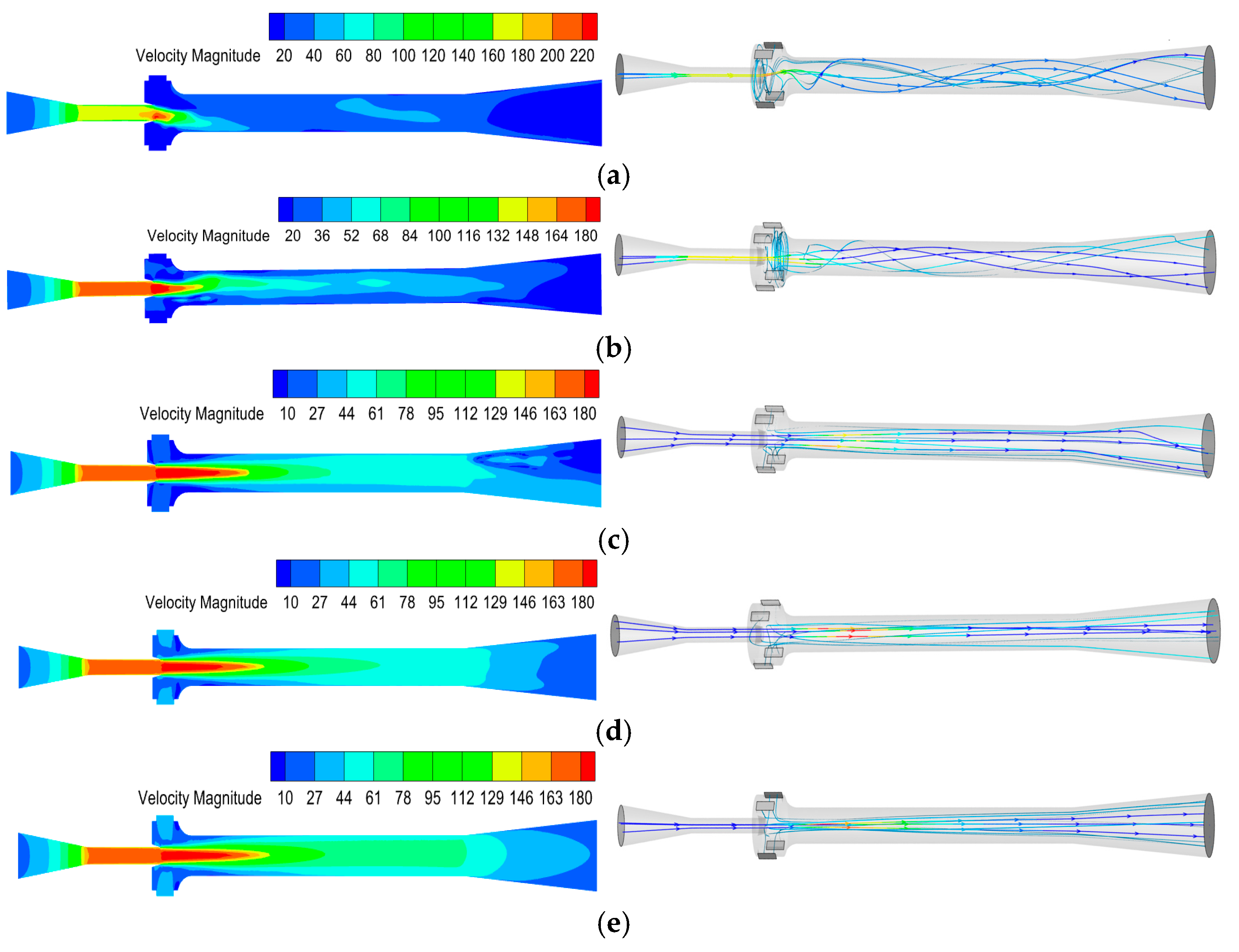
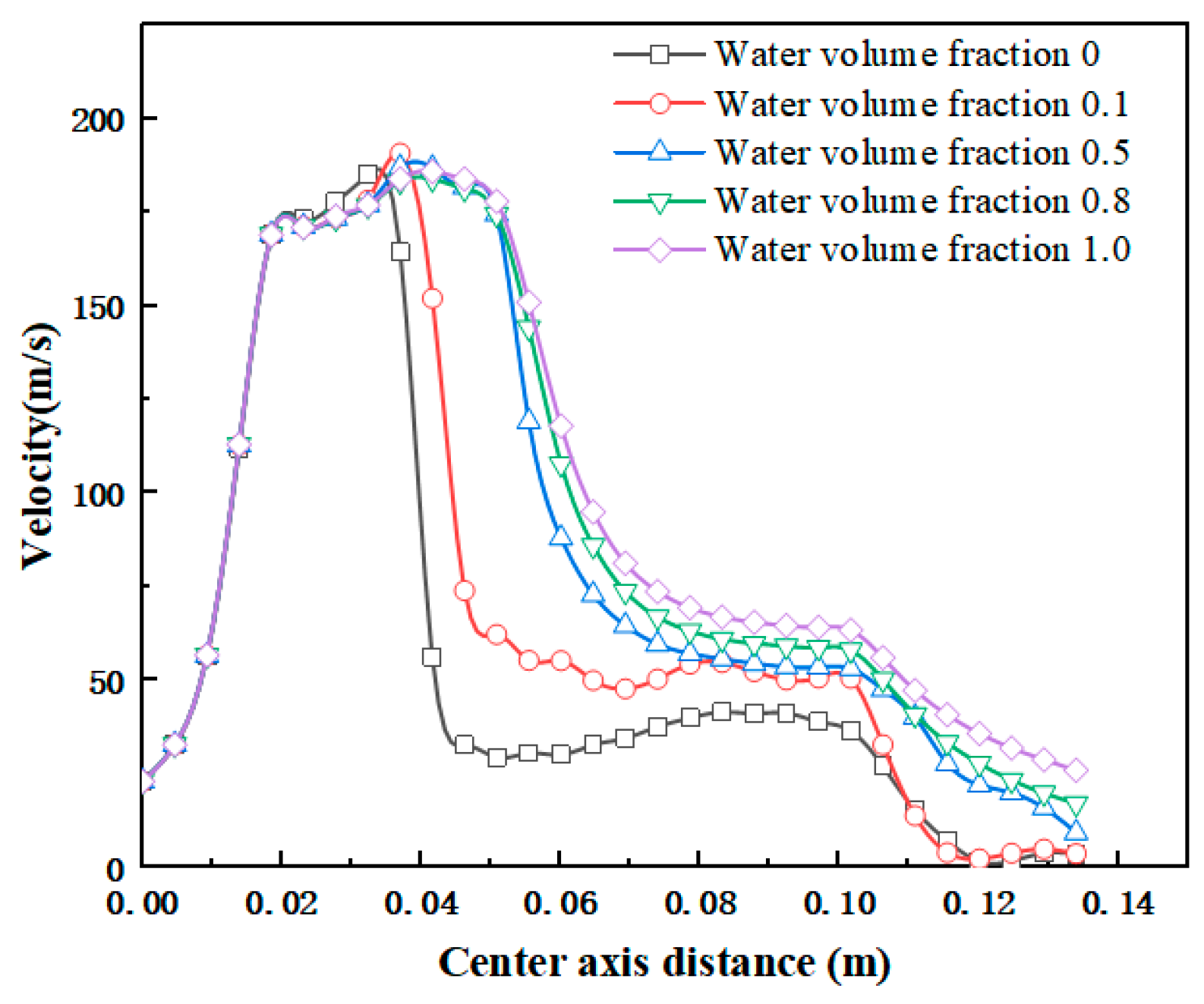
3.1.2. Velocity Distribution
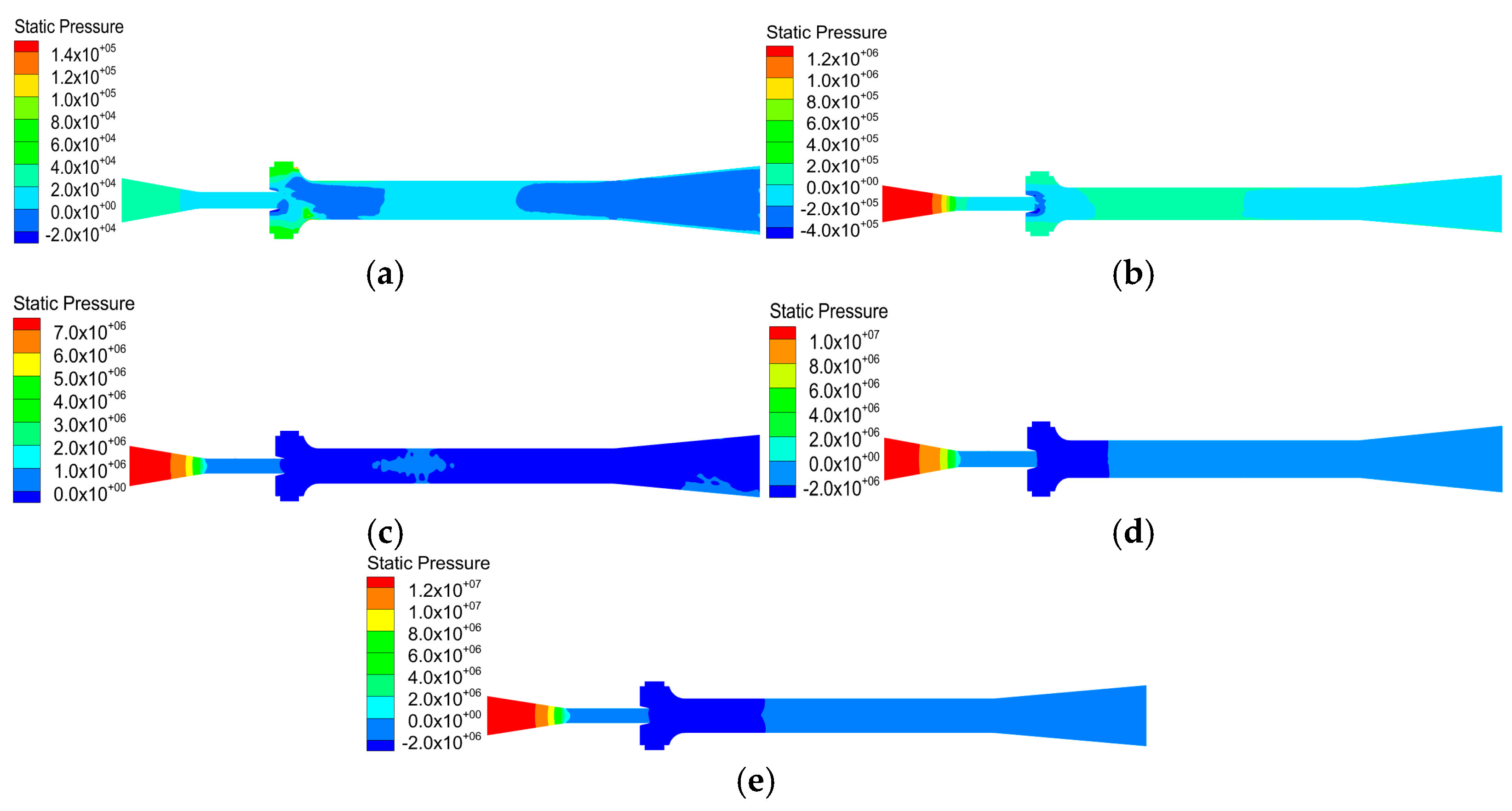
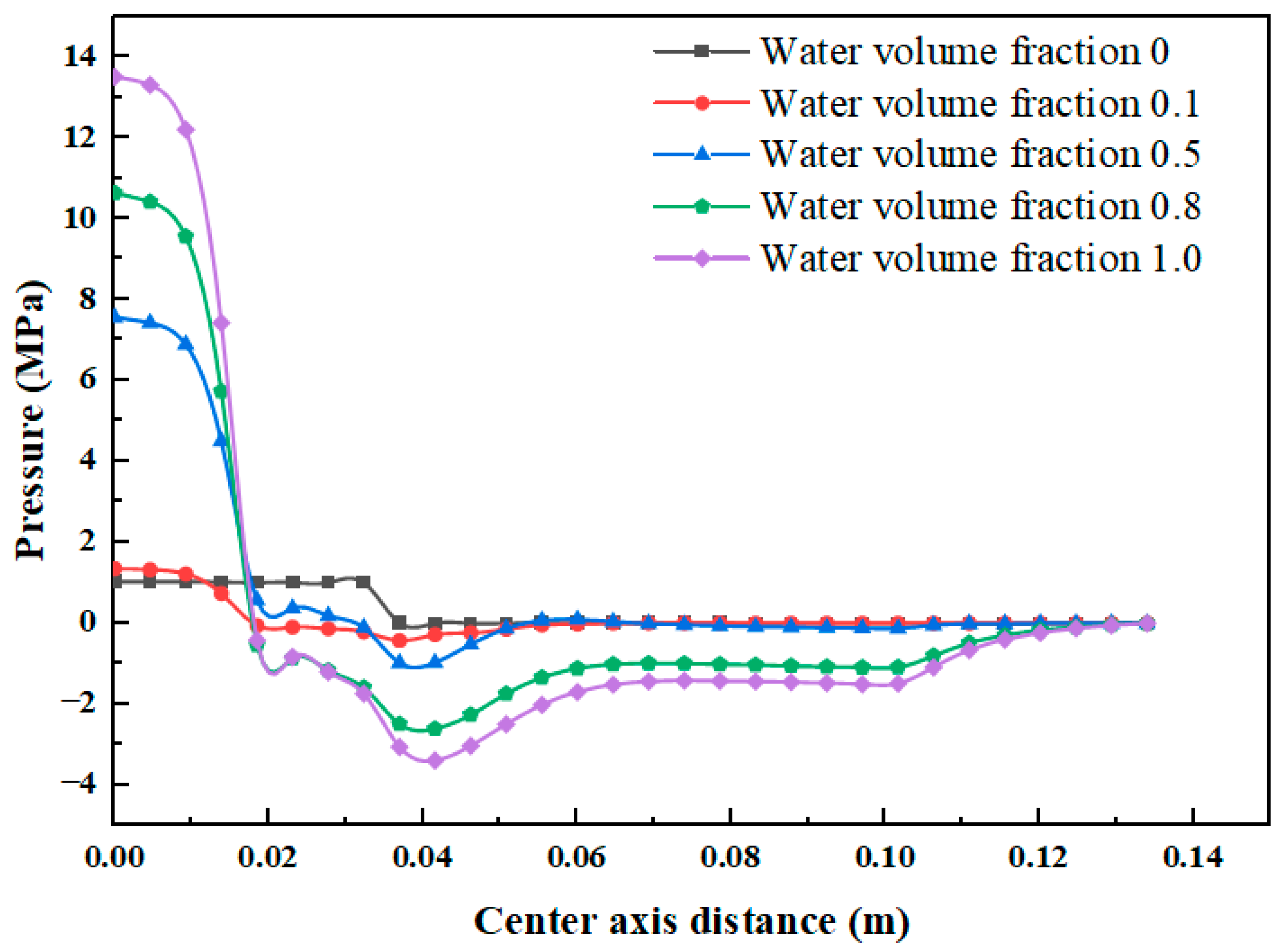
3.1.3. Pressure Distribution
3.1.4. Turbulent Kinetic Energy Distribution
3.2. Performance of Jet Pump
3.2.1. Pressure Ratio
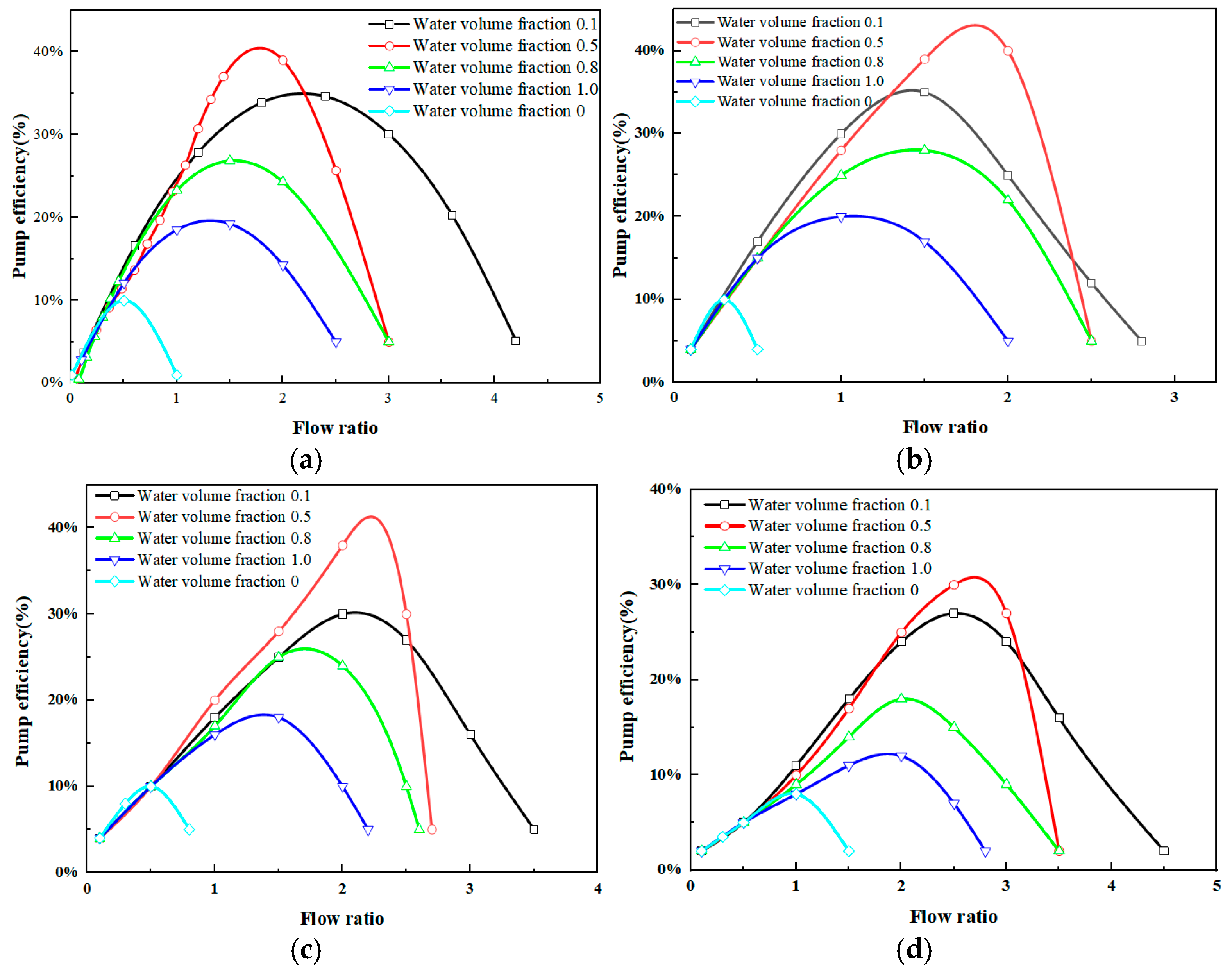
3.2.2. Pump Efficiency
4. Conclusions
- Exploration of pneumatic jet drainage and gas production in the Sulige Gas Field revealed that adding a certain volumetric fraction of water as the driving medium significantly improves drainage and gas production efficiency.
- The volumetric fraction of water has a significant impact on jet pump performance. Simulation results show that the volumetric fraction of water can significantly enhance jet pump efficiency. When the water volumetric fraction is 0.5, the jet pump efficiency reaches its maximum value (exceeding 40%), and the corresponding dimensionless mass flow rate is approximately 2.0, which represents the highest energy utilization efficiency of the jet pump.
- As the volumetric fraction of water increases, the optimal working point of the jet pump (i.e., the dimensionless mass flow rate corresponding to the peak pump efficiency) gradually decreases. It drops from 2.0 at water volumetric fractions of 0.1 and 0.5, to 1.8 at 0.8, and then to 1.5 at 1.0. This indicates that higher water volumetric fractions affect the flow characteristics of the jet pump, shifting the optimal working point to lower dimensionless mass flow rates.
- The simulation results provide valuable data support for optimizing jet pump performance. Future research can further consider factors such as fluid properties and nozzle-throat spacing in combination with mixed gas-liquid driving media to comprehensively improve jet pump efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Bai, J.; Jiang, Z.; Yu, F.; Hou, X.; Yu, X. Optimal design of pump selection for jet pump lift in offshore heavy oil thermal recovery. China Pet. Chem. Stand. Qual. 2023, 43, 154–157. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, D.; Chu, H.; Yao, J.; Zhang, M.; Liao, R. Simulation analysis of flow field of jet pump for co-production of high and low pressure reservoirs. Mach. Tools Hydraul. 2023, 51, 127–134. [Google Scholar] [CrossRef]
- Wang, X. Progress in the test of new drainage gas recovery technology in Qingshimao water-bearing gas reservoir. Petrochem. Appl. 2024, 43, 51–55. [Google Scholar]
- Ge, L.; Han, M.; Liu, X. Application of hydraulic jet pump in oil and gas wells. Equip. Manag. Maint. 2023, 17, 41–43. [Google Scholar]
- Mallela, R.; Chatterjee, D. Numerical investigation of the effect of geometry on the performance of a jet pump. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2011, 225, 1614–1625. [Google Scholar] [CrossRef]
- Girgidov, A.D. Efficiencies of jet pumps. Power Technol. Eng. 2015, 48, 366–370. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A.; Andresen, T. Experimental and numerical investigation of the influence of the two-phase ejector geometry on the performance of the R744 heat pump. Int. J. Refrig. 2012, 35, 1617–1625. [Google Scholar] [CrossRef]
- Kwon, O.B.; Kim, M.K.; Kwon, H.C.; Bae, D.S. Two-dimensional numerical simulations on the performance of an annular jet pump. J. Vis. 2002, 5, 21–28. [Google Scholar] [CrossRef]
- Long, X. Numerical simulation of internal flow in jet pump. J. Wuhan Univ. Hydraul. Electr. Eng. 2002, 6, 125054705. [Google Scholar]
- Zhu, X.; Wang, D.; Xu, C.; Zhu, Y.; Zhou, W.; He, F. Structure influence on jet pump operating limits. Chem. Eng. Sci. 2018, 192, 143–160. [Google Scholar] [CrossRef]
- Wang, C.; Lin, J.Z.; Shi, X. Numerical simulation and experimental study of turbulent flow in jet pump. J. Chem. Eng. Univ. 2006, 2, 175–179. [Google Scholar]
- Wu, J. Current Status and Prospects of Jet Pump Development. Irrig. Drain. Mach. 2007, 2, 65–68. [Google Scholar]
- Kumar, R.S.; Kumaraswamy, S.; Mani, A. Experimental investigations on a two-phase jet pump used in desalination systems. Desalination 2007, 204, 437–447. [Google Scholar] [CrossRef]
- Yadav, R.L.; Patwardhan, A.W. Design aspects of ejectors: Effects of suction chamber geometry. Chem. Eng. Sci. 2008, 63, 3886–3897. [Google Scholar] [CrossRef]
- Shah, A.; Chughtai, I.R.; Inayat, M.H. Experimental and numerical analysis of steam jet pump. Int. J. Multiph. Flow 2011, 37, 1305–1314. [Google Scholar] [CrossRef]
- Ge, Y. Modeling and simulation of steam jet refrigeration system. Cryog. Supercond. 2011, 39, 48–52. [Google Scholar]
- Liu, X. Numerical Analysis of Solid-Liquid Two-Phase Flow Field of Oil Well Jet Sand Pump. Master’s Thesis, Jilin University, Changchun, China, 2011. [Google Scholar]
- Wang, L.H.; Gao, C.C.; Wang, W.S.; Qin, H.X. Experimental study on the effect of pulse frequency on the performance of liquid jet pump. J. Hydraul. Eng. 2008, 03, 318–324. [Google Scholar]
- Chen, Y.; Danye, C.; Qizhi, Y. Calculation and analysis of ejector flow field based on FLUENT. Coal Mine Mach. 2012, 33, 108–109. [Google Scholar]
- Wu, Y.; Xiang, Q.; Li, H.; Chen, S. Experimental study on bubble size in the diffuser of liquid-gas jet pump. Fluid Mach. 2012, 40, 1–5. [Google Scholar]
- Aldaş, K.; Yapıcı, R. Investigation of Effects of Scale and Surface Roughness on Efficiency of Water Jet Pumps Using CFD. Eng. Appl. Comput. Fluid Mech. 2014, 8, 14–25. [Google Scholar] [CrossRef]
- Wang, Y. Research on Fluid Characteristics of Liquid-Gas Jet Pump. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2015. [Google Scholar]
- Chen, W. A brief discussion on the current status of numerical simulation of internal flow field of jet pumps. Chem. Eng. Des. Commun. 2016, 42, 88–110. [Google Scholar]
- Ran, L. Numerical simulation of flow field of jet pump with streamline nozzle. Hydropower Energy Sci. 2018, 36, 150–153. [Google Scholar]
- Tan, J. Numerical Analysis of Basic Performance and Cavitation Performance of Adjustable Jet Pump. Master’s Thesis, Wuhan University, Wuhan, China, 2019. [Google Scholar]
- Wang, W. Structure and working principle of venturi jet device. J. Southwest Univ. Sci. Technol. 2004, 2, 41–44. [Google Scholar] [CrossRef]
- Gao, G.; Yadong, X.; Yingliang, W. Numerical study on the effect of throat-mouth contraction half angle on flow characteristics of liquid-gas jet pump. J. Vac. Sci. Technol. 2020, 40, 174–179. [Google Scholar]
- Morrall, A.; Quayle, S.; Campobasso, M.S. Turbulence modelling for RANS CFD analyses of multi-nozzle annular jet pump swirling flows. Int. J. Heat Fluid Flow. 2020, 85, 108652. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Zhou, T. Computational fluid dynamics-based structure optimization of ultra-high-pressure water-jet nozzle using approximation method. arXiv 2025, arXiv:2501.01137. [Google Scholar]
- Liu, B. Structural Optimization of Jet Pump Based on Bp Neural Network. Quimica Nova 2024, 47, e-20230127. [Google Scholar] [CrossRef]
- AlSarkhi, A.; Kassar, A.; Sahu, Q.; Gajbhiye, R. Optimizing jet pump efficiency via drag reducing polymers and enhanced efficiency definitions. Sci. Rep. 2024, 14, 1–17. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, X.; Wang, H.; Wu, S.; Jiao, W.; Ji, L.; Shi, W.; He, Z.; Agarwal, R.K.; Wang, C. Multifactor response-based optimization for enhancing cavitation performance of short injection self-priming pumps. Phys. Fluids 2024, 36, 045116. [Google Scholar] [CrossRef]
- Wang, Z.; Lei, Y.; Wu, Z.; Wu, J.; Zhang, M.; Liao, R. Structure Size Optimization and Internal Flow Field Analysis of a New Jet Pump Based on the Taguchi Method and Numerical Simulation. Processes 2023, 11, 341. [Google Scholar] [CrossRef]
- Wang, D. Experimental study on needle valve regulated liquid jet pump. Trans. Chin. Soc. Agric. Mach. 1993, 4, 37–41. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Yokoi, K. Efficient implementation of THINC scheme: A simple and practical smoothed VOF algorithm. J. Comput. Phys. 2007, 226, 1985–2002. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- ESDU 93022. Ejectors and Jet Pumps: Computer Program for Design and Performance for Liquid Flow. 2011. Available online: https://www.esdu.com/cgi-bin/ps.pl?t=doc&p=esdu_93022b-r1 (accessed on 19 January 2024).


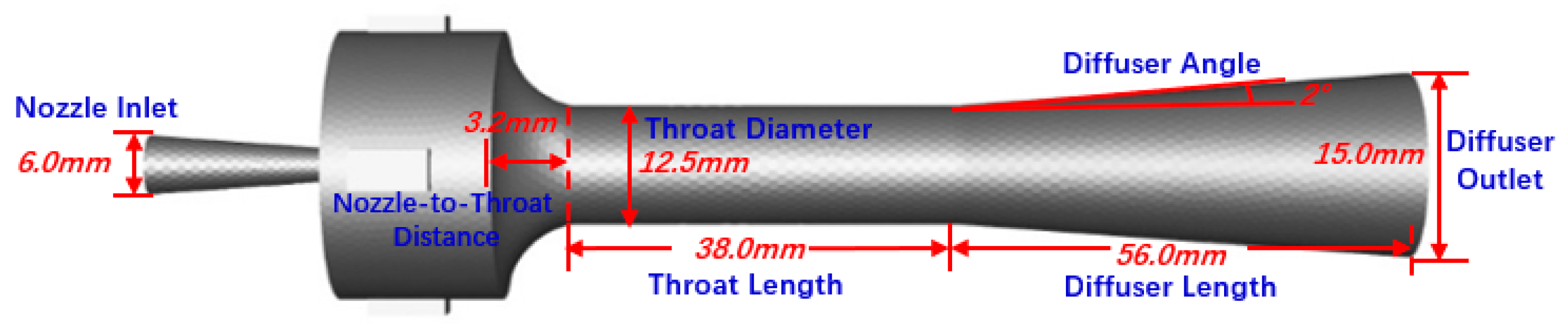



| Nozzle Inlet Diameter (mm) | Nozzle Outlet Diameter (mm) | Nozzle-to-Throat Distance (mm) | Throat Diameter (mm) | Throat Length (mm) | Diffuser Length(mm) | Diffuser Oulet Diameter(mm) | Diffuser Angle (°) |
|---|---|---|---|---|---|---|---|
| 6 | 3.2 | 3.2 | 12.5 | 38 | 56 | 15 | 4 |
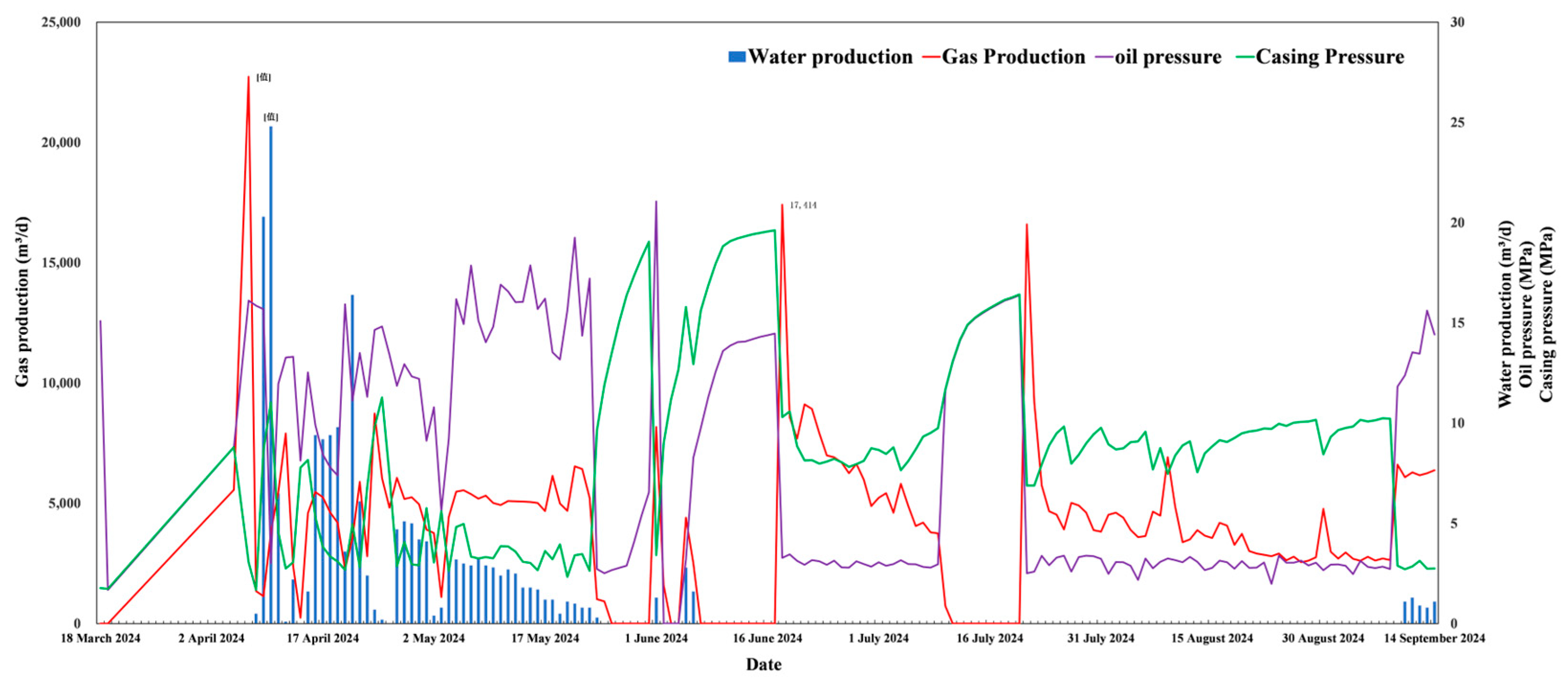
| Mode | Date | Oil Pressure (MPa) | Casing Pressure (MPa) | Water Production(m3/d) | Accumulated Water Production (m3/d) | Gas Production (m3/d) | Accumulated Gas Production (m3/d) |
|---|---|---|---|---|---|---|---|
| Self-flowing | 5 September 2024 | 2.83 | 10.08 | 0.0 | 193.9 | 2777 | 604,441 |
| 6 September 2024 | 2.77 | 10.14 | 0.0 | 193.9 | 2620 | 607,061 | |
| 7 September 2024 | 2.84 | 10.24 | 0.0 | 193.9 | 2708 | 609,769 | |
| 8 September 2024 | 2.72 | 10.22 | 0.0 | 193.9 | 2644 | 612,413 | |
| 9 September 2024 | 11.82 | 2.89 | 0.0 | 193.9 | 6611 | 619,024 | |
| Jet pump | 10 September 2024 | 12.38 | 2.71 | 1.1 | 195.0 | 6084 | 625,108 |
| 11 September 2024 | 13.53 | 2.85 | 1.3 | 196.3 | 6287 | 631,395 | |
| 12 September 2024 | 13.46 | 3.13 | 0.9 | 197.2 | 6165 | 637,560 | |
| 13 September 2024 | 15.61 | 2.74 | 0.8 | 198.0 | 6251 | 643,811 | |
| 14 September 2024 | 14.42 | 2.75 | 1.1 | 199.1 | 6374 | 650,185 | |
| 15 September 2024 | 2.83 | 10.08 | 0.0 | 193.9 | 2777 | 604,441 |
| Gas Phase | Liquid Phase | Gas Flow Rate | Water Flow Rate | Water Volume Fraction (Power Medium) |
|---|---|---|---|---|
| Air | Water | 23.04 m/s | 3.61~90.42 m/s | 0~1.0 |
| Fluid | Density/(kg·m−3) | Viscosity/(mPa·s) | Surface Tension/(M·m−1) |
|---|---|---|---|
| Water | 998.2 | 1.003 | 0.072 |
| Air | 1.225 | 1.798 × 10−2 |
| Section | Theoretical Pressure (MPa) | Simulated Pressure (MPa) | Relative Errors (%) |
|---|---|---|---|
| Pressure of the power fluid at inlet 1 | 13.57 | 13.85 | 2.1 |
| Pressure of the intake fluid at inlet 2 | 4.21 | 4.03 | 4.3 |
| Pressure of the mixture fluid at outlet 3 | 0.3 | 0.32 | 6.7 |
| Serial Number | Nozzle Inlet Diameter (mm) | Nozzle Outlet Diameter (mm) | Nozzle-to-Throat Distance (mm) | Throat Diameter (mm) | Throat Length (mm) | Diffuser Length (mm) | Diffuser OuletDiameter (mm) | Diffuser Angle (°) |
|---|---|---|---|---|---|---|---|---|
| #1 | 6 | 3.2 | 3.2 | 12.5 | 38 | 56 | 15 | 4 |
| #2 | 6 | 2.3 | 2.3 | 3.9 | 32 | 54 | 8 | 4 |
| #3 | 6 | 4.02 | 4.02 | 19 | 114 | 120 | 26 | 4 |
| #4 | 6 | 2.88 | 2.88 | 4.88 | 42 | 65 | 7 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Shi, S.; Zhao, Z.; Zhang, Y.; Cai, J.; Lin, S.; Mao, J. Numerical Simulation Study on Internal Flow Law and Efficiency of Gas-Liquid Mixed Jet Pump. Processes 2025, 13, 495. https://doi.org/10.3390/pr13020495
Wang X, Shi S, Zhao Z, Zhang Y, Cai J, Lin S, Mao J. Numerical Simulation Study on Internal Flow Law and Efficiency of Gas-Liquid Mixed Jet Pump. Processes. 2025; 13(2):495. https://doi.org/10.3390/pr13020495
Chicago/Turabian StyleWang, Xiongxiong, Shuqiang Shi, Zhengyan Zhao, Yongcai Zhang, Jiaming Cai, Shaokang Lin, and Jincheng Mao. 2025. "Numerical Simulation Study on Internal Flow Law and Efficiency of Gas-Liquid Mixed Jet Pump" Processes 13, no. 2: 495. https://doi.org/10.3390/pr13020495
APA StyleWang, X., Shi, S., Zhao, Z., Zhang, Y., Cai, J., Lin, S., & Mao, J. (2025). Numerical Simulation Study on Internal Flow Law and Efficiency of Gas-Liquid Mixed Jet Pump. Processes, 13(2), 495. https://doi.org/10.3390/pr13020495






