Study on the Influence of Crystal Plugging on the Mechanical Behavior of Karst Tunnel Lining Structure
Abstract
1. Introduction
2. Experimental Study on the Influence of CaCO3 Crystallization on the Mechanical Properties of Initial Support Concrete for Karst Tunnel
2.1. Solution Preparation and Specimen Preparation
2.2. Test Steps
- (1)
- The prepared concrete sample was immersed in the test solution to produce crystallization. The test was divided into five groups, and each group was soaked for 0 d (blank control group), 10 d, 20 d, 30 d and 40 d, respectively. After the test time of each group of concrete samples was completed, the corresponding samples were taken out and dried for 24 h to carry out the follow-up test;
- (2)
- After the crystallization test, we took out the static dry sample for appearance inspection, and observed the crystallization precipitation and surface changes of the sample. After observation and recording, we cleaned the crystal on the surface of the sample, weighed the sample with an electronic scale with an accuracy of 0.1 g and recorded it, and calculated the average mass and mass damage rate of each group of samples;
- (3)
- Uniaxial compression tests with a stress loading rate of 0.5 mpa/s were carried out on different groups of samples. The changes of compressive strength and elastic modulus after crystallization were measured to evaluate the mechanical properties of concrete.
2.3. Indoor Test Results and Analysis
2.3.1. Analysis of Concrete Appearance Changes in Different Crystallization Days
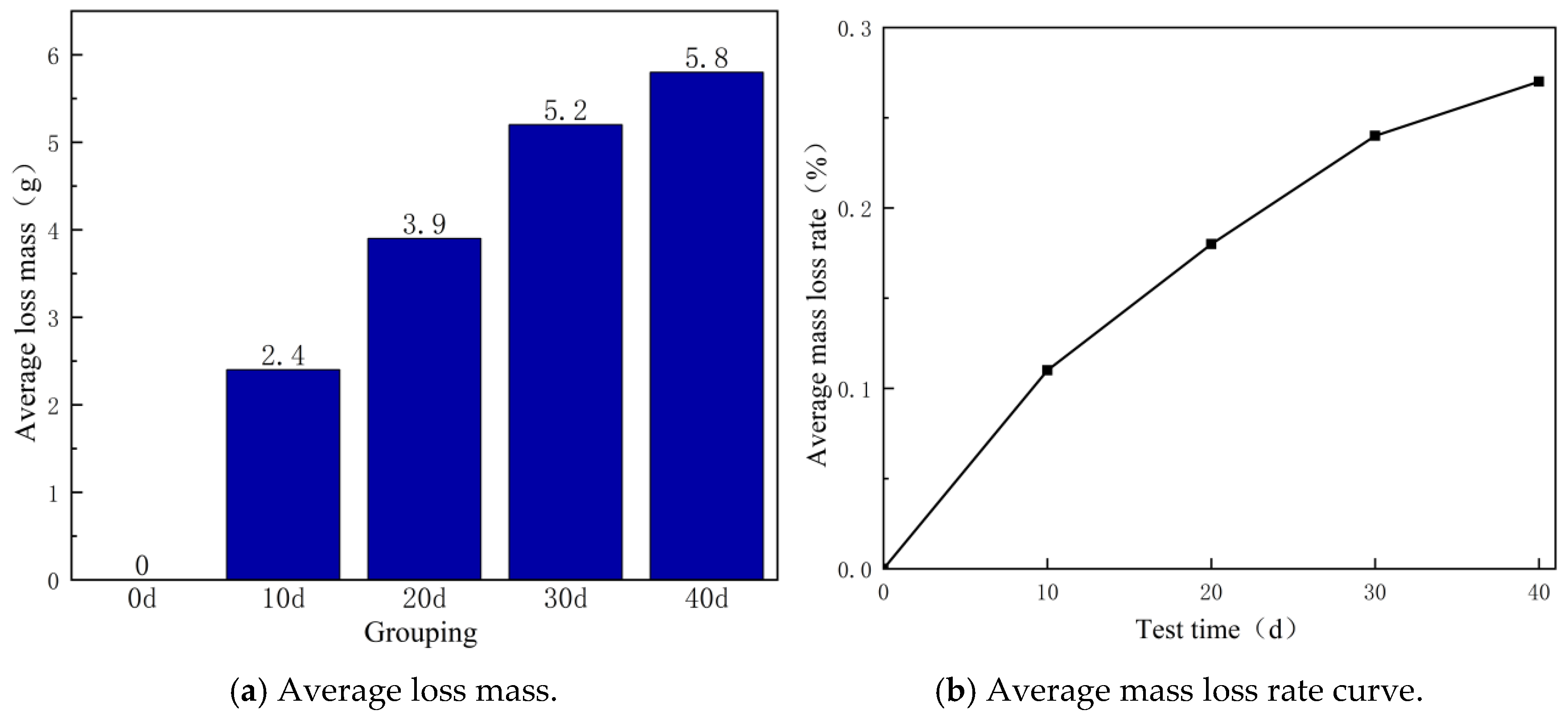
2.3.2. Analysis of Concrete Quality Change in Different Crystallization Days
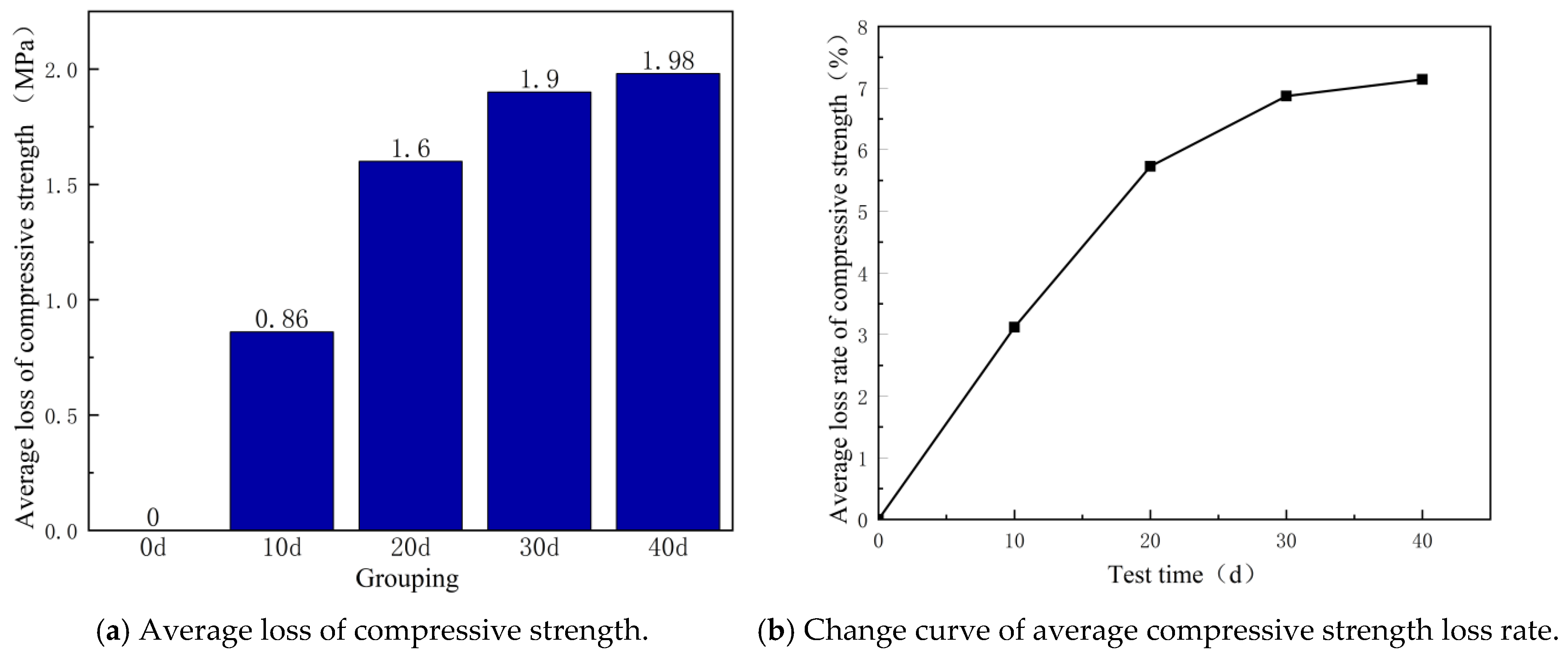
2.3.3. Analysis of Compressive Strength Changes of Concrete with Different Crystallization Days
2.3.4. Analysis of Elastic Modulus Change of Concrete with Different Crystallization Days
3. Numerical Simulation Method and Scheme
3.1. Determination of Mechanical Properties of Primary Support Concrete
3.2. Determination of Drainage Capacity of Tunnel Drainage System
3.3. Selection of Groundwater Level
3.4. Numerical Simulation Scheme
4. Result Analysis and Discussion
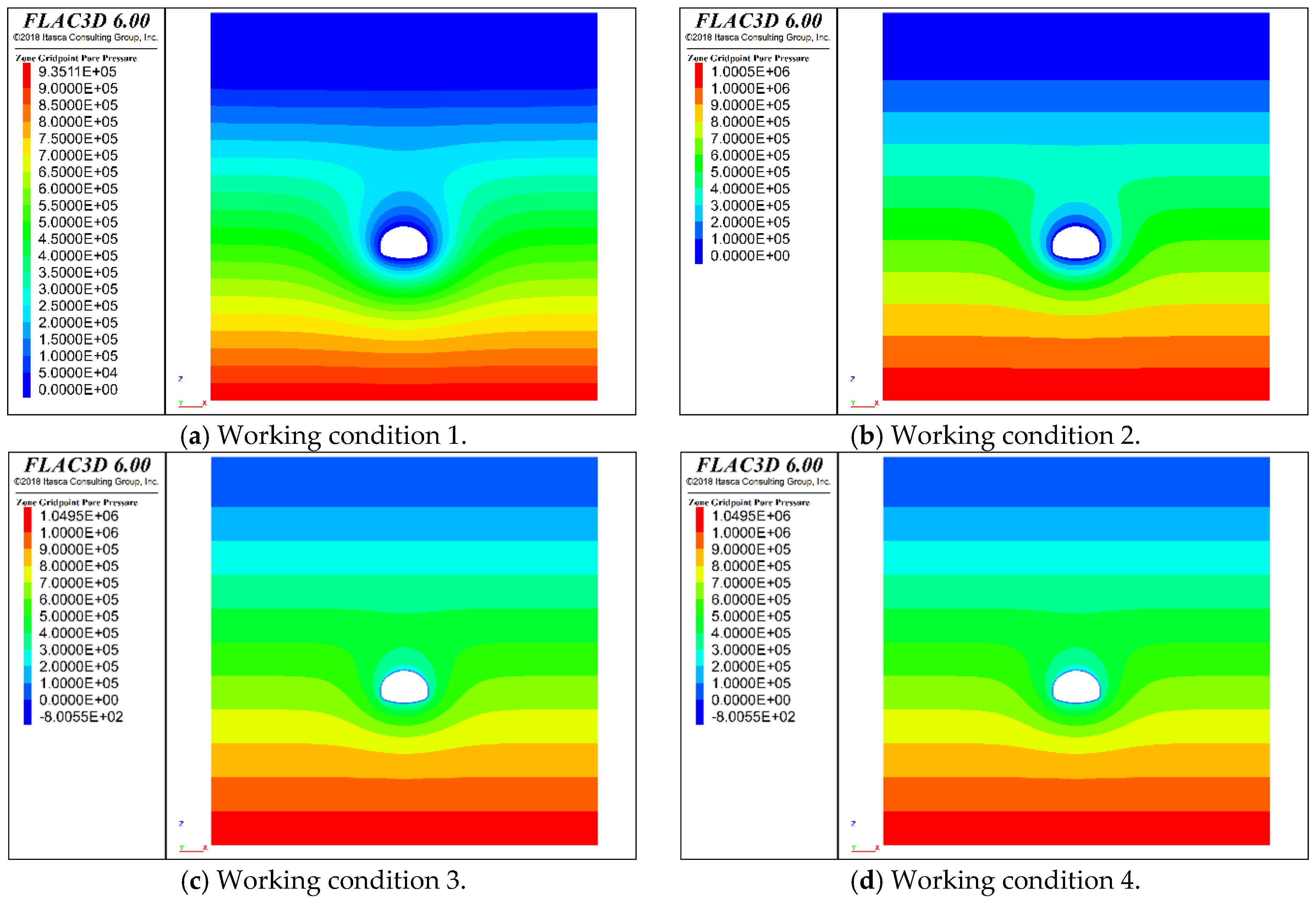
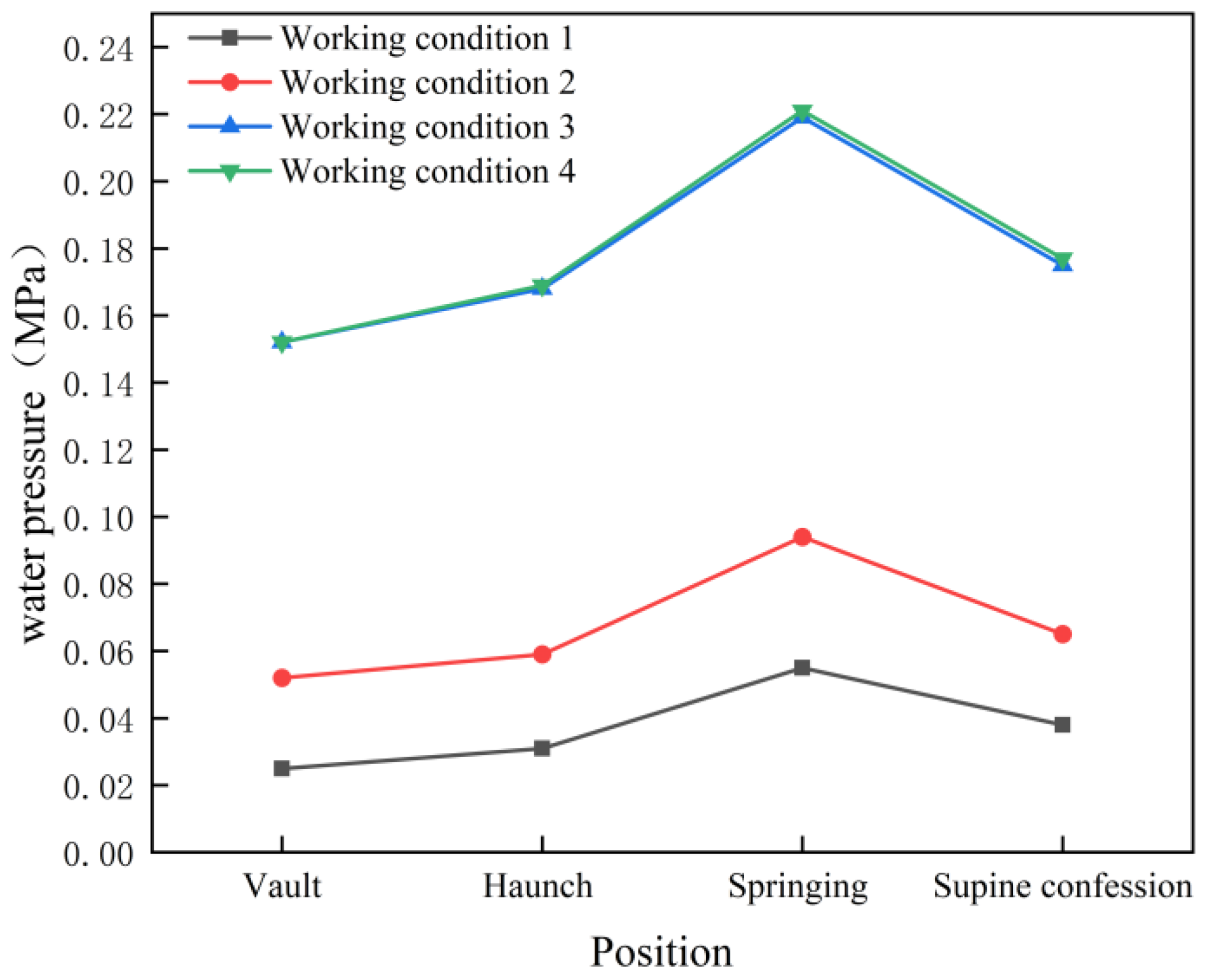
4.1. Pore Water Pressure Analysis
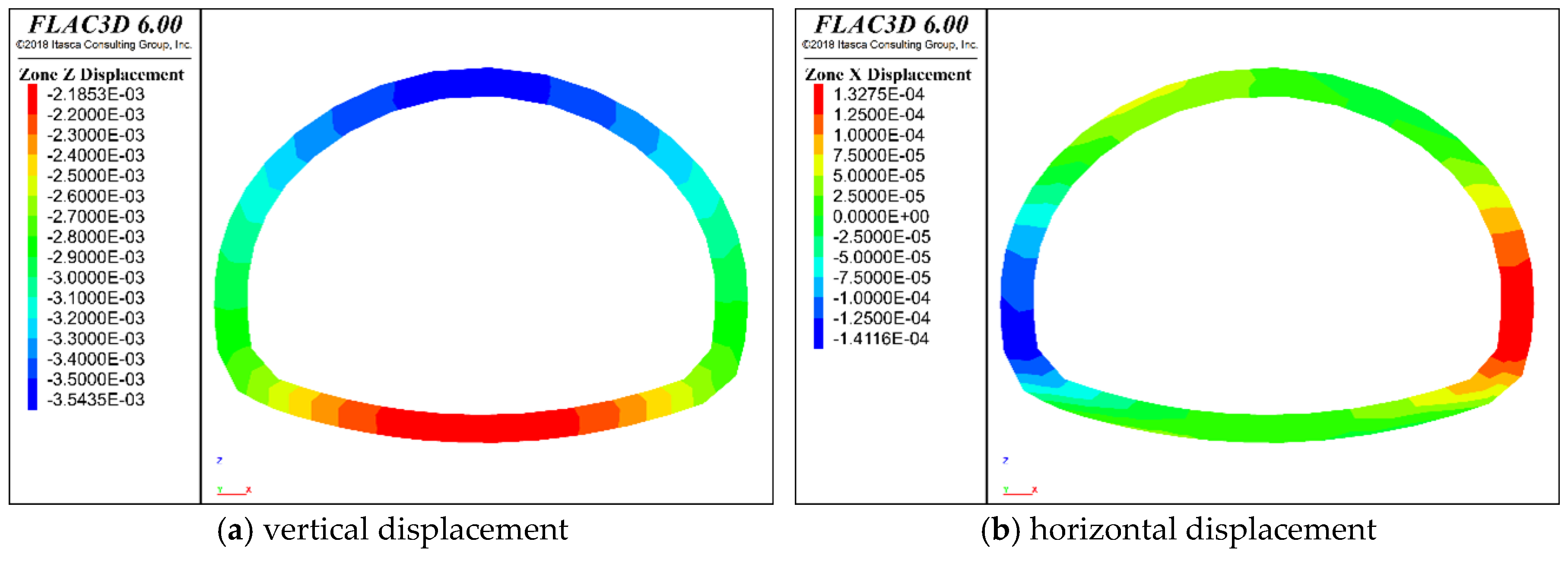
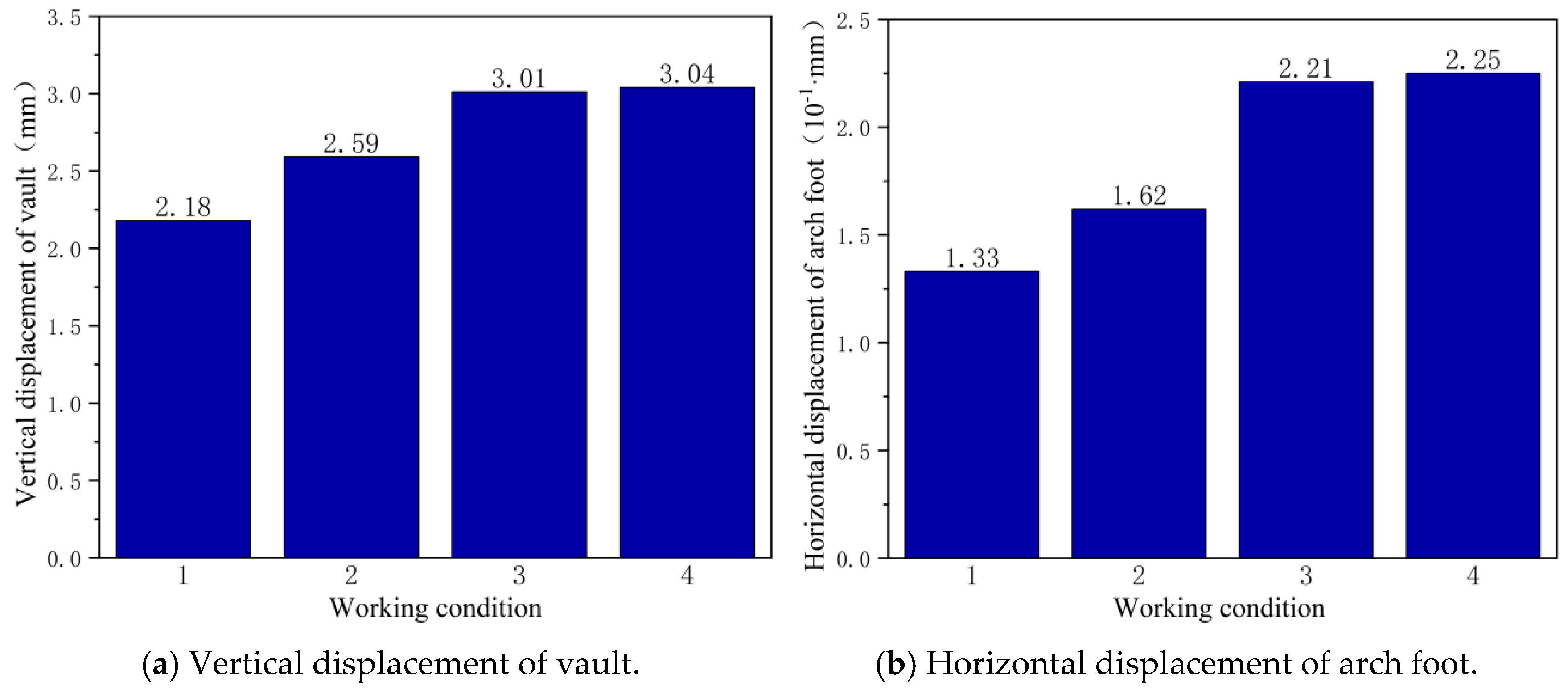
4.2. Displacement Analysis
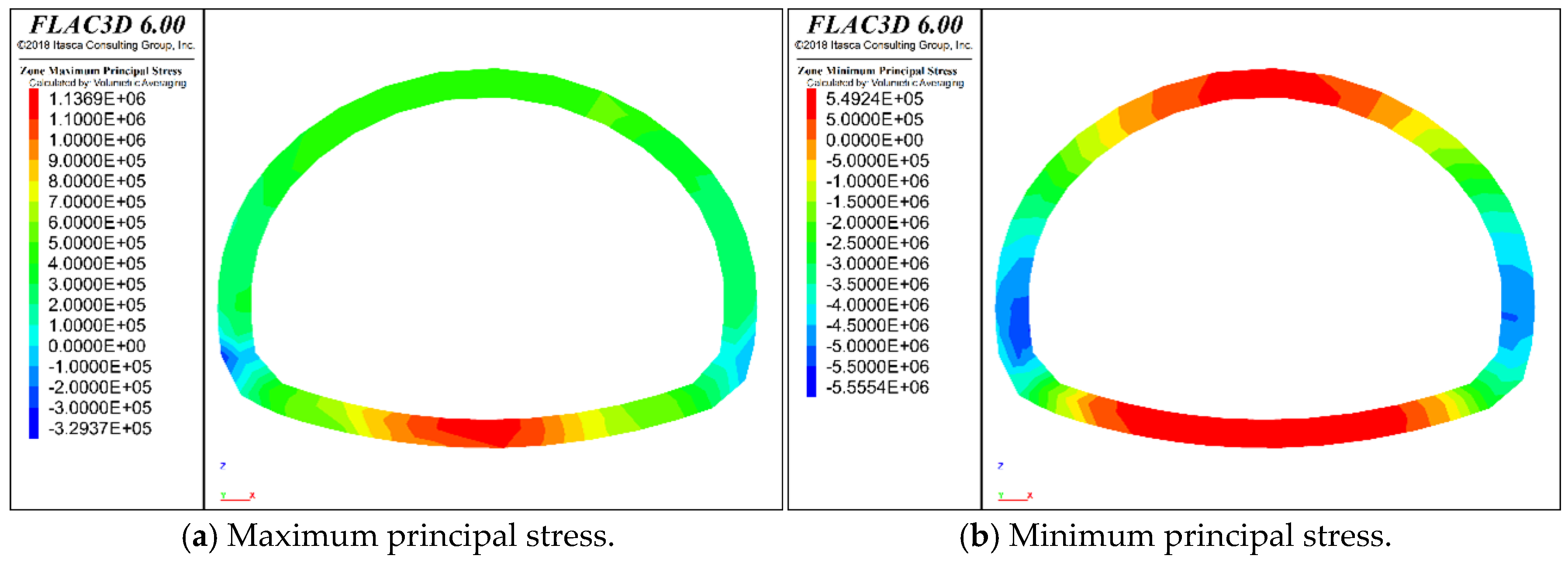
4.3. Stress Analysis
5. Conclusions
- (1)
- The phenomenon of calcium carbonate crystallization in the tunnel initial support concrete gradually appears with the passage of time. The area of the crystalline region diffuses from the edge to the center, accompanied by the formation of holes;
- (2)
- With the passage of time, the precipitation of calcium ions generated by the cement hydration reaction in concrete gradually increases, leading to the crystallization of calcium carbonate and the increase in pores on the surface of concrete, resulting in the decline of concrete quality, compressive strength and elastic modulus. However, the change range of concrete quality, compressive strength and elastic modulus shows a gradually decreasing trend;
- (3)
- The change of pore water pressure is mainly caused by the rise of groundwater level caused by the blockage of drainage system. The pore water pressure distribution of each part of tunnel lining shows the rule of arch foot > inverted arch > arch waist > arch crown;
- (4)
- The stress and displacement of the tunnel lining are affected by the crystallization of the primary support concrete and the blockage degree of the drainage system. With the increase in concrete crystallization and drainage system blockage, the stress and displacement increase accordingly. However, within 0–40 d, the effect of concrete crystallization on lining stress and displacement is relatively small.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, S.; Wang, W.; Gong, J. Development and Prospects of Railway Tunnels in China (including statistical data of railway tunnels in China as of the end of 2020). Tunn. Constr. (Chin. Engl.) 2021, 41, 308–325. [Google Scholar]
- Jiang, S. China highway tunnel data statistics. Tunn. Constr. 2017, 37, 643–644. [Google Scholar]
- Wu, M.; Zhang, Y.; Liu, X. Research on disease treatment technology of highway tunnel. J. Undergr. Space Eng. 2007, 3, 967–971. [Google Scholar]
- Dai, G.; Zhu, H.; Xia, C. Cause analysis and treatment of a highway tunnel disease. Chin. J. Saf. Sci. 2005, 89–92+139. [Google Scholar]
- Miao, X. Analysis of disease causes of JIUYANSHAN tunnel and suggestions on treatment measures. J. Railw. Eng. 2003, 2, 70–72. [Google Scholar]
- Li, Z.; Zhang, Y. Stability analysis and treatment technology of lining cracking tunnel. Mod. Tunn. Technol. 2004, 41, 26–31+40. [Google Scholar]
- Pan, H.; Yang, L.; Huang, K. Research on bias effect and lining crack of highway tunnel. J. Rock Mech. Eng. 2005, 3311–3315. [Google Scholar]
- Wang, J.; Zhu, H.; Tang, Y.; Zhou, N.; Ye, C.; Lu, Y. Monitoring and analysis of crack movement in multi arch tunnel. J. Civ. Eng. 2007, 40, 69–73. [Google Scholar]
- Li, H.; Ye, F.; Yang, Y.; Xie, X.; Sheng, J. Cause analysis and control technology of water leakage in power tunnel. East China Power 2011, 39, 1311–1313. [Google Scholar]
- Lin, C. Research on the Mechanism of Water Leakage and Grouting Treatment of Operating Tunnel Lining. Ph.D. Thesis, Shandong University, Jinan, China, 2017. [Google Scholar]
- Liu, T.; Zhu, H.; Xia, C.; Li, Z.; Li, G. Investigation results and analysis of lining cracking and leakage of multi arch tunnels in Yunnan Province. Chin. J. Highw. 2004, 65–68. [Google Scholar]
- Li, G.; Guo, J. Causes, prevention and treatment of tunnel lining cracks and leakage. Railw. Constr. 2003, 23–25. [Google Scholar]
- Shi, J. Research on the Mechanism and Prevention Technology of Water Leakage in Multi Arch Tunnel. Ph.D. Thesis, Chongqing University, Chongqing, China, 2012. [Google Scholar]
- Fu, J. Research on the Causes of Water Leakage in Highway Tunnels and Its Impact on Lining Structures. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2012. [Google Scholar]
- Zhai, M. Study on the Law of Crystal Blockage in Tunnel Drainage System in Limestone Area. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2016. [Google Scholar]
- Ye, F.; Tian, C.; He, B.; Zhao, M.; Wang, J.; Han, X.; Song, G. Crystallization blockage test of under construction tunnel drainage system. Chin. J. Highw. 2021, 34, 159–170. [Google Scholar]
- Zhou, Z. Mechanism Research and Treatment Suggestions on Tunnel Drainage Pipe Blockage by Groundwater Seepage Crystallization in Karst Area. Master’s Thesis, Chang’an University, Xi’an, China, 2015. [Google Scholar]
- Jian, B.; Lu, T.; Li, S.; Yin, K. Influence of groundwater buoyancy on the safety of underground building structures. Civ. Archit. Environ. Eng. 2010, 32, 56–60. [Google Scholar]
- Li, P.; Zhang, D.; Fang, Q.; Liu, Y.; Li, B. Mechanical characteristics of subsea tunnel support structure based on continuum model. J. Beijing Jiaotong Univ. 2009, 33, 7–12. [Google Scholar]
- Fang, Q.; Zhang, D.; Huang, M. Analysis of seepage in subsea tunnel based on continuum model. J. Rock Mech. Eng. 2007, 26 (Suppl. S2), 3776–3784. [Google Scholar]
- Jiang, H. Comprehensive Study on Drainage Hole Simulation Method in Seepage Calculation. Master’s Thesis, Hohai University, Nanjing, China, 2007. [Google Scholar]
- Wang, E.; Wang, H.; Sun, Y. Study on numerical model of three-dimensional fracture network seepage. In The Professional Committee of Structural Engineering of the Chinese Society of Mechanics, the Editorial Board of Engineering Mechanics of the Chinese Society of Mechanics, the Science and Technology Association of Guangxi Autonomous Region, Guangxi University, and the Department of Civil Engineering of Tsinghua University Proceedings of the Sixth National Conference on Structural Engineering (Volume II); Department of water conservancy and Hydropower Engineering, Tsinghua University: Beijing, China, 1997. [Google Scholar]
- Wang, E.; Wang, H.; Wang, H. Discussion on the Simulation Method of Drainage Hole Curtain “Replacing Wells with Cracks”. J. Rock Mech. Eng. 2002, 21, 98–101. [Google Scholar]
- Negi, A.S.; Kumar, B.; Kumar, A.; Rawat, S.K.; Yaseen, M. Investigation of heat flux and heat source/sink effect on heat transfer ferrofluid (CoFe2O4-H2O) flow in an induced magnetic field with porous medium within the horizontal channel. Int. J. Ambient. Energy 2025, 46, 2447939. [Google Scholar] [CrossRef]
- Negi, A.S.; Kumar, B. Nano-ferrofluid (Mn–Zn, CoFe2O4, Fe3O4) flow in a permeable channel with induced magnetic field. Waves Random Complex Media 2023, 1–28. [Google Scholar] [CrossRef]
- Saini, A.; Negi, A.S.; Kumar, A.; Chamkha, A.J. Radiative convective heat transfer and magneto-hydrodynamic flow in a viscous fluid-saturated porous channel with variable thermal conductivity. Int. J. Ambient. Energy 2024, 45, 2406908. [Google Scholar] [CrossRef]
- Tong, Y.; Ye, F.; Tian, C.; Zhang, J.; Jiang, Y.; Han, X.; Li, Y. Optimizing the development and field application of calcium stabilizing agents for preventing calcium leaching in tunnels. J. Clean. Prod. 2024, 449, 141757. [Google Scholar] [CrossRef]
- Liu, L.; Xie, M.; He, Y.; Li, Y.; Huang, X.; Cui, X.; Shi, C. Expansion behavior and microstructure change of alkali-activated slag grouting material in sulfate environment. Constr. Build. Mater. 2020, 260, 119909. [Google Scholar] [CrossRef]
- Liu, L.; Liu, H.; Xu, Y.; Xiang, J.; He, Y.; Zheng, G. Mechanical Properties and Microstructure of Alkali-Activated Slag Grouting Materials Exposed to Flowing NaHCO3 Solution. J. Mater. Civ. Eng. 2022, 34, 04022332. [Google Scholar] [CrossRef]
- Cang, L.; Qiu, B. Qiu Buyi Hypothesis, and Qiu Buyi Formula. Hydrogeol. Eng. Geol. 1983, 54–55. [Google Scholar]
- Zheng, B.; Wang, J.; Wu, J. Study on calculation method of lining water pressure based on equivalent permeability coefficient. Mod. Tunn. Technol. 2011, 48, 43–46+57. [Google Scholar]
- Zheng, B. Study on Practical Calculation of Water Pressure Load on Tunnel Lining. Ph.D. Thesis, China Academy of Railway Sciences, Beijing, China, 2010. [Google Scholar]




| Test Point | Water Depth (cm) | Ditch Width (cm) | Average Velocity (m/s) | Drainage (m3/d) |
|---|---|---|---|---|
| 1 | 25 | 30 | 0.80 | 5203 |
| 2 | 33 | 30 | 0.51 | 4362 |
| 3 | 14 | 30 | 0.61 | 2210 |
| 4 | 10 | 30 | 0.34 | 876 |
| 5 | 4 | 30 | 0.20 | 207 |
| 6 | 26 | 30 | 0.25 | 1678 |
| 7 | 15 | 30 | 0.32 | 1224 |
| 8 | / | / | / | 2251 |
| Total discharge 18,011 m3/d | ||||
| Degree of Crystalline Blockage of Drainage System (%) | Initial Groundwater Level Height (m) | Groundwater Level Drawdown (m) | Height of Groundwater Level After Stabilization (m) |
|---|---|---|---|
| 0 | 60 | 16.35 | 43.65 |
| 40 | 60 | 9.81 | 50.19 |
| 80 | 60 | 4.91 | 55.09 |
| Material | Elastic Modulus E (GPa) | Poisson’s Ratioμ | Bulk Density γ (kN/m3) | Internal Friction Angle φ (°) | Cohesion c (MPa) | Permeability Coefficient K (m3/Pa-sec) | Porosity n |
|---|---|---|---|---|---|---|---|
| Class IV surrounding rock | 3.90 | 0.30 | 22 | 37 | 1.60 | 3.3 × 10−8 | 0.32 |
| Primary support | 28 | 0.25 | 24 | / | / | 5.0 × 10−13 | 0.14 |
| Initial branch of crystallization for 20 d | 27.44 | 0.25 | 23.96 | / | / | 5.0 × 10−13 | 0.14 |
| 40 d primary crystallization | 27.30 | 0.25 | 23.93 | / | / | 5.0 × 10−13 | 0.14 |
| Secondary lining | 32 | 0.20 | 26 | / | / | 5.0 × 10−14 | 0.09 |
| 40% clogged secondary lining | 32 | 0.20 | 26 | / | / | 3.0 × 10−14 | 0.09 |
| 80% secondary lining blocked | 32 | 0.20 | 26 | / | / | 1.0 × 10−14 | 0.09 |
| Working Condition | Crystallization Days (d) | Blockage Degree of Drainage System (%) | Height of Underground Water Level from Tunnel Top (m) |
|---|---|---|---|
| 1 | 0 | 0 | 43.65 |
| 2 | 40 | 40 | 50.19 |
| 3 | 20 | 80 | 55.09 |
| 4 | 40 | 80 | 55.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, S.; Zhang, L.; Guan, S.; Li, Z.; Cheng, L.; Liu, J.; Chen, J. Study on the Influence of Crystal Plugging on the Mechanical Behavior of Karst Tunnel Lining Structure. Processes 2025, 13, 568. https://doi.org/10.3390/pr13020568
Wang Y, Liu S, Zhang L, Guan S, Li Z, Cheng L, Liu J, Chen J. Study on the Influence of Crystal Plugging on the Mechanical Behavior of Karst Tunnel Lining Structure. Processes. 2025; 13(2):568. https://doi.org/10.3390/pr13020568
Chicago/Turabian StyleWang, Yehao, Shiyang Liu, Li Zhang, Shaojie Guan, Zongzhi Li, Liang Cheng, Jie Liu, and Jie Chen. 2025. "Study on the Influence of Crystal Plugging on the Mechanical Behavior of Karst Tunnel Lining Structure" Processes 13, no. 2: 568. https://doi.org/10.3390/pr13020568
APA StyleWang, Y., Liu, S., Zhang, L., Guan, S., Li, Z., Cheng, L., Liu, J., & Chen, J. (2025). Study on the Influence of Crystal Plugging on the Mechanical Behavior of Karst Tunnel Lining Structure. Processes, 13(2), 568. https://doi.org/10.3390/pr13020568







