Pressure Relief-Type Overpressure Prediction in Sand Body Based on BP Neural Network
Abstract
:1. Introduction
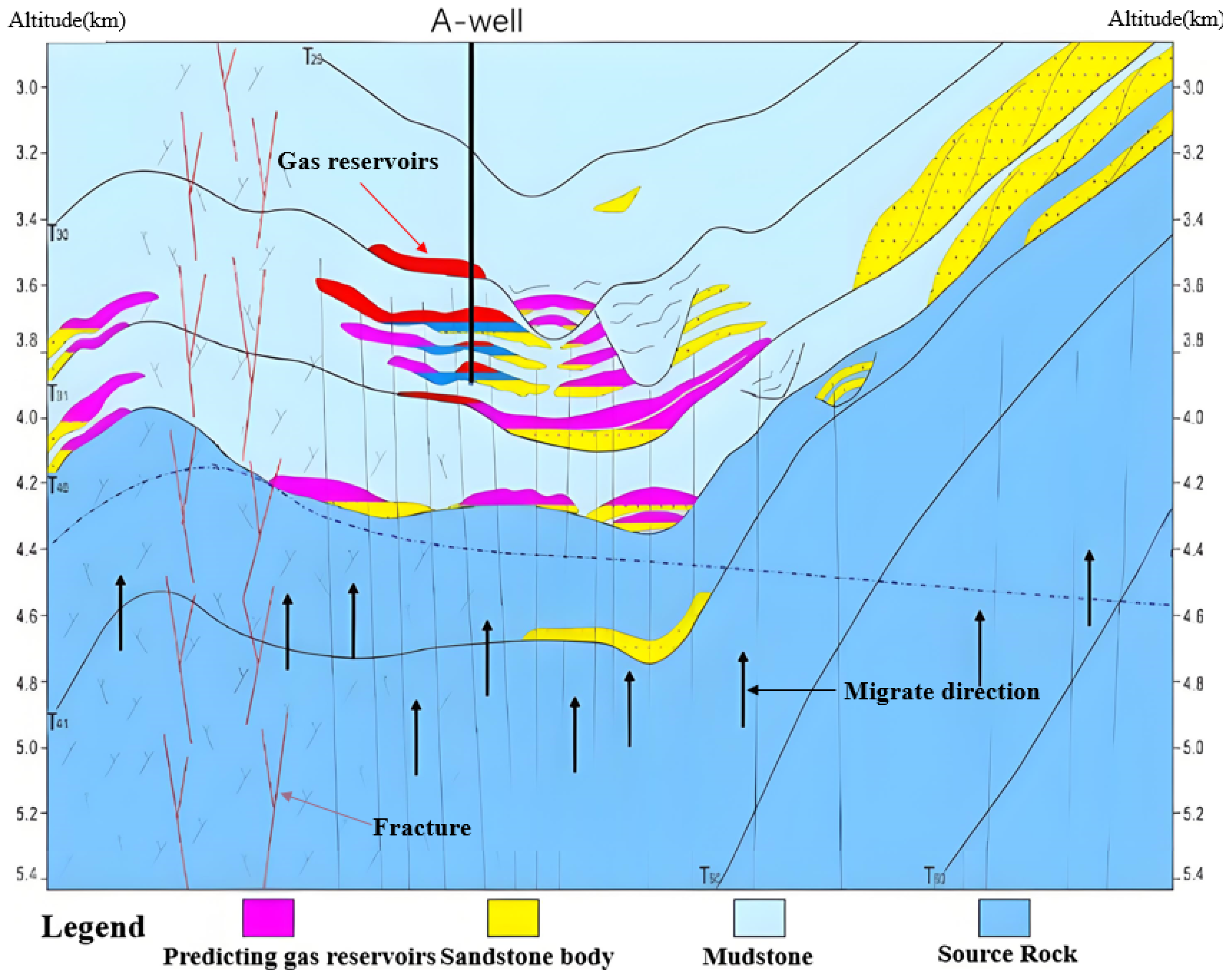
2. Anomaly Formation Pressure of Other Source Relief Type
3. Materials and Methods
3.1. Traditional Model—Bowers Method
- (1)
- Establishment of Bowers method detection model
- (2)
- Determination of Model Parameters
- (3)
- Characteristics of the method
3.2. Traditional Model—Eaton Method
- (1)
- Model Introduction
- (2)
- Normal compaction trend line
3.3. Neural Network Prediction Method
- (1)
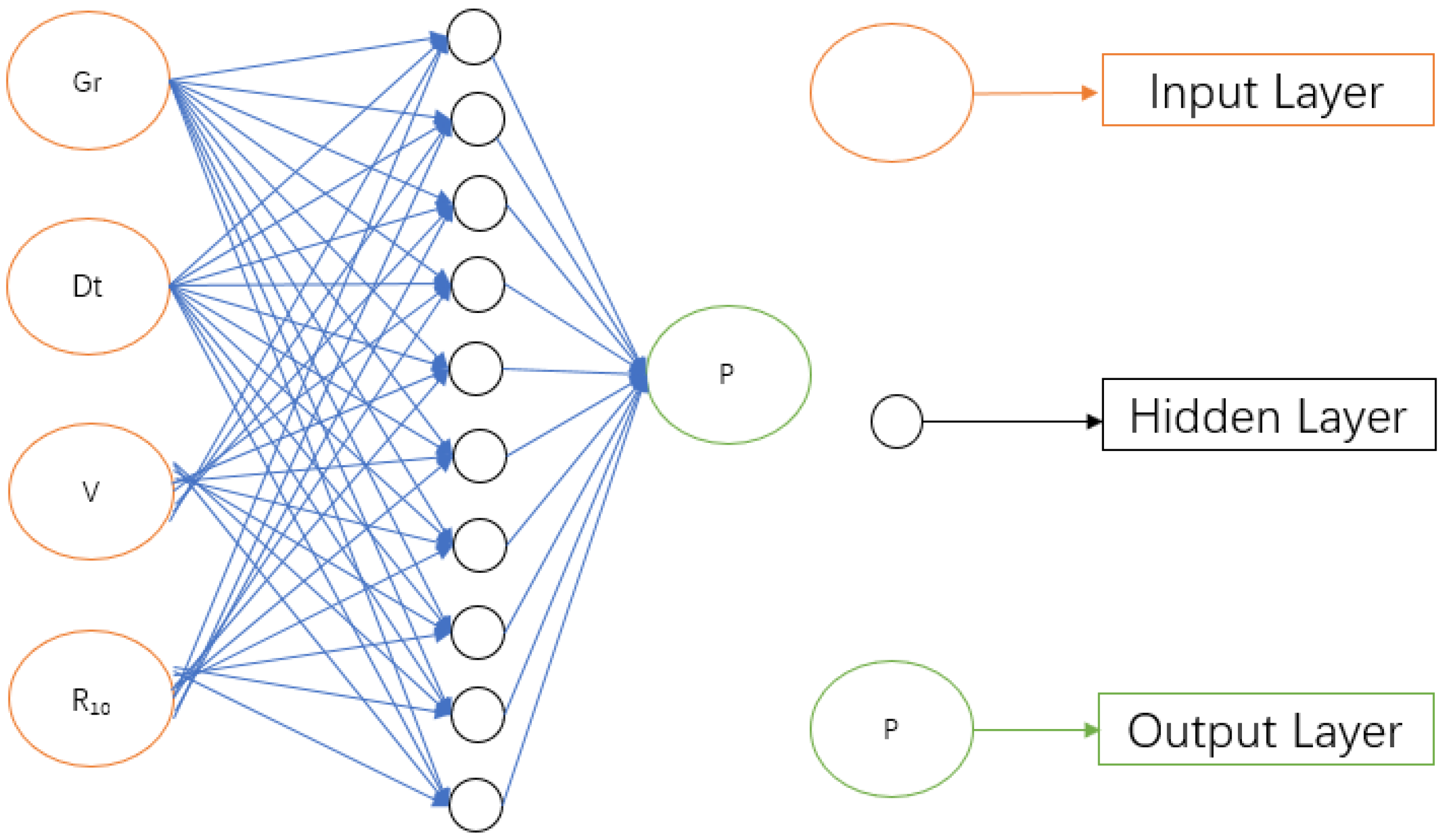
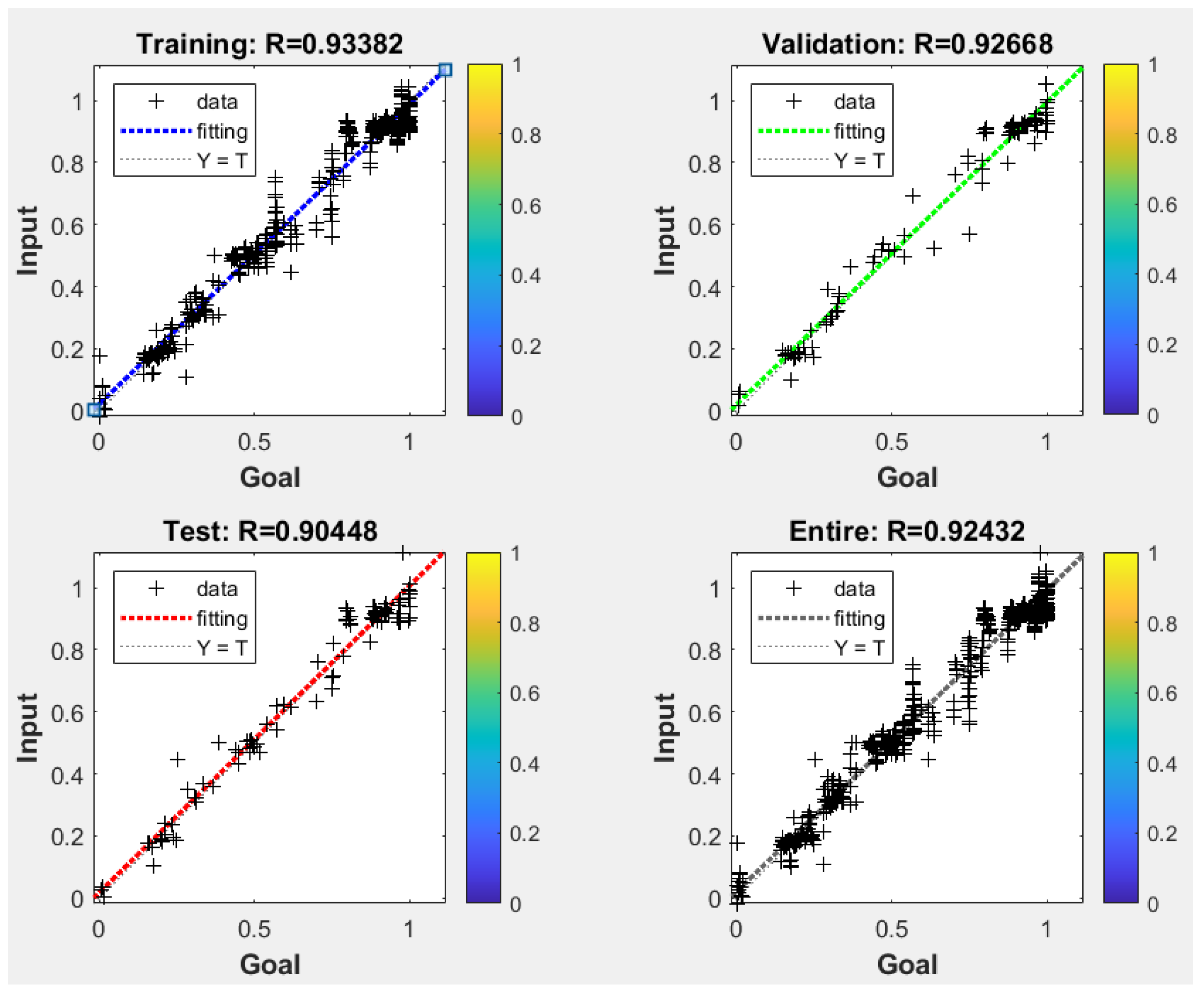
- Establishment of Neural Network Model
- (2)
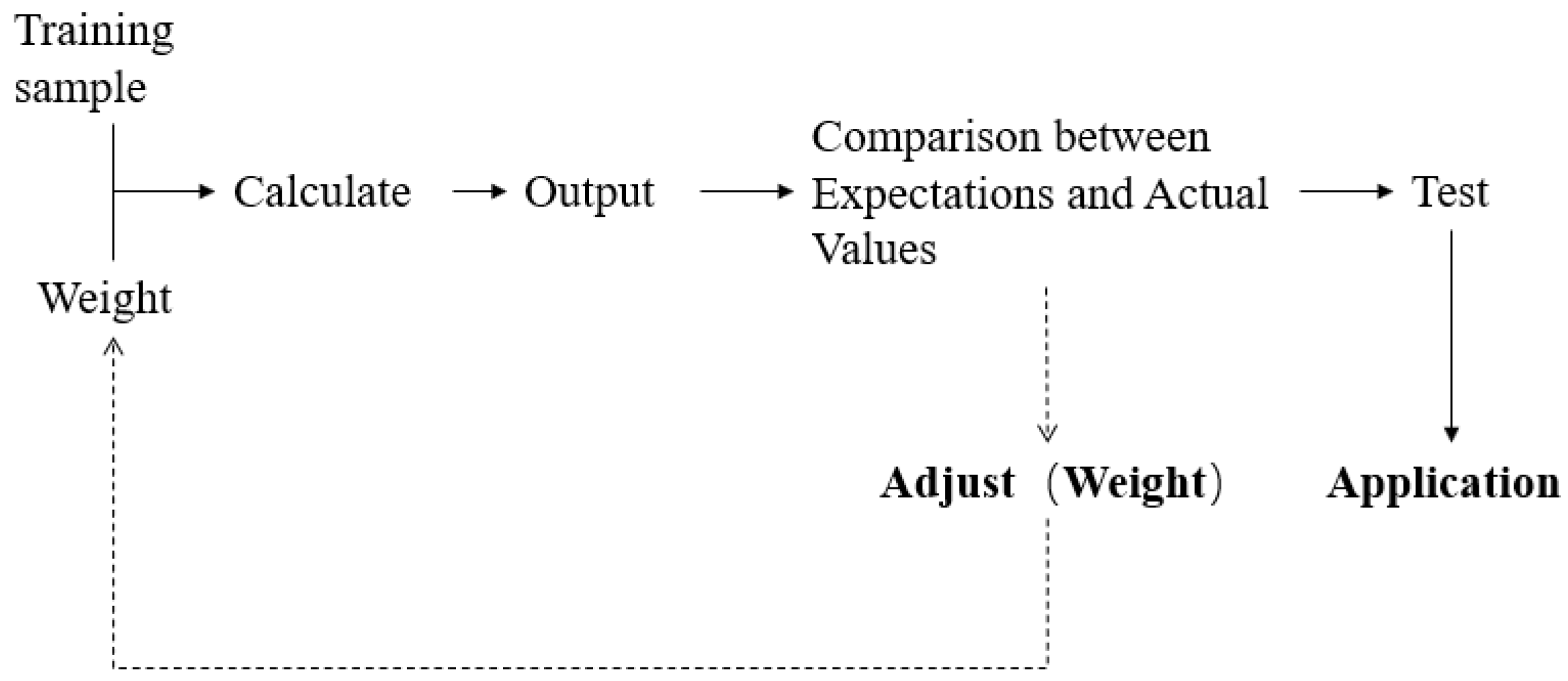
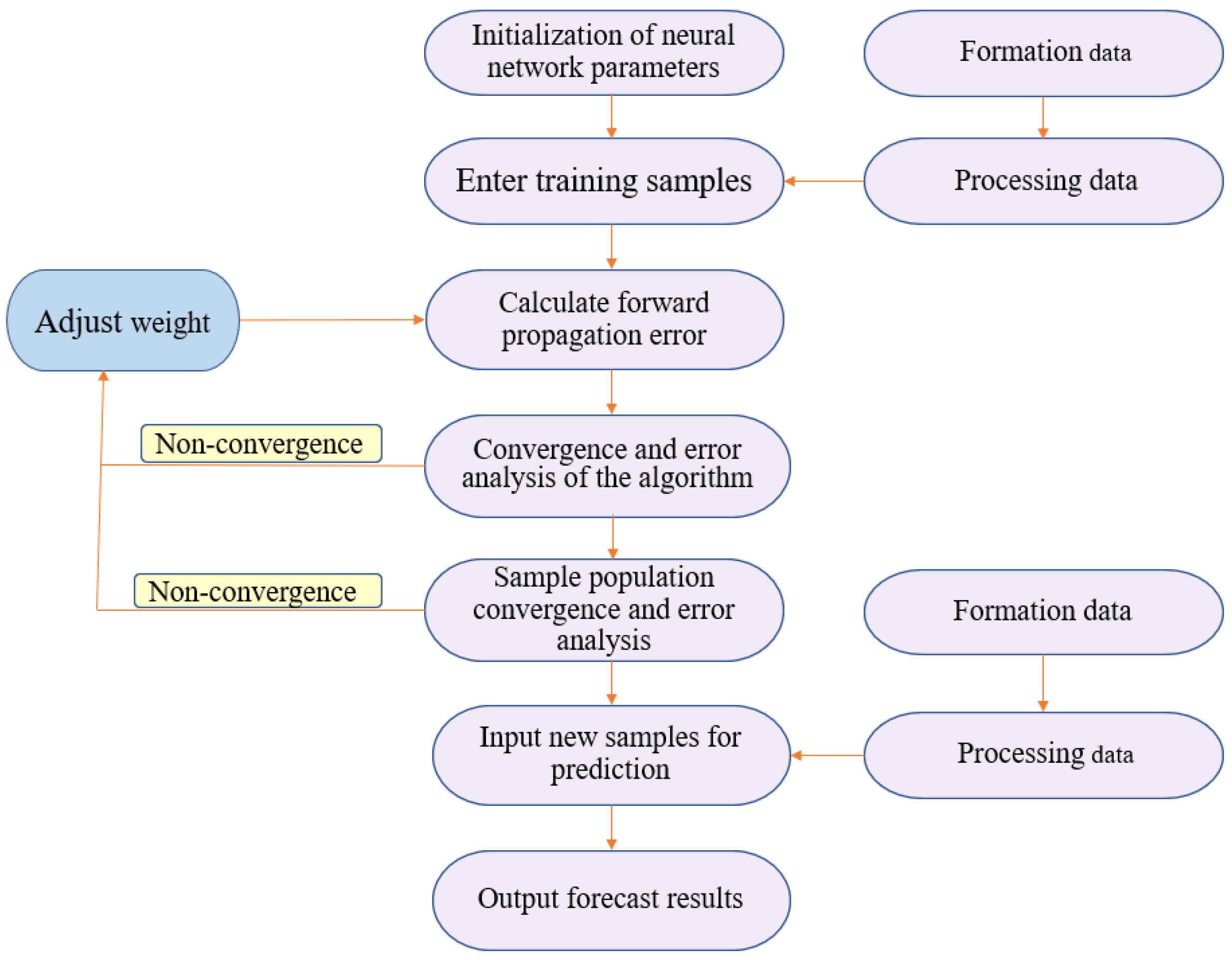
- Neural Network Workflow
- (3)
- The Limitations of Using BPNNs
4. Data Processing and Application Analysis
4.1. Data Cleaning
4.2. Data Standardization Processing
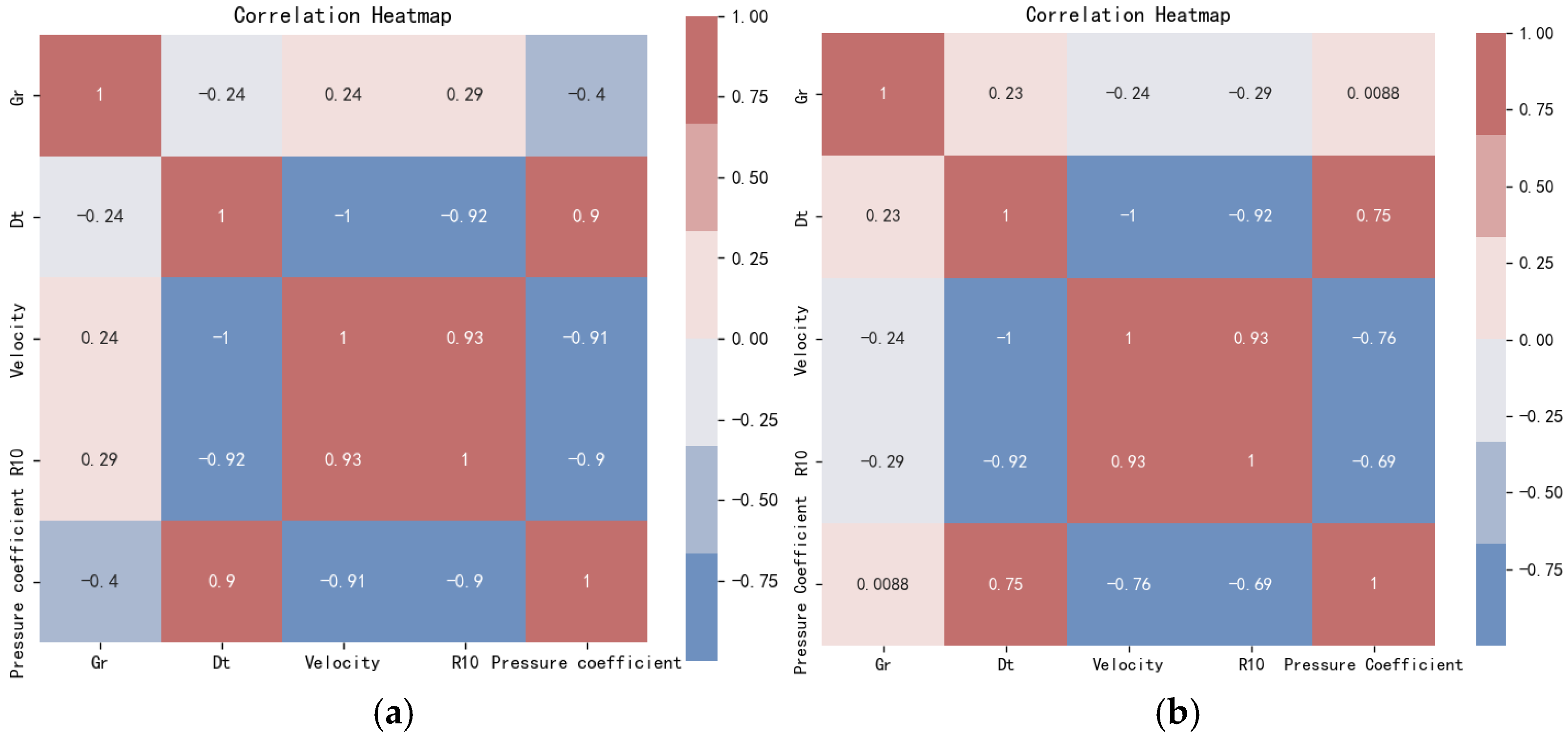
4.3. Correlation Analysis
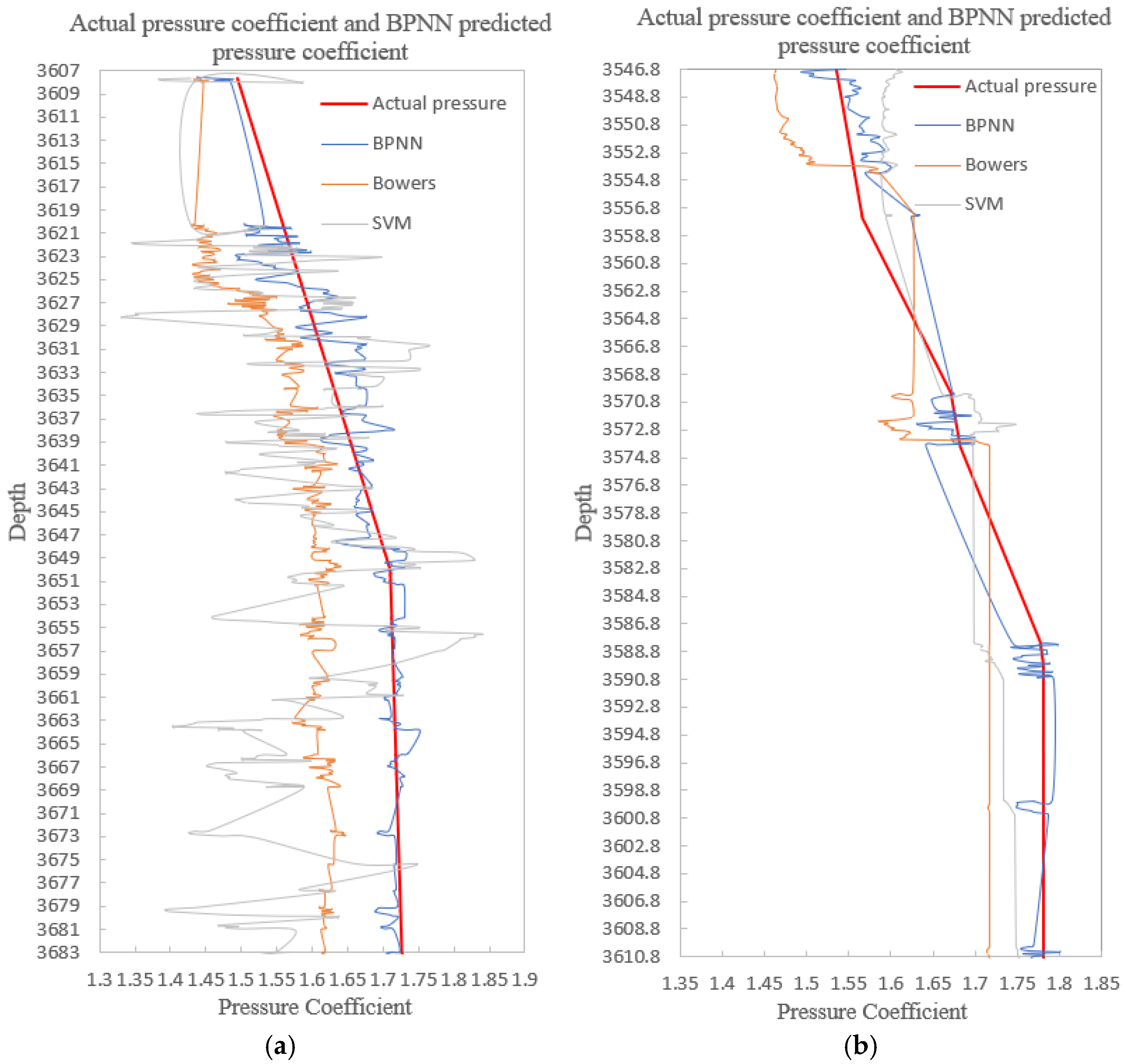
4.4. Example Applications
5. Discussion
6. Summary and Conclusions
- (1)
- Most stages of oil and gas exploration and development require precise prediction of formation pressure. Empirical and artificial intelligence methods have been developed to predict formation pressure. This study highlights the potential of the BP neural network (BPNN) in predicting the anomaly formation pressure of relief type and demonstrates sufficient effectiveness in prediction.
- (2)
- The correlation between logging parameters and the data of formation pressure of relief type indicates a good correlation between logging parameters such as GR, Dt, Velocity, and R10 and formation pressure of relief type. They are selected as input neurons. Define the number of neurons in the hidden layer as 10 through multiple optimization methods. The iteration selection is 42 to minimize the average absolute error of the validation data.
- (3)
- Based on the research results, a BP neural network model was trained using the provided data on the decrease in downhole pressure to accurately predict anomaly pore pressure, resulting in an AAPE of 4.22% and an R of 0.875. When applying the equations extracted by the model to well B in the same area, further testing was conducted on the data obtained from the same training well, resulting in a predicted pore pressure of AAPE of 5.44% and R of 0.864.
- (4)
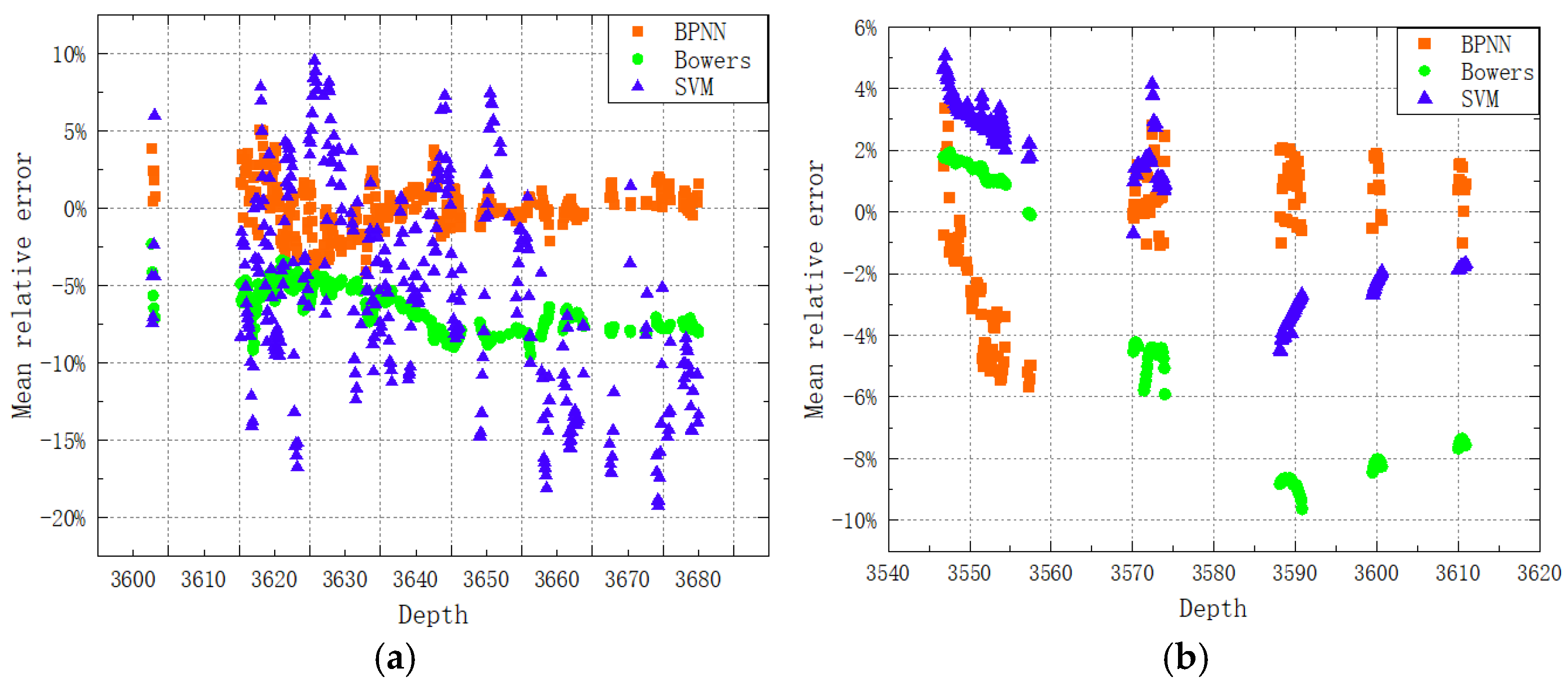
- Using the BP neural network to predict pore pressure in anomaly formations with pressure relief from other sources is a relatively new method. When multiple possible factors affect the formation’s pore pressure, using BP neural network processing has significant advantages. The proposed model has several advantages in terms of accuracy and universality. Firstly, it can handle nonlinear and complex relationships between input and output variables. Secondly, it is necessary to accurately predict the formation pore pressure values of relief type through this model, as it can optimize drilling parameters such as mud weight, significantly reducing drilling costs. At the same time, comparing and observing the graph, it is found that the BPNN model has substantially better prediction performance than the traditional towers model and can better meet engineering needs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Law, B.E.; Ulmishek, G.F.; Slavin, V.I. Abnormal Pressures in Hydrocarbon Environments. In AAPG Memoir 70; AAPG: Tulsa, OK, USA, 1998. [Google Scholar]
- Ernanda; Primasty, A.Q.T.; Akbar, K.A. Detecting Overpressure Using the Eaton and Equivalent Depth Methods in Offshore Nova Scotia, Canada. IOP Conf. Ser. Earth Environ. Sci. 2018, 132, 012016. [Google Scholar] [CrossRef]
- Gao, G.; Huang, Z.; Wang, Z. Study on the mechanisms of the formation of formation abnormal high-pressure. J. Xi’an Shiyou Univ. (Nat. Sci. Ed.) 2001, 20, 17. [Google Scholar]
- Fan, H. Research and Application of a New Method for Predicting and Detecting Formation Pore Pressure. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2001. [Google Scholar]
- Law, B.E.; Spenser, C.W. Abnormal Pressures in Hydrocarbon Environments; AAPG: New York, NY, USA, 1998; pp. 1–11. [Google Scholar]
- Neuzil, C.E. Abnormal pressures as hydrodynamic phenomena. Am. J. Sci. 1995, 295, 742–786. [Google Scholar] [CrossRef]
- Li, W.; Chen, Z.; Huang, P.; Yu, Z.; Min, L.; Lu, X. Formation of overpressure system and its relationship with the distribution of large gas fields in typical foreland basins in central and western China. Pet. Explor. Dev. 2021, 48, 536–548. [Google Scholar] [CrossRef]
- GB/T 26979—2011; China National Standardization Administration Committee. The Classification of Natural Gas Pool. Standards Press of China: Beijing, China, 2011.
- Li, M. Oil and Gas Migration; Petroleum Industry Press: Beijing, China, 2006; pp. 4–11. [Google Scholar]
- Adams, N.; Charrier, T. Drilling Engineering: A Complete Well Planning Approach; PennWell Publishing Company: Tulsa, OK, USA, 1985. [Google Scholar]
- Rabia, H. Well Engineering & Construction; Entrac Consulting: Houston, TX, USA, 2001; ISBN 9780954108700. [Google Scholar]
- Legkokonets, V.A.; Islamov, S.R.; Mardashov, D.V. Multifactor Analysis of Well Killing Operations on Oil and Gas Condensate Field with a Fractured Reservoir. In Proceedings of the International Forum-Contest of Young Researchers: Topical Issues of Rational Use of Mineral Resources; Taylor & Francis: London, UK, 2019; pp. 111–118. [Google Scholar]
- Islamov, S.; Bondarenko, A.; Korobov, G.; Podoprigora, D. Complex Algorithm for Developing Effective Kill Fluids for Oil and Gas Condensate Reservoirs. Int. J. Civ. Eng. Technol. 2019, 10, 2697–2713. [Google Scholar]
- Ganguli, S.S.; Sen, S. Investigation of Present-Day in-Situ Stresses and Pore Pressure in the South Cambay Basin, Western India: Implications for Drilling, Reservoir Development and Fault Reactivation. Mar. Pet. Geol. 2020, 118, 104422. [Google Scholar] [CrossRef]
- Radwan, A.E.; Abudeif, A.M.; Attia, M.M.; Mohammed, M.A. Pore and Fracture Pressure Modeline Using Direct and Indirect Methods in Badri Field, Gulf of Suez, Egypt. J. Afr. Earth Sci. 2019, 156, 133–143. [Google Scholar] [CrossRef]
- Singha, D.K.; Chatterjee, R.; Sen, M.K.; Sain, K. Pore Pressure Prediction in Gas-Hydrate Bearing Sediments of Krishna-Godavari Basin, India. Mar. Geol. 2014, 357, 1–11. [Google Scholar] [CrossRef]
- Zhang, J. Pore Pressure Prediction from Well Logs: Methods, Modifications, and New Approaches. Earth-Sci. Rev. 2011, 108, 50–63. [Google Scholar] [CrossRef]
- Xu, B.; Xu, H.; Yu, B.; Jing, H.; Guo, J. Application of Abnormal Formation Pressure Prediction Technologies in Junggar Basin. Xinjiang Pet. Geol. 2015, 36, 597–601. [Google Scholar]
- Kiss, A.; Fruhwirth, R.K.; Pongratz, R.; Maier, R.; Hofstätter, H. Formation breakdown pressure prediction with artificial neural networks. In Proceedings of the SPE International Hydraulic Fracturing Technology Conference and Exhibition, Muscat, Oman, 16–18 October 2018. [Google Scholar]
- Qian, L.; Wang, X.; Li, F.; Li, J.; Wang, J.; Qu, Y. Fillippone formula combined with equivalent medium theory to predict formation pressure. Oil Geophys. Prospect. 2018, 53, 224–229. [Google Scholar]
- Kun, W.; Jia, L.; Lin, Y.; Wei, Y.; Wu, K.; Li, J.; Chen, Z. Artificial neural network accelerated flash calculation for compositional simulations. In Proceedings of the SPE Reservoir Simulation Conference, Galveston, TX, USA, 10–11 April 2019. [Google Scholar]
- Li, Y.; Sun, W.; He, W.; Yang, Y.; Zhang, X.; Yan, Y. Prediction method of shale formation pressure based on pre-stack inversion. Lithol. Reserv. 2019, 31, 113–121. [Google Scholar]
- Clifford, A.; Aminzadeh, F. Gas detection from absorption attributes and amplitude versus offset with artificial neural networks in grand bay field. In SEG Technical Program Expanded Abstracts 2011; Society of Exploration Geophysicists: Houston, TX, USA, 2011; pp. 375–380. [Google Scholar]
- Ogiesoba, O.; Ambrose, W. Ambrosew Seismic attributes investigation of depositional environments and hydrocarbon sweet-spot distribution in Serbin Field, TaylorGroup, Central Texas. In SEG Technical Program Expanded Abstracts 2017; Society of Exploration Geophysicists: Houston, TX, USA, 2011; pp. 2274–2278. [Google Scholar]
- Fogg, A.N. Petro-seismic classification using neural networks: UK onshore. In SEG Technical Program Expanded Abstracts 2017; Society of Exploration Geophysicists: Houston, TX, USA, 2011; pp. 1426–1429. [Google Scholar]
- Zhang, T.F.; Tilke, P.; Dupont, E.; Zhu, L.C.; Liang, L.; Bailey, W. Generating geologically realistic 3D reservoir facies models using deep learning of sedimentary architecture with generative adversarial networks. Pet. Sci. 2019, 16, 541–549. [Google Scholar] [CrossRef]
- Noshi, C.I.; Eissa, R.M.; Abdallar, M. An intelligent data driven approach for production prediction. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019; p. OTC-29243-MS. [Google Scholar]
- Rui, Z.; Hu, J. Production performance forecasting method based on multivariate time series and vector autoregressive machine learning model for waterflooding reservoirs. Pet. Explor. Dev. 2021, 48, 175–184. [Google Scholar]
- Jia, D.L.; Guo, T.; Pei, X.H.; Zhang, J.; Ye, Q.; Jin, X.G.; Tang, X. Intelligent waterflooding development of high-permeability reservoirs at the late development stage. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 29–31 October 2018; p. SPE-192067MS. [Google Scholar]
- Zang, K.; Zhao, X.; Zhang, L.; Zhang, H.; Wang, H.; Chen, G.; Zhao, M.; Jiang, Y.; Yao, J. Current status and prospect for the research and application of big data and intelligent optimization methods in oilfield development. J. China Univ. Pet. (Ed. Nat. Sci.) 2020, 44, 28–38. [Google Scholar]
- Liao, G.; Guo, S.; Wang, C.; Shen, Y.; Gao, Y. Pressure Relief-Type Overpressure Distribution Prediction Model Based on Seepage and Stress Coupling. Processes 2023, 11, 480. [Google Scholar] [CrossRef]
- Adiche, S.; Larbi, M.; Toumi, D.; Bouddou, R.; Bajaj, M.; Bouchikhi, N.; Zaitsev, I. Advanced control strategy for AC microgrids: A hybrid ANN-based adaptive PI controller with droop control and virtual impedance technique. Sci. Rep. 2024, 14, 31057. [Google Scholar] [CrossRef]
- Liu, T.; Ye, X.; Cheng, L.; Hu, Y.; Guo, D.; Huang, B.; Li, Y.; Su, J. Intelligent Pressure Monitoring Method of BP Neural Network Optimized by Genetic Algorithm: A Case Study of X Well Area in Yinggehai Basin. Processes 2024, 12, 2439. [Google Scholar] [CrossRef]
- Sarra, Z.; Bouziane, M.; Bouddou, R.; Benbouhenni, H.; Mekhilef, S.; Elbarbary, Z.M.S. Intelligent control of hybrid energy storage system using NARX-RBF neural network techniques for microgrid energy management. Energy Rep. 2024, 12, 5445–5461. [Google Scholar] [CrossRef]
- Zaidi, S.; Meliani, B.; Bouddou, R.; Belhadj, S.M.; Bouchikhi, N. Comparative study of different types of DC/DC converters for PV systems using RBF neural network-based MPPT algorithm. J. Renew. Energ. 2024, 1, 13. [Google Scholar] [CrossRef]
- Berrouk, A.S.; Nandakumar, K. Special issue section on process system safety and risk engineering. Can. J. Chem. Eng. 2024, 103, 4–7. [Google Scholar] [CrossRef]
- Abdulmalek, A.S.; Elkatatny, S.; Abdulraheem, A.; Mahmoud, M.; Abdulwahab, Z.A.; Mohamed, I.M. Pore pressure prediction while drilling using fuzzy logic. In Proceedings of the SPE kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 23–26 April 2018; p. SPE-192318-MS. [Google Scholar]
- Hadi, F.; Eckert, A.; Almahdawi, F. Real-time pore pressure prediction in depleted reservoirs using regression analysis and artificial neural networks. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 18–21 March 2019; p. SPE-194851-MS. [Google Scholar]
- Rashidi, M.; Hajipour, M.; Asadi, A. Correlation between static and dynamic elastic modulus of limestone formations using artificial neural networks. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Rashidi, M.; Asadi, A. An artificial intelligence approach in estimation of formation pore pressure by critical drilling data. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Fan, H. Analysis Methods and Applications of Abnormal Formation Pressures; Science Press: Beijing, China, 2016. [Google Scholar]
- Bowers, G.L. Pore pressure estimation from velocity data: Accounting for overpressure mechanisms besides undercompaction. SPE Drill. Competion 1995, 10, 89–95. [Google Scholar] [CrossRef]
- Eaton, B.A. The equation for geopressure prediction from well logs. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, Dallas, TX, USA, 28 September–1 October 1975; p. SPE-5544-MS. [Google Scholar]
- Gamal, H.; Abdelaal, A.; Elkatatny, S. Machine learning models for equivalent circulating density prediction from drilling data. ACS Omega 2021, 8, 4363. [Google Scholar] [CrossRef] [PubMed]
- Asadisaghandi, J.; Pejman, T. Comparative evaluation of back-propagation neural network learning algorithms and empirical correlations for prediction of oil PVT properties in Iran oilfields. J. Pet. Sci. Eng. 2011, 78, 464–475. [Google Scholar] [CrossRef]

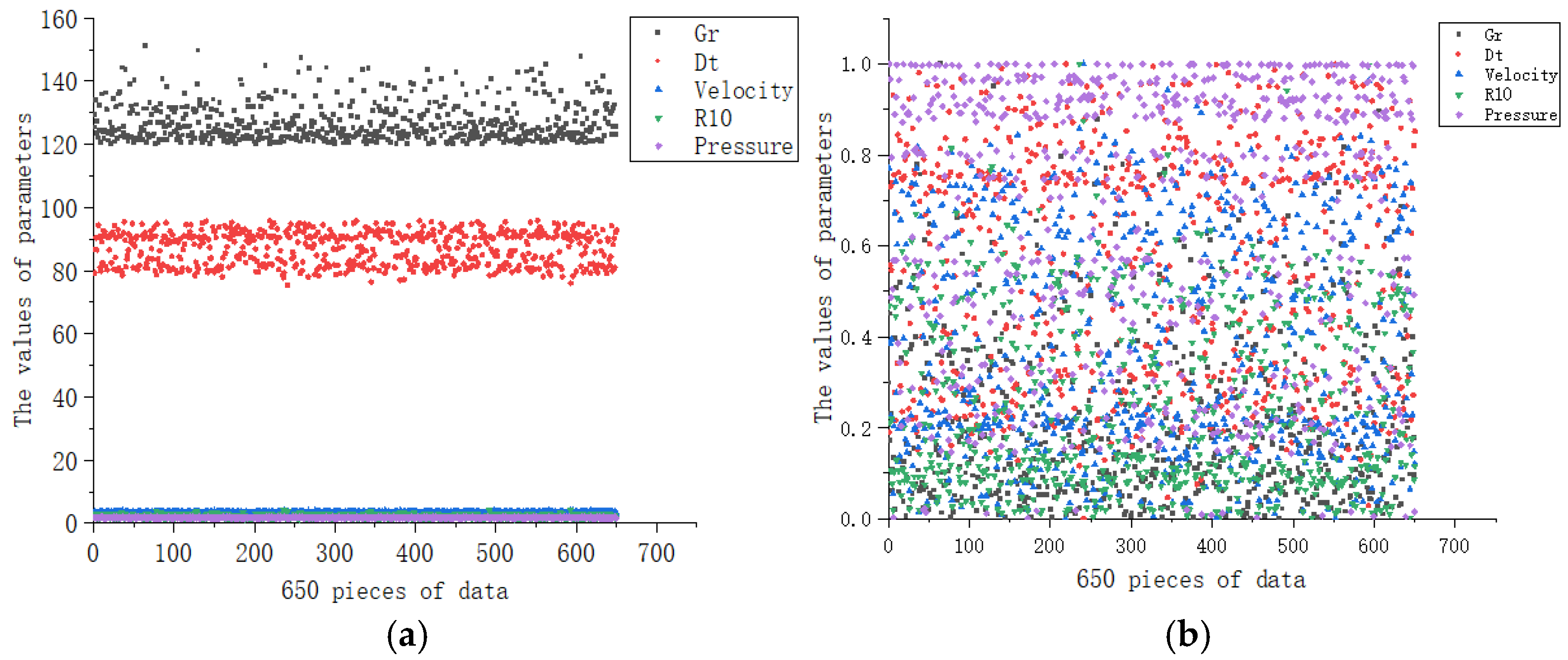

| Statistical Parameter | Depth (m) | Gr (dpi) | Dt (μs/ft) | Vp (km/s) | R10 (Ω·m) | Pressure Coefficient |
|---|---|---|---|---|---|---|
| Maximum | 3930.9 | 164.02 | 107.41 | 4.59 | 8.39 | 1.93 |
| Minimum | 2552.6 | 120.01 | 66.40 | 2.84 | 0.72 | 1.48 |
| Mean | 3118.9 | 128.07 | 95.79 | 3.21 | 1.79 | 1.83 |
| Standard deviation | 313.21 | 6.5833 | 7.91 | 0.31 | 0.82 | 0.09 |
| Skewness | 0.3205 | 1.6178 | −1.52 | 1.84 | 3.90 | −1.20 |
| Kurtosis | 2.4111 | 6.6667 | 4.52 | 5.64 | 21.63 | 3.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Li, Y.; Yu, H.; Shen, S.; Chen, Z.; Li, D.; Liang, X.; Huang, Z. Pressure Relief-Type Overpressure Prediction in Sand Body Based on BP Neural Network. Processes 2025, 13, 616. https://doi.org/10.3390/pr13030616
Gao Y, Li Y, Yu H, Shen S, Chen Z, Li D, Liang X, Huang Z. Pressure Relief-Type Overpressure Prediction in Sand Body Based on BP Neural Network. Processes. 2025; 13(3):616. https://doi.org/10.3390/pr13030616
Chicago/Turabian StyleGao, Yanfang, Yanchao Li, Hongyan Yu, Shijie Shen, Zupeng Chen, Dengke Li, Xuelin Liang, and Zhi Huang. 2025. "Pressure Relief-Type Overpressure Prediction in Sand Body Based on BP Neural Network" Processes 13, no. 3: 616. https://doi.org/10.3390/pr13030616
APA StyleGao, Y., Li, Y., Yu, H., Shen, S., Chen, Z., Li, D., Liang, X., & Huang, Z. (2025). Pressure Relief-Type Overpressure Prediction in Sand Body Based on BP Neural Network. Processes, 13(3), 616. https://doi.org/10.3390/pr13030616






