SPH Simulation of Gear Meshing with Lubricating Fluid–Solid Coupling and Heat-Transfer Process
Abstract
1. Introduction
2. Numerical Modeling Based on SPH
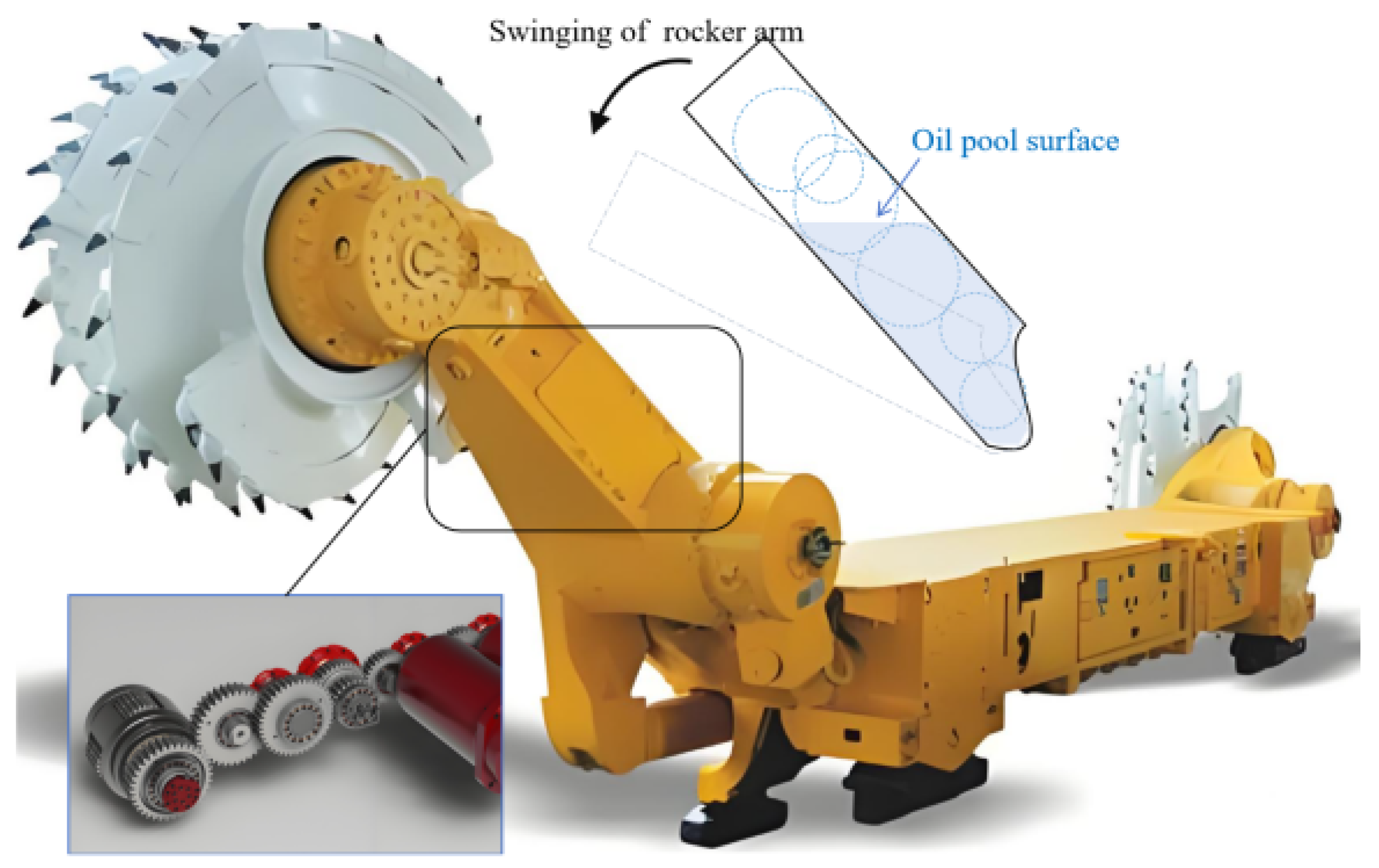
2.1. Model Description
2.2. Governing Equations of Fluid Dynamics
2.3. Rigid Body Motion Equations
2.4. Governing Equations of Thermal Dynamics
3. Model Implementation and Numerical Solution
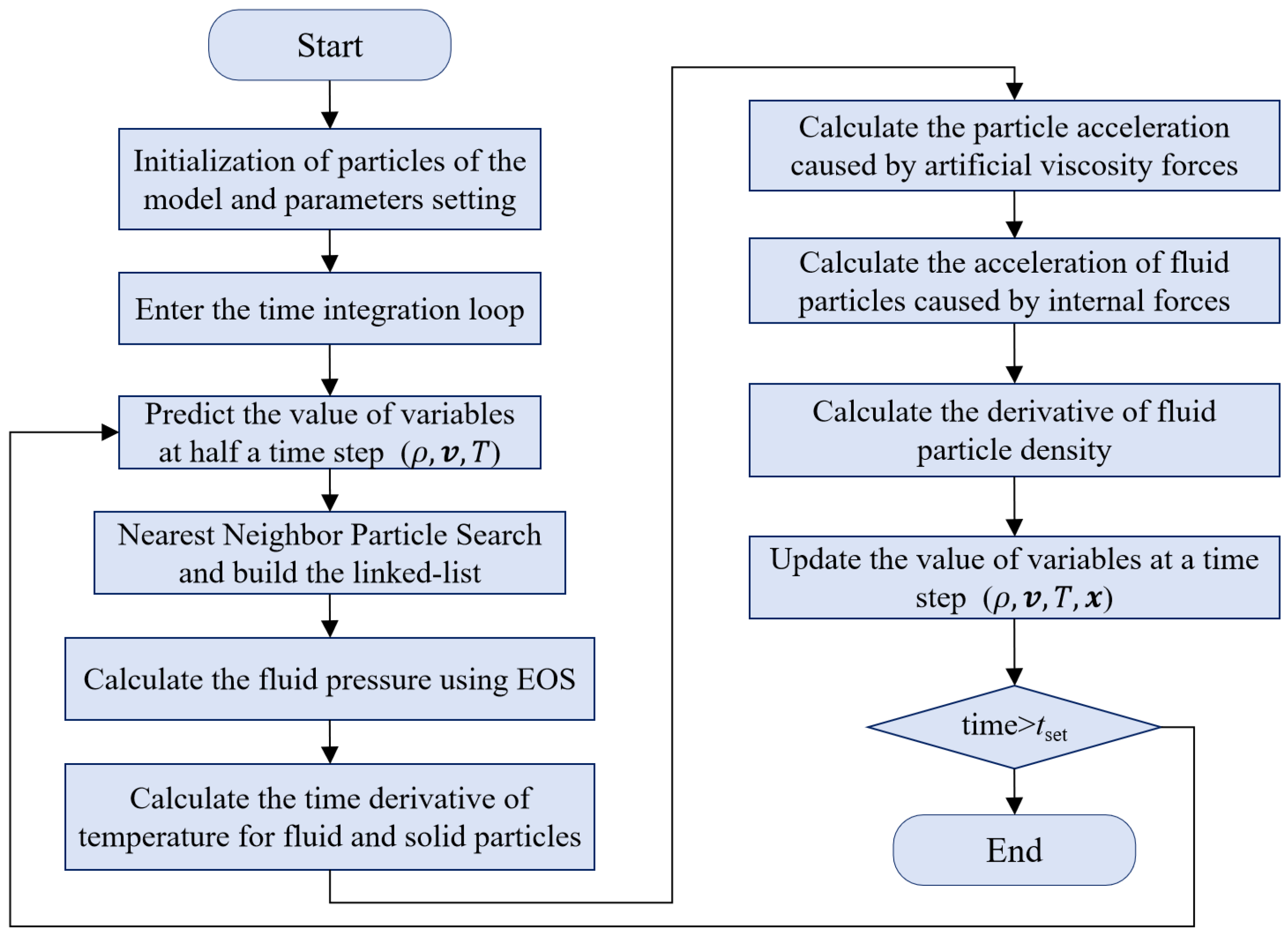
3.1. Numerical Solution Strategy
- (1)
- The gears are considered as rigid bodies, and their positions are updated according to the equations of rigid body rotation.
- (2)
- The gears are also discretized into SPH particles, which are used to discretize the thermodynamic equations. These particles possess physical properties such as temperature, mass, and density.
- (3)
- The fluid–solid coupling is achieved through the interaction between fluid particles and adjacent solid SPH particles (i.e., gear particles). The motion of the gears is according to the given rotational speed.
- (4)
- The thermal expansion characteristics of the oil and the variation of oil viscosity with temperature are not considered.
- (5)
- The heat dissipation of the gears to the air is not considered; only the heat exchange between the gears and the lubricating oil is considered, which is completed through the interaction between fluid particles and gear particles that support each other’s domains.
3.2. Time Integration Scheme
4. Results and Analysis
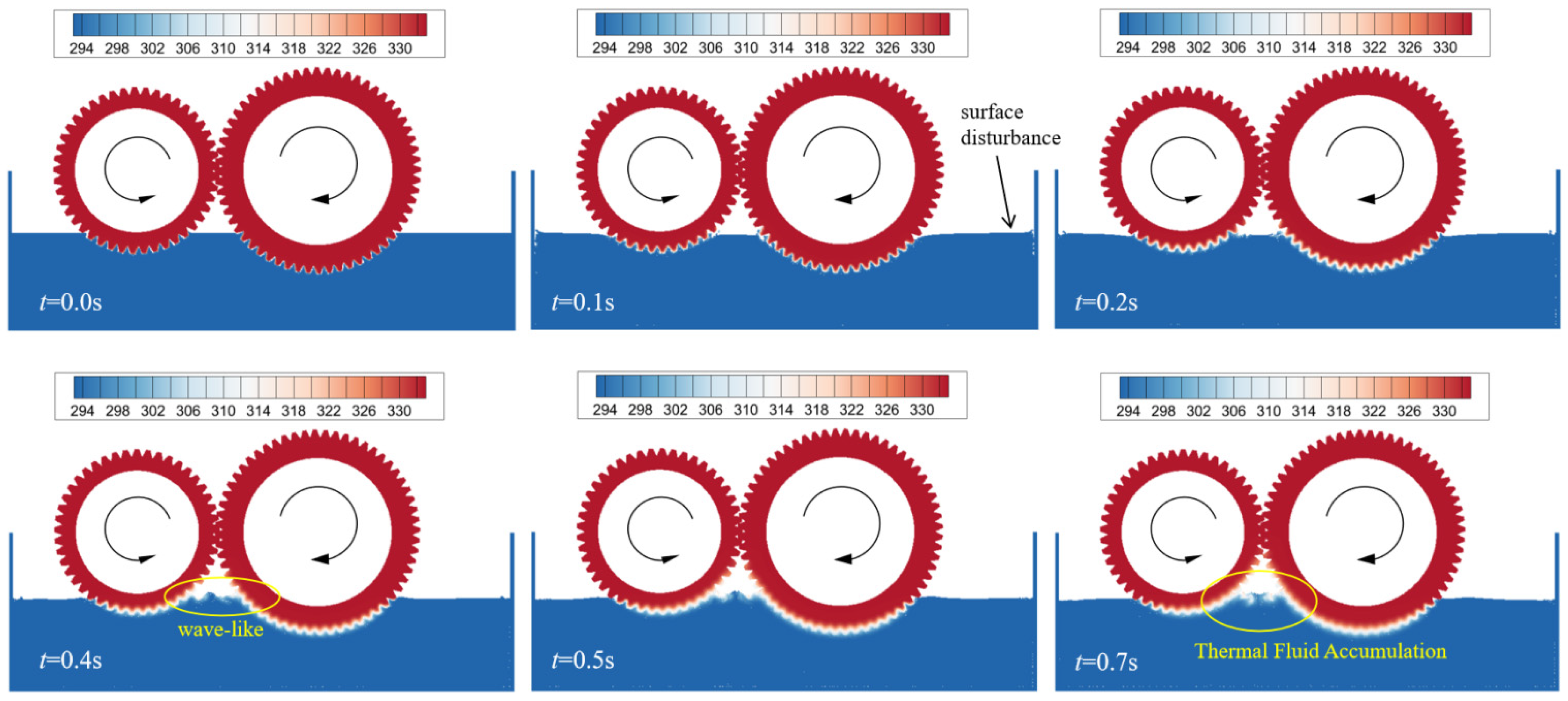
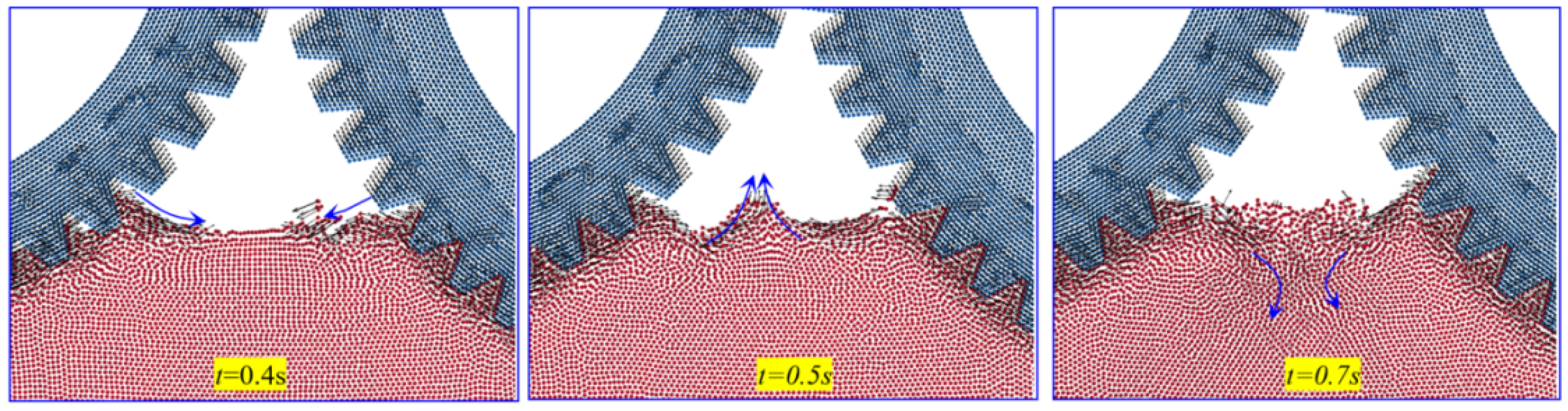
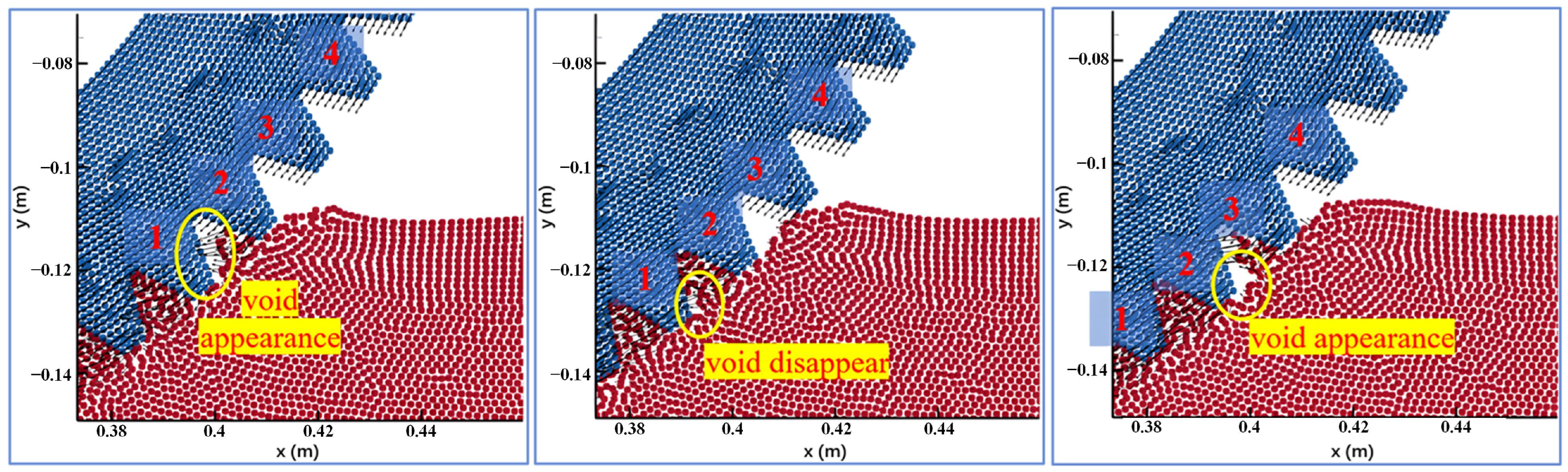
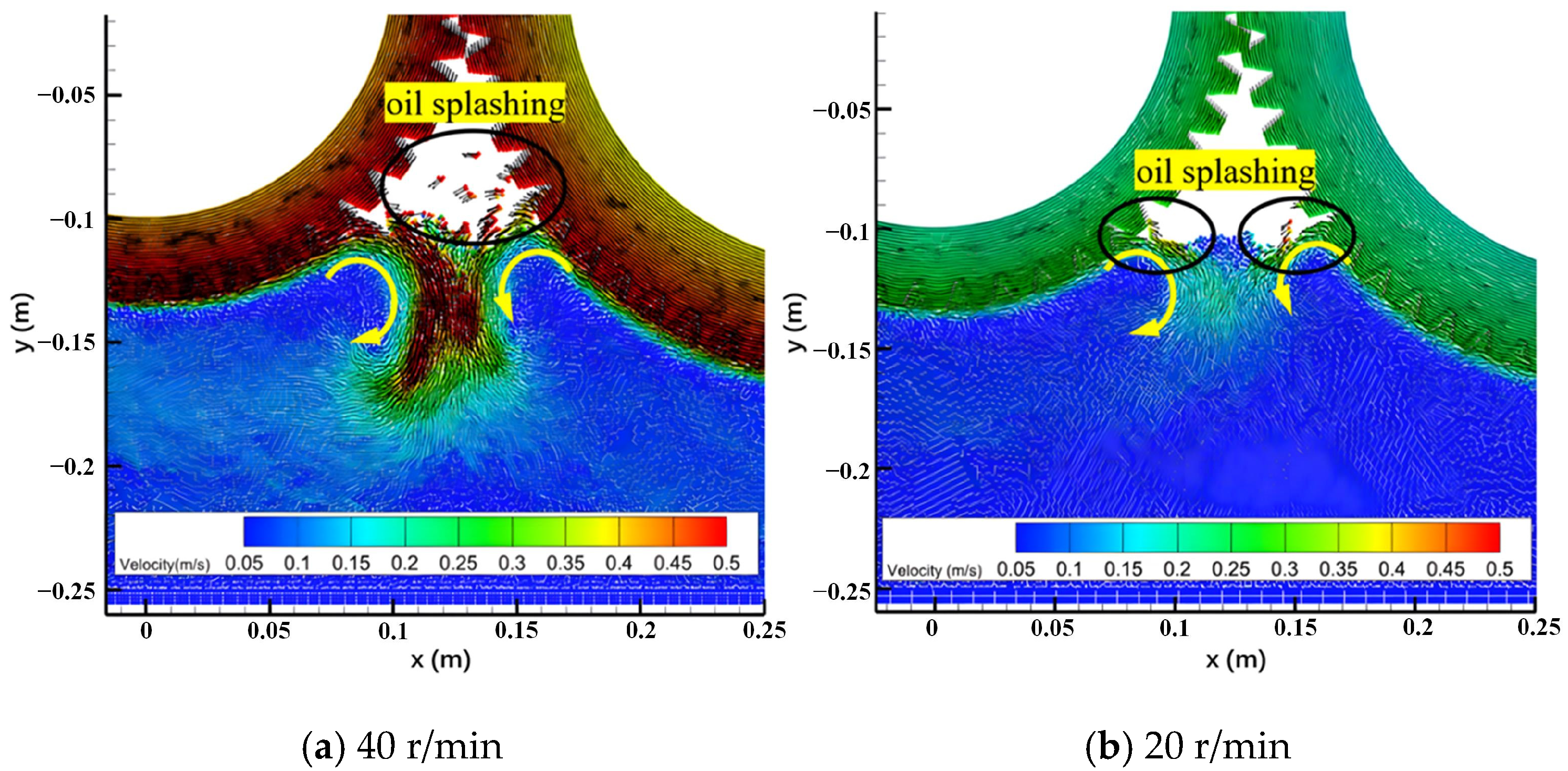
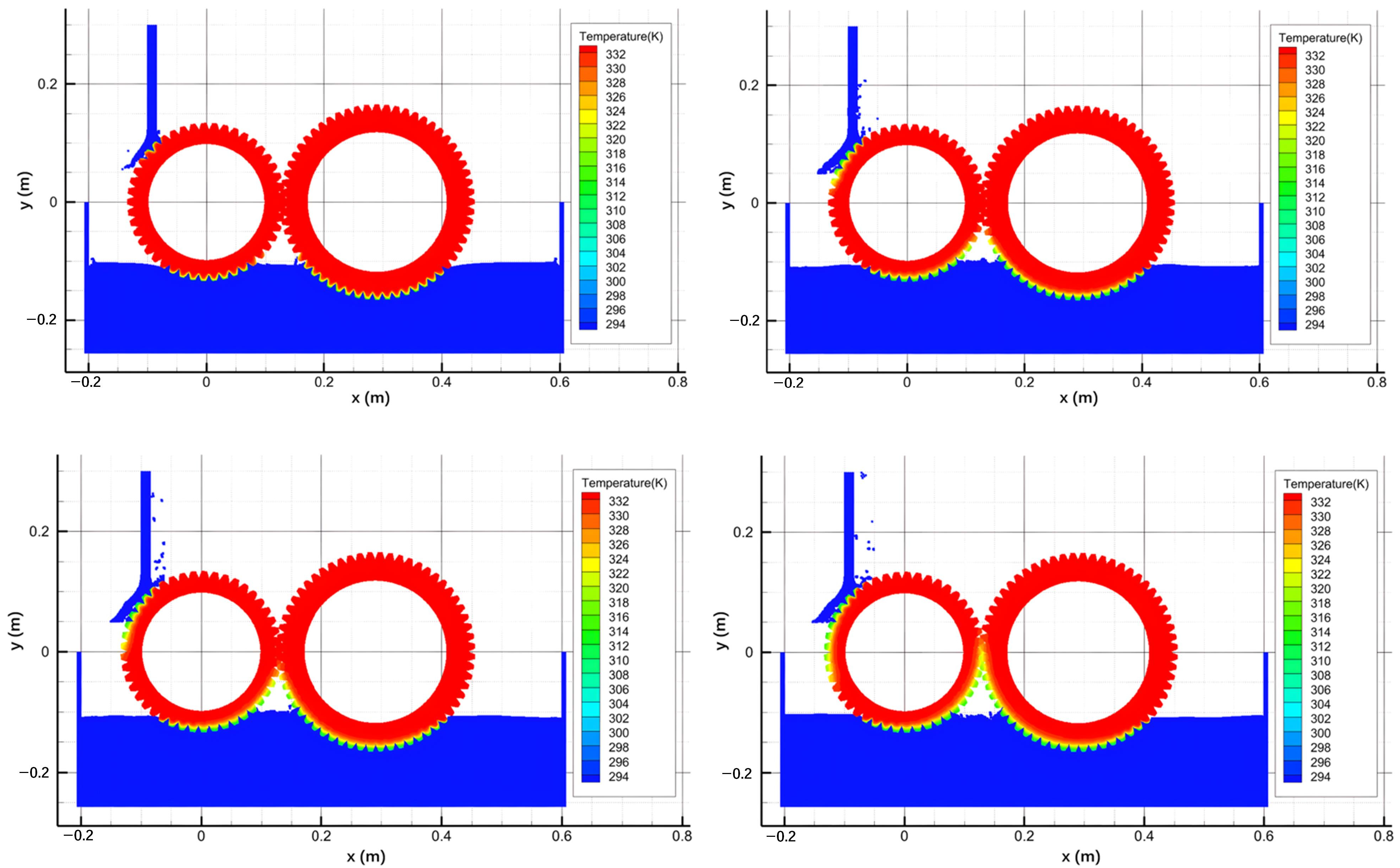
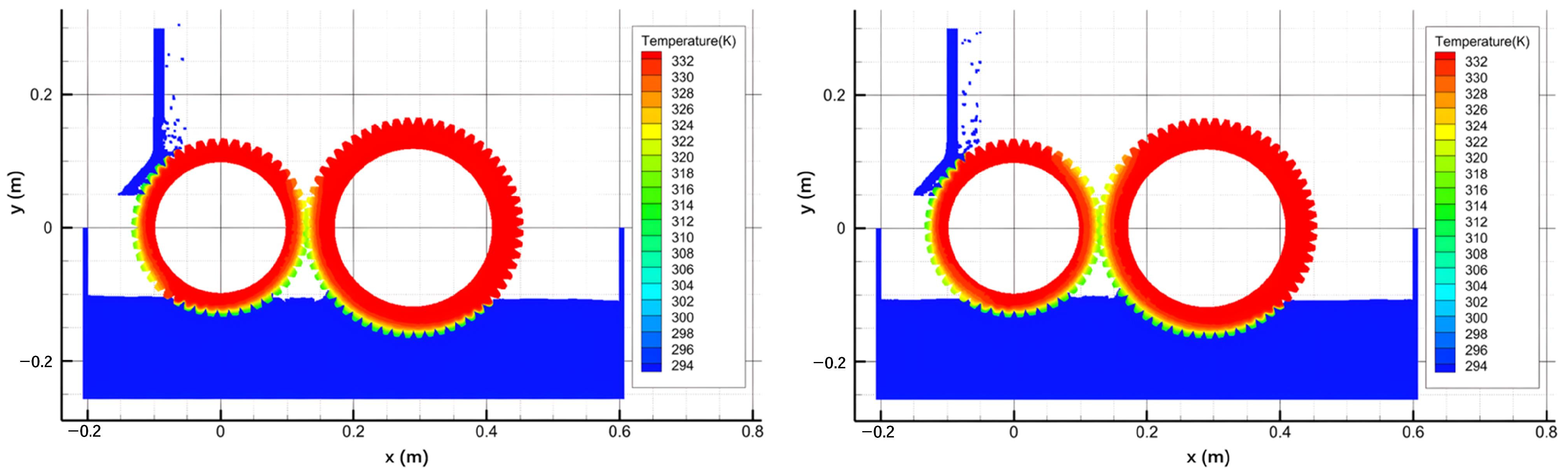
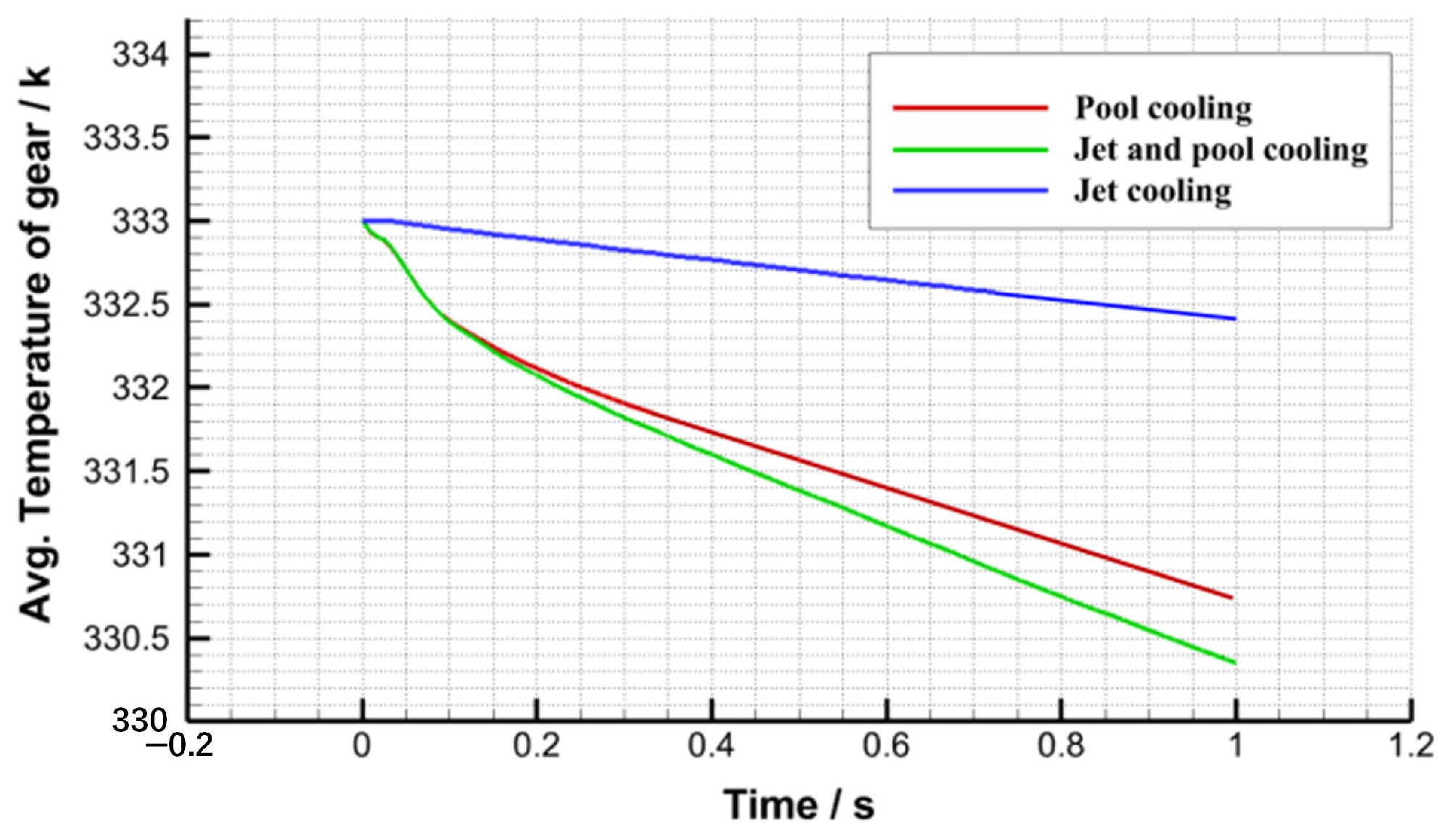
4.1. Results of Transmission Gear with Oil Pool Cooling
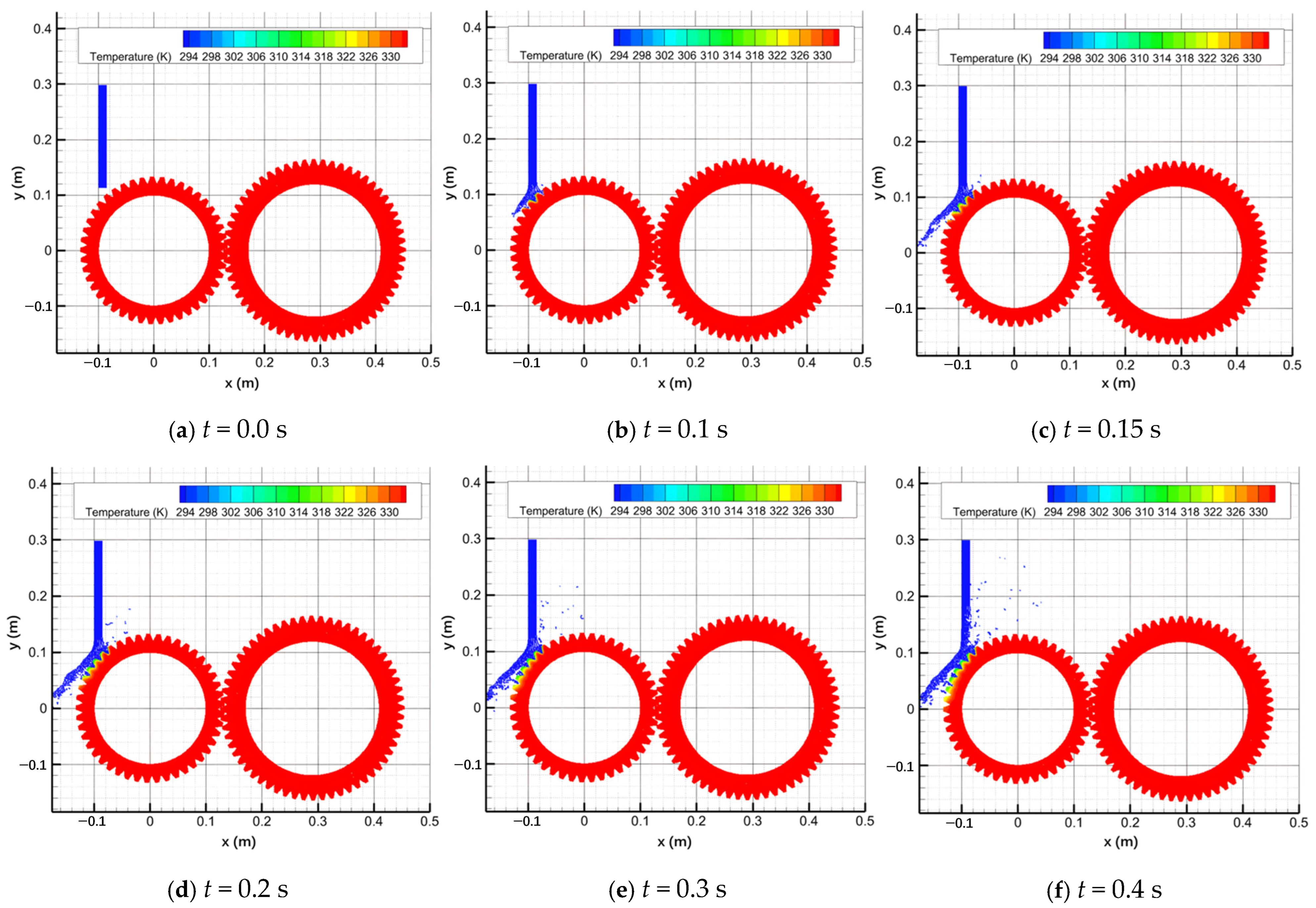
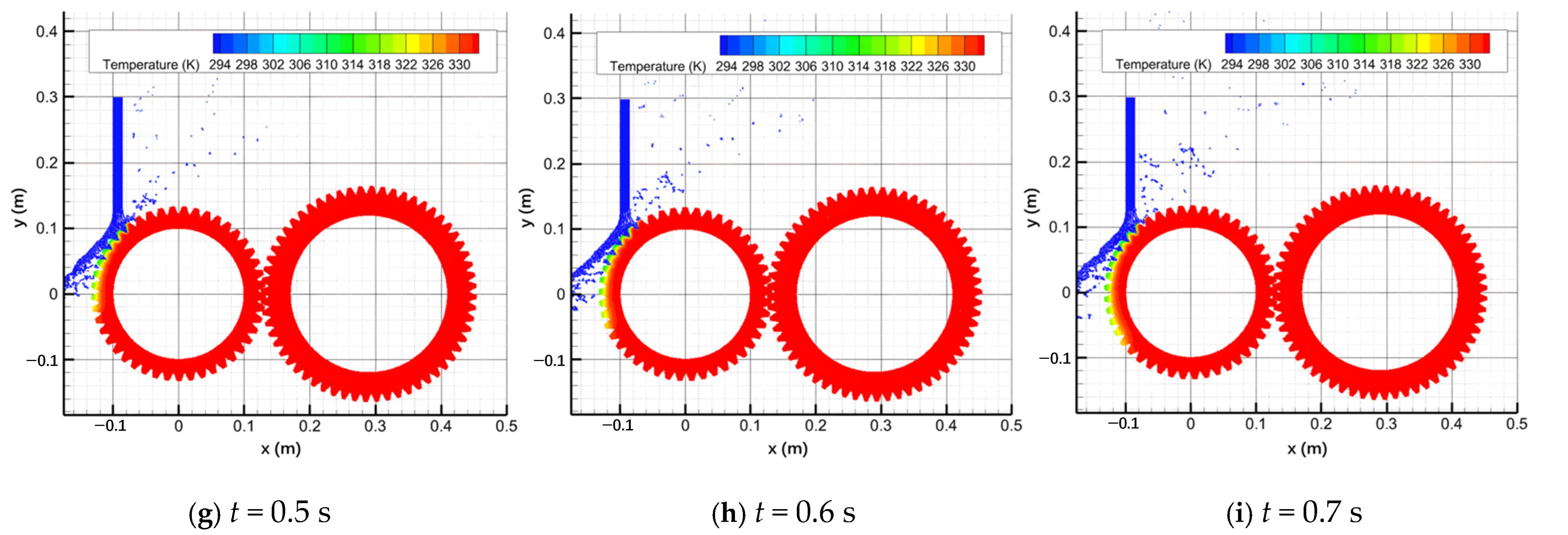
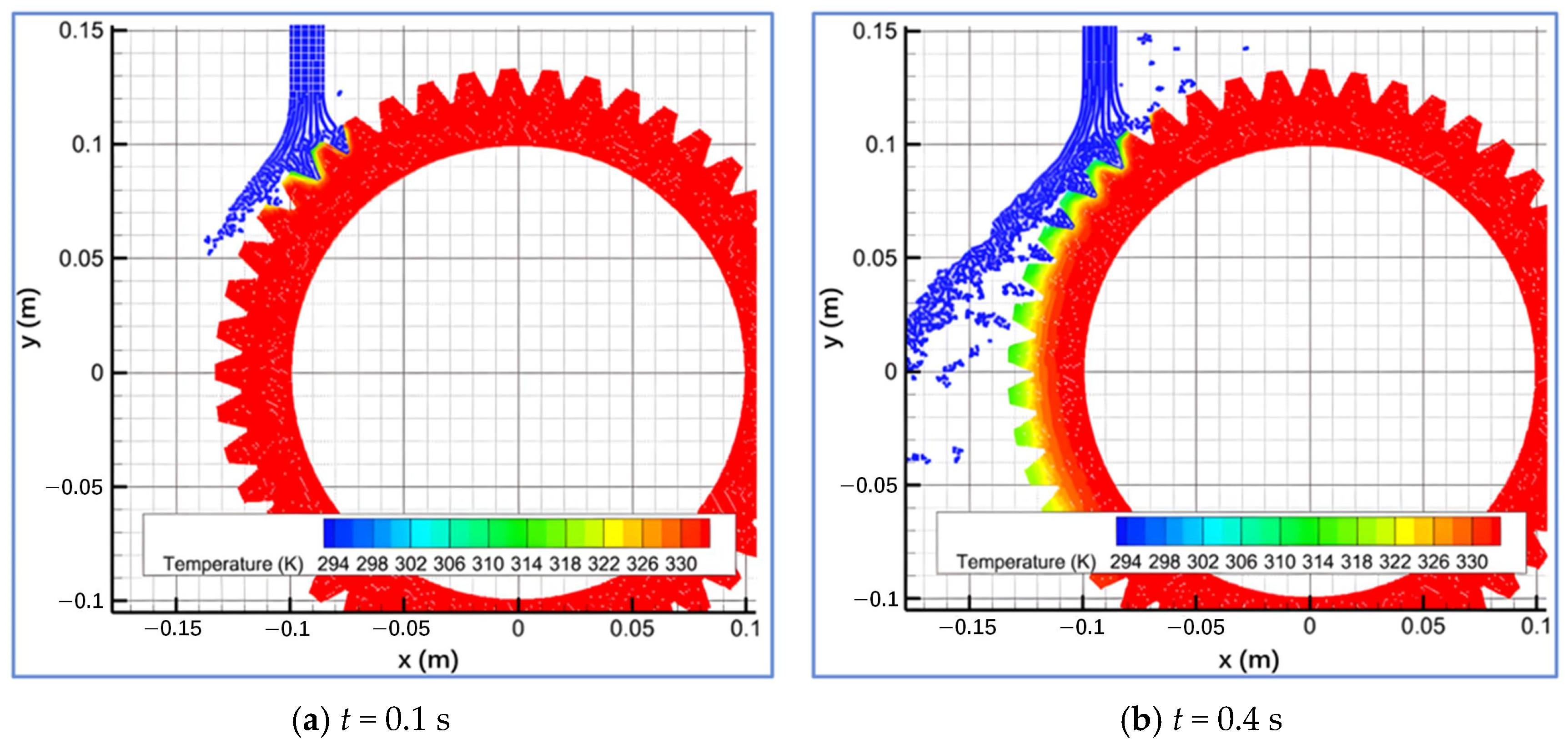
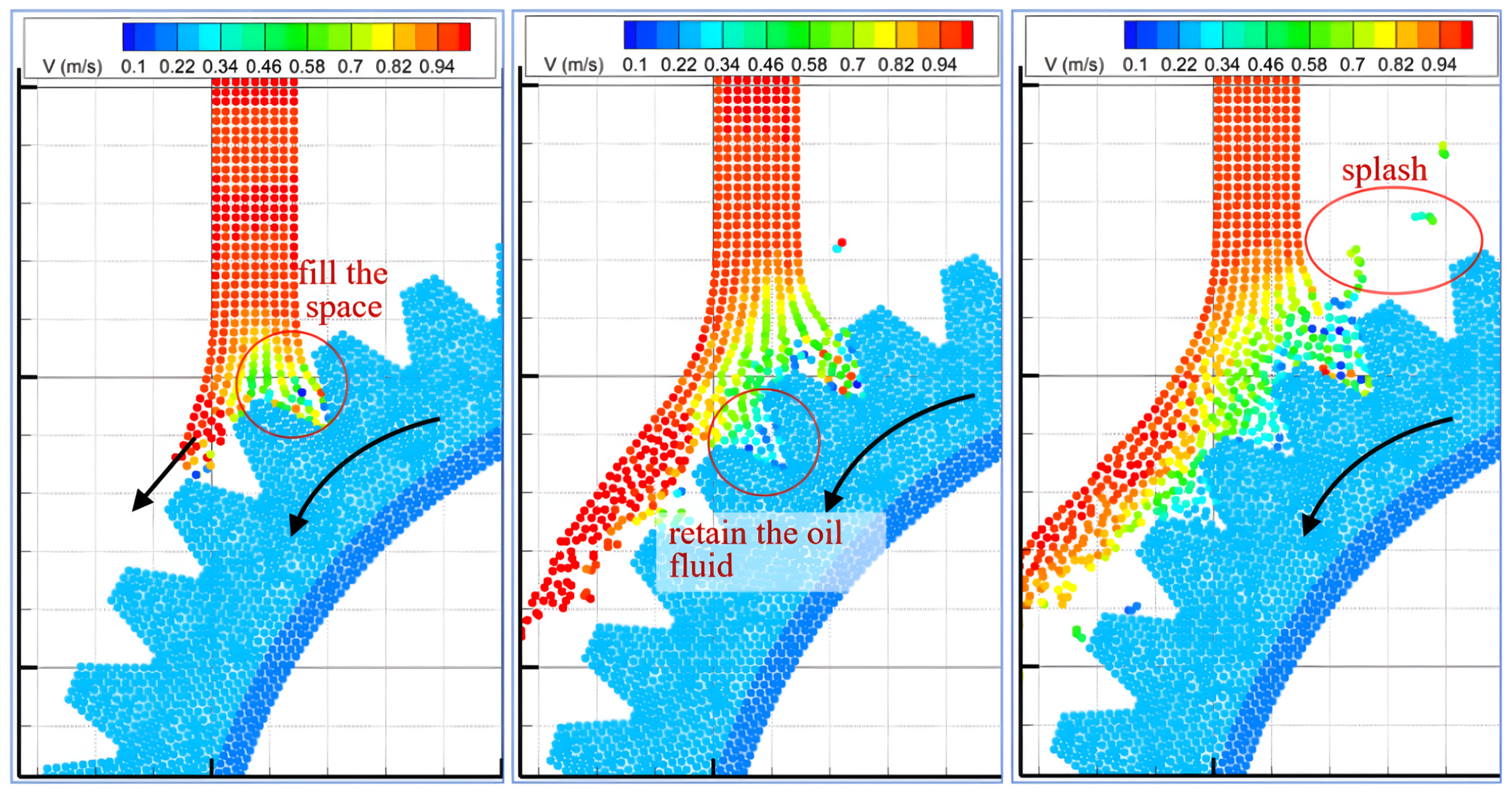
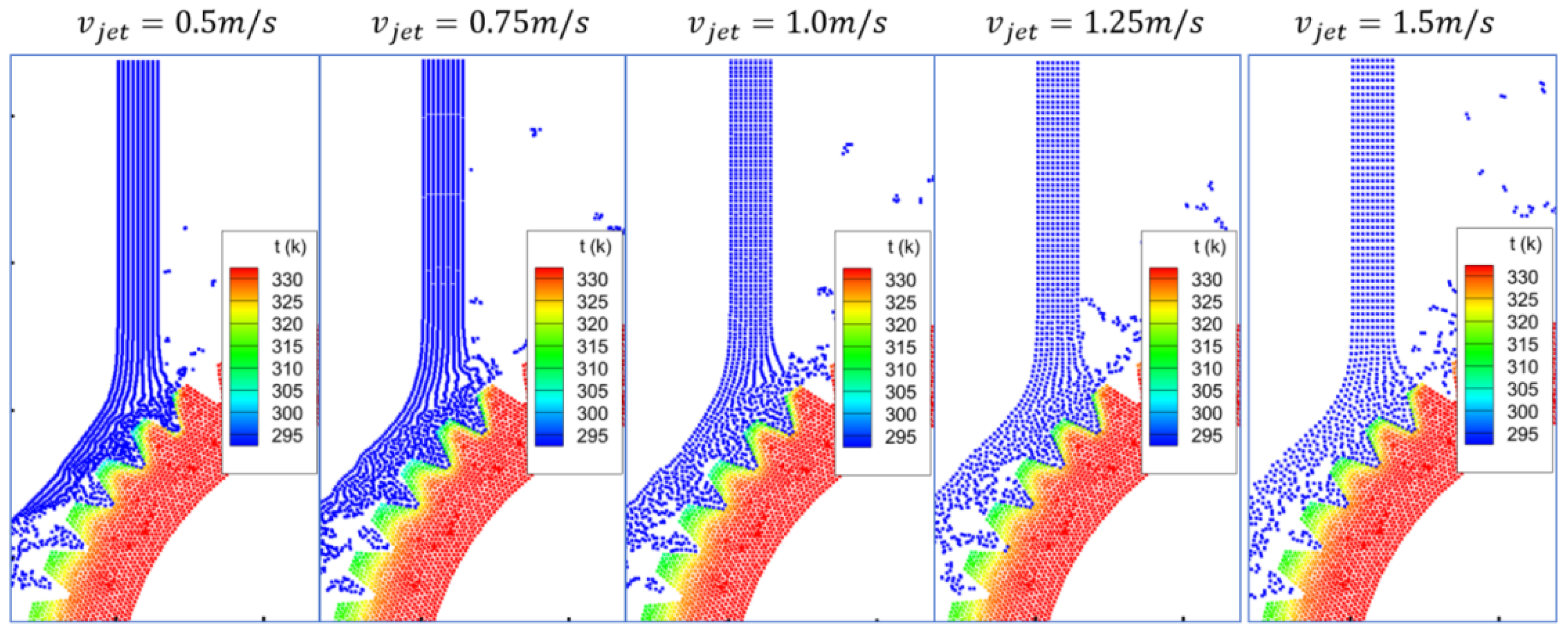
4.2. Results of Transmission Gear Oil Jet Cooling
5. Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| SPH | Smoothed Particle Hydrodynamics |
| CFD | Computational Fluid Dynamics |
| MLS | Moving Least Squares |
| MPM | Material Point Method |
| PIV | Particle Image Velocimetry |
| SPH–FE | Smoothed Particle Hydrodynamics–Finite Element |
| VPS | Virtual Performance Solution |
| EOS | Equation of State |
| RPM | Revolutions Per Minute |
| Parameters | |
| t | Time |
| ρ | Fluid density |
| Velocity vector | |
| External forces or body forces | |
| Fluid pressure | |
| Kinematic viscosity of the fluid | |
| I | Index for fluid particles |
| j | Index for neighboring particles |
| Value of the kernel gradient between particles i and j | |
| h | Smoothing length |
| γ | Coefficient |
| c | Artificial speed of sound |
| Initial density of the fluid phase or reference density | |
| Linear velocity vectors of the I-th rigid body | |
| Angular velocity vectors of the I-th rigid body | |
| External forces acting on the rigid body | |
| Torques acting on the rigid body | |
| Mass of the rigid body | |
| Moment of inertia of the rigid body | |
| Position vector of particle i | |
| Position vector of the center of mass of rigid body | |
| Number of discrete particles constituting rigid body | |
| Mass of particle i | |
| Position vector of particle | |
| Position vector of the center of mass of rigid body | |
| Velocity vectors of particle on gears 1 | |
| Velocity vectors of particle on gears 2 | |
| Angular velocity vectors of gears 1 | |
| Angular velocity vectors of gears 2 | |
| Position vectors of particle on gears 1 | |
| Position vectors of particle on gears 2 | |
| Thermal conductivity coefficients of particles i | |
| Thermal conductivity coefficients of particles j | |
| Temperatures of particles i | |
| Temperatures of particles j | |
| Time step size | |
| Current time step | |
| Maximum time step values derived from the flow characteristics | |
| Maximum time step values derived from the heat transfer characteristics | |
| Specific heat capacity of particle i | |
| Thermal conductivity of particle |
References
- Burberi, E.; Fondelli, T.; Andreini, A.; Facchini, B.; Cipolla, L. CFD simulations of a meshing gear pair. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, New York, NY, USA, 13 June 2016; p. V05AT15A024. [Google Scholar] [CrossRef]
- Ouyang, T.; Mo, X.; Lu, Y.; Wang, J. CFD-vibration coupled model for predicting cavitation in gear transmissions. Int. J. Mech. Sci. 2022, 225, 107377. [Google Scholar] [CrossRef]
- Marchesse, Y.; Changenet, C.; Ville, F.; Velex, P. Investigations on CFD simulations for predicting windage power losses in spur gears. J. Mech. Des. 2011, 133, 024501. [Google Scholar] [CrossRef]
- Keller, M.C.; Kromer, C.; Cordes, L.; Schwitzke, C.; Bauer, H.J. CFD study of oil-jet gear interaction flow phenomena in spur gears. Aeronaut. J. 2020, 124, 1301–1317. [Google Scholar] [CrossRef]
- Hildebrand, L.; Dangl, F.; Paschold, C.; Lohner, T.; Stahl, K. Cfd analysis on the heat dissipation of a dry-lubricated gear stage. Appl. Sci. 2022, 12, 10386. [Google Scholar] [CrossRef]
- Strasser, W. CFD investigation of gear pump mixing using deforming/agglomerating mesh. J. Fluids Eng. 2007, 129, 476–484. [Google Scholar] [CrossRef]
- Mastrone, M.N.; Concli, F. CFD simulations of gearboxes: Implementation of a mesh clustering algorithm for efficient simulations of complex system’s architectures. Int. J. Mech. Mater. Eng. 2021, 16, 12. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Wu, J.; Li, L.; Tan, D. Machinability evolution of gas–liquid-solid three-phase rotary abrasive flow finishing. Int. J. Adv. Manuf. Technol. 2024, 131, 2145–2164. [Google Scholar] [CrossRef]
- Mastrone, M.N.; Concli, F. A multi domain modeling approach for the CFD simulation of multi-stage gearboxes. Energies 2022, 15, 837. [Google Scholar] [CrossRef]
- Felter, C.L.; Walther, J.H.; Henriksen, C. Moving least squares simulation of free surface flows. Comput. Fluids 2014, 91, 47–56. [Google Scholar] [CrossRef]
- Spandan, V.; Lohse, D.; de Tullio, M.D.; Verzicco, R. A fast moving least squares approximation with adaptive Lagrangian mesh refinement for large scale immersed boundary simulations. J. Comput. Phys. 2018, 375, 228–239. [Google Scholar] [CrossRef]
- Hu, M.; Tan, Q.; Feng, D.; Ren, Y.; Huang, Y. Simulation of rock crack propagation and failure behavior based on a mixed failure model with SPH. Rock Mech. Rock Eng. 2024, 57, 9575–9596. [Google Scholar] [CrossRef]
- Feng, D.; Yi, C.; Hu, M.; Gao, T.; Huang, Y. Simulation of non-cohesive soil turning based on an SPH model. Comput. Geotech. 2023, 160, 105502. [Google Scholar] [CrossRef]
- Dong, X.; Hao, G.; Yu, R. Two-dimensional smoothed particle hydrodynamics (SPH) simulation of multiphase melting flows and associated interface behavior. Eng. Appl. Comp. Fluid Mech. 2022, 16, 588–629. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, Q.; Liu, Y.; Liu, X. Improved mesh-free SPH approach for loose top coal caving modeling. Particuology 2024, 95, 1–27. [Google Scholar] [CrossRef]
- Hu, W.; Chen, Z. A multi-mesh MPM for simulating the meshing process of spur gears. Comput. Struct. 2003, 81, 1991–2002. [Google Scholar] [CrossRef]
- Lei, Z.; Wu, B.; Wu, S.; Nie, Y.; Cheng, S.; Zhang, C. A material point-finite element (MPM-FEM) model for simulating three-dimensional soil-structure interactions with the hybrid contact method. Comput. Geotech. 2022, 152, 105009. [Google Scholar] [CrossRef]
- Dong, X.; Feng, L.; Zhang, Q. Droplet asymmetry bouncing on structured surfaces: A simulation based on SPH method. Int. J. Adhes. Adhes. 2024, 132, 103734. [Google Scholar] [CrossRef]
- Dong, X.; Hao, G.; Liu, Y. Efficient mesh-free modeling of liquid droplet impact on elastic surfaces. Eng. Comput. 2023, 39, 3441–3471. [Google Scholar] [CrossRef]
- Huang, C.; Hu, C.; An, Y.; Shi, C.; Feng, C.; Wang, H.; Liu, Q.; Wang, X. Numerical simulation of the large-scale Huangtian (China) landslide-generated impulse waves by a GPU-accelerated three-dimensional soil–water coupled SPH model. Water Resour. Res. 2023, 59, e2022WR034157. [Google Scholar] [CrossRef]
- Imin, R.; Geni, M. Stress analysis of gear meshing impact based on SPH method. Math. Probl. Eng. 2014, 2014, 328216. [Google Scholar] [CrossRef]
- Ji, Z.; Stanic, M.; Hartono, E.A.; Chernoray, V. Numerical simulations of oil flow inside a gearbox by Smoothed Particle Hydrodynamics (SPH) method. Tribol. Int. 2018, 127, 47–58. [Google Scholar] [CrossRef]
- Keller, M.C.; Braun, S.; Wieth, L.; Chaussonnet, G.; Dauch, T.F.; Koch, R.; Schwitzke, C.; Bauer, H.J. Smoothed particle hydrodynamics simulation of oil-jet gear interaction. J. Tribol. 2019, 141, 071703. [Google Scholar] [CrossRef]
- Groenenboom, P.; Cartwright, B.; McGuckin, D.; Amoignon, O.; Mettichi, M.Z.; Gargouri, Y.; Kamoulakos, A. Numerical studies and industrial applications of the hybrid SPH-FE method. Comput. Fluids 2019, 184, 40–63. [Google Scholar] [CrossRef]
- Sun, P.N.; Pilloton, C.; Antuono, M.; Colagrossi, A. Inclusion of an acoustic damper term in weakly-compressible SPH models. J. Comput. Phys. 2023, 483, 112056. [Google Scholar] [CrossRef]
- Guan, X.S.; Sun, P.N.; Xu, Y.; Lyu, H.G.; Geng, L.M. Numerical studies of complex fluid-solid interactions with a six degrees of freedom quaternion-based solver in the SPH framework. Ocean Eng. 2024, 291, 116484. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, H.; Qian, Z.; Liu, M. Smoothed-interface SPH model for multiphase fluid-structure interaction. J. Comput. Phys. 2024, 518, 113336. [Google Scholar] [CrossRef]
- Ma, Y.; Zhou, X.; Zhang, F.; Weißenfels, C.; Liu, M. A novel smoothed particle hydrodynamics method for multi-physics simulation of laser powder bed fusion. Comput. Mech. 2024, 74, 1009–1036. [Google Scholar] [CrossRef]
- Guo, X.; Yang, M.; Li, F.; Zhu, Z.; Cui, B. Investigation on cryogenic cavitation characteristics of an inducer considering thermodynamic effects. Energies 2024, 17, 3627. [Google Scholar] [CrossRef]
- Zheng, B.X.; Cai, Z.W.; Zhao, P.D.; Xu, X.Y.; Chan, T.S.; Yu, P. A generalized density dissipation for weakly compressible smoothed particle hydrodynamics. Phys. Fluids 2024, 36, 083325. [Google Scholar] [CrossRef]
- Becker, M.; Teschner, M. Weakly compressible SPH for free surface flows. In Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 2 August 2007; p. 209. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical diffusive terms in weakly-compressible SPH schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Cleary, P.W.; Monaghan, J.J. Conduction modelling using smoothed particle hydrodynamics. J. Comput. Phys. 1999, 148, 227–264. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Method Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, C.; Song, X.; Xu, W.; Tian, Y.; Yang, L.; Dong, X.; Zhang, Q. SPH Simulation of Gear Meshing with Lubricating Fluid–Solid Coupling and Heat-Transfer Process. Processes 2025, 13, 730. https://doi.org/10.3390/pr13030730
Shi C, Song X, Xu W, Tian Y, Yang L, Dong X, Zhang Q. SPH Simulation of Gear Meshing with Lubricating Fluid–Solid Coupling and Heat-Transfer Process. Processes. 2025; 13(3):730. https://doi.org/10.3390/pr13030730
Chicago/Turabian StyleShi, Chunxiang, Xiangkun Song, Weipeng Xu, Ying Tian, Liu Yang, Xiangwei Dong, and Qiang Zhang. 2025. "SPH Simulation of Gear Meshing with Lubricating Fluid–Solid Coupling and Heat-Transfer Process" Processes 13, no. 3: 730. https://doi.org/10.3390/pr13030730
APA StyleShi, C., Song, X., Xu, W., Tian, Y., Yang, L., Dong, X., & Zhang, Q. (2025). SPH Simulation of Gear Meshing with Lubricating Fluid–Solid Coupling and Heat-Transfer Process. Processes, 13(3), 730. https://doi.org/10.3390/pr13030730






