Experimental Dielectric Properties and Temperature Measurement Analysis to Assess the Thermal Distribution of a Multimode Microwave-Assisted Susceptor Fixed-Bed Reactor
Abstract
:1. Introduction
2. Materials and Methods
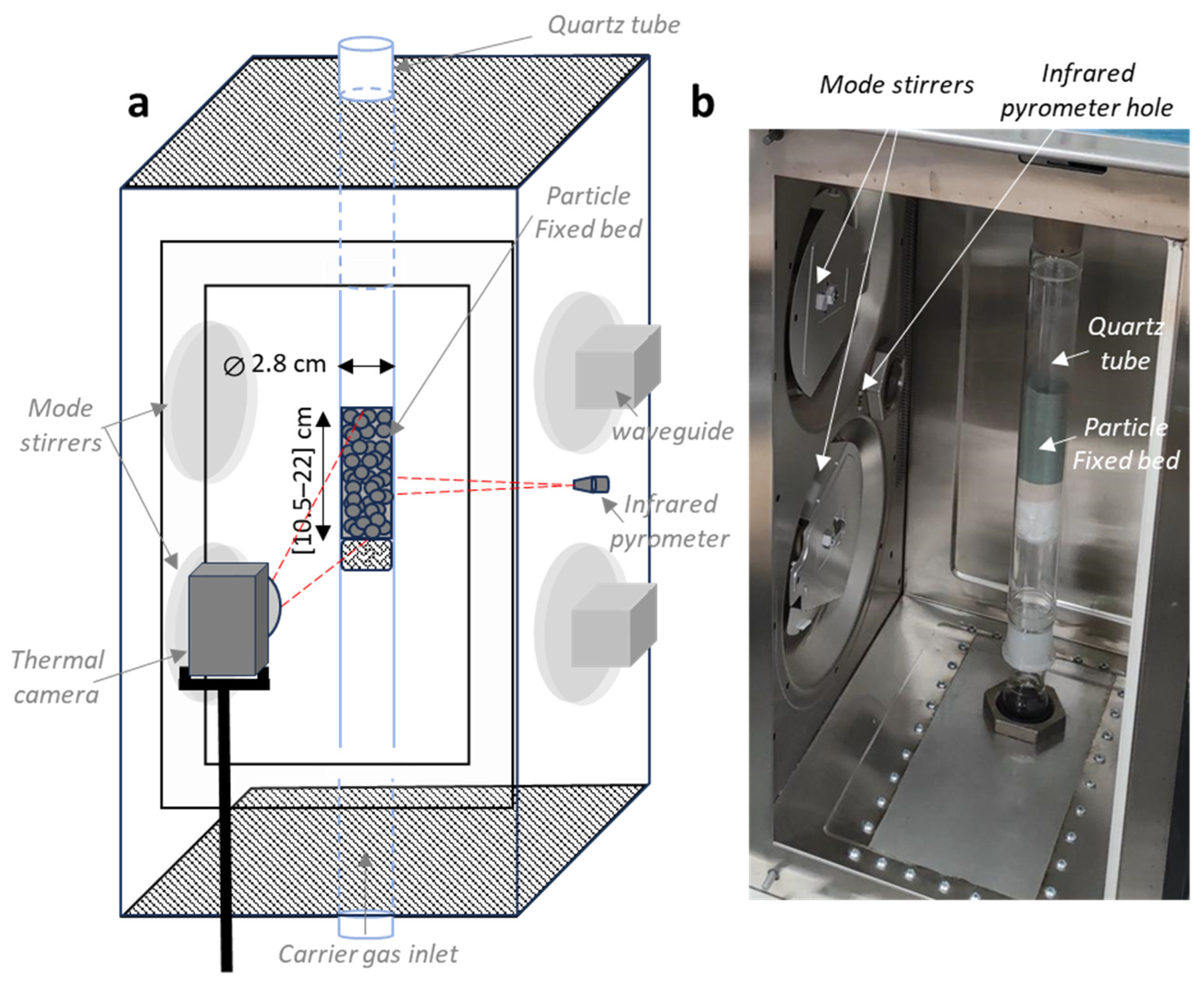
2.1. Microwave Cavity Configuration
2.2. Non-Contact Temperature Measurement Devices
2.3. Dielectric Properties Characterization
2.4. Microwave Susceptor Heating Curves and Thermal Homogeneity Characterization
3. Results
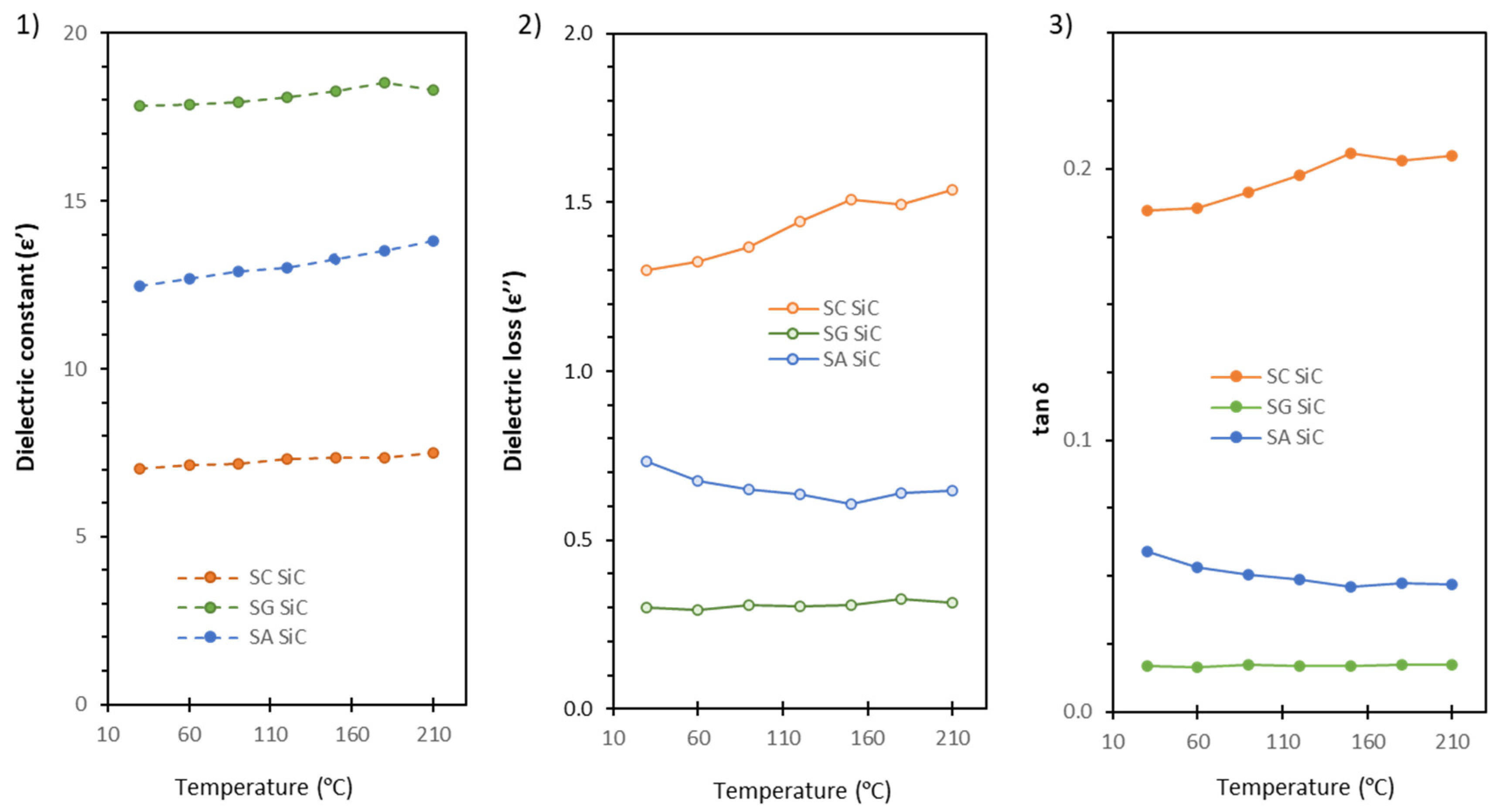
3.1. Dielectric Properties Measurement
3.2. Susceptor’s Heating Rate Characterization
3.3. Fixed-Bed Thermal Distribution Homogeneity
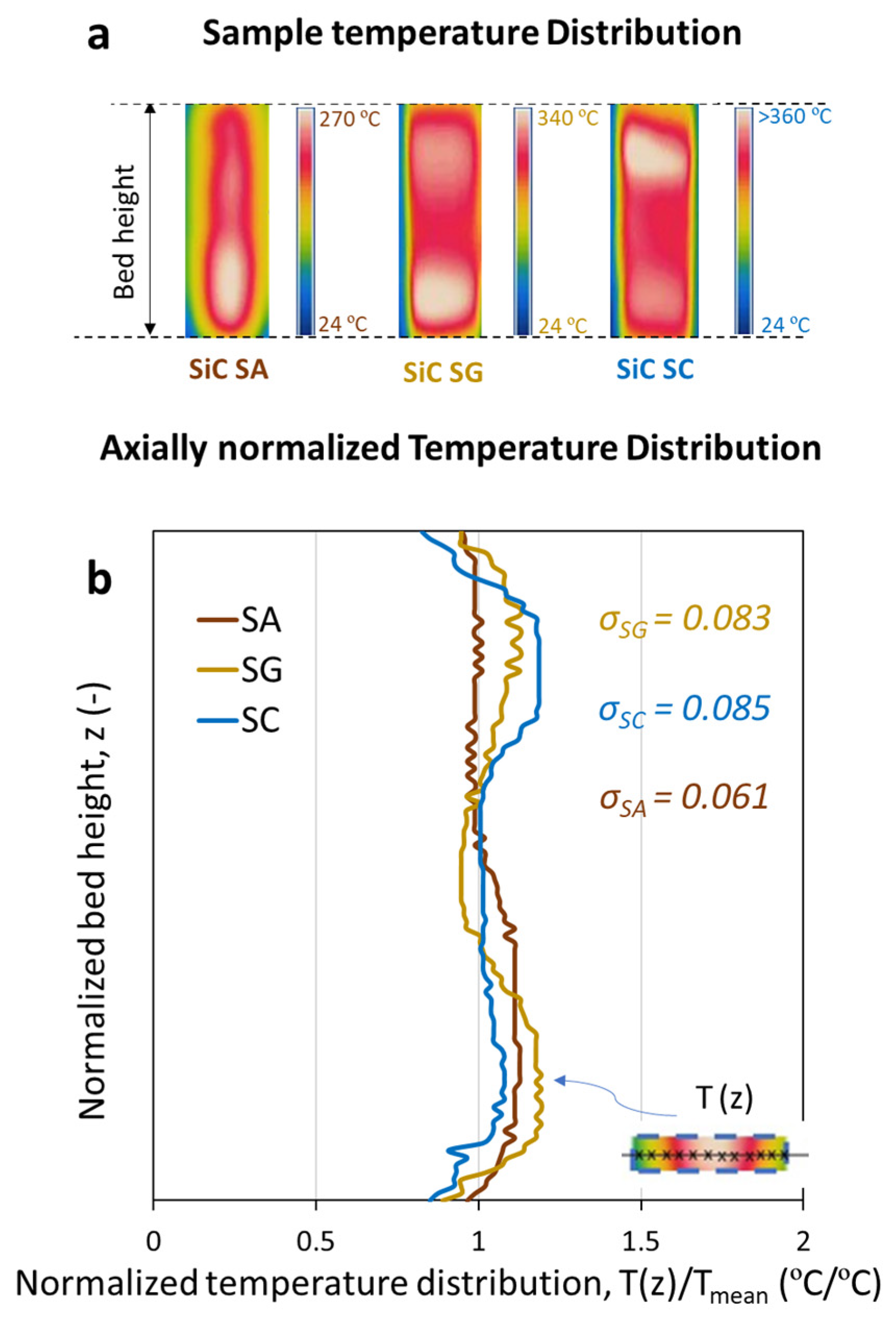
3.3.1. Impact of Susceptor Material Nature on the Temperature Distribution
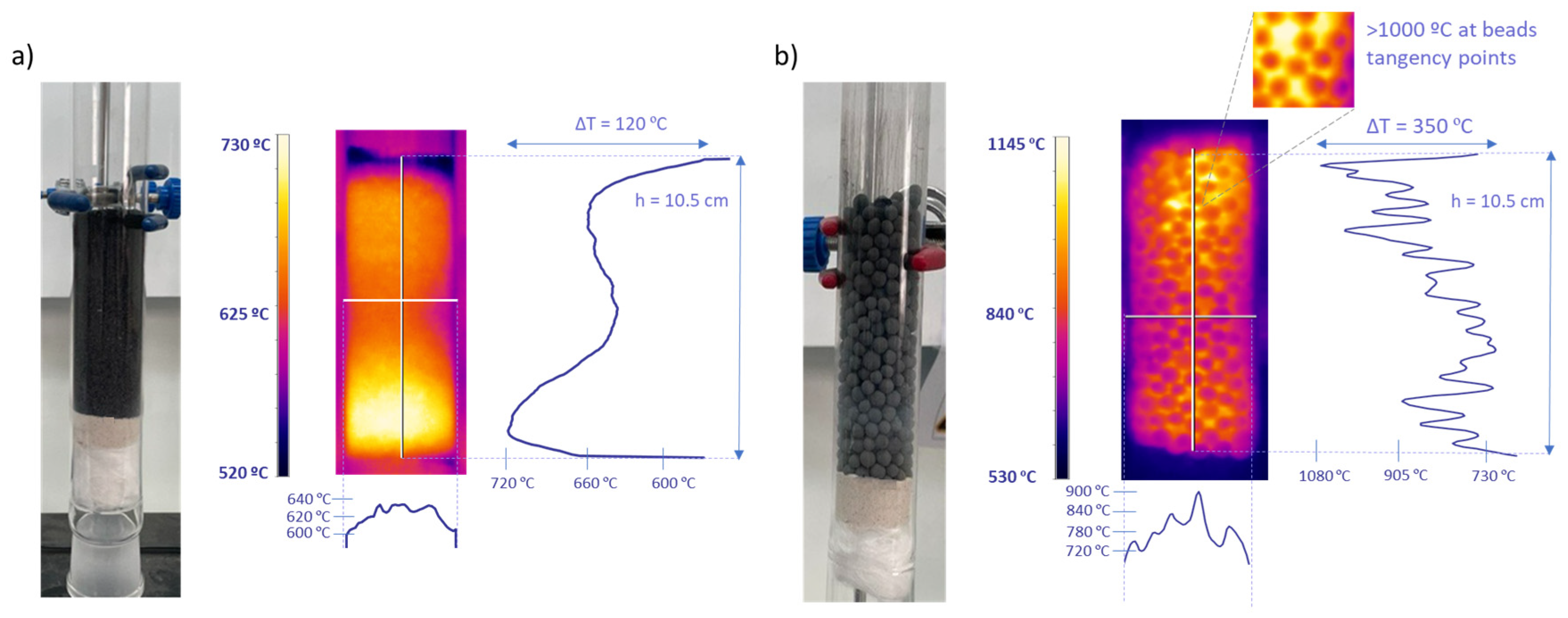
3.3.2. Assessment of Temperature Measurement in Microwave Reactor
3.3.3. Impact of Fixed-Bed Length and Feedstock Load on Temperature Distribution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martínez–Castelló, A.; Tejeda–Serrano, M.; Nowacka, A.E.; Oliver–Meseguer, J.; Leyva–Pérez, A. Solid–Catalyzed Esterification Reaction of Long–Chain Acids and Alcohols in Fixed–Bed Reactors at Pilot Plant Scale. Chem. Eng. Process.-Process Intensif. 2022, 178, 109038. [Google Scholar] [CrossRef]
- Kiefer, F.; Nikolic, M.; Borgschulte, A.; Dimopoulos Eggenschwiler, P. Sorption-Enhanced Methane Synthesis in Fixed-Bed Reactors. Chem. Eng. J. 2022, 449, 137872. [Google Scholar] [CrossRef]
- Nahes, A.L.M.; Bagajewicz, M.J.; Costa, A.L.H. A Novel Method for the Globally Optimal Design of Fixed Bed Catalytic Reactors. Chem. Eng. Sci. 2023, 271, 118524. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, Y.; Peng, Y.-L.; Zou, J.-S.; Yang, T.; Liu, Z.; Qiu, F.; Liu, C.; Jiang, S. Probing the Differences in CO2 Adsorption/Desorption Behaviors of Solid Amine Sorbents in Fixed and Fluidized Beds. Sep. Purif. Technol. 2024, 343, 127171. [Google Scholar] [CrossRef]
- Choi, Y.; Wang, S.; Yoon, Y.M.; Jang, J.J.; Kim, D.; Ryu, H.-J.; Lee, D.; Won, Y.; Nam, H.; Hwang, B. Sustainable Strategy for Converting Plastic Waste into Energy over Pyrolysis: A Comparative Study of Fluidized-Bed and Fixed-Bed Reactors. Energy 2024, 286, 129564. [Google Scholar] [CrossRef]
- Aysu, T.; Küçük, M.M. Biomass Pyrolysis in a Fixed-Bed Reactor: Effects of Pyrolysis Parameters on Product Yields and Characterization of Products. Energy 2014, 64, 1002–1025. [Google Scholar] [CrossRef]
- Le Brech, Y.; Jia, L.; Cissé, S.; Mauviel, G.; Brosse, N.; Dufour, A. Mechanisms of Biomass Pyrolysis Studied by Combining a Fixed Bed Reactor with Advanced Gas Analysis. J. Anal. Appl. Pyrolysis 2016, 117, 334–346. [Google Scholar] [CrossRef]
- Kurkela, E.; Kurkela, M.; Hiltunen, I. Pilot-Scale Development of Pressurized Fixed-Bed Gasification for Synthesis Gas Production from Biomass Residues. Biomass Convers. Bioref. 2023, 13, 6553–6574. [Google Scholar] [CrossRef]
- Jiang, W.; Li, D.; Chen, S.; Ye, Y.; Kang, J.; Tang, Q.; Ren, Y.; Liu, D.; Li, D. Design and Operation of a Fixed-Bed Pyrolysis-Gasification-Combustion Pilot Plant for Rural Solid Waste Disposal. Bioresour. Technol. 2022, 362, 127799. [Google Scholar] [CrossRef]
- Jerzak, W.; Reinmöller, M.; Magdziarz, A. Estimation of the Heat Required for Intermediate Pyrolysis of Biomass. Clean Technol. Environ. Policy 2022, 24, 3061–3075. [Google Scholar] [CrossRef]
- Ábrego, J.; Atienza-Martínez, M.; Plou, F.; Arauzo, J. Heat Requirement for Fixed Bed Pyrolysis of Beechwood Chips. Energy 2019, 178, 145–157. [Google Scholar] [CrossRef]
- Radoiu, M.; Mello, A. Technical Advances, Barriers, and Solutions in Microwave—Assisted Technology for Industrial Processing. Chem. Eng. Res. Des. 2022, 181, 331–342. [Google Scholar] [CrossRef]
- Appleton, T.J.; Colder, R.I.; Kingman, S.W.; Lowndes, I.S.; Read, A.G. Microwave Technology for Energy-Efficient Processing of Waste. Appl. Energy 2005, 81, 85–113. [Google Scholar] [CrossRef]
- Lam, S.S.; Chase, H.A. A Review on Waste to Energy Processes Using Microwave Pyrolysis. Energies 2012, 5, 4209–4232. [Google Scholar] [CrossRef]
- Liang, J.; Morgan Jr, H.M.; Liu, Y.; Shi, A.; Lei, H.; Mao, H.; Bu, Q. Enhancement of Bio-Oil Yield and Selectivity and Kinetic Study of Catalytic Pyrolysis of Rice Straw over Transition Metal Modified ZSM-5 Catalyst. J. Anal. Appl. Pyrolysis 2017, 128, 324–334. [Google Scholar] [CrossRef]
- Zhang, Y.; Fu, Z.; Wang, W.; Ji, G.; Zhao, M.; Li, A. Kinetics, Product Evolution, and Mechanism for the Pyrolysis of Typical Plastic Waste. ACS Sustain. Chem. Eng. 2022, 10, 91–103. [Google Scholar] [CrossRef]
- Goyal, H.; Chen, T.Y.; Chen, W.; Vlachos, D.G. A Review of Microwave-Assisted Process Intensified Multiphase Reactors. Chem. Eng. J. 2022, 430, 133183. [Google Scholar] [CrossRef]
- Omoriyekomwan, J.E.; Tahmasebi, A.; Yu, J. Production of Phenol-Rich Bio-Oil during Catalytic Fixed-Bed and Microwave Pyrolysis of Palm Kernel Shell. Bioresour. Technol. 2016, 207, 188–196. [Google Scholar] [CrossRef]
- Fresneda-Cruz, A.; Murillo-Ciordia, G.; Figueirêdo, M.B.; Tovar-Lasheras, F.; Farra, A.A.; Arauzo, J.; Julian, I. Microwave-Assisted Pyrolysis of Waste LDPE: Unveiling the Role of Induced Gas-Solid Thermal Gradients on Pyrolysis Oil Product Distribution. J. Anal. Appl. Pyrolysis 2025, 187, 106984. [Google Scholar] [CrossRef]
- Xie, Q.; Pan, T.; Zheng, G.; Zhou, Y.; Yu, S.; Duan, Y.; Nie, Y. Microwave Fixed-Bed Reactor for Gas-Phase Glycerol Dehydration: Experimental and Simulation Studies. Ind. Eng. Chem. Res. 2022, 61, 10723–10735. [Google Scholar] [CrossRef]
- Chen, W.; Malhotra, A.; Yu, K.; Zheng, W.; Plaza-Gonzalez, P.J.; Catala-Civera, J.M.; Santamaria, J.; Vlachos, D.G. Intensified Microwave-Assisted Heterogeneous Catalytic Reactors for Sustainable Chemical Manufacturing. Chem. Eng. J. 2021, 420, 130476. [Google Scholar] [CrossRef]
- Malhotra, A.; Chen, W.; Goyal, H.; Plaza-Gonzalez, P.J.; Julian, I.; Catala-Civera, J.M.; Vlachos, D.G. Temperature Homogeneity under Selective and Localized Microwave Heating in Structured Flow Reactors. Ind. Eng. Chem. Res. 2021, 60, 6835–6847. [Google Scholar] [CrossRef]
- Bartoli, M.; Frediani, M.; Briens, C.; Berruti, F.; Rosi, L. An Overview of Temperature Issues in Microwave-Assisted Pyrolysis. Processes 2019, 7, 658. [Google Scholar] [CrossRef]
- Ye, J.; Hong, T.; Wu, Y.; Wu, L.; Liao, Y.; Zhu, H.; Yang, Y.; Huang, K. Model Stirrer Based on a Multi-Material Turntable for Microwave Processing Materials. Materials 2017, 10, 95. [Google Scholar] [CrossRef] [PubMed]
- Frisa-Rubio, A.; González-Niño, C.; Royo, P.; García-Polanco, N.; Martínez-Hernández, D.; Royo-Pascual, L.; Fiesser, S.; Žagar, E.; García-Armingol, T. Chemical Recycling of Plastics Assisted by Microwave Multi-Frequency Heating. Clean. Eng. Technol. 2021, 5, 100297. [Google Scholar] [CrossRef]
- Durka, T.; Stefanidis, G.D.; Gerven, T.V.; Stankiewicz, A. On the Accuracy and Reproducibility of Fiber Optic (FO) and Infrared (IR) Temperature Measurements of Solid Materials in Microwave Applications. Meas. Sci. Technol. 2010, 21, 045108. [Google Scholar] [CrossRef]
- Temperature Assessment of Microwave-Enhanced Heating Processes|Scientific Reports. Available online: https://www-nature-com.cuarzo.unizar.es:9443/articles/s41598-019-47296-0 (accessed on 21 March 2024).
- Gangurde, L.S.; Sturm, G.S.J.; Devadiga, T.J.; Stankiewicz, A.I.; Stefanidis, G.D. Complexity and Challenges in Noncontact High Temperature Measurements in Microwave-Assisted Catalytic Reactors. Ind. Eng. Chem. Res. 2017, 56, 13379–13391. [Google Scholar] [CrossRef]
- Malkina, S.D.; Malkin, A.I.; Korotkov, A.N. Permittivity Measurement Technique for Solid and Powder Materials. In Proceedings of the 2022 IEEE 23rd International Conference of Young Professionals in Electron Devices and Materials (EDM), Altai, Russia, 30 June–4 July 2022; pp. 84–87. [Google Scholar]
- Laboratory Microwave Ovens—Microwave Research Applications, Laboratory Microwave Ovens Used for Chemical, Medical, Food and Material Laboratory Applications. Available online: https://www.microwaveresearch.com/ (accessed on 24 February 2025).
- Whittington, B.I.; Milestone, N.B. The Microwave Heating of Zeolites. Zeolites 1992, 12, 815–818. [Google Scholar] [CrossRef]
- Pérez-Botella, E.; Peumans, D.; Vandersteen, G.; Baron, G.V.; Catalá-Civera, J.M.; Gutiérrez-Cano, J.D.; Van Assche, G.; Costa Cornellà, A.; Denayer, J.F.M. Challenges in the Microwave Heating of Structured Carbon Adsorbents. Chem. Eng. J. 2023, 476, 146632. [Google Scholar] [CrossRef]
- Gutierrez-Cano, J.D.; Plaza-Gonzalez, P.; Canos, A.J.; Garcia-Banos, B.; Catala-Civera, J.M.; Penaranda-Foix, F.L. A New Stand-Alone Microwave Instrument for Measuring the Complex Permittivity of Materials at Microwave Frequencies. IEEE Trans. Instrum. Meas. 2020, 69, 3595–3605. [Google Scholar] [CrossRef]
- Rajasekhar Reddy, B.; Malhotra, A.; Najmi, S.; Baker-Fales, M.; Coasey, K.; Mackay, M.; Vlachos, D.G. Microwave Assisted Heating of Plastic Waste: Effect of Plastic/Susceptor (SiC) Contacting Patterns. Chem. Eng. Process.-Process Intensif. 2022, 182, 109202. [Google Scholar] [CrossRef]
- Rayssi, C.; El. Kossi, S.; Dhahri, J.; Khirouni, K. Frequency and Temperature-Dependence of Dielectric Permittivity and Electric Modulus Studies of the Solid Solution Ca 0.85 Er 0.1 Ti 1−x Co 4x/3 O 3 (0 ≤ x ≤ 0.1). RSC Adv. 2018, 8, 17139–17150. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Cheng, J.; Wen, W.; Wang, Q.; Gao, X.; Zhu, Z. Study on Effective Dielectric Properties of Silicon Carbide Composites. Phys. B Condens. Matter 2020, 595, 412376. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Qi, F.; Wang, C. Preparation, Characterization and Microwave Absorption Properties of Electroless Ni–Co–P-Coated SiC Powder. Appl. Surf. Sci. 2008, 254, 4708–4715. [Google Scholar] [CrossRef]
- Wang, W.; Wang, B.; Sun, J.; Mao, Y.; Zhao, X.; Song, Z. Numerical Simulation of Hot-Spot Effects in Microwave Heating Due to the Existence of Strong Microwave-Absorbing Media. RSC Adv. 2016, 6, 52974–52981. [Google Scholar] [CrossRef]
- Julian, I.A.; Fresneda-Cruz, A. Scale-up of Microwave-Assisted Heterogeneous Catalytic Processes. In Advances in Microwave-Assisted Heterogeneous Catalysis; Royal Society of Chemistry: London, UK, 2023. [Google Scholar] [CrossRef]
- Siddique, I.J.; Salema, A.A.; Antunes, E.; Vinu, R. Technical Challenges in Scaling up the Microwave Technology for Biomass Processing. Renew. Sustain. Energy Rev. 2022, 153, 111767. [Google Scholar] [CrossRef]
- Campañone, L.A.; Zaritzky, N.E. Mathematical Analysis of Microwave Heating Process. J. Food Eng. 2005, 69, 359–368. [Google Scholar] [CrossRef]
- Ayappa, K.G.; Davis, H.T.; Crapiste, G.; Davis, E.A.; Gordon, J. Microwave Heating: An Evaluation of Power Formulations. Chem. Eng. Sci. 1991, 46, 1005–1016. [Google Scholar] [CrossRef]
- Haneishi, N.; Tsubaki, S.; Abe, E.; Maitani, M.M.; Suzuki, E.; Fujii, S.; Fukushima, J.; Takizawa, H.; Wada, Y. Enhancement of Fixed-Bed Flow Reactions under Microwave Irradiation by Local Heating at the Vicinal Contact Points of Catalyst Particles. Sci. Rep. 2019, 9, 222. [Google Scholar] [CrossRef]
- Adavi, K.; Shabanian, J.; Chaouki, J. Temperature Distribution Assessment in Gas–Solid Reactive and Nonreactive Systems Heated by Microwaves. Ind. Eng. Chem. Res. 2023, 62, 9970–9982. [Google Scholar] [CrossRef]
- Ramirez, A.; Hueso, J.L.; Mallada, R.; Santamaria, J. In Situ Temperature Measurements in Microwave-Heated Gas-Solid Catalytic Systems. Detection of Hot Spots and Solid-Fluid Temperature Gradients in the Ethylene Epoxidation Reaction. Chem. Eng. J. 2017, 316, 50–60. [Google Scholar] [CrossRef]
- Hamzehlouia, S.; Shabanian, J.; Latifi, M.; Chaouki, J. Effect of Microwave Heating on the Performance of Catalytic Oxidation of N-Butane in a Gas-Solid Fluidized Bed Reactor. Chem. Eng. Sci. 2018, 192, 1177–1188. [Google Scholar] [CrossRef]
- Julian, I.; Ramirez, H.; Hueso, J.L.; Mallada, R.; Santamaria, J. Non-Oxidative Methane Conversion in Microwave-Assisted Structured Reactors. Chem. Eng. J. 2019, 377, 119764. [Google Scholar] [CrossRef]
- Ramirez, A.; Hueso, J.L.; Abian, M.; Alzueta, M.U.; Mallada, R.; Santamaria, J. Escaping Undesired Gas-Phase Chemistry: Microwave-Driven Selectivity Enhancement in Heterogeneous Catalytic Reactors. Sci. Adv. 2019, 5. [Google Scholar] [CrossRef] [PubMed]
- Hueso, J.L.; Mallada, R.; Santamaria, J. Gas-Solid Contactors and Catalytic Reactors with Direct Microwave Heating: Current Status and Perspectives. Catal. Today 2023, 423, 113927. [Google Scholar] [CrossRef]
- Plaza-Gonzalez, P.; Monzo-Cabrera, J.; Catala-Civera, J.M.; Sanchez-Hernandez, D. Effect of Mode-Stirrer Configurations on Dielectric Heating Performance in Multimode Microwave Applicators. IEEE Trans. Microw. Theory Tech. 2005, 53, 1699–1706. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, Y.; Cui, L.; Xiong, Q.; Mostafa, E. Microwave-Assisted Fluidized Bed Reactor Pyrolysis of Polypropylene Plastic for Pyrolysis Gas Production towards a Sustainable Development. Appl. Energy 2023, 342, 121099. [Google Scholar] [CrossRef]


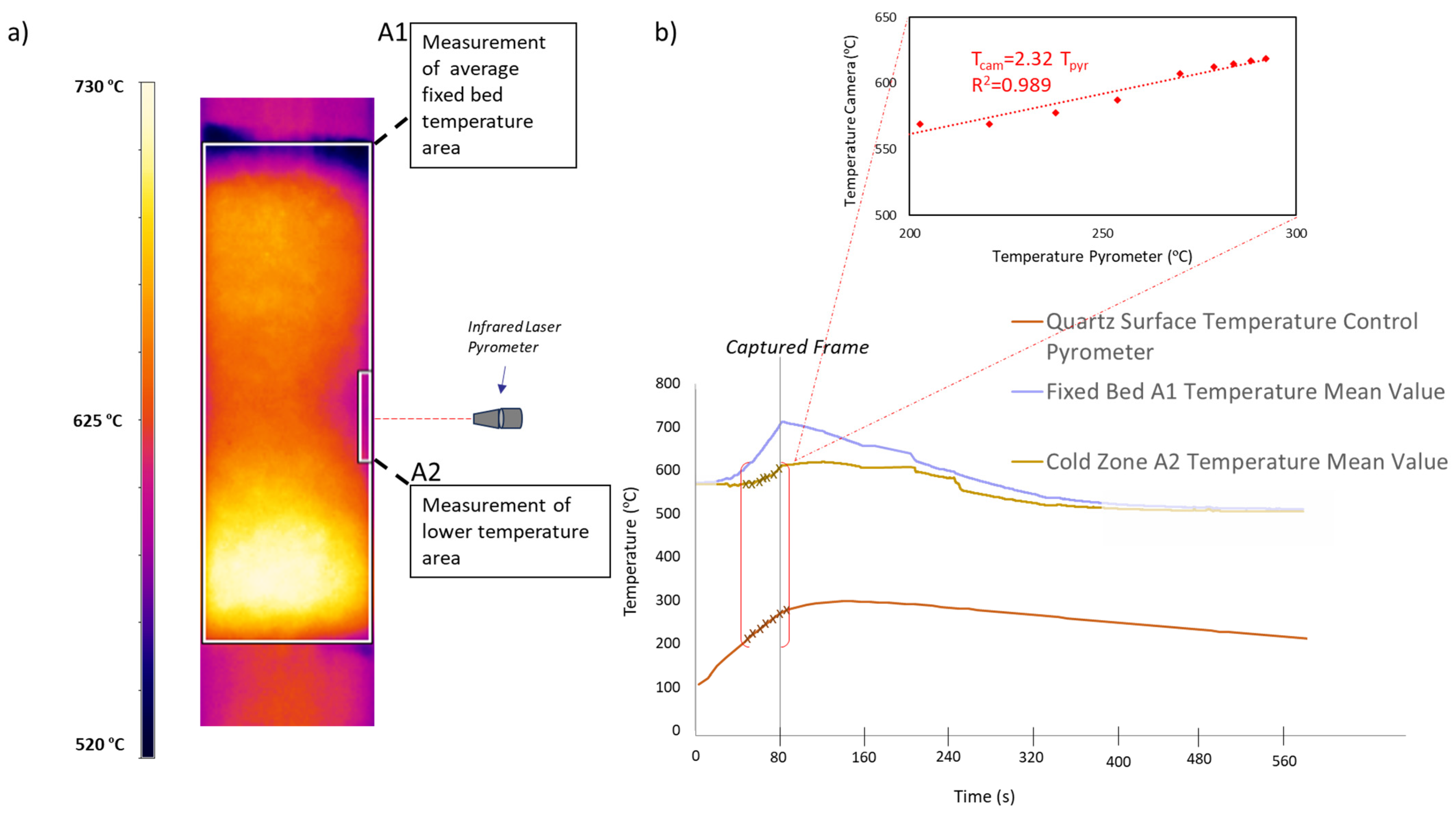
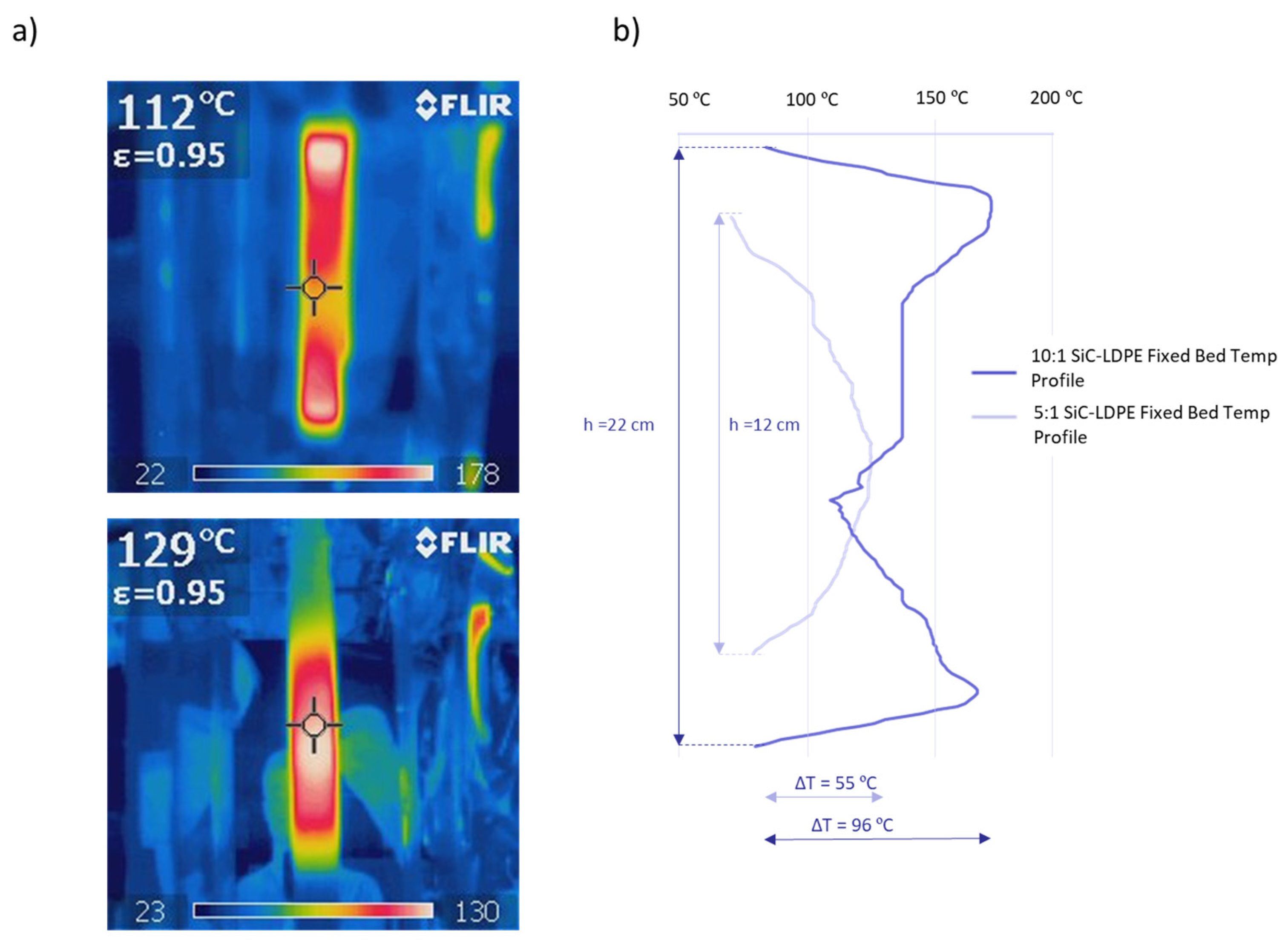
| Property | SA | SG | SC |
|---|---|---|---|
| SiC density (g/cm3) | 3.21 | 3.21 | 3.21 |
| Bed weight (g) | 146 | 120 | 70 |
| Bed volume (cm3) | 64.6 | 64.6 | 64.6 |
| Bulk density (g/cm3) | 2.26 | 1.86 | 1.08 |
| Fixed-bed void fraction (%) | 30% | 42% | 66% |
| Gas Flow (L/min) | Sample | Susceptor Mass (g) | Power (W) |
|---|---|---|---|
| 0 | SA | 146 | 565 |
| 1903 | |||
| 3200 | |||
| SG | 120 | 565 | |
| 1903 | |||
| 3200 | |||
| SC | 70 | 565 | |
| 1903 | |||
| 3200 | |||
| 2 | SA | 146 | 1903 |
| 3200 | |||
| SG | 120 | 1903 | |
| 3200 | |||
| SC | 70 | 1903 | |
| 3200 |
| Fixed Bend Length (cm) | Waste LDPE Feedstock Chips (g) | SiC (g) | Ratio Susceptor: SiC | T ªset (°C) |
|---|---|---|---|---|
| 12 | 28 | 140 | 5:1 | 100 °C |
| 22 | 116 | 168 | 1.5:1 | 100 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fresneda-Cruz, A.; Murillo-Ciordia, G.; Julian, I. Experimental Dielectric Properties and Temperature Measurement Analysis to Assess the Thermal Distribution of a Multimode Microwave-Assisted Susceptor Fixed-Bed Reactor. Processes 2025, 13, 774. https://doi.org/10.3390/pr13030774
Fresneda-Cruz A, Murillo-Ciordia G, Julian I. Experimental Dielectric Properties and Temperature Measurement Analysis to Assess the Thermal Distribution of a Multimode Microwave-Assisted Susceptor Fixed-Bed Reactor. Processes. 2025; 13(3):774. https://doi.org/10.3390/pr13030774
Chicago/Turabian StyleFresneda-Cruz, Alejandro, Gonzalo Murillo-Ciordia, and Ignacio Julian. 2025. "Experimental Dielectric Properties and Temperature Measurement Analysis to Assess the Thermal Distribution of a Multimode Microwave-Assisted Susceptor Fixed-Bed Reactor" Processes 13, no. 3: 774. https://doi.org/10.3390/pr13030774
APA StyleFresneda-Cruz, A., Murillo-Ciordia, G., & Julian, I. (2025). Experimental Dielectric Properties and Temperature Measurement Analysis to Assess the Thermal Distribution of a Multimode Microwave-Assisted Susceptor Fixed-Bed Reactor. Processes, 13(3), 774. https://doi.org/10.3390/pr13030774






