CFD Simulation Analysis of a Diesel Generator Exhaust Muffler and Performance-Based Optimization
Abstract
:1. Introduction
2. Materials and Methods
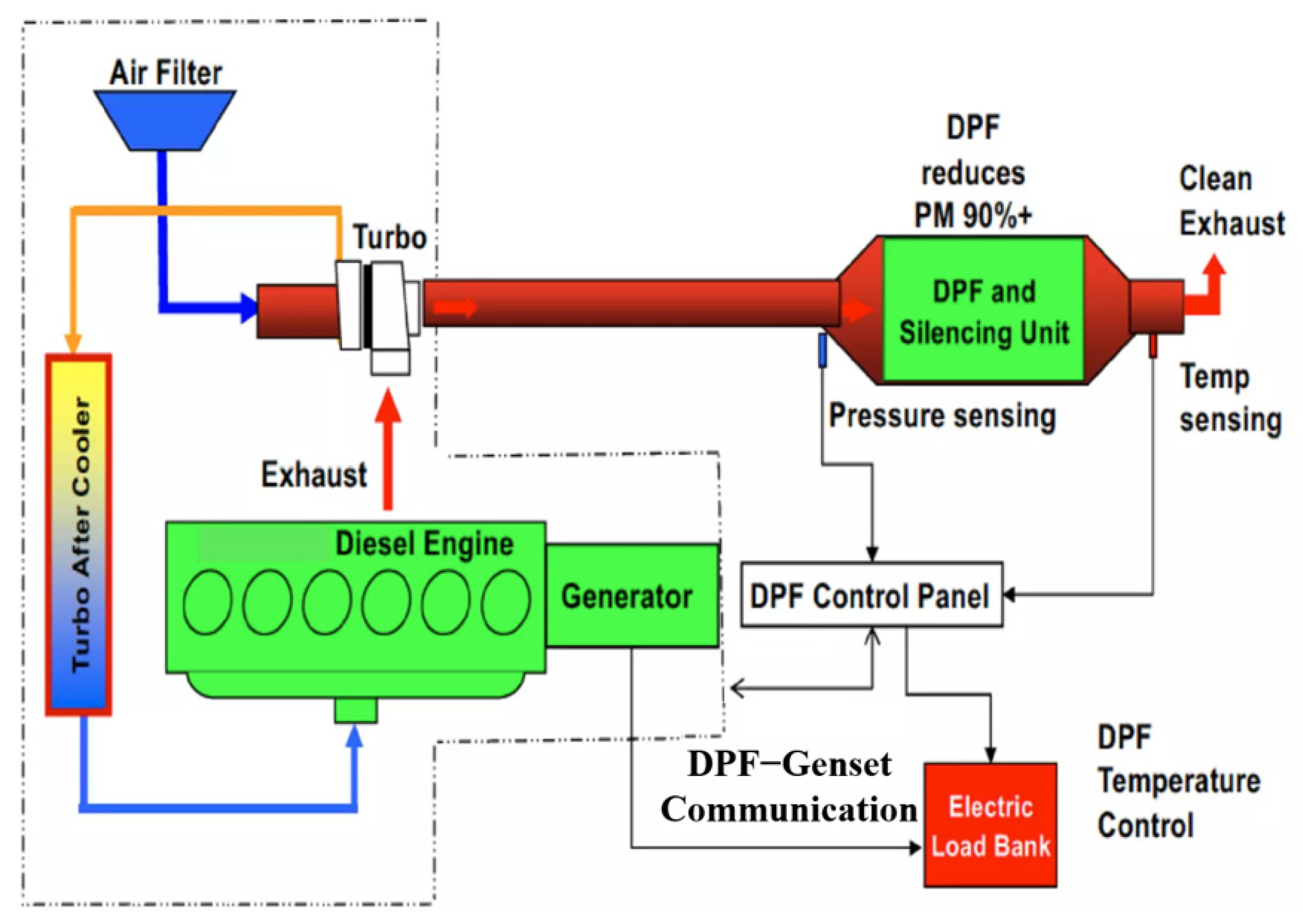
2.1. Material
2.2. Method
3. Result and Discussion
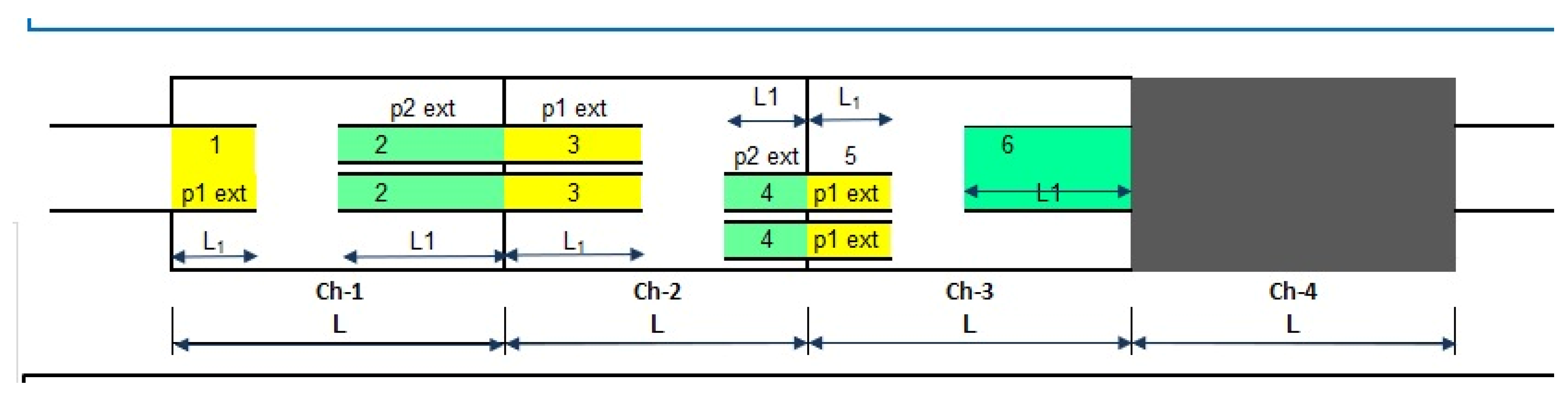
3.1. Mathematical Modeling
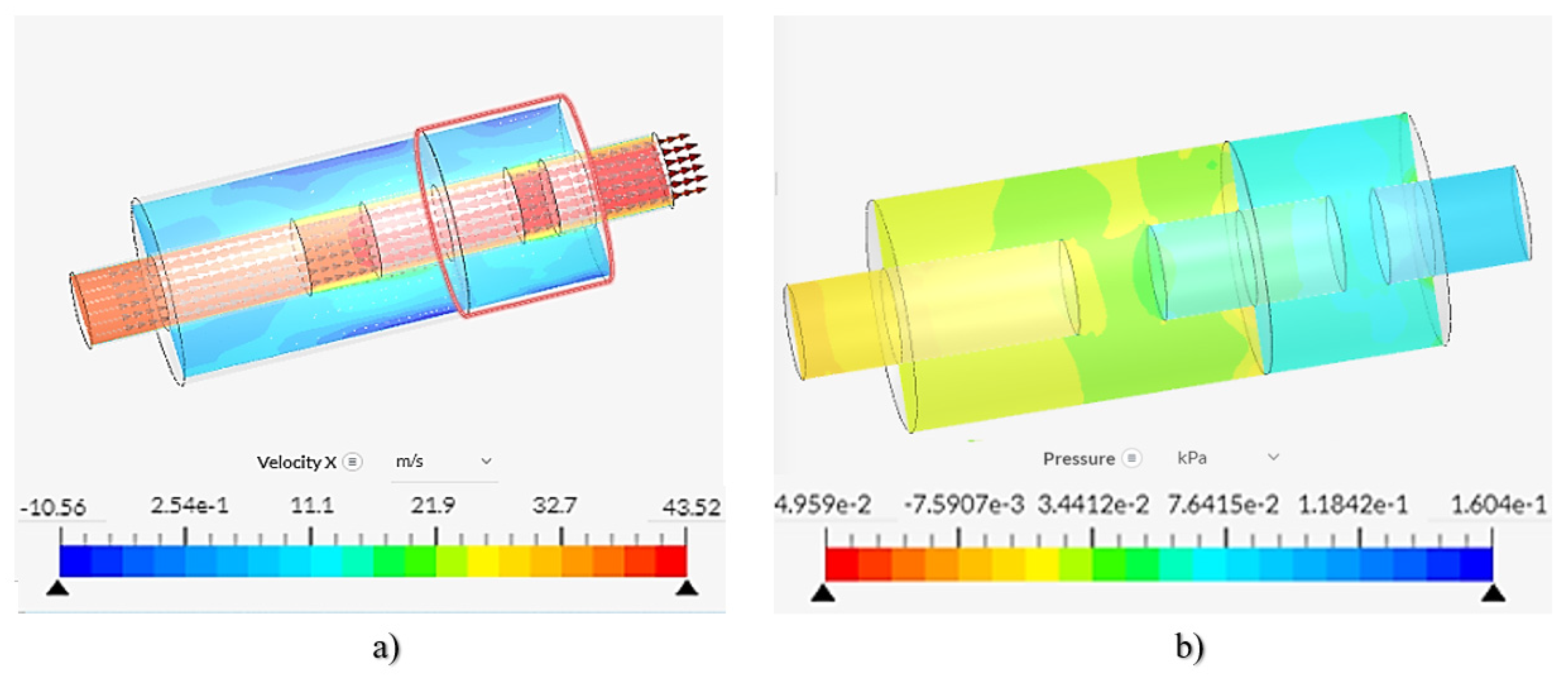
3.2. CFD Modeling
3.3. Case Study: Industrial Implementation of the Novel Silencer Design
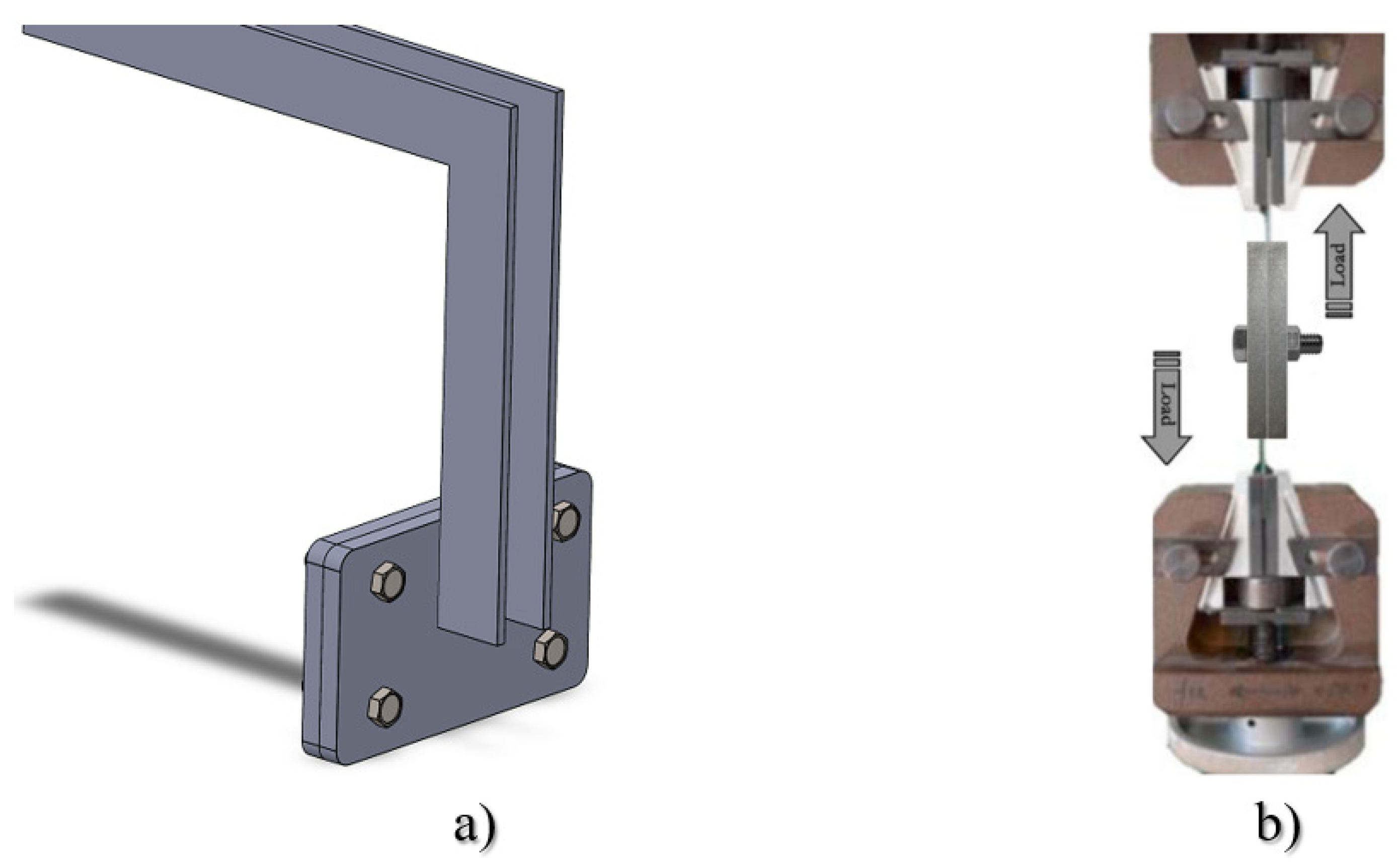
3.4. Structural Design Experimental Study and Finite Element Analysis
3.5. Error Analysis
4. Optimization
4.1. Performance-Based Optimization
4.2. Structural Optimization
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tanriver, K.; Dilibal, S.; Sahin, H. A novel design on polymeric material recycling technology. Acta Sci. Technol. 2021, 43, e56211. [Google Scholar] [CrossRef]
- Asaduzzaman, M.; Ali, M.H.; Pratik, N.A.; Lubaba, N. Exhaust heat harvesting of automotive engine using thermoelectric generation technology. Energy Convers. Manag. X 2023, 19, 100398. [Google Scholar] [CrossRef]
- Bönnen, D.; Bamdad-Soufi, D.; Steinkilberg, H.; Abram, K. Possibilities and Constraints for Lightweight in Exhaust Systems. In Proceedings of the 8th International Styrian Noise, Vibration, Harshness Congress (ISNVH), Graz, Austria, 2–4 July 2014; pp. 81–97. [Google Scholar]
- Huang, L.; Simon, T.; Zhang, M.; Yeom, T.; North, M.; Cui, T.H. Noise Measurements and Reduction for High-Frequency Vibrating Devices in the Application of Cooling Electronics. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 1497–1504. [Google Scholar]
- Kang, I.S.; Yang, S.M. Effect of Confluence Geometry of Dual Exhaust System on Quietness and Power. Int. J. Automot. Technol. 2021, 22, 27–36. [Google Scholar] [CrossRef]
- Lin, T.-H.; Deng, J.; Chen, Y.-C. Using Response Surface for Searching the Nearly Optimal Parameters Combination of the Foam Concrete Muffler. Materials 2022, 15, 8128. [Google Scholar] [CrossRef]
- Kadyrov, A.; Bembenek, M.; Sarsembekov, B.; Kukesheva, A.; Nurkusheva, S. The Influence of the Frequency of Ultrasound on the Exhaust Gas Purification Process in a Diesel Car Muffler. Appl. Sci. 2024, 14, 5027. [Google Scholar] [CrossRef]
- Nursal, R.S.; Hashim, A.H.; Nordin, N.I.; Abdul Hamid, M.A.; Danuri, M.R. CFD analysis on the effects of exhaust backpressure generated by four-stroke marine diesel generator after modification of silencer and exhaust flow design. ARPN J. Eng. Appl. Sci. 2017, 12, 1271–1280. [Google Scholar]
- Gupta, A.; Mishra, P.C. Optimization of emission characteristics of spark ignition engine with chambered straight muffler running in methanol blend: An engine development technique for environmental sustainability. J. Clean. Prod. 2019, 238, 117778. [Google Scholar] [CrossRef]
- Sunny Manohar, D.; Krishnaraj, J. Modeling and analysis of Exhaust Manifold using CFD. IOP Conf. Ser. Mater. Sci. Eng. 2018, 455, 012132. [Google Scholar] [CrossRef]
- Altun, A.; Adin, M.; İlçin, K. Monohydric aliphatic alcohols as liquid fuels for using in internal combustion engines: A review. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2023, 238, 1941–1975. [Google Scholar] [CrossRef]
- Uyar, M.; Aydın, H. Production of low sulfur diesel-like fuel from crude oil wastes by pyrolytic distillation and its usage in a diesel engine. Energy 2022, 244, 122683. [Google Scholar] [CrossRef]
- Yadav, G.P.K.; Dwivedi, Y.D.; Kumar, M.L.; Sonia, P.; Bandhu, D.; Nagendra, J.; Abass, M.A. CFD simulation analysis of a rectangular chambered muffler model for a C.I. engine. Int. J. Interact. Des. Manuf. 2024, 18, 3183–3192. [Google Scholar] [CrossRef]
- Peng, Q.; Liu, R.; Zhou, G.; Zhao, X.; Dong, S.; Zhang, Z.; Zhang, H. Summary of Turbocharging as a Waste Heat Recovery System for a Variable Altitude Internal Combustion Engine. ACS Omega 2023, 8, 27932–27952. [Google Scholar] [CrossRef]
- Li, S.; Zang, Z.; Zhang, S.; Zhao, X. Low-frequency duct noise control using coupled loudspeakers. J. Acoust. Soc. Am. 2023, 153, 1163–1178. [Google Scholar] [CrossRef]
- Archana, S.K.; Surve, F. Transmission loss and end-correction modeling of extended inlet-outlet expansion chamber muffler and the concentric tube resonator. J. Acoust. Soc. Am. 2022, 151, A55. [Google Scholar]
- Dogra, S.; Gulia, P.; Gupta, A. Noise isolation in building HVAC system using recyclable plastic bottles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 238, 3327–3337. [Google Scholar] [CrossRef]
- Rahmani, N.; Khastavan, Y.; Variani, A.S.; Ahmadi, S. Compressor pulsation noise attenuation using reactive silencer with various configurations: A theoretical and experimental study. Heliyon 2024, 10, e27263. [Google Scholar] [CrossRef]
- Villau, M.; Rämmal, H.; Lavrentjev, J. Acoustic analysis of compact silencer solution based on microperforated panel. AIP Conf. Proc. 2024, 2989, 030014. [Google Scholar]
- Fu, J.; Gu, S.; Wu, L.; Wang, N.; Lin, L.; Chen, Z. Research on Optimization of Diesel Engine Speed Control Based on UKF-Filtered Data and PSO Fuzzy PID Control. Processes 2025, 13, 777. [Google Scholar] [CrossRef]
- Kang, I.-S.; Yang, S.-M. The Effect of Back Pressure Change on Exhaust Emissions According to the Confluence Geometry of a Dual Exhaust System in Idling. Appl. Sci. 2022, 12, 1855. [Google Scholar] [CrossRef]
- Li, F.; Yuan, W.; Ma, Y.; Fu, J. Structural Performance Analysis and Optimization of Small Diesel Engine Exhaust Muffler. Processes 2024, 12, 2186. [Google Scholar] [CrossRef]
- Li, K.; Xiao, B.; Wang, Y.; Jia, J.; Wu, X. Applications of Electric Heating Technology in Vehicle Exhaust Pollution Control. Processes 2024, 12, 298. [Google Scholar] [CrossRef]
- Wansom, A.; Maneechot, P.; Jiteurtragool, N.; Vitidsant, T. PM2.5 Collection Enhancement in a Smart Hybrid Wet Scrubber Tower. Processes 2023, 11, 3306. [Google Scholar] [CrossRef]
- Mikky, Y.A.; Bhran, A.A.; El-Araby, R.Y.; Mohamed, A.M.A.; Gadallah, A.G.; Shoaib, A.M. Optimization of Biodiesel–Nanoparticle Blends for Enhanced Diesel Engine Performance and Emission Reduction. Processes 2024, 12, 2471. [Google Scholar] [CrossRef]
- Ma, Q.; Luo, C.; Wan, X.; Xu, Z. Numerical Investigation into Acoustics Characteristics towards Pressure Reducing Valve with High Ratio of Reduced Pressure. Processes 2024, 12, 2110. [Google Scholar] [CrossRef]
- Zhang, S.-W.; Wang, F.; Li, C.; Zhu, S.-M.; Lan, H.-Q. Study on Acoustic–Vibration Characteristics and Noise Reduction Methods for Elbows. Processes 2025, 13, 389. [Google Scholar] [CrossRef]
- Alexanda Petrovic, B.; Masoudi Soltani, S. Optimization of Post Combustion CO2 Capture from a Combined-Cycle Gas Turbine Power Plant via Taguchi Design of Experiment. Processes 2019, 7, 364. [Google Scholar] [CrossRef]
- Tanriver, K.; Ay, M. Modifying the Refuse Chute Design to Prevent Infection Spread: Engineering Analysis and Optimization. Appl. Sci. 2024, 14, 9638. [Google Scholar] [CrossRef]
- Binh Pham, V.; Hung Pham, C.; Gregory, J.H. Block shear and tear-out in bolted connections as limited by curling. Thin-Walled Struct. 2023, 187, 110754. [Google Scholar] [CrossRef]
- Li, Y.; Long, T.; Luo, Z.; Wen, C.; Zhu, Z.; Jin, L.; Li, B. Numerical and experimental investigations on dynamic behaviors of a bolted joint rotor system with pedestal looseness. J. Sound Vib. 2024, 571, 118036. [Google Scholar] [CrossRef]
- Cheng, L.; Huan, H.; Ke, Y. Elastic-plastic analysis, and riveting energy control for dual-robot pneumatic riveting system. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1836–1847. [Google Scholar] [CrossRef]
- Tanriver, K.; Ay, M. Investigation of flue gas temperature effects in natural gas fueled Systems: Experimental thermal performance and structural optimization. Int. J. Heat Fluid Flow 2024, 107, 109428. [Google Scholar] [CrossRef]
- Kong, F.; Zhen, X.; Yuqi, Y.; Wang, Z. Analysis of Fracture Damage Mechanical Properties of Particle Reinforced Polymer Composite Film Based on Micro-macro–Finite Element Method. Model. Simul. Mater. Sci. Eng. 2024, 32, 065010. [Google Scholar] [CrossRef]
- Yi, W.; Zhu, L.; Wang, M. Sun Experimental and numerical study on mechanical performance of single shear bolted connections with novel elliptical one-sided bolts. Structures 2024, 62, 106223. [Google Scholar] [CrossRef]
- He, M.; Zhang, Q.; Sun, X.; Alhaddad, W. An experimental and numerical study on the shear performance of friction-type high-strength bolted connections used for CLT-steel hybrid shear walls. Eng. Struct. 2024, 306, 117868. [Google Scholar] [CrossRef]
- Gao, X.; Wang, W. Bolt load looseness measurement for slip-critical blind bolt by ultrasonic technique: A feasibility study with calibration and experimental verification. Struct. Health Monit. 2024, 23, 527–538. [Google Scholar] [CrossRef]
- Ye, J.; Quan, G.; Yun, X.; Guo, X.; Chen, J. An improved and robust finite element model for simulation of thin-walled. Eng. Struct. 2022, 250, 113368. [Google Scholar] [CrossRef]
- ISO 14163:1998; Acoustics—Guidelines for Noise Control by Silencers. ISO: Geneva, Switzerland, 1998.
- Kovachev, N.Y.; Mihova, V.A.; Georgiev, I.R.; Pavlov, V.T. Assessing the Impact of Speed and Type of Road Surface on the Noise Level in a Passenger Car Cabin. J. Phys. Conf. Ser. 2023, 2675, 012014. [Google Scholar] [CrossRef]
- EN 1090-1:2009+A1:2011; Execution of Steel Structures and Aluminium Structures—Part 1: Requirements for Conformity Assessment of Structural Components. BSI: London, UK, 2011.
- ISO 3834-2:2021; Quality Requirements for Fusion Welding of Metallic Materials—Part 2: Comprehensive Quality Requirements. ISO: Geneva, Switzerland, 2021.
- ISO 6892-1:2016; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. ISO: Geneva, Switzerland, 2016.
- İncesu, A.; Ercan, B.; Çevik, E.; Akgül, Y. Reference material development process for tensile test method. Pamukkale Univ. J. Eng. Sci. 2022, 28, 58–62. [Google Scholar] [CrossRef]
- Tanriver, K.; Ay, M. Experimental and numerical analysis of bolted two plates using a developed shear theory. J. Theor. Appl. Mech. 2023, 61, 509–520. [Google Scholar] [CrossRef]
- Uysal, M.; Bakar, O.; Doğan, Y. Comparison of Noise Analysis with Finite Elements Method and Test Values in Diesel Generator Sets. DEU FMD 2022, 24, 463–474. [Google Scholar] [CrossRef]
- Perkins Engine Datasheet—4008-30TAG3 Diesel Engine—Electropak. Available online: https://www.gucbirjenerator.com/engine/perkins/4008-30TAG3.pdf (accessed on 4 March 2025).
- Nohutcu, O. CFD Simulation of Airflow in a New Receiver Concept for High-Temperature Solar Heating. Master’s Thesis, FH Aachen University of Applied Sciences, Aachen, Germany, 2023. [Google Scholar]
- Kubenova, M.; Kuterbekov, K.; Bekmyrza, K.; Kabyshev, A.; Kabdrakhimova, G.; Atamurotov, F.; Ibrahim, W. Exhaust waste heat recovery system using thermoelectric generator: A prospective of novel simulation technique toward low-carbon technology. Int. J. Low-Carbon Technol. 2025, 20, 8–24. [Google Scholar] [CrossRef]
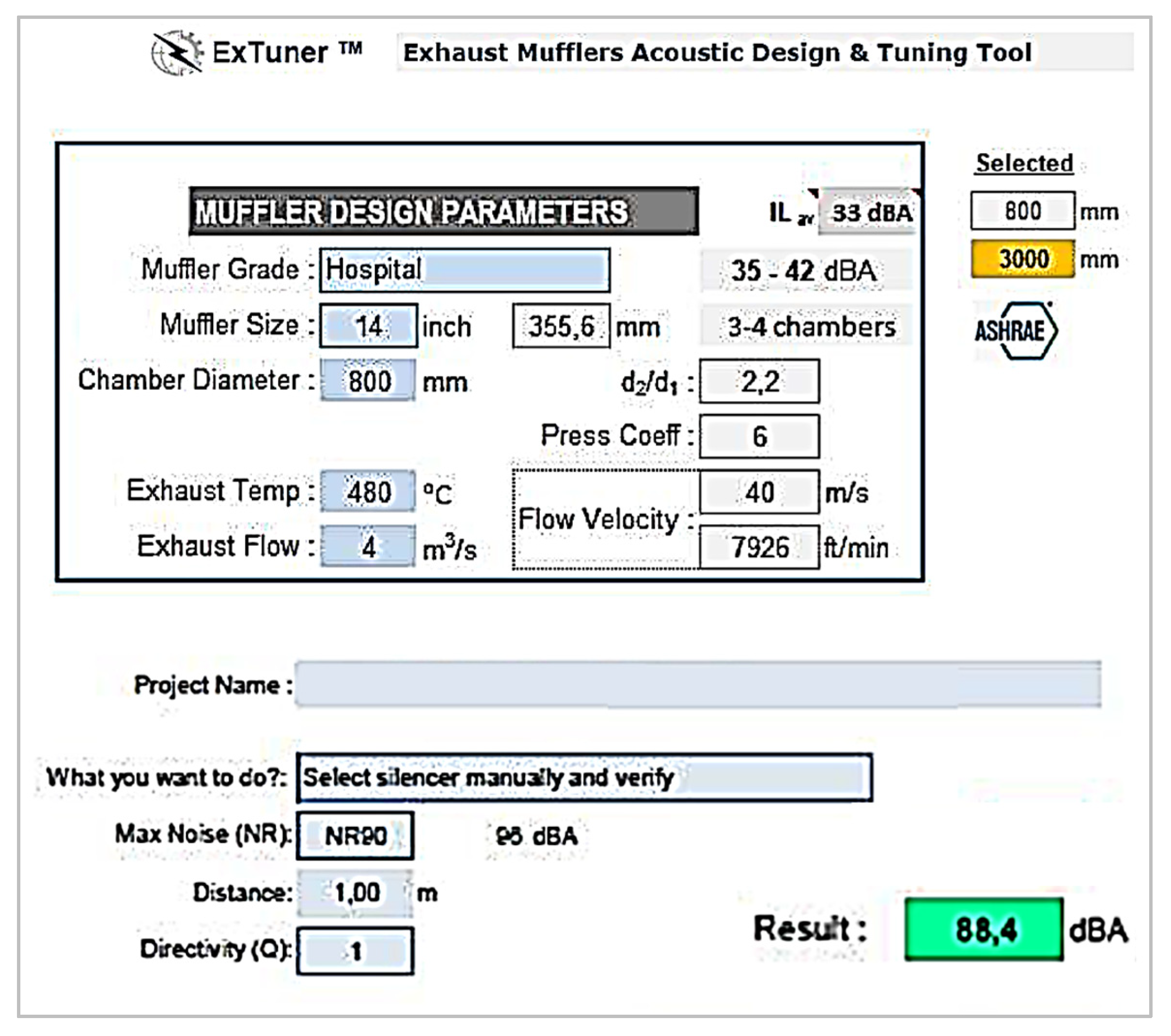
- NEC Najah Engineering Consultants LLC-NEC Acostix-ExTuner Program Sheets. Available online: https://najahengineering.com/acostix.html (accessed on 4 March 2025).
- EN 13384-1:2015; Chimneys—Thermal and Fluid Dynamic Calculation Methods—Part 1: Chimneys Serving One Heating Appliance. BSI: London, UK, 2015.
- Tzouka, E.; Karavasilis, T.; Kashani, M.M.; Afshan, S. Finite element modelling of push-out tests for novel locking nut shear connectors. Structures 2021, 33, 1020–1032. [Google Scholar] [CrossRef]
- Navarro, M.; Ivorra, S.; Varona, F.B. Parametric finite element analysis of punching shear behaviour of RC slabs reinforced with bolts. Comput. Struct. 2020, 228, 106147. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Mashiri, F.; Mirza, O. Parametric study of innovative bolted shear connectors using 3D finite element modelling. J. Constr. Steel Res. 2021, 179, 106565. [Google Scholar] [CrossRef]
- Tanriver, K.; Ay, M. Topology Optimization of a Steel Construction Bolt Under Boundary Conditions. Euroasia J. Math. Eng. Nat. Med. Sci. 2020, 7, 31–47. [Google Scholar]
- Tanriver, K.; Ay, M. Experimental, Software and Topological Optimization Study of Unpredictable Forces in Bolted Connections. Tech. Gaz. 2023, 30, 1175–1184. [Google Scholar]
- Tanriver, K.; Ay, M. Efficient Path Planning for Drilling Processes: A Hybrid Approach of Genetic Algorithm and Ant Colony Optimization. Trans. Famena 2024, 48, 125–140. [Google Scholar] [CrossRef]
- Tanriver, K.; Ay, M. Simulation of Speed Reducer Design with the Modified Ant Colony Optimization Algorithm. J. Eng. Sci. Res. 2024, 6, 53–64. [Google Scholar]
- Andersen, P.R.; Henríquez, V.C.; Aage, N. On the validity of numerical models for Visco thermal losses in structural optimization for micro-acoustics. J. Sound Vib. 2023, 547, 117455. [Google Scholar] [CrossRef]
- Cool, V.; Sigmund, O.; Aage, N.; Naets, F.; Deckers, E. Vibroacoustic topology optimization for sound transmission minimization through sandwich structures. J. Sound Vib. 2024, 568, 117959. [Google Scholar] [CrossRef]
- Fischer, S.; Szürke, S.K. Detection Process of Energy Loss in Electric Railway Vehicles. Facta Univ. Ser. Mech. Eng. 2023, 21, 81–99. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Brennan, M.J.; Yang, T. Design and optimization of a two-degrees-of-freedom single-sided vibro-impact nonlinear energy sink for transient vibration suppression of a thin plate. J. Sound Vib. 2024, 587, 118512. [Google Scholar] [CrossRef]
- Maury, C.; Bravo, T.; Amielh, M.; Mazzoni, D. Acoustic Pressure Amplification through In-Duct Sonic Black Holes. Appl. Sci. 2024, 14, 4699. [Google Scholar] [CrossRef]




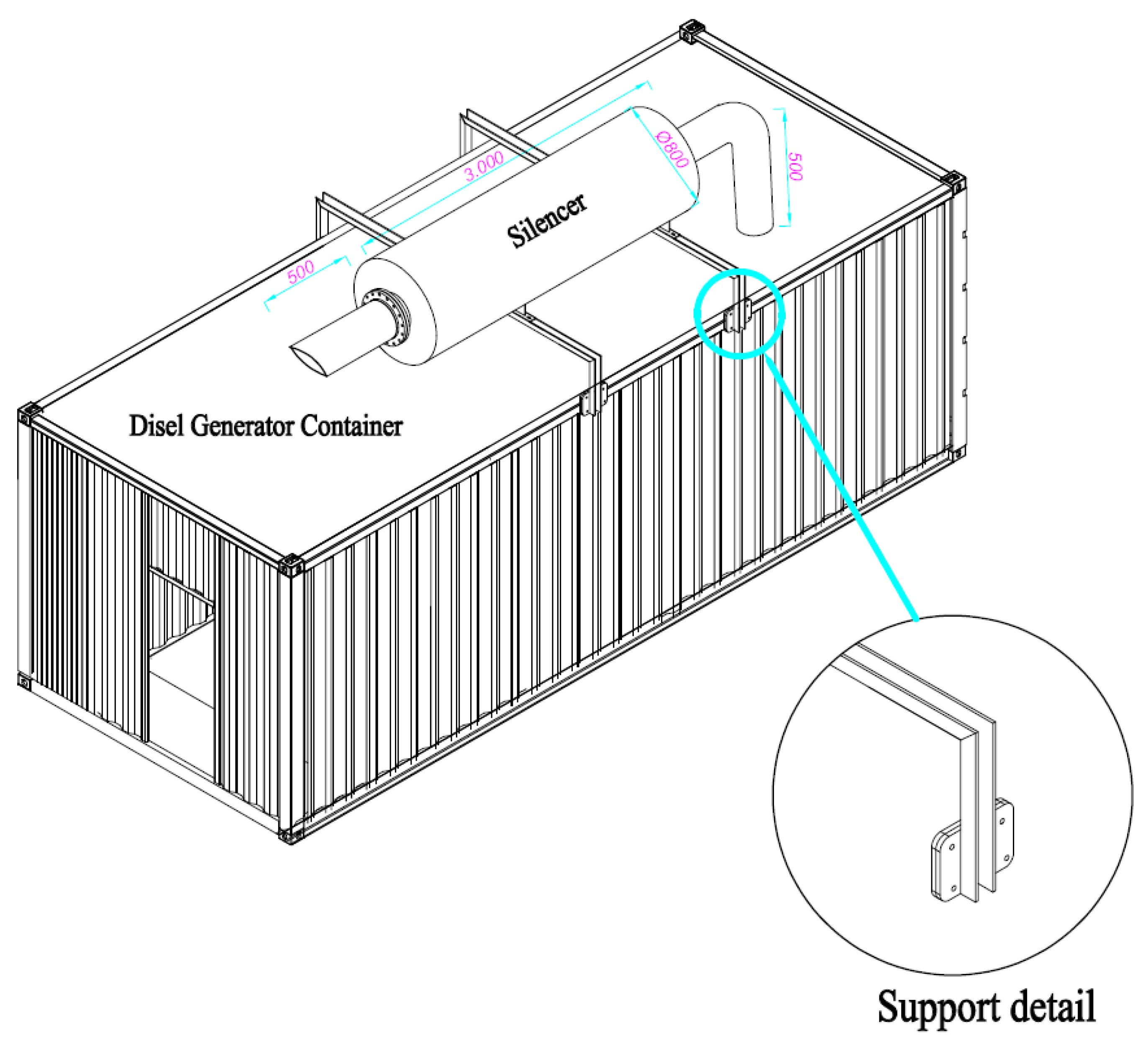



| Part No | Diameter | Thick | Material Specification | Welding Process |
|---|---|---|---|---|
| (mm) | (mm) | |||
| Silencer body | Ø 800 | 3.0 | ST 37 | Manuel 135 MAG |
| Sound absorber isolation | Ø 796 | 100.0 | Rockwool 100 kg/m3 | - |
| Isolation Cover | Ø 596 | 3.0 | ST 37 perforated sheet | Manuel 135 MAG |
| Inlet Pipe | Ø 355.6 | 3.0 | ST 37 | Manuel 135 MAG |
| Outlet Pipe | Ø 355.6 | 3.0 | ST 37 | Manuel 135 MAG |
| Description | Units | Type of Operation and Application 50 Hz @1500 rev/min | |||
|---|---|---|---|---|---|
| Base Load | Prime Power | Standby Power | Data Used | ||
| Exhaust Gas Flow | m3/min | 180 | 203 | 240 | 240 |
| Exhaust Gas Temp. | °C | 460 | 473 | 482 | 482 |
| Allowable Back Pressure | KPa | 7 | 7 | ||
| Performance Criteria | Conventional Silencer | The Novel Designed Silencer | ||
|---|---|---|---|---|
| Preliminary Calculation (Design, Pressure Loss, Noise Level) | - | The same calculations previously performed are used for the entire design | + | A preliminary calculation is performed before each design |
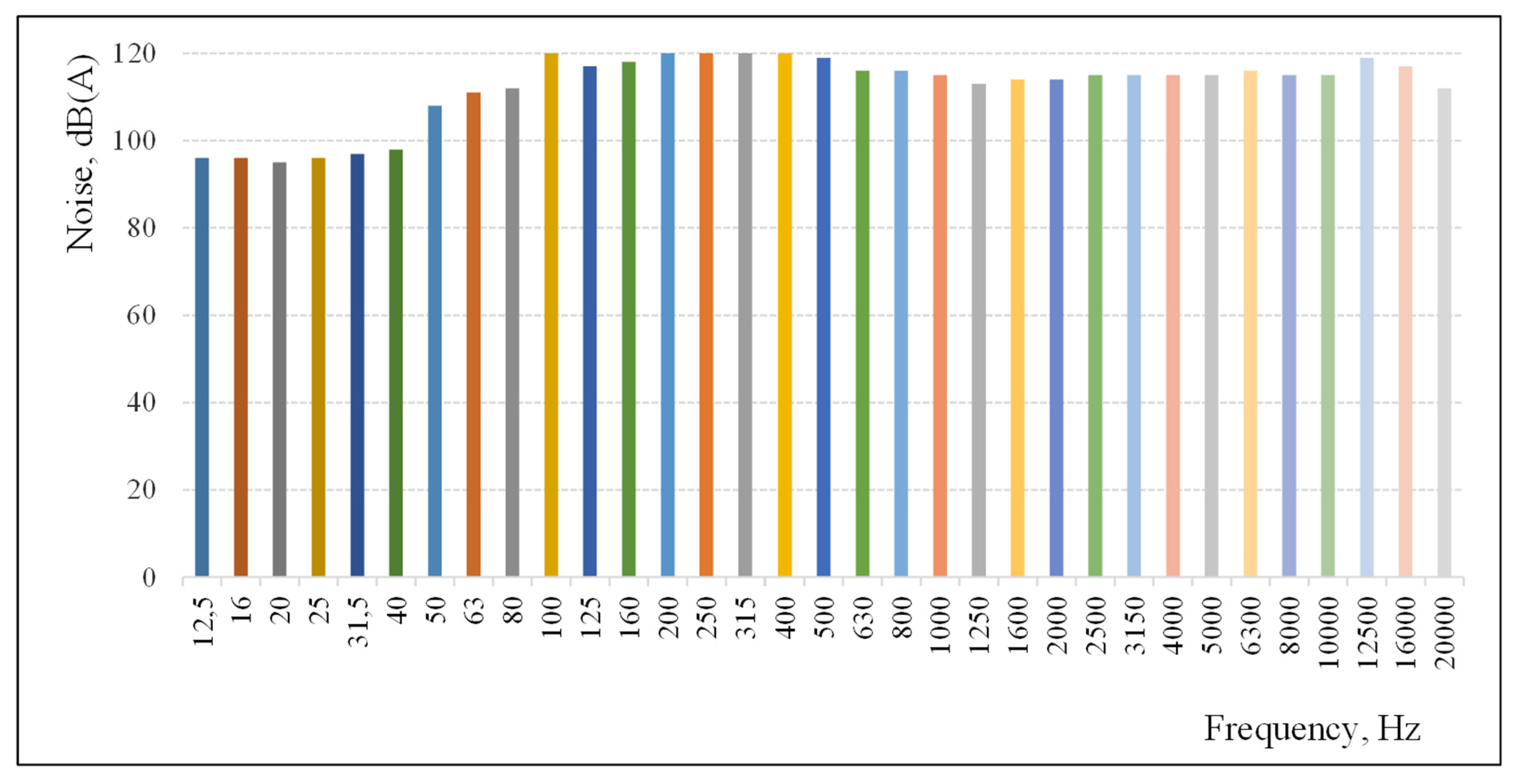
| Noise Level ≤ 96 dB(A) at 1 m. | 110 | It does not meet the design requirements | 88.1 | It meets the design requirements |
| Pressure Loss ≤ 7 KPa dB(A) | 0.160 | It meets the design requirements, but it is too tolerant from an engineering perspective | 6.149 | It meets the design requirements |
| Dimension ≤ Container Dimensions | + | Outer dimensions remain the same | + | Outer dimensions remain the same |
| Structural Optimization | - | None | + | An optimization model has been proposed to be calculated for the users |
| Bold Diameter | Plate Dimensions | Sample Name | Tensile Stress (MPa) | Load (N) |
|---|---|---|---|---|
| M12 × 50 | 12 × 100 × 120 | Bold Sample 1 | 273.00 | 39,312.45 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 2 | 267.49 | 38,518.27 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 3 | 269.06 | 38,744.56 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 4 | 282.30 | 40,651.37 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 5 | 265.81 | 38,276.59 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 6 | 272.53 | 39,243.84 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 7 | 275.06 | 39,609.19 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 8 | 267.99 | 38,590.41 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 9 | 267.28 | 38,488.92 |
| M12 × 50 | 12 × 100 × 120 | Bold Sample 10 | 271.56 | 39,104.78 |
| Parameter | Experimental Result | Simulation Result | Total Error (%) |
|---|---|---|---|
| Front Noise Reduction (dB(A)) | 85.5 | 88.1 | −3.04% |
| Side Noise Reduction (dB(A)) | 74.4 | 88.1 | −18.41% |
| Pressure Loss (KPa) | 6.00 | 6.15 | −2.48% |
| Structural Stress (MPa) | 271.21 | 271.99 | −0.29% |
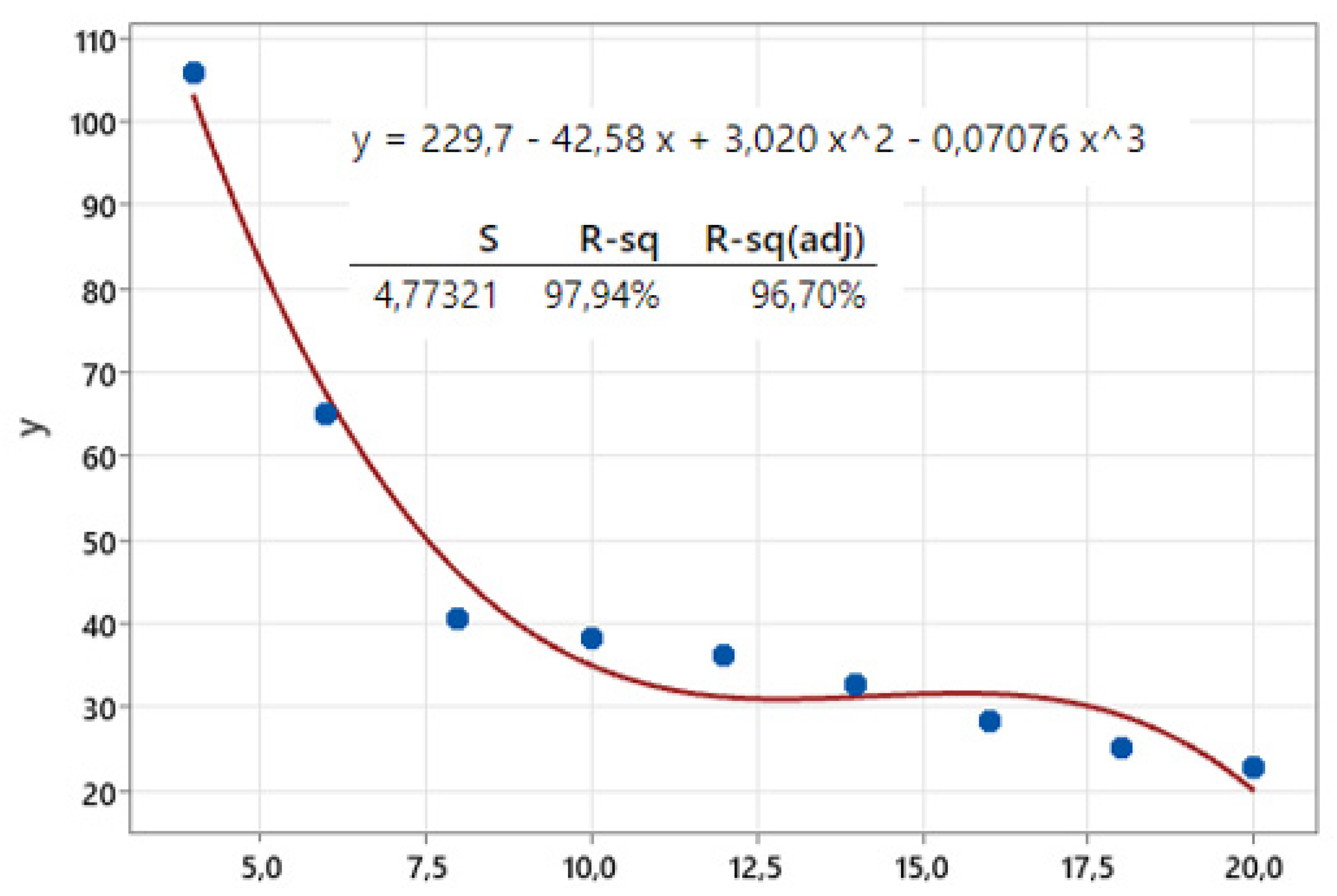
| Load (N) | Bolt Diameter (mm) | Stress Analysis Result (MPa) |
|---|---|---|
| 11,722 | 4 | 105.77 |
| 6 | 65.11 | |
| 8 | 40.62 | |
| 10 | 38.45 | |
| 12 | 37.03 | |
| 14 | 32.89 | |
| 16 | 28.42 | |
| 18 | 25.41 | |
| 20 | 22.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanriver, K. CFD Simulation Analysis of a Diesel Generator Exhaust Muffler and Performance-Based Optimization. Processes 2025, 13, 887. https://doi.org/10.3390/pr13030887
Tanriver K. CFD Simulation Analysis of a Diesel Generator Exhaust Muffler and Performance-Based Optimization. Processes. 2025; 13(3):887. https://doi.org/10.3390/pr13030887
Chicago/Turabian StyleTanriver, Kursat. 2025. "CFD Simulation Analysis of a Diesel Generator Exhaust Muffler and Performance-Based Optimization" Processes 13, no. 3: 887. https://doi.org/10.3390/pr13030887
APA StyleTanriver, K. (2025). CFD Simulation Analysis of a Diesel Generator Exhaust Muffler and Performance-Based Optimization. Processes, 13(3), 887. https://doi.org/10.3390/pr13030887






