An Unresolved SPH-DEM Coupling Framework for Bubble–Particle Interactions in Dense Multiphase Systems

Abstract

This study presents a novel unresolved SPH-DEM coupling framework to investigate the complex interactions between rising gas bubbles and sinking solid particles in multiphase systems. Traditional numerical methods often struggle with large deformations, multiphase interfaces, and computational efficiency when simulating dense particle-laden flows. To address these challenges, the proposed model leverages SPH’s Lagrangian nature to resolve fluid motion and bubble dynamics, while the DEM captures particle–particle and particle–bubble interactions. An unresolved coupling strategy is introduced to bridge the scales between fluid and particle phases, enabling efficient simulations of large-scale systems with discrete bubbles/particles. The model is validated against benchmark cases, including single bubbles rising and single particle’s sedimentation. Simulation studies reveal the effects of particle/bubble number and initial distance on phase interaction patterns and clustering behaviors. Results further illustrate the model’s capability to capture complex phenomena such as particle entrainment by bubble wakes and hindered settling in dense suspensions. The framework offers a robust and efficient tool for optimizing industrial processes like mineral flotation, where bubble–particle dynamics play a critical role.

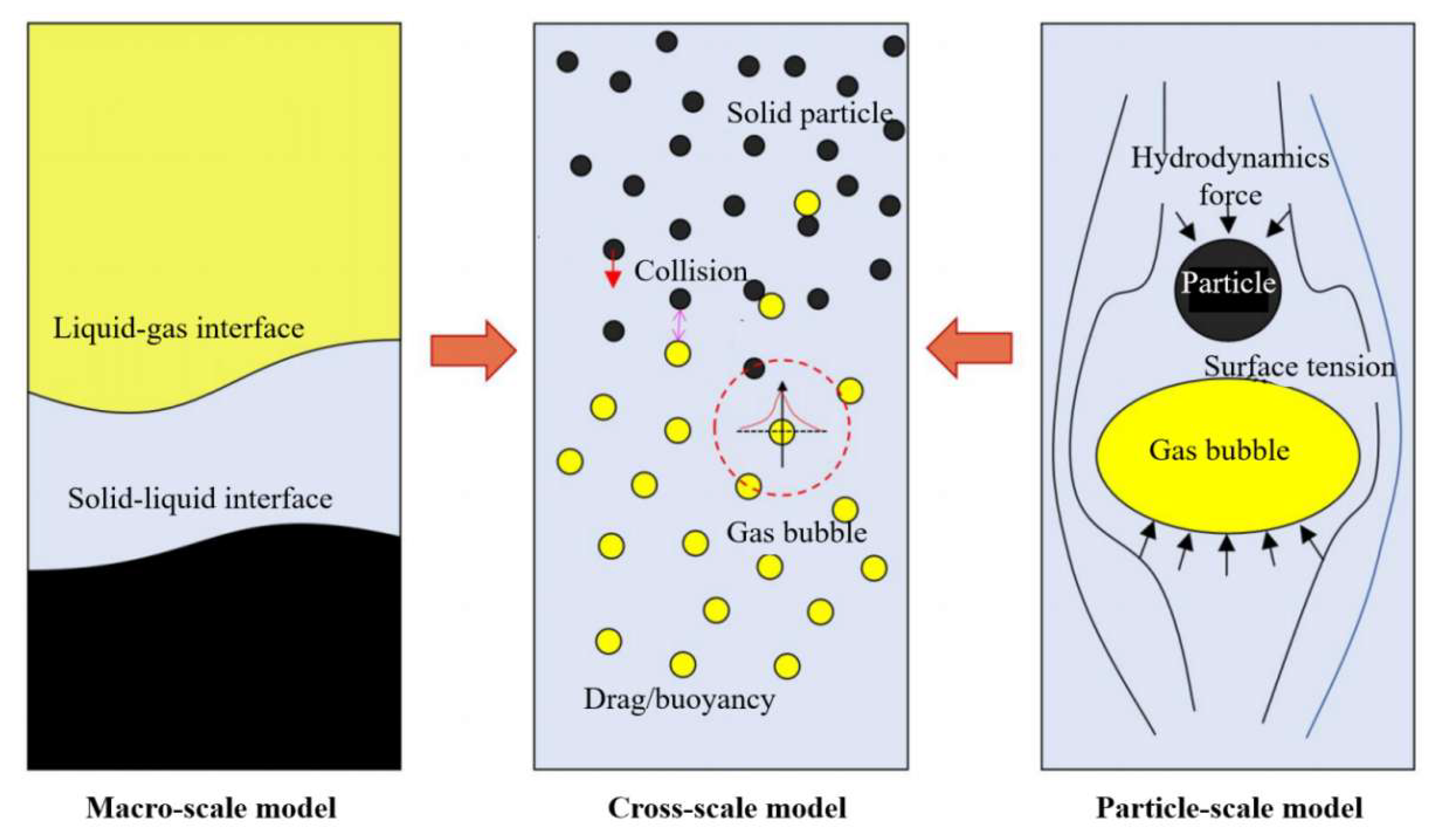
1. Introduction

The interaction between rising gas bubbles and sinking solid particles is a critical phenomenon in multiphase systems, influencing industrial processes such as mineral flotation [1], wastewater treatment [2], and chemical reactor design [3]. These interactions govern mass transfer efficiency, phase separation dynamics, and energy consumption, making their understanding essential for optimizing engineering applications. Traditional approaches to modeling bubble–particle dynamics, such as resolved/unresolved CFD-DEM [4,5] or Eulerian–Eulerian frameworks [6], face significant limitations in handling large deformations, multiphase interfaces, and computational efficiency—particularly in dense particle-laden flows.

In mineral flotation, hydrophobic particles attach to rising bubbles, enabling their separation from hydrophilic waste materials [7]. Similarly, in bioreactors, oxygen transfer via bubbles dictates microbial activity [8], while in environmental engineering, bubble-induced mixing enhances pollutant degradation. However, these processes are highly sensitive to hydrodynamic forces, particle–bubble collision efficiency, and adhesion mechanisms, which remain challenging to model accurately [9]. Recent studies on cavitation bubbles, for instance, reveal that bubble collapse can generate microjets, capable of propelling particles and exacerbating material erosion—a phenomenon critical to hydraulic machinery operating in sediment-laden flows [10]. Such findings underscore the need for robust numerical tools to capture transient bubble–particle interactions [11].

Current CFD-DEM frameworks often rely on Eulerian grids, which struggle with free-surface flows and large interfacial deformations [12]. While volume-of-fluid methods improve interface tracking [13], they have high computational costs in systems with dense particle suspensions. The interaction between particles and bubbles involves complex physical phenomena such as multiphase flow coupling, interfacial deformation, and particle collision. Although traditional grid-based numerical methods dominate in engineering simulations [14], they face significant challenges when dealing with such problems [15]. The intense deformation of the free surface during the rising of bubbles or the settling of particles requires frequent grid reconstruction, leading to the accumulation of calculation errors and a decrease in computational efficiency [16]. Coupling methods such as CFD-DEM require two-way force mapping between the fluid grid and discrete particles [17]. However, in a dense particle system, the grid division needs to meet the resolution of the particle scale, resulting in an exponential increase in the computational load [18].

The mesh-less particle method, due to its characteristics of the Lagrangian framework and discrete particle representation, has gradually become an important tool for multiphase flow simulation [19], especially demonstrating unique advantages in the particle–bubble coupling system [20]. SPH directly solves the fluid motion through kernel function interpolation without the need for explicit interface tracking and can naturally simulate the deformation and coalescence of bubbles as well as the entrainment of particles in vortices [21]. The MPS method enforces incompressibility through the particle number density constraint and has been successfully applied to the direct simulation of the rising motion of bubbles in gas–liquid two-phase flows [22]. However, current SPH or MPS-based simulations of bubbles remain largely confined to resolved regimes [23,24,25]. While these methods accurately capture bubble deformation, breakup, and coalescence by explicitly resolving gas–liquid interfaces, they inherently demand higher resolution to maintain interface sharpness and numerical stability [26]. This requirement renders them computationally prohibitive for large-scale industrial systems involving dense particle–bubble interactions, where unresolved coupling strategies are more pragmatic for balancing accuracy and efficiency [27].

As shown in Figure 1, the gas–liquid two-phase flow phenomena can be defined at three scales. Previous CFD simulations either focus on the macro scale or the micro scale of bubbles, making it challenging to balance large-scale computations with detailed modeling. This study, for the first time, introduces an unresolved SPH-DEM coupling framework to address these gaps. By leveraging SPH for fluid dynamics and DEM for discrete phase interactions, the framework combines the Lagrangian meshless advantage of SPH—ideal for free surfaces and multiphase interfaces—with DEM’s granular-scale resolution of collisions and cohesion. Key innovations include: (1) a porosity-based local averaging technique bridges fluid and discrete phases, enabling efficient momentum exchange while avoiding the computational overhead of fully resolved methods; (2) bubbles and particles are modeled as discrete entities with distinct mechanical properties, allowing simultaneous simulation of buoyancy-driven bubble rise and particle sedimentation; (3) hydrodynamic forces (drag, buoyancy) and contact mechanics are coupled through SPH interpolation and DEM contact models, capturing phenomena like particle entrainment in bubble wakes and hindered settling.

The present study focuses on two-dimensional simulations to establish foundational insights into unresolved SPH-DEM coupling mechanisms. The remainder of this paper is organized as follows. Section 2 systematically presents the unresolved SPH-DEM coupling framework, including the SPH fluid dynamics equations based on local averaging techniques and the discrete element models for particle/bubble interactions. Section 3 validates the model through benchmark cases and investigates bubble–particle interaction mechanisms in dense systems, highlighting phase segregation and hindered settling phenomena. Section 4 discusses the computational efficiency advantages and inherent limitations of the framework while outlining future research directions.

2. Methodology

2.1. SPH Equations for Continuous Flow Based on Local Average Technique

This section outlines the governing equations, numerical implementation, and specific adaptations for modeling fluid flows. In fluid media with high concentrations of solid particles and bubbles, solving the Navier–Stokes equations directly via fully resolved coupling approaches imposes significant computational costs. However, a coarse-grained coupling framework offers a more efficient solution. This method employs a local averaging technique to model the coupling forces between the fluid phase and discrete particle/bubble phase. It defines local average variables to characterize momentum transfer in particle/bubble suspensions. These spatially averaged variables at any point x within the fluid domain are derived through a convolution operation with a smoothing kernel, as described below:

$$〈\overline{f}(x)〉=ϵ(x)f(x)={\displaystyle {\int }_{\mathrm{fluid}}\overline{f}(x^{\text{'}})}W(x-x^{\text{'}})dV,$$

(1)

$$ϵ(x)=1-{\displaystyle {\int }_{\mathrm{particle}}W(x-x^{\text{'}})dV},$$

(2)

where $\overline{f}(x)$ denotes the local average value of f$\left(x\right)$. $ϵ(x)$ denotes the porosity, for no particle/bubble around, $ϵ(x)$ = 1.

SPH represents a continuous fluid, and an SPH particle represents a fluid particle. The porosity at the location of the fluid particle a can be calculated by the following equation:

$${ϵ}_a=1-{\displaystyle \sum _j{W}_{aj}(h_c)}{V}_j,$$

(3)

where V_j is the volume of particle/bubble j and h_c is the smoothing length.

From Equation (3), if the area surrounding SPH particle a is filled with solid particles or bubbles, the normalization property of the kernel function W implies that the summation $\sum W_{aj}\left(h_c\right)$ results in a value of 1, that is, the porosity ${ϵ}_a$ is 0.

We tested the calculation results of the porosity through two types of densely arranged particles. As shown in Figure 2, they are regularly arranged and staggeredly arranged, respectively. The porosities corresponding to these two arrangement patterns are approximately 0.21 and 0.1, respectively. We also arranged SPH particles uniformly distributed within the test computational domain, as shown in Figure 3. Then, we calculated the porosity values of all SPH particles at the central position of the computational domain and plotted Figure 4 with the X-coordinate of the particles as the abscissa and the porosity as the ordinate. As shown in the figure, the porosity results calculated according to Equation (3) are basically consistent with the theoretical results.

For fluid SPH particles, the local density value needs to be scaled according to the porosity, as shown in the following:

$${\overline{\rho }}_a={\epsilon }_a{\rho }_a,$$

(4)

where ${\rho }_a$ and ${\overline{\rho }}_a$ represent the actual density and the scaled density, respectively.

The motion equations of the fluid phase are derived from the Navier–Stokes equations. Regarding the continuity and momentum equations in the SPH framework, when adopting the local average technique, they can be expressed as follows:

$${\displaystyle \frac{\mathrm{d}{\overline{\rho }}_a}{\mathrm{d}t}}={\overline{\rho }}_a{\displaystyle \sum _{b=1}^N\frac{m_b}{{\overline{\rho }}_b}(}{\overrightarrow{v}}_a^{\alpha }-{\overrightarrow{v}}_b^{\alpha })\cdot {\displaystyle \frac{\partial W_{ab}}{\partial {\overrightarrow{x}}_a^{\alpha }}},$$

(5)

$${\displaystyle \frac{\mathrm{d}{\overrightarrow{v}}_a^{\alpha }}{\mathrm{d}t}}={\displaystyle \sum _{b=1}^N{m}_b\left[-\left(\frac{P_a}{{\overline{\rho }}_a^2}+\frac{P_b}{{\overline{\rho }}_b^2}\right)+{\Pi }_{ab}^{visc}-{\mathsf{\pi }}_{ab}^{art}\right]}\cdot {\displaystyle \frac{\partial W_{ab}}{\partial {\overrightarrow{x}}_a^{\alpha }}}+{\overrightarrow{F}}_{f-a}^{\alpha }+{\overrightarrow{F}}_{f-s}^{\alpha }+{\overrightarrow{g}}^{\alpha },$$

(6)

where ${\overrightarrow{v}}_{\mathrm{a}}$ and P_a are the velocity and pressure, respectively. ${\overrightarrow{F}}_{f-a}$ and ${\overrightarrow{F}}_{f-s}$ are the particle–fluid coupling force and the bubble–fluid coupling force, respectively.

The term ${\Pi }_{ab}^{visc}$ is the viscous term and is written as:

$${\Pi }_{ab}^{visc}={\displaystyle \sum _{b=1}^N{m}_b\left[\frac{4{\mu }_f{\overrightarrow{r}}_{ab}}{({\overline{\rho }}_a+{\overline{\rho }}_b){\left|{\overrightarrow{r}}_{ab}\right|}^2}\right]}\cdot {\overrightarrow{v}}_{ab},$$

(7)

where ${\mu }_f$ is the fluid viscosity.

The third term ${\mathsf{\pi }}_{\mathrm{ab}}^{\mathrm{art}}$ corresponds to the so-called artificial viscous force suppressing the numerical oscillations. It is written as:

$$\begin{gathered} {\mathsf{\pi }}_{ab}^{art}=\left\{\begin{array}{ll}{\displaystyle \frac{-{\alpha }_{\mathsf{\pi }}{\overline{c}}_{ab}{\varphi }_{ab}+{\beta }_{\mathsf{\pi }}{{\varphi }_{ab}}^2}{{\overline{\rho }}_{ab}}}\hfill & ,{\overrightarrow{v}}_{ij}\cdot {\overrightarrow{x}}_{ij}<0\hfill \\ 0,\hfill & {\overrightarrow{v}}_{ij}\cdot {\overrightarrow{x}}_{ij}\ge 0\hfill \end{array}\right., \\ {\stackrel{\mathrm{-}}{c}}_{\mathrm{ab}}={\displaystyle \frac{c_{\mathrm{a}}+c_{\mathrm{b}}}{2}},{\stackrel{\mathrm{-}}{\rho }}_{\mathit{ab}}={\displaystyle \frac{{\stackrel{\mathrm{-}}{\rho }}_a+{\stackrel{\mathrm{-}}{\rho }}_b}{2}},{\varphi }_{ab}={\displaystyle \frac{{\overline{h}}_{ab}\left({\overrightarrow{v}}_{ab}\cdot {\overrightarrow{x}}_{ab}\right)}{{\left|{\overrightarrow{x}}_{ab}\right|}^2+{\left(0.1{\overline{h}}_{ab}\right)}^2}} \end{gathered}$$

(8)

where c_a denotes the speed of sound, ${\stackrel{\mathrm{-}}{h}}_{\mathrm{ab}}=({\mathrm{h}}_{\mathrm{a}}+h_{\mathrm{b}})/2$, ${\overrightarrow{V}}_{\mathrm{ab}}={\overrightarrow{V}}_{\mathrm{a}}-{\overrightarrow{V}}_{\mathrm{b}}$ and ${\overrightarrow{X}}_{\mathrm{ab}}={\overrightarrow{X}}_{\mathrm{a}}-{\overrightarrow{X}}_{\mathrm{b}}$

2.2. DEM for Particles and Bubbles

The DEM is employed to resolve the motion and interactions of solid particles and gas bubbles, treating them as discrete Lagrangian entities, as shown in Figure 5. This section details the motion equations, contact mechanics, and adaptations for modeling bubble dynamics within the unresolved SPH-DEM framework.

For each discrete element (particle or bubble), the following equations govern its dynamics:

$$\left\{\begin{array}{c}{m}_i{\displaystyle \frac{d{\overrightarrow{v}}_i}{dt}}={\overrightarrow{F}}_{a-a}+{\overrightarrow{F}}_{a-s}+{\overrightarrow{F}}_{a-f}+m_i\overrightarrow{g}\hfill \\ I_i{\displaystyle \frac{d{\overrightarrow{\omega }}_i}{dt}}={\overrightarrow{T}}_{a-a}+{\overrightarrow{T}}_{a-s}\hfill \end{array}\right.,$$

(9)

where m_i stands for its mass, I_i is its moment of inertia, v_i is the centroid velocity, and ${\omega }_i$ is the angular velocity. T_a-a represents the total contact torque resulting from particle–particle interactions, and T_a-s is the total contact torque due to particle–bubble interactions. The indices i and j are used to denote the DEM, while the indices a and b are assigned to SPH particles.

Hydrodynamic forces, F_a-f: Drag, buoyancy, and pressure gradient forces mapped from the SPH fluid phase (see Section 2.3).

Body forces, m_ig: Gravity and other external forces.

Bubble–particle/particle–particle interaction forces, F_a-a, F_a-s.

Bubbles are modeled as DEM elements with reduced stiffness compared to solid particles. Buoyancy-driven motion is dominated by density contrast between gas and liquid phases. Bubble coalescence/breakup is neglected in this study.

As shown in Figure 6, for each pair of interacting DEM particles, contact force is enforced by a spring, a damper, and a slider. It can be divided into normal contact force ${\overrightarrow{F}}_{\mathrm{ij}}^{\mathrm{n}}$ and tangential contact force ${\overrightarrow{F}}_{\mathrm{ij}}^{\mathrm{t}}$:

$$\left\{\begin{array}{c}{\overrightarrow{F}}_{ij}^n=-k_n{\delta }_n\overrightarrow{n}-d_n{\overrightarrow{v}}_{ij}^n\\ {\overrightarrow{F}}_{ij}^t=-k_t{\delta }_t\overrightarrow{t}-d_t{\overrightarrow{v}}_{ij}^t\end{array}\right.,$$

(10)

where $\overrightarrow{n}$ and $\overrightarrow{t}$ denote the normal and tangent vectors. k and η are the stiffness and damping coefficients. δ and ${\overrightarrow{v}}_{\mathit{ij}}$ denote the overlap and relative velocity.

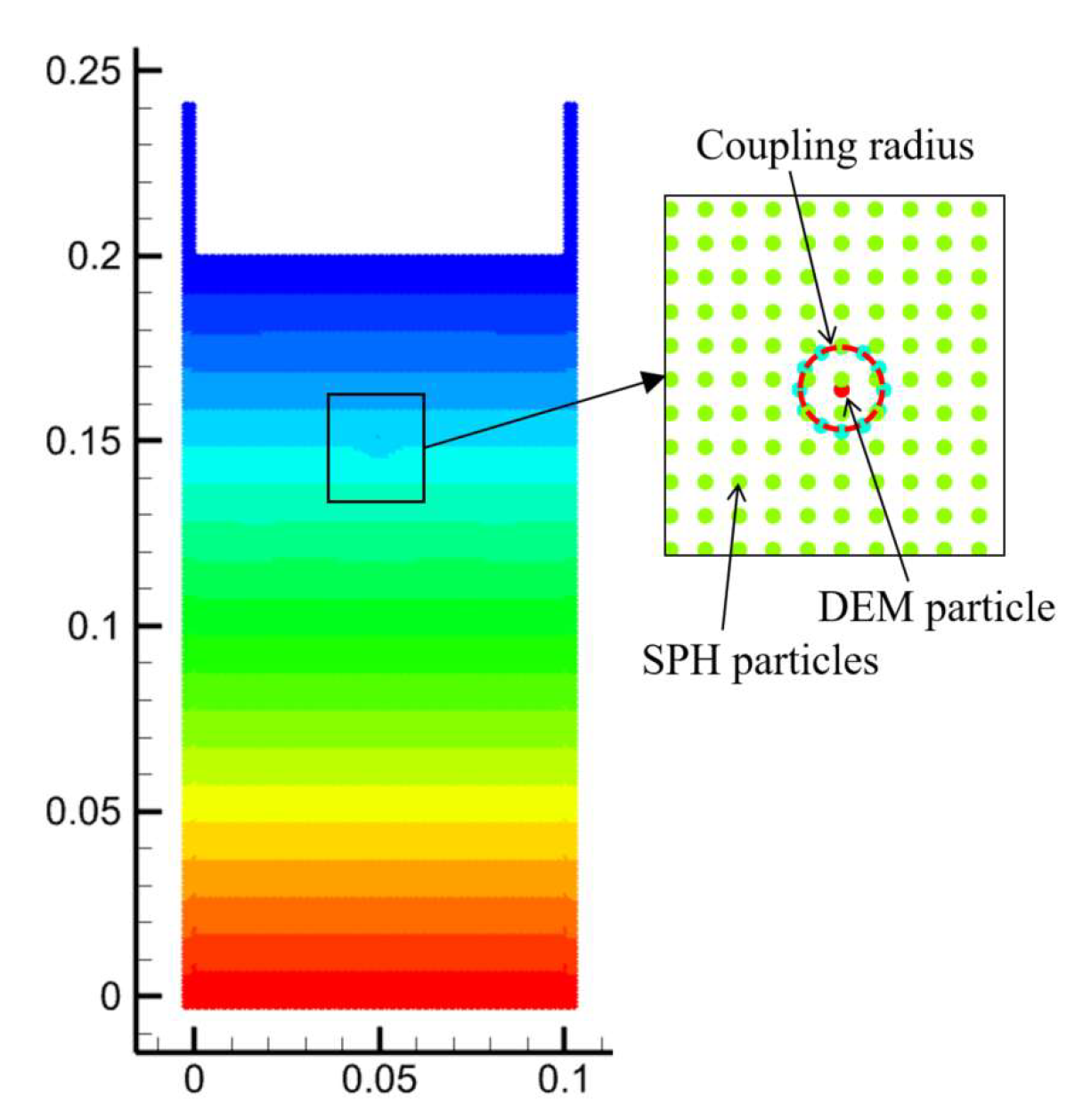
2.3. Coupling Strategy

The unresolved SPH-DEM coupling strategy bridges the fluid phase and discrete phases (particles/bubbles) through two-way coupling momentum exchange, leveraging the porosity field from Section 2.1 and DEM contact forces from Section 2.2. This section outlines the force mapping algorithms and numerical implementation techniques.

2.3.1. Fluid-to-Discrete-Phase Coupling

The core of SPH-DEM coupling lies in enabling interactions between the two particle types. In the unresolved coupling framework, the coupling forces governing the solid–fluid interactions presented are illustrated in Figure 7. By leveraging the kernel smoothing technique, the interphase coupling radius is defined as R_c = 2h_c. For a discrete element particle i, the governing relation can be formulated as:

$${\overrightarrow{F}}_{a-f}=V_i{(-\nabla P+\nabla \cdot \overrightarrow{\tau })}_i+{\overrightarrow{F}}_d,$$

(11)

where the first term represents hydrodynamic force, including the buoyancy and shear force acting on DEM within R_c. The second term ${\overrightarrow{F}}_d$ denotes drag force.

The Shepard SPH kernel is employed to solve the hydrodynamic force terms:

$$\left\{\begin{array}{l}{V}_i{(-\nabla P+\nabla \cdot \overrightarrow{\tau })}_i={\displaystyle \frac{1}{{\displaystyle \sum _a\frac{m_a}{{\rho }_a}{W}_{ia}(h_c)}}}{\displaystyle \sum _a{m}_a{\theta }_a}{W}_{ia}(h_c)\hfill \\ {\theta }_a={\displaystyle \sum _b{m}_b\left[-\left(\frac{P_a}{{\overline{\rho }}_a^2}+\frac{P_b}{{\overline{\rho }}_b^2}\right)+{\Pi }_{ab}^{visc}\right]}\cdot {\nabla }_a{W}_{ab}(h)\hfill \end{array}\right.,$$

(12)

where the subscript a represents the SPH particle within the coupling radius of the DEM particle i, and the subscript b represents the SPH particle within the support domain of the particle a.

2.3.2. Discrete-to-Fluid-Phase Coupling

The fluid–particle/bubble hydrodynamic interactions are incorporated into the SPH framework through kernel-based force interpolation, where the discrete forces are spread to neighboring SPH particles using the smoothing kernel W. In order to satisfy Newton’s third law, the coupling force ${\overrightarrow{F}}_{f-a}$ of the SPH particle a subjected to the DEM particles in Equation (6) is the weighted average of ${\overrightarrow{F}}_{a-f}$ acting on the DEM particles nearby (Figure 8), given by:

$$\left\{\begin{array}{l}{\overrightarrow{F}}_{f-a}=-{\displaystyle \frac{m_a}{{\overline{\rho }}_a}}{\displaystyle \sum _i\frac{1}{S_i}}{\overrightarrow{F}}_{a-f}{W}_{ai}(h_c)\hfill \\ S_i={\displaystyle \sum _b\frac{m_b}{{\overline{\rho }}_b}}{W}_{bi}(h_c)\hfill \end{array}\right.,$$

(13)

where the subscript b represents the SPH particle within the coupling radius R_c of the DEM particle i.

2.4. Numerical Implementation

The selection of time step Δt plays a critical role in explicit dynamic simulations. On one hand, large time steps can lead to insufficient temporal resolution for capturing SPH/DEM particle contacts and compromising numerical stability that terminate computations. On the other hand, overly small Δt requires an impractical number of iterations to resolve the same physical time, escalating computational costs and degrading efficiency.

For SPH fluid particles, the time step is governed by the CFL criterion. In the DEM framework, temporal discretization is controlled by the normal stiffness parameter k_n to maintain contact mechanics fidelity. The resultant time step formulation is given by:

$$\left\{\begin{array}{c}\Delta t=\min \left(\Delta t_{sph},\Delta t_{dem}\right)\\ \Delta t_{sph}={\min }_{a\mathrm{th}-\mathrm{particle}}\left({\displaystyle \frac{C_F{h}_a}{c_a+\left|{\overrightarrow{v}}_a\right|}}\right)\hfill \\ \Delta t_{dem}={\displaystyle \frac{2\pi }{{\alpha }_{tn}}}\sqrt{{\displaystyle \frac{m_i}{k_n}}}\hfill \end{array}\right.,$$

(14)

where C_F = 0.1 is the coefficient. To maintain numerical stability, the coupled SPH-DEM framework adopts the smaller time step when Δt_sph and Δt_dem differ within an order of magnitude. This strategy ensures temporal synchronization between the fluid and discrete phases.

The overall solution procedure of the coupled model is outlined in Figure 9. The time integration employs the leap-frog scheme, while neighbor particle searching utilizes the linked-list algorithm to enhance computational efficiency.

3. Model Validation and Simulation Results

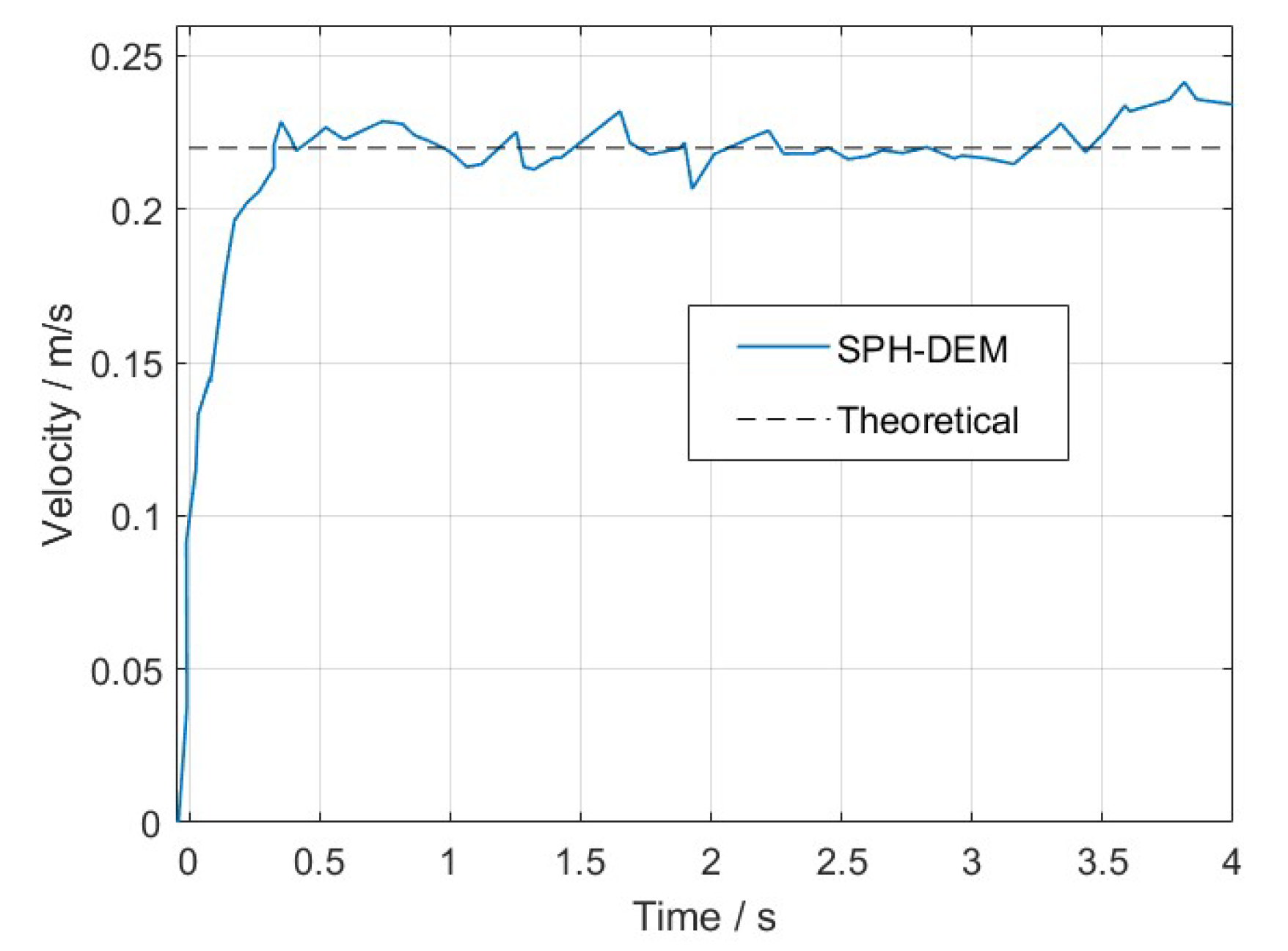
3.1. Single Bubble Rising in Quiescent Fluid

This work investigates the velocity evolution of an R = 16 mm buoyant bubble ascending in a quiescent fluid. A steady state is attained after an initial transient period, where buoyancy and drag forces achieve equilibrium. The computational domain is designed with sufficient width to eliminate wall effects and height to allow the bubble to traverse multiple radii after reaching terminal velocity. With a low Reynolds number (Re = 5), viscous forces dominate the flow dynamics. Strong surface tension maintains a cylindrical bubble shape. The bubble’s velocity is defined as the translational speed of its centroid. Figure 10 demonstrates velocity convergence across all resolutions toward its terminal rising velocity. For this configuration, the hydrodynamic force on the bubble can be analogous to that on an infinite rigid cylinder in uniform, gravity-free flow. For spherical bubbles, this force ranges from 2/3 to 1 times the force on a solid sphere, dependent on the fluid viscosity ratio. With our chosen viscosities, the force on a spherical bubble is 80% of that on a rigid sphere, described by the following expression [21]:

$$F_{c\infty }={\displaystyle \frac{4\pi {\mu }_x{u}_{c\infty }}{\frac{1}{2}-\gamma -\ln \left(\frac{R{u}_{c\infty }{\rho }_x}{4{\mu }_x}\right)}}.$$

(15)

Numerical approximation yields a terminal velocity of V = 0.22 m/s, plotted in Figure 10 and closely matching converged simulation results. As expected, this value is slightly lower than the theoretical prediction for a rigid cylinder due to minor flow separation behind the bubble. Nevertheless, the close agreement between numerical and theoretical outcomes validates the realism of the terminal velocity.

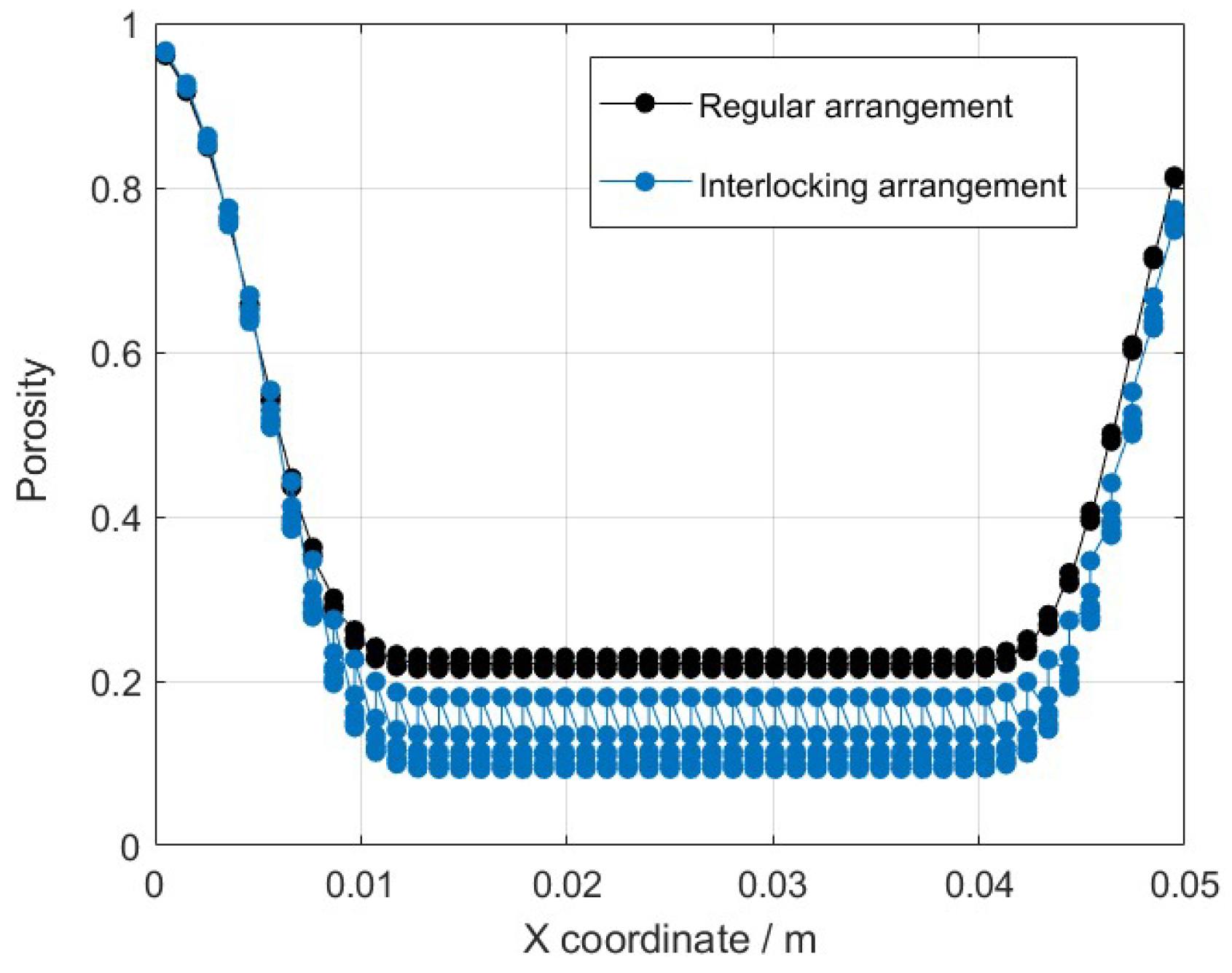
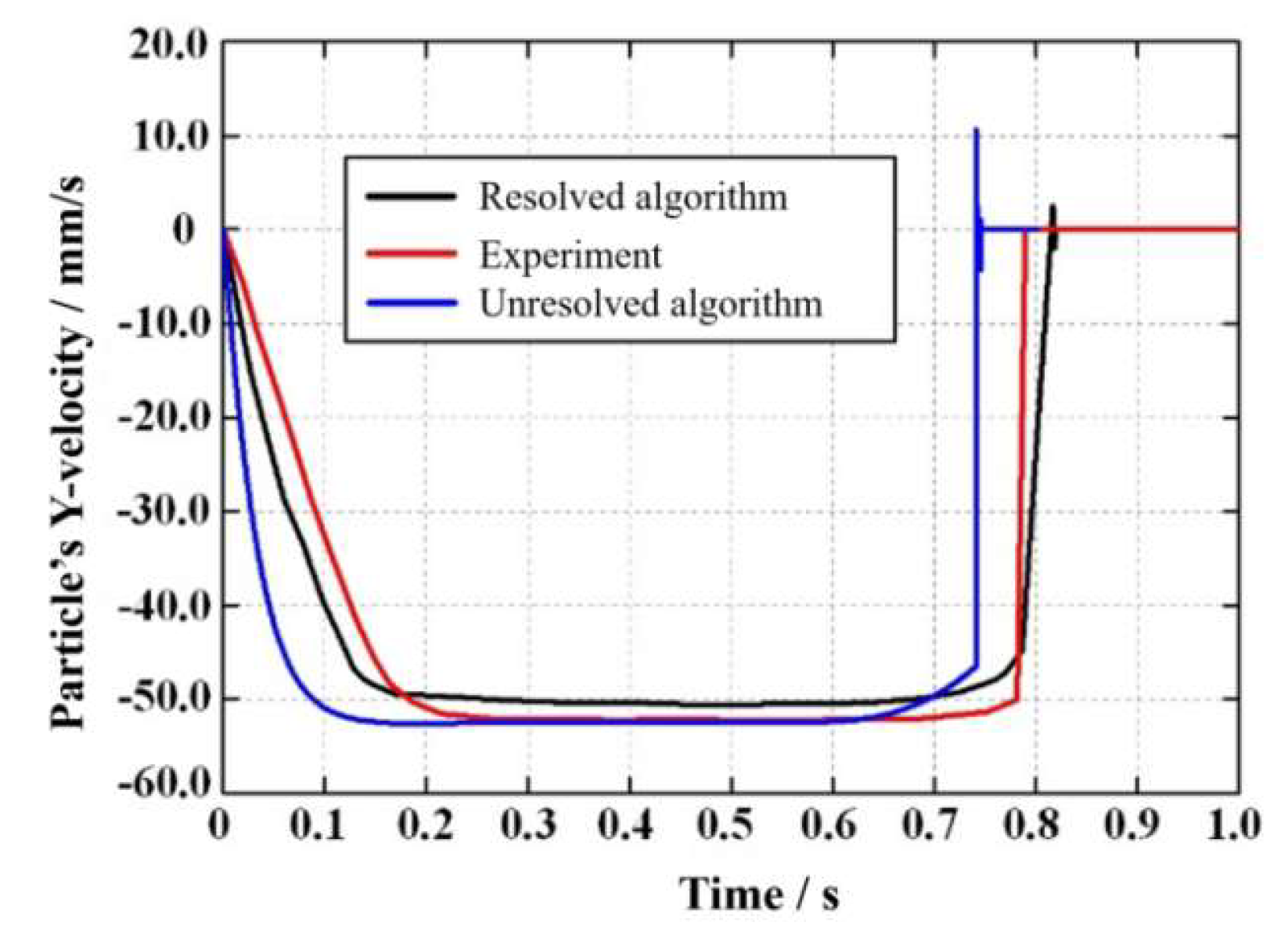
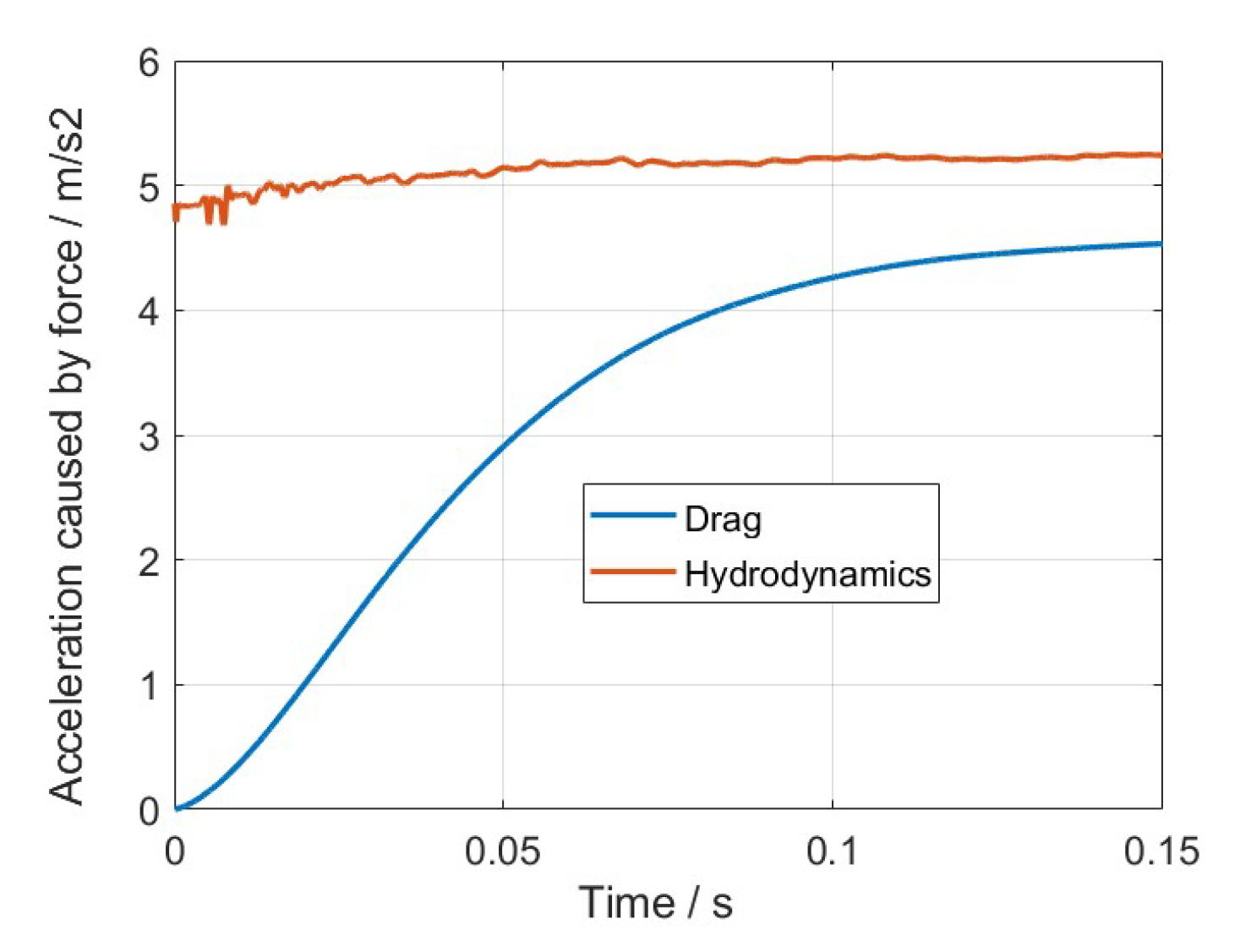
3.2. Particle Settling in Viscous Fluid

To verify the effectiveness of the SPH-DEM coupling algorithm, a numerical model of single-particle sedimentation is constructed, as shown in Figure 11. The initial spacing of the fluid SPH particles is d_ini = 1.0 × 10⁻³ m, the smoothing length is h = 1.25 d_ini, the SPH-DEM coupling radius is R_c = 2d = 5 × 10⁻³ m, and the time step is Δt = 2.5 × 10⁻⁷ s. There are a total of 2970 SPH particles and 1 DEM particle.

The curve of the relationship between the particle velocity and time is shown in Figure 12. The simulated particle sedimentation process by the coupling algorithm is in good agreement with the experimental results, with only some differences in the acceleration stage (0 < t < 0.20 s), the deceleration stage (0.64 < t < 0.74 s), and the collision moment (t = 0.74 s). As in Figure 13, when the particle settles with acceleration, as the relative velocity between the DEM particle and the fluid SPH particles increases, the drag force term gradually increases, while the hydrodynamic term has no obvious change, causing the force exerted on the DEM particle by the fluid to gradually increase and approach its own gravity, and the acceleration of the particle decreases to zero. The acceleration process is non-linear. When t = 0.74 s, the particle makes contact with the bottom boundary. Under the action of the soft-sphere contact model, the particle rebounds multiple times, and the potential energy is gradually consumed until it finally stops at the bottom boundary.

Figure 14 shows the distribution of the velocity of the flow field during the single-particle sedimentation process. When t = 0.33 s, as can be seen, the particle is in a state of uniform motion. The surrounding fluid SPH particles form a stable eddy current under the action of the fluid–solid coupling force, as shown in Figure 14a. When t = 0.64 s, the DEM particle approaches the bottom boundary. The fluid SPH particles located below the particle start to move upward under the squeezing action of the DEM particle and the bottom boundary, as shown in Figure 14b. For the fluid SPH particles within the coupling radius R_c of the DEM particle, their porosity is less than 1.0 and they are subjected to the local averaging effect. When the particle approaches the bottom boundary (t = 0.64 s), the fluid forms a local pressure concentration near the bottom boundary, causing the hydrodynamic term of the DEM particle to increase and become greater than its own gravity, resulting in the deceleration of the particle.

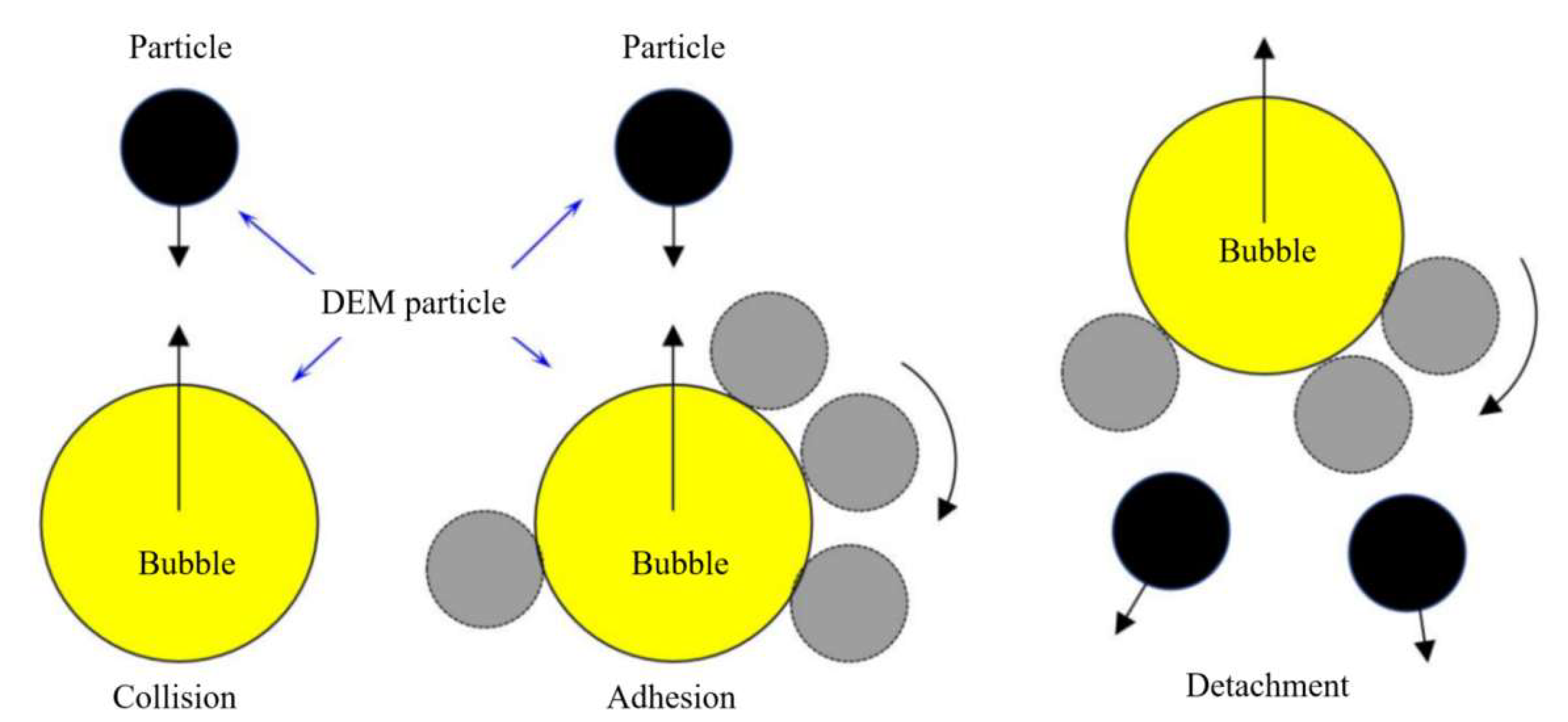
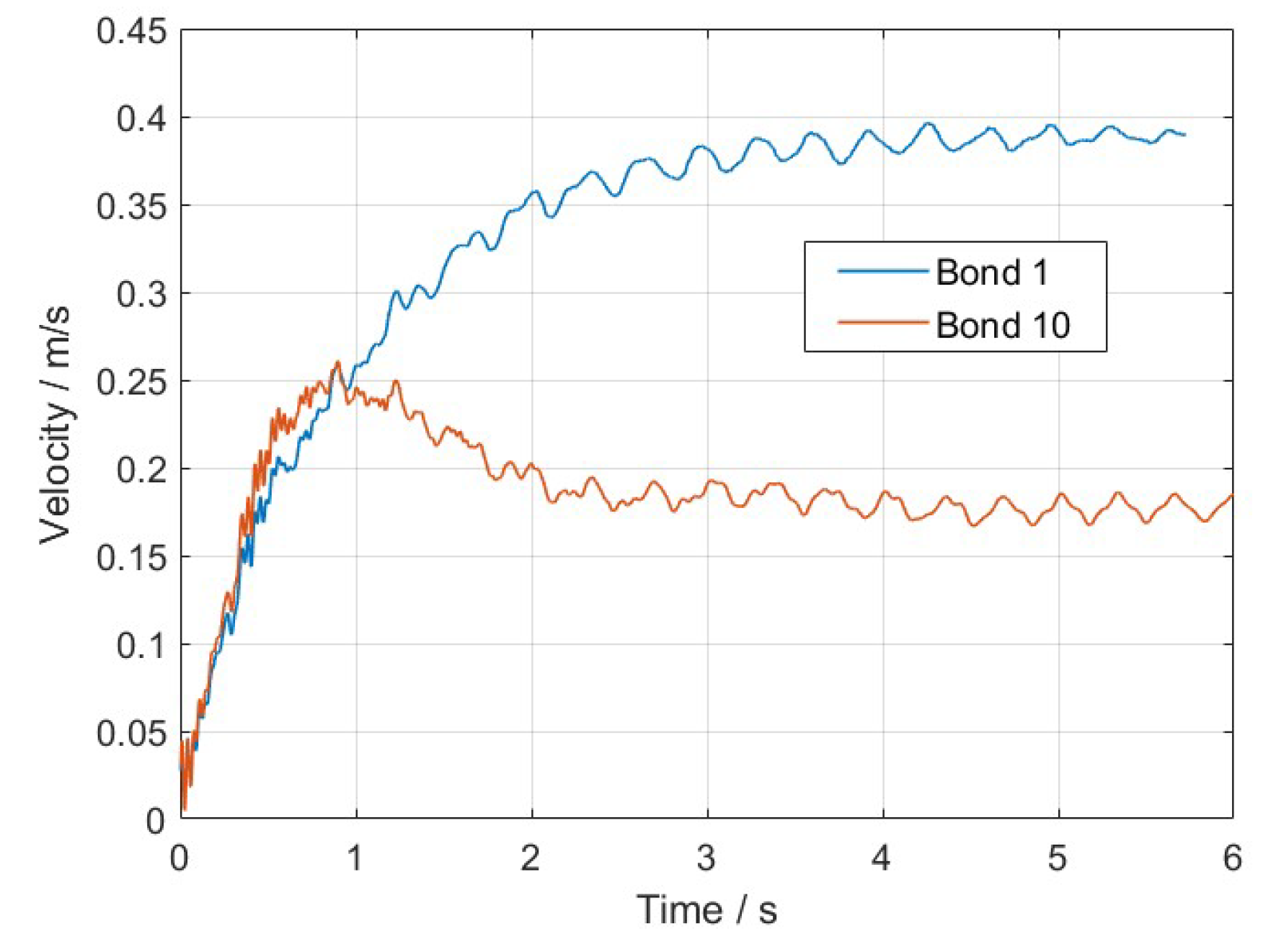
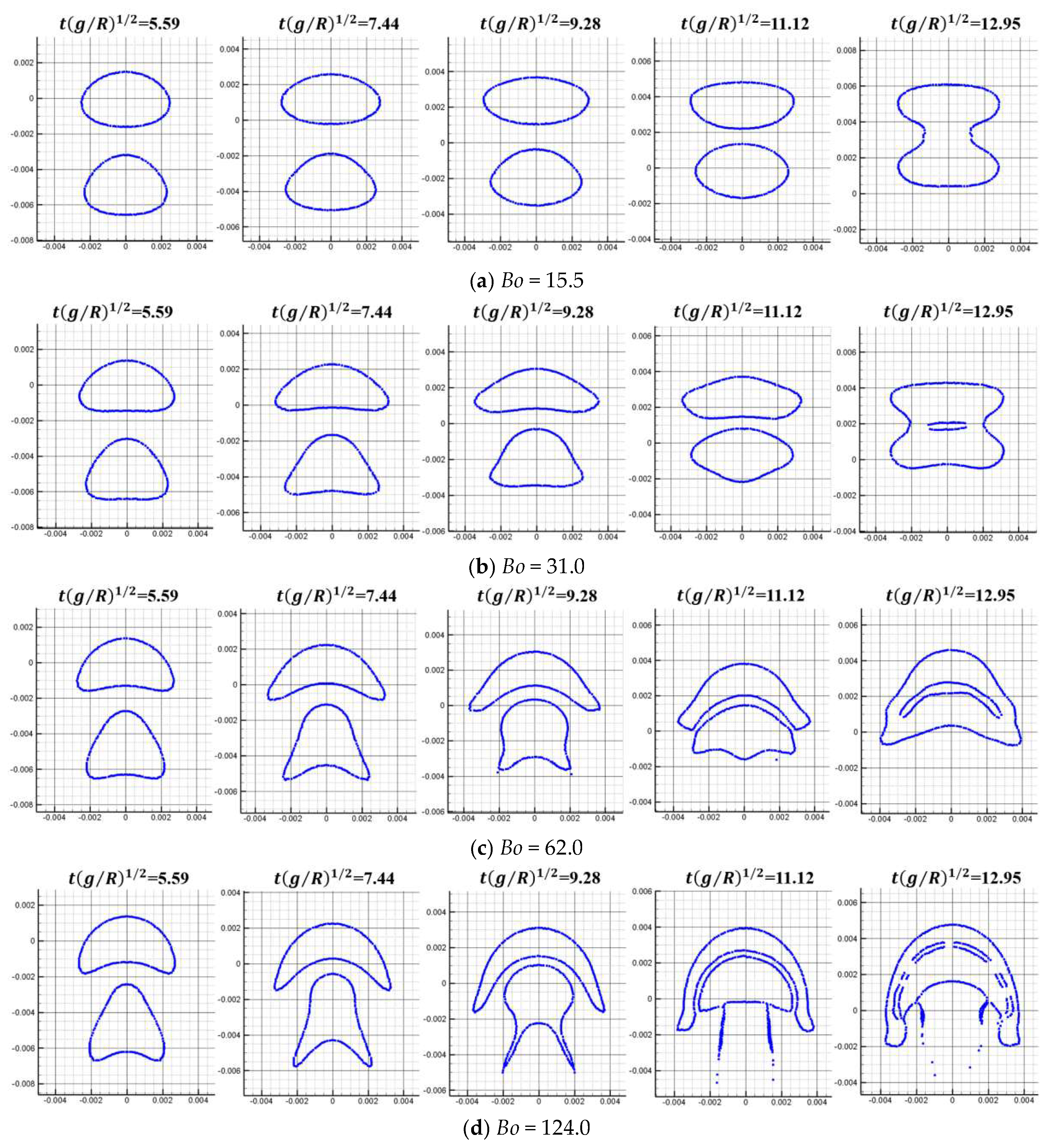
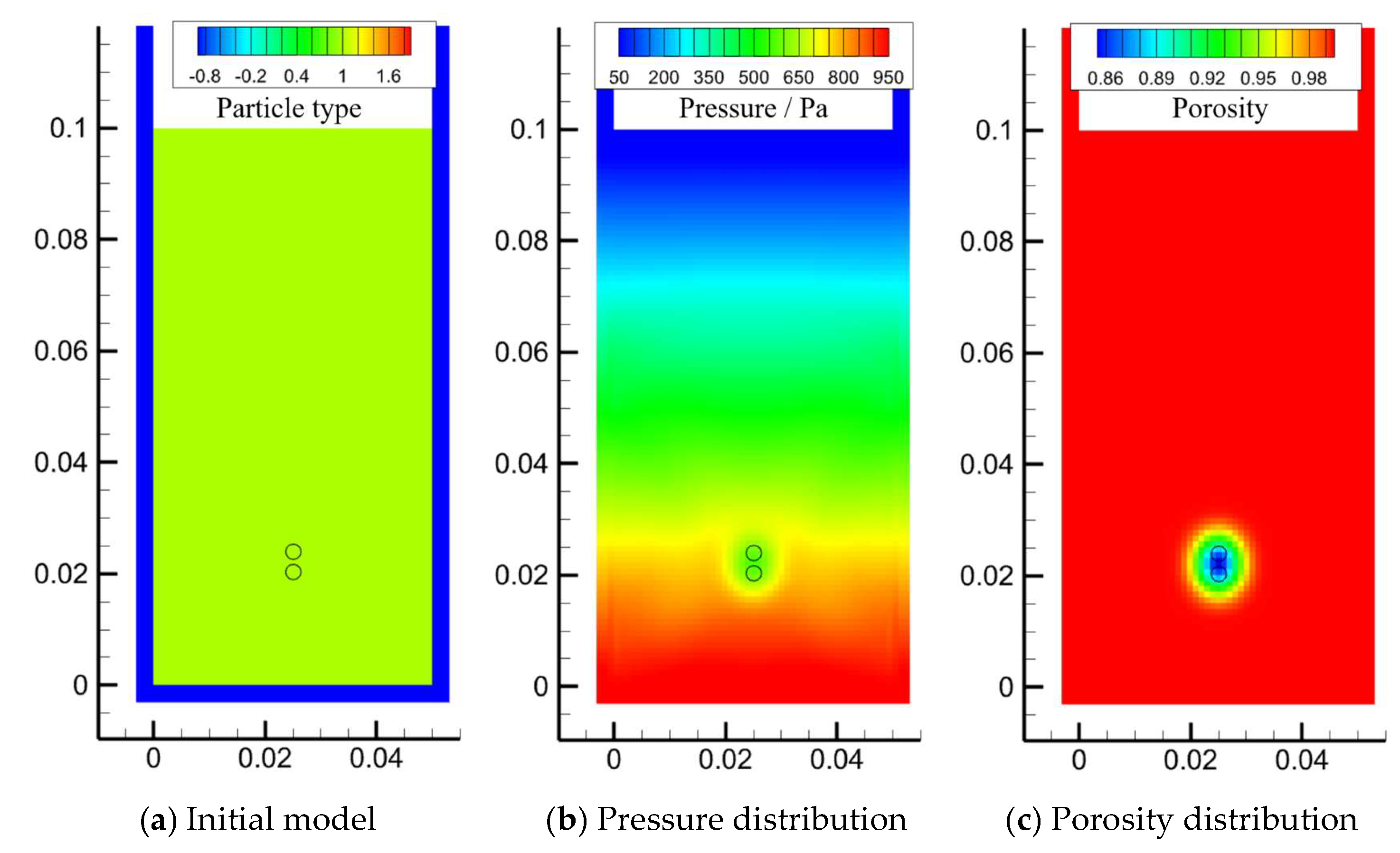
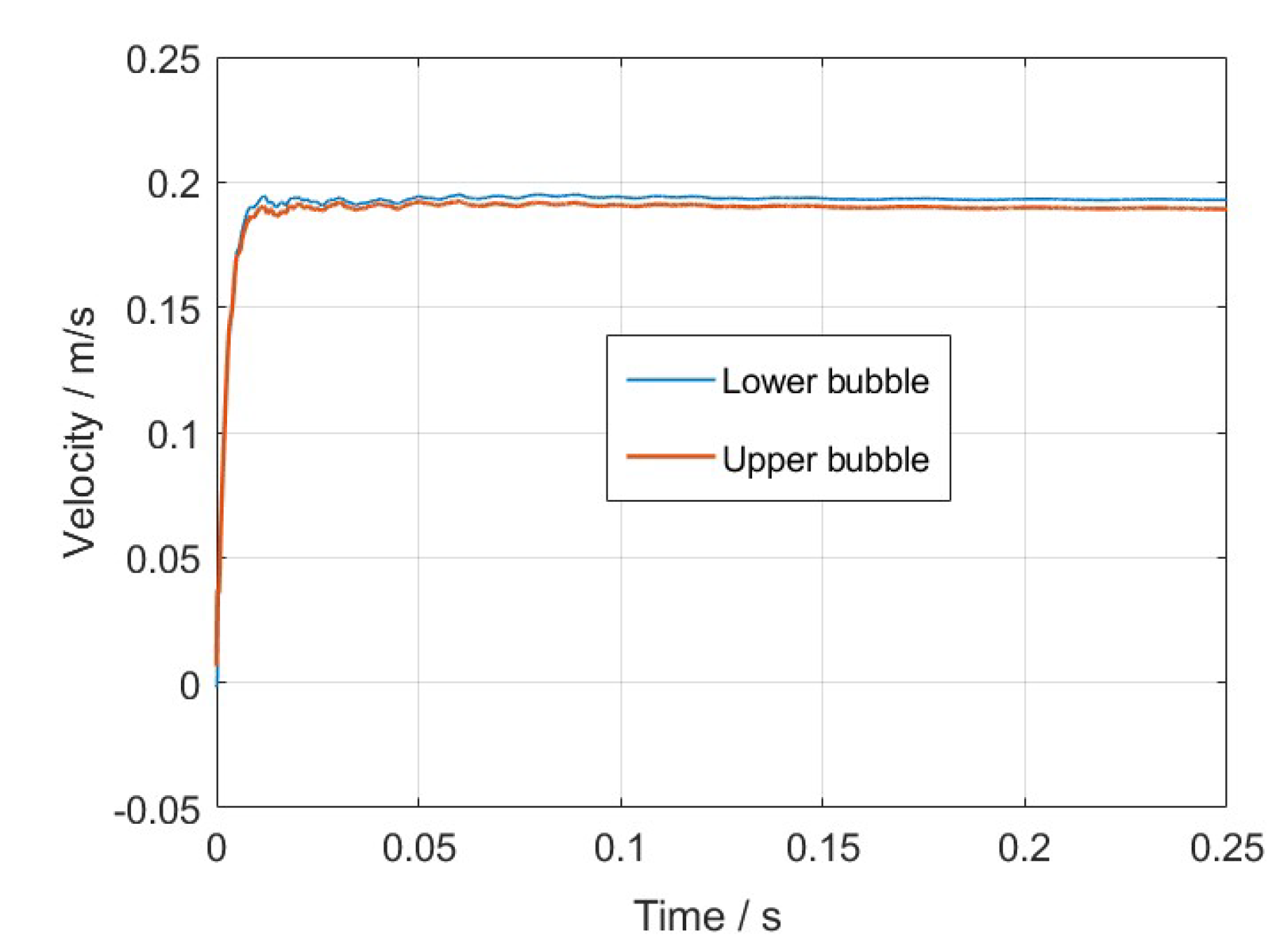
3.3. Bubble–Particle Interaction Mechanisms

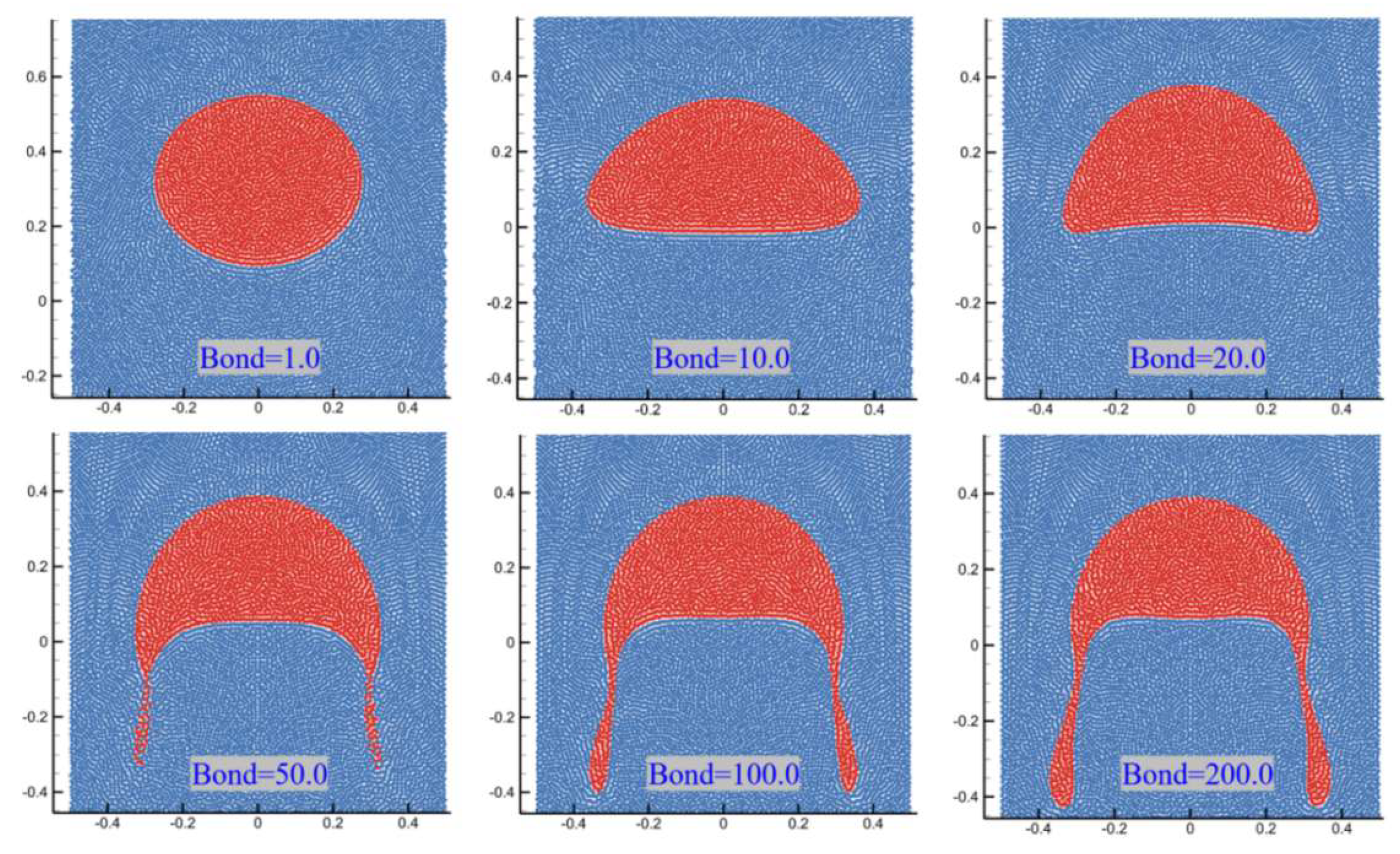
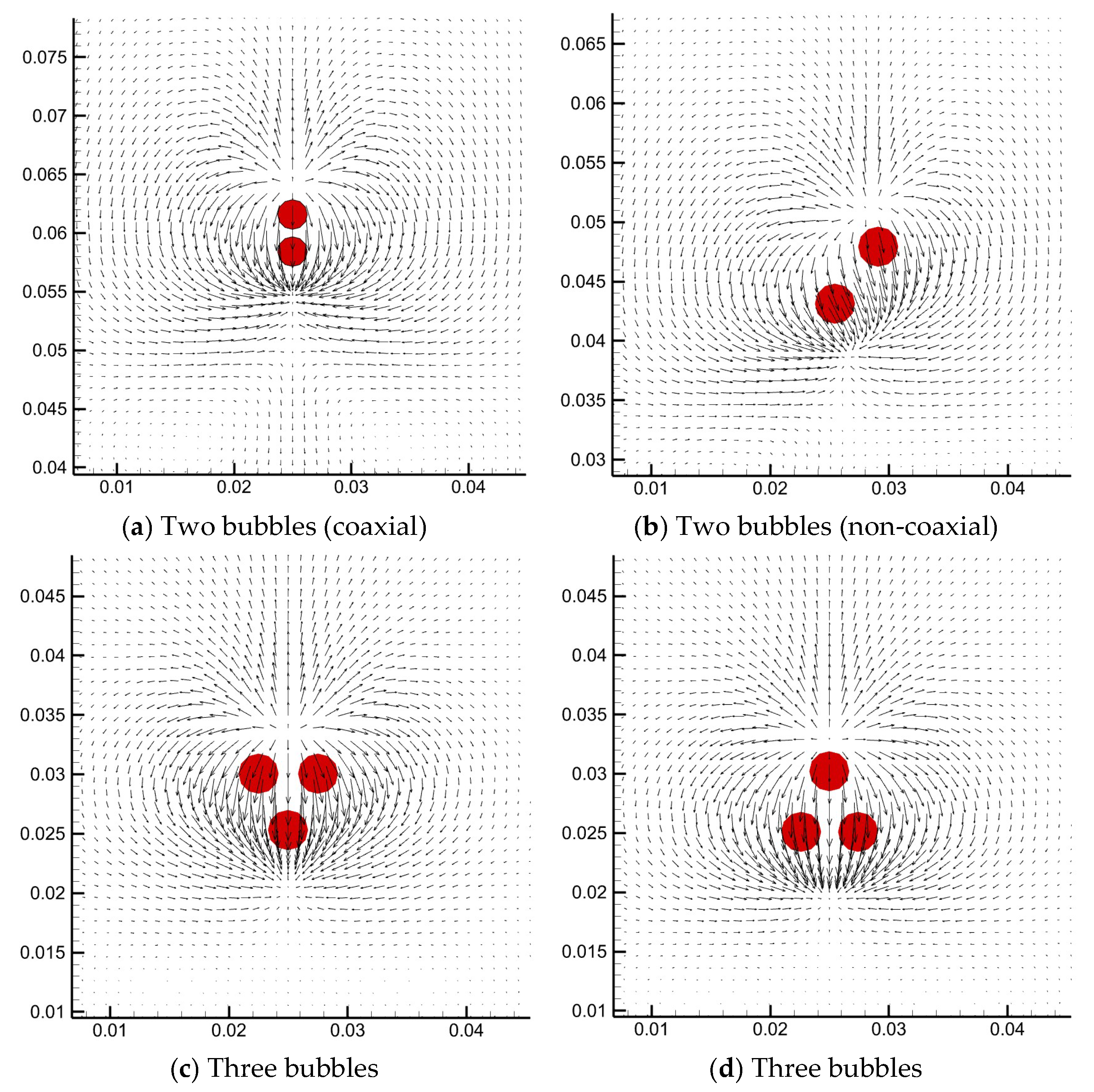
3.3.1. Single Bubble and Multiple Bubbles

This section investigates the fundamental physical processes governing interactions between rising gas bubbles and sinking solid particles, using the established SPH-DEM model. Rising bubbles generate low-pressure wake regions behind them, which entrain nearby particles. The Lagrangian nature of SPH captures the transient vortical structures, while the DEM tracks particle trajectories influenced by these hydrodynamic forces.

In the present SPH-DEM model, bubbles are approximated as rigid spherical/circular entities. However, bubble deformation during buoyancy-driven ascent is governed by the dimensionless Bond number ($Bo={\displaystyle \frac{\mathsf{\Delta }\mathsf{\rho }\mathrm{g}\mathrm{R}2}{\mathsf{\sigma }}}$), which quantifies the ratio of hydrodynamic to surface tension forces. To evaluate the impact of this simplification, fully resolved SPH simulations of bubble dynamics across a wide Bo range (1.0 ≤ Bo ≤ 200) were conducted using the methodology detailed in our previous work [15]. Figure 15 presents the simulation results of bubble morphology under different Bond numbers. As shown, as the Bond number increases, the deformation of the bubble becomes more severe; when the Bond number exceeds 50, the rising bubble will experience wake detachment, indicating that surface tension is no longer sufficient to maintain a stable bubble morphology.

Figure 16 presents a comparison of the bubble-rising velocity–time curves for Bond numbers of 1 and 10. It can be observed that, when the Bond number is 1, the surface tension effect is significant, and the morphology of the bubble after it stabilizes is close to circular, with the peak in the bubble-rising velocity curve also disappearing. The evolution of the rising velocity curve for the bubble with a Bond number of 1 is more consistent with the description of Stokes’ law.

Figure 17 shows the simulation results of the rising and coalescence of two coaxial bubbles. At the beginning of the calculation, two bubbles float up under the action of buoyancy. The wake of the upper bubble produces an adsorption effect on the lower bubble. At low Bond numbers, the lower bubble presents a nearly triangular shape. As the Bond number increases, as shown in Figure 17c,d, the lower bubble presents a horseshoe shape at time 6.79. The adsorption effect of the upper bubble makes the lower bubble rise faster than the upper bubble, and finally the two bubbles merge at time 13.51. With a lower Bond number, as shown in Figure 17a,b, at time 16.83, two bubbles merge into a bubble with a larger diameter, and the Bond number also increases. Therefore, the overall floating topography presents an approximately triangular shape.

Figure 18 illustrates the numerical setup for simulating the buoyancy-driven motion of two gas bubbles using the coupled SPH-DEM model. The bubble dynamics are represented by two distinct DEM particles, with a prescribed density ratio of 0.01 between the gas phase and surrounding fluid. In the initialization configuration (Figure 18a), the computational domain comprises boundary particles (blue), fluid SPH particles (green), and DEM particles (black hollow circles). Due to overlapping configurations between SPH and DEM particles, the DEM particles are visually obscured in the initial particle arrangement and are therefore schematically represented by outlined circles. Figure 18b presents the initial fluid pressure distribution under gravitational acceleration acting downward along the Y-axis, exhibiting a characteristic hydrostatic pressure gradient. Notably, localized pressure reductions are observed near the DEM particles (Figure 18c), attributable to porosity variations induced by the particle–fluid interactions.

The transient velocity fields during bubble ascension are depicted in Figure 19. The initial acceleration phase demonstrates buoyancy-driven upward motion accompanied by fluid entrainment. A velocity disparity between the upper and lower bubbles emerges due to hydrodynamic interactions, with the trailing bubble exhibiting higher ascent velocity as a result of wake-induced effects from the leading bubble. Quantitative velocity evolution (Figure 20) reveals rapid acceleration to terminal velocity followed by steady-state motion. It should be emphasized that the current SPH-DEM framework excludes coalescence mechanisms, thereby maintaining independent bubble trajectories throughout the simulation.

Figure 21 provides vector field visualizations of fluid–bubble interactions, demonstrating the model’s capability to resolve two-way coupled phenomena. The simulations successfully capture characteristic flow patterns around rising bubbles, validating the numerical implementation. However, the coarse-grained modeling approach introduces limitations in resolving fine-scale wake structures between adjacent DEM particles—a capability demonstrated in fully resolved models (as in Figure 15 and Figure 17).

Despite this resolution constraint, the SPH-DEM framework demonstrates significant computational efficiency, requiring only 5000 particles compared to 100,000 particles in fully resolved simulations (Figure 15), achieving a 20-fold reduction in computational cost. Simulations were performed on a workstation with an Intel Xeon Gold 6248R CPU (3.0 GHz, 24 cores) and 128 GB RAM. For the three-bubble case, the unresolved SPH-DEM model required 0.75 h to simulate 0.2 s of physical time, whereas a resolved multiphase SPH simulation with equivalent bubble counts (using the in-house SPH code) required 15 h (20× longer). This efficiency–performance tradeoff positions the proposed methodology as particularly suitable for engineering-scale multiphase flow simulations.

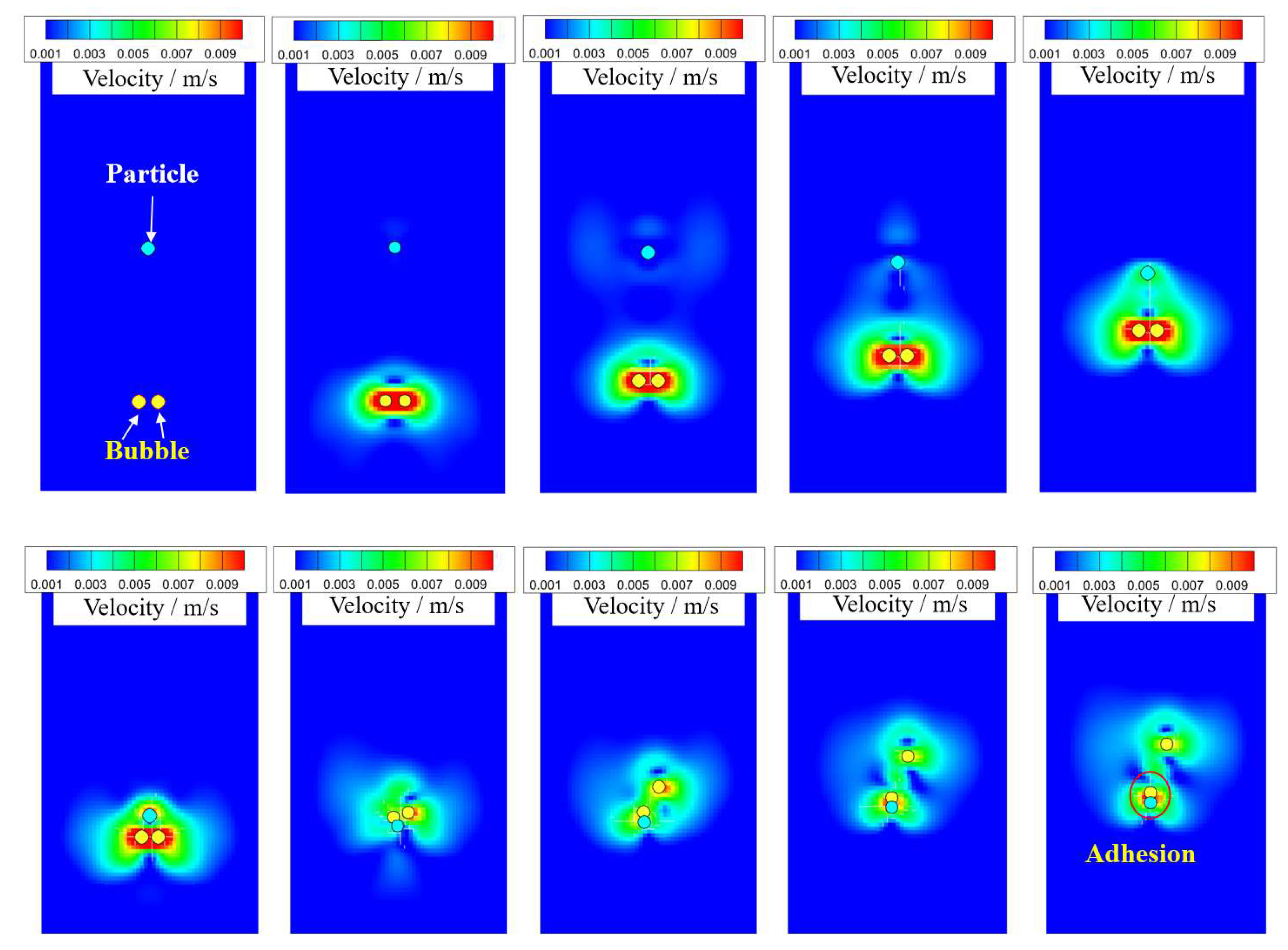
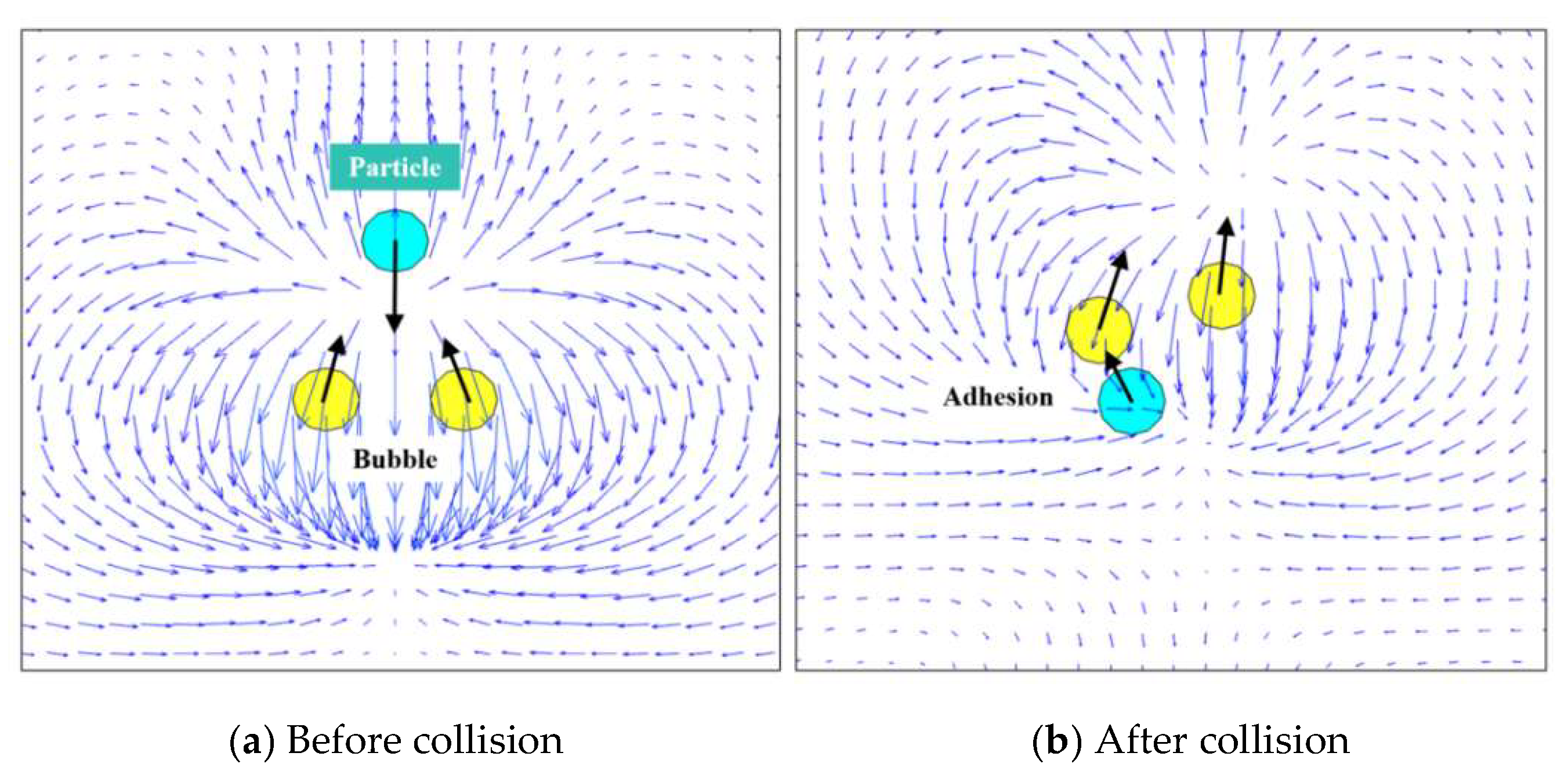
3.3.2. Interaction Between Bubble and Solid Particles

The SPH-DEM framework demonstrates robust capability in resolving hydrodynamic interactions between buoyant bubbles and settling particles. As illustrated in Figure 22, rising bubbles generate low-pressure wake regions that entrain adjacent particles, altering their trajectories. The Lagrangian nature of SPH enables precise tracking of vortical structures induced by bubble motion, while the DEM captures particle dynamics under combined hydrodynamic and contact forces.

This section investigates the dynamic interaction between two rising bubbles and a settling solid particle using the SPH-DEM framework. The numerical setup, as illustrated in Figure 22, initializes two bubbles (radius R = 1.25 mm) at y = 0.02 m and a spherical particle (radius r = 1.25 mm, density ratio ρ_p/ρ_f = 1.25) at y = 0.06 m. All phases start with zero initial velocity under gravitational acceleration (g = 9.81 m/s²). The fluid domain (0.05 m × 0.1 m) employs 5775 SPH particles with a smoothing length h = 1.2d_ini (initial particle spacing d_ini = 1 × 10⁻³ m), ensuring sufficient resolution to capture hydrodynamic interactions.

At the initial stage (Figure 22), buoyancy drives the bubbles upward, while gravity accelerates the particle downward. The velocity field (Figure 23) reveals symmetric vortices forming around the rising bubbles, with a stagnation zone developing between them due to opposing pressure gradients. The particle’s descent generates a localized high-pressure region beneath it, inducing upward fluid motion. During this phase, the leading bubble attains a velocity of 0.18 m/s, while the particle accelerates to 0.12 m/s.

By t = 0.25 s, the trailing bubble overtakes the leading one due to wake-induced acceleration, a phenomenon consistent with Figure 23. Concurrently, the particle enters the low-pressure wake region of the leading bubble, reducing its effective drag and delaying sedimentation. The velocity vector plot (Figure 23b) highlights recirculating flows that redirect the particle toward the bubble interface. At t = 0.32 s, the particle collides with the trailing bubble’s upper surface. The soft-sphere contact model governs this interaction, with adhesion enforced via a cohesion force threshold, calibrated to mimic hydrophobic attachment in flotation systems.

Following adhesion (t > 0.32 s), the particle–bubble aggregate ascends at a reduced terminal velocity of 0.14 m/s, 22% lower than the isolated bubble’s velocity. This deceleration arises from the added inertial load of the particle and disturbed wake symmetry. The porosity distribution shows a localized void fraction reduction (ε ≈ 0.85) near the adhered particle, amplifying local drag forces. Remarkably, the SPH-DEM framework captures the transient redistribution of fluid momentum, with vorticity magnitudes near the aggregate decreasing by 35% compared to pre-collision levels. This case study demonstrates the SPH-DEM framework’s capability to resolve multiscale interactions in bubble–particle systems, providing critical insights for optimizing collision efficiency in industrial applications like mineral flotation.

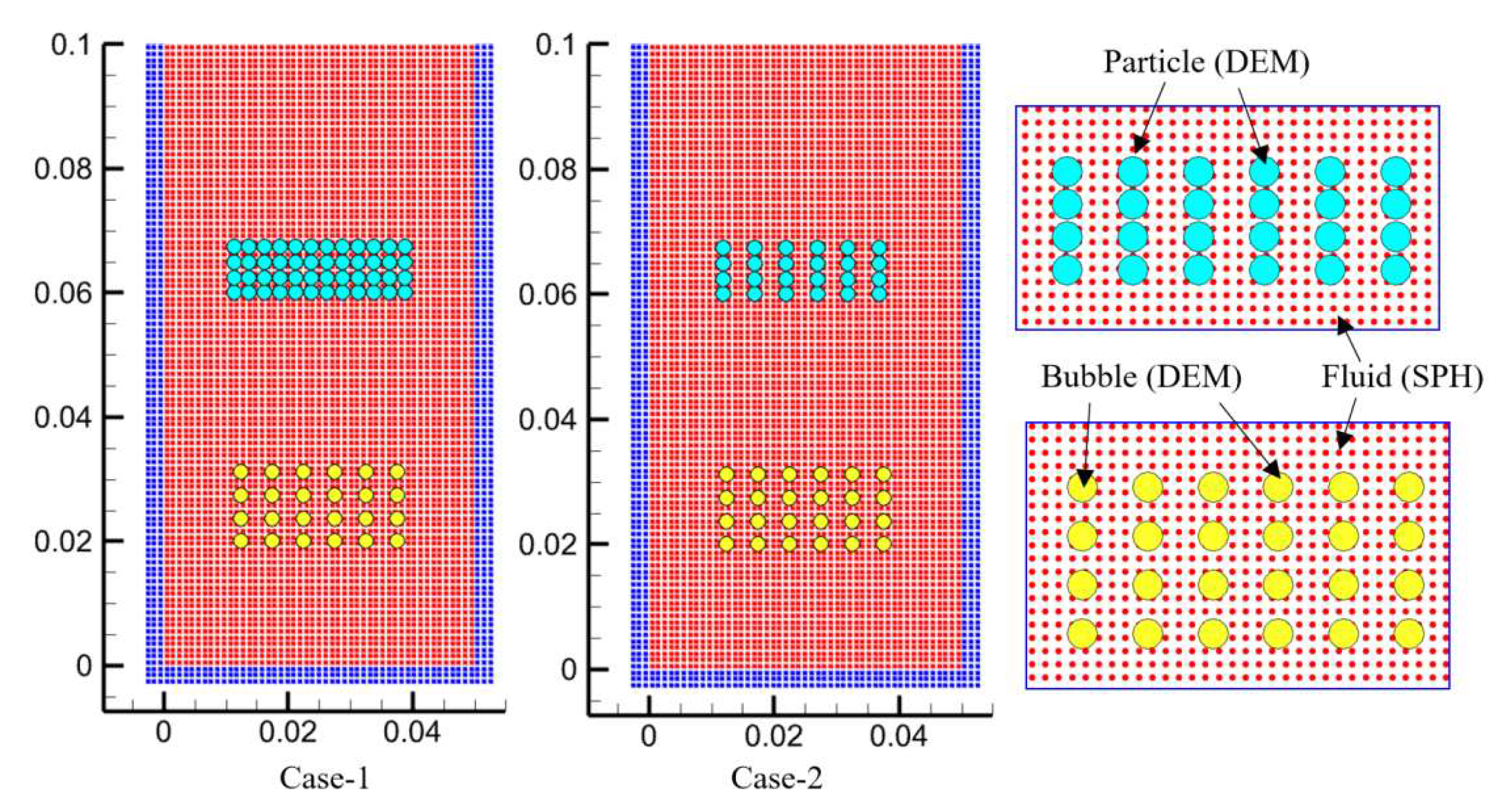
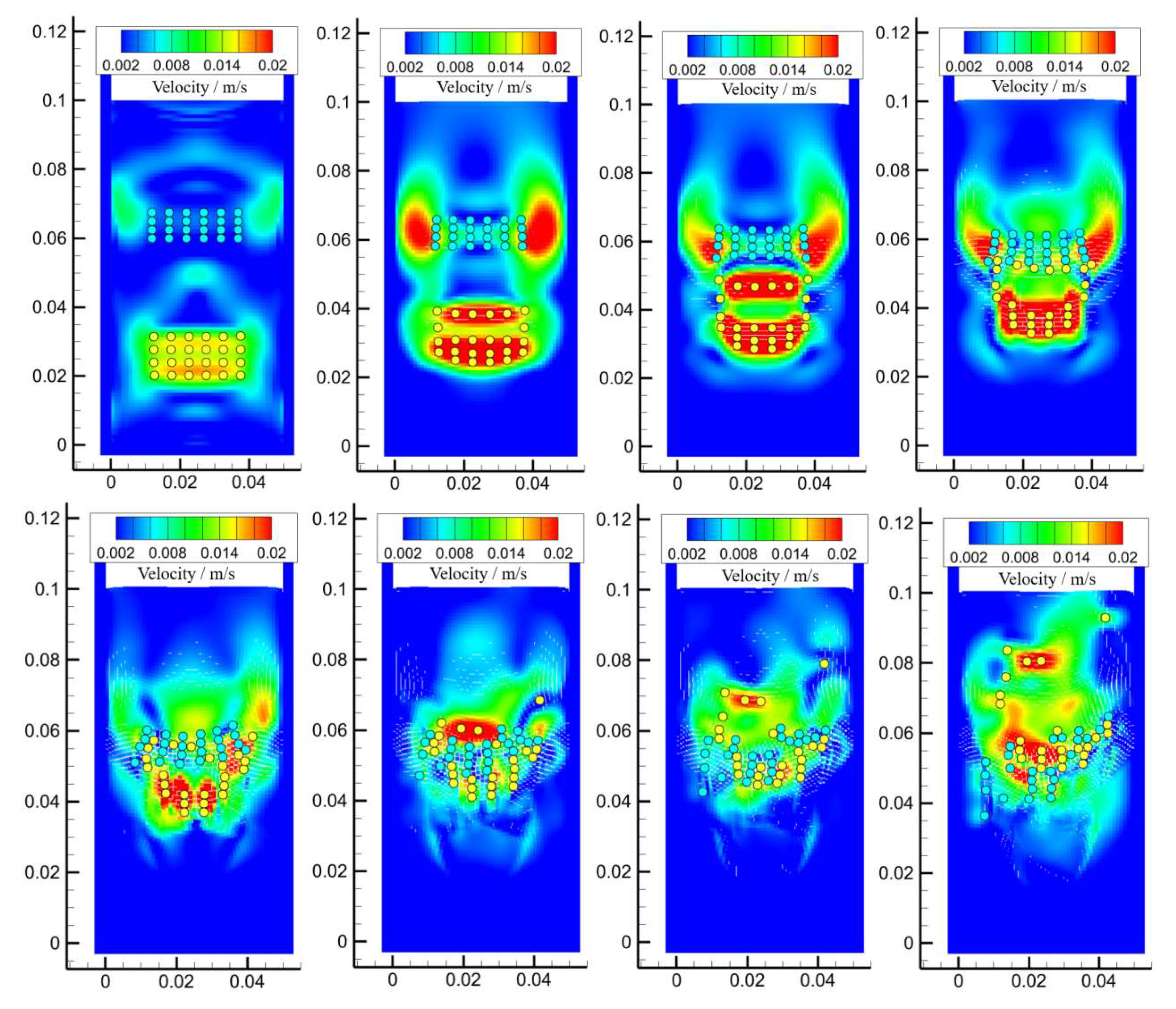
3.3.3. Dense Particle and Bubble Systems

This section investigates the dynamic interactions between dense particle suspensions and bubbles using the SPH-DEM model. Two configurations are analyzed to evaluate the model’s capability in capturing hindered settling, as shown in Figure 24, bubble-induced fluidization, and phase segregation in high-concentration systems.

As shown in Figure 25, a total of 24 bubbles (radius R = 1.25 mm) are arranged in a 4 × 6 grid at y = 0.02 m, with row and column spacings of 1.5R and 2R, respectively. Above them, 24 particles (radius r = 1.25 mm) are positioned in a 4 × 6 grid at y = 0.06 m, with tighter spacing (row: 1.0r, column: 2.0r). Initial velocities for all phases are zero. At the initial stage, buoyancy drives bubbles upward while particles descend under gravity. The velocity field (Figure 25) reveals staggered vortices forming between bubble columns, creating alternating high- and low-pressure zones. Particles initially accelerate downward at 0.15 m/s² but decelerate to 0.08 m/s² as they enter the bubbles’ wake regions. The porosity distribution shows localized reductions near particle clusters, amplifying drag forces on ascending bubbles.

By t = 0.4 s, hydrodynamic interactions dominate. Bubbles rising through particle-laden regions experience a 30% velocity reduction compared to isolated bubbles, attributed to increased effective viscosity from particle-induced turbulence. Meanwhile, particles in bubble wakes exhibit 40% slower settling rates due to upward fluid entrainment. A critical particle volume fraction is observed, beyond which bubble motion transitions from laminar to chaotic, marked by sudden velocity fluctuations (Figure 26).

In Figure 27, particle density is doubled (48 particles in a 4 × 12 grid with 1r spacing). This configuration intensifies phase coupling, with particle volume fraction reaching ϕ = 0.35. Initial bubble rise velocities are 0.12 m/s, 33% lower than in Case 1. By t = 0.3 s, particle jamming near the domain center creates a “bridging” effect, temporarily trapping bubbles and reducing their ascent velocity to 0.05 m/s. The porosity field shows extreme gradients, driving localized fluid recirculation that disperses particle clusters.

4. Limitations, Advantages, and Future Works

The unresolved SPH-DEM framework, despite its computational efficiency, exhibits several inherent limitations stemming from its coarse-grained nature. In bubble–particle contact scenarios, the model cannot resolve liquid film thickness, leading to empirical treatment of capillary forces and contact angles. Turbulent vortex streets in bubble wakes are homogenized, underestimating particle drag coefficients. The model neglects bubble coalescence/breakup, limiting applicability to high-viscosity systems or shear-thickening slurries. The exclusion of bubble coalescence and breakup mechanisms restricts the model’s applicability to high-velocity or turbulent flows, such as froth flotation systems with dynamic bubble swarms. To address this, future iterations will integrate population balance models or interface-tracking SPH formulations to resolve coalescence criteria and breakup thresholds.

The unresolved SPH-DEM framework employs a smoothing length h_c comparable to the particle/bubble diameter, which homogenizes subparticle wake structures and thin liquid films. While this ensures computational efficiency, it limits the resolution of micro-scale vortices and interfacial phenomena critical to processes like bubble coalescence. Future work will explore adaptive resolution strategies, such as variable smoothing lengths or hybrid resolved–unresolved coupling, to mitigate these limitations.

• Nevertheless, the framework’s advantages are summarized:
• Inherent stability for large-density-ratio systems;
• Scalable Lagrangian handling of free surfaces;
• Efficient model for large-scale applications. Future enhancements will focus on three-dimensional extensions incorporating turbulence closure models and dynamic bubble morphology via interface-aware SPH formulations.

Future extensions will focus on 3D implementations, turbulence modeling, and experimental validation to further enhance predictive accuracy for complex engineering systems. The population balance modeling can be used for model bubble coalescence/breakup resolving wake turbulence effects. Extending the framework to three dimensions introduces computational and algorithmic challenges, such as increased neighbor-search complexity, higher memory demands for particle tracking, and the need for advanced kernel functions to handle 3D free-surface dynamics. Furthermore, modeling irregularly shaped particles or non-spherical bubbles in 3D would require adaptive contact mechanics and refined porosity calculations, which are subjects of ongoing research.

5. Summary

This study presents a novel unresolved SPH-DEM coupling framework to efficiently simulate multiphase interactions between rising bubbles and sinking particles in dense systems. By leveraging SPH’s Lagrangian meshless approach for fluid dynamics and the DEM’s granular-scale resolution for discrete phase interactions, the framework bridges macro- and micro-scale phenomena through a porosity-based averaging technique, enabling large-scale simulations with reduced computational costs. Validated against benchmark cases of single bubble rising and particle sedimentation, the model demonstrates robust capabilities in capturing hydrodynamic coupling, wake entrainment, and hindered settling. Case studies reveal key mechanisms governing bubble–particle adhesion, clustering, and phase segregation, highlighting its applicability to industrial processes like mineral flotation. While the coarse-grained approach achieves a 20-fold efficiency gain over resolved methods, limitations persist in resolving subparticle wake structures and bubble coalescence.