Evolution Characteristics of Roof Stress in Horizontal Segmental Mining of Steeply Inclined Coal Seams
Abstract
:1. Introduction
2. Overview of the Coal Mine
3. Orthogonal Test Modeling
4. Analyzing the Stress of the Roof Through Numerical Simulation
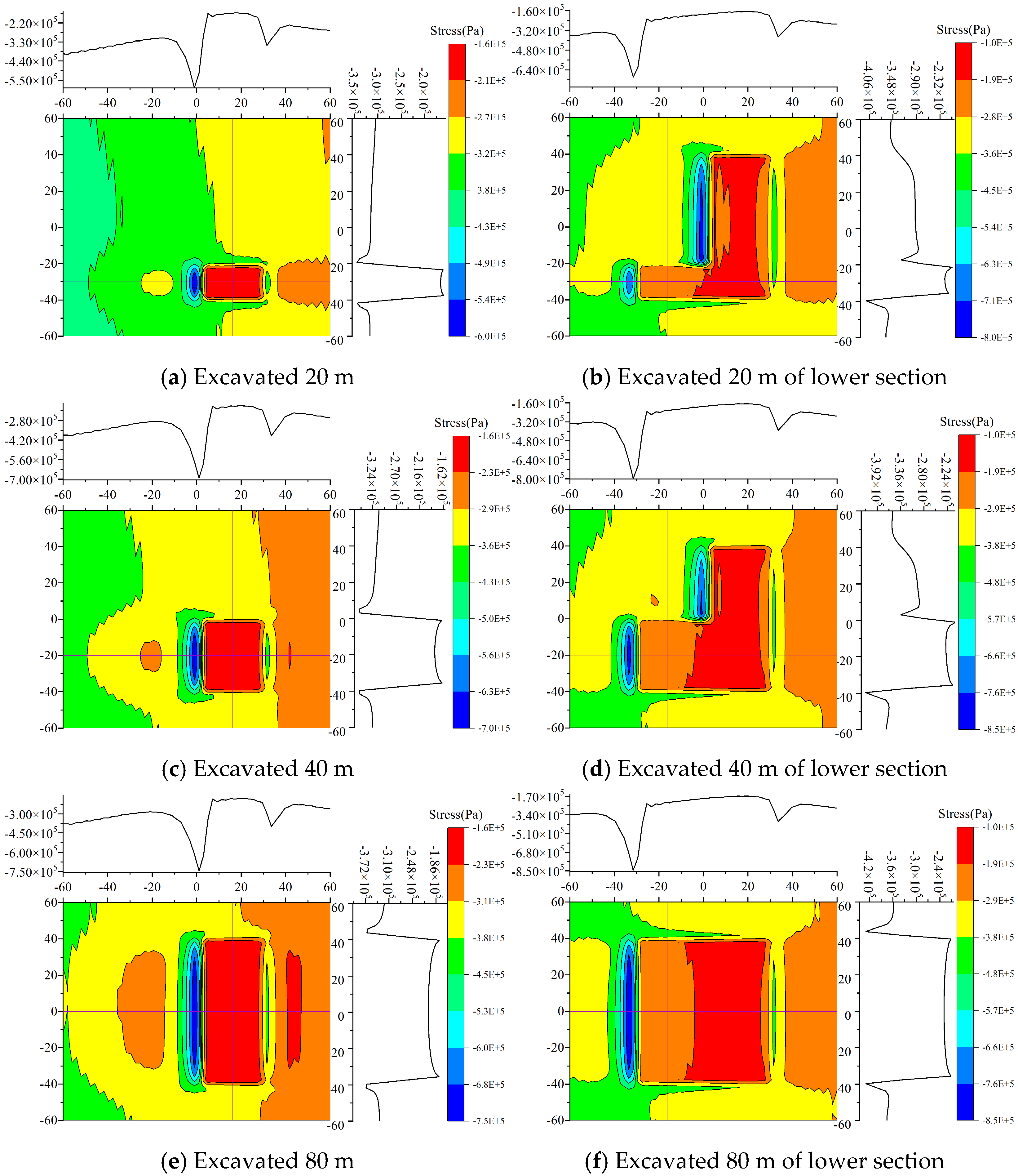
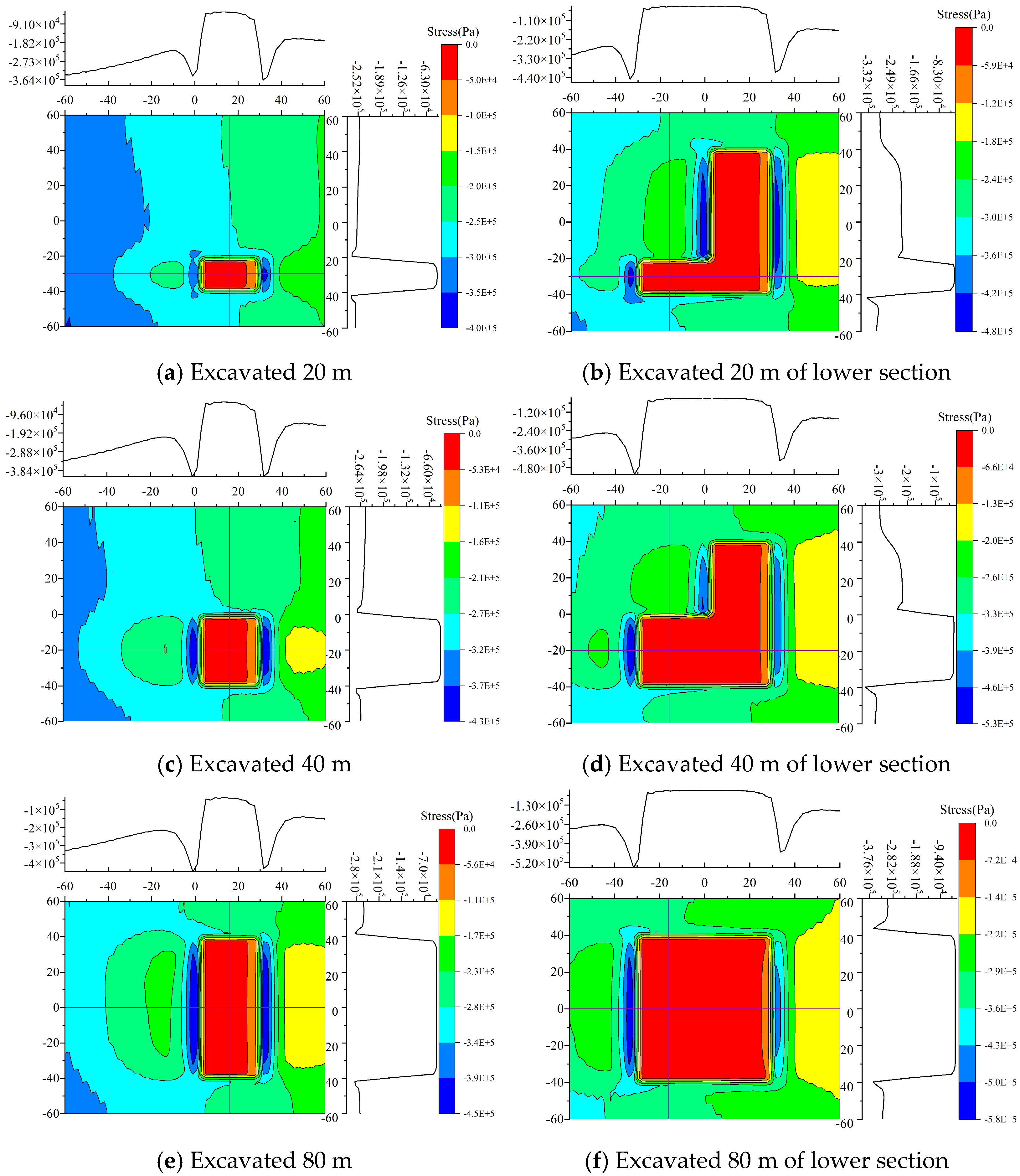
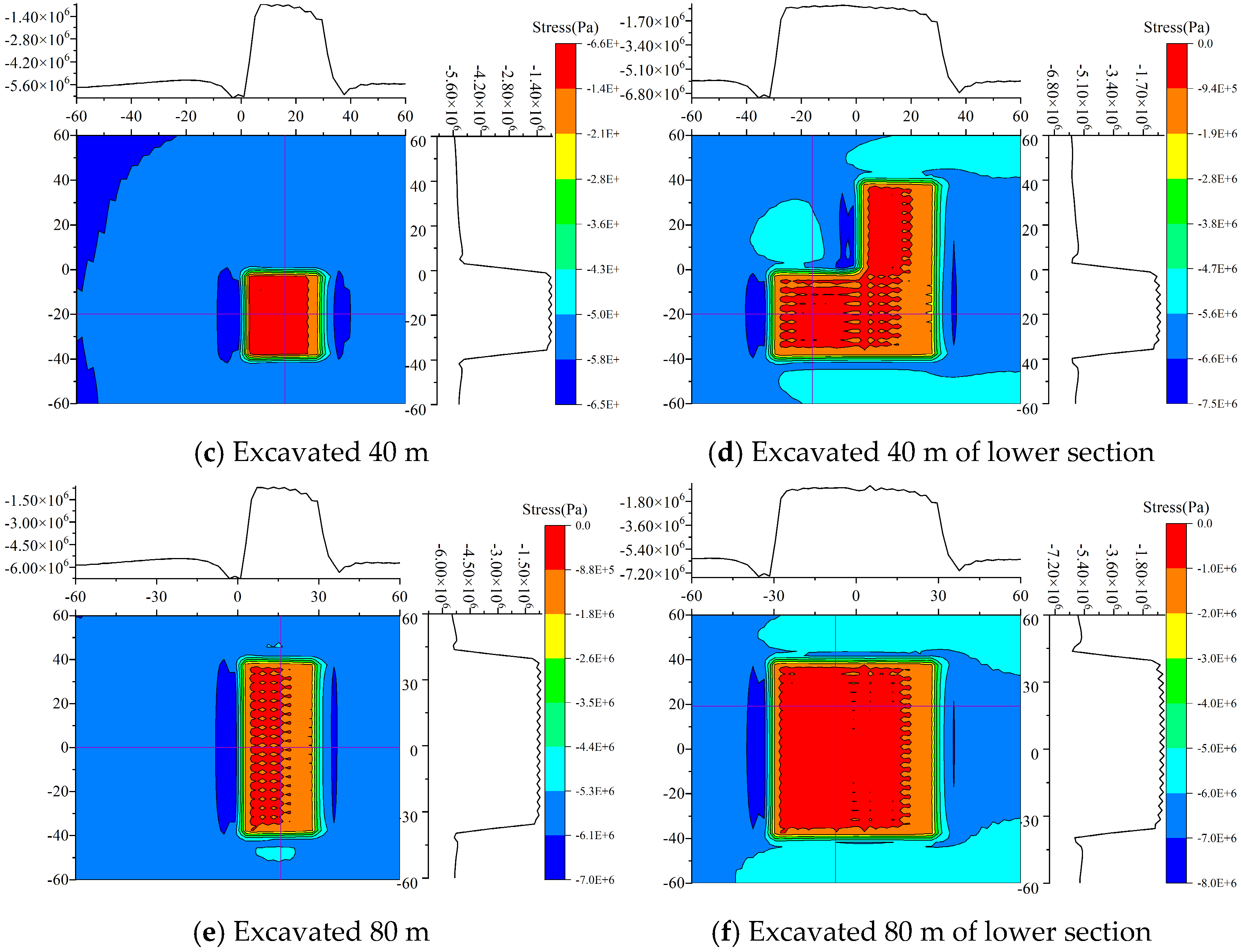
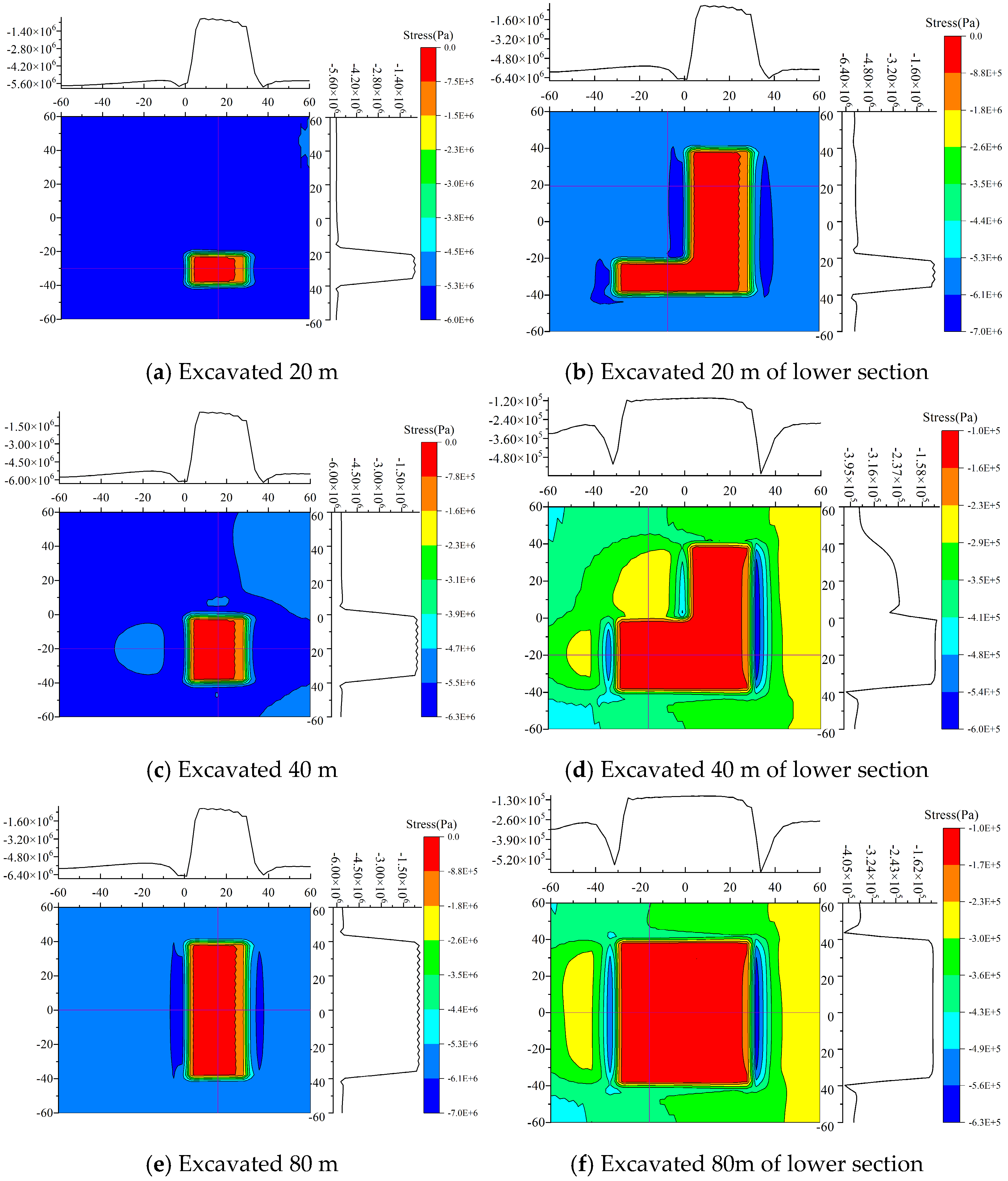
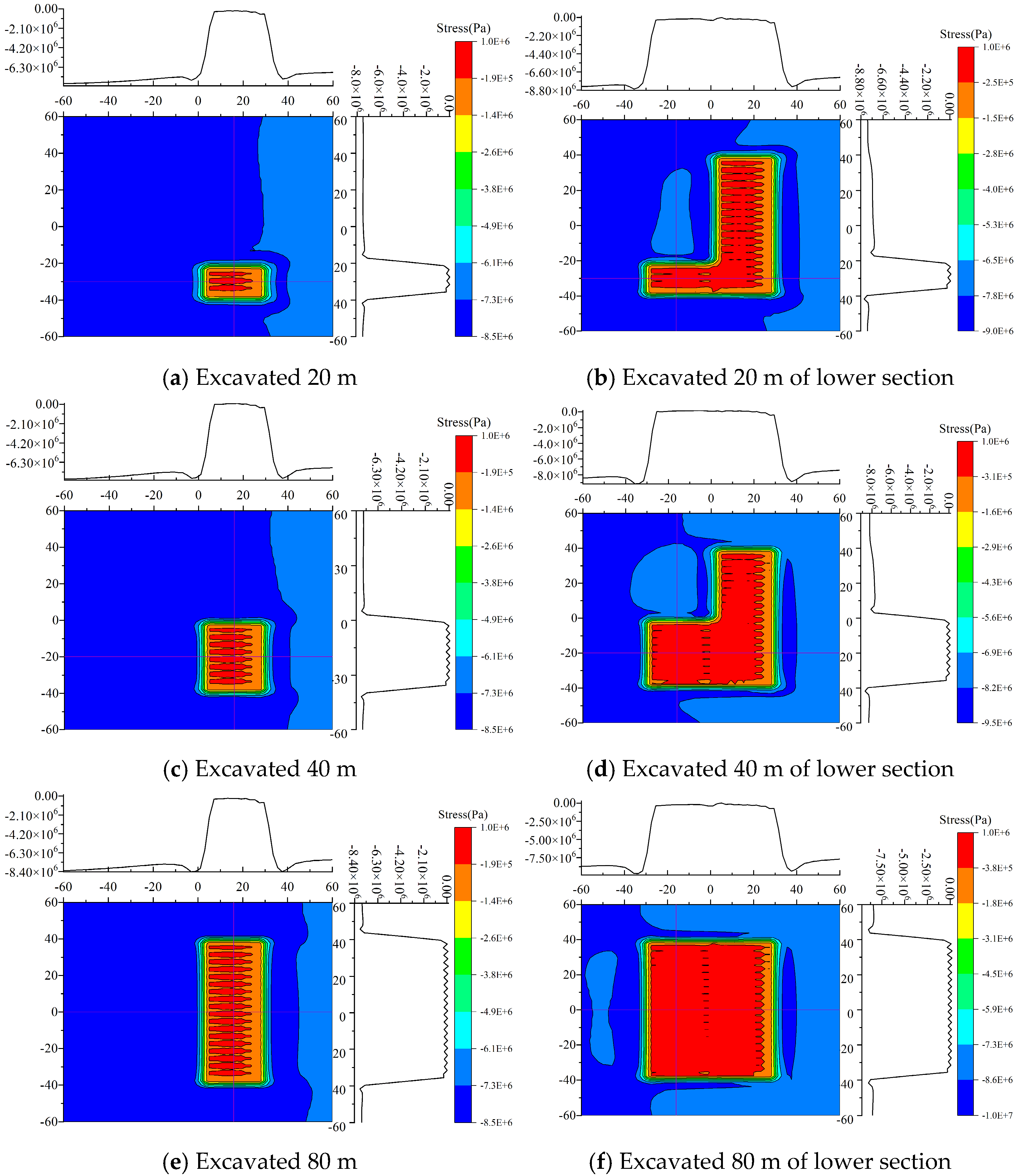
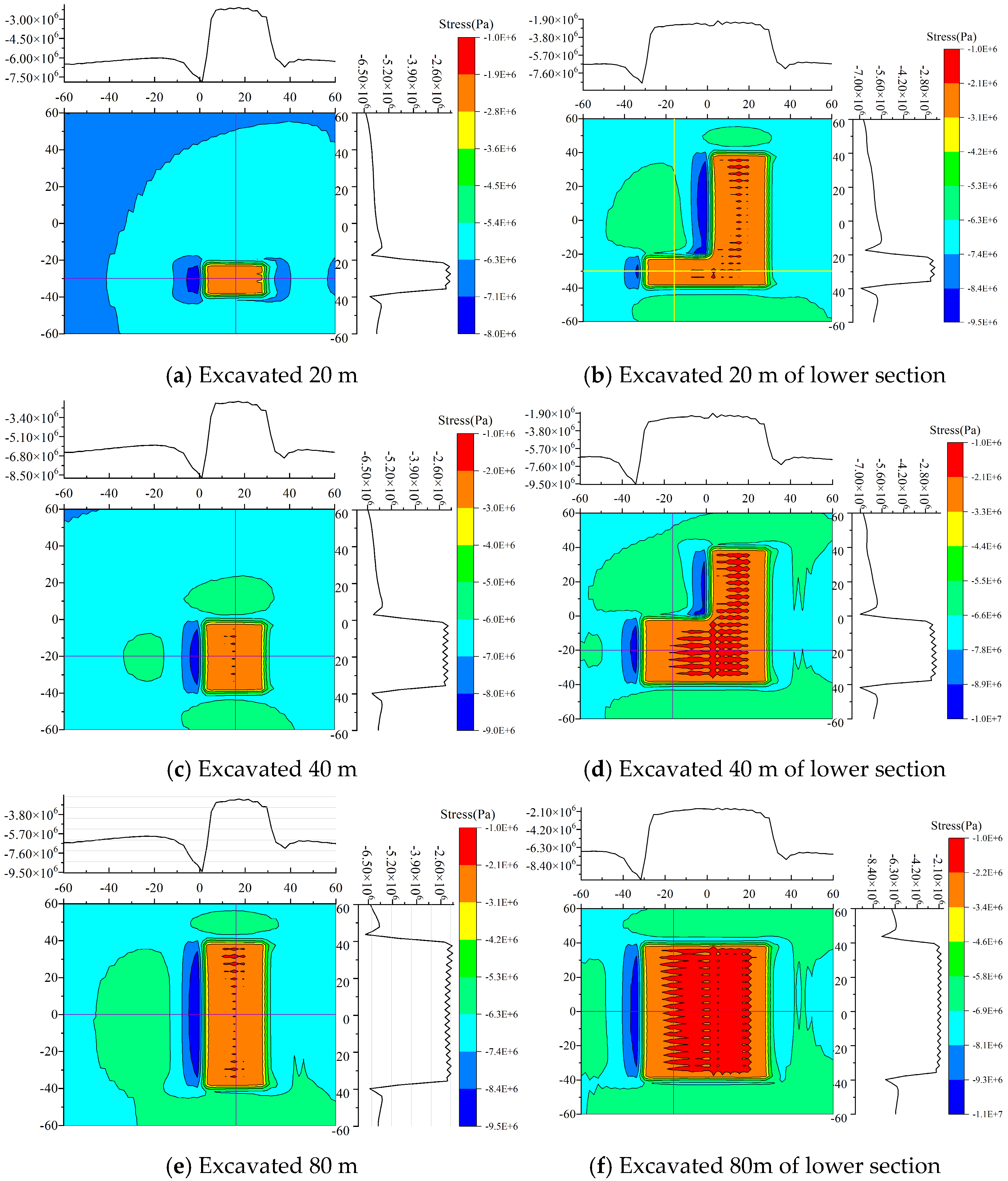
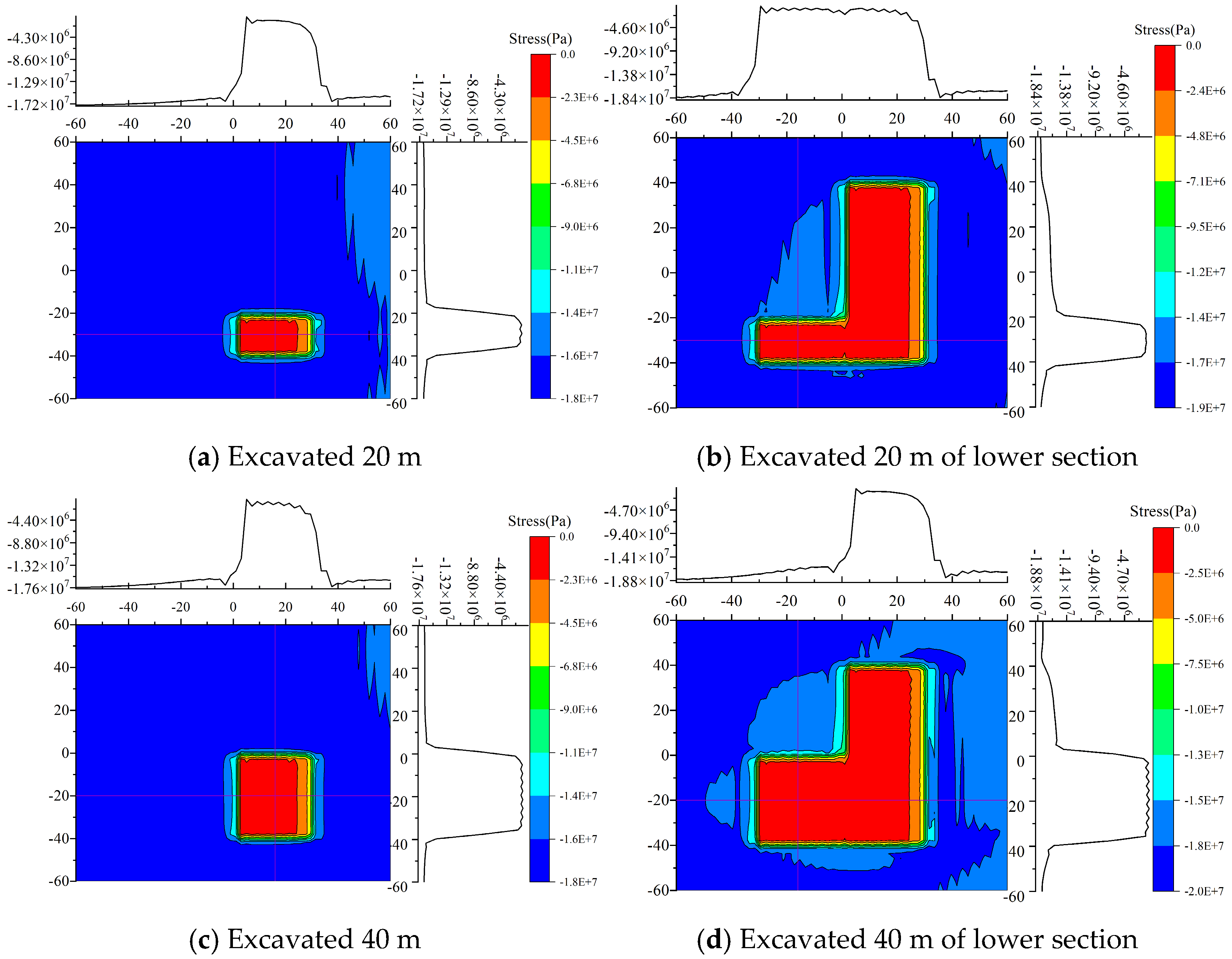
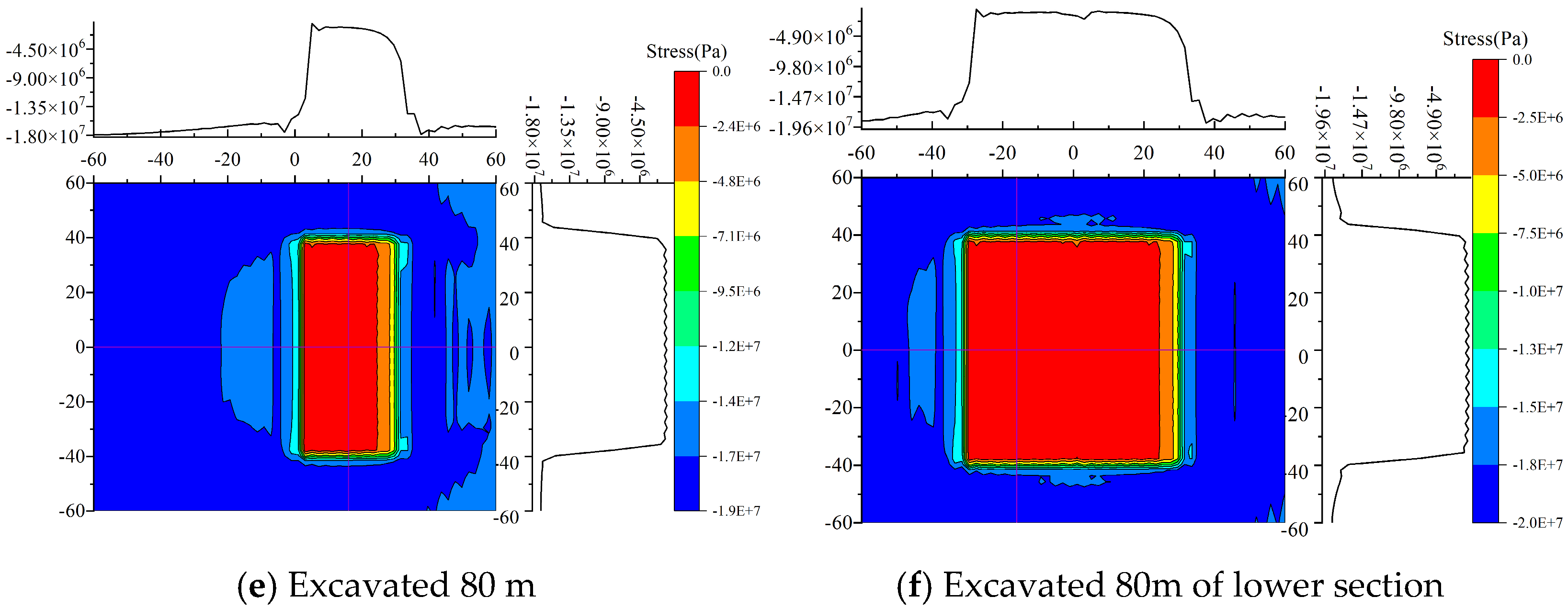
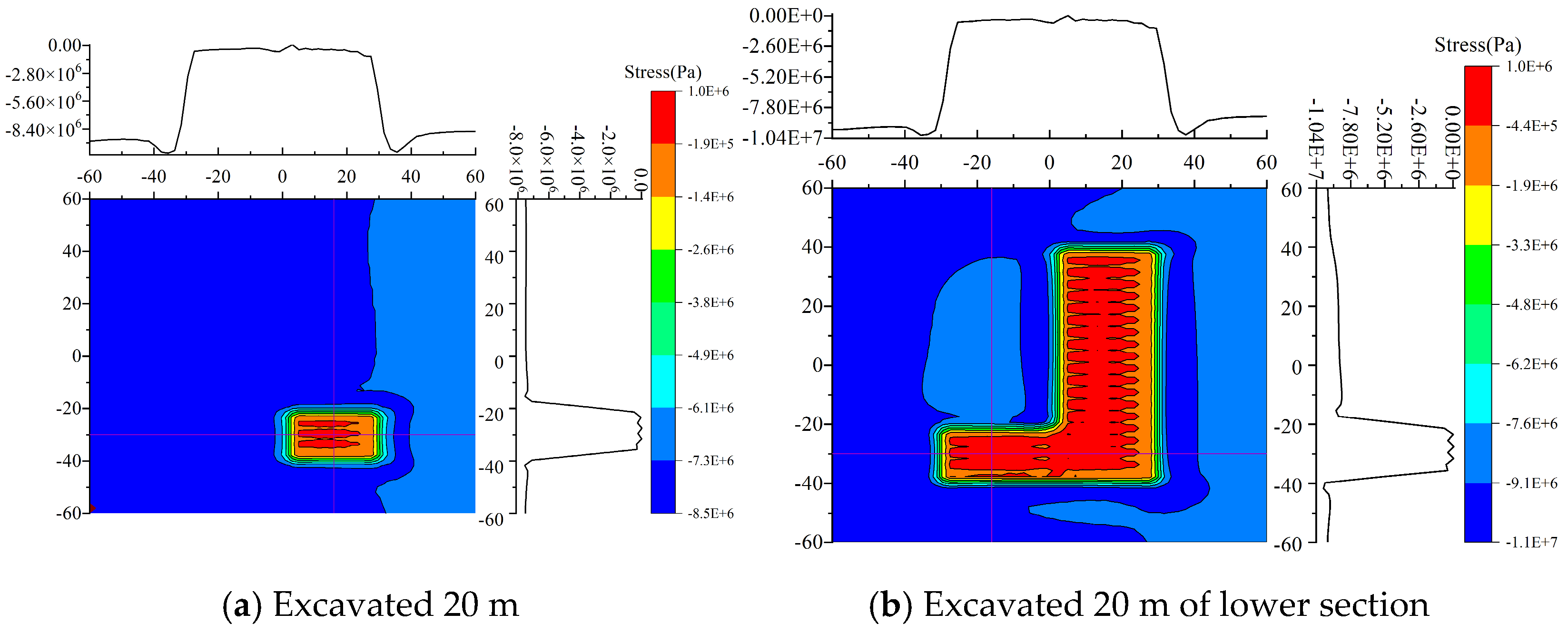
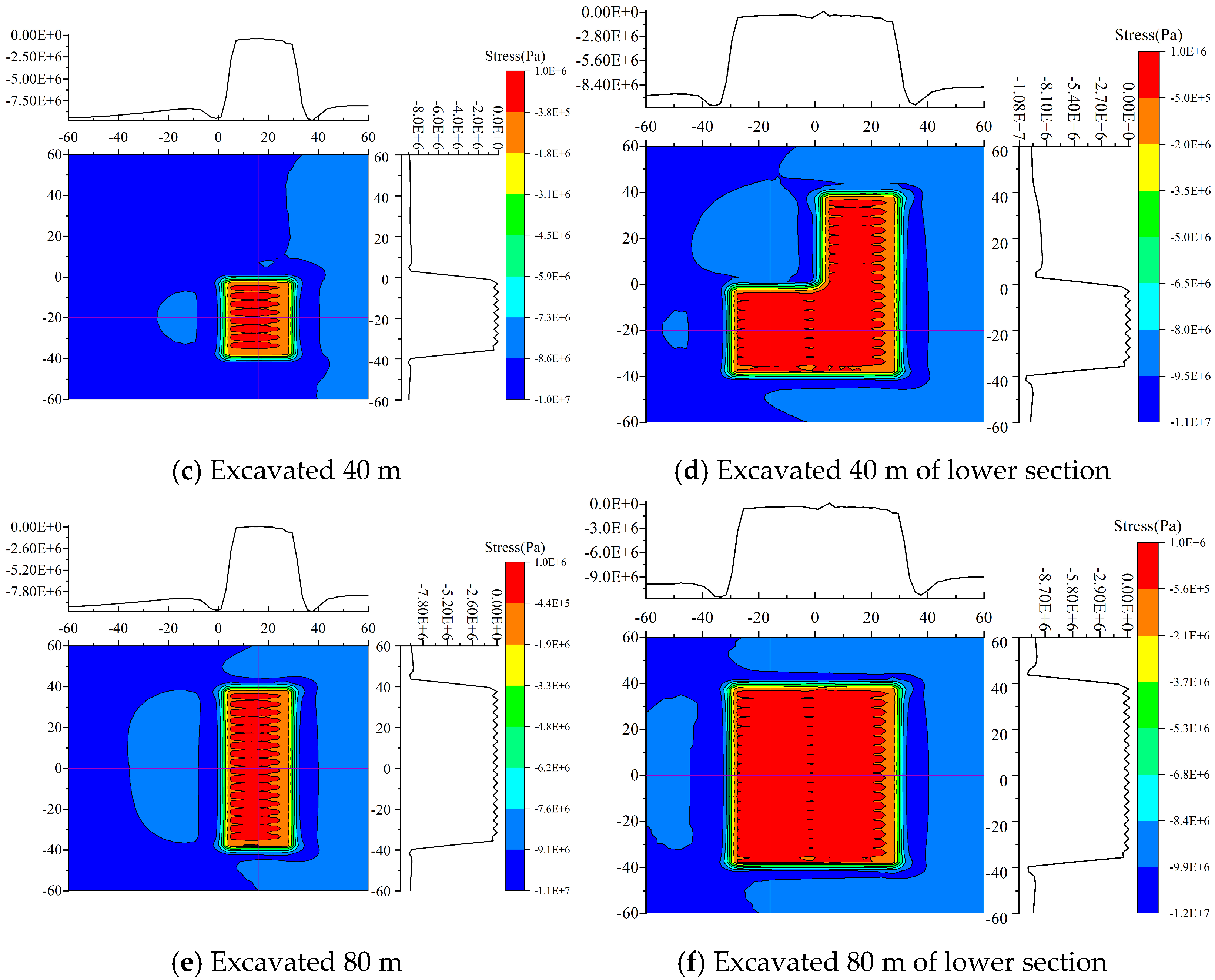
4.1. Processing Simulation Result Data
4.2. Analysis of Simulation Results
4.3. Comparative Analysis of Rock Tilt Directions
4.4. Comparative Analysis of Rock Strike Directions
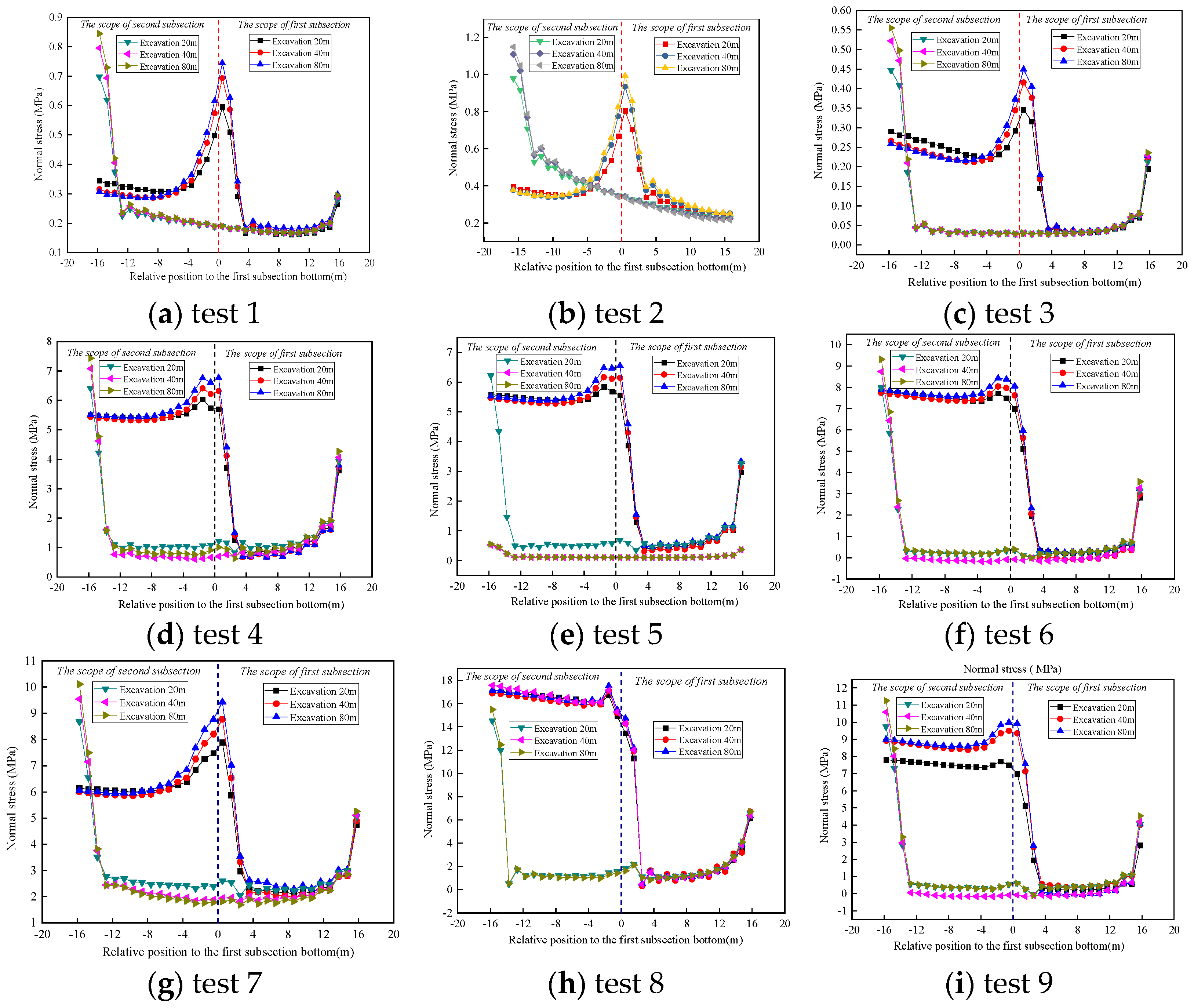
5. Orthogonal Analysis of Normal Stresses in the Top Rock Layer
6. Discussion
- (1)
- Identifying High-Risk Zones: By understanding stress distributions, mining engineers can identify areas with high stress concentration, which are more prone to rock bursts, collapses, or other failures. This allows for targeted monitoring and reinforcement in these zones to prevent accidents.
- (2)
- Optimizing Mine Design: The findings can inform the design of mine layouts, including the placement of tunnels, pillars, and extraction sequences. By avoiding high-stress areas or redistributing stress more evenly, the risk of structural failures can be minimized.
- (3)
- Support System Design: knowledge of stress patterns helps to design more effective support systems, such as rock bolts, shotcrete, or steel arches, which are tailored to the specific stress conditions of different areas within the mine.
- (4)
- Predicting and Mitigating Hazards: Stress distribution data can be used to predict potential hazards, including rock bursts or ground subsidence. Early warning systems and preventive measures, such as controlled blasting or stress relief techniques, can be implemented to mitigate these risks.
- (5)
- Improving Worker Safety Protocols: by mapping stress patterns, mining operators can develop safer work practices, such as restricting access to high-stress areas during critical periods or scheduling maintenance activities when stress levels are lower.
- (6)
- Enhancing Monitoring Systems: The research results can guide the deployment of advanced monitoring technologies, such as micro-seismic sensors or stress meters, in order to continuously track stress changes and provide real-time data for decision making.
7. Conclusions
- (1)
- The normal stress distribution is approximately linear within 4 m of the top edge of the rock formation. The influences of the factors on the mean values are, in descending order, inclination angle > burial depth > angle between the maximum horizontal principal stress and the strike of the formation > lateral pressure coefficient.
- (2)
- In other parts of the top plate of the formation, the normal stresses are approximately uniformly distributed. The four influencing factors on these mean values are, in descending order, angle between the maximum horizontal principal stress and the strike of the formation > inclination angle > burial depth > lateral pressure coefficient.
- (3)
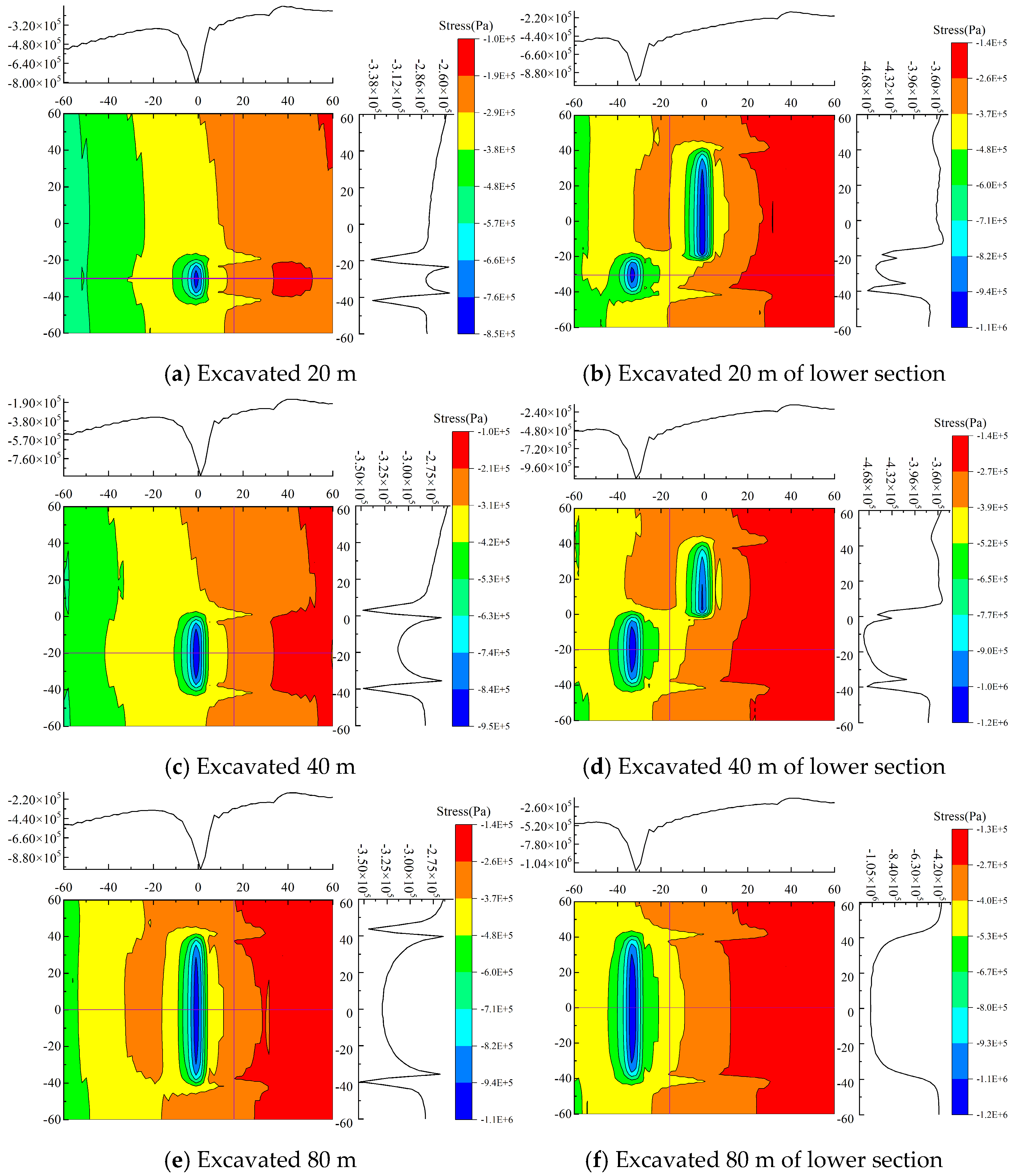
- During mining of the upper section, the normal stress in the hollow area above the working face increases with greater burial depth. In the lower section, the stress distribution characteristics are similar to those of the upper section; however, the rate of change in the normal stress within the range from −32 to −24 in the coordinate axis gradually increases, while it tends to flatten in the range from−24 to 0. Regarding coal seam inclination, the normal stress in the hollow area decreases as the inclination increases during upper-section mining, with the rate of change in the lower part (−32 to −24 on the axes) increasing and the stress in other regions (−24 to 0) approaching a flat distribution. During lower-section mining, although the normal stress increases in the range of −32 to −24, the stress distribution in other regions (−24 to 0) also tends to flatten. Overall, the characteristics of stress distribution during lower-section mining are similar to those for the upper section.
- (4)
- The normal stress in the mining hollow area above the working face increases with an increase in the lateral pressure coefficient. This study provided new insights into the distribution pattern of normal stresses on the roof of the working face and clarified the order of importance of each influencing factor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Jiao, J.; Wu, Y.; Jiang, B.; Luo, S.; Wang, T. Mining stress evolution law of surrounding rock in short wall fully mechanized caving stope of steeply inclined coal seam. J. Min. Saf. Eng. 2024, 41, 462–471. [Google Scholar] [CrossRef]
- Wang, J.; Yang, S.; Liu, S.; Liu, J.; Zhang, J. Technology status and fluidized mining conception for steeply inclined coal seams. Coal Sci. Technol. 2022, 50, 48–59. [Google Scholar]
- Wu, Y.P.; Liu, K.Z.; Yuan, D.F.; Jie, P.D.; Wang, G.W. Research progress on the safe and efficient mining technology of steeply dipping seam. J. China Coal Soc. 2014, 39, 1611–1618. [Google Scholar] [CrossRef]
- Ross, C.; Conover, D.; Baine, J. Highwall mining of thick, steeply dipping coal: A case study in geotechnical design and recovery optimization. Int. J. Min. Sci. Technol. 2019, 29, 777–780. [Google Scholar] [CrossRef]
- Jawed, M.; Sinha, R.K. Design of rhombus coal pillars and support for roadway stability and mechanizing loading of face coal using SDLs in a steeply inclined thin coal seam: A technical feasibility study. Arab. J. Geosci. 2018, 11, 415. [Google Scholar] [CrossRef]
- Xie, P.; Zhang, Y.; Wu, Y.; Huang, B.; Feng, K.; Chen, X. Experimental study on roof fracture and gangue filling in pitching oblique mining area of steeply dipping medium thick coal seam. J. Min. Saf. Eng. 2023, 40, 534–542. [Google Scholar] [CrossRef]
- Wu, Y.; Huangfu, J.; Xie, P.; Hu, B.; Liu, K. Mechanism of instability of section coal pillar in steeply dipping seam based on large-scale strata control technology. J. China Coal Soc. 2018, 43, 3062–3071. [Google Scholar]
- Xie, P.S.; Zhang, Y.Y.; Zhang, Y.L.; Chen, J.J.; Zhang, X.B.; Duan, J.J. Instability law of the coal-rock interbedded roof and its influence on supports in large mining height working face with steeply dipping coal seam. J. China Coal Soc. 2021, 46, 344–356. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Y. The immediate roof first fractures of suberect and extremely thick coal. J. China Coal Soc. 2018, 43, 1220–1229. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Q.; Xu, Z.; Zhang, Y. Roof fractures of near-vertical and extremely thick coal seams in horizontally grouped top-coal drawing method based on the theory of a thin plate. Sustainability 2022, 14, 10285. [Google Scholar] [CrossRef]
- Yang, S.; Li, Q.; Yue, H.; Yang, S.; Liu, F. Study on coal wall spalling characteristics and stability control of steeply inclined coal seam mining face. Comput. Part. Mech. 2025, 1–22. [Google Scholar] [CrossRef]
- Lu, A.; Song, D.; Li, Z.; He, X.; Zhou, C.; Qiu, L. Numerical Simulation Study on Microseismic Characteristics and Rockburst Hazard Prediction in Deep Mining of Steeply Inclined Coal Seams. Rock Mech. Rock Eng. 2024, 58, 2465–2486. [Google Scholar] [CrossRef]
- Xiong, Y.; Kong, D.; Song, G.; He, Y. Failure mechanism and 3D physical modeling test of coal face pyramid sliding in steeply inclined working face: A case study. Eng. Fail. Anal. 2024, 159, 108064. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, J.; Zhang, N.; Guo, F.; He, Z.; Xiang, Z.; Zhang, C. Study on Time-Dependent Failure Mechanisms and CBAG Differential Support Technology of Roadway in Steeply Inclined Coal Seam. Processes 2023, 11, 866. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Y.; Zhu, Y.; Cai, J.; Wang, J. Quantitative Study on the Law of Surface Subsidence Zoning in Steeply Inclined Extra-Thick Coal Seam Mining. Sustainability 2022, 14, 6758. [Google Scholar] [CrossRef]
- Kong, D.; Xiong, Y.; Cheng, Z.; Wang, N.; Wu, G.; Liu, Y. Stability analysis of coal face based on coal face-support-roof system in steeply inclined coal seam. Geomech. Eng. 2021, 25, 233–243. [Google Scholar] [CrossRef]
- He, S.Q.; Song, D.Z.; Li, Z.L.; He, X.Q.; Chen, J.Q.; Li, D.H.; Tian, X.H. Precursor of Spatio-temporal Evolution Law of MS and AE Activities for Rock Burst Warning in Steeply Inclined and Extremely Thick Coal Seams Under Caving Mining Conditions. Rock Mech. Rock Eng. 2019, 52, 2415–2435. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, J. Stability of roof structure and its control in steeply inclined coal seams. Int. J. Min. Sci. Technol. 2017, 27, 359–364. [Google Scholar] [CrossRef]
- Wang, J.-A.; Jiao, J.-L. Criteria of support stability in mining of steeply inclined thick coal seam. Int. J. Rock Mech. Min. Sci. 2016, 82, 22–35. [Google Scholar] [CrossRef]
- Feng, C.; Lei, Z.; Chen, J.; Chang, B.; Yang, Y.; Li, C.; Jia, C. Research on Reducing Mining-Induced Disasters by Filling in Steeply Inclined Thick Coal Seams. Sustainability 2019, 11, 5802. [Google Scholar] [CrossRef]




| Test | Depth (m) | Dip of a Coal Seam (°) | Lateral Pressure Coefficient | Angle Between Maximum Principal Stress and Coal Seam Strike (°) |
|---|---|---|---|---|
| 1 | 100 | 65 | 1 | 0 |
| 2 | 100 | 75 | 1.25 | 45 |
| 3 | 100 | 85 | 1.5 | 90 |
| 4 | 300 | 65 | 1.5 | 45 |
| 5 | 300 | 75 | 1 | 90 |
| 6 | 300 | 85 | 1.25 | 0 |
| 7 | 500 | 65 | 1.25 | 90 |
| 8 | 500 | 75 | 1.5 | 0 |
| 9 | 500 | 85 | 1 | 45 |
| Dip of a Coal Seam/° | Lengths/m | Width/m | Height/m | Number of Units | Number of Nodes |
|---|---|---|---|---|---|
| 65 | 277 | 200 | 120 | 553,750 | 586,921 |
| 75 | 257 | 200 | 120 | 516,250 | 550,685 |
| 85 | 239 | 200 | 120 | 515,000 | 549,155 |
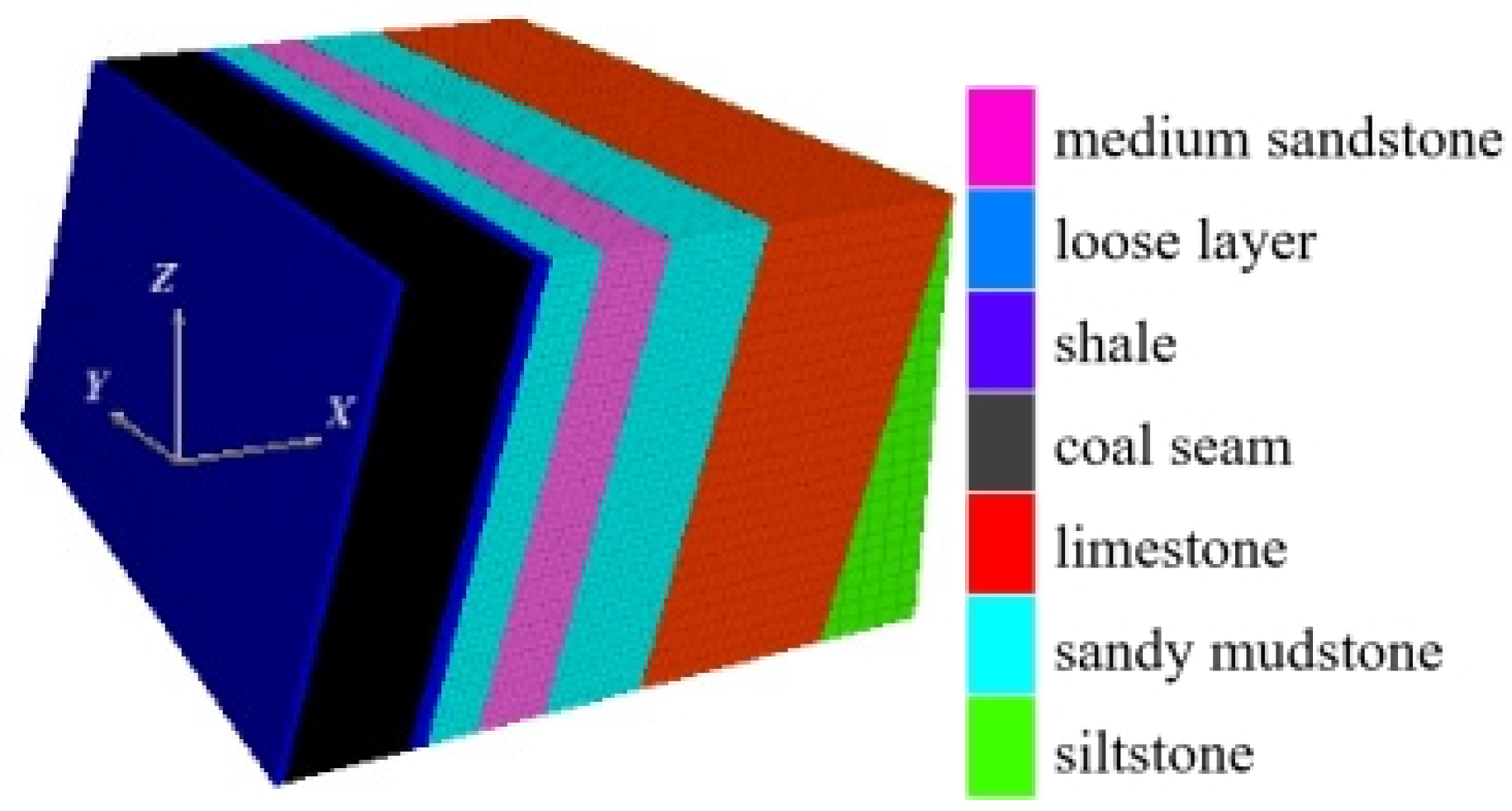
| NO. | Lithology | Thickness/m | Density Kg/m3 | Bulk Modulus/GPa | Shear Modulus/GPa | Friction Angle/degree (°) | Cohesion/MPa | Tensile Strength/GPa |
|---|---|---|---|---|---|---|---|---|
| 1 | Loose layer | 20 | 2100 | 7.0 | 3.5 | 25° | 5.5 | 1.6 |
| 2 | Sandy mudstone | Variable | 2600 | 8.1 | 6.0 | 36° | 18.8 | 3.5 |
| 3 | Mudstone | 48 | 2470 | 2.6 | 2.0 | 38° | 4.5 | 1.0 |
| 4 | Sandy mudstone | 24 | 2450 | 8.1 | 6.0 | 36° | 18.8 | 3.5 |
| 5 | Medium sandstone | 16 | 2430 | 10.9 | 6.9 | 31° | 39.5 | 5.1 |
| 6 | Sandstone | 8 | 2600 | 4.9 | 3.7 | 30° | 27.2 | 6.1 |
| 7 | Mudstone | 2 | 2430 | 2.6 | 2.0 | 38° | 4.5 | 1.0 |
| 8 | Coal seam | 28 | 1330 | 1.2 | 0.8 | 28° | 4.2 | 0.9 |
| 9 | Mudstone | 4 | 2400 | 2.6 | 2.0 | 38° | 4.5 | 1.0 |
| 10 | Sandstone | 12 | 2450 | 4.9 | 3.7 | 30° | 27.2 | 6.1 |
| 11 | Medium sandstone | 16 | 2650 | 10.9 | 6.9 | 31° | 39.5 | 5.1 |
| 12 | Sandy mudstone | 24 | 2500 | 8.1 | 6.0 | 36° | 18.8 | 3.5 |
| 13 | Coarse sandstone | 48 | 2500 | 12.5 | 9.4 | 35° | 35.6 | 3.5 |
| NO. | Geostress Test Location | Depth/m | σ1/MPa | σ2/MPa | σH/MPa | σ1/σ2 |
|---|---|---|---|---|---|---|
| 1 | Stone gate at +1126 m level of Adohai Mine | 367.5 | 18.03 | 10.9 | 9.25 | 1.95 |
| 2 | Winch chamber at +1228 m level of Adohai Mine | 206.9 | 12.26 | 6.84 | 6.27 | 1.96 |
| 3 | Roadway 2–106b2 of Xinzhi Mine | 600 | 14.7 | 8.53 | 17.03 | 1.72 |
| 4 | Roadway 2–1022 of Ganhe Mine | 461 | 16.18 | 8.38 | 11 | 1.93 |
| 5 | Railroad track end in the second mining area of Ganhe Mine | 529 | 14.78 | 7.92 | 12.77 | 1.87 |
| 6 | Roadway 10–2151 of Tuanbai Mine | 33 | 9.27 | 5.32 | 7.8 | 1.74 |
| 7 | Return lane 310 of Tuanbai Mine | 405 | 12.37 | 6.7 | 9.67 | 1.8 |
| 8 | System roadway 10–1021 of Huipodi Mine | 367.9 | 9.32 | 4.99 | 8.77 | 1.87 |
| 9 | East first mining area railroad track of Huipodi Mine | 355.1 | 10.32 | 5.57 | 8.33 | 1.85 |
| 10 | East five mining area two link alley of Huipodi Mine | 271 | 7.38 | 4.84 | 6.28 | 1.52 |
| 11 | Lane 1051, central part of the yard of Pangpang Mine | 490 | 9.63 | 5.1 | 12.26 | 1.89 |
| 12 | Lane 1092 at 560 m of Pangpang Mine | 592 | 11.68 | 6.16 | 14.8 | 1.90 |
| 13 | Rubber wheelbarrow alley of Changping Mine | 348.1 | 10.81 | 5.6 | 8.7 | 1.93 |
| 14 | Explosives magazine return airway of Changping Mine | 336.3 | 8.85 | 5.15 | 8.41 | 1.72 |
| 15 | First contact lane exit of Changping Mine | 343.9 | 9.64 | 4.99 | 8.6 | 1.93 |
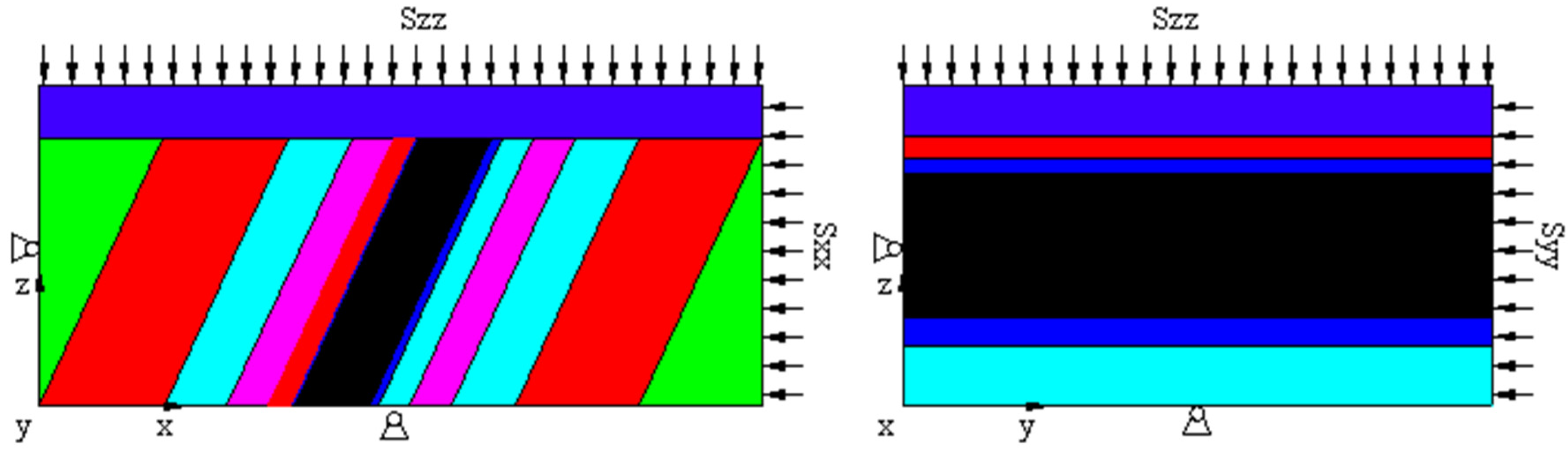
| NO. | Lower z-Direction | Upper z-Direction | x-Negative Direction | x-Positive Direction | y-Negative Direction | y-Positive Direction |
|---|---|---|---|---|---|---|
| Szz/Mpa | Sxx/Mpa | Sxx/Mpa | Syy/Mpa | Syy/Mpa | ||
| 1 | Fixed | 0.25 | Fixed | 0.32 | Fixed | 0.18 |
| 2 | Fixed | 0.25 | Fixed | 0.31 | Fixed | 0.31 |
| 3 | Fixed | 0.25 | Fixed | 0.27 | Fixed | 0.48 |
| 4 | Fixed | 5.25 | Fixed | 7.88 | Fixed | 7.88 |
| 5 | Fixed | 5.25 | Fixed | 6.78 | Fixed | 3.72 |
| 6 | Fixed | 5.25 | Fixed | 8.47 | Fixed | 4.65 |
| 7 | Fixed | 10.25 | Fixed | 9.09 | Fixed | 16.54 |
| 8 | Fixed | 10.25 | Fixed | 19.85 | Fixed | 10.90 |
| 9 | Fixed | 10.25 | Fixed | 10.25 | Fixed | 10.25 |
| NO. | Location of Statistics | Mean Normal Corresponding Force (Mpa) | |||||
|---|---|---|---|---|---|---|---|
| Excavation Distance of the Upper Section | Distance of Excavation in the Lower Section | ||||||
| 20 | 40 | 80 | 20 | 40 | 80 | ||
| 1 | Mean value of the edge portion | 0.73 | 0.84 | 0.89 | 0.81 | 0.90 | 0.92 |
| Smoothed section mean | 0.30 | 0.33 | 0.34 | 0.45 | 0.34 | 0.33 | |
| 2 | Mean value of the edge portion | 0.53 | 0.62 | 0.66 | 0.50 | 0.55 | 0.58 |
| Smoothed section mean | 0.18 | 0.19 | 0.20 | 0.22 | 0.19 | 0.19 | |
| 3 | Mean value of the edge portion | 0.32 | 0.38 | 0.41 | 0.30 | 0.34 | 0.36 |
| Smoothed section mean | 0.05 | 0.05 | 0.06 | 0.03 | 0.03 | 0.03 | |
| 4 | Mean value of the edge portion | 5.04 | 5.52 | 5.87 | 2.88 | 3.12 | 3.18 |
| Smoothed section mean | 0.66 | 0.62 | 0.75 | 1.04 | 0.71 | 0.96 | |
| 5 | Mean value of the edge portion | 5.05 | 5.55 | 5.93 | 2.91 | 0.33 | 0.35 |
| Smoothed section mean | 1.09 | 0.99 | 1.00 | 0.51 | 0.11 | 0.11 | |
| 6 | Mean value of the edge portion | 6.53 | 7.07 | 7.47 | 4.06 | 4.41 | 4.76 |
| Smoothed section mean | 0.45 | 0.21 | 0.53 | 0.22 | −0.09 | 0.29 | |
| 7 | Mean value of the edge portion | 7.08 | 7.84 | 8.41 | 5.03 | 5.45 | 5.65 |
| Smoothed section mean | 2.37 | 2.31 | 2.63 | 2.52 | 1.93 | 1.82 | |
| 8 | Mean value of the edge portion | 13.22 | 13.80 | 14.14 | 6.25 | 17.39 | 6.49 |
| Smoothed section mean | 1.47 | 1.50 | 1.54 | 1.26 | 13.86 | 1.71 | |
| 9 | Mean value of the edge portion | 6.53 | 8.67 | 9.16 | 5.06 | 5.49 | 5.88 |
| Smoothed section mean | 0.45 | 0.73 | 0.34 | 0.39 | −0.10 | 0.48 | |
| Classifications | Depth | Inclination Angle | Lateral Pressure Coefficient | Angle of Principal Stress | Depth | Inclination Angle | Lateral Pressure Coefficient | Angle of Principal Stress |
|---|---|---|---|---|---|---|---|---|
| Excavation | Upper Section Excavation 20 m | Lower Section Excavation 20 m | ||||||
| K1 | 1.58 | 12.84 | 12.31 | 20.48 | 1.61 | 8.73 | 8.78 | 11.12 |
| K2 | 16.62 | 18.81 | 14.15 | 12.11 | 9.85 | 9.65 | 9.59 | 8.44 |
| K3 | 26.83 | 45.03 | 18.58 | 12.44 | 16.34 | 27.79 | 9.43 | 8.23 |
| k1 | 0.53 | 4.28 | 4.10 | 6.83 | 0.54 | 2.91 | 2.93 | 3.71 |
| k2 | 5.54 | 6.27 | 4.72 | 4.04 | 3.28 | 3.22 | 3.20 | 2.81 |
| k3 | 8.94 | 15.01 | 6.19 | 4.15 | 5.45 | 9.26 | 3.14 | 2.74 |
| R (Level) | 8.42 (2) | 10.73 (1) | 2.09 (4) | 2.68 (3) | 4.91 (2) | 6.36 (1) | 0.27 (3) | 0.96 (3) |
| K1′ | 0.53 | 7.01 | 1.84 | 2.22 | 0.70 | 6.63 | 1.34 | 1.93 |
| K2′ | 2.20 | 2.75 | 2.99 | 9.22 | 1.77 | 1.99 | 2.95 | 8.36 |
| K3′ | 4.28 | 0.94 | 2.18 | 3.51 | 4.16 | 0.64 | 2.34 | 3.06 |
| k1′ | 0.18 | 2.34 | 0.61 | 0.74 | 0.23 | 2.21 | 0.45 | 0.64 |
| k2′ | 0.73 | 0.92 | 1.00 | 3.07 | 0.59 | 0.66 | 0.98 | 2.79 |
| k3′ | 1.43 | 0.31 | 0.73 | 1.17 | 1.39 | 0.21 | 0.78 | 1.02 |
| R’ (Level) | 1.25 (3) | 2.02 (2) | 0.39 (4) | 2.34 (1) | 1.16 (3) | 2.00 (2) | 0.54 (4) | 2.14 (1) |
| Excavation | Upper section excavation 40 m | Lower section excavation 40 m | ||||||
| K1 | 1.84 | 14.20 | 15.06 | 21.71 | 1.79 | 9.47 | 6.72 | 22.70 |
| K2 | 18.15 | 19.96 | 15.53 | 14.81 | 7.87 | 18.27 | 10.41 | 9.17 |
| K3 | 30.30 | 50.28 | 19.70 | 13.77 | 28.33 | 37.98 | 20.85 | 6.12 |
| k1 | 0.61 | 4.73 | 5.02 | 7.24 | 0.60 | 3.16 | 2.24 | 7.57 |
| k2 | 6.05 | 6.65 | 5.18 | 4.94 | 2.62 | 6.09 | 3.47 | 3.06 |
| k3 | 10.10 | 16.76 | 6.57 | 4.59 | 9.44 | 12.66 | 6.95 | 2.04 |
| R (Level) | 9.49 (2) | 12.03 (1) | 1.55 (4) | 2.65 (3) | 8.85 (2) | 9.51 (1) | 4.71 (4) | 5.53 (3) |
| K1′ | 0.57 | 6.93 | 2.05 | 2.03 | 0.55 | 16.96 | 0.34 | 14.11 |
| K2′ | 1.81 | 2.68 | 2.71 | 8.75 | 0.72 | 14.16 | 2.02 | 17.70 |
| K3′ | 4.54 | 0.99 | 2.17 | 3.35 | 15.69 | -0.17 | 14.61 | 2.06 |
| k1′ | 0.19 | 2.31 | 0.68 | 0.68 | 0.18 | 5.65 | 0.11 | 4.70 |
| k2′ | 0.60 | 0.89 | 0.90 | 2.92 | 0.24 | 4.72 | 0.67 | 5.90 |
| k3′ | 1.51 | 0.33 | 0.72 | 1.12 | 5.23 | -0.06 | 4.87 | 0.69 |
| R′ (Level) | 1.32 (3) | 1.98 (2) | 0.22 (4) | 2.24 (1) | 5.04 (3) | 5.71 (2) | 0.56 (4) | 1.20 (1) |
| Excavation | Upper section excavation 80 m | Lower section excavation 80 m | ||||||
| K1 | 1.96 | 15.17 | 15.98 | 22.50 | 1.85 | 9.75 | 7.14 | 12.17 |
| K2 | 19.27 | 20.73 | 16.54 | 15.69 | 8.29 | 7.41 | 10.99 | 9.64 |
| K3 | 31.70 | 52.93 | 20.42 | 14.74 | 18.02 | 28.17 | 10.03 | 6.36 |
| k1 | 1.96 | 15.17 | 15.98 | 22.50 | 0.62 | 3.25 | 2.38 | 4.06 |
| k2 | 19.27 | 20.73 | 16.54 | 15.69 | 2.76 | 2.47 | 3.66 | 3.21 |
| k3 | 31.70 | 52.93 | 20.42 | 14.74 | 6.01 | 9.39 | 3.34 | 2.12 |
| R (Level) | 29.74 (2) | 37.77 (1) | 4.44 (4) | 7.76 (3) | 5.39 (2) | 6.14 (1) | 1.28 (4) | 1.94 (3) |
| K1′ | 0.60 | 7.38 | 1.67 | 2.41 | 0.55 | 5.92 | 0.92 | 2.33 |
| K2′ | 2.28 | 2.74 | 3.36 | 9.67 | 1.35 | 2.01 | 2.30 | 7.28 |
| K3′ | 4.51 | 0.92 | 2.35 | 3.68 | 4.02 | 0.80 | 2.70 | 1.96 |
| k1′ | 0.60 | 7.38 | 1.67 | 2.41 | 0.18 | 1.97 | 0.31 | 0.78 |
| k2′ | 2.28 | 2.74 | 3.36 | 9.67 | 0.45 | 0.67 | 0.77 | 2.43 |
| k3′ | 4.51 | 0.92 | 2.35 | 3.68 | 1.34 | 0.27 | 0.90 | 0.65 |
| R’ (Level) | 3.91 (3) | 6.46 (2) | 1.68 (4) | 7.26 (1) | 1.16 (3) | 1.71 (2) | 0.46 (4) | 1.65 (1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhang, Y.; Fu, S.; Chi, M. Evolution Characteristics of Roof Stress in Horizontal Segmental Mining of Steeply Inclined Coal Seams. Processes 2025, 13, 1317. https://doi.org/10.3390/pr13051317
Zhang G, Zhang Y, Fu S, Chi M. Evolution Characteristics of Roof Stress in Horizontal Segmental Mining of Steeply Inclined Coal Seams. Processes. 2025; 13(5):1317. https://doi.org/10.3390/pr13051317
Chicago/Turabian StyleZhang, Guojun, Yong Zhang, Shigen Fu, and Mingbo Chi. 2025. "Evolution Characteristics of Roof Stress in Horizontal Segmental Mining of Steeply Inclined Coal Seams" Processes 13, no. 5: 1317. https://doi.org/10.3390/pr13051317
APA StyleZhang, G., Zhang, Y., Fu, S., & Chi, M. (2025). Evolution Characteristics of Roof Stress in Horizontal Segmental Mining of Steeply Inclined Coal Seams. Processes, 13(5), 1317. https://doi.org/10.3390/pr13051317







