A Collaborative Optimization Approach for Configuring Energy Storage Systems and Scheduling Multi-Type Electric Vehicles Using an Improved Multi-Objective Particle Swarm Optimization Algorithm
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contributions
- (1)
- A multidimensional collaborative optimization framework is proposed for high-penetration renewable energy systems, which uncovers the nonlinear coupling mechanisms between the configuration of ESS and the scheduling of multi-type EVs. This framework aims to maximize the coordinated operation of ESS and EVs, thereby enhancing the integration of renewable energy.
- (2)
- A differentiated charging demand model for private cars, taxis, and buses is developed based on real-world operational data, with the Monte Carlo algorithm employed for load forecasting. This approach improves upon existing EV studies by better capturing user behavior heterogeneity and enhancing the accuracy of time distribution modeling for charging demand.
- (3)
- An IMOPSO algorithm is proposed, combining dynamic crowding distance Pareto front updates, adaptive inertia weights, and entropy-weighted technique for order preference by similarity to an ideal solution (TOPSIS) selection. This effectively addresses high-dimensional nonlinear constraints and fixed weight limitations, outperforming non-dominated sorting genetic algorithm-II (NSGA-II) and traditional multi-objective particle swarm optimization (MOPSO) in convergence speed and solution uniformity.
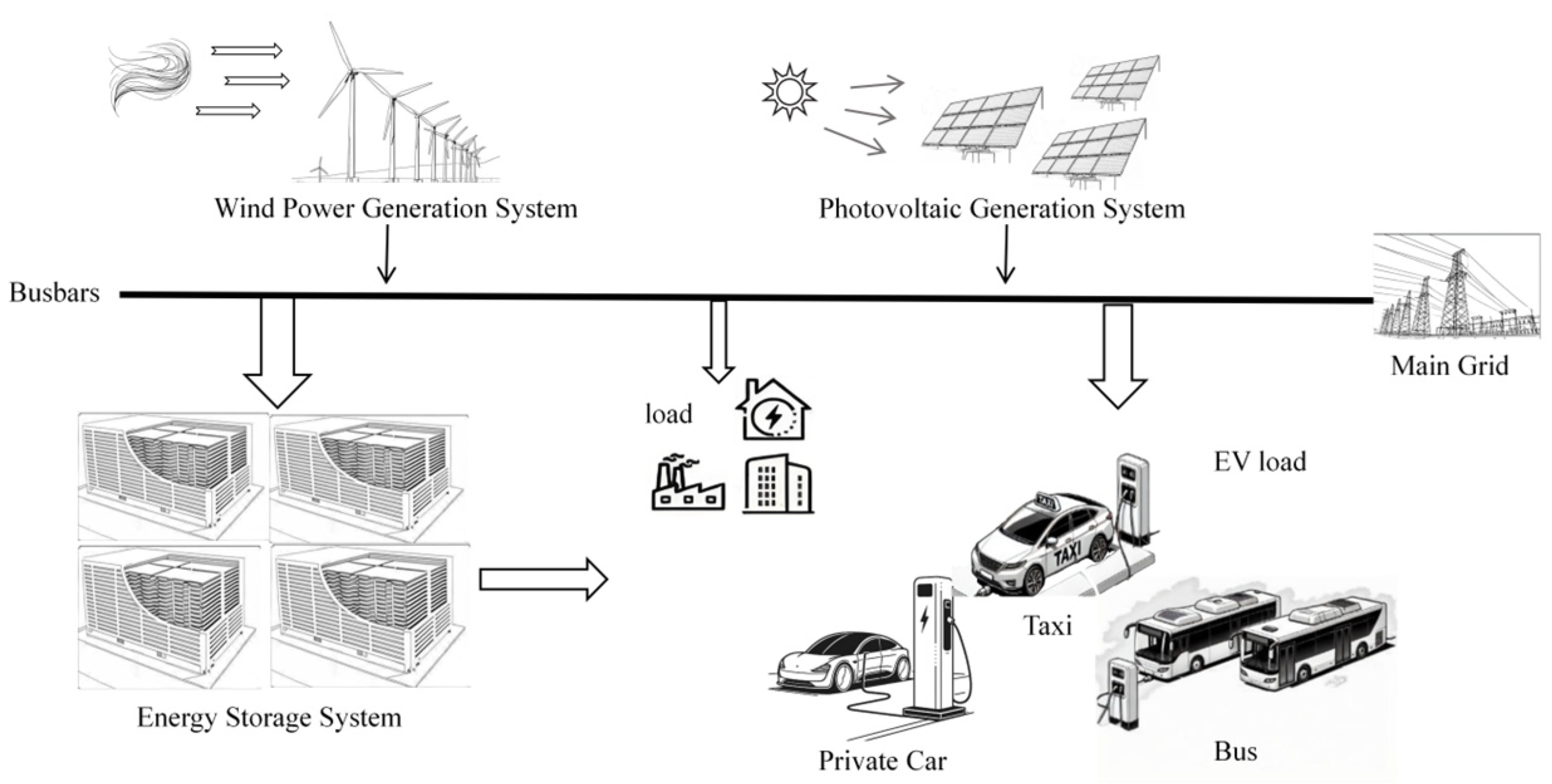
2. Wind–Solar Storage-Load System Model
2.1. Wind Power Generation Model
2.2. Photovoltaic Power Generation Model
2.3. ESS Model
2.4. Multi-Type EVs Flexible Load Model
2.4.1. Modeling of Daily Driving Distance
2.4.2. Model of Charging Start Time
2.4.3. Charging Power for EVs
2.4.4. Charging Duration
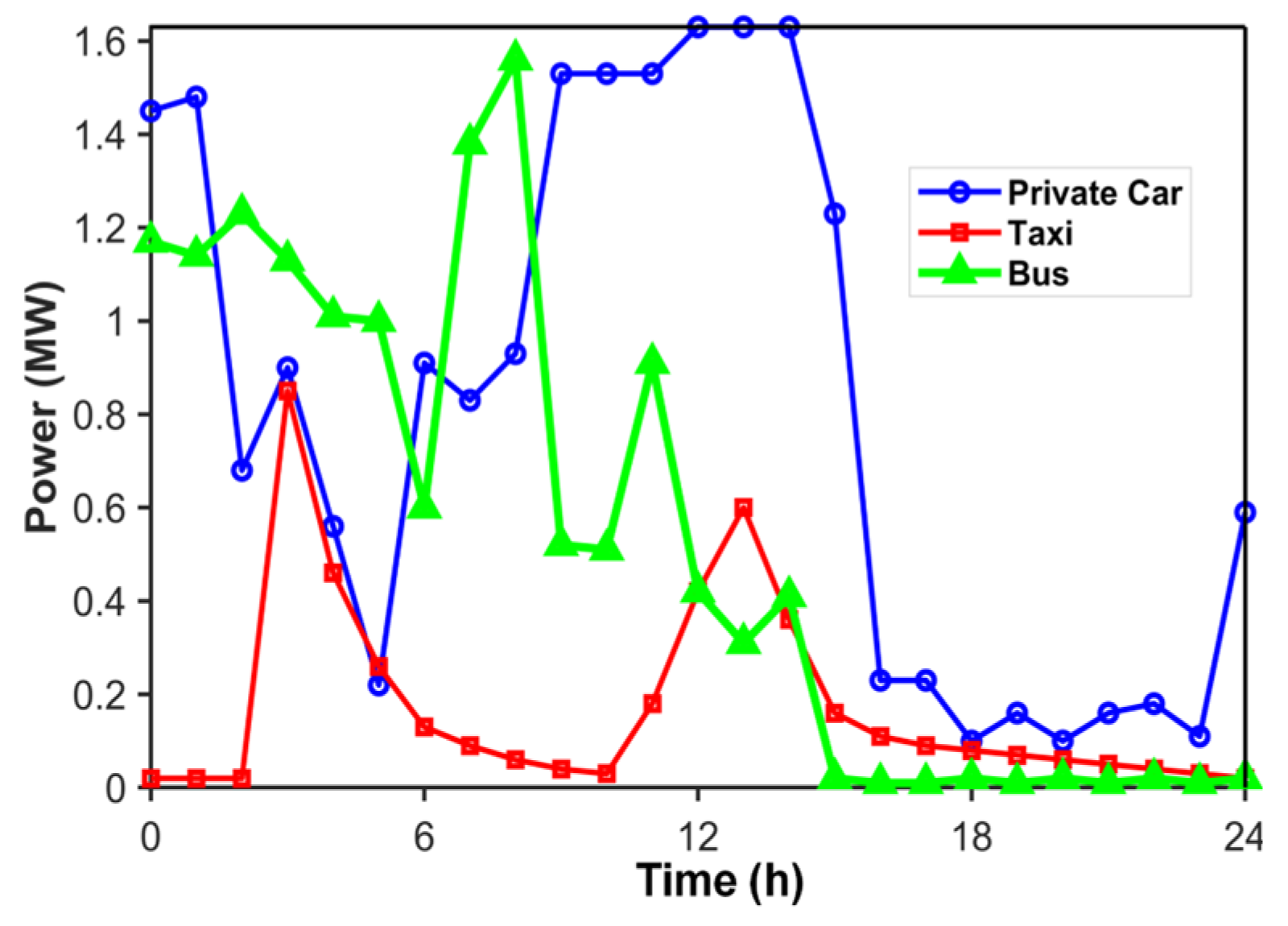
2.5. Multi-Type EVs Load Setting
2.5.1. Electric Private Car
2.5.2. Electric Taxi
2.5.3. Electric Bus
2.6. Monte Carlo-Based Multi-Type EV Charging Load Forecasting Process
3. Collaborative Optimization for the Configuration of ESS and the Scheduling of EVs
3.1. Optimization Configuration of ESS
3.1.1. Annual Total Cost
- (1)
- Construction Cost
- (2)
- Maintenance Costs
- (3)
- Incremental Annual Grid Revenue from the ESS
3.1.2. Wind–Solar Integration Rate
3.1.3. System Electricity Deficit
3.1.4. Constraints
- (1)
- Load Balance Constraint
- (2)
- ESS Constraints
- (3)
- System Deficit Constraint
3.2. Multi-Type EV Optimization Dispatch Objective Function
3.2.1. Charging Cost for EV Users
3.2.2. Load Factor
3.2.3. Constraints
- (1)
- Load Balance Constraint
- (2)
- Multi-Type EVs Load Constraints
3.3. Solution Algorithm—IMOPSO
3.3.1. Classical PSO Algorithm
3.3.2. Pareto Solution Set Update Strategy
3.3.3. Adaptive Adjustment of Inertia Weight
3.3.4. Selection of the Optimal Solution
3.3.5. Solution Process
4. Simulation Analysis
4.1. Simulation Setting
4.2. Case Study Analysis
- Scenario 1: only optimizing the configuration of ESS;
- Scenario 2:optimizing the configuration of ESS and the scheduling of single-type EVs;
- Scenario 3: optimizing the configuration of ESS and the scheduling of multi-type EVs.
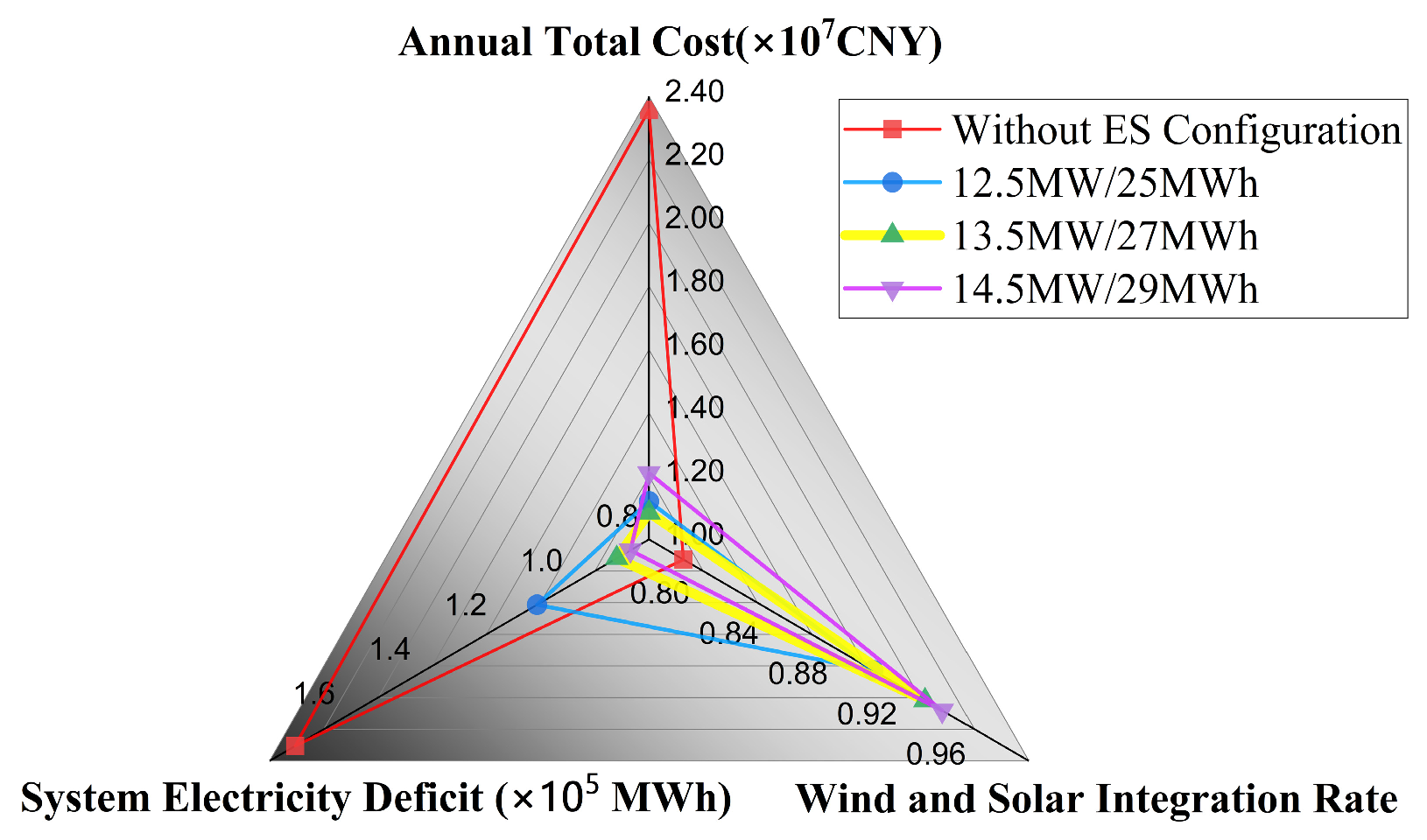
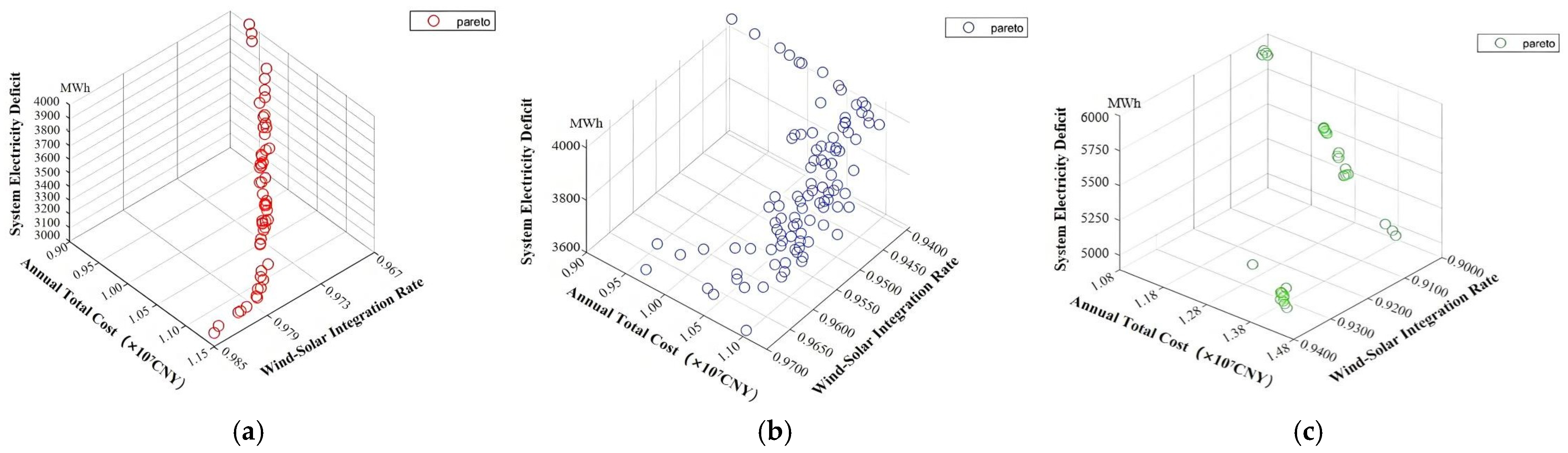
4.3. Optimization Results of ESS Configuration
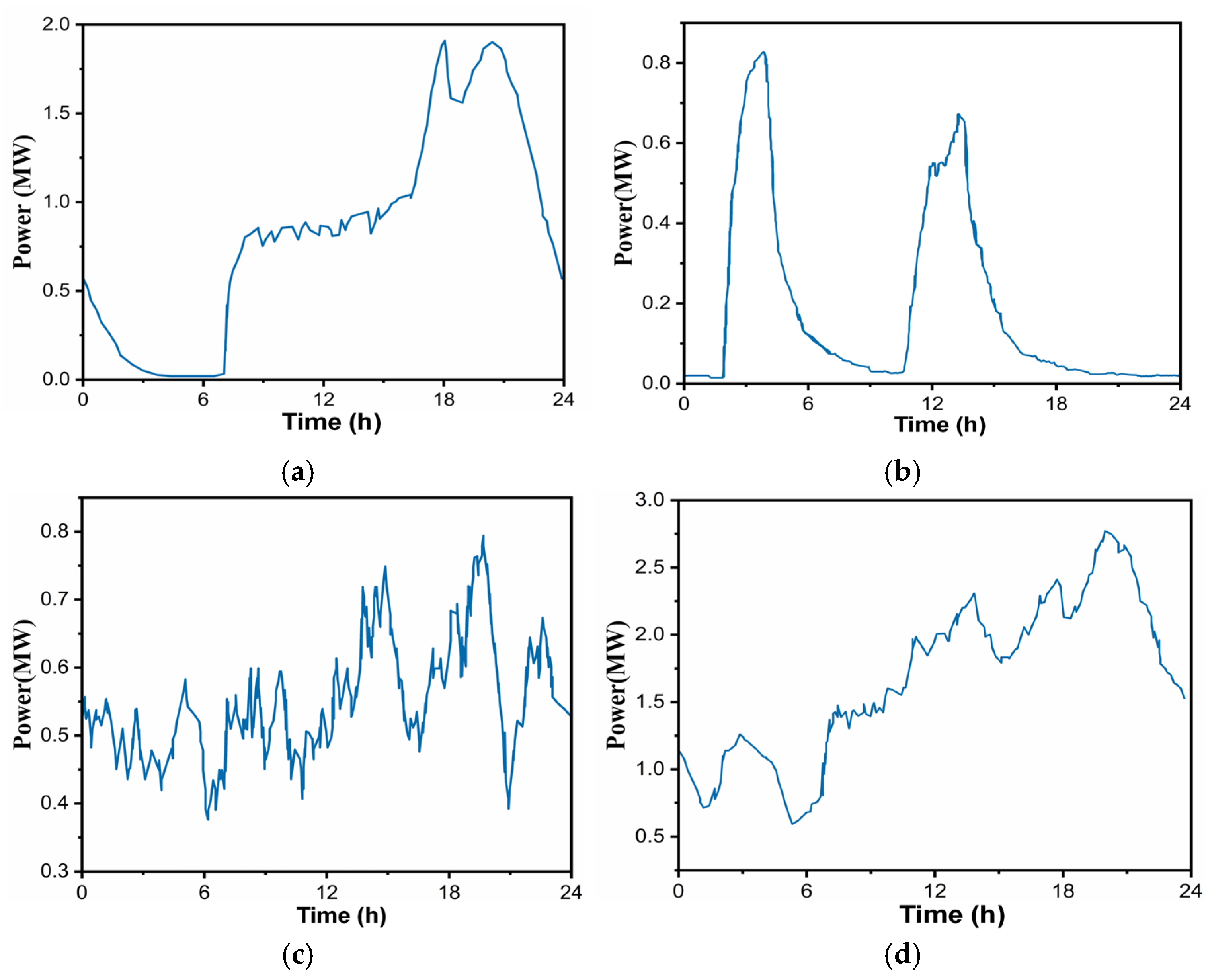
4.4. Monte Carlo Simulation for Multi-Type EV Load Forecasting
- Situation 1: disordered EV charging;
- Situation 2: ordered EV charging.
4.5. Sensitivity Analysis of Key Parameters
4.6. The Comparison of Algorithms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ESS | energy storage systems |
| EVs | electric vehicles |
| IMOPSO | improved multi-objective particle swarm optimization |
| ES | energy storage |
| BESS | battery energy storage systems |
| PSO | particle swarm optimization |
| TOPSIS | technique for order preference by similarity to an ideal solution |
| NSGA-II | non-dominated sorting genetic algorithm-II |
| MOPSO | multi-objective particle swarm optimization |
| WT | wind turbine |
| PV | photovoltaic |
| SOC | state of charge |
| output power of the WT, (kW) | |
| PV output power, (kW) | |
| ESS charging and discharging power, (kW) | |
| total charging load of EVs, (kW) | |
| annual total cost of the wind–solar storage system, (CNY) | |
| wind–solar integration rate, (%) | |
| system electricity deficit, (kWh) | |
| curtailment power, (kW) | |
| charging cost for EV users, (CNY) | |
| Lr | load factor, (%) |
References
- Jiang, B.; Raza, M.Y. Research on China’s renewable energy policies under the dual carbon goals: A political discourse analysis. Energy Strat. Rev. 2023, 48, 101118. [Google Scholar] [CrossRef]
- Xia, P.; Lu, G.; Yuan, B.; Gong, Y.; Chen, H. Analysis of China’s Low-Carbon Power Transition Path Considering Low-Carbon Energy Technology Innovation. Appl. Sci. 2025, 15, 340. [Google Scholar] [CrossRef]
- Wei, H.; Zhuo, Z.; Zhang, N.; Du, E.; Xiao, J.; Wang, P.; Kang, C. Transition Path Optimization and Influencing Factor Analysis of Carbon Emission Peak and Carbon Neutrality for Power System of China. Autom. Electr. Power Syst. 2022, 46, 1–12. [Google Scholar] [CrossRef]
- Zhu, L.; Liang, Z.; Zhang, L.; Meng, W.; Yao, X.; Su, B.; Tao, Z. Assessing the impacts of coal-to-electricity transition in China’s regional power system and “2 + 26” cities. iScience 2025, 28, 111775. [Google Scholar] [CrossRef] [PubMed]
- Hoicka, C.E.; Zhao, Y.; McMaster, M.L.; Das, R.R. Diffusion of demand-side low-carbon innovations and socio-technical energy system change. Renew. Sustain. Energy Transit. 2022, 2, 100034. [Google Scholar] [CrossRef]
- Chen, Y.; Dai, X.; Fu, P.; Luo, G.; Shi, P. A review of China’s automotive industry policy: Recent developments and future trends. J. Traffic Transp. Eng. 2024, 11, 867–895. [Google Scholar] [CrossRef]
- Wang, Z. Charging of New Energy Vehicles. In Annual Report on the Development of the Pure Electric New Energy Vehicle Market and Vehicle Usage (2023), 1st ed; Springer Singapore: Singapore, 2024; Volume 5, pp. 141–209. Available online: https://link.springer.com/book/10.1007/978-981-97-4840-2 (accessed on 1 December 2024).
- China Association of Automobile Manufacturers. Annual Report on the Development of China Automotive Industry; Social Sciences Academic Press: Beijing, China, 2023. [Google Scholar]
- Oladigbolu, J.O.; Mujeeb, A.; Li, L. Optimization and energy management strategies, challenges, advances, and prospects in electric vehicles and their charging infrastructures: A comprehensive review, Computers and Electrical Engineering. Comput. Electr. Eng. 2024, 120, 109842. [Google Scholar] [CrossRef]
- Prakhar, P.; Jaiswal, R.; Gupta, S.; Tiwari, A.K. Electric vehicles in transition: Opportunities, challenges, and research agenda—A systematic literature review. J. Environ. Manag. 2024, 372, 123415. [Google Scholar] [CrossRef]
- Zhan, C.; Ge, J.; Hao, F.; Zhu, H.; Wang, C.; Wang, N. Assuring Security and Stability of a Remote/Islanded Large Electric Power System with High Penetration of Variable Renewable Energy Resources. IEEE Power Electron. Mag. 2025, 12, 53–63. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, B.; Wang, L.; Zeng, J.; Jiao, R.; Gong, C. Research on Participation of Electric Vehicles in Microgrid Load Power Fluctuation Mitigation Based on Digital Twin Hybrid Energy Storage. Automot. Eng. 2024, 46, 1046–1054. [Google Scholar] [CrossRef]
- Sun, B.; Dong, H.; Chen, G.; Liu, A.; Li, S. An intraday optimal scheduling model for joint operation of electric vehicles and wind-storage hybrid systems. Renew. Energy Resour. 2018, 36, 1033–1038. [Google Scholar] [CrossRef]
- Zheng, J.; Lai, H.; Zheng, W.; Xi, H.; Zhou, Z.; Qi, F.; Yu, K.; Yang, J. Capacity optimization configuration of WT-PV-DE-BES independent microgrid with electric vehicles. Power Demand Side Manag. 2024, 26, 31–36. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y. Research on Two-stage Optimal Dispatching Strategy of Distribution Network Considering EV and BESS. J. Power Supply 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Wang, T.; Liu, H.; Su, M. Energy Optimization for Microgrids Based on Uncertainty-Aware Deep Deterministic Policy Gradient. Processes 2025, 13, 1047. [Google Scholar] [CrossRef]
- Li, S.; Zhang, T.; Liu, X.; Xue, Z.; Liu, X. Performance investigation of a grid-connected system integrated photovoltaic, battery storage and electric vehicles: A case study for gymnasium building. Energy Build. 2022, 270, 112255. [Google Scholar] [CrossRef]
- Motevakel, P.; Roldán-Blay, C.; Roldán-Porta, C.; Escrivá-Escrivá, G.; Dasí-Crespo, D. Hybrid Energy Solutions for Enhancing Rural Power Reliability in the Spanish Municipality of Aras de los Olmos. Appl. Sci. 2025, 15, 3790. [Google Scholar] [CrossRef]
- Ahmed, H.Y.; Ali, Z.M.; Refaat, M.M.; Aleem, S.H.E.A. A Multi-Objective Planning Strategy for Electric Vehicle Charging Stations towards Low Carbon-Oriented Modern Power Systems. Sustainability 2023, 15, 2819. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, J.; Liu, Y.; Fan, J.; Lan, J.; Zhang, L. Renewable Energy Accommodation Strategy Based on Cyber-Physical-Social Integration. Autom. Electr. Power Syst. 2021, 46, 127–136. [Google Scholar] [CrossRef]
- Dong, X.-J.; Shen, J.-N.; Liu, C.-W.; Ma, Z.-F.; He, Y.-J. Simultaneous capacity configuration and scheduling optimization of an integrated electrical vehicle charging station with photovoltaic and battery energy storage system. Energy 2024, 289, 129991. [Google Scholar] [CrossRef]
- El Mezdi, K.; El Magri, A.; Bahatti, L. Advanced control and energy management algorithm for a multi-source microgrid incorporating renewable energy and electric vehicle integration. Results Eng. 2024, 48, 102642. [Google Scholar] [CrossRef]
- Chai, X.; Zhang, Y.; Du, D.; Sun, Y. Bi-level optimization scheduling of electric vehicle-distribution network considering demand response and carbon quota. J. Phys. Conf. Ser. 2024, 2849, 012075. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, B.; Deng, J. Multi-objective optimization strategy for distribution network considering V2G-enabled electric vehicles in building integrated energy system. Prot. Contr. Mod. Pow. 2020, 5, 278–283. [Google Scholar] [CrossRef]
- Elghanam, E.; Abdelfatah, A.; Hassan, M.S.; Osman, A.H. Optimization Techniques in Electric Vehicle Charging Scheduling, Routing and Spatio-Temporal Demand Coordination: A Systematic Review. IEEE Open J. Veh. Tech. 2024, 5, 1294–1313. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, J.; Liu, Y. Daily Travel Characteristics and the Development Strategy of Private Motor Vehicles in Beijing. In Proceedings of the International Conference of Transportation Professionals, Dalian, China, 23–26 June 2006. [Google Scholar]
- Xing, Y.; Li, F.; Sun, K.; Wang, D.; Chen, T.; Zhang, Z. Multi-type electric vehicle load prediction based on Monte Carlo simulation. Energy Rep. 2022, 8, 966–972. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proc. ICNN Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar] [CrossRef]
- Ang, K.H.; Lim, W.H.; Mat Isa, N.A.; Tiang, S.S.; Wong, C.H. A constrained multi- swarm particle swarm optimization without velocity for constrained optimization problems. Expert. Syst. Appl. 2020, 140, 2461–2468. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An Overview of Variants and Advancements of PSO Algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]





| Vehicle Type | Charging Strat Time | Daily Driving Distance | Charging Power | Number of Vehicles |
|---|---|---|---|---|
| Electric Bus | U (0, 24) | U (150, 200) | 80 kW | 90 units |
| Electric Taxi | U (2, 4) | N (275, 152) | 35 kW | 225 units |
| U (11, 14) | ||||
| Electric Private Car (Weekdays) | U (7, 18) | X~E (0.020) | 30 kW | 1950 units |
| N (19.2, 1.72) | 7 kW | |||
| Electric Private Car (non-working days) | U (7, 18) | X~E (0.018) | 30 kW | |
| N (19.2, 2.52) | 7 kW |
| WT Construction Cost/(CNY/kW) | 1801 |
|---|---|
| PV Construction Cost/(CNY/kW) | 3167 |
| PV Operation and Maintenance Cost/(CNY/kW) | 37 |
| WT Operation and Maintenance Cost/(CNY/kW) | 50 |
| Wind–solar-Storage Discount Rate | 8% |
| WT Construction Generation Capacity/MW | 55 |
| PV Construction Generation Capacity/MW | 20 |
| System Life Cycle/year | 15 |
| Off-Peak Electricity Price (0–6, 11–13)/(CNY/kWh) | 0.5998 |
| Peak Electricity Price (19–23)/(CNY/kWh) | 1.8322 |
| Off-Peak Electricity Price (7–10, 14–18)/(CNY/kWh) | 1.2322 |
| ES Unit Capacity Price/(CNY/kWh) | 1080 |
| ES Unit Power Price/(CNY/kW) | 850 |
| ESS Loss Efficiency | 95% |
| Scenario | CT (Million CNY) | R (%) | H (MWh) |
|---|---|---|---|
| 1 | 10.85 | 93.16 | 7853 |
| 2 | 10.01 | 94.96 | 6040 |
| 3 | 8.96 | 97.73 | 3553 |
| Scenario | CEV (Million CNY) | Lr (%) | |
| 1 | 6.62 | 85.19% | |
| 2 | 5.76 | 87.41% | |
| 3 | 4.62 | 90.01% | |
| Algorithms | CT (Million CNY) | R (%) | H (MWh) | ESS Solution | CEV RR (%) | Lr GR (%) |
|---|---|---|---|---|---|---|
| MOPSO | 12.23 | 91.20 | 5435 | 14.6 MW/29.2 MWh | 20.61 | 1.11 |
| IMOPSO | 8.96 | 97.73 | 3553 | 13.5 MW/27.0 MWh | 30.21 | 2.61 |
| NSGA-II | 10.83 | 95.21 | 3916 | 13.9 MW/27.8 MWh | 27.21 | 2.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wu, X. A Collaborative Optimization Approach for Configuring Energy Storage Systems and Scheduling Multi-Type Electric Vehicles Using an Improved Multi-Objective Particle Swarm Optimization Algorithm. Processes 2025, 13, 1343. https://doi.org/10.3390/pr13051343
Liu Y, Wu X. A Collaborative Optimization Approach for Configuring Energy Storage Systems and Scheduling Multi-Type Electric Vehicles Using an Improved Multi-Objective Particle Swarm Optimization Algorithm. Processes. 2025; 13(5):1343. https://doi.org/10.3390/pr13051343
Chicago/Turabian StyleLiu, Yirun, and Xiaolong Wu. 2025. "A Collaborative Optimization Approach for Configuring Energy Storage Systems and Scheduling Multi-Type Electric Vehicles Using an Improved Multi-Objective Particle Swarm Optimization Algorithm" Processes 13, no. 5: 1343. https://doi.org/10.3390/pr13051343
APA StyleLiu, Y., & Wu, X. (2025). A Collaborative Optimization Approach for Configuring Energy Storage Systems and Scheduling Multi-Type Electric Vehicles Using an Improved Multi-Objective Particle Swarm Optimization Algorithm. Processes, 13(5), 1343. https://doi.org/10.3390/pr13051343






