A Hybrid Method of Moving Mesh and RCM for Microwave Heating Calculation of Large-Scale Moving Complex-Shaped Objects
Abstract
1. Introduction
2. Methodology and Methods
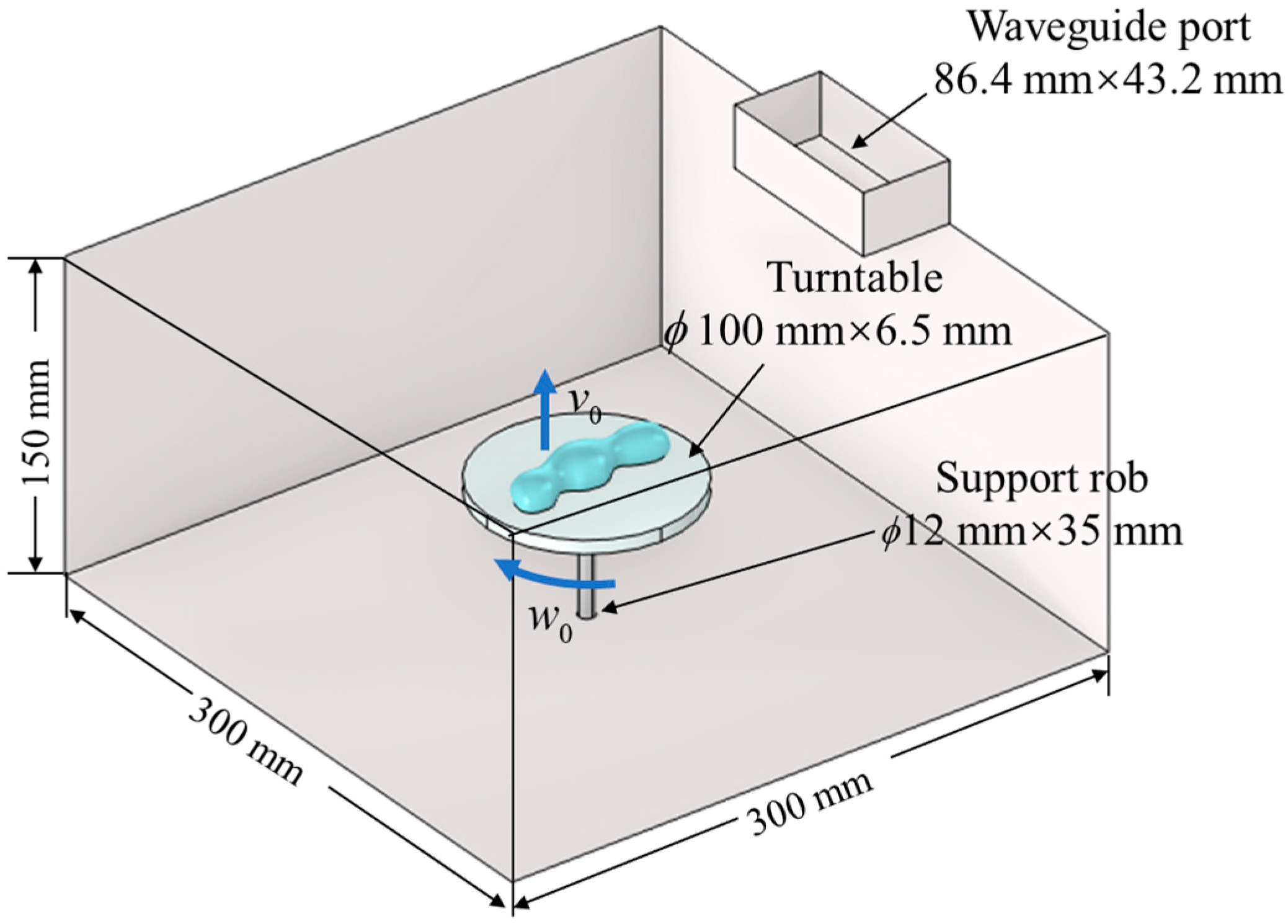
2.1. Simulation Model Geometry
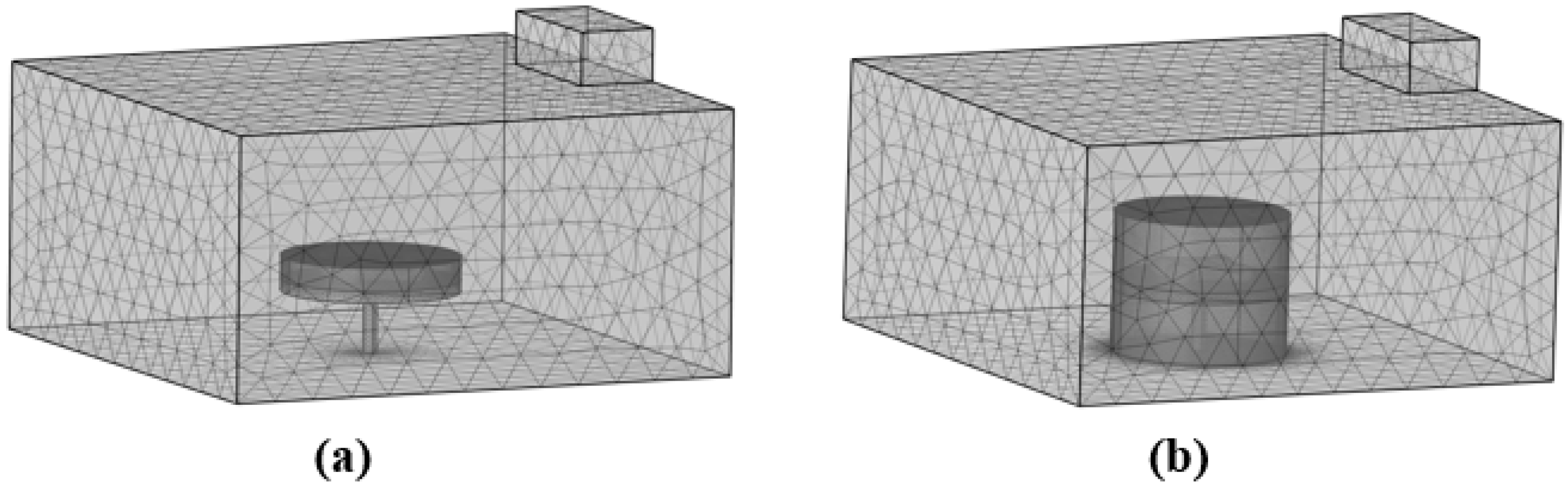
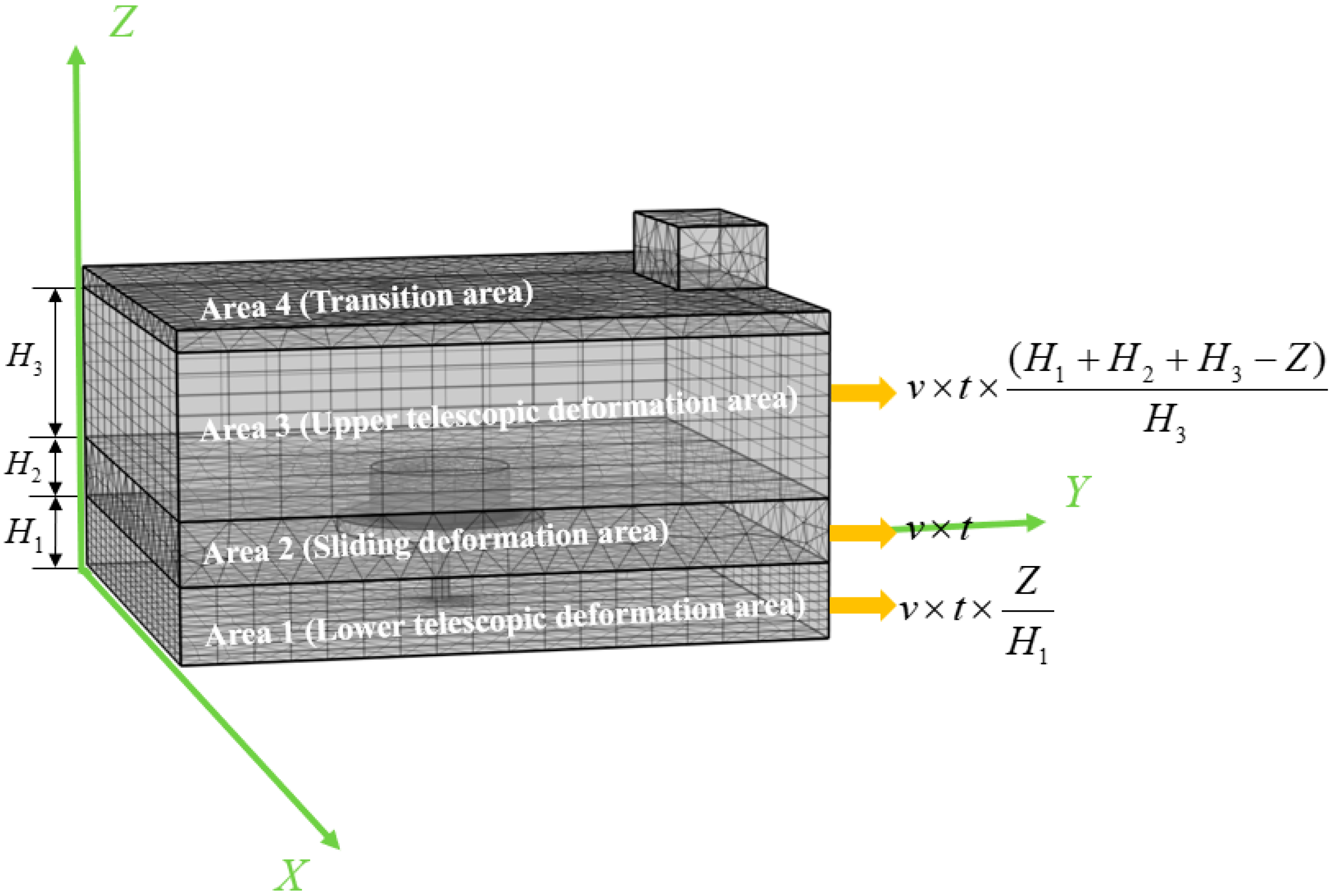
2.2. Design of Moving Mesh in Microwave Heating Calculation
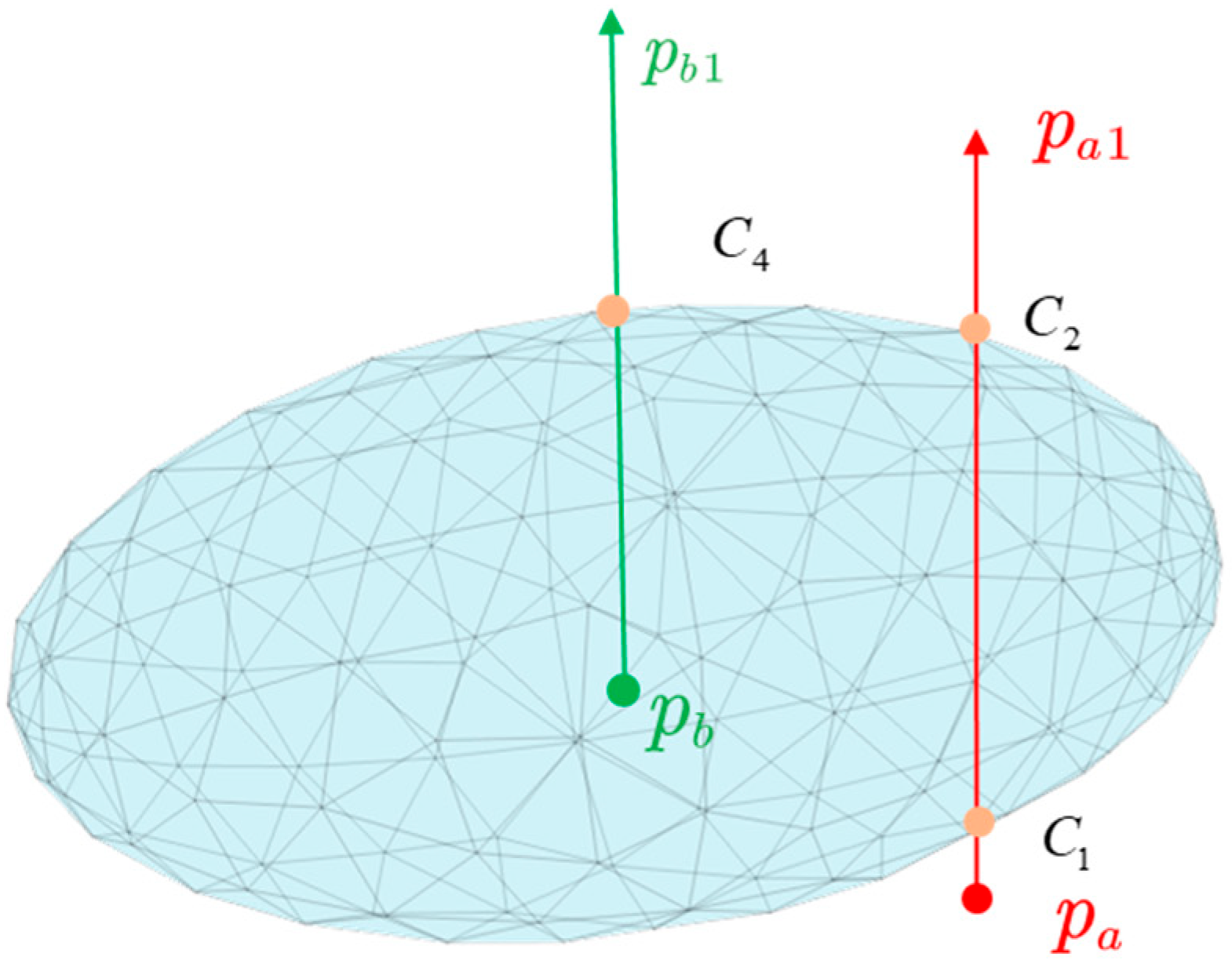
2.3. Representation of Sample in the Model
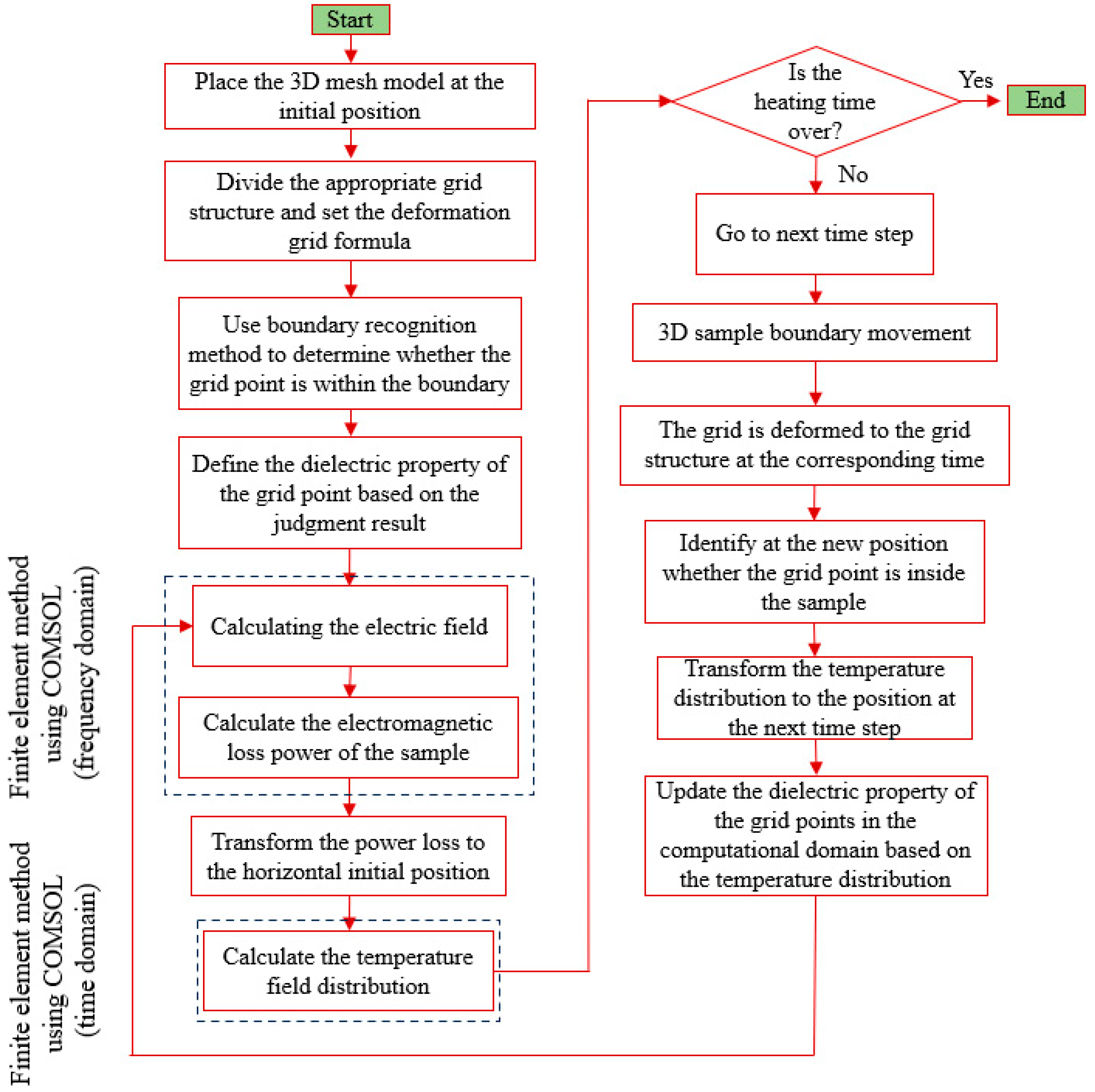
2.4. Microwave Heating Multi-Physics Simulation Process
2.5. Experimental Settings
3. Results and Discussion
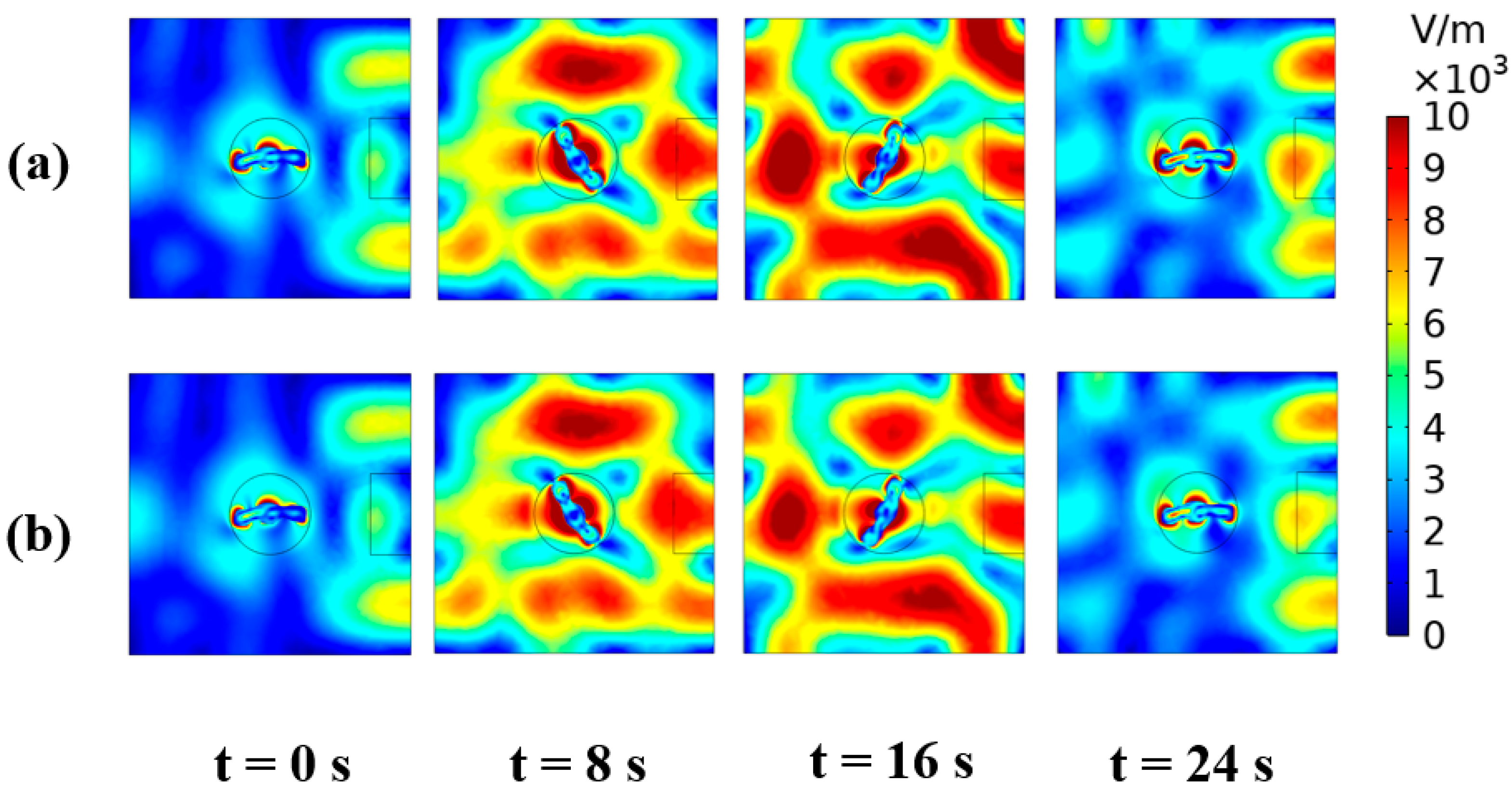
3.1. Validation of Electromagnetic Field Model
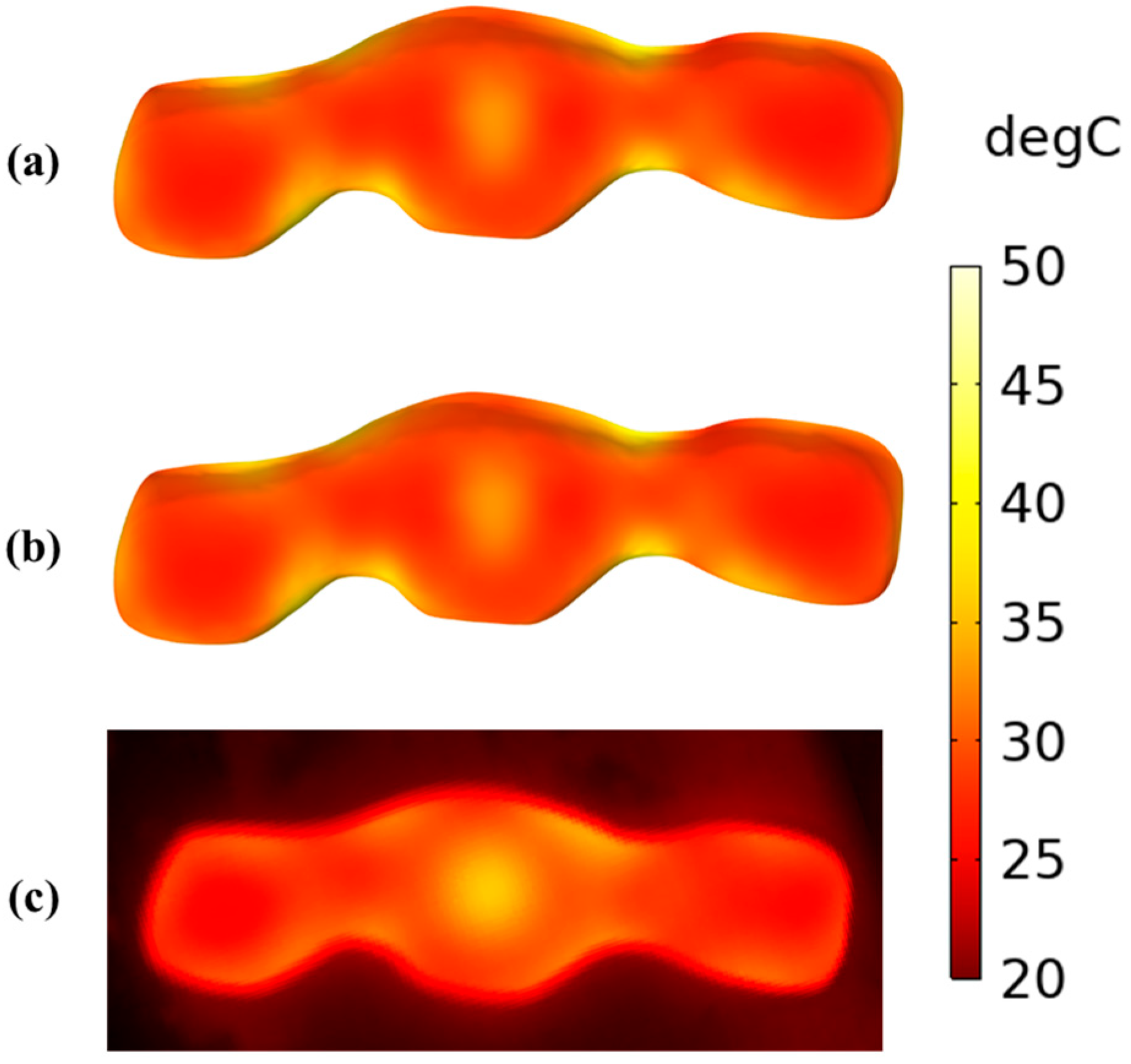
3.2. Temperature Distribution
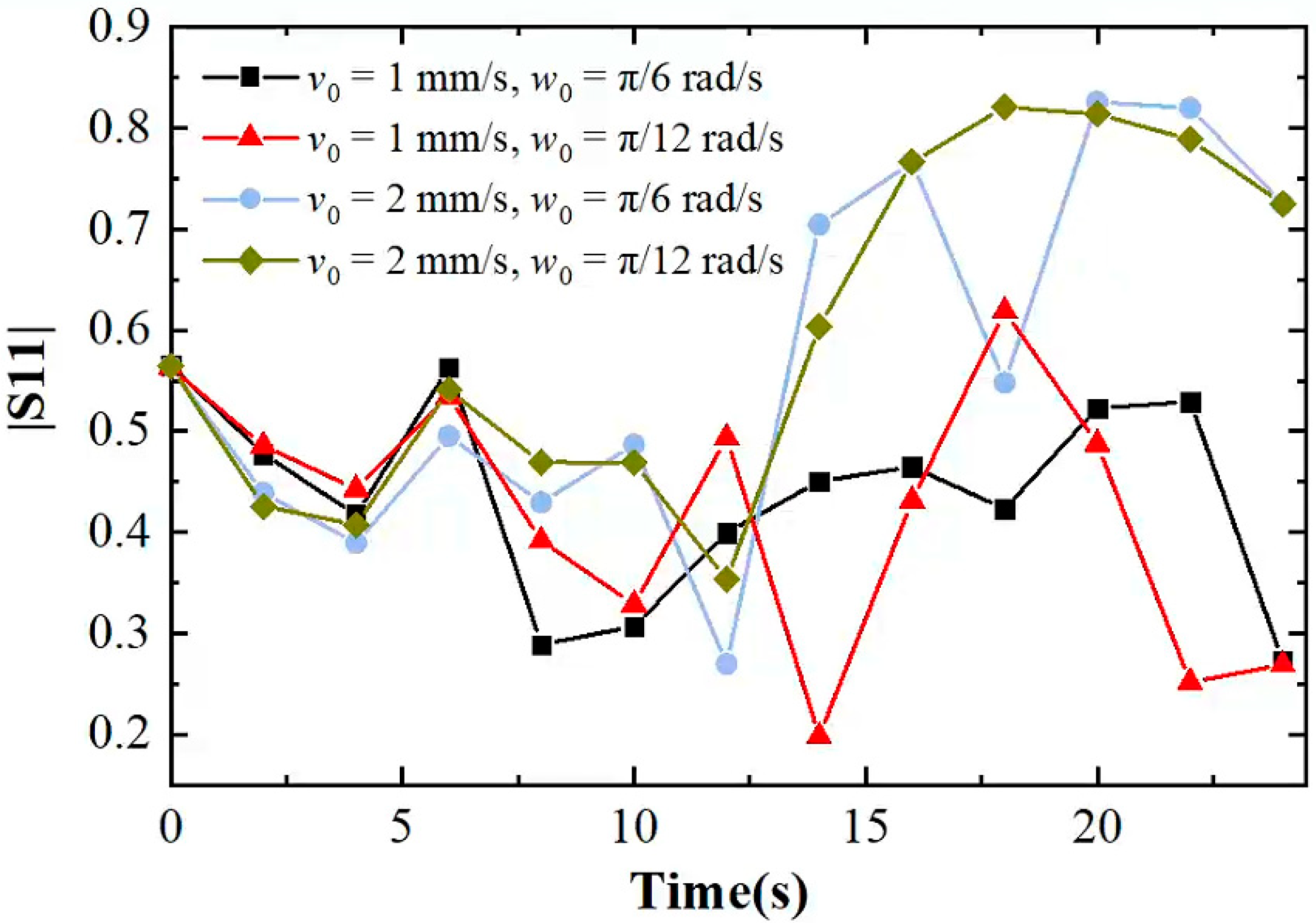
3.3. Effects of Rotating Speed and Lifting Speed on Heating Efficiency and Uniformity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, Y.; Zhou, D.; Chen, H.; Liu, M.; Tang, Z.; Hong, T. Resonance-Driven Microwave Heating of Low-Loss Cylindrical Substances in Waveguide Systems. IEEE Trans. Microw. Theory Tech. 2024, 72, 3722–3733. [Google Scholar] [CrossRef]
- Yin, C. Microwave-Assisted Pyrolysis of Biomass for Liquid Biofuels Production. Bioresour. Technol. 2012, 120, 273–284. [Google Scholar] [CrossRef] [PubMed]
- Kappe, C.O.; Stadler, A.; Dallinger, D. Microwaves in Organic and Medicinal Chemistry; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Chandrasekaran, S.; Ramanathan, S.; Basak, T. Microwave Food Processing—A Review. Food Res. Int. 2013, 52, 243–261. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, D.; Peng, Y.; Tang, Z.; Huang, K.; Hong, T. High-Efficiency Continuous-Flow Microwave Heating System Based on Metal-Ring Resonant Structure. Innov. Food Sci. Emerg. Technol. 2023, 85, 103330. [Google Scholar] [CrossRef]
- Tang, J.; Hao, F.; Lau, M. Microwave Heating in Food Processing. In Advances in Bioprocessing Engineering; Springer: Dordrecht, The Netherlands, 2002; pp. 1–44. [Google Scholar]
- Ye, J.; Lan, J.; Xia, Y.; Yang, Y.; Zhu, H.; Huang, K. An Approach for Simulating the Microwave Heating Process with a Slow-Rotating Sample and a Fast-Rotating Mode Stirrer. Int. J. Heat Mass Transf. 2019, 140, 440–452. [Google Scholar] [CrossRef]
- Kurniawan, H.; Alapati, S.; Che, W.S. Effect of Mode Stirrers in a Multimode Microwave-Heating Applicator with the Conveyor Belt. Int. J. Precis. Eng. Manuf.-Green Technol. 2015, 2, 31–36. [Google Scholar] [CrossRef]
- Chen, J.; Pitchai, K.; Birla, S.; Jones, D.D.; Subbiah, J. Modeling Heat and Mass Transport during Microwave Heating of Frozen Food Rotating on a Turntable. Food Bioprod. Process. 2016, 99, 116–127. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Y.; Zhang, Y.; Tang, J. Modeling the RF Heating Uniformity Contributed by a Rotating Turntable. J. Food Eng. 2023, 339, 111289. [Google Scholar] [CrossRef]
- Rodriguez, J.; Morona, L.; Erans, M.; Buttress, A.J.; Nicholls, M.; Batchelor, A.R.; Duran-Jimenez, G.; Kingman, S.; Groszek, D.; Dodds, S. Solving the microwave heating uniformity conundrum for scalable high-temperature processes via a toroidal fluidised-bed reactor. Chem. Eng. Process.-Process Intensif. 2024, 202, 109838. [Google Scholar] [CrossRef]
- Bae, S.-H.; Jeong, M.-G.; Kim, J.-H.; Lee, W.-S. A Continuous Power-Controlled Microwave Belt Drier Improving Heating Uniformity. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 527–529. [Google Scholar] [CrossRef]
- Yi, Q.; Lan, J.; Ye, J.; Zhu, H.; Yang, Y.; Wu, Y.; Huang, K. A Simulation Method of Coupled Model for a Microwave Heating Process with Multiple Moving Elements. Chem. Eng. Sci. 2021, 231, 116339. [Google Scholar] [CrossRef]
- Geedipalli, S.S.R.; Rakesh, V.; Datta, A.K. Modeling the Heating Uniformity Contributed by a Rotating Turntable in Microwave Ovens. J. Food Eng. 2007, 82, 359–368. [Google Scholar] [CrossRef]
- Pitchai, K.; Chen, J.; Birla, S.; Gonzalez, R.; Subbiah, J. A Microwave Heat Transfer Model for a Rotating Multi-Component Meal in a Domestic Oven: Development and Validation. J. Food Eng. 2014, 128, 60–71. [Google Scholar] [CrossRef]
- Zhu, H.-C.; Liao, Y.-H.; Xiao, W.; Ye, J.-H.; Huang, K.-M. Transformation Optics for Computing Heating Process in Microwave Applicators with Moving Elements. IEEE Trans. Microw. Theory Tech. 2017, 65, 1434–1442. [Google Scholar] [CrossRef]
- Lian, C.; Li, J.-J.; Zhang, Y.; Ye, J.-H.; Zhu, H.-C.; Huang, K.-M. A General Inheritance Algorithm for Calculating of Arbitrary Moving Samples during Microwave Heating. IEEE Trans. Microw. Theory Tech. 2022, 70, 1964–1974. [Google Scholar] [CrossRef]
- Ye, J.-H.; Zhu, H.-C.; Liao, Y.-H.; Xiao, W.; Huang, K.-M. Implicit Function and Level Set Methods for Computation of Moving Elements during Microwave Heating. IEEE Trans. Microw. Theory Tech. 2017, 65, 4773–4784. [Google Scholar] [CrossRef]
- Zhang, M.; Jia, X.; Tang, Z.; Li, Y.; Wang, Y. A Fast and Accurate Method for Computing the Microwave Heating of Moving Objects. Appl. Sci. 2020, 10, 2985. [Google Scholar] [CrossRef]
- Li, R.; Hong, T.; Liu, R.; Chen, H.; Yang, Y.; Zhu, H. Microwave Heating Multiphysics Computation of Moving Complex-Shaped Samples Based on Ray Casting Method. IEEE Trans. Microw. Theory Tech. 2024, 72, 1234–1245. [Google Scholar] [CrossRef]
- Ye, J.; Xu, C.; Zhang, C.; Zhu, H.; Huang, K.; Li, Q.; Wang, J.; Zhou, L.; Wu, Y. A Hybrid ALE/Implicit Function Method for Simulating Microwave Heating with Rotating Objects of Arbitrary Shape. J. Food Eng. 2021, 302, 110551. [Google Scholar] [CrossRef]
- Farag, K.W.; Lyng, J.G.; Morgan, D.J.; Cronin, D.A. A Comparison of Conventional and Radio Frequency Thawing of Beef Meats: Effects on Product Temperature Distribution. Food Bioprocess Technol. 2011, 4, 1128–1136. [Google Scholar] [CrossRef]
- Ye, J.; Zhu, H.; Lan, J.; Xia, Y.; Yang, Y.; Huang, K. Dynamic Analysis of a Continuous-Flow Microwave-Assisted Screw Propeller System for Biodiesel Production. Chem. Eng. Sci. 2019, 202, 146–156. [Google Scholar] [CrossRef]
- Tezduyar, T.E. Finite element methods for flow problems with moving boundaries and interfaces. Arch. Comput. Methods Eng. 2001, 8, 83–130. [Google Scholar] [CrossRef]
- Teixeira, P.R.F.; Awruch, A.M. Numerical Simulation of Fluid–Structure Interaction Using the Finite Element Method. Comput. Fluids 2005, 34, 249–273. [Google Scholar] [CrossRef]
- Küttler, U.; Wall, W.A. Fluid-Structure Interactions Using Different Mesh Motion Techniques. Comput. Struct. 2008, 86, 1523–1532. [Google Scholar]
- Gu, B.; Yang, C. A Review of the Computational Investigation of Three-Dimensional Transient Magneto-Thermal Coupling Characteristics of Electromagnetic Railgun Armature and Rail in High-Speed Sliding Electrical Contact. J. Phys. Conf. Ser. 2023, 2478, 082007. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, X.; Chu, Y.; Li, X.; Yuan, J. A Novel Algorithm Approach for Rapid Simulated Microwave Heating of Food Moving on a Conveyor Belt. J. Food Eng. 2020, 282, 110029. [Google Scholar] [CrossRef]
- Roth, S.D. Ray Casting for Modeling Solids. Comput. Graph. Image Process. 1982, 18, 109–144. [Google Scholar] [CrossRef]
- Purcell, T.J.; Buck, I.; Mark, W.R.; Hanrahan, P. Ray Tracing on Programmable Graphics Hardware. In ACM SIGGRAPH 2005 Courses; ACM: Los Angeles, CA, USA, 2005. [Google Scholar]
- Rossi, S.; Benaglia, M.; Brenna, D.; Porta, R.; Orlandi, M. Three Dimensional (3D) Printing: A Straightforward, User-Friendly Protocol to Convert Virtual Chemical Models to Real-Life Objects. J. Chem. Educ. 2015, 92, 1398–1401. [Google Scholar] [CrossRef]






| Property | Physical Domains | Value | Source |
|---|---|---|---|
| Relative permittivity | Agar | [20] | |
| Air | 1 | ||
| Turntable | 4.2 | [30] | |
| Support rod | 2.3 | [31] | |
| ) | Agar | 1000 | [28] |
| Thermal conductivity ) | Agar | 0.609 | |
| Specific heat Capacity ) | Agar | 4190 |
| RCM | Proposed Method | |
|---|---|---|
| Total number of meshes | 2,114,187 | 490,907 |
| Calculation time | 221 min | 21.6 min |
| v0 = 1 mm/s, w0 = π/6 rad/s | v0 = 1 mm/s, w0 = π/12 rad/s | v0 = 2 mm/s, w0 = π/6 rad/s | v0 = 2 mm/s, w0 = π/12 rad/s | |
|---|---|---|---|---|
| COV | 0.423 | 0.424 | 0.4 | 0.36 |
| (°C) | 17.11 | 16.74 | 13.15 | 11.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Wu, Y.; Yang, F.; Xiao, W.; Dong, L. A Hybrid Method of Moving Mesh and RCM for Microwave Heating Calculation of Large-Scale Moving Complex-Shaped Objects. Processes 2025, 13, 2109. https://doi.org/10.3390/pr13072109
Huang Y, Wu Y, Yang F, Xiao W, Dong L. A Hybrid Method of Moving Mesh and RCM for Microwave Heating Calculation of Large-Scale Moving Complex-Shaped Objects. Processes. 2025; 13(7):2109. https://doi.org/10.3390/pr13072109
Chicago/Turabian StyleHuang, Yulin, Yuanyuan Wu, Fengming Yang, Wei Xiao, and Lu Dong. 2025. "A Hybrid Method of Moving Mesh and RCM for Microwave Heating Calculation of Large-Scale Moving Complex-Shaped Objects" Processes 13, no. 7: 2109. https://doi.org/10.3390/pr13072109
APA StyleHuang, Y., Wu, Y., Yang, F., Xiao, W., & Dong, L. (2025). A Hybrid Method of Moving Mesh and RCM for Microwave Heating Calculation of Large-Scale Moving Complex-Shaped Objects. Processes, 13(7), 2109. https://doi.org/10.3390/pr13072109






