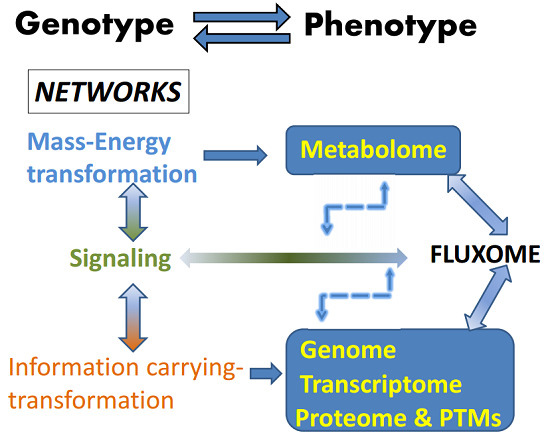
Systems Biology of the Fluxome
Abstract
:1. Introduction
2. Limitations of the “Big Data” Approach and the Ubiquitous Cyclic Topologies of the Living

3. Metabolism and the Fluxome as a Phenotypic Signature
4. From Metabolomics to Fluxomics: A Brief Survey of Existing Methodologies

5. Prediction, Control and Modulation of Complex Dynamic Behavior
6. The Next Frontier: Multiscale Systems Biology
7. Concluding Remarks
Author Contributions
Conflicts of Interest
References
- Aon, M.A. Complex systems biology of networks: The riddle and the challenge. In Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, 1st ed.; Aon, M.A., Saks, V., Schlattner, U., Eds.; Springer-Verlag: Berlin, Germany, 2013; pp. 19–35. [Google Scholar]
- Aon, M.A.; Lloyd, D.; Saks, V. From physiology, genomes, systems, and self-organization to systems biology: The historical roots of a twenty-first century approach to complexity. In Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, 1st ed.; Aon, M.A., Saks, V., Schlattner, U., Eds.; Springer-Verlag: Berlin, Germany, 2013; pp. 3–17. [Google Scholar]
- Cortassa, S.; Aon, M.A.; Iglesias, A.A.; Aon, J.C.; Lloyd, D. An Introduction to Metabolic and Cellular Engineering, 2nd ed.; World Scientific Publishers: Singapore, 2012; p. 448. [Google Scholar]
- Aon, M.A.; Cortassa, S. Chaotic dynamics, noise and fractal space in biochemistry. In Encyclopedia of Complexity and Systems Science; Meyers, R., Ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Lloyd, D.; Rossi, E.L. Epilogue: A new vision of life. In Ultradian Rhythms from Molecules to Mind; Lloyd, D., Rossi, E.L., Eds.; Springer Science+Business Media B.V.: New York, NY, USA, 2008; pp. 431–439. [Google Scholar]
- Vidal, M. A unifying view of 21st century systems biology. FEBS Lett. 2009, 583, 3891–3894. [Google Scholar] [CrossRef] [PubMed]
- Barabasi, A.L.; Oltvai, Z.N. Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Agren, R.; Bordel, S.; Nielsen, J. Use of genome-scale metabolic models for understanding microbial physiology. FEBS Lett. 2010, 584, 2556–2564. [Google Scholar] [CrossRef] [PubMed]
- Cortassa, S.; Aon, M.A. Computational modeling of mitochondrial function. Methods Mol. Biol. 2012, 810, 311–326. [Google Scholar] [PubMed]
- Cortassa, S.; Aon, M.A. Dynamics of mitochondrial redox and energy networks: Insights from an experimental-computational synergy. In Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, 1st ed.; Aon, M.A., Saks, V., Schlattner, U., Eds.; Springer-Verlag: Berlin, Germany, 2013; pp. 115–144. [Google Scholar]
- Cortassa, S.; O’Rourke, B.; Winslow, R.L.; Aon, M.A. Control and regulation of mitochondrial energetics in an integrated model of cardiomyocyte function. Biophys. J. 2009, 96, 2466–2478. [Google Scholar] [CrossRef] [PubMed]
- Cortassa, S.; O’Rourke, B.; Winslow, R.L.; Aon, M.A. Control and regulation of integrated mitochondrial function in metabolic and transport networks. Int. J. Mol. Sci. 2009, 10, 1500–1513. [Google Scholar] [CrossRef] [PubMed]
- De Vargas Roditi, L.; Claassen, M. Computational and experimental single cell biology techniques for the definition of cell type heterogeneity, interplay and intracellular dynamics. Curr. Opin. Biotechnol. 2014, 34, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Kurz, F.T.; Aon, M.A.; O’Rourke, B.; Armoundas, A.A. Spatio-temporal oscillations of individual mitochondria in cardiac myocytes reveal modulation of synchronized mitochondrial clusters. Proc. Natl. Acad. Sci. USA 2010, 107, 14315–14320. [Google Scholar] [CrossRef] [PubMed]
- Kurz, F.T.; Aon, M.A.; O’Rourke, B.; Armoundas, A.A. Cardiac mitochondria exhibit dynamic functional clustering. Front. Physiol. 2014, 5, 329. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Aon, M.A.; Almas, T.; Cortassa, S.; Winslow, R.L.; O’Rourke, B. A reaction-diffusion model of ROS-induced ROS release in a mitochondrial network. PLoS Comput. Biol. 2010, 6, e1000657. [Google Scholar] [CrossRef] [PubMed]
- Aon, M.A.; Cortassa, S. Dynamic Biological Organization. Fundamentals as Applied to Cellular Systems; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Cortassa, S.; Aon, M.A.; Westerhoff, H.V. Linear nonequilibrium thermodynamics describes the dynamics of an autocatalytic system. Biophys. J. 1991, 60, 794–803. [Google Scholar] [CrossRef]
- Lloyd, D.; Poole, R.K.; Edwards, S.W. The Cell Division Cycle: Temporal Organization and Control of Cellular Growth and Reproduction; Academic Press: London, UK, 1982; p. 523. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations; Wiley: New York, NY, USA, 1977; p. xii, 491. [Google Scholar]
- Schneider, E.D.; Sagan, D. Into the Cool. Energy Flow, Thermodynamics and Life; The University of Chicago Press: Chicago, IL, USA, 2005. [Google Scholar]
- Yates, E.F. Self-Organizing Systems. The Emergence of Order; Plenum Press: New York, NY, USA, 1987; pp. 1–14. [Google Scholar]
- Hood, L.; Tian, Q. Systems approaches to biology and disease enable translational systems medicine. Genomics Proteomics Bioinform. 2012, 10, 181–185. [Google Scholar] [CrossRef] [PubMed]
- Gleick, J. The Information: A History, a Theory, a Flood; Vintage Books: New York, NY, USA, 2011. [Google Scholar]
- Varela, F.; Maturana, H.; Uribe, R. Autopoiesis: The organization of living sytems, its characterization and a model. Biosystems 1974, 5, 187–196. [Google Scholar] [CrossRef]
- Maturana, H.; Varela, F. De Maquinas y Seres Vivos. Autopoiesis: La Organizacion de lo Vivo; Editorial Universitaria: Santiago de Chile, Chile, 1994; (in French). [Google Scholar]
- McKnight, S.L. On getting there from here. Science 2010, 330, 1338–1339. [Google Scholar] [CrossRef] [PubMed]
- Capra, F. The Web of Life; Anchor books Doubleday: New York, NY, USA, 1996. [Google Scholar]
- Kitano, H. Computational systems biology. Nature 2002, 420, 206–210. [Google Scholar] [CrossRef] [PubMed]
- Lanpher, B.; Brunetti-Pierri, N.; Lee, B. Inborn errors of metabolism: The flux from mendelian to complex diseases. Nat. Rev. Genet. 2006, 7, 449–460. [Google Scholar] [CrossRef] [PubMed]
- Cascante, M.; Marin, S. Metabolomics and fluxomics approaches. Essays Biochem. 2008, 45, 67–81. [Google Scholar] [CrossRef] [PubMed]
- Cortassa, S.; Caceres, V.; Bell, L.N.; O’Rourke, B.; Paolocci, N.; Aon, M.A. From metabolomics to fluxomics: A computational procedure to translate metabolite profiles into metabolic fluxes. Biophys. J. 2015, 108, 163–172. [Google Scholar] [CrossRef] [PubMed]
- Niedenfuhr, S.; Wiechert, W.; Noh, K. How to measure metabolic fluxes: A taxonomic guide for 13C fluxomics. Curr. Opin. Biotechnol. 2014, 34, 82–90. [Google Scholar] [CrossRef] [PubMed]
- Raamsdonk, L.M.; Teusink, B.; Broadhurst, D.; Zhang, N.; Hayes, A.; Walsh, M.C.; Berden, J.A.; Brindle, K.M.; Kell, D.B.; Rowland, J.J.; et al. A functional genomics strategy that uses metabolome data to reveal the phenotype of silent mutations. Nat. Biotechnol. 2001, 19, 45–50. [Google Scholar] [PubMed]
- Griffin, J.L. The Cinderella story of metabolic profiling: Does metabolomics get to go to the functional genomics ball? Philos. Trans. R. Soc. Lond. B Biol. Sci. 2006, 361, 147–161. [Google Scholar] [CrossRef] [PubMed]
- Kell, D.B.; Goodacre, R. Metabolomics and systems pharmacology: Why and how to model the human metabolic network for drug discovery. Drug Discov. Today 2014, 19, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Winter, G.; Kromer, J.O. Fluxomics―connecting 'omics analysis and phenotypes. Environ. Microbiol. 2013, 15, 1901–1916. [Google Scholar] [CrossRef] [PubMed]
- Orth, J.D.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Savinell, J.M.; Palsson, B.O. Optimal selection of metabolic fluxes for in vivo measurement. II. Application to escherichia coli and hybridoma cell metabolism. J. Theor. Biol. 1992, 155, 215–242. [Google Scholar] [CrossRef]
- Feist, A.M.; Henry, C.S.; Reed, J.L.; Krummenacker, M.; Joyce, A.R.; Karp, P.D.; Broadbelt, L.J.; Hatzimanikatis, V.; Palsson, B.O. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007, 3, 121. [Google Scholar] [CrossRef] [PubMed]
- Sauer, U. Metabolic networks in motion: 13C-based flux analysis. Mol. Syst. Biol. 2006, 2, 62. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, D. Oscillations, synchrony and deterministic chaos. Prog. Bot. 2009, 70, 70–91. [Google Scholar]
- Lloyd, D.; Murray, D.B. Redox rhythmicity: Clocks at the core of temporal coherence. Bioessays 2007, 29, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Murray, D.B.; Amariel, C.; Sasidharan, K.; Machne, R.; Aon, M.A.; Lloyd, D. Temporal partitioning of the yeast cellular network. In Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer; Aon, M.A., Saks, V., Schlattner, U., Eds.; Springer-Verlag: Berlin, Germany, 2013; pp. 323–349. [Google Scholar]
- Aon, M.A.; Cortassa, S.; Lloyd, D. Chaos in biochemistry and physiology. In Encyclopedia of Molecular Cell Biology and Molecular Medicine: Systems Biology; Meyers, R., Ed.; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Asher, G.; Sassone-Corsi, P. Time for food: The intimate interplay between nutrition, metabolism, and the circadian clock. Cell 2015, 161, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Grieson, C.S.; Webb, A.A.; Hussey, P.J. Modelling dynamic plant cells. Curr. Opin. Plant Biol. 2010, 13, 744–749. [Google Scholar] [CrossRef] [PubMed]
- Aon, J.C.; Cortassa, S. Involvement of nitrogen metabolism in the triggering of ethanol fermentation in aerobic chemostat cultures of saccharomyces cerevisiae. Metab. Eng. 2001, 3, 250–264. [Google Scholar] [CrossRef] [PubMed]
- Fu, Z.; Verderame, T.D.; Leighton, J.M.; Sampey, B.P.; Appelbaum, E.R.; Patel, P.S.; Aon, J.C. Exometabolome analysis reveals hypoxia at the up-scaling of a saccharomyces cerevisiae high-cell density fed-batch biopharmaceutical process. Microb. Cell Factories. 2014, 13, 32. [Google Scholar] [CrossRef] [PubMed]
- Akar, F.G.; Aon, M.A.; Tomaselli, G.F.; O’Rourke, B. The mitochondrial origin of postischemic arrhythmias. J. Clin. Investig. 2005, 115, 3527–3535. [Google Scholar] [CrossRef] [PubMed]
- Aon, M.A.; Cortassa, S.; Akar, F.G.; Brown, D.A.; Zhou, L.; O’Rourke, B. From mitochondrial dynamics to arrhythmias. Int. J. Biochem. Cell Biol. 2009, 41, 1940–1948. [Google Scholar] [CrossRef] [PubMed]
- Kurz, F.T.; Aon, M.A.; O’Rourke, B.; Armoundas, A.A. Wavelet analysis reveals heterogeneous time-dependent oscillations of individual mitochondria. Am. J. Physiol. Heart Circ. Physiol. 2010, 299, H1736–H1740. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z. Network dynamics in cardiac electrophysiology. In Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, 1st ed.; Aon, M.A., Saks, V., Schlattner, U., Eds.; Springer-Verlag: Berlin, Germany, 2013; pp. 243–260. [Google Scholar]
- Aon, M.A.; Cortassa, S.; O’Rourke, B. Percolation and criticality in a mitochondrial network. Proc. Natl. Acad. Sci. USA 2004, 101, 4447–4452. [Google Scholar] [CrossRef] [PubMed]
- Kembro, J.M.; Cortassa, S.; Aon, M.A. Mitochondrial ros and arrhythmias. In Systems Biology of Free Radicals and Anti-oxidants; Laher, I., Ed.; Springer-Verlag: Berlin, Germany, 2014. [Google Scholar]
- Zhou, L.; Cortassa, S.; Wei, A.C.; Aon, M.A.; Winslow, R.L.; O’Rourke, B. Modeling cardiac action potential shortening driven by oxidative stress-induced mitochondrial oscillations in guinea pig cardiomyocytes. Biophys. J. 2009, 97, 1843–1852. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Solhjoo, S.; Millare, B.; Plank, G.; Abraham, M.R.; Cortassa, S.; Trayanova, N.; O’Rourke, B. Effects of regional mitochondrial depolarization on electrical propagation: Implications for arrhythmogenesis. Circ. Arrhythm. Electrophysiol. 2014, 7, 143–151. [Google Scholar] [CrossRef] [PubMed]
- Roussel, M.R.; Lloyd, D. Observation of a chaotic multioscillatory metabolic attractor by real-time monitoring of a yeast continuous culture. FEBS J. 2007, 274, 1011–1018. [Google Scholar] [CrossRef] [PubMed]
- Aon, M.A.; Roussel, M.R.; Cortassa, S.; O’Rourke, B.; Murray, D.B.; Beckmann, M.; Lloyd, D. The scale-free dynamics of eukaryotic cells. PLoS ONE 2008, 3, e3624. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sasidharan, K.; Tomita, M.; Aon, M.; Lloyd, D.; Murray, D.B. Time-structure of the yeast metabolism in vivo. Adv. Exp. Med. Biol. 2012, 736, 359–379. [Google Scholar] [PubMed]
- Hartwell, L.H.; Hopfield, J.J.; Leibler, S.; Murray, A.W. From molecular to modular cell biology. Nature 1999, 402, C47–C52. [Google Scholar] [CrossRef] [PubMed]
- Cortassa, S.; Aon, M.A.; O’Rourke, B.; Jacques, R.; Tseng, H.J.; Marban, E.; Winslow, R.L. A computational model integrating electrophysiology, contraction, and mitochondrial bioenergetics in the ventricular myocyte. Biophys. J. 2006, 91, 1564–1589. [Google Scholar] [CrossRef] [PubMed]
- Del Vecchio, D. Modularity, context-dependence, and insulation in engineered biological circuits. Trends Biotechnol. 2015, 33, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Freddolino, P.L.; Tavazoie, S. The dawn of virtual cell biology. Cell 2012, 150, 248–250. [Google Scholar] [CrossRef] [PubMed]
- Karr, J.R.; Sanghvi, J.C.; Macklin, D.N.; Gutschow, M.V.; Jacobs, J.M.; Bolival, B., Jr.; Assad-Garcia, N.; Glass, J.I.; Covert, M.W. A whole-cell computational model predicts phenotype from genotype. Cell 2012, 150, 389–401. [Google Scholar] [CrossRef] [PubMed]
- Plank, G.; Zhou, L.; Greenstein, J.L.; Cortassa, S.; Winslow, R.L.; O’Rourke, B.; Trayanova, N.A. From mitochondrial ion channels to arrhythmias in the heart: Computational techniques to bridge the spatio-temporal scales. Philos. Trans. A Math. Phys. Eng. Sci. 2008, 366, 3381–3409. [Google Scholar] [CrossRef] [PubMed]
- Ducat, D.C.; Silver, P.A. Improving carbon fixation pathways. Curr. Opin. Chem. Biol. 2012, 16, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Long, S.P.; Marshall-Colon, A.; Zhu, X.-G. Meeting the global food demand of the future by engineering crop photosynthesis and yield potential. Cell 2015, 161, 56–66. [Google Scholar] [CrossRef] [PubMed]
- Chew, Y.H.; Wenden, B.; Flis, A.; Mengin, V.; Taylor, J.; Davey, C.L.; Tindal, C.; Thomas, H.; Ougham, H.J.; de Reffye, P.; et al. Multiscale digital arabidopsis predicts individual organ and whole-organism growth. Proc. Natl. Acad. Sci. USA 2014, 111, E4127–E4136. [Google Scholar] [CrossRef] [PubMed]
- Xin, C.P.; Tholen, D.; Devloo, V.; Zhu, X.G. The benefits of photorespiratory bypasses: How can they work? Plant Physiol. 2015, 167, 574–585. [Google Scholar] [CrossRef] [PubMed]
- Obituary intimation Prof. Daniel Thomas, UTC pioneer. Available online: http://www.utc.fr/utc_espacepresse/iso_album/cp_danielthomas_gb.pdf (accessed on 10 July 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aon, M.A.; Cortassa, S. Systems Biology of the Fluxome. Processes 2015, 3, 607-618. https://doi.org/10.3390/pr3030607
Aon MA, Cortassa S. Systems Biology of the Fluxome. Processes. 2015; 3(3):607-618. https://doi.org/10.3390/pr3030607
Chicago/Turabian StyleAon, Miguel A., and Sonia Cortassa. 2015. "Systems Biology of the Fluxome" Processes 3, no. 3: 607-618. https://doi.org/10.3390/pr3030607
APA StyleAon, M. A., & Cortassa, S. (2015). Systems Biology of the Fluxome. Processes, 3(3), 607-618. https://doi.org/10.3390/pr3030607