Polymerization Kinetics of Poly(2-Hydroxyethyl Methacrylate) Hydrogels and Nanocomposite Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Polymerization Kinetics
2.3. Synthesis of Nanocomposites
2.4. Measurements
3. Results
3.1. Polymerization Kinetics of HEMA
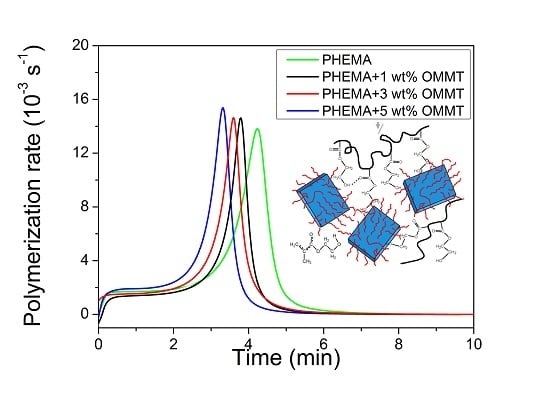
3.2. Polymerization Kinetics during the Formation of PΗΕΜΑ/OMMT Nanocomposites
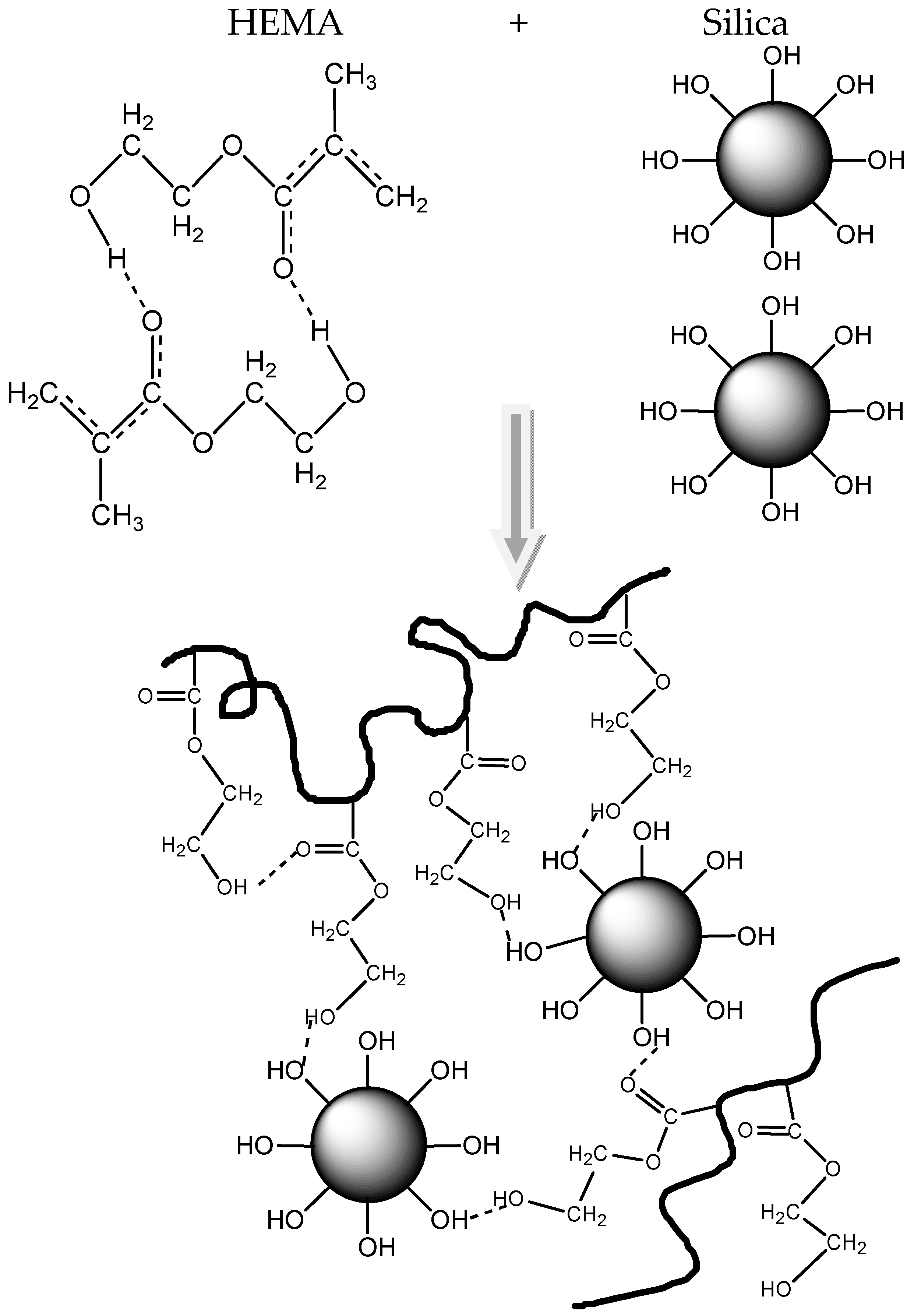
3.3. Polymerization Kinetics during the Formation of PΗΕΜΑ/Silica Nanocomposites
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Nogueira, N.; Conde, O.; Minones, M.; Trillo, J.M.; Minones, J.R. Characterization of poly(2-hydroxyethyl methacrylate) contact lens using the Langmuir monolayer technique. J. Colloid Interface Sci. 2012, 385, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Montheard, J.P.; Chatzopoulos, M.; Chappard, D. 2-Hydroxyethyl methacrylate (HEMA): Chemical properties and applications in biomedical fields. J. Macromol. Sci. C Polym. Rev. 1992, 32, 1–34. [Google Scholar] [CrossRef]
- Gupta, M.K.; Bajpai, J.; Bajpai, A.K. Optimizing the release process and modelling of in vitro release data of cis-dichlorodiamminoplatinum (II) encapsulated into poly(2-hydroxyethyl methacrylate) nanocarriers. Mater. Sci. Eng. C 2016, 58, 852–862. [Google Scholar] [CrossRef] [PubMed]
- Costantini, A.; Luciani, G.; Annunziata, G.; Silvestri, B.; Branda, F. Swelling properties and bioactivity of silica gel/pHEMA Nanocomposites. J. Mater. Sci. Mater. Med. 2006, 17, 319–325. [Google Scholar] [CrossRef] [PubMed]
- Kharismadewi, D.; Haldorai, Y.; Nguyen, V.H.; Tuma, D.; Shim, J.-J. Synthesis of graphene oxide-poly(2-hydroxyethyl methacrylate) composite by dispersion polymerization in supercritical CO2: Adsorption behavior for the removal of organic dye. Compos. Interfaces 2016, 23, 7. [Google Scholar] [CrossRef]
- Moradi, O.; Aghaie, M.; Zare, K.; Monajjemi, M.; Aghaie, H. The study of adsorption characteristics Cu2+ and Pb2+ ions onto PHEMA and P(MMA-HEMA) surfaces from aqueous single solution. J. Hazard. Mater. 2009, 170, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Bolbukh, Y.; Klonos, P.; Roumpos, K.; Chatzidogiannaki, V.; Tertykh, V.; Pissis, P. Glass transition and hydration properties of polyhydroxyethylmethacrylate filled with modified silica nanoparticles. J. Therm. Anal. Calorim. 2016, 125, 1387–1398. [Google Scholar] [CrossRef]
- Nikolaidis, A.K.; Achilias, D.S.; Karayannidis, G.P. Synthesis and characterization of PMMA/organomodified montmorillonite nanocomposites prepared by in situ bulk polymerization. Ind. Eng. Chem. Res. 2011, 50, 571–579. [Google Scholar] [CrossRef]
- Achilias, D.S.; Siafaka, P.I.; Nikolaidis, A.K. Polymerization kinetics and thermal properties of poly(alkyl methacrylate)/organomodifiend montmorillonite nanocomposites. Polym. Int. 2012, 61, 1510–1518. [Google Scholar] [CrossRef]
- Passos, M.F.; Dias, D.R.C.; Bastos, G.N.T.; Jardini, A.L.; Benatti, A.C.B.; Dias, C.G.B.T.; Maciel Filho, R. PHEMA Hydrogels. J. Therm. Anal. Calorim. 2016, 125, 361–368. [Google Scholar] [CrossRef]
- Ning, L.; Xu, N.; Xiao, C.; Wang, R.; Liu, Y. Analysis for the reaction of hydroxyethyl methacrylate/benzoyl peroxide/polyethacrylate through DSC and viscosity changing and their resultants as oil absorbent. J. Macromol. Sci. Part A Pure Appl. Chem. 2015, 52, 1017–1027. [Google Scholar] [CrossRef]
- Huang, C.-W.; Sun, Y.-M.; Huang, W.-F. Curing kinetics of the synthesis of poly(2-hydroxyethyl methacrylate) (PHEMA) with ethylene glycol dimethacrylate (EGDMA) as a crosslinking agent. J. Polym. Sci. A Polym. Chem. 1997, 35, 1873–1889. [Google Scholar] [CrossRef]
- Kaddami, H.; Gerard, J.F.; Hajji, P.; Pascault, J.P. Silica-filled poly(hema) from hema/grafted SiO2 nanoparticles: Polymerization kinetics and rheological changes. J. Appl. Polym. Sci. 1999, 73, 2701–2713. [Google Scholar] [CrossRef]
- Li, L.; Lee, L.J. Photopolymerization of HEMA/DEGDMA hydrogels in solution. Polymer 2005, 46, 11540–11547. [Google Scholar] [CrossRef]
- Mikos, A.G.; Peppas, N.A. A model for prediction of the structural characteristics of EGDMA crosslinked PHEMA microparticles produced by suspension copolymerization/crosslinking. J. Controll. Release 1987, 5, 53–62. [Google Scholar] [CrossRef]
- Goodner, M.D.; Lee, H.R.; Bowman, C.N. Method for determining the inetic parameters in diffusion-controlled free-radical homopolymerizations. Ind. Eng. Chem. Res. 1997, 36, 1247–1252. [Google Scholar] [CrossRef]
- Hacioglu, B.; Berchtold, K.A.; Lovell, L.G.; Nie, J.; Bowman, C.N. Polymerization kinetics of HEMA/DEGDMA: using changes in initiation and chain transfer rates to explore the effects of chain-length-dependent termination. Biomaterials 2002, 23, 4057–4064. [Google Scholar] [CrossRef]
- Achilias, D.S. Investigation of the radical polymerization kinetics using DSC and mechanistic or isoconversional methods. J. Therm. Anal. Calorim. 2014, 116, 1379–1386. [Google Scholar] [CrossRef]
- Siafaka, P.; Achilias, D.S. Polymerization kinetics and thermal degradation of poly(2-hydroxyethyl methacylate)/organomodified montmorillonite nanocomposites prepared by in situ bulk polymerization. Macromol. Symp. 2013, 331–332, 166–172. [Google Scholar] [CrossRef]
- Achilias, D.S. A review of modeling of diffusion controlled polymerization reactions. Macromol. Theory Simul. 2007, 16, 319–347. [Google Scholar] [CrossRef]
- Achilias, D.S.; Verros, G.D. Modeling of Diffusion-Controlled Reactions in Free Radical Solution and Bulk Polymerization: Model Validation by DSC Experiments. J. Appl. Polym. Sci. 2010, 116, 1842–1856. [Google Scholar] [CrossRef]
- Buback, M.; Kurz, C.H. Free-radical propagation coefficients for cyclohexyl methacrylate, glycidyl methacrylate and 2-hydroxyethyl methacrylate homopolymerizations. Macromol. Chem. Phys. 1998, 199, 2301–2310. [Google Scholar] [CrossRef]
- Siddiqui, M.N.; Redhwi, H.H.; Vakalopoulou, E.; Tsagkalias, I.; Ioannidou, M.D.; Achilias, D.S. Synthesis, characterization and reaction kinetics of PMMA/silver nanocomposites prepared via in situ radical polymerization. Eur. Polym. J. 2015, 72, 256–269. [Google Scholar] [CrossRef]
- Zoller, A.; Gigmes, D.; Guillaneuf, Y. Simulation of radical polymerization of methyl methacrylate at room temperature using a tertiary amine/BPO initiating system. Polym. Chem. 2015, 6, 5719–5727. [Google Scholar] [CrossRef]
- Achilias, D.S.; Kiparissides, C. Development of a general mathematical framework for modeling of diffusion-controlled free-radical polymerization reactions. Macromolecules 1992, 25, 3739–3750. [Google Scholar] [CrossRef]
- Morita, S. Hydrogen-bonds structure in poly(2-hydroxyethyl methacrylate) studied by temperature- dependent infrared spectroscopy. Front. Chem. 2014, 2, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Liang, K.; Hutchinson, R.A. Solvent Effects on Free-Radical Copolymerization Propagation Kinetics of Styrene and Methacrylates. Macromolecules 2010, 43, 6311–6320. [Google Scholar] [CrossRef]
- Furuncuoglu Ozaltin, T.; Dereli, B.; Karahan, O.; Salman, S.; Aviyente, V. Solvent effects on free-radical copolymerization of styrene and 2-hydroxyethyl methacrylate: A DFT study. New J. Chem. 2014, 38, 170–178. [Google Scholar] [CrossRef]















| T (°C) | keff (min−1) | kp0/√kt0 (L/mol/s)1/2 | kp0 [22] (L/mol/s) | kt0 (L/mol/s) | R (L/mol) | Ap | fcp | At | fct |
|---|---|---|---|---|---|---|---|---|---|
| 52 | 0.00597 | 1.1278 | 2685 | 5.667E6 | 3.20 | 0.595 | 0.0500 | 1.40 | 0.083 |
| 60 | 0.01400 | 1.4014 | 3262 | 5.78E6 | 2.01 | 0.64 | 0.0485 | 1.35 | 0.084 |
| 72 | 0.04235 | 1.7257 | 4295 | 6.195E6 | 1.34 | 0.85 | 0.0481 | 1.28 | 0.0876 |
| 82 | 0.10222 | 2.0641 | 5326 | 6.657E6 | 0.91 | 1.14 | 0.0445 | 1.39 | 0.0858 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achilias, D.S.; Siafaka, P.I. Polymerization Kinetics of Poly(2-Hydroxyethyl Methacrylate) Hydrogels and Nanocomposite Materials. Processes 2017, 5, 21. https://doi.org/10.3390/pr5020021
Achilias DS, Siafaka PI. Polymerization Kinetics of Poly(2-Hydroxyethyl Methacrylate) Hydrogels and Nanocomposite Materials. Processes. 2017; 5(2):21. https://doi.org/10.3390/pr5020021
Chicago/Turabian StyleAchilias, Dimitris S., and Panoraia I. Siafaka. 2017. "Polymerization Kinetics of Poly(2-Hydroxyethyl Methacrylate) Hydrogels and Nanocomposite Materials" Processes 5, no. 2: 21. https://doi.org/10.3390/pr5020021
APA StyleAchilias, D. S., & Siafaka, P. I. (2017). Polymerization Kinetics of Poly(2-Hydroxyethyl Methacrylate) Hydrogels and Nanocomposite Materials. Processes, 5(2), 21. https://doi.org/10.3390/pr5020021