Energy Optimization of Gas–Liquid Dispersion in Micronozzles Assisted by Design of Experiment
Abstract
:1. Introduction
2. Theoretical Background
2.1. Gas–Liquid Flow and Bubble Generation
2.2. Two-Phase Flow
2.3. Primary Bubble Generation at T-Junction
2.4. Bubbly Flow Refinement via Micronozzle
3. Materials and Methods
3.1. Design of Experiment for Efficient Turbulent Redispersion
3.1.1. Determination of Process Inputs, Process Outputs, and Disturbance Variables
3.1.2. Selection and Generation of an Experimental Design
3.2. Experimental Set-Up
3.3. Bubble Measurement
4. Results
4.1. Flow Regimes
4.1.1. Primary Bubble Generation at T-Mixer
4.1.2. Jet Flow Induced Bubble Redispersion
4.1.3. Relation between Mother and Daughter Bubble Size
4.2. Redispersion Parameters
4.2.1. Influence of Hydraulic Diameter
4.2.2. Influence of Length of Smallest Cross Section
4.2.3. Influence of Diffusor Angle
4.2.4. Influence of Downstream Channel Hydraulic Diameter
4.2.5. Influence of Volumetric Flow Rate
4.2.6. Evaluation of Energy Efficacy of Redispersion
4.3. Energy Optimization of Turbulent Bubble Breakup Assisted by Design of Experiment
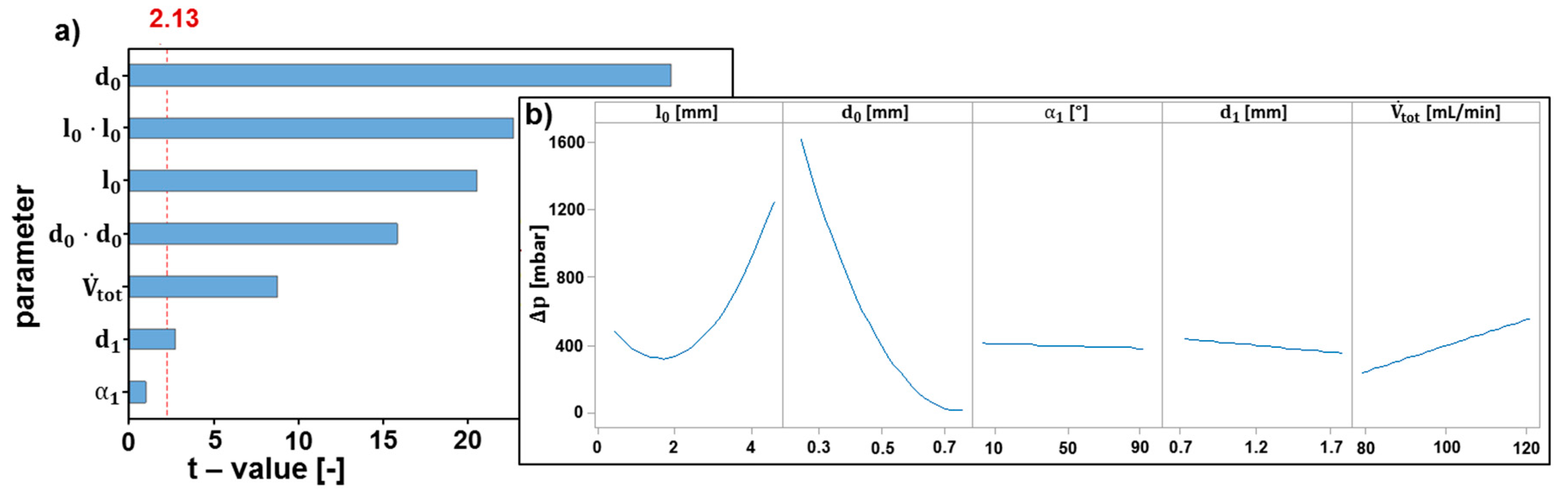
4.3.1. Regression Models for Daughter Bubble Size and Pressure Drop Derived from DoE
4.3.2. Geometry for Energy-Optimized Bubble Breakup
4.3.3. Model Validation Experiment Using Optimal Parameter Settings
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| a | aspect ratio, - |
| channel width, m | |
| Sauter diameter, m | |
| bubble diameter, m | |
| hydraulic diameter, m | |
| channel height, m | |
| number of parameters, - | |
| length, m | |
| Kolmogorov length scale, m | |
| extent of DoE, - | |
| number of experiments, - | |
| pressure difference, bar | |
| relative frequency of size distribution, m−1 | |
| cumulative size distribution, - | |
| area, m2 | |
| mean velocity, m·s−1 | |
| velocity, m·s−1 | |
| perimeter, m | |
| temperature | |
| volumetric flow rate, m3 s−1 | |
| volume, m3 | |
| number of repetitions of one experimental point, - | |
| Greek Symbols | |
| angle, ° | |
| mean energy dissipation rate, m2 s−3 | |
| local energy dissipation rate, m2 s−3 | |
| dynamic viscosity, kg·m−1·s−1 | |
| kinematic viscosity, m2·s−1 | |
| density, kg·m−3 | |
| surface tension, kg·s−2 | |
| void fraction, % | |
| Subscripts | |
| parameter regarding upstream channel of the nozzle, - | |
| parameter regarding nozzle’s smallest cross section, - | |
| parameter regarding downstream channel of the nozzle, - | |
| bubble | |
| critical number for laminar breakup | |
| critical number for turbulent breakup | |
| dissipation | |
| gaseous phase | |
| component , … | |
| component , … | |
| liquid phase | |
| pressure loss | |
| relative | |
| total | |
| Abbreviations | |
| DoE | Design of Experiment |
| LED | light-emitting diode |
| Dimensionless Numbers | |
| Capillary number, - | |
| Reynolds number, - | |
| Weber number, - | |
References
- Gutmann, B.; Cantillo, D.; Kappe, C.O. Continuous-flow technology—A tool for the safe manufacturing of active pharmaceutical ingredients. Angew. Chem. Int. Ed. 2015, 54, 6688–6728. [Google Scholar] [CrossRef] [PubMed]
- Roberge, D.M.; Ducry, L.; Bieler, N.; Cretton, P.; Zimmermann, B. Microreactor Technology: A Revolution for the Fine Chemical and Pharmaceutical Industries? Chem. Eng. Technol. 2005, 28, 318–323. [Google Scholar] [CrossRef]
- Brzozowski, M.; O’Brien, M.; Ley, S.V.; Polyzos, A. Flow chemistry: Intelligent processing of gas-liquid transformations using a tube-in-tube reactor. Acc. Chem. Res. 2015, 48, 349–362. [Google Scholar] [CrossRef] [PubMed]
- Cantillo, D.; Kappe, C.O. Halogenation of organic compounds using continuous flow and microreactor technology. React. Chem. Eng. 2017, 2, 7–19. [Google Scholar] [CrossRef]
- Jähnisch, K.; Baerns, M.; Hessel, V.; Ehrfeld, W.; Haverkamp, V.; Löwe, H.; Wille, C.; Guber, A. Direct fluorination of toluene using elemental fluorine in gas/liquid microreactors. J. Fluor. Chem. 2000, 105, 117–128. [Google Scholar] [CrossRef]
- Irfan, M.; Glasnov, T.N.; Kappe, C.O. Heterogeneous catalytic hydrogenation reactions in continuous-flow reactors. ChemSusChem 2011, 4, 300–316. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.X. Multiphase flow microfluidics for the production of single or multiple emulsions for drug delivery. Adv. Drug Deliv. Rev. 2013, 65, 1420–1446. [Google Scholar] [CrossRef] [PubMed]
- Plutschack, M.B.; Pieber, B.; Gilmore, K.; Seeberger, P.H. The Hitchhiker’s Guide to Flow Chemistry. Chem. Rev. 2017, 117, 11796–11893. [Google Scholar] [CrossRef] [PubMed]
- Mallia, C.J.; Baxendale, I.R. The Use of Gases in Flow Synthesis. Org. Process Res. Dev. 2016, 20, 327–360. [Google Scholar] [CrossRef] [Green Version]
- Elvira, K.S.; i Solvas, X.C.; Wootton, R.C.R.; deMello, A.J. The past, present and potential for microfluidic reactor technology in chemical synthesis. Nat. Chem. 2013, 5, 905–915. [Google Scholar] [CrossRef] [PubMed]
- Hartman, R.L.; Jensen, K.F. Microchemical systems for continuous-flow synthesis. Lab Chip 2009, 9, 2495–2507. [Google Scholar] [CrossRef] [PubMed]
- Kockmann, N.; Gottsponer, M. Heat Transfer Limitations of Gas-Liquid Exothermic Reactions in Microchannels. In Proceedings of the 8th International Conference on Nanochannels, Microchannels and Minichannels-2010, Montreal, QC, Canada, 1–5 August 2010; ASME: New York, NY, USA, 2011; pp. 193–199. [Google Scholar] [CrossRef]
- Kockmann, N.; Roberge, D.M. Harsh Reaction Conditions in Continuous-Flow Microreactors for Pharmaceutical Production. Chem. Eng. Technol. 2009, 32, 1682–1694. [Google Scholar] [CrossRef]
- Chen, G.; Yue, J.; Yuan, Q. Gas-Liquid Microreaction Technology: Recent Developments and Future Challenges. Chin. J. Chem. Eng. 2008, 16, 663–669. [Google Scholar] [CrossRef]
- Kashid, M.N.; Renken, A.; Kiwi-Minsker, L. Gas–liquid and liquid–liquid mass transfer in microstructured reactors. Chem. Eng. Sci. 2011, 66, 3876–3897. [Google Scholar] [CrossRef]
- Kashid, M.N.; Kiwi-Minsker, L. Microstructured Reactors for Multiphase Reactions: State of the Art. Ind. Eng. Chem. Res. 2009, 48, 6465–6485. [Google Scholar] [CrossRef]
- Noël, T.; Hessel, V. Membrane microreactors: Gas-liquid reactions made easy. ChemSusChem 2013, 6, 405–407. [Google Scholar] [CrossRef] [PubMed]
- Ward, K.; Fan, Z.H. Mixing in microfluidic devices and enhancement methods. J. Micromech. Microeng. 2015, 25. [Google Scholar] [CrossRef] [PubMed]
- Hessel, V.; Angeli, P.; Gavriilidis, A.; Löwe, H. Gas−Liquid and Gas−Liquid−Solid Microstructured Reactors: Contacting Principles and Applications. Ind. Eng. Chem. Res. 2005, 44, 9750–9769. [Google Scholar] [CrossRef]
- Abiev, R.; Svetlov, S.; Haase, S. Hydrodynamics and Mass Transfer of Gas-Liquid and Liquid-Liquid Taylor Flow in Microchannels. Chem. Eng. Technol. 2017, 60, 5895. [Google Scholar] [CrossRef]
- Fu, T.; Ma, Y. Bubble formation and breakup dynamics in microfluidic devices: A review. Chem. Eng. Sci. 2015, 135, 343–372. [Google Scholar] [CrossRef]
- Xu, J.; Cheng, P.; Zhao, T. Gas–liquid two-phase flow regimes in rectangular channels with mini/micro gaps. Int. J. Multiph. Flow 1999, 25, 411–432. [Google Scholar] [CrossRef]
- Triplett, K.A.; Ghiaasiaan, S.M.; Abdel-Khalik, S.I.; Sadowski, D.L. Gas–liquid two-phase flow in microchannels Part I: Two-phase flow patterns. Int. J. Multiph. Flow 1999, 25, 377–394. [Google Scholar] [CrossRef]
- Hessel, V.; Renken, A.; Schouten, J.C.; Yoshida, J. Micro Process Engineering: A Comprehensive Handbook; Wiley-VCH: Berlin, Germany, 2009. [Google Scholar]
- Hessel, V.; Löwe, H.; Schönfeld, F. Micromixers—A review on passive and active mixing principles. Chem. Eng. Sci. 2005, 60, 2479–2501. [Google Scholar] [CrossRef]
- Anna, S.L.; Bontoux, N.; Stone, H.A. Formation of dispersions using “flow focusing” in microchannels. Appl. Phys. Lett. 2003, 82, 364–366. [Google Scholar] [CrossRef]
- Garstecki, P.; Gitlin, I.; DiLuzio, W.; Whitesides, G.M.; Kumacheva, E.; Stone, H.A. Formation of monodisperse bubbles in a microfluidic flow-focusing device. Appl. Phys. Lett. 2004, 85, 2649–2651. [Google Scholar] [CrossRef]
- Nguyen, N.T. Micromixers: Fundamentals, Design and Fabrication, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Nagy, K.D.; Shen, B.; Jamison, T.F.; Jensen, K.F. Mixing and Dispersion in Small-Scale Flow Systems. Org. Process Res. Dev. 2012, 16, 976–981. [Google Scholar] [CrossRef]
- Reichmann, F.; Tollkötter, A.; Körner, S.; Kockmann, N. Gas-liquid dispersion in micronozzles and microreactor design for high interfacial area. Chem. Eng. Sci. 2017, 169, 151–163. [Google Scholar] [CrossRef]
- Rothstock, S.; Hessel, V.; Löb, P.; Werner, B. Characterization of a Redispersion Microreactor by Studying its Dispersion Performance. Chem. Eng. Technol. 2008, 31, 1124–1129. [Google Scholar] [CrossRef]
- Reichmann, F.; Tollkötter, A.; Kockmann, N. Investigation of Bubble Break-Up in Microchannel Orifices. In Proceedings of the ASME 14th International Conference on Nanochannels, Microchannels, and Minichannels-2016, Washington, DC, USA, 10–13 July 2016; The American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Zheng, C.; Tan, J.; Wang, K.; Luo, G.S. Stability and pressure drop of gas–liquid micro-dispersion flows through a capillary. Chem. Eng. Sci. 2016, 140, 134–143. [Google Scholar] [CrossRef]
- Gordiychuk, A.; Svanera, M.; Benini, S.; Poesio, P. Size distribution and Sauter mean diameter of micro bubbles for a Venturi type bubble generator. Exp. Therm. Fluid Sci. 2016, 70, 51–60. [Google Scholar] [CrossRef]
- Uesawa, S.I.; Kaneko, A.; Nomura, Y.; Abe, Y. Fluctuation of Void Fraction in the Microbubble Generator with a Venturi Tube. In Proceedings of the ASME/JSME/KSME Joint Fluids Engineering Conference-2011, Hamamatsu, Japan, 24–29 July 2011; The American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 2483–2492. [Google Scholar] [CrossRef]
- Reichmann, F.; Koch, M.J.; Kockmann, N. Investigation of Bubble Breakup in Laminar, Transient, and Turbulent Regime behind Micronozzles. In Proceedings of the ASME 15th International Conference on Nanochannels, Microchannels, and Minichannels-2017, Cambridge, MA, USA, 27–30 August 2017; The American Society of Mechanical Engineers: New York, NY, USA, 2017. in press. [Google Scholar]
- Nomura, Y.; Uesawa, S.I.; Kaneko, A.; Abe, Y. Study on Bubble Breakup Mechanism in a Venturi Tube. In Proceedings of the ASME/JSME/KSME Joint Fluids Engineering Conference-2011, Hamamatsu, Japan, 24–29 July 2011; The American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 2533–2540. [Google Scholar] [CrossRef]
- Reichmann, F.; Koch, M.J.; Körner, S.; Kockmann, N. Internal Jet Formation during Bubble Generation in Microchannels. In Proceedings of the ASME 15th International Conference on Nanochannels, Microchannels, and Minichannels-2017, Cambridge, MA, USA, 27–30 August 2017; The American Society of Mechanical Engineers: New York, NY, USA, 2017. in press. [Google Scholar]
- Tollkötter, A. Mikrostrukturierte Baukastensysteme für Mehrphasenströmungen. Ph.D. Thesis, TU Dortmund University, Dortmund, Germany, 2016. [Google Scholar]
- Garstecki, P.; Stone, H.A.; Whitesides, G.M. Mechanism for flow-rate controlled breakup in confined geometries: A route to monodisperse emulsions. Phys. Rev. Lett. 2005, 94, 164501. [Google Scholar] [CrossRef] [PubMed]
- Munson, B.R. Fundamentals of Fluid Mechanics, 7th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Verein Deutscher Ingenieure. In VDI Heat Atlas, 2nd ed.; Springer: Berlin, Germany, 2010.
- Jensen, K.F.; Reizman, B.J.; Newman, S.G. Tools for chemical synthesis in microsystems. Lab Chip 2014, 14, 3206–3212. [Google Scholar] [CrossRef] [PubMed]
- Anna, S.L. Droplets and Bubbles in Microfluidic Devices. Annu. Rev. Fluid Mech. 2016, 48, 285–309. [Google Scholar] [CrossRef]
- Oliveira, M.S.N.; Ni, X.W. Characterization of a gas-liquid OBC: Bubble size and gas holdup. AIChE J. 2004, 50, 3019–3033. [Google Scholar] [CrossRef]
- Moruzzi, R.B.; Reali, M.A.P. Characterization of micro-bubble size distribution and flow configuration in DAF contact zone by a non-intrusive image analysis system and tracer tests. Water Sci. Technol. 2010, 61, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Sevik, M.; Park, S.H. The Splitting of Drops and Bubbles by Turbulent Fluid Flow. J. Fluids Eng. 1973, 95, 53–60. [Google Scholar] [CrossRef]
- Fu, T.; Ma, Y.; Funfschilling, D.; Zhu, C.; Li, H.Z. Squeezing-to-dripping transition for bubble formation in a microfluidic T-junction. Chem. Eng. Sci. 2010, 65, 3739–3748. [Google Scholar] [CrossRef]
- Garstecki, P.; Fuerstman, M.J.; Stone, H.A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction-scaling and mechanism of break-up. Lab Chip 2006, 6, 437–446. [Google Scholar] [CrossRef] [PubMed]
- Oertel, H.; Böhle, M.; Reviol, T. Strömungsmechanik: Für Ingenieure und Naturwissenschaftler, 7 überarb. Aufl. ed; Springer: Wiesbaden, Germany, 2015. [Google Scholar]
- Martínez-Bazán, C.; Montanés, J.L.; Lasheras, J.C. On the breakup of an air bubble injected into a fully developed turbulent flow. Part 2. Size PDF of the resulting daughter bubbles. J. Fluid Mech. 1999, 401, 183–207. [Google Scholar] [CrossRef] [Green Version]
- Herwig, H. Strömungsmechanik: Einführung in die Physik von Technischen Strömungen, 2. überarb. und erw. Aufl. ed; Springer: Wiesbaden, Germany, 2016. [Google Scholar]
- Mersmann, A.; Großmann, H. Dispergieren im flüssigen Zweiphasensystem. Chem. Ing. Tech. 1980, 52, 621–628. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Dissipation of Energy in the Locally Isotropic Turbulence. Proc. Math. Phys. Sci. 1991, 434, 15–17. [Google Scholar] [CrossRef]
- Matsuyama, K.; Mine, K.; Kubo, H.; Aoki, N.; Mae, K. Optimization methodology of operation of orifice-shaped micromixer based on micro-jet concept. Chem. Eng. Sci. 2010, 65, 5912–5920. [Google Scholar] [CrossRef] [Green Version]
- Van Steijn, V. Formation and Transport of Bubbles in Microfluidic Systems; Ponsen en Looijen: Wageningen, The Netherlands, 2010. [Google Scholar]
- Antony, J. Design of Experiments for Engineers and Scientists, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Siebertz, K.; van Bebber, D.; Hochkirchen, T. Statistische Versuchsplanung: Design of Experiments (DoE); Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Stieß, M. Mechanische Verfahrenstechnik 1; Zweite, Neubearbeitete Auflage; Springer: Berlin, Germany, 1995. [Google Scholar]
- Qian, D.; McLaughlin, J.B.; Sankaranarayanan, K.; Sundaresan, S.; Kontomaris, K. Simulation of bubble breakup dynamics in homogeneous turbulence. Chem. Eng. Commun. 2006, 193, 1038–1063. [Google Scholar] [CrossRef]
- Risso, F.; Fabre, J. Oscillations and breakup of a bubble immersed in a turbulent field. J. Fluid Mech. 1998, 372, 323–355. [Google Scholar] [CrossRef]
- Galinat, S.; Risso, F.; Masbernat, O.; Guiraud, P. Dynamics of drop breakup in inhomogeneous turbulence at various volume fractions. J. Fluid Mech. 2007, 578, 85. [Google Scholar] [CrossRef]
- Ryan, B.F.; Joiner, B.L.; Cryer, J.D. Minitab Handbook: Updated for Release 16, 6th ed.; Brooks/Cole: Boston, MA, USA, 2013. [Google Scholar]
- Kleppmann, W. Taschenbuch Versuchsplanung: Produkte und Prozesse Optimieren, 4. überarb. Aufl. ed; Hanser: Munich, Germany, 2006. [Google Scholar]



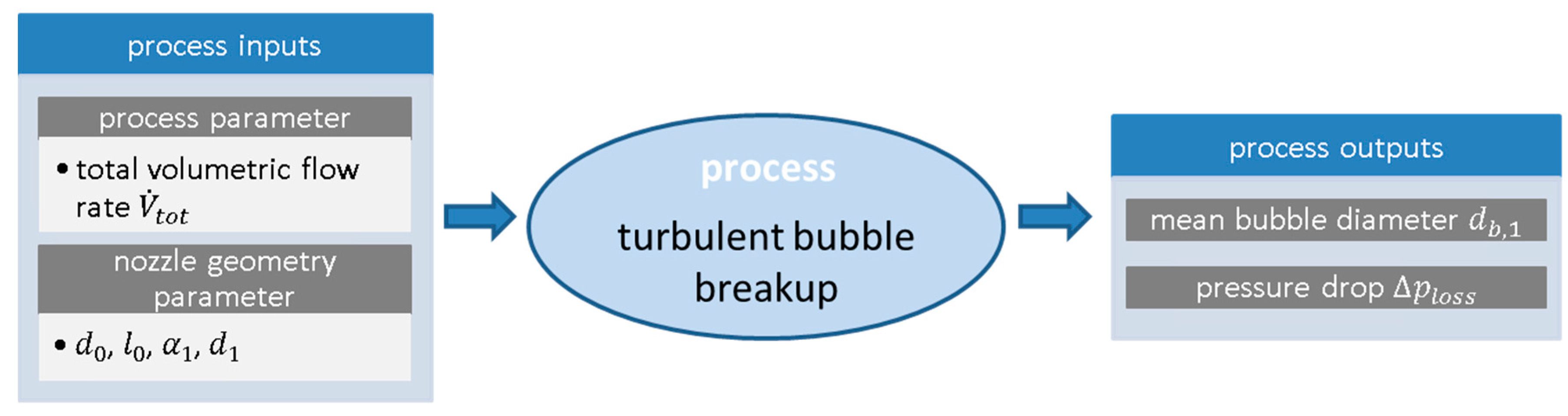

















| Process Parameters | Nozzle Parameters |
|---|---|
|
|
| Parameters [Unit] | Minimum Value | Maximum Value |
|---|---|---|
| [mm] | 0.25 | 0.75 |
| [mm] | 0.5 | 4.5 |
| [°] | 5 | 90 |
| [mm] | 0.75 | 1.75 |
| [mL/min] | 80 | 120 |
| Experiment No. | [mm] | [mm] | [°] | [mm] | [mL/min] | Point Type |
|---|---|---|---|---|---|---|
| 1 | 2.5 | 0.5 | 47.5 | 1.25 | 100 | central point |
| 2 | 0.9 | 0.7 | 81.5 | 1.65 | 84 | corner point |
| 3 | 0.9 | 0.7 | 13.5 | 0.85 | 84 | corner point |
| 4 | 4.1 | 0.7 | 81.5 | 1.65 | 116 | corner point |
| 5 | 4.1 | 0.3 | 13.5 | 1.65 | 116 | corner point |
| 6 | 0.9 | 0.3 | 13.5 | 0.85 | 116 | corner point |
| 7 | 2.5 | 0.5 | 47.5 | 1.25 | 120 | star point |
| 8 | 4.1 | 0.3 | 81.5 | 1.65 | 84 | corner point |
| 9 | 0.5 | 0.5 | 47.5 | 1.25 | 100 | star point |
| 10 | 2.5 | 0.5 | 47.5 | 1.25 | 100 | central point |
| 11 | 2.5 | 0.5 | 90 | 1.25 | 100 | star point |
| 12 | 2.5 | 0.5 | 47.5 | 1.25 | 100 | central point |
| 13 | 2.5 | 0.5 | 47.5 | 0.75 | 100 | star point |
| 14 | 0.9 | 0.3 | 81.5 | 0.85 | 84 | corner point |
| 15 | 4.1 | 0.7 | 13.5 | 0.85 | 116 | corner point |
| 16 | 2.5 | 0.5 | 5 | 1.25 | 100 | star point |
| 17 | 0.9 | 0.3 | 81.5 | 1.65 | 116 | corner point |
| 18 | 2.5 | 0.5 | 47.5 | 1.25 | 100 | central point |
| 19 | 2.5 | 0.5 | 47.5 | 1.25 | 80 | star point |
| 20 | 2.5 | 0.5 | 47.5 | 1.25 | 100 | central point |
| 21 | 2.5 | 0.25 | 47.5 | 1.25 | 100 | star point |
| 22 | 2.5 | 0.5 | 47.5 | 1.75 | 100 | star point |
| 23 | 4.1 | 0.3 | 81.5 | 0.85 | 116 | corner point |
| 24 | 0.9 | 0.7 | 81.5 | 0.85 | 116 | corner point |
| 25 | 4.1 | 0.7 | 13.5 | 1.65 | 84 | corner point |
| 26 | 2.5 | 0.5 | 47.5 | 1.25 | 100 | central point |
| 27 | 4.5 | 0.5 | 47.5 | 1.25 | 100 | star point |
| 28 | 0.9 | 0.7 | 13.5 | 1.65 | 116 | corner point |
| 29 | 4.1 | 0.7 | 81.5 | 0.85 | 84 | corner point |
| 30 | 4.1 | 0.3 | 13.5 | 0.85 | 84 | corner point |
| 31 | 0.9 | 0.3 | 13.5 | 1.65 | 84 | corner point |
| 32 | 2.5 | 0.75 | 47.5 | 1.25 | 100 | star point |
| Name | Picture | [mm] | [mm] | [°] | [mm] |
|---|---|---|---|---|---|
| A |  | 0.5 | 2.5 | 47.5 | 1.25 |
| B |  | 0.3 | 0.9 | 13.5 | 0.85 |
| C |  | 0.3 | 0.9 | 81.5 | 1.65 |
| D |  | 0.7 | 0.9 | 13.5 | 1.65 |
| E |  | 0.3 | 0.9 | 13.5 | 1.65 |
| F |  | 0.5 | 0.5 | 47.5 | 1.25 |
| G |  | 0.5 | 4.5 | 47.5 | 1.25 |
| H |  | 0.25 | 2.5 | 47.5 | 1.25 |
| I |  | 0.75 | 2.5 | 47.5 | 1.25 |
| J |  | 0.5 | 2.5 | 5 | 1.25 |
| K |  | 0.5 | 2.5 | 90 | 1.25 |
| L |  | 0.5 | 2.5 | 47.5 | 0.75 |
| M |  | 0.5 | 2.5 | 47.5 | 1.75 |
| N |  | 0.3 | 4.1 | 13.5 | 1.65 |
| O |  | 0.3 | 4.1 | 81.5 | 0.85 |
| P |  | 0.3 | 4.1 | 13.5 | 0.85 |
| Q |  | 0.7 | 4.1 | 81.5 | 1.65 |
| R |  | 0.3 | 4.1 | 81.5 | 1.65 |
| S |  | 0.7 | 4.1 | 13.5 | 1.65 |
| T |  | 0.3 | 0.9 | 81.5 | 0.85 |
| U |  | 0.7 | 0.9 | 81.5 | 1.65 |
| reference |  | 1 | - | - | 1 |
| Parameter | Value |
|---|---|
| 2.5 mm | |
| 0.9 mm | |
| 80° | |
| 1.0 mm | |
| 115 mL/min |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reichmann, F.; Varel, F.; Kockmann, N. Energy Optimization of Gas–Liquid Dispersion in Micronozzles Assisted by Design of Experiment. Processes 2017, 5, 57. https://doi.org/10.3390/pr5040057
Reichmann F, Varel F, Kockmann N. Energy Optimization of Gas–Liquid Dispersion in Micronozzles Assisted by Design of Experiment. Processes. 2017; 5(4):57. https://doi.org/10.3390/pr5040057
Chicago/Turabian StyleReichmann, Felix, Fabian Varel, and Norbert Kockmann. 2017. "Energy Optimization of Gas–Liquid Dispersion in Micronozzles Assisted by Design of Experiment" Processes 5, no. 4: 57. https://doi.org/10.3390/pr5040057
APA StyleReichmann, F., Varel, F., & Kockmann, N. (2017). Energy Optimization of Gas–Liquid Dispersion in Micronozzles Assisted by Design of Experiment. Processes, 5(4), 57. https://doi.org/10.3390/pr5040057




