A General Model for Estimating Emissions from Integrated Power Generation and Energy Storage. Case Study: Integration of Solar Photovoltaic Power and Wind Power with Batteries
Abstract
:1. Introduction
1.1. Background
1.2. Motivation for PV LCA
1.3. Motivation for Modeling Emissions from Coupled Generation and Energy Storage
2. Methodology
2.1. Model of Combined Generation and Storage
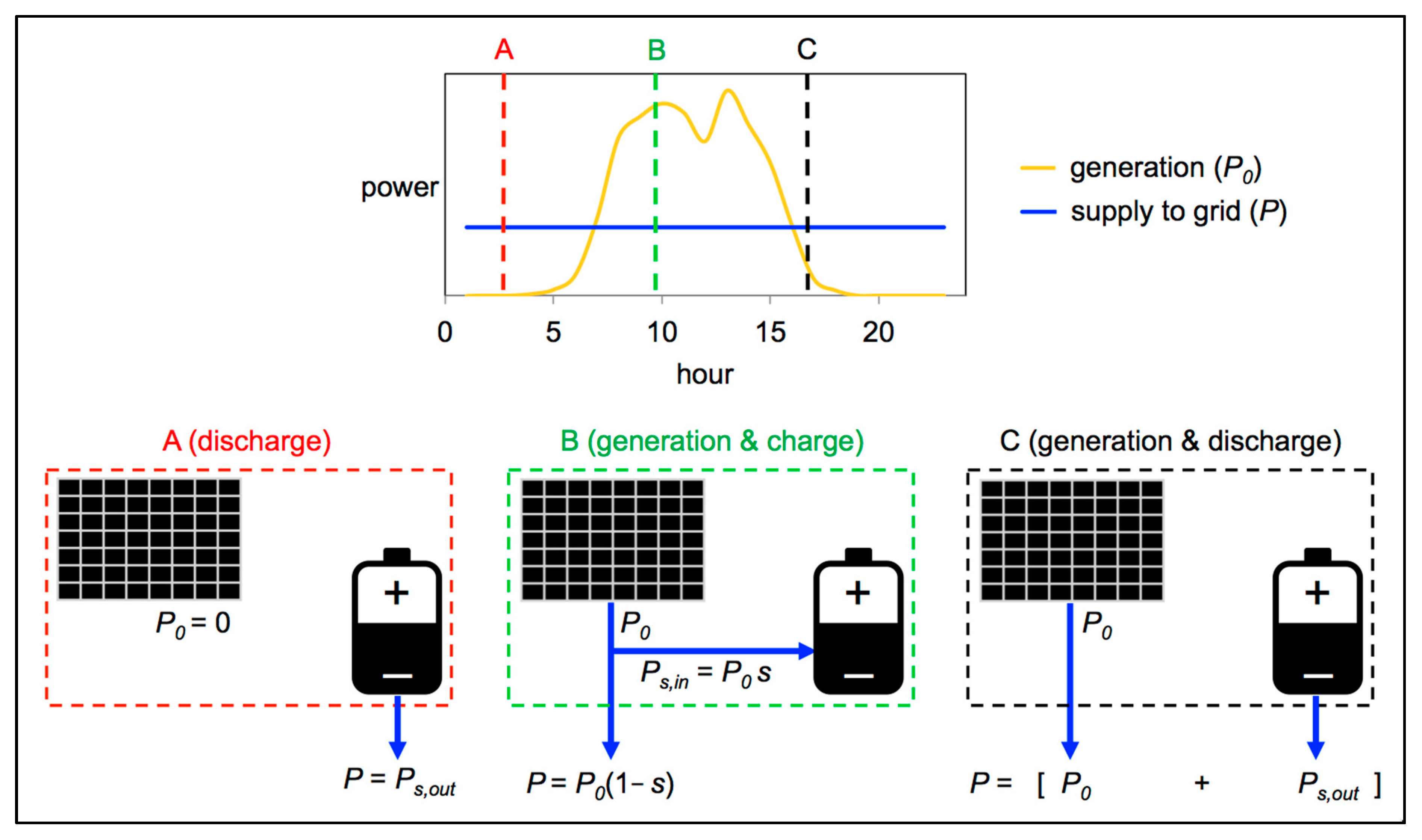
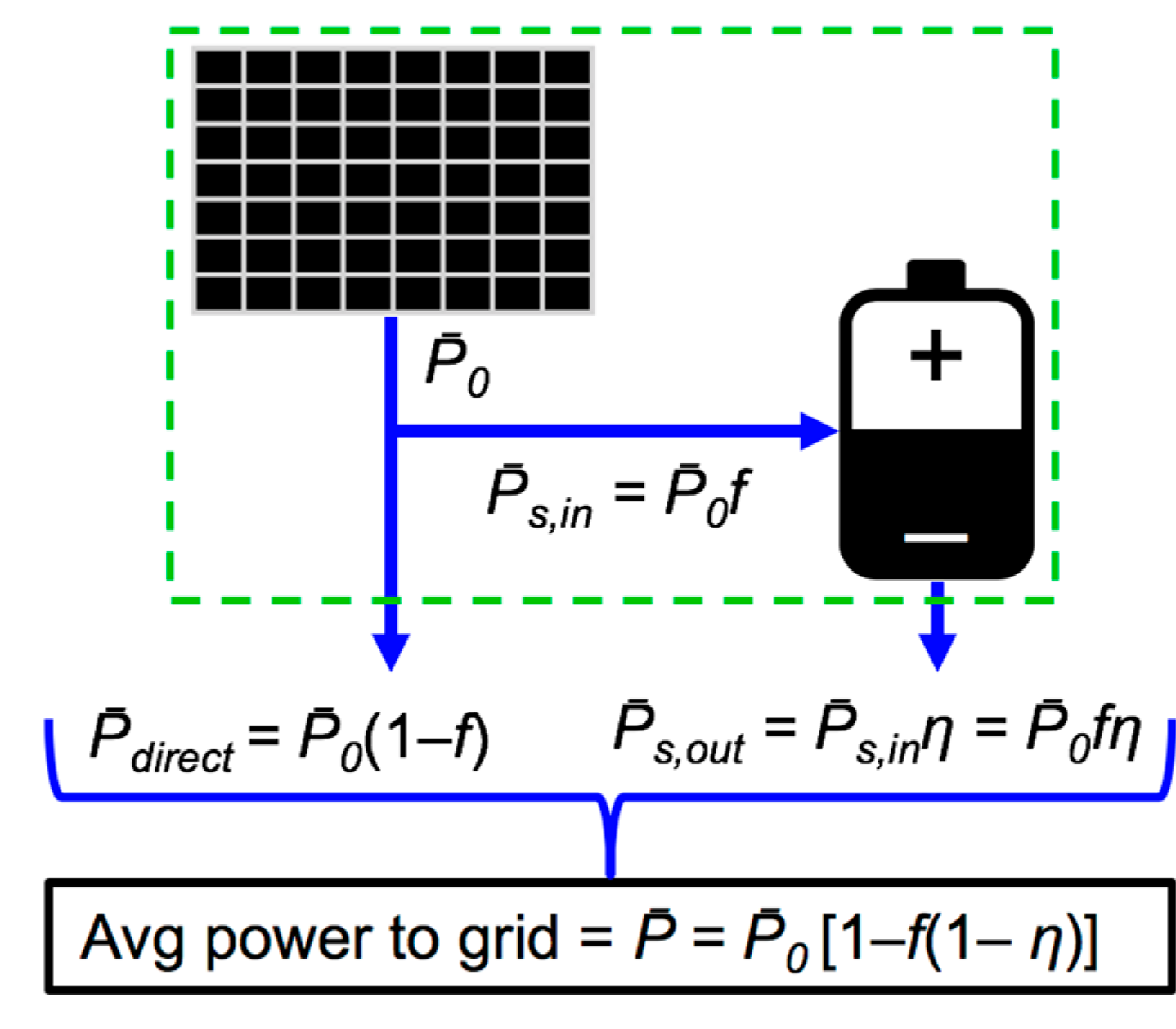
2.1.1. Model of Electricity Supply to Grid
2.1.2. Model Equations and Parameters
2.1.3. Model Equations Derivations
2.1.4. Model Assumptions and Approximations Include the Following:
- (1)
- Storage efficiency is treated as constant.
- (2)
- The number of storage units retired over the system’s lifetime is treated as continuous in the model (see Equation (5)).
- (3)
- In Table 2, the battery production emissions (es) do not include emissions from producing the battery inverter and control system, because of a lack of data. An alternative is estimating battery inverter emissions by approximating that the battery inverters are equivalent to PV inverters, and then using the PV inventories discussed in Section 2.2.1. [40,41]. These inventories report inverter production GHGs of ~27.4 gCO2e per watt of AC inverter capacity, and inverter lifetime of 15 years. For the cases analyzed in this paper, this would add approximately 1.5 gCO2e/kWh to the total carbon intensity, and increase the storage production emissions by ~15% for LBs and ~30% for VFBs. Unlike the battery inverter case, we do not identify a reasonable approximation for the emissions from producing the battery control system.
- (4)
- Charging from the grid is not analyzed. Such an analysis would include the expansion of the generator definition to encompass all generators connected to a grid.
- (5)
- Cycle life is considered as controlling, not calendar life. Our analysis is focused on storage applications that require regular cycling at high DoD, and thus cause cycling-induced degradation to be the primary degradation mode. The storage unit is assumed to reach its cycle life before its calendar life. For applications that do not involve a high-use of battery capacity, such as frequency regulation, this might not be a valid approximation [37].
- (6)
- (7)
- DC–DC coupling is possible for PV and battery storage, but is not analyzed here. It is unclear whether DC–DC coupling of PV and batteries actually increases the round-trip efficiency, given the particular equipment and system architecture required. For more discussions, see the literature [42].
- (8)
- Possible storage impacts on curtailment and generator efficiency are not analyzed. For example, storage can be used to store off-peak wind generation that would otherwise be curtailed, for later supply to the grid. Thus, in some cases, storage might actually increase the generator capacity factor F by offsetting storage efficiency losses with curtailment reductions. As another example, storage can be used to increase the fuel-to-power efficiency of the simple cycle gas turbines (SCGT). A preliminary analysis suggests that, for an SCGT with an original generation profile typical of California peaker plants, adding enough storage to allow for flat generation might increase generation-averaged fuel-to-power efficiency by up to ~3%, thus partly offsetting efficiency losses in storage.
2.2. Life Cycle Assessments of Generation
2.2.1. PV LCA Methodology
PV LCA-Goal, System Boundary, and Functional Unit
PV LCA-Data Sources
PV LCA-Model Structure
PV LCA-Converting GHGs per Capacity to GHGs per Generation (Carbon Intensity)
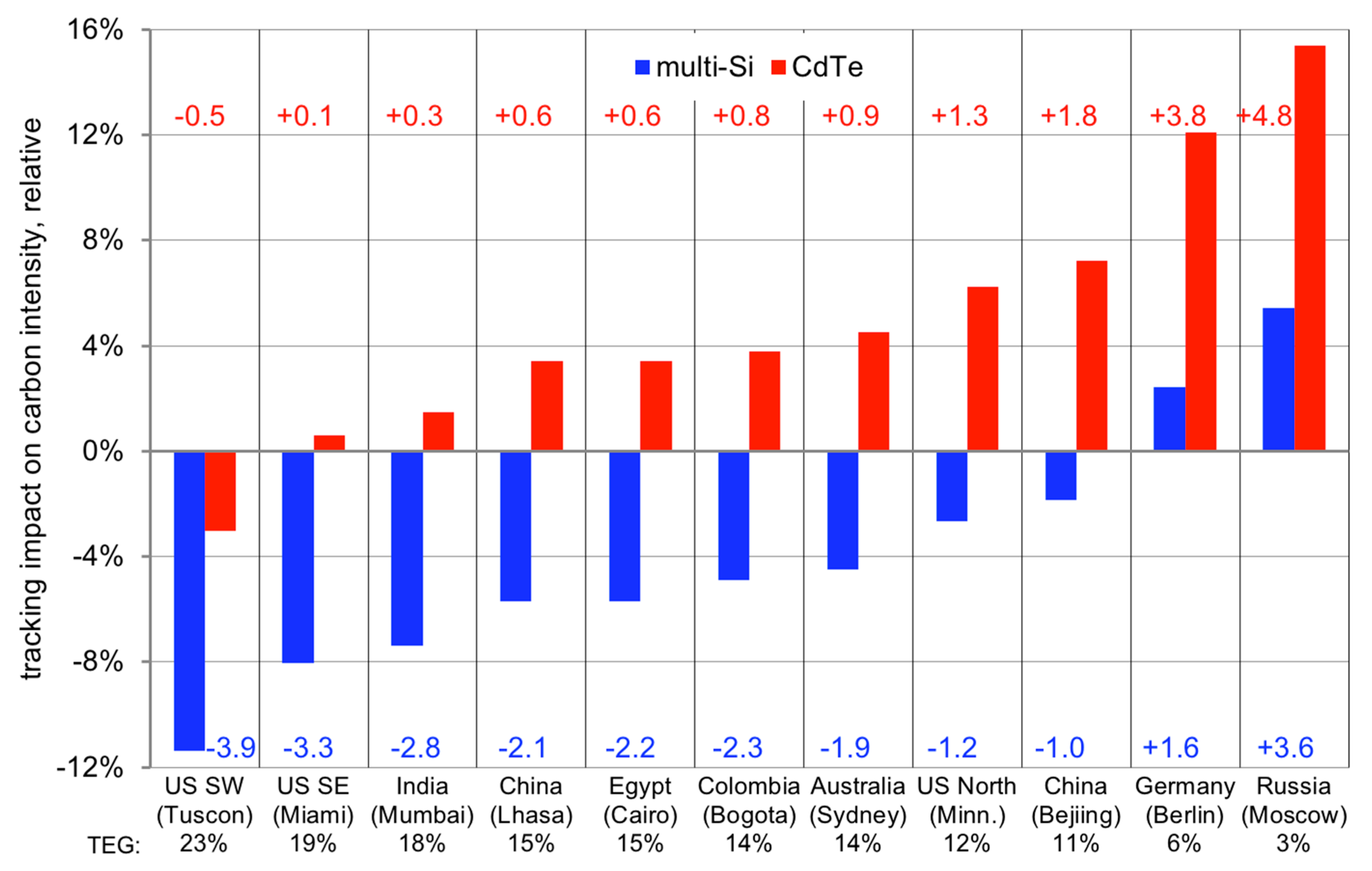
PV LCA-Tracking Energy Gain Methodology
2.2.2. Wind LCA Synthesis
3. Results and Discussion
3.1. Base Cases for PV Generation (No Tracking, No Storage)
3.2. The Impact of Solar Tracking
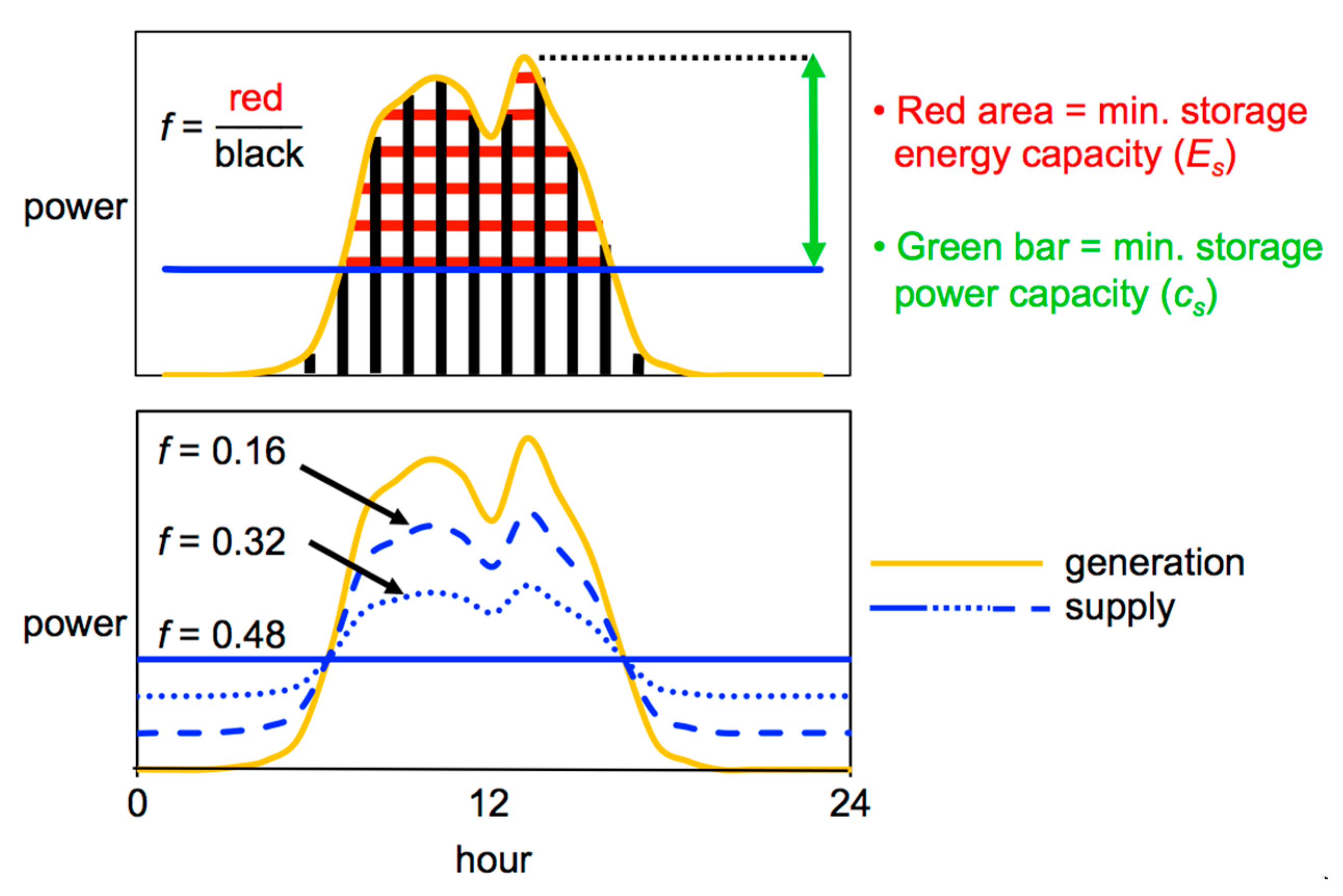
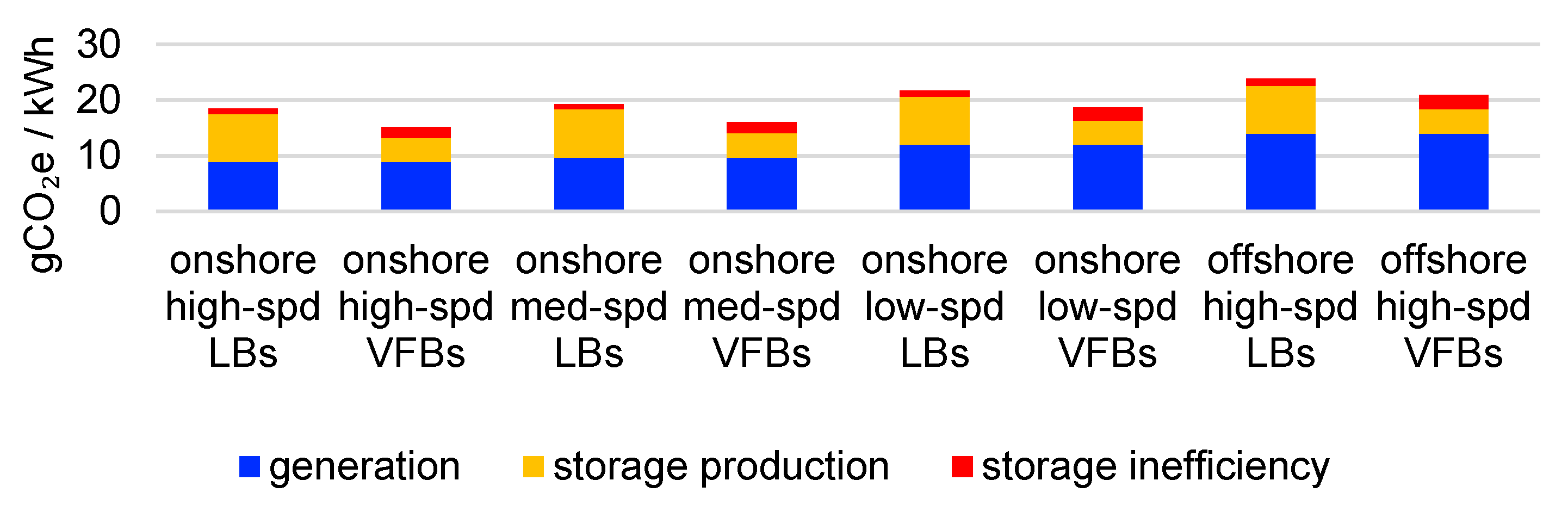
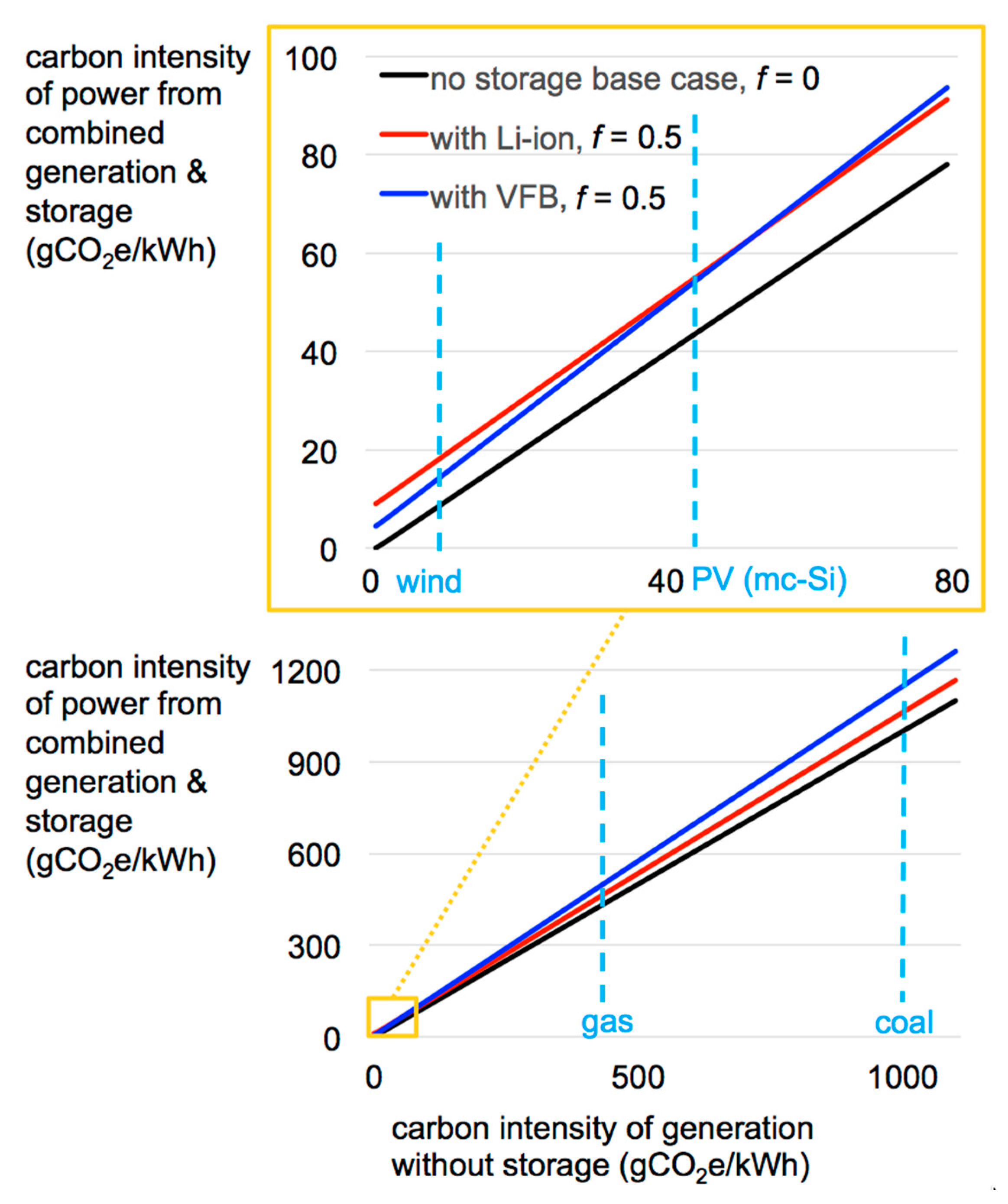
3.3. Hybrid Power Generation and Storage
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature (In Order of Appearance)
| GHG | greenhouse gas |
| IEA | International Energy Agency |
| PV | photovoltaic |
| mc-Si | multi-crystalline silicon |
| sc-Si | single-crystalline silicon |
| CdTe | cadmium telluride |
| gCO2e | grams CO2 equivalent |
| CCNG | combined cycle natural gas |
| SCPC | supercritical pulverized coal |
| cradle-to-grave | covering all parts of a product’s life cycle from raw material acquistion (cradle) through disposal and/or recycling (grave) |
| cradle-to-gate | covering all parts of a product’s life cycle from raw material acquistion (cradle) through production (factory gate) |
| LCA | life cycle assessment |
| utility-scale | having AC capacity >5 MW, used to describe power plants |
| LB | lithium-ion battery |
| VFB | vanadium redox flow battery |
| LAB | lead acid battery |
| SSB | sodium sulfur battery |
| PHS | pumped hydroelectric storage |
| CAES | compressed air energy storage |
| P0 | power generation (kW) |
| P | power supply to grid (kW) |
| Ps,in | is the amount of power generation sent to storage (kW) |
| s | is the instantaneous fraction of power generation going to storage |
| Ps,out | is the power supply to grid from storage |
| η | round-trip efficiency of the storage |
| the fraction of energy generation sent to storage (vs. directly to grid) | |
| E | lifetime electricity supply to grid from power plant (kWh) |
| E0 | lifetime electricity supply to grid from power plant without storage (kWh) |
| I | emissions intensity (g/kWh) |
| the life emissions of the generator (g) | |
| the life emissions of the storage (g) | |
| or DoD | the average depth of discharge of the storage (DoD) |
| the total rated energy capacity of storage used over the power plant life (kWh) | |
| the cycle life of the storage (the number of charge–discharge cycles before a storage unit is retired) | |
| the mass of batteries used over the power plant life (kg) | |
| the specific energy capacity of the batteries (kWh/kg) | |
| the total rated energy capacity of all storage used and retired over the power plant life | |
| cg | rated power capacity |
| F | capacity factor |
| TEG | tracking energy gain |
| EOL | end of life |
References
- IEA. Energy, Climate Change & Environment; IEA: Paris, France, 2016. [Google Scholar]
- The Energy Initiative MIT. The Future of Solar Energy: An Interdiscipinary MIT Stud; MIT: Cambridge, MA, USA, 2015; pp. 3–6. [Google Scholar] [CrossRef]
- GlobalData. Solar PV Generation Statistics, Wind Generation Statistics; GlobalData: London, UK, 2018. [Google Scholar]
- ExxonMobil. 2017 Outlook for Energy: A View to 2040; ExxonMobil: Irving, TX, USA, 2017. [Google Scholar]
- BNEF. Bloomberg New Energy Finance Report 2017; BNEF: New York, NY, USA, 2017. [Google Scholar]
- Fraunhofer Institute for Solar Energy Systems. Photovoltaics Report; Fraunhofer Institute for Solar Energy Systems: Freiburg, Germany, 2017. [Google Scholar]
- WindEurope. The European Offshore Wind Industry—Key Trends And Statistics 2017; WindEurope: Brussels, Belgium, 2018. [Google Scholar]
- EIA. Form EIA-860: Annual Electric Generator Report; EIA: Paris, France, 2016. [Google Scholar]
- Leccisi, E.; Raugei, M.; Fthenakis, V. The energy and environmental performance of ground-mounted photovoltaic systems—A timely update. Energies 2016, 9, 622. [Google Scholar] [CrossRef]
- Garrett, P.; Rønde, K. Life Cycle Assessment of Electricity Production from an Onshore V90-3.0 MW Wind Plant September 2012; Vestas Wind Systems A/S: Aarhus, Denmark, 2012; pp. 1–106. [Google Scholar]
- Garrett, P.; Rønde, K.; Finkbeiner, M. Life Cycle Assessment of Electricity Production from an Onshore V110-2.0 MW Wind Plant; Vestas Wind Systems A/S: Aarhus, Denmark, 2012; pp. 1–106. [Google Scholar]
- Garrett, P.; Klaus, R. Life Cycle Assessment of Electricity Production from a V100-1.8 MW Gridstreamer Wind Plant; Vestas Wind Systems A/S: Aarhus, Denmark, 2011; p. 105. [Google Scholar]
- Razdan, A.P.; Garrett, P. Life Cycle Assessment of Electricity Production from an Onshore V100-2.0 MW Wind Plant; Vestas Wind Systems A/S: Aarhus, Denmark, 2015. [Google Scholar]
- Siemens. Onshore Wind Power Plant Employing SWT-2.3-108. In A Clean Energy Solut—From Cradle to Grave; Siemens: Munich, Germany, 2014; 16p. [Google Scholar]
- Siemens. Onshore Wind Power Plant Employing SWT-3.2-113. In A Clean Energy Solut—From Cradle to Grave; Siemens: Munich, Germany, 2014; 16p. [Google Scholar]
- Siemens. Offshore Wind Power Plant Employing SWT-4.0-130. In A Clean Energy Solut—From Cradle to Grave; Siemens: Munich, Germany, 2014; 16p. [Google Scholar]
- Siemens. Offshore Wind Power Plant Employing SWT-7.0-154. In A Clean Energy Solut—From Cradle to Grave; Siemens: Munich, Germany, 2014; 16p. [Google Scholar]
- Weinzettel, J.; Reenaas, M.; Solli, C.; Hertwich, E.G. Life cycle assessment of a floating offshore wind turbine. Renew. Energy 2009, 34, 742–747. [Google Scholar] [CrossRef]
- Skone, T.J.; Littefield, J.; Cooney, G.; Marriott, J. Power Generation Technology Comparison from a Life Cycle Perspective; National Energy Technology Laboratory: Pittsburgh, PA, USA, 2013.
- Peng, J.; Lu, L.; Yang, H. Review on life cycle assessment of energy payback and greenhouse gas emission of solar photovoltaic systems. Renew. Sustain. Energy Rev. 2013, 19, 255–274. [Google Scholar] [CrossRef]
- Hsu, D.D.; O’Donoughue, P.; Fthenakis, V.; Heath, G.A.; Kim, H.C.; Sawyer, P.; Choi, J.K.; Turney, D.E. Life Cycle Greenhouse Gas Emissions of Crystalline Silicon Photovoltaic Electricity Generation: Systematic Review and Harmonization. J. Ind. Ecol. 2012, 16, S122–S135. [Google Scholar] [CrossRef]
- Frischknecht, R.; Heath, G.; Raugei, M.; Sinha, P.; de Wild-Scholten, M.; Fthenakis, V. Methodology Guidelines on Life Cycle Assessment of Photovoltaic Electricity, 3rd ed.; IEA PVPS Task 12; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2016.
- Bayod-Rújula, Á.A.; Lorente-Lafuente, A.M.; Cirez-Oto, F. Environmental assessment of grid connected photovoltaic plants with 2-axis tracking versus fixed modules systems. Energy 2011, 36, 3148–3158. [Google Scholar] [CrossRef]
- Desideri, U.; Zepparelli, F.; Morettini, V.; Garroni, E. Comparative analysis of concentrating solar power and photovoltaic technologies: Technical and environmental evaluations. Appl. Energy 2013, 102, 765–784. [Google Scholar] [CrossRef]
- Beylot, A.; Payet, J.Ô.; Puech, C.; Adra, N.; Jacquin, P.; Blanc, I.; Beloin-Saint-Pierre, D. Environmental impacts of large-scale grid-connected ground-mounted PV installations. Renew. Energy 2014, 61, 2–6. [Google Scholar] [CrossRef] [Green Version]
- Bolinger, M.; Seel, J.; La Commare, K.H. Utility-Scale Solar 2016; LBNL-2001055; Lawrence Berkeley National Laboratory: Foshan, Guangdong, China, September 2017.
- Sinha, P.; Schneider, M.; Dailey, S.; Jepson, C.; De Wild-Scholten, M. Eco-efficiency of CdTe photovoltaics with tracking systems. In Proceedings of the 39th IEEE Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013. [Google Scholar]
- Sivaram, V.; Kann, S. Solar power needs a more ambitious cost target. Nat. Energy 2016, 1, 16036. [Google Scholar] [CrossRef]
- Zhuk, A.; Zeigarnik, Y.; Buzoverov, E.; Sheindlin, A. Managing peak loads in energy grids: Comparative economic analysis. Energy Policy 2016, 88, 39–44. [Google Scholar] [CrossRef]
- Krieger, E.M.; Casey, J.A.; Shonkoff, S.B.C. A framework for siting and dispatch of emerging energy resources to realize environmental and health benefits: Case study on peaker power plant displacement. Energy Policy 2016, 96, 302–313. [Google Scholar] [CrossRef]
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energy Policy 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Simon, B.; Finn-Foley, D.; Gupta, D. GTM Research/ESA U.S. Energy Storage Monitor; GTM: Boston, MA, USA, 2018. [Google Scholar]
- Yang, G. Is this the ultimate grid battery? IEEE Spectrum 2017, 54, 36–41. [Google Scholar] [CrossRef]
- Spanos, C.; Turney, D.E.; Fthenakis, V. Life-cycle analysis of flow-assisted nickel zinc-, manganese dioxide-, and valve-regulated lead-acid batteries designed for demand-charge reduction. Renew. Sustain. Energy Rev. 2015, 43, 478–494. [Google Scholar] [CrossRef]
- Rydh, C.J.; Sandén, B.A. Energy analysis of batteries in photovoltaic systems. Part I: Performance and energy requirements. Energy Convers. Manag. 2005, 46, 1957–1979. [Google Scholar] [CrossRef]
- Denholm, P.; Kulcinski, G.L. Life cycle energy requirements and greenhouse gas emissions from large scale energy storage systems. Energy Convers. Manag. 2004, 45, 2153–2172. [Google Scholar] [CrossRef]
- Mitavachan, H.; Derendorf, K.; Vogt, T. Comparative life cycle assessment of battery storage systems for stationary applications. Environ. Sci. Technol. 2015. [Google Scholar] [CrossRef]
- Cui, Y.; Du, C.; Yin, G.; Gao, Y.; Zhang, L.; Guan, T.; Yang, L.; Wang, F. Multi-stress factor model for cycle lifetime prediction of lithium ion batteries with shallow-depth discharge. J. Power Source 2015, 279, 123–132. [Google Scholar] [CrossRef]
- Alsaidan, I.; Khodaei, A.; Gao, W. A Comprehensive Battery Energy Storage Optimal Sizing Model for Microgrid Applications. IEEE Trans. Power Syst. 2018, 33, 3968–3980. [Google Scholar] [CrossRef]
- Jungbluth, N.; Stucki, M.; Flury, K.; Frischknecht, R.; Büsser, S. Life Cycle Inventories of Photovoltaics; ESU-services Ltd.: Ulster, Switzerland, 2012. [Google Scholar]
- Frischknecht, R.; Itten, R.; Sinha, P.; de Wild-Scholten, M.; Zhang, J.; Fthenakis, V. Life Cycle Inventories and Life Cycle Assessment of Photovoltaic Systems; Report IEA-PVPS T12-04:2015; International Energy Agency (IEA): Paris, France, 2015. [Google Scholar]
- Eaton, C.T. AC vs. DC Coupling in Utility-Scale Solar Plus Storage Projects; Eaton: Cleveland, OH, USA, 2016. [Google Scholar]
- Miller, I.; Gençer, E.; Vogelbaum, H.S.; Brown, P.R.; Torkamani, S.; O’Sullivan, F.M. Parametric modeling of life cycle greenhouse gas emissions from photovol-taic power. Appl. Energy 2018. Under Review. [Google Scholar]
- ISO 14040. The International Standards Organisation. Environmental Management—Life cycle Assessment—Principles and Framework; ISO 14040 2006; ISO: Geneva, Switzerland, 2006; pp. 1–28. [Google Scholar] [CrossRef]
- Steubing, B.; Wernet, G.; Reinhard, J.; Bauer, C.; Moreno-Ruiz, E. The ecoinvent database version 3 (part II): Analyzing LCA results and comparison to version 2. Int. J. Life Cycle Assess. 2016, 21, 1269–1281. [Google Scholar] [CrossRef]
- Gagnon, P.; Margolis, R.; Melius, J.; Phillips, C.; Elmore, R. Rooftop Solar Photovolatic Technical Potential in the United States: A Detailed Assessment; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2016; p. 82. [CrossRef]
- Jean, J.; Brown, P.R.; Jaffe, R.L.; Buonassisi, T.; Bulović, V. Pathways for solar photovoltaics. Energy Environ. Sci. 2015, 8, 1200–1219. [Google Scholar] [CrossRef]
- Gençer, E.; Miskin, C.; Sun, X.; Khan, M.R.; Bermel, P.; Alam, M.A.; Agrawal, R. Directing solar photons to sustainably meet food, energy, and water needs. Sci. Rep. 2017, 7, 3133. [Google Scholar] [CrossRef] [PubMed]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P. Climate Change 2014: Synthesis Report; Contribution of Working Groups, I II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar] [CrossRef]
- Gilman, P.; Dobos, A.; DiOrio, N.; Freeman, J.; Janzou, S.; Ryberg, D. SAM Photovoltaic Model Technical Reference Update; NREL: Golden, CO, USA, 2018.
- Dobos, A.P. PVWatts Version 5 Manual; NREL/TP-6A20-62641; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014.
- Garrett, P.; Ronde, K. Life Cycle Assessment of Electricity Production from an Onshore V90-2.6 MW Wind Plant; Vestas Wind Systems A/S: Aarhus, Denmark, 2013; p. 107. [Google Scholar]
- Razdan, A.P.; Garrett, P. December 2015 Life Cycle Assessment of Electricity Production from an Onshore V110-2.0 MW Wind Plant; Vestas Wind Systems A/S: Aarhus, Denmark, 2015. [Google Scholar]
- GWEC. Global Wind Statistics 2016; GWEC: Brussels, Beligum, 2017. [Google Scholar]
- Siemens. Offshore wind power plant employing SWT-6.0-154. In A Clean Energy Solut—From Cradle to Grave; Siemens: Munich, Germany, 2014; 16p. [Google Scholar]
- Jordan, D.C.; Kurtz, S.R.; VanSant, K.; Newmiller, J. Compendium of photovoltaic degradation rates. Prog. Photovolt. Res. Appl. 2016, 24, 978–989. [Google Scholar] [CrossRef]
- IEA. CO2 Emissions from Fuel Combustion 2017; International Energy Agency: Paris, France, 2017. [Google Scholar] [CrossRef]










| Symbol | Description | Units | Example of Dependence on Technology | Example of Dependence on Design |
|---|---|---|---|---|
| emissions intensity of electricity w/o storage | g/kWh | Coal gen. has higher GHG emissions than wind generation | ||
| fraction of electricity generation that is stored | Greater smoothing of generation peaks requires greater f (see Figure 3) | |||
| round-trip efficiency of storage | LBs usually have higher η than VFBs | |||
| emissions per unit of rated storage energy capacity produced | g/kWh | Compared to LABs, LBs generally have higher GHG emissions per rated energy | Two VFBs w/same rated energy and different rated power will have different emissions | |
| emissions per unit of storage mass produced | g/kg | |||
| specific energy capacity | kWh/kg | Two VFBs w/same rated energy but different power will have different ρ | ||
| average depth of discharge (DoD) | LBs are usually run at higher DoD than LABs | More “excess” storage energy capacity means lower D for same f | ||
| cycle life | cycles | LBs have higher C than LABs |
| Carbon Intensity (gCO2e/kWh) | |||
|---|---|---|---|
| Avg | Low | High | |
| Onshore high wind speed (~9 m/s) | 8.9 | 5.5 | 12 |
| Onshore med wind speed (~8 m/s) | 9.7 | 6.4 | 12 |
| Onshore low wind speed (~7 m/s) | 12 | 7.3 | 15.8 |
| Onshore high wind speed (~9 m/s) | 14 | 10.8 | 18.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, I.; Gençer, E.; O’Sullivan, F.M. A General Model for Estimating Emissions from Integrated Power Generation and Energy Storage. Case Study: Integration of Solar Photovoltaic Power and Wind Power with Batteries. Processes 2018, 6, 267. https://doi.org/10.3390/pr6120267
Miller I, Gençer E, O’Sullivan FM. A General Model for Estimating Emissions from Integrated Power Generation and Energy Storage. Case Study: Integration of Solar Photovoltaic Power and Wind Power with Batteries. Processes. 2018; 6(12):267. https://doi.org/10.3390/pr6120267
Chicago/Turabian StyleMiller, Ian, Emre Gençer, and Francis M. O’Sullivan. 2018. "A General Model for Estimating Emissions from Integrated Power Generation and Energy Storage. Case Study: Integration of Solar Photovoltaic Power and Wind Power with Batteries" Processes 6, no. 12: 267. https://doi.org/10.3390/pr6120267
APA StyleMiller, I., Gençer, E., & O’Sullivan, F. M. (2018). A General Model for Estimating Emissions from Integrated Power Generation and Energy Storage. Case Study: Integration of Solar Photovoltaic Power and Wind Power with Batteries. Processes, 6(12), 267. https://doi.org/10.3390/pr6120267





