Modelling and Simulation of Biochemical Processes Using Petri Nets
Abstract
:1. Introduction
1.1. Context
1.2. Problems & Issues
1.3. Contribution & Contents
2. Methionine Metabolic Pathway: The Studied Biochemical System
3. Petri Nets
4. Model Construction
- Enzymes and metabolites are represented by entities. These entities are continuous since they contain quantities representing concentrations.
- Processes represent all reactions taking place in these pathway. These processes are continuous since they are supposed to assure the execution permanency. One process is discrete, namely , in order to control Methionine input quantities since it is provided by diet intake.
- Metabolites and processes are linked via normal connectors which allow the representation of degradation or production of metabolites.
- Enzymes and processes are linked via test connectors which represent the catalysis of reactions while maintaining the quantity of the source entity.
- Test connectors are used also to play the role of reactions activation, in some cases, in the purpose of maintaining “the system equilibrium”. In this case they are in blue (see the blue arcs from to and from to in Figure 7).
- Red arcs linking some metabolites and some enzymes, are inhibitory connectors. They allow to stop and inhibit some reactions when the contents of the source place is more than its weight.
- V is the velocity at any time (M/h);
- is the maximum rate achieved by the system at maximum substrate concentration (M/h);
- is the substrate concentration (M/L);
- is the Michaelis constant = Substrate concentration at which the reaction rate is half of (M).
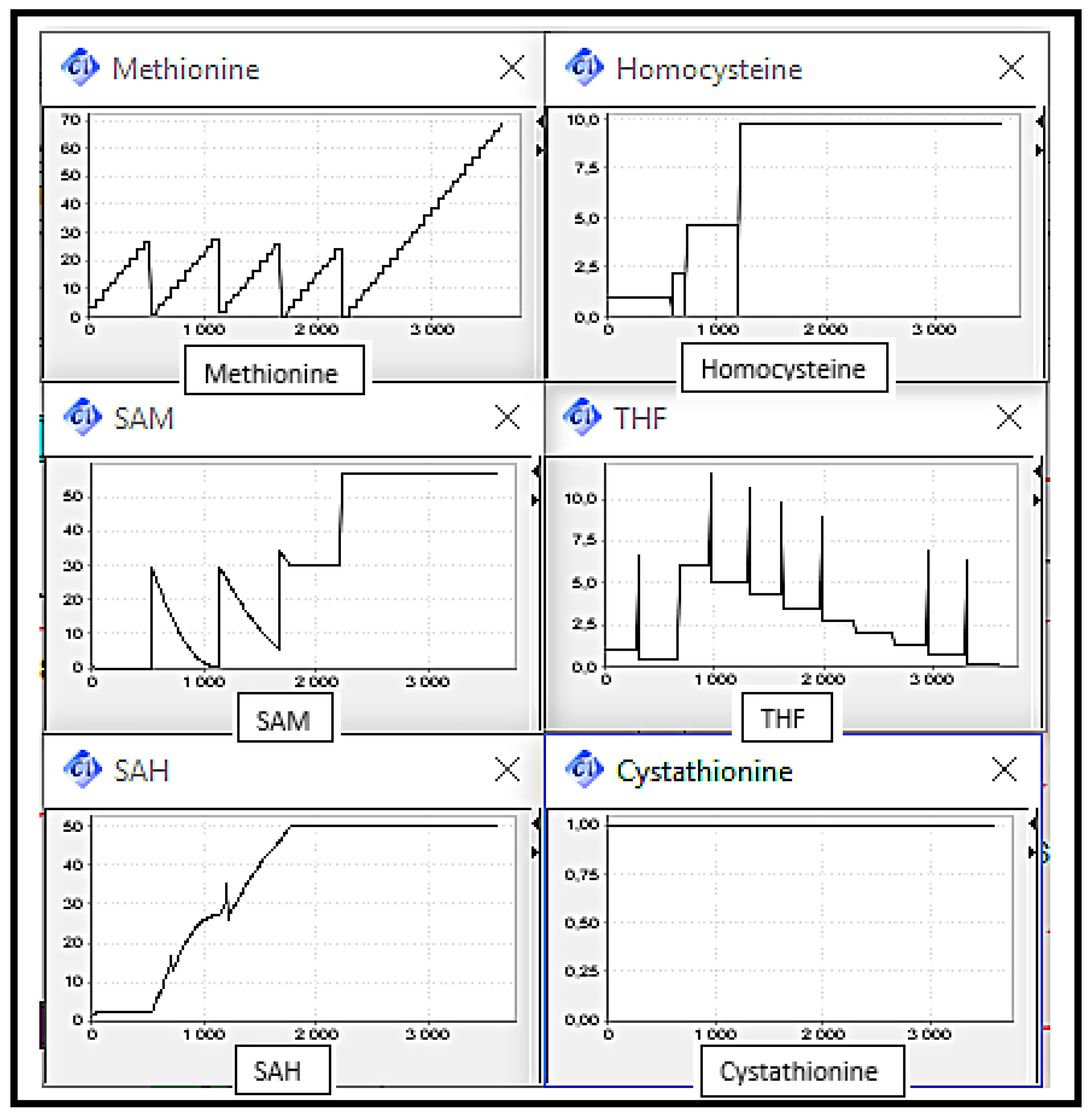
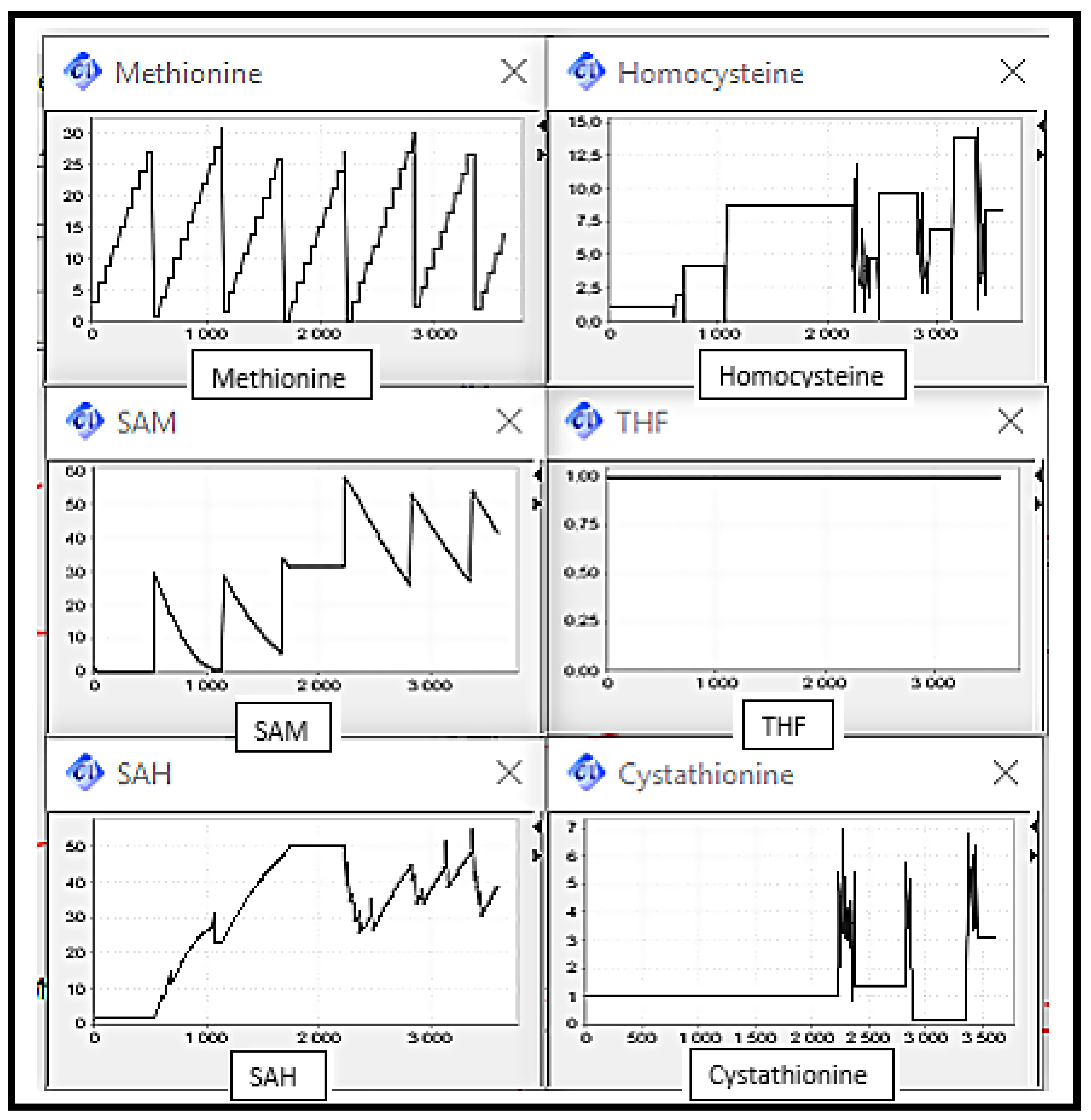
5. Simulation and Validation
- -
- Scenario 1: Normal Case
- -
- Scenario 2: MS, BHSM and CBS Deficiencies, the enzymes catalysing reactions converting Homocysteine to Methionine and Cysthationine respectively.
- -
- Scenario 3: MS and BHSM Deficiencies, the enzymes catalysing reactions converting Homocysteine to Methionine.
- -
- Scenario 4: CBS and BHSM Deficiencies, the enzymes catalysing reactions converting Homosycteine to Methionine and Cysthationine respectively.
- -
- Scenario 5: MS and CBS Deficiencies, the enzymes catalysing reactions converting Homosycteine to Methionine and Cysthationine respectively.
6. Conclusions & Future Works
6.1. Conclusions
6.2. Future Works
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 5MethylTHF | 5-Methyl Tetrahydrofolate |
| BHSM | Betaine-Homocysteine S-Methyltransferase |
| CBS | Cystathionine Beta Synthase |
| MATII | Methionine Adenosyl Transferase |
| METH | Methyltransferase |
| MS | Methionine Synthase |
| SAH | S-Adenosyl-Homocysteine |
| SAHH | S-Adenosyl-Homocysteine Hydrolase |
| SAM | S-Adenosyl-Methionine |
| THF | Tetrahydrofolate |
References
- De Jong, H. Modeling and simulation of genetic regulatory systems: A literature review. J. Comput. Biol. 2002, 9, 67–103. [Google Scholar] [CrossRef] [PubMed]
- Kitano, H. Computational systems biology. Nature 2002, 420, 206–210. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Makkena, R.; McGeary, F.; Decker, K.; Gillis, W.; Schmidt, C. A multi-agent system for the quantitative simulation of biological networks. In Proceedings of the Second International Joint Conference On Autonomous Agents and Multiagent Systems, Melbourne, Australia, 14–18 July 2003; pp. 385–392. [Google Scholar]
- Guerriero, M.L. Qualitative and quantitative analysis of a Bio-PEPA model of the gp130/JAK/STAT signalling pathway. In Transactions on Computational Systems Biology XI; Springer: Berlin/Heidelberg, Germany, 2009; pp. 90–115. [Google Scholar]
- Koch, I. Petri nets in systems biology. Softw. Syst. Model. 2015, 14, 703–710. [Google Scholar] [CrossRef]
- Reddy, V.N.; Mavrovouniotis, M.L.; Liebman, M.N. Petri net representations in metabolic pathways. In Proceedings of the 1st International Conference on Intelligent Systems for Molecular Biology, Bethesda, MD, USA, 6–9 July 1993; Volume 93, pp. 328–336. [Google Scholar]
- Liu, F.; Heiner, M. Petri nets for modeling and analyzing biochemical reaction networks. In Approaches in Integrative Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 245–272. [Google Scholar]
- Heiner, M.; Koch, I.; Will, J. Model validation of biological pathways using Petri nets—Demonstrated for apoptosis. Biosystems 2004, 75, 15–28. [Google Scholar] [CrossRef] [PubMed]
- Herajy, M.; Liu, F.; Rohr, C.; Heiner, M. Coloured Hybrid Petri Nets: an Adaptable Modelling Approach for Multi-scale Biological Networks. Comput. Biol. Chem. 2018, 76, 87–100. [Google Scholar] [CrossRef] [PubMed]
- Herajy, M.; Liu, F.; Heiner, M. Efficient modelling of yeast cell cycles based on multisite phosphorylation using coloured hybrid Petri nets with marking-dependent arc weights. Nonlinear Anal. Hybrid Syst. 2018, 27, 191–212. [Google Scholar] [CrossRef]
- Cao, R.; Hao, L.; Wang, F.; Qiang, G. Modelling and analysis of hybrid stochastic timed Petri net. J. Control Decis. 2018, 1–21. [Google Scholar]
- Hardy, S.; Robillard, P.N. Modeling and simulation of molecular biology systems using Petri nets: Modeling goals of various approaches. J. Bioinform. Comput. Biol. 2004, 2, 619–637. [Google Scholar] [CrossRef]
- Peleg, M.; Rubin, D.; Altman, R.B. Using Petri net tools to study properties and dynamics of biological systems. J. Am. Med. Inform. Assoc. 2005, 12, 181–199. [Google Scholar] [CrossRef] [PubMed]
- Herajy, M.; Liu, F.; Rohr, C. Coloured hybrid Petri nets for systems biology. In Proceedings of the 5th International Workshop on Biological Processes & Petri Nets (BioPPN 2014), Satellite Event of Petri Nets 2014, Tunis, Tunisia, 23 June 2014; Volume 1159, p. 60. [Google Scholar]
- Cherdal, S.; Mouline, S. A petri net model for a composed biological system. Proceeding of the 5th International Conference on Information & Communication Technology and Accessibility (ICTA), Marrakesh, Morocco, 21–23 December 2016; pp. 1–6. [Google Scholar]
- Koch, I.; Reisig, W.; Schreiber, F. Modeling in Systems Biology: The Petri Net Approach; Springer Science & Business Media: Berlin, Germany, 2011; Volume 16. [Google Scholar]
- Formanowicz, D.; Kozak, A.; Głowacki, T.; Radom, M.; Formanowicz, P. Hemojuvelin–hepcidin axis modeled and analyzed using Petri nets. J. Biomed. Inform. 2013, 46, 1030–1043. [Google Scholar] [CrossRef] [PubMed]
- Martinov, M.; Vitvitsky, V.; Mosharov, E.; Banerjee, R.; Ataullakhanov, F. A substrate switch: A new mode of regulation in the methionine metabolic pathway. J. Theor. Biol. 2000, 204, 521–532. [Google Scholar] [CrossRef] [PubMed]
- Reed, M.C.; Nijhout, H.F.; Sparks, R.; Ulrich, C.M. A mathematical model of the methionine cycle. J. Theor. Biol. 2004, 226, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Reed, M.C.; Nijhout, H.F.; Neuhouser, M.L.; Gregory, J.F.; Shane, B.; James, S.J.; Boynton, A.; Ulrich, C.M. A mathematical model gives insights into nutritional and genetic aspects of folate-mediated one-carbon metabolism. J. Nutr. 2006, 136, 2653–2661. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Sharpnack, J.; Tello, D.; Grajdeanu, P. Cell Metabolism, Methionine and Neurodiseases. 2007. Available online: https://www.researchgate.net/publication/266346273_Cell_Metabolism_Methionine_and_Neurodiseases (accessed on 20 July 2018).
- Duncan, T.M.; Reed, M.; Nijhout, H.F. The relationship between intracellular and plasma levels of folate and metabolites in the methionine cycle: A model. Mol. Nutr. Food Res. 2013, 57, 628–636. [Google Scholar] [CrossRef] [PubMed]
- Martinov, M.; Vitvitsky, V.; Banerjee, R.; Ataullakhanov, F. The logic of the hepatic methionine metabolic cycle. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2010, 1804, 89–96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piazza, M.; Feng, X.J.; Rabinowitz, J.D.; Rabitz, H. Diverse metabolic model parameters generate similar methionine cycle dynamics. J. Theor. Biol. 2008, 251, 628–639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Z.E.; Chen, A.H. Constructing the Methionine cycle and its related disease model with Hybrid Functional Petri Nets. In Proceedings of the Asia Pacific Association of Medical Informatics (APAMI), Taipei, Taiwan, 27–29 October 2006; pp. 24–30. [Google Scholar]
- Matsuno, H.; Tanaka, Y.; Aoshima, H.; Doi, A.; Matsui, M.; Miyano, S. Biopathways representation and simulation on hybrid functional Petri net. In Silico Biol. 2003, 3, 389–404. [Google Scholar] [PubMed]
- Brosnan, J.T.; Brosnan, M.E. The sulfur-containing amino acids: An overview. J. Nutr. 2006, 136, 1636S–1640S. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.W.; Nadeau, M.R.; Smith, D.; Selhub, J. Vitamin B-6 deficiency vs folate deficiency: Comparison of responses to methionine loading in rats. Am. J. Clin. Nutr. 1994, 59, 1033–1039. [Google Scholar] [CrossRef] [PubMed]
- Carson, N.A.; Cusworth, D.; Dent, C.; Field, C.; Neill, D.; Westall, R. Homocystinuria: A new inborn error of metabolism associated with mental deficiency. Arch. Dis. Child. 1963, 38, 425–436. [Google Scholar] [CrossRef] [PubMed]
- Schimke, R.N.; McKusick, V.A.; Huang, T.; Pollack, A.D. Homocystinuria: Studies of 20 families with 38 affected members. JAMA 1965, 193, 711–719. [Google Scholar] [CrossRef] [PubMed]
- Kronenberg, G.; Harms, C.; Sobol, R.W.; Cardozo-Pelaez, F.; Linhart, H.; Winter, B.; Balkaya, M.; Gertz, K.; Gay, S.B.; Cox, D.; et al. Folate deficiency induces neurodegeneration and brain dysfunction in mice lacking uracil DNA glycosylase. J. Neurosci. 2008, 28, 7219–7230. [Google Scholar] [CrossRef] [PubMed]
- Cherdal, S.; Mouline, S. Petri nets for modelling and analysing a complex system related to alzheimer’s disease. In Proceedings of the 31st Annual ACM Symposium on Applied Computing (SAC), Pisa, Italy, 4–8 April 2016; pp. 309–312. [Google Scholar]
- Smith, A.D.; Smith, S.M.; De Jager, C.A.; Whitbread, P.; Johnston, C.; Agacinski, G.; Oulhaj, A.; Bradley, K.M.; Jacoby, R.; Refsum, H. Homocysteine-lowering by B vitamins slows the rate of accelerated brain atrophy in mild cognitive impairment: A randomized controlled trial. PLoS ONE 2010, 5, e12244. [Google Scholar] [CrossRef] [PubMed]
- Miller, A.L. The methionine-homocysteine cycle and its effects on cognitive diseases. Altern. Med. Rev. 2003, 8, 7–19. [Google Scholar] [PubMed]
- Tchantchou, F.; Shea, T.B. Folate deprivation, the methionine cycle, and Alzheimer’s disease. Vitam. Horm. 2008, 79, 83–97. [Google Scholar] [PubMed]
- Refsum, H.; Ueland, P.; Nygård, O.; Vollset, S. Homocysteine and cardiovascular disease. Annu. Rev. Med. 1998, 49, 31–62. [Google Scholar] [CrossRef] [PubMed]
- Potter, J.D. Colorectal cancer: Molecules and populations. J. Natl. Cancer Inst. 1999, 91, 916–932. [Google Scholar] [CrossRef] [PubMed]
- Mattson, M.P.; Shea, T.B. Folate and homocysteine metabolism in neural plasticity and neurodegenerative disorders. Trends Neurosci. 2003, 26, 137–146. [Google Scholar] [CrossRef]
- Eskes, T. Neural tube defects, vitamins and homocysteine. Eur. J. Pediatr. 1998, 157, S139–S141. [Google Scholar] [CrossRef] [PubMed]
- Cherdal, S.; Mouline, S. A Petri Net model to simulate and analyse cerebral folate deficiency and hyperhomocysteinemia effects in Autism Spectrum Disorder. In Proceedings of the 7th International Conference on Sciences of Electronics, Technologies of Information and Telecommunications (SETIT), Hammamet, Tunisia, 18–20 December 2016; pp. 279–284. [Google Scholar]
- Alla, H.; David, R. Continuous and hybrid Petri nets. J. Circuits Syst. Comput. 1998, 8, 159–188. [Google Scholar] [CrossRef]
- Drath, R. Hybrid object nets: An object oriented concept for modeling complex hybrid systems. In Proceedings of the 3rd International Conference on Automation of Mixed Processes (ADPM’98), Reims, France, 19–20 March 1998; pp. 436–442. [Google Scholar]
- Hofestädt, R.; Thelen, S. Quantitative modeling of biochemical networks. In Silico Biol. 1998, 1, 39–53. [Google Scholar] [PubMed]
- Miyano, S.; Matsuno, H. How to Model and Simulate Biological Pathways with Petri nets-A new challenge for systems Biology. In Proceedings of the 25th International Conference on Application and Theory of Petri Nets, Bologna, Italy, 23–25 June 2004. [Google Scholar]
- Li, C.; Nagasaki, M.; Ueno, K.; Miyano, S. Simulation-based model checking approach to cell fate specification during Caenorhabditis elegans vulval development by hybrid functional Petri net with extension. BMC Syst. Biol. 2009, 3, 42. [Google Scholar] [CrossRef] [PubMed]
- Doi, A.; Fujita, S.; Matsuno, H.; Nagasaki, M.; Miyano, S. Constructing biological pathway models with hybrid functional Petri nets. In Silico Biol. 2004, 4, 271–291. [Google Scholar] [PubMed]
- Doi, A.; Nagasaki, M.; Matsuno, H.; Miyano, S. Simulation-based validation of the p53 transcriptional activity with hybrid functional Petri net. In Silico Biol. 2006, 6, 1–13. [Google Scholar] [PubMed]
- Akçay, N.İ.; Bashirov, R.; Tüzmen, Ş. Validation of signalling pathways: Case study of the p16-mediated pathway. J. Bioinform. Comput. Biol. 2015, 13, 1550007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nagasaki, M.; Saito, A.; Doi, A.; Matsuno, H.; Miyano, S. Foundations of Systems Biology: Using Cell Illustrator and Pathway Databases; Springer Science & Business Media: Berlin, Germany, 2009; Volume 13. [Google Scholar]
- Nijhout, H.; Reed, M.; Budu, P.; Ulrich, C. A mathematical model of the folate cycle: New insights into folate homeostasis. J. Biol. Chem. 2004, 279, 55008–55016. [Google Scholar] [CrossRef] [PubMed]
- Michaelis, L.; Menten, M.L. Die kinetik der invertinwirkung. Biochem. Z. 1913, 49, 333–369. [Google Scholar]
- Reed, M.C.; Thomas, R.L.; Pavisic, J.; James, S.J.; Ulrich, C.M.; Nijhout, H.F. A mathematical model of glutathione metabolism. Theor. Biol. Med. Model. 2008, 5, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, H.; Chi, J.; Xing, Y.; Wang, P. Influence of folic acid on plasma homocysteine levels & arterial endothelial function in patients with unstable angina. Indian J. Med. Res. 2009, 129, 279–284. [Google Scholar] [PubMed]










| Biological System | HFPN | ||
|---|---|---|---|
| Element | Symbol | Element | Symbol |
| Principal Metabolite |  | Continuous Entity | 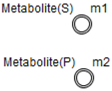 |
| Enzyme | 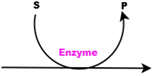 | Continuous Entity |  |
| Reaction | 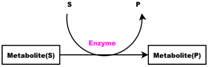 | Continuous Process | 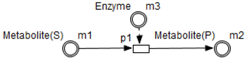 |
| Normal Arc |  | Normal Connector |  |
| Catalysis |  | Test Connector: Catalysis | 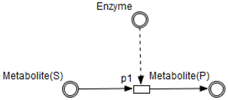 |
| Activator Arc |  | Test Connector: Activator | 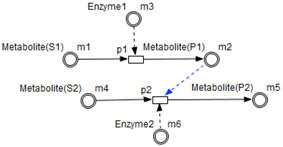 |
| Inhibitory Arc | 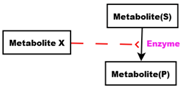 | Inhibitory Connector | 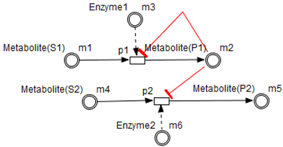 |
| Process | Process Type | Process Rate |
|---|---|---|
| P1 | Discrete | 3 |
| P2 | Continuous | |
| P3 | Continuous | |
| P4 | Continuous | |
| P5 | Continuous | |
| P6 | Continuous | |
| P7 | Continuous | |
| P8 | Continuous | 1 |
| P9 | Continuous | 1 |
| P10 | Continuous | 1 |
| P11 | Continuous | 1 |
| P12 | Continuous | 1 |
| P13 | Continuous | 1 |
| Entity Name | Entity Type | Variable | Initial Value | Value Type |
|---|---|---|---|---|
| Methionine | Continuous | m1 | 3 | Double |
| SAM | Continuous | m2 | 1 | Double |
| SAH | Continous | m3 | 1 | Double |
| Homocysteine | Continuous | m4 | 1 | Double |
| Cystathionine | Continuous | m5 | 1 | Double |
| 5MethylTHF | Continuous | m6 | 1 | Double |
| THF | Continuous | m7 | 1 | Double |
| MATII | Continuous | m8 | 1 | Double |
| METH | Continuous | m9 | 1 | Double |
| SAHH | Continuous | m10 | 1 | Double |
| CBS | Continuous | m11 | 1 | Double |
| BHSM | Continuous | m12 | 1 | Double |
| MS | Continuous | m13 | 1 | Double |
| Connector | Firing Style | Firing Script | Connector Type |
|---|---|---|---|
| c1-c14 | Threshold | 0 | Output Process |
| c15-c32 | Threshold | 0 | Input Process |
| c33-c39 | Threshold | 0 | Input Association |
| c40-c44 | Threshold | 50 | Input Inhibitor |
| Biological Phenomenon | Process | Process Type | Process Rate |
|---|---|---|---|
| Metabolites’ Degradation | P14-P19 | Continuous | mi × 0.0001 |
| Proteins’ Degradation | P20-P25 | Continuous | mi × 0.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherdal, S.; Mouline, S. Modelling and Simulation of Biochemical Processes Using Petri Nets. Processes 2018, 6, 97. https://doi.org/10.3390/pr6080097
Cherdal S, Mouline S. Modelling and Simulation of Biochemical Processes Using Petri Nets. Processes. 2018; 6(8):97. https://doi.org/10.3390/pr6080097
Chicago/Turabian StyleCherdal, Safae, and Salma Mouline. 2018. "Modelling and Simulation of Biochemical Processes Using Petri Nets" Processes 6, no. 8: 97. https://doi.org/10.3390/pr6080097
APA StyleCherdal, S., & Mouline, S. (2018). Modelling and Simulation of Biochemical Processes Using Petri Nets. Processes, 6(8), 97. https://doi.org/10.3390/pr6080097





