Next Article in Journal
Acknowledgement to Reviewers of Processes in 2018
Next Article in Special Issue
Enhanced Lifetime Cathode for Alkaline Electrolysis Using Standard Commercial Titanium Nitride Coatings
Previous Article in Journal
Ultrasonic-Assisted Extraction and Swarm Intelligence for Calculating Optimum Values of Obtaining Boric Acid from Tincal Mineral
Previous Article in Special Issue
Combining Microwave Pretreatment with Iron Oxide Nanoparticles Enhanced Biogas and Hydrogen Yield from Green Algae
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 7
Issue 1
10.3390/pr7010031
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

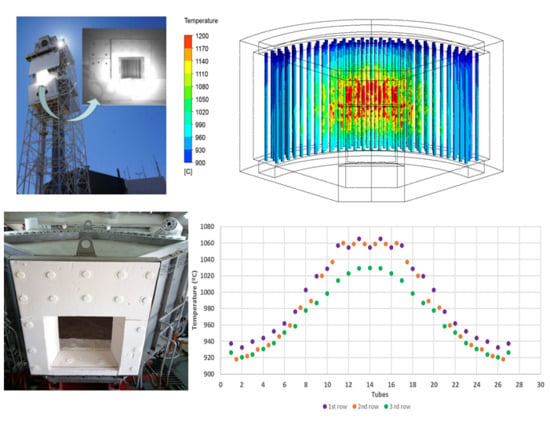
Multi-Tubular Reactor for Hydrogen Production: CFD Thermal Design and Experimental Testing †

by
Elvira Tapia
1,‡,
Aurelio González-Pardo
2,
Alfredo Iranzo
1,*,
Manuel Romero
3,
José González-Aguilar
3,
Alfonso Vidal
2,
Mariana Martín-Betancourt
4 and
Felipe Rosa
1
1
Thermal Engineering Group, Energy Engineering Department, School of Engineering, University of Seville, Camino de los Descubrimientos s/n, 41092 Sevilla, Spain
2
CIEMAT-PSA, Carretera de Senés, S/N Tabernas, 04200 Almería, Spain
3
IMDEA Energy Institute, Avda. Ramón de la Sagra, 3, 28935 Móstoles, Spain
4
ABENGOA Innovación–División de hidrógeno. C/Energía Solar,1 41014 Sevilla, Spain
*
Author to whom correspondence should be addressed.
†
This paper is an extended version of the conference paper published in SolarPACES 2016 International Conference, Santiago de Chile, Chile, 26–29 September, 2017.
‡
Present address: ABENGOA Innovación–División de hidrógeno. C/Energía Solar,1 41014 Sevilla, Spain.
Processes 2019, 7(1), 31; https://doi.org/10.3390/pr7010031
Submission received: 3 December 2018 / Revised: 21 December 2018 / Accepted: 27 December 2018 / Published: 11 January 2019
(This article belongs to the Special Issue Hydrogen Production Technologies)
Browse Figures
Versions Notes

Abstract

This study presents the Computational Fluid Dynamics (CFD) thermal design and experimental tests results for a multi-tubular solar reactor for hydrogen production based on the ferrite thermochemical cycle in a pilot plant in the Plataforma Solar de Almería (PSA). The methodology followed for the solar reactor design is described, as well as the experimental tests carried out during the testing campaign and characterization of the reactor. The CFD model developed for the thermal design of the solar reactor has been validated against the experimental measurements, with a temperature error ranging from 1% to around 10% depending on the location within the reactor. The thermal balance in the reactor (cavity and tubes) has been also solved by the CFD model, showing a 7.9% thermal efficiency of the reactor. CFD results also show the percentage of reacting media inside the tubes which achieve the required temperature for the endothermic reaction process, with 90% of the ferrite pellets inside the tubes above the required temperature of 900 °C. The multi-tubular solar reactor designed with aid of CFD modelling and simulations has been built and operated successfully.
Keywords: solar reactor; hydrogen production; solar receiver; thermal energy; computational fluid dynamics; CFD; model solar reactor; hydrogen production; solar receiver; thermal energy; computational fluid dynamics; CFD; model
Graphical Abstract

Share and Cite

MDPI and ACS Style

Tapia, E.; González-Pardo, A.; Iranzo, A.; Romero, M.; González-Aguilar, J.; Vidal, A.; Martín-Betancourt, M.; Rosa, F. Multi-Tubular Reactor for Hydrogen Production: CFD Thermal Design and Experimental Testing. Processes 2019, 7, 31. https://doi.org/10.3390/pr7010031

AMA Style

Tapia E, González-Pardo A, Iranzo A, Romero M, González-Aguilar J, Vidal A, Martín-Betancourt M, Rosa F. Multi-Tubular Reactor for Hydrogen Production: CFD Thermal Design and Experimental Testing. Processes. 2019; 7(1):31. https://doi.org/10.3390/pr7010031

Chicago/Turabian Style

Tapia, Elvira, Aurelio González-Pardo, Alfredo Iranzo, Manuel Romero, José González-Aguilar, Alfonso Vidal, Mariana Martín-Betancourt, and Felipe Rosa. 2019. "Multi-Tubular Reactor for Hydrogen Production: CFD Thermal Design and Experimental Testing" Processes 7, no. 1: 31. https://doi.org/10.3390/pr7010031

APA Style

Tapia, E., González-Pardo, A., Iranzo, A., Romero, M., González-Aguilar, J., Vidal, A., Martín-Betancourt, M., & Rosa, F. (2019). Multi-Tubular Reactor for Hydrogen Production: CFD Thermal Design and Experimental Testing. Processes, 7(1), 31. https://doi.org/10.3390/pr7010031

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop