Optimization of Reaction Selectivity Using CFD-Based Compartmental Modeling and Surrogate-Based Optimization

Abstract

Mixing is considered as a critical process parameter (CPP) during process development due to its significant influence on reaction selectivity and process safety. Nevertheless, mixing issues are difficult to identify and solve owing to their complexity and dependence on knowledge of kinetics and hydrodynamics. In this paper, we proposed an optimization methodology using Computational Fluid Dynamics (CFD) based compartmental modelling to improve mixing and reaction selectivity. More importantly, we have demonstrated that through the implementation of surrogate-based optimization, the proposed methodology can be used as a computationally non-intensive way for rapid process development of reaction unit operations. For illustration purpose, reaction selectivity of a process with Bourne competitive reaction network is discussed. Results demonstrate that we can improve reaction selectivity by dynamically controlling rates and locations of feeding in the reactor. The proposed methodology incorporates mechanistic understanding of the reaction kinetics together with an efficient optimization algorithm to determine the optimal process operation and thus can serve as a tool for quality-by-design (QbD) during product development stage.

1. Introduction

In chemical synthesis, many important reactions can be accompanied by undesired side-reactions. This leads to wastes and affects product quality. Therefore, incorporating knowledge of mixing can substantially improve reaction selectivity and yield, in addition to enhancing process safety. Furthermore, due to a growing variety of reactors, characterization of mixing has become vital in process development [1,2]. To achieve optimal selectivity and yield, appropriate modeling of the mass transport process in reactors is critical [3]. Nevertheless, owing to the complexity of mass transport in turbulent flow, analyzing mixing remains a difficult problem.

Frequently, mixing in reactor is approximated by residence time distribution (RTD) analysis, where residence time is experimentally measured through a tracer test. This approximation has been proved to work relatively well, however “RTD is not a complete description of structure for a particular reactor or system of reactors” [3]. Therefore, when reaction with high conversion rates are considered, analysis solely based on RTD can lead to significant error [4]. Based on local sensors, RTD characterization of tracer test can be improved by mixing time measurement [5,6]. However, considering potential bias and the requirement for specific equipment for tracer tests, RTD and mixing time measurement have become less preferable comparing to the more resource-effective benchmark reaction method [7]. Therefore, competitive reaction systems have become the standard for mixing analysis [7,8,9]. Among the competitive reaction systems, the “well-documented and highly reliable” [7] Bourne reaction and Villermaux reaction is most commonly adopted [10]. Nevertheless, benchmark reaction tests provide only the input-output relationship, without detailed description of the process dynamics. Therefore, developing optimal process operation experimentally remains challenging.

With rapid advances in computer technology, computational fluid dynamics (CFD) has become a powerful tool to study mixing. Comparing with the experimental methods, it provides detailed understanding of mixing phenomenon in a timely-efficient manner without requiring meticulous choice of equipment and sensors. In reaction engineering, CFD has been employed to study mixing in chemical reactors and bio-reactors. Mixing of liquid-liquid system [11], solid-liquid system [12] or non-Newtonian fluid [13] are studied with CFD, which agrees well with experimental data. In the presence of complex chemical reactions [14] or biological metabolism [15] CFD is implemented to provide detailed understanding of the mass transfer process. Complex hydrodynamics, mass transfer, heat transfer and reaction kinetic can be satisfactorily captured by CFD, making it a powerful tool in process design.

As a result, CFD has been implemented to optimize mixing by improve reactor design. Studies reported in the literature mainly focus on improving geometrical attributes of reactors. Researches that directly integrate detailed CFD simulation with optimization algorithms has successfully improved reactor design [16,17,18,19,20]. Due to the complexity of CFD simulations, the chosen optimization algorithms are often meta-heuristic, such as genetic algorithm (GA) [16,17,18] and particle swarm methodology [20]. They can address complex black-box problems, such as reactor geometry [16,17] or impeller configuration [18], but require a large number of function evaluations, which leads to a large number of computationally expensive CFD runs. To improve the computational efficiency of direct CFD simulations, hybrid methods have been proposed that replace direct CFD evaluation with simpler data-driven models [21,22,23,24,25], which are then integrated with GA. Successful implementation have been reported in the literature that use neural network [22,23], Gaussian process [24] and radial basis function (RBF) [25]. However, building confidence in those data-driven models requires large number of CFD runs, and balancing computational efficiency with accuracy is non-trivial [26].

Apart from improving mixing through optimized design, to the best of the authors’ knowledge, there is no work that improves mixing by optimizing dynamic process operation based on CFD simulations. The main reasons for the limited implementation is the complexity of CFD simulations. To optimize dynamic process operation, more decision variables should be considered. Since GA would suffer from “curse of dimensionality” [27], significantly more CFD runs would be required, leading to increasing computational expense and degrading performance.

In this work, a framework is developed trying to leverage CFD simulations to optimize process operation. Firstly, CFD-based compartmental model is built to replace direct CFD simulations. Comparing to the data-driven models implemented for reactor geometry optimization, compartmental models are finite-volume physical models, which provide satisfactory accuracy while requiring significantly less CFD runs. Secondly, a surrogate-based optimization algorithm using radial-basis function is implemented, which has been proven to be more efficient than GA [28]. This work offers a compact and systematic framework for improving reaction selectivity with a numerically efficient Quality-by-Design (QbD) tool. In a case study, Bourne reaction is employed as a benchmark, which serve as a more explicit quantification for the efficiency of mixing. The proposed framework is compared with process operations optimized based on ideal mixing model, suggesting great improvement by leveraging CFD simulations. By integrating CFD-based compartmental model with surrogate-based optimization, the proposed framework has shown a great potential for fast process development.

2. Integrating CFD-Based Compartmental Model with Surrogate Based Optimization

This section presents the development and implementation of the proposed methodology. Initially, a detail description of flow field in the reactor is generated by a CFD simulation. It should be noted that in stirred tank reactors the flow field are considered independent from chemical reactions. As a result, the fluid dynamics data can be used for different reactions, which could contribute to rapid process design and cost reduction. The result from CFD simulation is used to develop a compartmental model, which would be discussed in Section 2.1. Comparing to direct CFD simulation, computational complexity of compartmental model is significantly reduced. Therefore, the optimal process design can be determined numerically without prohibitive computational expense. The process selectivity is then optimized by integrating the compartmental model with surrogate-based optimization, as will be discussed in Section 2.2.

2.1. CFD-Based Compartmental Model

2.1.1. A Brief Review of Compartmental Model

Compartmental model defines a matrix of perfectly mixed control volumes interconnected by the exchanging mass flux. In this method the reactors are discretized into a set of homogeneous control volumes according to the defined mesh. The volume-averaged variable in all control volumes are solved together to represent the space distribution inside the reactor. Compartmental modeling was regarded as a crude tool to study transport process and only provide basic understandings [29]. However, by incorporating detailed CFD simulation to compartmental model, substantial improvement can be achieved leading to satisfactory agreement with experimental data without loss of computational efficiency [30,31].

Considering the excessive computational and economical expense usually required by CFD simulation, for Chemistry, Manufacturing, and Controls (CMC) development, CFD-based compartmental model have been adopted as computationally cheaper alternative [4,30,32,33,34] In addition to the reduced computational expense, CFD-based compartmental model provides the required simplifications for development work. Unlike CFD, which is not widely available and requires special know-how, CFD-based compartmental model can be easily implemented for different reaction systems based on flow field data determined beforehand. Adjustment in chemical kinetics do not usually require extra CFD simulation, which could save time and reduce cost.

In this proposed methodology, compartmental model is developed from CFD simulation based on the idea outlined by Bezzo et al. [33]. Two key steps are required for model construction: (1) Topological mapping between two models through aggregating CFD cells into compartments. (2) Quantifying mass flux between different compartments. Topology mapping between CFD and compartmental model can be done either manually or automatically. Manual allocation of CFD cells is based on preliminary knowledge of flow field, which can be conducted prior to CFD simulation [15,31,35,36]. Automatic mapping, on the other hand, merges computational cells based on CFD simulation to form meaningful homogeneous control volumes [4,37]. Manual allocation usually leads to simpler mesh structure, which allow for efficient implementation of optimization tools. Therefore, in this work manual allocation is conducted, as will be outlined in sub Section 2.1.3.

2.1.2. Compartmental Model Development

Mixing of particles inside the reactor is described by Equation (1), where c_i is the concentration of species i, N_i represents the mass flux of species i, and R_i denotes the source of species i. Compartmental models are obtained by volume averaging Equation (1) over each predefined compartment V, as described in Equation (2).

$$\frac{\partial C_i}{\partial \mathrm{t}}=-\nabla ·{\mathit{N}}_{\mathit{i}}+R_i,$$

(1)

$$\frac{d}{dx}{{\displaystyle \int }}_V^{ }\overline{C_i}dV=-{{\displaystyle \int }}_V^{ }\nabla ·{\mathit{N}}_{\mathit{i}}dV+{{\displaystyle \int }}_V^{ }{R}_{i}dV.$$

(2)

Adopting the divergence theorem and replacing C_i with the volume-averaged concentration $\overline{C_{\mathit{i},{\mathit{K}}_j}}$, Equation (2) is modified to Equation (3), where V_j is the volume of control volume K_j, and S_j is the surface of control volume K_j. The mass flux N consist of convection and diffusion, where the diffusion is modelled by Fick’s law with diffusion coefficient D. The source term R_i models the homogeneous consumption and generation of species i, which include chemical reactions and micro mixing. Due to the assumption of homogeneous compartments, the volume integral of source term in Equation (5) is modified as follows:

$$V_j\frac{d\overline{C_{i,K_j}}}{dx}+{{\displaystyle \oint }}_{S_j}^{ }{\mathit{N}}_{\mathit{i},{\mathit{K}}_{\mathit{j}}}·\mathit{n}dS={{\displaystyle \int }}_{K_j}^{ }{R}_{i}dV,$$

(3)

$$V_j\frac{d\overline{C_{i,K_j}}}{dx}=--{{\displaystyle \int }}_{S_j}^{ }\mathit{v}·\overline{C_{\mathit{i},{\mathit{K}}_j}}·\mathit{n} dS+{{\displaystyle \int }}_{S_j}^{ }D·\mathbf{\nabla }C·\mathit{n} dS+{{\displaystyle \int }}_{K_j}^{ }{R}_{i}dV,$$

(4)

$${{\displaystyle \int }}_{{\mathit{K}}_j}^{ }{R}_{\mathit{i},{\mathit{K}}_j}=V_j·R_{\mathit{i},{\mathit{K}}_j}.$$

(5)

It should be recognized that the homogeneous assumption depends upon the Damköhler number (Da) in each compartment, which is a strong function of grid size, as will be discussed in sub Section 2.1.3. Moreover, in this work diffusion mass transfer between different compartments are neglected, which is also justified in sub Section 2.1.3 based on an analysis of the Péclet number (Pe). The dominance of convective mass transfer would simplify 4 into Equation (6), where Q_jk denotes the flow rate from control volume j to control volume k.

$$V_j\frac{d\overline{C_{\mathit{i},{\mathit{K}}_j}} }{dt}=-\overline{C_{\mathit{i},{\mathit{K}}_j}}{{\displaystyle \sum }}_k^{ }{Q}_{j,k}+{{\displaystyle \sum }}_l^{ }\left(Q_{l,j}·\overline{C_{\mathit{i},{\mathit{K}}_j}}\right)+V_j·R_{\mathit{i},{\mathit{K}}_j}.$$

(6)

Equation (6) is a finite-volume mixing model parameterized by mass flow rate Q and compartment volumes V. Since CFD is also based on fine-volume models, parameters of this mixing model can be effectively determined from CFD simulations, based on the topology mapping and merging strategy proposed by Bezzo et al. [33].

Firstly, a steady-state CFD simulation should be developed and calibrated to yield a good prediction of flow field inside the reactor. Then the computational cells of CFD mapped to the same compartments are group into ensembles. Cells in the same ensemble are aggregated together, where, the volumes and mass flow rate and summed together to determine the parameters of each compartment. To achieve a good balance between computational complexity and model accuracy, the resolution of the compartmental model is determined based on a grid independence test as will be discussed in sub Section 2.1.3. For illustration purposes, a well-known pair of parallel competitive Bourne reactions is studied. As will be discussed later in the case study, this reaction system is composed of a first-order decay and a parallel second order coupling reaction [38].

2.1.3. Grid Independence

From numerical perspective, compartmental model is an upwind discretization of mass balance equation with finite volume method. Underlying this discretization scheme lies the assumption of homogeneity inside each control volume. Therefore, compartmental model would exhibit higher diffusivity than the true medium. The deviation caused by compartmentalization depends on the system being modelled and the type of discretization that is used.

One heuristic rule is that with higher resolution grid, the discretized model should behave more like the continuous case. However, with increasing resolution, the complexity of the model also increases, which leads to higher computational expenses. Moreover, decreasing grid size would lead to a decreasing Péclet number, which would undermine the assumption of ignoring diffusion mass transfer. Therefore, a grid independence analysis should be conducted to find the optimal grid density to map the CFD data to compartmental model.

In this work the grid independence test is performed in two steps. First the Damköhler number (Da) and Péclet number (Pe) are analyzed, as suggested in Equations (7) and (8), which are critical to justify the compartmentalization of model discussed in sub Section 2.1.2.

$$\mathrm{Da}=\frac{k_1{C}_A+k_2{C}_b{C}_A}{u{C}_A/L}<1,$$

(7)

$$\mathrm{Pe}=\frac{Lu}{D}>1.$$

(8)

This analysis determines the lower and upper bounds of length scale for the compartments, which could serve as a starting point for the grid independence test. Then the initial choice of length scale is improved in an iterative manner. Simulations based on compartmental models with decreasing length scale are tested. When the simulation results are no longer changing with the increasing grid density, the model resolution can be considered as sufficient.

It should be mentioned that the optimal grid density depends on reaction kinetics. If the time constant of chemical reactions is significantly larger than that of mixing, this process could be considered mixing-insensitive and perfect mixing assumption could be adopted without harming model precision. By contrast, for fast reaction, the deviation caused by perfect-mixing assumption could be significant, which require higher resolution. If the characteristic time scale of reaction is in orders of magnitude less than micro-mixing, which is in the order of 10⁻³ s [11], micro-mixing would dominate chemical reaction. As a result, the rate law of chemical reaction should be replaced with micro-mixing models. Although for different reaction kinetics we can use the same steady state solution from CFD, if new reaction kinetics are used, grid independence test should be conducted with the updated model.

2.2. Surrogate-Based Optimization

2.2.1. A Brief Review of Surrogate-Based Optimization

Surrogate-based optimization have been the focus of interest in the derivative-free optimization literature. Commonly seen in science and engineering studies are complex computer simulations and experiments conducted to gain understanding of systems. As a result, for these problems derivative information is either unavailable or prohibitively hard to get, making it impossible to implement deterministic optimization methods efficiently [39]. Therefore, there is a high interest in developing methods to handle the optimization problems where limited or noisy information is available [40].

Surrogate-based optimization use surrogate models, which are simpler models that can mimic complex phenomenon, to guide the search in derivative-free optimization problems. Since surrogate models are computationally less demanding, surrogate-based optimization is a good compromise between describing the complex process and remaining computationally feasible. It has been demonstrated that surrogate-based optimization displays superior performance for derivative-free optimization problems [41]. Most popular surrogate models implemented for optimization methods are RBF [42,43,44,45,46] and Kriging [47,48,49,50,51], due to their capability to provide prediction uncertainty. Artificial neural networks (ANN) have excellent fitting characteristics with low complexity, therefore implementations of ANN for surrogate-based optimization (SBO) is popular for various engineering applications [22,52,53,54].

SBO works in an iterative manner. In the initial step, several sampling point are chosen, and an initial surrogate model is built based on function evaluation at those sampled points. Then new sampling points are determined by evaluating the surrogate model. At new sampling point, the original model is evaluated and the surrogate model is updated. This process is conducted iteratively until a stopping criterion is met, and the best design point is chosen. In this work, the mixed-integer optimization problem is solved with SBO based on the work of Müller [55].

2.2.2. Problem Formulation

In this work, the location and rate of feeding are optimized to improve reaction selectivity. Due to the perfect mixing assumption of control volumes, feeding location is represented by the index of compartment it resides at. It is worth noting that while the feeding location should be fixed throughout the process, the feeding rate could change dynamically. Therefore, by taking advantage of the extra degree of freedom through adopting a changing feeding rate, reaction selectivity could be further improved comparing to a fixed rate feeding, as will be discussed in Section 3.5.2. Dynamic profile of feeding rate is defined by splitting the whole process time into N_s discrete feeding stages. Feeding rate is kept constant in each stage, but different feeding rate are employed for different stages. Each feeding stage m is specified by its duration t_m and the adopted feeding rate f_m, which are not defined a priori, instead they are determined by solving an optimization problem.

In order to solve for the optimal operating policy, reaction selectivity should be quantified based on analyzing product distribution. The most intuitive definition is by segregation index, which is based on the ratio of raw material consumed by the desired product to the total raw materials injected. This method was widely adopted in previous work [2,56,57], where the influence of feeding rate was not investigated. However, adopting segregation index as an objective function in this work could lead to trivial solutions, due to the fact that feeding rate usually contributes monotonically to product ratio. Without considering the economics of the process, solely focusing on the product ratio would lead to unsatisfactory process design. Thus, it is recommended to use revenue as a way to capture and optimize reaction selectivity. To maximize revenue of chemical processes, the optimization problem is defined as followed.

$$Maximiz{e}_{ n,t_i,f_i}\left(\sum P_R{y}_R-\sum P_A{y}_A\right),$$

(9)

Subject to:

$$\left[y_R,y_A\right]=\mathit{\phi }\left(n,t_1,f_1,t_2,f_2,\dots ,t_{N_p},f_{N_p}\right),$$

(10)

$$\sum t_m=\mathrm{T}, \forall m=1,\dots ,N_s,$$

(11)

$$t_m,f_m\ge 0, \forall m=1,\dots ,N_s,$$

(12)

$$n\in \left[0,N_c\right],$$

(13)

where P_R denotes the price of desired product R while y_R denotes its yield. P_A represents the unit cost of raw material A and its consumption is denoted as y_A. Both y_R and y_A are calculated through the simulation φ based on the compartmental model. Addition point n and addition rate profile which is defined by t₁, f₁, t₂, f₂…t_Ns, f_Ns are parameters of this simulation. The first set of constraints describe the simulation based on the compartmental model. The second constraint represents that the total time span of all stages is pre-defined as T.

Notice that the number of stages is introduced as a parameter instead of decision variable. This is based on the difficulty of penalizing the monotonic increase of the number of stages. By allowing extra degrees of freedom, an increasing number of stages is always preferred. Reaction selectivity would always benefit from higher degree of freedom provided by the increasing N_p, unless computational expense of solving this optimization problem is taken into consideration. However, this is beyond the scope of this paper. The duration of process T is defined as a parameter, which is usually determined in the production scheduling stage. It is recommended to define T similar to the timescale of mixing in mixing controlled processes to maximize time efficiency of reactors.

3. Case Study

In this section, a case study of a semi-batch process inside a dual-impeller stirred tank reactor is studied. The duration of the whole process is 150 s, in which a fed-batch process is analyzed and optimized. A well-known pair of competitive reactions [38] is introduced to study the influence of mixing on reaction selectivity. The overall objective for the optimization problem is to maximize process productivity, which is defined as the revenue from selling the products minus the total cost of raw materials injected. In this case study, process designed according to CFD-based compartmental model and perfect-mixing model are compared to illustrate the effectiveness of this methodology. Furthermore, constant feeding rate design is compared with time-varying feeding rate to demonstrate that this framework can further improve reaction selectivity by enabling dynamic design.

3.1. Reactor Setup

This study was carried out in a 74 L baffled stirred vessel agitated with a Rushton impeller and a pitched blade turbine, as illustrated in Figure 1. The diameter of the vessel is 0.5 m, and the liquid level is 0.4 m from the bottom of the vessel. The Rushton impeller is assembled 0.14 m below the pitched blade turbine, whose blade angle is 45°. The agitation system is operated at 12 rpm anticlockwise, which drives fluid downwards from the pitched blade turbine to the Rushton impeller.

3.2. Chemical Kinetics

To study the influence of mixing on reaction selectivity, a well-documented pair of parallel competitive Bourne reactions is integrated. This reaction system is composed of a first-order decay and a parallel second order coupling, where A is a diazonium salt (diazotized 2-chloro-4-nitroaniline) and B is pyrazolone (4-sulphophenyl-3-carboxypyrazol-5-one). R denotes the desirable product which is a dyestuff, and S is the unwanted product of decomposition. The rate constants at 40 °C are k₁ = 10⁻³ s⁻¹ and k₂ = 7000 m³ kmol⁻¹ s⁻¹ at a PH = 6.6 [38]. Both reactants are dissolved in aqueous solution.

$$\mathrm{A}\stackrel{k_1}{\to }\mathrm{S},$$

(14)

$$\mathrm{A}+\mathrm{B}\stackrel{k_2}{\to }\mathrm{R}$$

(15)

The vessel is initially charged with pyrazolone solution with a concentration of 1 × 10⁻³ M. diazonium solution is added into the stirred tank in a semi-batch manner, the concentration of which is 7.4 × 10⁻¹ M.

In this reaction system, the advantage of defining objective function in the form of productivity is pronounced. Considering that the desired reaction happens faster than side reactions, infinitely slow feeding would always be preferred if we want to maximize the ratio between desired product and side product. Based the time scale of mixing, the duration of process is set as 150 s.

3.3. Flow Field Simulation

CFD simulation is adopted to solve for velocity field inside this reactor based on the physical property of the solvent. The influence of the feeding pipe over the flow pattern is ignored. Since the flow rate of injection pipe is 10² order smaller than that of the bulk flow inside the reactor, influence of reagent injection over the flow pattern is ignored.

A steady state CFD simulation is conducted with the commercial code of Ansys Fluent 16.0 [58]. The Reynolds-Averaged-Navier-Stocks (RANS) equation was numerically solved with multi-reference frame (MRF) method. To close the equations, k-epsilon turbulence model with standard wall functions was adopted. The velocity field is shown in Figure 2.

It should be noted that it is necessary to calibrate CFD simulations so that can be confidently utilized. Since this case study is used for demonstration purposes, due to the lack of experimental data, validation of the numerical simulation is not conducted. This will be addressed in future work where this method is applied.

3.4. Compartmental Modeling and Grid Independence Test

To develop compartmental models from steady state CFD simulation, computational cells extracted from CFD are aggregated based on a predefined grid. The grid is defined by evenly dividing the reactor in radial, axial and angular directions. The grid density of each direction is determined based on the grid sensitivity test proposed in Section 2.1.3.

To justify the perfect-mixing assumptions in each compartment, local Damköhler number (Da) is analyzed. As suggested Figure 2, the bulk velocity inside the stirred tank is in the order of 10⁻² m/s. Based on Equation (7), the upper bound of length scale in each compartment should be 1 m. Furthermore, to justify neglecting diffusive mass transfer, Péclet number (Pe) is analyzed according to Equation (8). Since diffusion coefficient in aqueous solutions are in the order of 10⁻⁹ m²/s, the lower bound of compartment length scale is 10⁻⁷ m. It can be concluded that since in single phase turbulent flow convective mass transfer rate is usually several orders of magnitude higher than that of diffusion, compartmental model can be safely adopted in most single phase stirred tank reactors.

Starting from the upper bound indicated by the analysis of Damköhler number, length scale of the compartments is decreased to test the optimal grid density as discussed in Section 2.1.3. In this work, grid independence test is performed by simulating the injection of diazonium at the top free surface of liquid near the wall. Considering that the injection should be fast enough to show mixing effect, but not excessively fast so that the pyrazolone is instantly depleted and the mixing-sensitive coupling is dominated by the decaying, the feeding rate of diazonium solution is set as 0.5 mL/s, scaled from the work of Nienow [38]. The distribution of different chemical species at the end of process is predicted and monitored. The total number of compartments used for the grid sensitivity test varied from 384 (8 × 8 × 6: axial × radial × angular) to 2352 (12 × 14 × 14). The predicted amount of chemical species varies with the number of compartments and approaches asymptotic values as shown in Figure 3. In good agreement with the scaling analysis, convergence is achieved with 1920 (12 × 16 × 10) compartments for all species, which corresponds to Da < 0.1. For fast model development, Damköhler number can served as an efficient criterion for defining grids [30]. Further results presented in this paper are based on this discretization scheme.

3.5. Optimization and Results

The overall objective for the optimization problem is to maximize process productivity, which is defined based on the price of different materials. In this case study the price of desired product is assumed to be ten times as much as the price of diazonium, which is 10⁴ $/mol. The prices have profound influence on the optimal operating policy. Feeding points are defined with 3 integer variables, representing the corresponding radial, axial and angular index.

The optimization algorithm is first solved for the optimal static operating condition in which reagent is injected in a constant rate. To further improve the process productivity, dynamic operating conditions where the feeding rate changes dynamically are studied and optimized. Dynamic policies comprised of 2 and 3 feeding stages are discussed. Furthermore, by optimizing process design with perfect-mixing assumption, traditional design is compared with this proposed methodology.

3.5.1. Optimal Location of Feeding

In this section, the influence of feeding location on mixing and reaction selectivity is studied. Two operating conditions with different feeding locations are compared; one is at the bottom corner of the reactor while the other one is at the tip of Rushton impeller. The feeding rate (1 mL/s) is kept constant throughout the simulation. In Figure 4 the yield trajectories of desired product are displayed when different feeding locations are adopted. Considering that stronger convective flow presents near impellers, in industry the injection point is usually placed in that region. Consistent with this empirical rule, this simulation suggests that feeding at the corner of the reactor significantly hindered the progress of reaction.

The location for feeding is then numerically optimized with the proposed compartmental model. As suggested in

Table 1. Comparison of optimal feeding location for (a) constant rate feeding (b) two-stage dynamic feeding policy and (c) three-stage feeding policy.

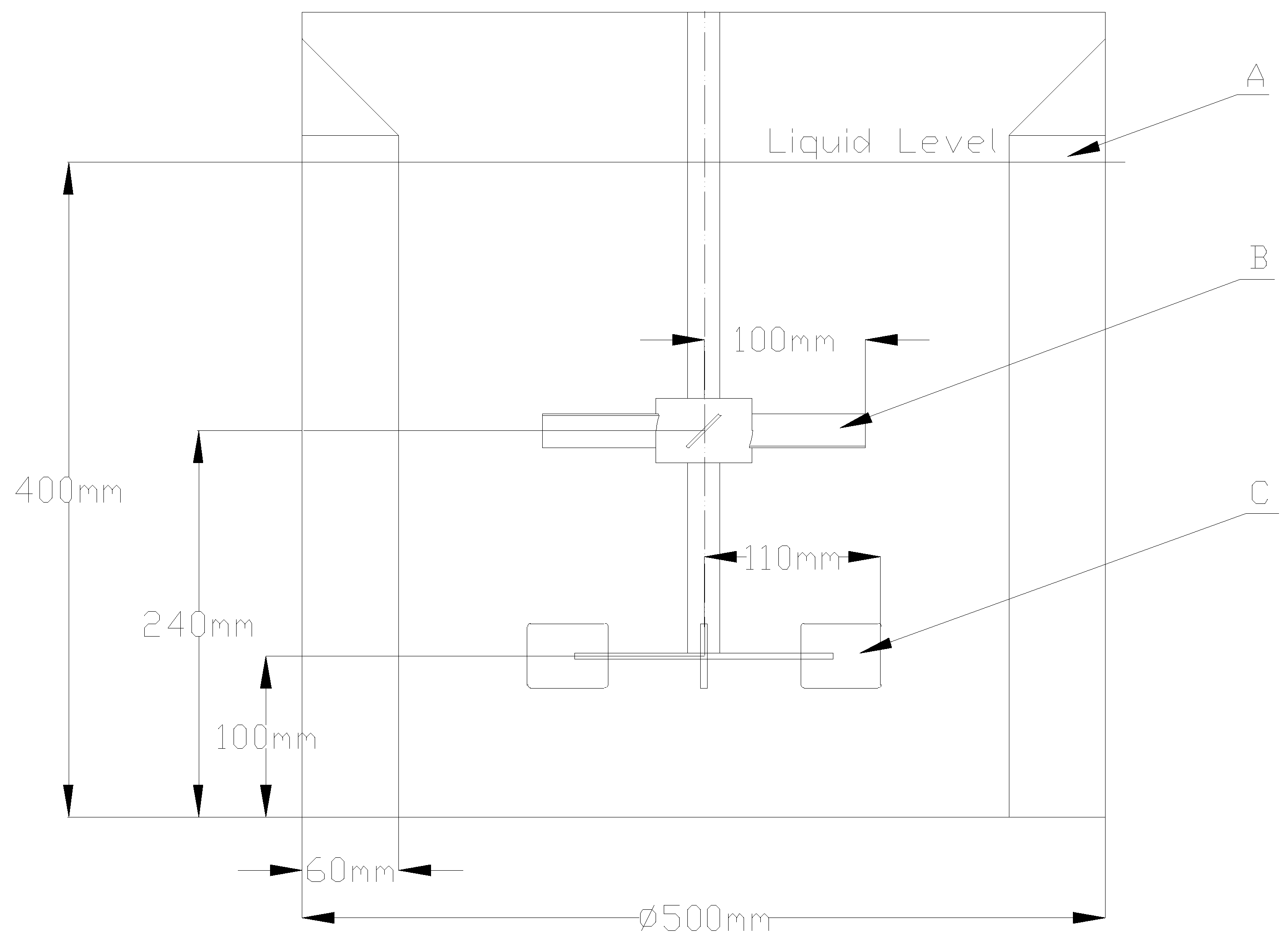
Reagent Injection Policy	Optimal Injection Location
	Height (m)	Radial Position (m)
Constant Rate Feeding	0.1–0.13	0.22–0.25
Two-stage Dynamic Feeding	0.1–0.13	0.22–0.25
Three-stage Dynamic Feeding	0.1–0.13	0.22–0.25

, it was found that irrespective of the number of stages, the maximum productivity is reached when reagents are injected at the tip of Rushton impeller, which suggests a higher mixing efficiency.

3.5.2. Optimal Rate of Feeding

The optimal feeding rate profiles determined for different reagent injection policies are illustrated in Figure 5. It can be concluded that the proposed methodology favors a decreasing feeding rate profile, which leads to an increased process productivity. The reason behind this productivity boost is studied through process dynamics. As illustrated in

Table 2. Comparison of optimal process productivity when (a) constant rate feeding (b) two-stage dynamic feeding policy and (c) three-stage feeding policy are adopted.

Reagent Injection Policy	Optimal Process Productivity ($)
Constant Rate Feeding	6162.90
Two-stage Dynamic Feeding	6410.43
Three-stage Dynamic Feeding	6411.76

, approximately 4% increase in process productivity is achieved by implementing a dynamic operation.

Simulated trajectories of chemical species when different injection policies are employed is illustrated in Figure 6. It is suggested that through employing dynamic policies, the yield of desired product is not significantly enhanced (Figure 6c), which can be explain by the way we formulate this problem. Since the price of the desired product is 10 times as high as the price of diazonium, through the effort to maximize the overall profit, sufficient diazonium is fed to exhaust pyrazolone, which lead to similar yield of the product.

Nevertheless, dynamic feeding rate can improve process productivity through reducing the waste of raw material. As suggested in Figure 6a, considerable amount of diazonium is wasted if constant rate feeding policy is adopted. When reactant is fed at a constant rate, with the consumption of pyrazolone, diazonium would inevitably accumulate faster, which lead to material waste that compromises economic performance. By adjusting feeding rate as pyrazolone is deleted, maximum process profit can be achieved.

3.5.3. Traditional Process Design with Perfect-Mixing Assumptions

To illustrate the improvement of reaction selectivity by implementing this proposed methodology, perfect-mixing model is studied and compared with compartmental model. The same optimization algorithm is applied to the process dynamics model developed under perfect mixing assumption. Specifically, in this section, three-stage dynamic feeding rate is considered.

Table 3. Comparison between optimal operating conditions solved with perfect mixing model and the proposed methodology.

Methodology	Simulated Process Productivity ($)
Perfect-mixing Model	6162.90
CFD-based Compartmental Model	6410.43

shows the simulated process productivity when different methodologies are employed. It can be concluded that by capturing the heterogeneity with CFD-based compartmental model, significant improvement to process productivity could be achieved. The reason behind this productivity boost is studied through process dynamics, as shown in Figure 7 and Figure 8.

Optimal feeding rate profiles determined with different methodologies are illustrated in Figure 7. It is suggested that process design based on perfect-mixing assumption would lead to faster feeding at earlier period of process. Therefore, a high quantity of diazonium is accumulated in the earlier stage of process (Figure 8a). As a result, the undesired decomposition of diazonium is accelerated, which compromise reaction selectivity (Figure 8d). Moreover, without considering the insufficient consumption of pyrazolone due to imperfect mixing, the overall yield of desired product is hindered, which further reduced product productivity.

4. Discussion

Mixing in turbulent flow can significantly influence reaction selectivity, therefore systematic analysis of mass transfer inside reactors is crucial for process design. Despite the increasing computational power available for gaining understanding of the mixing process, in-silico process design can still be inefficient in time and cost. In this proposed framework, by replacing repetitive dynamic CFD simulation with compartmental model, process design can be conducted in a timely and economically more efficient manner. Moreover, in this work surrogate-based optimization is implemented to numerically optimize process productivity. Comparing to genetic algorithm, which is most widely adopted in engineering design, surrogate–based method requires less simulations to find the optimal process design. As a result, the overall time efficiency can be significantly improved.

Rößger and Richter [25] have thoroughly compared state of the art CFD-based optimization methods based on a 2-parameter design problem. For that specific problem it has been demonstrated that direct optimization based on CFD simulation would require 1000 CFD simulations, which is computationally prohibitive. Hybrid methods based on data-driven models can reduce the required number of CFD simulations. However, as have been discussed, a large number of simulations are required to sufficiently train the data-driven model and prevent over-fitting. The reported computational time is 6.5 h running parallel on a 20-core Intel Xeon E5 V2 2.8 GHz processor.

In this manuscript, to optimize the process operation, 8 decision variables are considered. By implementing an efficient iterative SBO algorithm, 150 iterations are sufficient for the algorithm to converge to a good solution. Moreover, since each iteration is based on the compartmental model, which only require a single CFD simulation to construct. As presented in

Table 4. Comparing computational expense between the proposed methodology and direct CFD simulation.

Methodology	Computational Expense for One Simulation (s)
Dynamic CFD simulation	104
CFD-based Compartmental Model	70

, single simulations were performed to determine the computational effort for one design evaluation. The overall computational time is 3 h, running on a single-core of an Intel Xeon E5 V3 workstation. It can be concluded that by implementing CFD-based compartmental modeling, significant time saving could be achieved if same hardware system is applied. In active pharmaceutical ingredient (API) plant design where a large number of simulations are conducted, computational expense could be reduced from weeks to h through the implementation of the proposed methodology. Moreover, considering that CFD is not freely available and requires special know-how, by cutting back dynamics CFD simulations, implementing compartmental modeling is economically beneficial. This approach has shown a good potential to characterize mixing in all the reactors in an API plant.

Despite the reduced model complexity, in this work the grid density is determined so that inhomogeneity inside reactor is sufficiently captured. Comparing to traditional process design strategies which are based on perfect-mixing assumption, better reaction selectivity could be achieved through compartmental model. As has been discussed in sub Section 3.5.3, by replacing traditional process design strategy with this proposed compartmental model, more than 10% increase in process profit has been achieved (

Table 5. Comparison between optimal operating conditions solved with perfect mixing model and the proposed methodology.

Methodology	Simulated Process Productivity ($)
Perfect-mixing Model	5713.18
Compartmental Model (constant rate)	6126.90
Compartmental Model (dynamic rate)	6411.76

).

Furthermore, this proposed framework allows the design of dynamic operations. As illustrated in sub Section 3.5.2, by adapting feeding rate in time to account for the depletion of raw materials, material waste can be substantially reduced, which in turn leads to improved process productivity. Considering that for complex reaction networks commonly encountered in organic synthesis, process dynamics could be very complicated. By enabling the design of dynamic operations to fit the evolving chemical processes, this proposed framework has exhibited a great potential of productivity improvement.

5. Conclusions

CFD is a powerful tool to study mixing in chemical processes, and as such it has been applied widely for numerical optimization of reactor designs. Nevertheless, implementation of CFD to improve mixing through optimization of process operation is limited. A key reason is the computational complexity of CFD models. Even though some data-driven models are used to replace CFD to reduce time expense, to build confidence in the data-driven models requires large amount of CFD simulation. The implementation of meta-heuristic algorithms further increased the computational expense.

This paper has shown possible ways to address the inherent difficulty with two improvements. First, instead of using data-driven models to represent CFD simulation, compartmental model is implemented. Since compartmental model are built based on first-principle mass balance equations, it requires significantly less CFD simulations to drive, making it a better compromise between computational complexity and model accuracy. Second, GA is replaced with surrogate-based optimization based on RBF, which has been proven to be more efficient than GA. It should be noted that this surrogate-based optimization algorithm does not give global optimality guarantees, same as GA. The goals should be to find “good” or near optimal solutions when enough resources are provided.

The surrogate-based compartmental model optimization presented a compact and efficient structure, which can be easily implemented in other scenarios. Since in compartmental model space is discretized, which leads to mixed-integer nonlinear programing problems, surrogate-based optimization is an efficient way to address it. Moreover, compartmental model is built based on steady-state hydrodynamic solution from CFD, which is independent from models inside each compartment. Therefore, changing models in compartments does not require extra CFD simulations.

The proposed methodology allows for dynamic process operation design, which has shown a great potential of productivity improvement. Moreover, dynamic optimization of process operation improves process flexibility and agility to adjust to a more dynamic market. Finally, the developed simplification of complex transport model has the potential for advanced process monitoring and control for reactors with limited instrumentation, such as single-use bioreactors and fermenters.

It should be noted that, to leverage the result of CFD simulation, compartmental models are constructed based on steady-state hydrodynamic solution. However, this simplification is based on the assumption that the flow field is independent from chemical reaction. This assumption would limit the application of the proposed method in reactive flows. In addition, experimental calibration of CFD simulation is necessary build confidence in the predictive ability of the proposed methodology.