The Effect of Fines on Hydraulic Conductivity of Lawrencepur, Chenab and Ravi Sand

Abstract

The amount of fines in sand greatly influence the permeability of sandy soils. Thus, this research was conducted to study the effect of plastic and non-plastic fines on the permeability of three types of sands (Lawrencepur sand, Chenab sand and Ravi sand). For this purpose, plastic and non-plastic fines were collected from different location of Lahore. Samples were prepared by mixing plastic and non-plastic fines into each type of sand separately, in amounts ranging from 0% to 50% with increments of five percent. Overall 63 samples were prepared. Sieve analysis and hydrometric analysis were performed to obtain particle size distribution for each sample. Atterberg’s limits were also determined and each sample was classified according to the Unified Soil Classification System (USCS). Compaction tests were performed on all samples as per the procedure in a standard Proctor test. The test samples were compacted in permeability molds with optimum moisture contents to obtain the density, as per a standard Proctor test. Hydraulic conductivity tests were performed on all sixty-three samples using a constant head permeameter and a falling head permeameter. Permeability results were plotted against the percentage of fines added. It was noted from the curves that the permeability of sand-fine mixtures shows a decreasing trend with the addition of fine contents. A few trials were performed to formulate a correlation. Validation of the correlation was performed with the results of 52 data sets from the field. Finally, the devised correlation was compared with three empirical equations proposed by Mujtaba, Kozeny–Carman and Hazen.

1. Introduction

Permeability is an important physical property of soil whose understanding is essential in settlement, seepage and stability analyses [1,2]. The stability of structures depends to a large degree on the interaction of the said soil with water, or in other words, the ability of water to flow through the soil [3,4]. Moreover, in-depth understanding of soil permeability is needed to estimate the quantity of seepage under and through dams, levees and embankments etc. It also helps to plan dewatering methods to facilitate underground construction [5]. Furthermore, many dam failures have occurred due to insufficient geotechnical and geological investigations. The failure due to seepage through a dam body and/or foundation accounts for almost 30% of total failures [6].

While studying the soil properties, D represents the diameter of particles, and D50 means a cumulative 50% point of diameter (or 50% pass particle size); D10 means a cumulative 10% point of diameter. Numerous relationships between the permeability and grain size distribution indices (like uniformity coefficient, coefficient of gradation, median grain size (D50) and effective grain size (D10)) of the soil have been reported, such as those in Hazen [7], Zunker [8], Carman [9], Burmister [10], Michaels and Lin [11], Olsen [12], Mitchell et al. [13] and Wang and Huang [14]. Lately, Alyamani and Sen [15], Koltermann and Gorelick [16], D’Andrea and Boadu [17], Chapuis [18], Sinha and Wang [19] and Cote et al. [20] established different models to corelate the hydraulic conductivity of soils with their index properties. The hydraulic conductivity has been discussed with sand as well [21], focusing on grain size of soils [22]. However, equations based on grain size distribution do not yield good results for clayey soils and soils with effective grain sizes greater than 3 mm [23]. The presence of grains of extreme-size also produces inaccurate predictions of soil permeability. The prediction of permeability of well-graded soils is particularly difficult due to the void-filling trend of various-sized particles [24]. On the other hand, laboratory and field tests have their limitations and weaknesses, such as the variation of permeability in horizontal and vertical directions in soils [25]; disturbances in extracted samples and how closely they represent field conditions [26,27]; and costly and time-consuming field pumping tests [27].

Silica fume was used to improve the qualities of clay used as clay liners. It was observed that it reduced the plasticity index (from CH to CL), permeability and swelling pressure considerably and increased the compressive strength [28]. Two types of silts, fine sands and coarse sands were mixed with varying amounts of commercial bentonite, and hydraulic conductivity was determined with a consolidometer permeameter. It was found that when bentonite was mixed with coarser material, the hydraulic conductivity (log) changed linearly with void ratio [1]. The permeability of dune sand was greatly affected and reduced to 10⁻⁸ cm/s from 10⁻⁴ cm/s with the addition of 10% bentonite [29].

Shear strength and permeability are two important characteristics desirable for almost all geotechnical projects. In many cases, these two are required concurrently, meaning these should be attained at maximum dry density (MDD) and optimum moisture content (OMC) of soil. As laboratory tests for determining permeability and shear strength are time-consuming, it is desirable to devise models to predict compacted soil’s permeability based on the index properties of soils. Efforts have been made to relate these important parameters with the indices of soils, such as grain size distribution and plasticity characteristics [5].

Pakistan is a vast country having large plains. Rivers (Indus, Chenab, Jhelum, Ravi, Bias and Sutlej) along with other tributaries pass through these plains. Sands of different gradations are encountered in these rivers and are widely used in construction works. The areas near the rivers are regularly subjected to the erosive action of river flow, especially during flood seasons, also causing damage to the river training works along the rivers and other infrastructure. In most cases, a need arises to modify the properties of riverbed materials by mixing these with other, locally available, cheaper materials. In this context, the predicted permeability (hydraulic conductivity) values of these sands mixed with different proportions of fines will be very helpful. Thus, in this research sand samples from Chenab, Lawrencepur and Ravi rivers were used. The two fines (plastic and non-plastic) were added to each type of the sand separately to prepare representative samples on MDD and OMC determined through the standard Proctor test, and permeability tests were executed. The results were analyzed, and a correlation was developed to predict permeability values from the given parameters. Finally, the correlation developed was compared with three other permeability correlations.

2. Materials and Methods

Three types of sands (quartz as main mineral) were collected from Chenab, Lawrencepur and Ravi rivers. These are the main and the most common type of fine aggregates used in various civil engineering projects in Pakistan [30]. Plastic and non-plastic fines are predominantly clays and silts respectively, and were collected from different localities of Lahore, Pakistan. Chenab, Lawrencepur and Ravi sands are designated as CS, LS and RS respectively, in the following discussion. Furthermore, PF represents plastic fines and NPF represents non-plastic fines. PF were collected from near Expo Centre Lahore, whereas NPF from the Habanspura area of Lahore.

All sands and fine samples were separated from vegetation, clods and other materials of larger sizes. Larger sizes in PF and NPF were broken into small fractions. All materials were then passed through sieve number 4. Each PF and NPF were added separately to each type of sand, ranging from 0% to 50% of the total weight of sample. Overall 63 samples were prepared and following tests were performed in the laboratory:

(a)

Grain size analysis (ASTM D-422);

(b)

Standard Proctor test (ASTM D-422);

(c)

Atterberg limits (ASTM D-4318);

(d)

Constant head permeability test (ASTM-D 2434);

(e)

Falling head permeability test.

3. Results and Discussion

3.1. Grain Size Analysis

The gradation curves of CS, LS and RS are given in Figure 1, along with curves of NPF and PF. The LS was well graded when compared to CS and RS, whereas RS was the most uniformly graded and CS lies somewhere between the two. Understandably, the curve of PF is on the finer side of the curve of NPF. Gradation curves were drawn for all 63 samples and observations were made to calculate the uniformity coefficient (C_u) and coefficient of gradation (C_c). Consistency limits (liquid limit and plastic limit) were determined for the soil samples attaining some plasticity due to the addition of fines. All samples were then classified according to Unified Soil Classification System (USCS). The median grain size (D₅₀, diameter corresponding to 50% finer) varied between 0.01 and 0.9 mm, whereas the effective grain size (D₁₀) varied from 0.005 to 0.33 mm. The gradation of all samples is not shown here due to a very large number of curves, though the observations from the gradation curves, consistency limits and soil symbols of all the samples are listed in

Table 1. Data from gradation curves, consistency limits and soil symbols of all the samples.

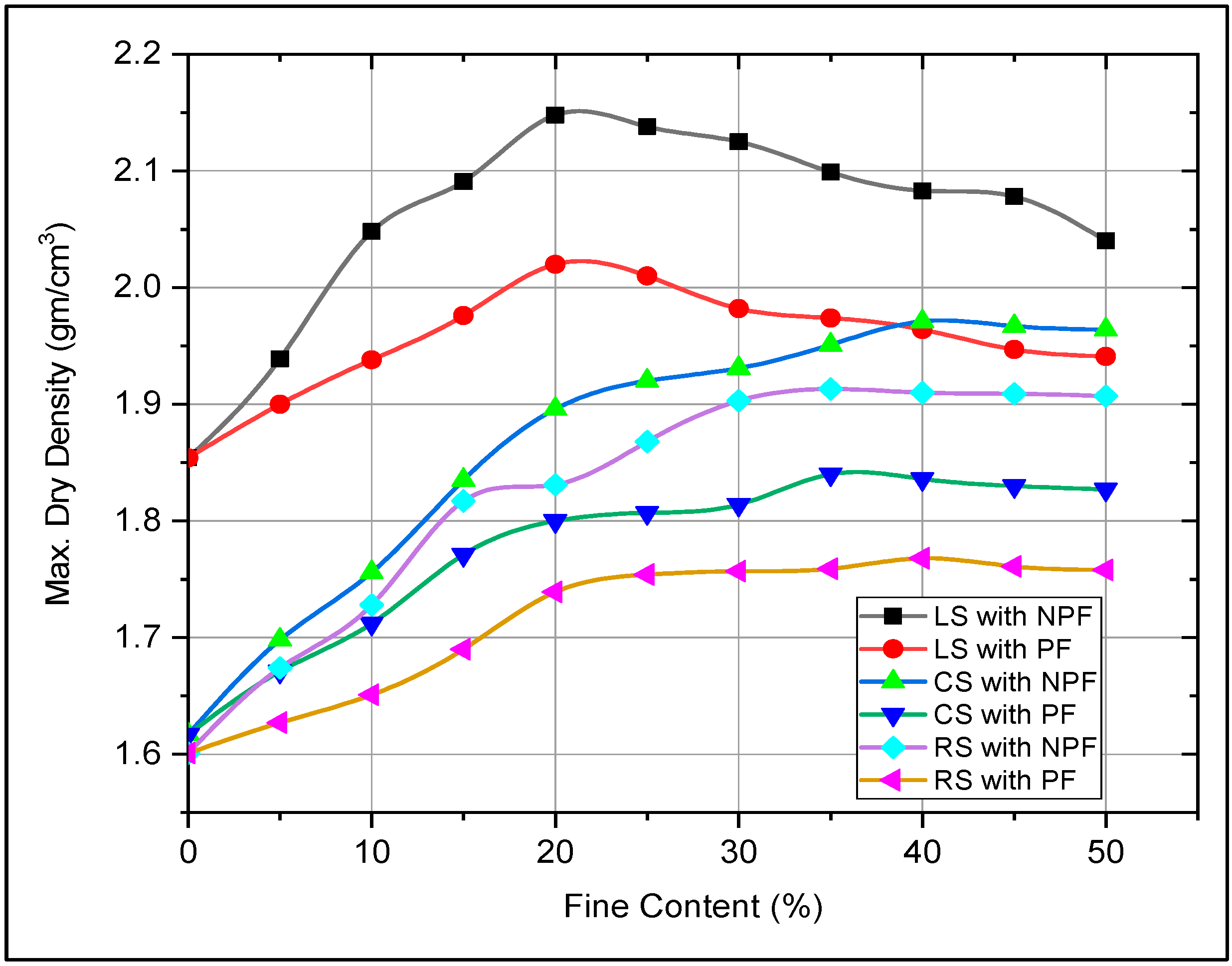
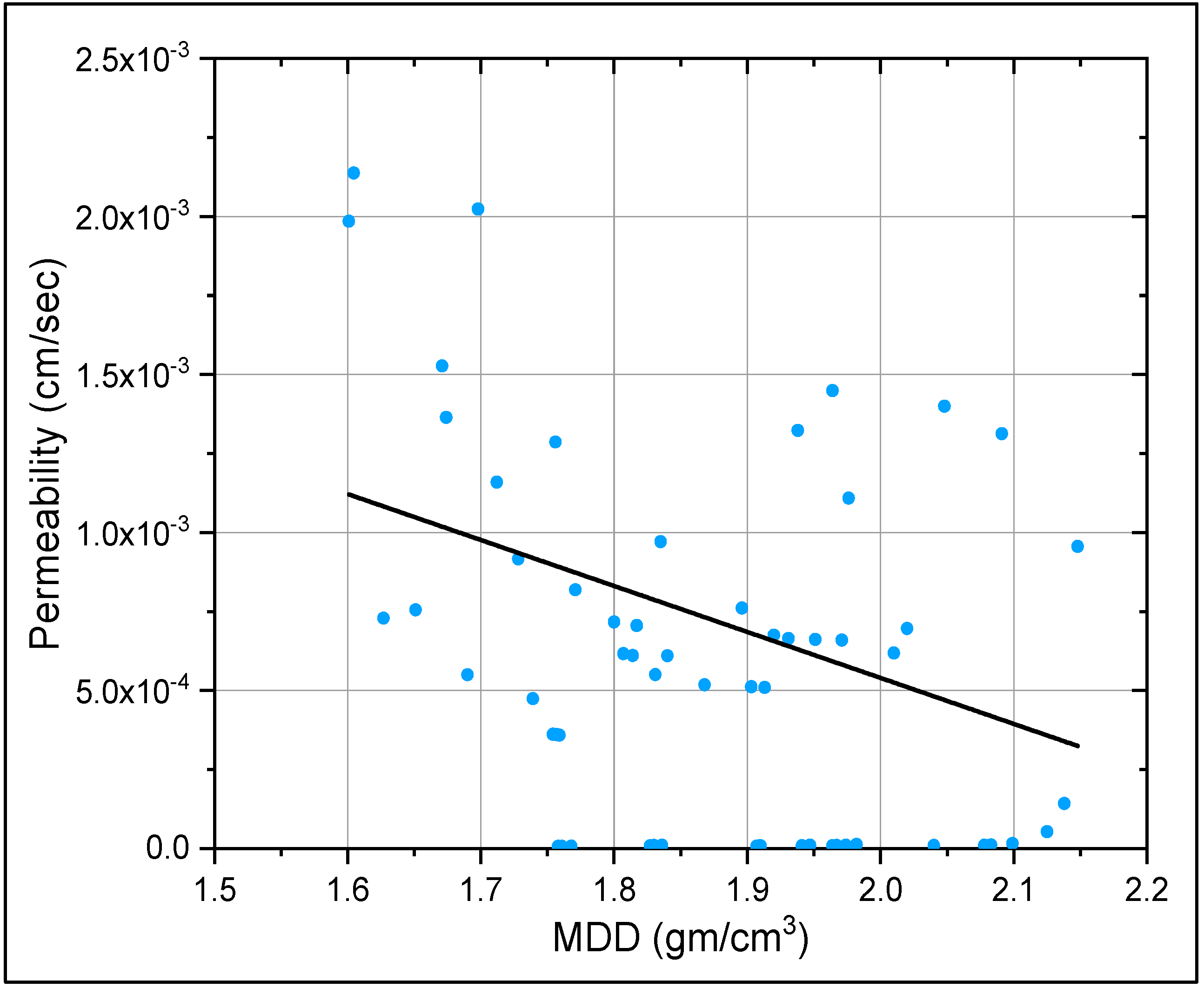
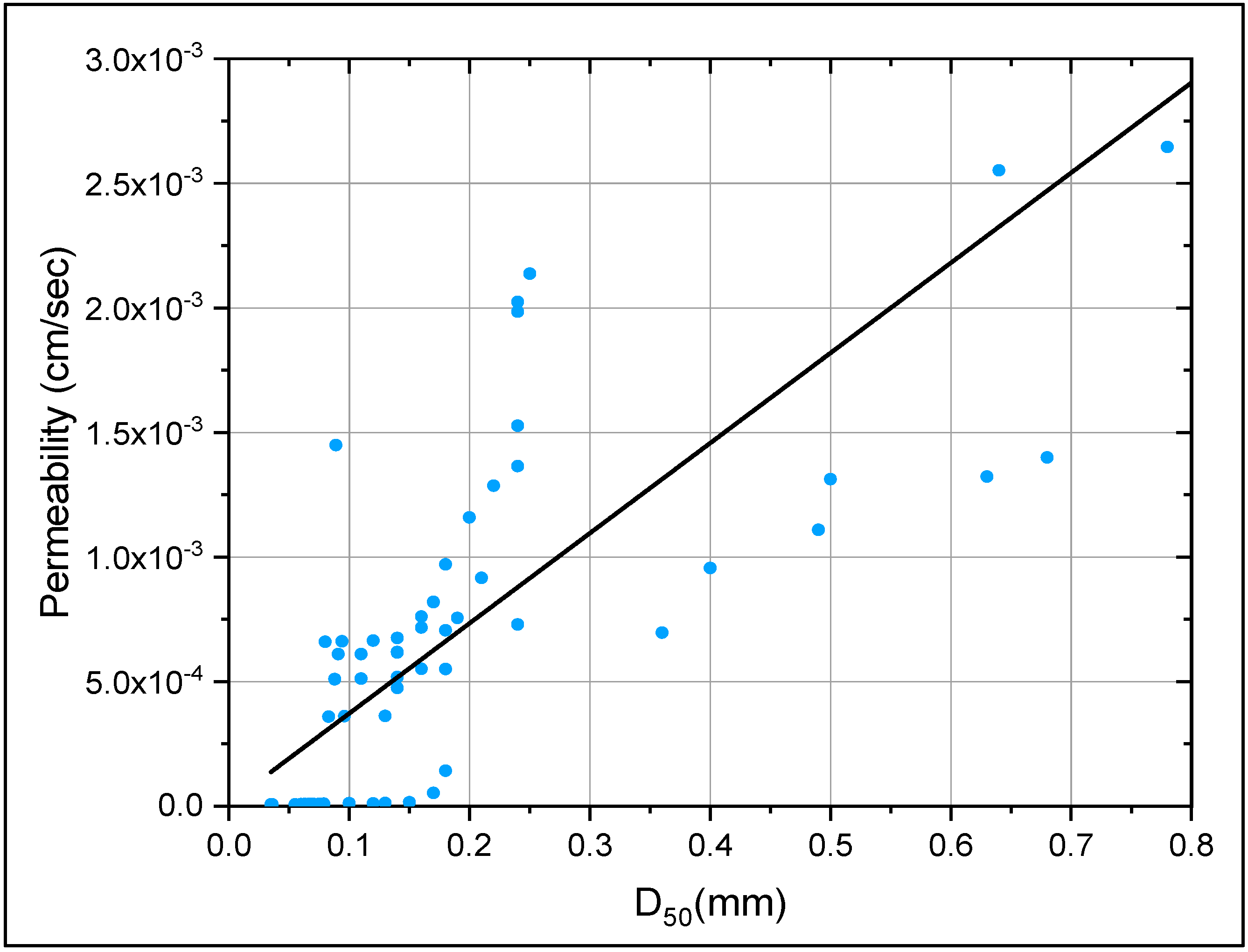
Sample No	Sand Type	FINES TYPE	Fines (%)	D10 (mm)	D30 (mm)	D60 (mm)	D50 (mm)	Cu	Cc	Liquid Limit	Plastic Limit	Plasticity Index	Soil Classification
1	CS	---	---	0.09	0.16	0.31	0.25	3.44	0.92	-	-	NP	SP
2	CS	NPF	5	0.076	0.16	0.28	0.25	3.68	1.20	-	-	NP	SP-SM
3	CS	NPF	10	0.055	0.15	0.28	0.23	5.09	1.46	-	-	NP	SM
4	CS	NPF	15	0.043	0.13	0.27	0.21	6.28	1.46	-	-	NP	SM
5	CS	NPF	20	0.025	0.098	0.22	0.16	8.80	1.75	-	-	NP	SM
6	CS	NPF	25	0.026	0.081	0.23	0.18	8.85	1.10	-	-	NP	SM
7	CS	NPF	30	0.024	0.067	0.22	0.17	9.17	0.85	-	-	NP	SM
8	CS	NPF	35	0.016	0.05	0.19	0.14	11.88	0.82	-	-	NP	SM
9	CS	NPF	40	0.015	0.042	0.18	0.12	12.00	0.65	16.85	-	NP	SM
10	CS	NPF	45	0.013	0.033	0.17	0.077	13.08	0.49	18.25	-	NP	SM
11	CS	NPF	50	0.013	0.028	0.14	0.067	10.77	0.43	19.30	-	NP	ML
12	CS	PF	5	0.053	0.16	0.28	0.24	5.28	1.73	-	-	NP	SP-SM
13	CS	PF	10	0.051	0.14	0.28	0.22	5.49	1.37	-	-	NP	SM
14	CS	PF	15	0.03	0.13	0.26	0.22	8.67	2.17	-	-	NP	SM
15	CS	PF	20	0.018	0.098	0.26	0.18	14.44	2.05	-	-	NP	SM
16	CS	PF	25	0.017	0.077	0.23	0.17	13.53	1.52	-	-	NP	SM
17	CS	PF	30	0.013	0.055	0.22	0.17	16.92	1.06	-	-	NP	SM
18	CS	PF	35	0.012	0.039	0.19	0.14	15.83	0.67	-	-	NP	SM
19	CS	PF	40	0.0094	0.03	0.18	0.13	19.15	0.53	18.80	-	NP	SM
20	CS	PF	45	0.0085	0.027	0.17	0.087	20.00	0.50	19.75	18.14	1.61	SM
21	CS	PF	50	0.0078	0.023	0.14	0.058	17.95	0.48	20.25	17.97	2.28	ML
22	LS	---	---	0.26	0.57	1.2	0.87	4.62	1.04	-	-	NP	SP
23	LS	NPF	5	0.17	0.54	1.1	0.86	6.47	1.56	-	-	NP	SP-SM
24	LS	NPF	10	0.06	0.49	1	0.78	16.67	4.00	-	-	NP	SM
25	LS	NPF	15	0.046	0.45	0.94	0.74	20.43	4.68	-	-	NP	SM
26	LS	NPF	20	0.039	0.41	0.9	0.7	23.08	4.79	-	-	NP	SM
27	LS	NPF	25	0.029	0.26	0.87	0.67	30.00	2.68	-	-	NP	SM
28	LS	NPF	30	0.026	0.17	0.8	0.6	30.77	1.39	14.30	-	NP	SM
29	LS	NPF	35	0.016	0.066	0.7	0.51	43.75	0.39	15.40	-	NP	SM
30	LS	NPF	40	0.015	0.041	0.6	0.41	40.00	0.19	16.70	-	NP	SM
31	LS	NPF	45	0.014	0.028	0.51	0.17	36.43	0.11	18.72	-	NP	SM
32	LS	NPF	50	0.013	0.028	0.45	0.07	34.62	0.13	19.80	-	NP	ML
33	LS	PF	5	0.18	0.55	1.1	0.84	6.11	1.53	-	-	NP	SP-SM
34	LS	PF	10	0.07	0.49	1	0.77	14.29	3.43	-	-	NP	SM
35	LS	PF	15	0.032	0.45	0.94	0.73	29.38	6.73	-	-	NP	SM
36	LS	PF	20	0.023	0.4	0.9	0.7	39.13	7.73	-	-	NP	SM
37	LS	PF	25	0.019	0.26	0.87	0.66	45.79	4.09	16.80	16.17	0.63	SM
38	LS	PF	30	0.016	0.17	0.8	0.6	50.00	2.26	17.85	16.87	0.98	SM
39	LS	PF	35	0.013	0.05	0.7	0.5	53.85	0.27	19.60	17.88	1.72	SM
40	LS	PF	40	0.01	0.034	0.62	0.42	62.00	0.19	20.30	17.84	2.46	SM
41	LS	PF	45	0.0092	0.028	0.52	0.18	56.52	0.16	22.77	19.57	3.20	SM
42	LS	PF	50	0.0085	0.024	0.46	0.068	54.12	0.15	23.20	20.03	3.17	ML
43	RS	---	---	0.085	0.17	0.26	0.22	3.06	1.31	-	-	NP	SP-SM
44	RS	NPF	5	0.066	0.16	0.26	0.21	3.94	1.49	-	-	NP	SP-SM
45	RS	NPF	10	0.036	0.14	0.24	0.19	6.67	2.27	-	-	NP	SM
46	RS	NPF	15	0.027	0.13	0.23	0.18	8.52	2.72	-	-	NP	SM
47	RS	NPF	20	0.017	0.09	0.22	0.18	12.94	2.17	-	-	NP	SM
48	RS	NPF	25	0.017	0.075	0.2	0.17	11.76	1.65	-	-	NP	SM
49	RS	NPF	30	0.014	0.05	0.19	0.16	13.57	0.94	-	-	NP	SM
50	RS	NPF	35	0.013	0.038	0.18	0.15	13.85	0.62	-	-	NP	SM
51	RS	NPF	40	0.013	0.031	0.017	0.11	1.31	4.35	17.70	-	NP	SM
52	RS	NPF	45	0.013	0.029	0.16	0.084	12.31	0.40	18.90	-	NP	SM
53	RS	NPF	50	0.013	0.021	0.14	0.048	10.77	0.24	19.70	-	NP	ML
54	RS	PF	5	0.066	0.16	0.24	0.2	3.64	1.62	-	-	NP	SP-SM
55	RS	PF	10	0.03	0.12	0.24	0.19	8.00	2.00	-	-	NP	SM
56	RS	PF	15	0.021	0.14	0.23	0.18	10.95	4.06	-	-	NP	SM
57	RS	PF	20	0.014	0.09	0.22	0.18	15.71	2.63	-	-	NP	SM
58	RS	PF	25	0.013	0.075	0.2	0.17	15.38	2.16	-	-	NP	SM
59	RS	PF	30	0.011	0.047	0.18	0.16	16.36	1.12	-	-	NP	SM
60	RS	PF	35	0.0084	0.032	0.18	0.15	21.43	0.68	-	-	NP	SM
61	RS	PF	40	0.0088	0.028	0.17	0.12	19.32	0.52	17.90	-	NP	SM
62	RS	PF	45	0.0083	0.025	0.16	0.084	19.28	0.47	19.50	18.32	1.18	SM
63	RS	PF	50	0.0063	0.019	0.13	0.045	20.63	0.44	20.10	17.94	2.16	ML

.

Most samples were non-plastic (NP) except some with higher percentages of plastic fines. It is also noted that most of the samples were silty sand (SM). As per USCS, both LS and CS were poorly graded sand (SP) while RS was poorly graded sand with silt (SP-SM).

3.2. Compaction Tests

Standard Proctor tests were performed on all 63 samples in accordance with the guidelines of ASTM D-698. The lowest value of MDD (1.6 g/cm³) was observed for Ravi sand. This was obvious, as RS was the most uniformly graded soil (mentioned earlier). The highest MDD was for Lawrencepur sand mixed with 20% non-plastic fines (LS20NPF). Figure 2 shows the compaction curves of the lowest dry density (RS), highest dry density (LS20NPF), CS and LS soil samples.

The variations in MDD and OMC with the addition of two fines are shown in Figure 3 and Figure 4 respectively. For LS mixed with both fines, MDD increased up to 20% fine content and then started to decrease, whereas, for both CS and RS, MDD increased for up to 35% fine content and then either remained the same or decreased a small amount. The initial increase in MDD may be attributable to the occupation of voids in sand by the fines. The decline in density after reaching the peak may be due to the bouncing of particles, thereby increasing the space within particles and reducing dry density.

3.3. Permeability

Constant head permeability tests were performed in accordance with the guidelines of ASTM D-2434 on LS mixed with up to 25% and 20% of NPF and PF respectively. The same test was conducted on CS and RS mixed with both fines up to 20%. Falling head permeability tests were performed on all remaining samples. The results of the tests are shown in Figure 5. The figure shows that the permeability of all three types of sands decreases with increasing fine contents. The rate of decrease in permeability is very weighty up until 20% fine content and then reduces significantly. Amongst the nonamended sands, LS had a maximum permeability value of 4.63 × 10⁻³ cm/sec, whereas for CS and RS, the observed values were 2.14 × 10⁻³ cm/sec and 1.98 × 10⁻³ cm/sec respectively. These values seem to be related with their median grain size (D50). D50s for CS, LS and RS were 0.25, 0.87 and 0.22 mm respectively. In amended soils, the minimum permeability of 6.39 × 10⁻⁶ cm/sec was noted for RS mixed with 50% PF.

3.4. The Development of Correlations

Analyses were performed with the set of ρ_d (dry density), D₁₀, D₃₀, D₅₀, D₆₀, C_u, and C_c values to select the most suitable independent variables to develop correlations as D60 defines 60 % of the soil particles are finer than this size, D30 defines 30% of the particles are finer than this size and D10 defines 10% of the particles are finer than this size. The results of the analysis of ρ_d, D₁₀ and D₅₀ on permeability are shown in Figure 6, Figure 7 and Figure 8 respectively. The trend for permeability versus ρ_d is a decreasing one, though the data is somewhat scattered. For both D₁₀ and D₅₀, the permeability increases with an increase in particle size.

Computer software “IBM SPSS Version 22” was used IBM SPSS Statistics (V22.0. 2016, IBM Corp, Armonk, NY, USA) for carrying out linear regression analysis to develop a correlation. A few trials were made and the best fit was obtained with D₁₀, D₅₀ and ρ_d. The value of coefficient of determination/R squared (R²) was determined as 0.95. The following equation was obtained.

$$k=0.012D_{10}+0.002D_{50}-0.001 {\gamma }_d+0.002(\mathrm{cm}/\sec )$$

(1)

Values predicted by the above equation were plotted against experimental values and the graph in Figure 9 was obtained. An 8.5% residual standard error of estimate (RSE) was found.

3.5. Data Validation

To investigate the validity of the equation, 52 data sets from the field were obtained from different areas of Pakistan. Nine data sets were from Lahore’s Sewerage system (sample numbers: S1 to S9), 11 from the Taunsa Hydro Power Plant (sample numbers: S10 to S20), five from Defence Housing Authority (DHA) Lahore (sample numbers: S21 to S25) and 27 from Bhikki Power Plant Bhikki (sample numbers: S26 to S52). The characteristics of the data are listed in

Table 2. Field permeability data for validation.

Sample No.	Gravel	Sand	Fines	Soil Class.	γd	Field Permeability
	%	%	%	USCS	gm/cm3	cm/sec
S1	0	89	11	SP-SM	1.727	2.00 × 10−3
S2	0	65	35	SM	1.688	2.83 × 10−3
S3	0	91	9	SP-SM	1.748	7.37 × 10−4
S4	0	81	19	SM	1.794	9.69 × 10−5
S5	0	94	6	SP-SM	1.827	1.0 × 10−3
S6	0	92	8	SP-SM	1.764	5.99 × 10−4
S7	0	93	7	SP-SM	1.589	3.60 × 10−4
S8	0	86	14	SM	1.836	1.29 × 10−3
S9	0	90	10	SP-SM	1.735	1.08 × 10−3
S10	0	57	43	SM	1.769	8.38 × 10−5
S11	0	3	97	ML	1.782	7.42 × 10−4
S12	0	2	98	ML	1.79	9.73 × 10−4
S13	0	92	8	SP-SM	1.621	1.37 × 10−3
S14	0	85	15	SM	1.6	5.59 × 10−4
S15	0	85	15	SM	1.651	1.16 × 10−3
S16	0	92	8	SP-SM	1464	2.12 × 10−3
S17	0	97	3	SP	1.534	7.72 × 10−4
S18	0	97	3	SP	1.596	1.81 × 10−3
S19	0	91	9	SP-SM	1.526	1.54 × 10−3
S20	0	88	12	SP-SM	1.527	1.75 × 10−3
S21	0	91	9	SP-SM	1.675	2.61 × 10−3
S22	0	85	15	SM	1.576	5.31 × 10−3
S23	0	54	46	SM	1.775	6.92 × 10−3
S24	3	11	86	CL	1.528	6.47 × 10−4
S25	0	4	96	CL	1.625	4.58 × 10−4
S26	0	93	7	SP-SM	1.499	2.39 × 10−3
S27	2	87	11	SP-SM	1.479	5.71 × 10−4
S28	1	95	4	SP	1.97	2.75 × 10−3
S29	0	75	26	SM	1.719	5.46 × 10−3
S30	0	49	41	SM	1.485	6.70 × 10−4
S31	0	82	18	SM	1.79	5.00 × 10−4
S32	0	73	27	SM	1.77	8.60 × 10−4
S33	0	95	5	SP-SM	1.822	4.11 × 10−3
S34	0	87	13	SM	1.777	3.20 × 10−3
S35	1	94	5	SP-SM	1.698	9.720 × 10−4
S36	0	80	20	SM	1.858	6.80 × 10−4
S37	0	70	30	SM	1.82	8.43 × 10−4
S38	0	83	17	SM	1.837	6.78 × 10−4
S39	0	79	21	SM	1.988	5.99 × 10−4
S40	0	59	41	SM	1.871	8.28 × 10−4
S41	0	92	8	SP-SM	1.8	9.83 × 10−4
S42	0	82	18	SM	1.821	2.99 × 10−4
S43	0.5	84	15.5	SM	1.883	3.28 × 10−4
S44	0.7	6.2	93.1	CL-ML	2.104	7.94 × 10−05
S45	0	82.6	17.4	SM	1.901	2.28 × 10−03
S46	0	85.3	14.7	SM	1.792	2.73 × 10−03
S47	4.5	8.2	87.3	CL	2.056	6.68 × 10−4
S48	0	86.8	13.2	SM	1.867	6.31 × 10−3
S49	0	80	20	SM	1.849	6.97 × 10−3
S50	0	79	21	SM	1.837	6.10 × 10−3
S51	0	73.4	26.6	SM	1.816	7.66 × 10−4
S52	0	73	27	SM	1.898	2.26 × 10−3

.

The data was tested with other familiar equations available in the literature; i.e., the Mujtaba equation [31], Kozeny–Carman equation [32,33,34] and Hazen equation [7,35]. The results are presented in Figure 10. The permeability values predicted by Mujtaba, Hazen and Kozeny–Carman equations do not really match with experimental values for hydraulic conductivity less than 3 × 10⁻³ cm/sec. The equation proposed by present research (Equation (1)) also produced scattered data but that is only for hydraulic conductivity less than 1 × 10⁻³ cm/sec. Interestingly, these predicted values (for hydraulic conductivity less than 1 × 10⁻³ cm/sec) are greater than the experimental values. Thus, the predicted values are conservative and can be tolerated. The reason may be that the equation was developed for the mixes of local sands and fines. As mentioned earlier, it is somewhat difficult to predict the hydraulic conductivity of fine-grained soils. For hydraulic conductivity greater than 3 × 10⁻³ cm/sec, all the equations yielded fairly good results. It is noted that the observed data best fits with the equation developed in the current research.

4. Conclusions

In this experimental work, the effect of adding fines to three different river sands on permeability (at maximum dry density and optimum moisture content) was studied. Moreover, an equation was developed to predict the permeability of sand and fine mixes. According to test observations and analyses, the outcomes can be summarized, as follows:

• The study of literature indicates that most equations developed for predicting the permeability are for granular soils with little effort being made for fine-grained soils. Analysis showed that the equation developed in this research is very much suitable for soils of local formations when fine content ranges from 0% to 50%.
• The equation formulated with the experimental data was compared with three empirical equations and it was found that this equation predicted better with fine-grained soils (hydraulic conductivity value less than 3 × 10⁻³ cm/sec) than the other three. The analysis also demonstrated that at lower ranges of fine contents, other equations perform well; however, as the percentages of fine content increases, their adaptability is questioned.