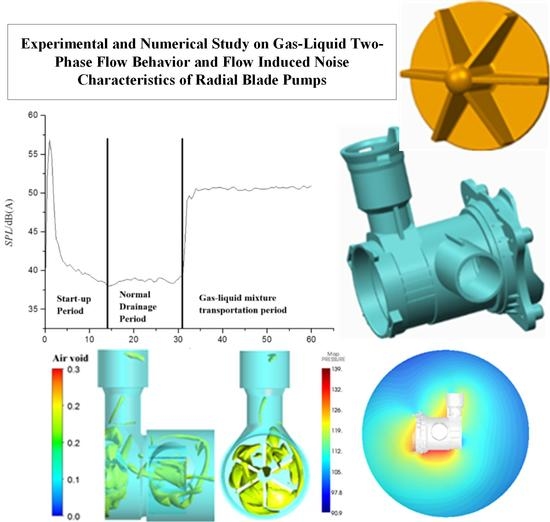
Experimental and Numerical Study on Gas-Liquid Two-Phase Flow Behavior and Flow Induced Noise Characteristics of Radial Blade Pumps
Abstract
1. Introduction
2. Experimental Setup and Calculation of Boundary Conditions for Pump Model
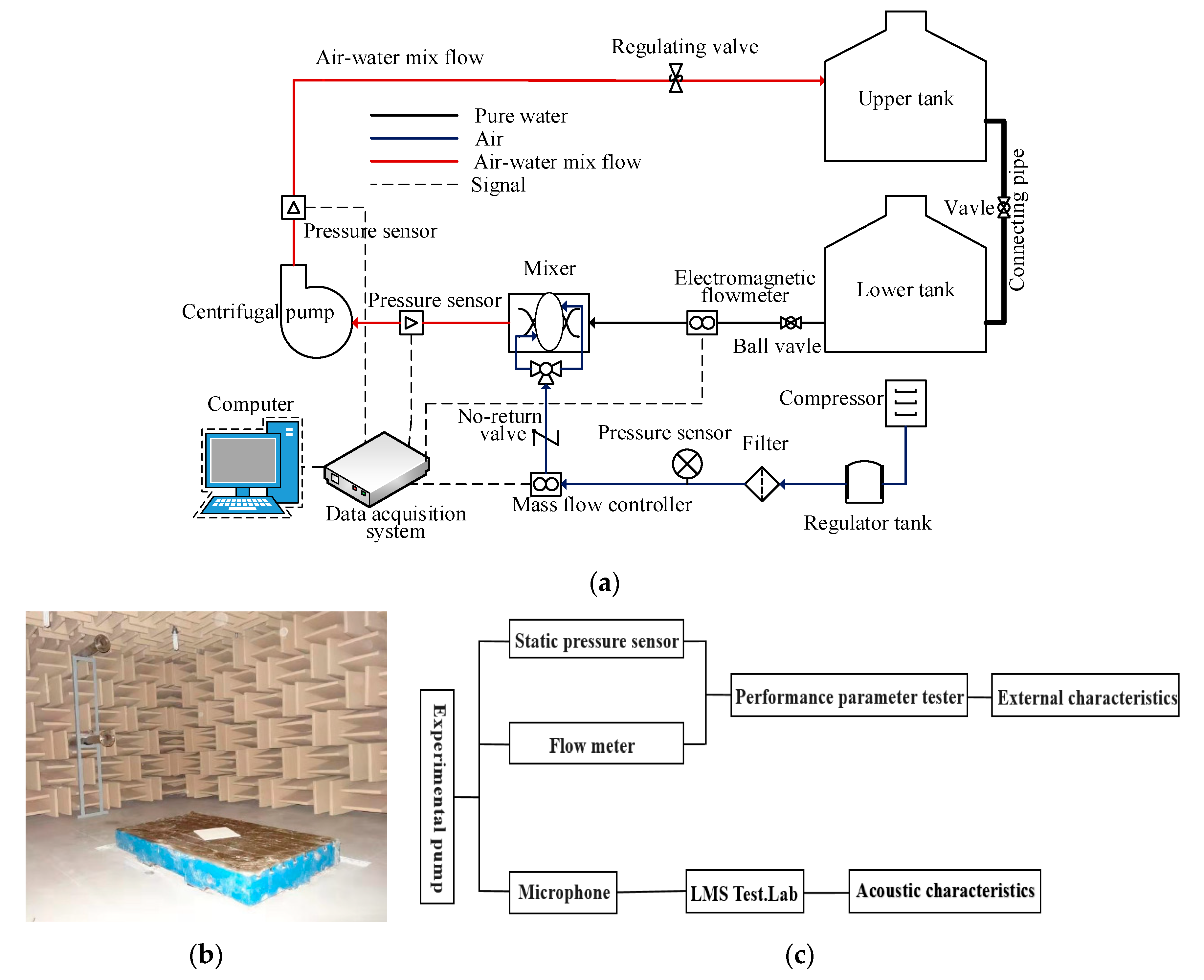
2.1. Test Equipment and Loop
2.2. Experimental Results Analysis
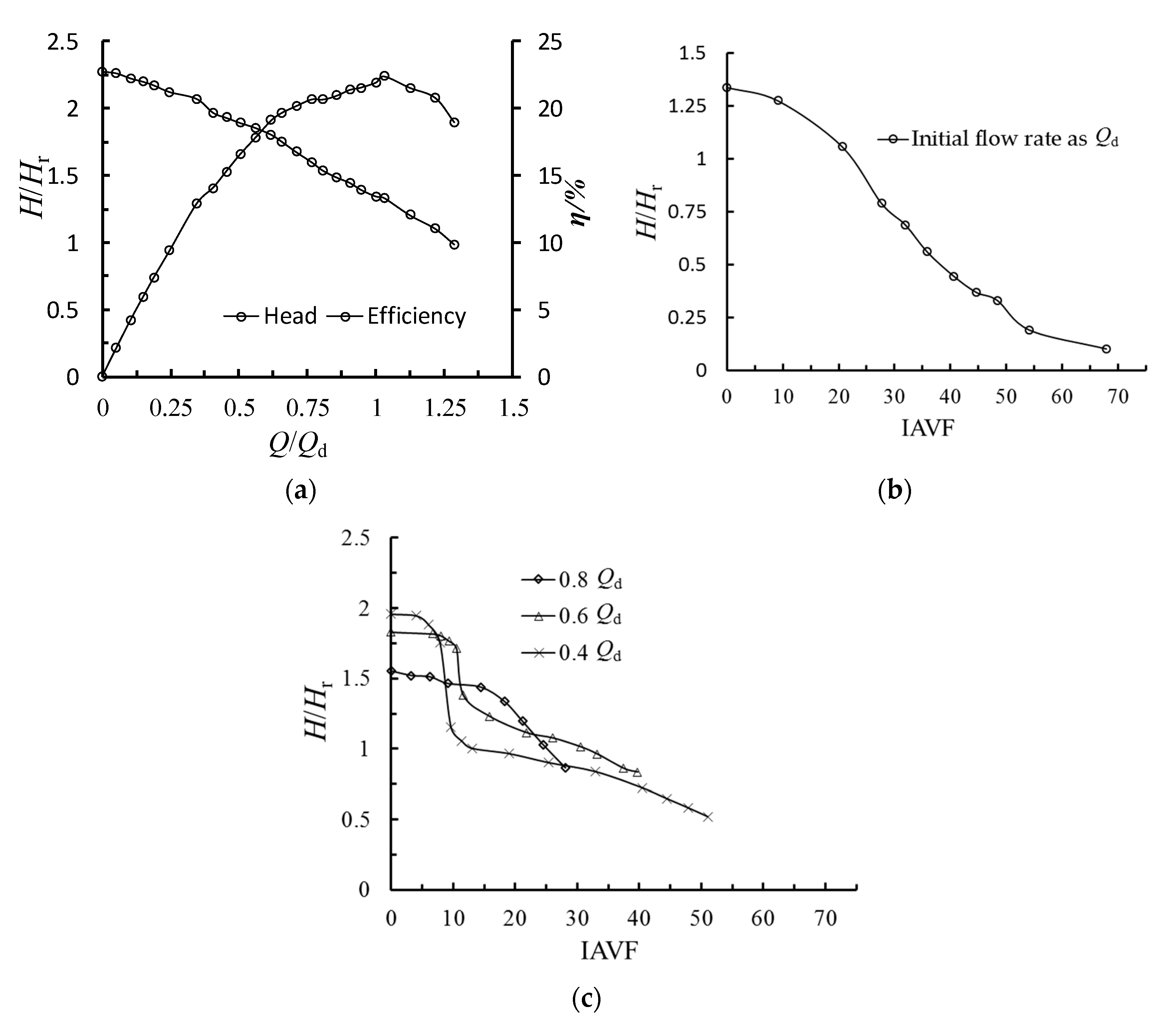
2.2.1. Pump Performance
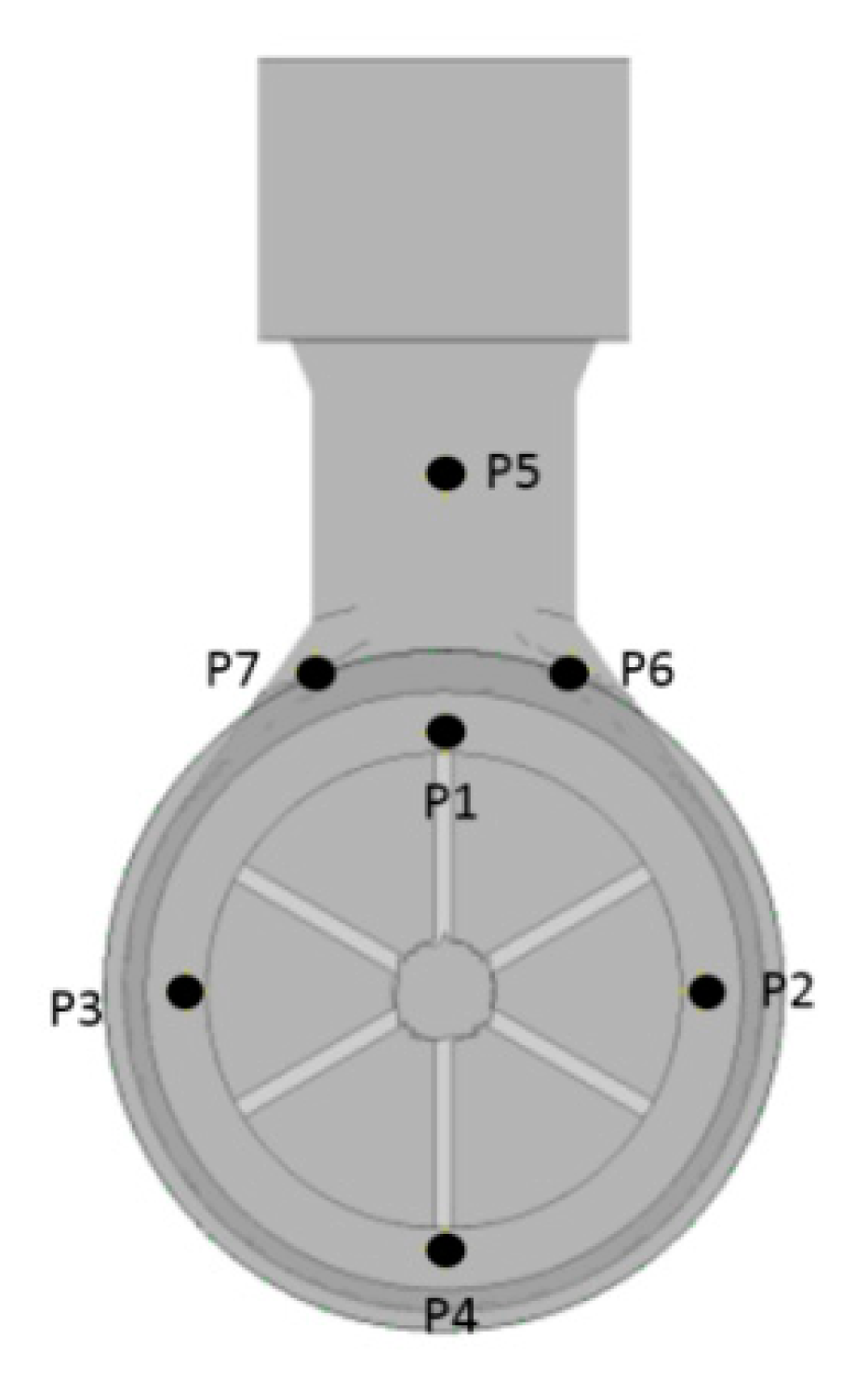
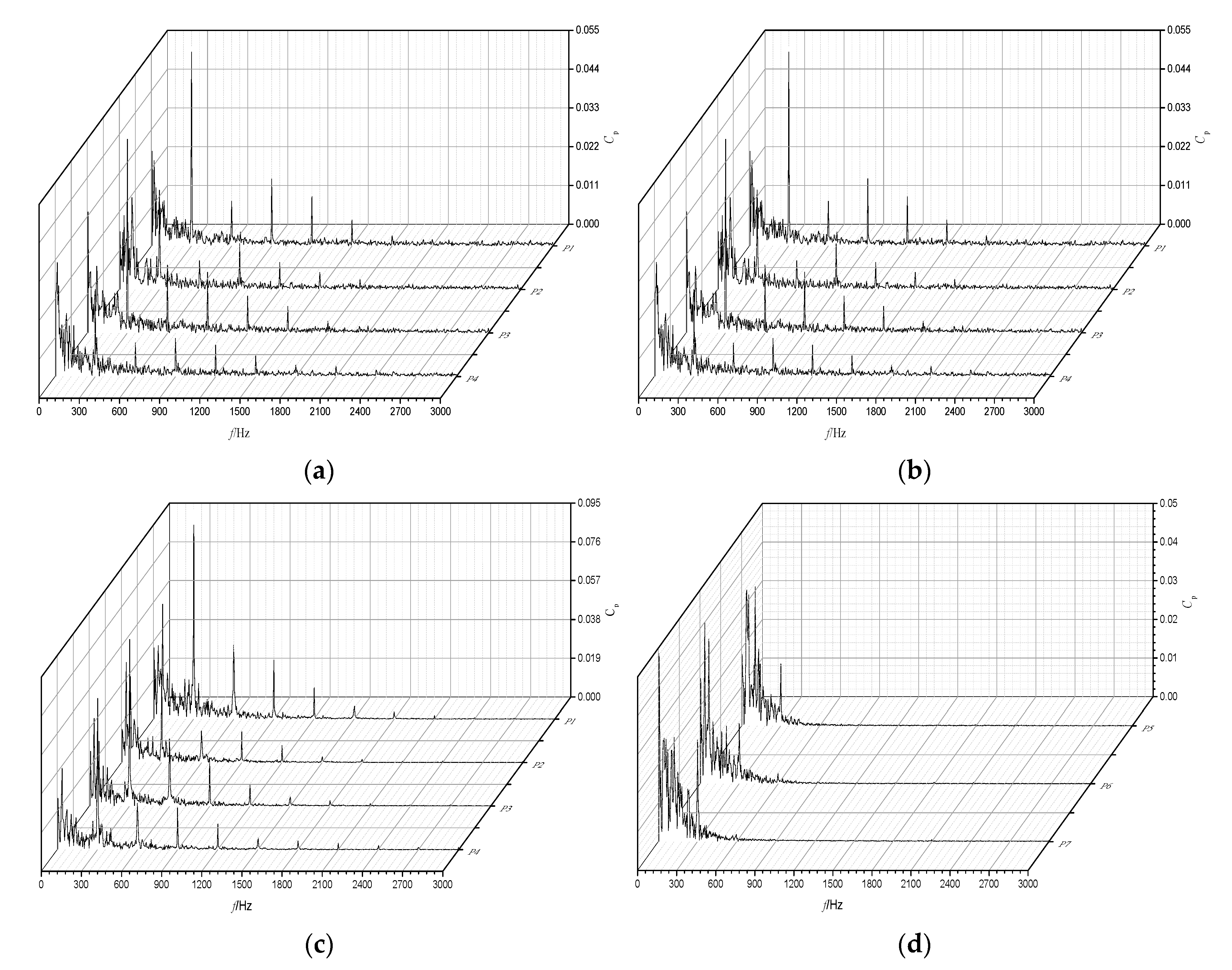
2.2.2. Radiated Noise of the Drain Pump at Different Measuring Points
3. Numerical Simulation Study on the Inner Flow Behavior
3.1. The Eulerian–Eulerian Inhomogeneous Two-Phase Flow Modeling Method
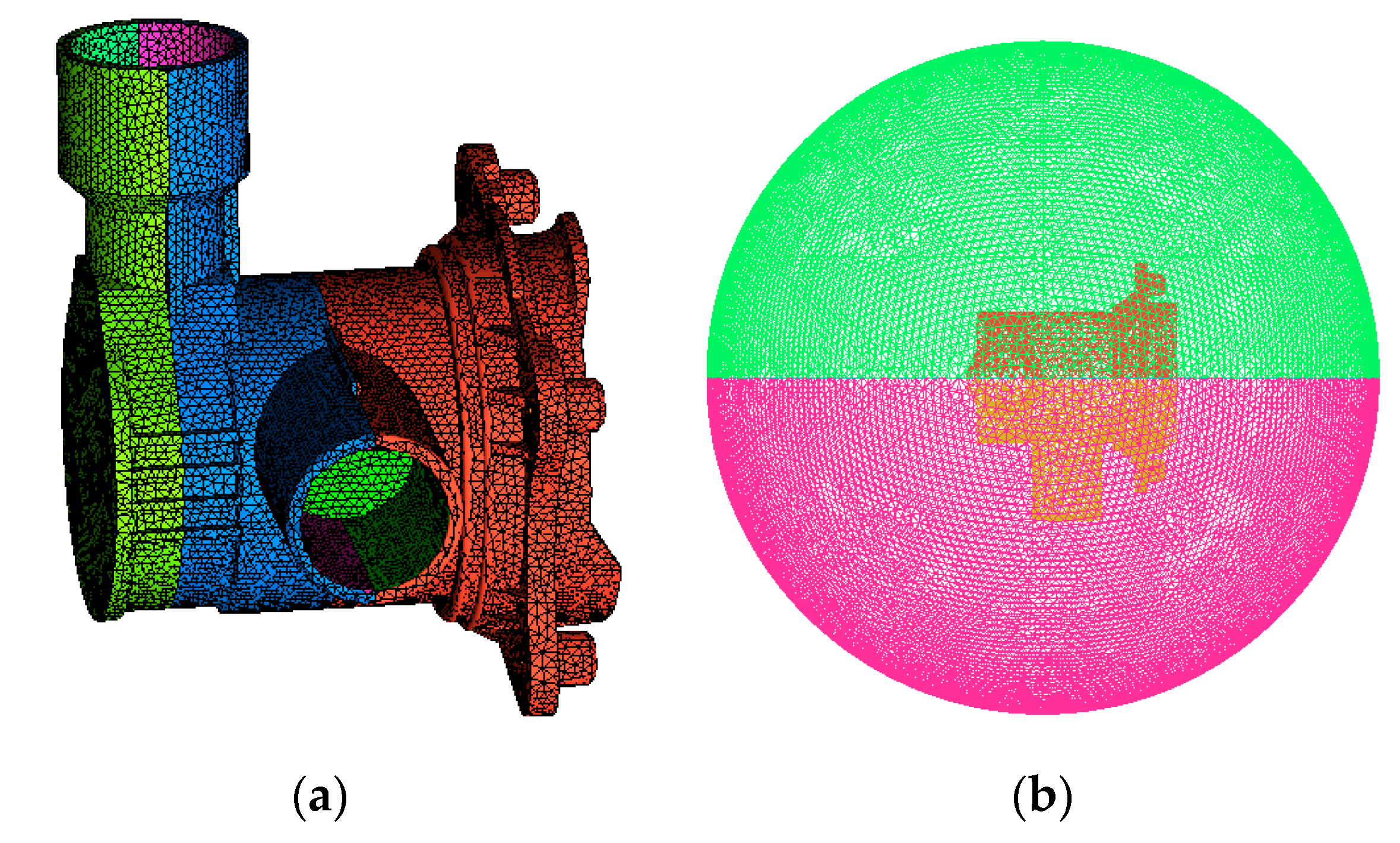
3.2. Computational Domain, Meshing and Boundary Setting
3.3. Simulation Results Analysis from CFD
3.3.1. Pump Performance Degradation
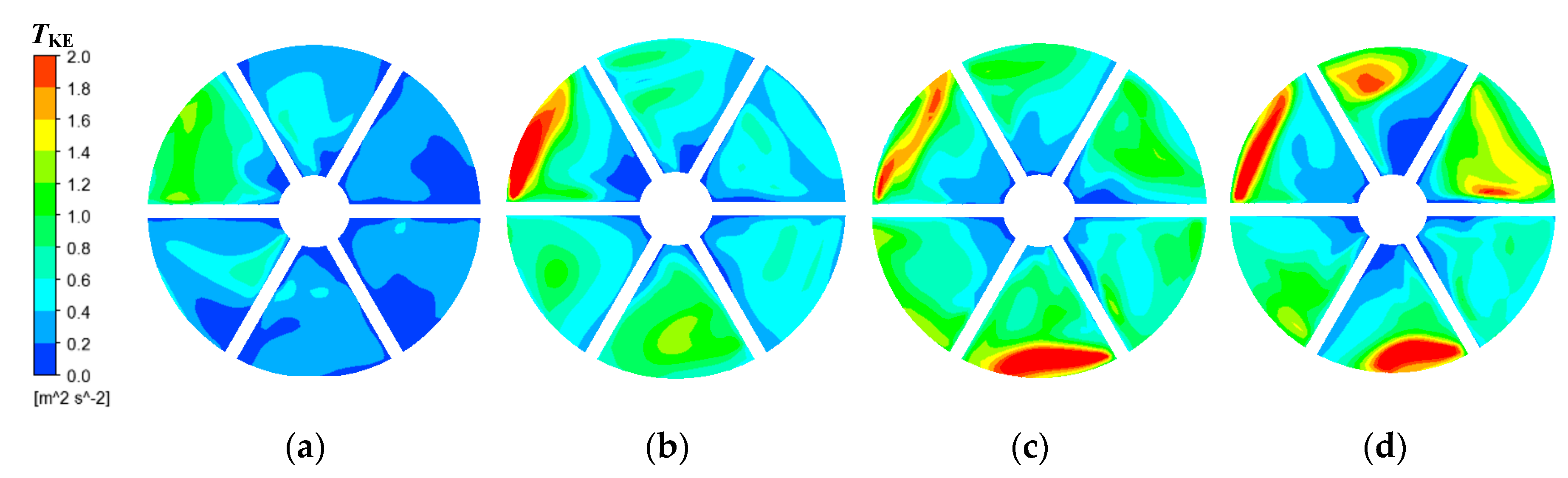
3.3.2. Two Phase Flow Behavior Analysis
3.3.3. Analysis of Pressure Fluctuations
4. Radiated Noise Simulation
4.1. Computational Acoustic Theory and Method
4.2. Computational Domain, Mesh Generation and Boundary Condition of the Acoustic
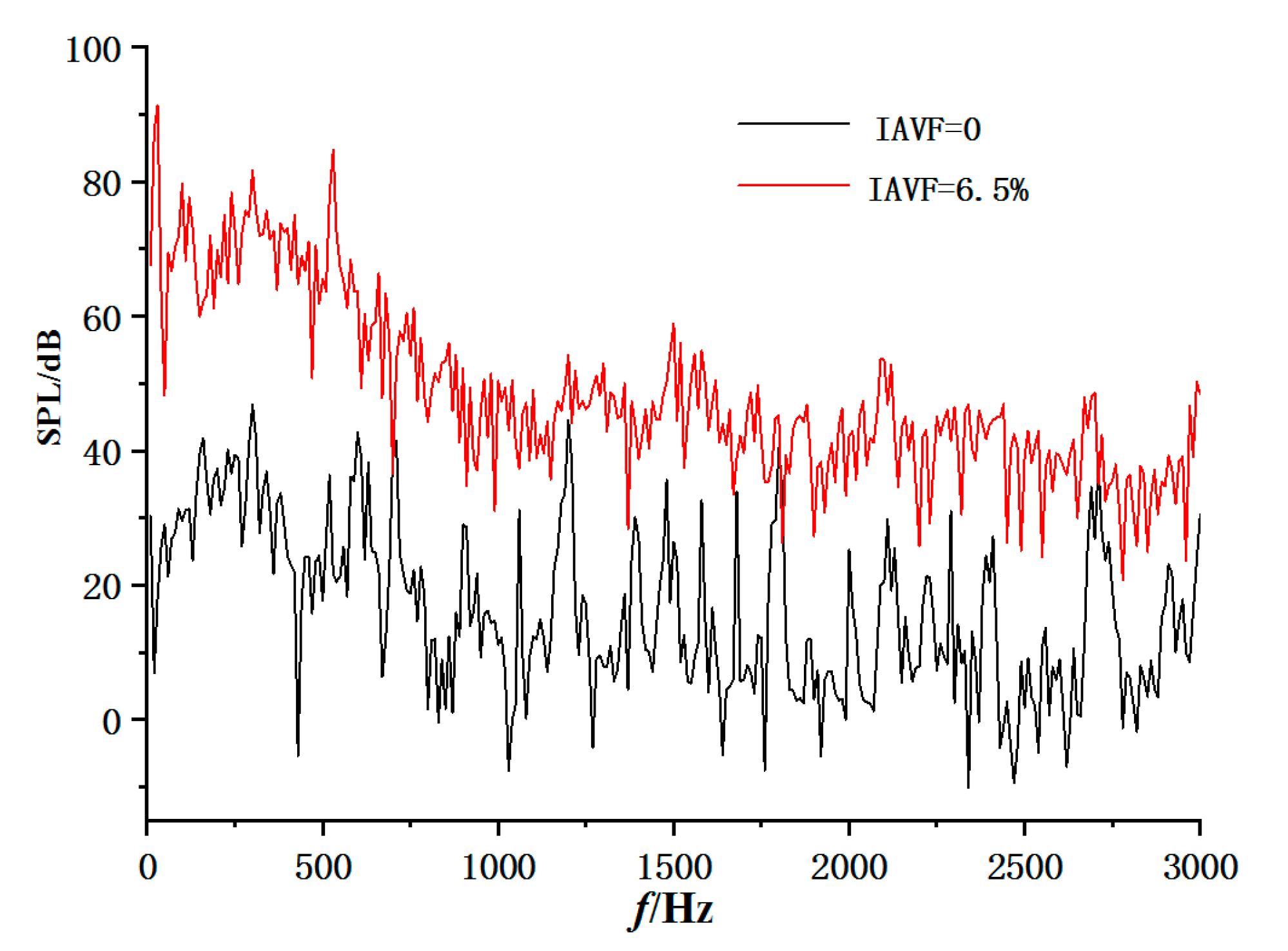
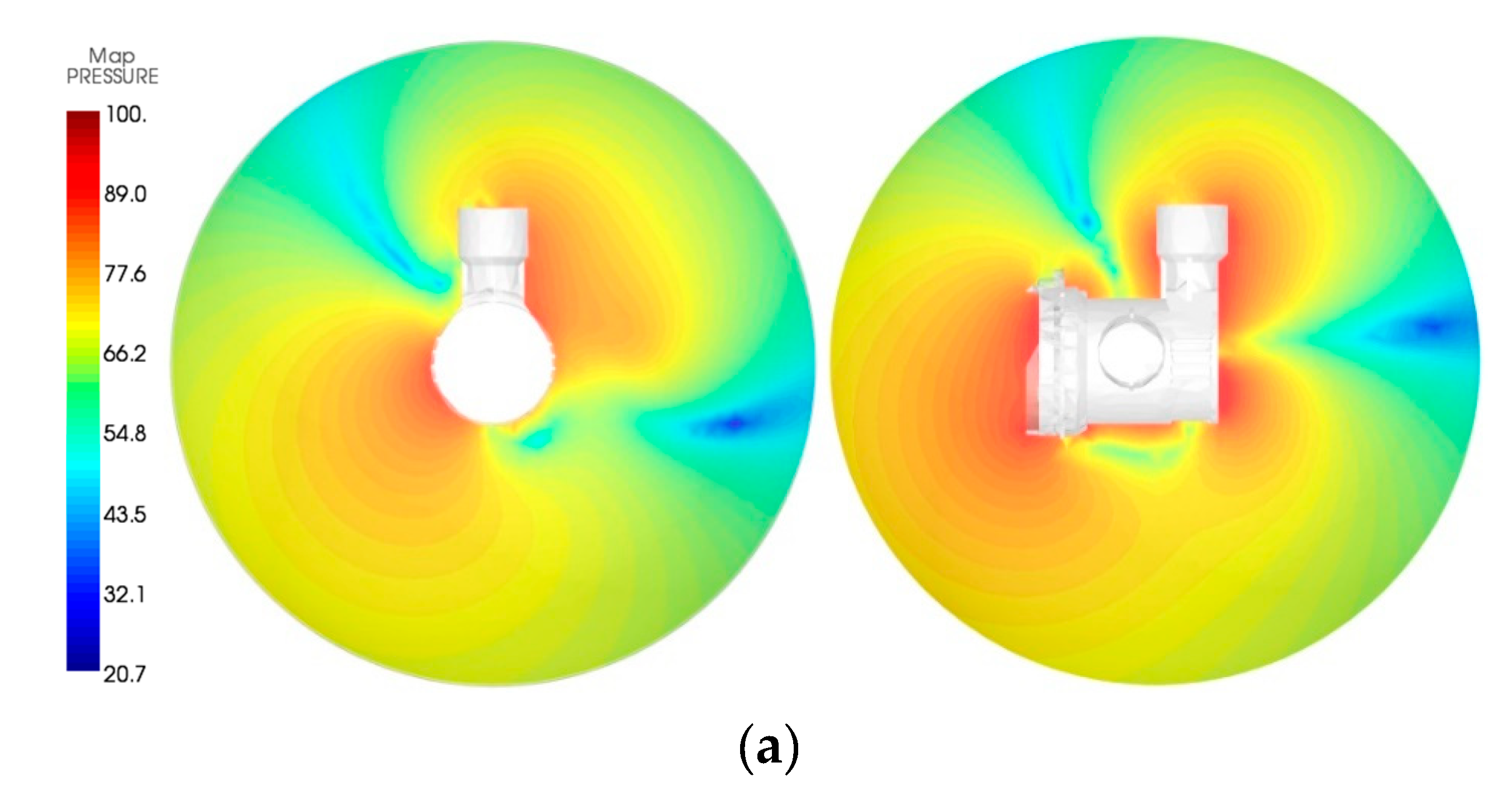
4.3. Acoustic Field Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| IAVF | inlet air void fraction |
| b | impeller blade width |
| d | diameter of bubble |
| D | diameter |
| H | pump head |
| M | shaft torque |
| n | rotational speed |
| p | local static pressure |
| P | shaft power |
| Q | volume water flow rate |
| R | radius |
| SPL | sound pressure level |
| v | velocity |
| z | height level |
| Z | impeller blade number |
| Greek Symbols | |
| α | local gas void fraction |
| η | global efficiency of the pump |
| ρ | density of fluid mixture |
| ω | angular velocity |
| δ | blade thickness |
| Subscripts | |
| B | bubble |
| d | design condition |
| g | gas |
| l | liquid |
| r | required |
| 1 | inlet of the impeller |
| 2 | outlet of the impeller |
| 3 | inlet of the volute |
| 4 | outlet of the pump |
References
- Wang, C.; Hu, B.; Zhu, Y.; Wang, X.; Luo, C.; Cheng, L. Numerical Study on the Gas-Water Two-Phase Flow in the Self-Priming Process of Self-Priming Centrifugal Pump. Processes 2019, 7, 330. [Google Scholar] [CrossRef]
- He, X.K.; Jiao, W.X.; Wang, C.; Cao, W.D. Influence of Surface Roughness on the Pump Performance Based on Computational Fluid Dynamics. IEEE Access 2019, 7, 105331–105341. [Google Scholar] [CrossRef]
- Wang, C.; He, X.K.; Shi, W.D.; Wang, X.K.; Wang, X.L.; Qiu, N. Numerical study on pressure fluctuation of a multistage centrifugal pump based on whole flow field. AIP Adv. 2019, 9, 035118. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, S.; Ye, S.; Xu, B.; Song, W.; Zhu, S.; Xiang, J. Experimental investigation on the noise reduction of an axial piston pump using free-layer damping material treatment. Appl. Acoust. 2018, 139, 1–7. [Google Scholar] [CrossRef]
- Ye, S.G.; Zhang, J.H.; Xu, B.; Zhu, S.Q.; Xiang, J.; Tang, H. Theoretical investigation of the contributions of the excitation forces to the vibration of an axial piston pump. Mech. Syst. Signal Process. 2019, 129, 201–217. [Google Scholar] [CrossRef]
- Kaigala, G.V.; Hoang, V.N.; Stickel, A.; Lauzon, J.; Manage, D.; Pilarski, L.M.; Backhouse, C.J. An inexpensive and portable microchip-based platform for integrated RT–PCR and capillary electrophoresis. Analyst 2008, 133, 331–338. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.C.; Ng, B.T.; Chan, W.K.; Chua, L.P. The flow patterns within the impeller passages of a centrifugal blood pump model. Med. Eng. Phys. 2000, 22, 381–393. [Google Scholar] [CrossRef]
- Orue, R. Drain Pump for Home Appliances. U.S. Patent 2007/0071617 A1, 29 March 2007. [Google Scholar]
- Marioni, E.; Cavalcante, V. Centrifugal Pump for Electric Household Appliances such as Washing Machines, Dishwashers and the Like. U.S. Patent 4861240 A, 29 August 1989. [Google Scholar]
- Luo, X.W.; Nishi, M.; Yoshida, K.; Dohzono, H.; Miura, K. Cavitation Performance of a Centrifugal Impeller Suitable for a Mini Turbo-Pump. In Proceedings of the Fifth International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Zhuang, B.; Luo, X.; Zhang, Y.; Wang, X.; Xu, H.; Nishi, M. Design optimization for a shaft-less double suction mini turbo pump. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012049. [Google Scholar] [CrossRef]
- Jiang, Q.F.; Heng, Y.G.; Liu, X.B.; Zhang, W.B.; Bois, G.; Si, Q.R. A review on design considerations of centrifugal pump capability for handling inlet gas-liquid two-phase flows. Energies 2019, 12, 1078. [Google Scholar] [CrossRef]
- Jang, J.H.; Lim, D.B. Washing Machine Having a Drain Pump to Reduce Vibration. U.S. Patent 7966848 B2, 28 June 2011. [Google Scholar]
- Murakami, M.; Minemura, K. Effects of Entrained Air on the Performance of a Centrifugal Pump: 1st Report, Performance and Flow Conditions. Bull. JSME 1974, 17, 1047–1055. [Google Scholar] [CrossRef]
- Murakami, M.; Minemura, K. Effects of Entrained Air on the Performance of Centrifugal Pumps: 2nd Report, Effects of Number of Blades. Bull. JSME 1974, 17, 1286–1295. [Google Scholar] [CrossRef]
- Pessoa, R.; Prado, M. Two-Phase Flow Performance for Electrical Submersible Pump Stages. SPE Prod. Facil. 2003, 18, 13–27. [Google Scholar] [CrossRef]
- Serena, A.; Bakken, L.E. Design of a Multiphase Pump Test Laboratory Allowing to Perform Flow Visualization and Instability Analysis. In Proceedings of the ASME 2015 Power Conference, San Diego, CA, USA, 28 June–2 July 2015. [Google Scholar]
- Schäfer, T.; Bieberle, A.; Neumann, M.; Hampel, U. Application of gamma-ray computed tomography for the analysis of gas holdup distributions in centrifugal pumps. Flow Meas. Instrum. 2015, 46, 262–267. [Google Scholar] [CrossRef]
- Verde, W.M.; Biazussi, J.L.; Sassim, N.A.; Bannwart, A.C. Experimental study of gas-liquid two-phase flow patterns within centrifugal pumps impellers. Exp. Therm. Fluid Sci. 2017, 85, 37–51. [Google Scholar] [CrossRef]
- Wang, C.; Shi, W.D.; Wang, X.K.; Jiang, X.P.; Yang, Y.; Li, W.; Zhou, L. Optimal design of multistage centrifugal pump based on the combined energy loss model and computational fluid dynamics. Appl. Energy 2017, 187, 10–26. [Google Scholar] [CrossRef]
- Wang, C.; He, X.K.; Zhang, D.S.; Hu, B.; Shi, W.D. Numerical and experimental study of the self-priming process of a multistage self-priming centrifugal pump. Int. J. Energy Res. 2019, 43, 4074–4092. [Google Scholar] [CrossRef]
- Qian, J.Y.; Chen, M.R.; Liu, X.L.; Jin, Z.J. A numerical investigation of the flow of nanofluids through a micro Tesla valve. J. Zhejiang Univ. Sci. A 2019, 20, 50–60. [Google Scholar] [CrossRef]
- Qian, J.-Y.; Gao, Z.-X.; Liu, B.-Z.; Jin, Z.-J. Parametric Study on Fluid Dynamics of Pilot-Control Angle Globe Valve. J. Fluids Eng. 2018, 140, 111103. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Yuan, X.; Lei, Y. Bifurcation Characteristic Research on the Load Vertical Vibration of a Hydraulic Automatic Gauge Control System. Processes 2019, 7, 718. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Quan, L.; Jiang, W.; Zhou, L. Extraction method for signal effective component based on extreme-point symmetric mode decomposition and Kullback-Leibler divergence. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 100. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, H.-Q. Numerical Study on Electrical Submersible Pump Two-Phase Performance and Bubble-Size Modeling. SPE Prod. Oper. 2017, 32, 267–278. [Google Scholar] [CrossRef]
- Si, Q.R.; Bois, G.; Jiang, Q.F.; He, W.T.; Ali, A.; Yuan, S.Q. Investigation on the Handling Ability of Centrifugal Pump Under Air-Water Two-Phase Inflow: Model and Experimental Validation. Energies 2018, 11, 3048. [Google Scholar] [CrossRef]
- Si, Q.R.; Asad, A.; Yuan, J.P.; Ibra, F.; Yasin, M.F. Flow-Induced Noises in a Centrifugal Pump: A Review. Sci. Adv. Mater. 2019, 11, 909–924. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). ISO 9906: 2012 Rotodynamic Pumps-Hydraulic Performance Acceptance Tests—Grades 1, 2 and 3; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Wang, C.; Chen, X.X.; Qiu, N.; Zhu, Y.; Shi, W.D. Numerical and experimental study on the pressure fluctuation, vibration, and noise of multistage pump with radial diffuser. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 481. [Google Scholar] [CrossRef]
- Jiao, W.X.; Cheng, L.; Zhang, D.; Zhang, B.W.; Su, Y.P.; Wang, C. Optimal Design of Inlet Passage for Waterjet Propulsion System Based on Flow and Geometric Parameters. Adv. Mater. Sci. Eng. 2019, 2019, 2320981. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Si, Q.R.; He, W.T.; Cui, Q.L.; Bois, G.; Yuan, S.Q. Experimental and numerical studies on inner flow characteristics of centrifugal pump under air-water inflow. Int. J. Fluid Mach. Syst. 2019, 12, 31–38. [Google Scholar]
- Gao, M.; Dong, P.X.; Lei, S.H.; Turan, A. Computational Study of the Noise Radiation in a Centrifugal Pump When Flow Rate Changes. Energies 2017, 10, 221. [Google Scholar] [CrossRef]
- Si, Q.; Wang, B.; Yuan, J.; Huang, K.; Lin, G.; Wang, C. Numerical and Experimental Investigation on Radiated Noise Characteristics of the Multistage Centrifugal Pump. Processes 2019, 7, 793. [Google Scholar] [CrossRef]










| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Design Flow rate Qd | 1.08 m3/h | Blade thickness | 1.5 mm |
| Head Hd | 1.2 m | Blades number Z | 6 |
| Rotating speed n | 3000 r/min | Specific speed ns | 68 |
| Impeller outlet diameter D2 | 37 mm | Volute base circle diameter D3 | 50 mm |
| Blade outlet width b2 | 6.25 mm | Diameter of outlet pipe D4 | 30 mm |
| Material | Density/(kg/m3) | Young’s Modulus/GPa | Poisson’s Ratio |
|---|---|---|---|
| PP | 910 | 0.896 | 0.4103 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, Q.; Shen, C.; Ali, A.; Cao, R.; Yuan, J.; Wang, C. Experimental and Numerical Study on Gas-Liquid Two-Phase Flow Behavior and Flow Induced Noise Characteristics of Radial Blade Pumps. Processes 2019, 7, 920. https://doi.org/10.3390/pr7120920
Si Q, Shen C, Ali A, Cao R, Yuan J, Wang C. Experimental and Numerical Study on Gas-Liquid Two-Phase Flow Behavior and Flow Induced Noise Characteristics of Radial Blade Pumps. Processes. 2019; 7(12):920. https://doi.org/10.3390/pr7120920
Chicago/Turabian StyleSi, Qiaorui, Chunhao Shen, Asad Ali, Rui Cao, Jianping Yuan, and Chuan Wang. 2019. "Experimental and Numerical Study on Gas-Liquid Two-Phase Flow Behavior and Flow Induced Noise Characteristics of Radial Blade Pumps" Processes 7, no. 12: 920. https://doi.org/10.3390/pr7120920
APA StyleSi, Q., Shen, C., Ali, A., Cao, R., Yuan, J., & Wang, C. (2019). Experimental and Numerical Study on Gas-Liquid Two-Phase Flow Behavior and Flow Induced Noise Characteristics of Radial Blade Pumps. Processes, 7(12), 920. https://doi.org/10.3390/pr7120920